Towards robust deconvolution of low-dose perfusion CT: Sparse perfusion deconvolution using online dictionary learning

Abstract

Computed tomography perfusion (CTP) is an important functional imaging modality in the evaluation of cerebrovascular diseases, particularly in acute stroke and vasospasm. However, the post-processed parametric maps of blood flow tend to be noisy, especially in low-dose CTP, due to the noisy contrast enhancement profile and the oscillatory nature of the results generated by the current computational methods. In this paper, we propose a robust sparse perfusion deconvolution method (SPD) to estimate cerebral blood flow in CTP performed at low radiation dose. We first build a dictionary from high-dose perfusion maps using online dictionary learning and then perform deconvolution-based hemodynamic parameters estimation on the low-dose CTP data. Our method is validated on clinical data of patients with normal and pathological CBF maps. The results show that we achieve superior performance than existing methods, and potentially improve the differentiation between normal and ischemic tissue in the brain.

1. Introduction

Stroke is the third-leading cause of death in the United States after heart disease and cancer. Early and rapid diagnosis of stroke can save critical time for thrombolytic therapy. Cerebral perfusion imaging via computed tomography perfusion (CTP) has become more commonly used in clinical practice for the evaluation of patients with cerebrovascular disease such as acute stroke and vasospasm after subarachnoid hemorrhage (SAH) (Miles and Griffiths, 2003; König, 2003; Hoeffner et al., 2004). Various mathematical models have been used to process the acquired temporal data to ascertain quantitative information, such as cerebral blood flow (CBF), cerebral blood volume (CBV) and mean transit time (MTT), with higher radiation dosage compared to a standard CT of the head (Østergaard et al., 1996a; Hoeffner et al., 2004; Harrigan et al., 2005; Wittsack et al., 2008; He et al., 2010). However, recent reports on the overexposure of radiation in CTP imaging have brought the dosage problem to the limelight because many patients suffered biologic effects from radiation exposure, including hair loss, skin burns and even cancer risk (Wintermark and Lev, 2010). A key challenge in CTP is to obtain a high-quality CBF image using low radiation dose.

The most commonly used deconvolution method to quantify the perfusion parameters in CTP is truncated singular value decomposition (TSVD) and its variants, such as circular TSVD (cTSVD) (Cenic et al., 1999, 2000; Østergaard et al., 1996b,a; Wu et al., 2003; Wittsack et al., 2008). When TSVD deconvolution algorithm was first introduced in 1996, it calculates the perfusion parameters for each tissue voxel independently. It assumes the X-ray radiation and intravenous injection were high enough to generate accurate tissue enhancement curve (TEC) and arterial input function (AIF) for deconvolution. However, TSVD-based methods tend to introduce unwanted oscillations (Calamante et al., 2003; Mouridsen et al., 2006) and results in overestimation of perfusion parameters, particularly CBF. Numerous works have been proposed to denoise the reconstructed CT images and therefore successfully improved the quality of CBF maps, including bilateral filtering (Mendrik et al., 2011), non-local mean (Ma et al., 2011), nonlinear diffusion filter (Saito et al., 2008), and wavelet-based methods (Lin et al., 2001). However, these works improve the quality of the reconstructed CT data only and do not take the convolution flow model of CTP into consideration. The oscillatory nature of the TSVD-based method has initiated research that incorporates different regularization methods to stabilize the deconvolution, and have shown varying degrees of success in stabilizing the residue functions by enforcing both temporal (Calamante et al., 2003; Nathan et al., 2008; Andersen et al., 2002; Wong et al., 2009) and spatial regularization (He et al., 2010; Fang et al., 2012a) on the residue function. However, prior studies have focused exclusively on imposing regularizations on the noisy low-dose CTP, without considering the corpus of high-dose CTP data.

Since perfusion images tend to be noisy at low-dose, our aim is to develop a method to perform deconvolution-based first-pass hemodynamic parameter estimation that is more robust to noisy input at low radiation dosage by learning from high-dose data, and to produce perfusion parameter maps with better signal-to-noise characteristics. To that end, we have developed a formulation that utilizes a sparse representation functional to enforce both temporal convolution and spatial regularization using example-based restoration learned from high-dose CTP parametric maps. Because TSVD-based approaches estimate the residue function (and hence the perfusion parameters) for each voxel independently of its neighbors, our sparse perfusion deconvolution approach with dictionaries learned from high-dose perfusion maps mitigates the noise issue associated with the traditional approaches. Although sparse representation image models have been used in several context (Aharon et al., 2006; Mairal et al., 2008), to date we are not aware of any such work in the context of perfusion parameter estimation to bridge the gap between high- and low-dose CTP data.

In this paper, we propose a robust sparsity-based deconvolution method to estimate CBF in CTP at low radiation dose We first learned a dictionary of CBF maps from a corpus of high-dose CTP data using online dictionary learning and then perform deconvolution-based hemodynamic parameter estimation of the low-dose CTP. This method produces perfusion parameter maps with better signal-to-noise characteristics.

The main contributions of our work are threefold: (1) We propose to train a dictionary of perfusion parameter maps from the high-dose CT data in an online fashion to improve the quantification of low-dose CTP. (2) We combine the temporal convolution model with the dictionary mapping term and the sparsity term to enforce spatio-temporal regularization. (3) In vivo brain aneurysmal SAH patient data, we demonstrate that our estimated CBF values lead to better separation between ischemic tissue — which by its angiogenic nature tends to have less blood flow — and normal tissue.

2. Related work

Since we use sparsity prior and example-based restoration to enhance low-dose perfusion CT images, we review relevant work in both sparsity prior and example-based restoration work.

2.1. Sparsity prior and dictionary learning

Sparsity methods have been vastly investigated in recent years. Candès et al. (2006) and Donoho (2006b) have shown that a sparse signal can be recovered from a small number of its linear measurements with high probability. Various greedy algorithms have been proposed to solve the problems with sparsity priors, including basis pursuit (BP) (Chen et al., 2001), matching pursuit (Mallat and Zhang, 1993), orthogonal maching pursuit (OMP) Chen et al. (1989) and stagewise OMP (stOMP) (Donoho, 2006a). Another approach is to use l₁ norm relaxation and convex optimization (Candès et al., 2006; Kim et al., 2007; Figueiredo et al., 2007), which is employed in our work.

Sparse representation and dictionary learning has been widely used in computer vision and multimedia communities, such as, but not limited to, natural image and video denosing (Elad and Aharon, 2006; Protter and Elad, 2009), image restoration (Mairal et al., 2009b), image super-resolution (Yang et al., 2008), robust face recognition (Wright et al., 2009), automatic image annotation (Zhang et al., 2010). In medical image analysis, sparsity prior has been applied to MR reconstruction (Lustig et al., 2007; Huang et al., 2011), shape modeling (Zhang et al., 2012a), deformable segmentation (Zhang et al., 2012b), etc. However, to the best of our knowledge, it is the first time sparse prior and learned dictionaries are used in a spatio-temporal model to address the challenging task of low-dose CTP enhancement. The sparsity prior leads to more robust solution in face of over-complete bases in signal recovery, and removes noise existent in the captured signal. Specifically, Wright et al. (2009) have shown that sparse representation is critical for high-performance classification of high-dimensional data, and occlusion and corruption can be handled uniformly and robustly with this framework.

To learn a compact representation from the original dataset due to computational cost when the training datasets have thousands or millions of samples, extensive studies in dictionary learning have been done. A brief introduction of the relevant algorithms are presented here. Dictionary learning typically consists of two steps: sparse coding and codebook update. Sparse coding can implemented using greedy algorithms such as matching pursuit (MP) (Mallat and Zhang, 1993) and orthogonal matching pursuit (OMP) (Chen et al., 1989) by finding the sparsest coefficients. And codebook update employs optimal direction (MOD) (Engan et al., 1999), K-SVD (Aharon et al., 2006) or the recently proposed online dictionary learning (Mairal et al., 2009a). Online dictionary learning is used in this work because it can handle large training dataset with higher efficiency and achieves more robust dictionary compared to MOD and K-SVD.

2.2. Example-based Restoration

Redundancy representation and sparsity have been the driving forces for signal denoising for the research in the past decades or so, leading to what is considered today as some of the best available image denoising methods (Portilla et al., 2003; Starck et al., 2002; Eslami and Radha, 2006; Matalon et al., 2005). While this work is built on the very same concept of sparsity and redundancy concepts for restoration, it is adopting a different point of view, drawing resources from yet another recent line of work on example-based restoration. Traditionally, the image prior to address the general inverse problem in image processing using Bayesian approach has been based on some simplifying assumptions, such as spatial smoothness, low/max-entropy, or sparsity in transform domain. On the other hand, example-based approach resorts to the images themselves for the optimal prior, for instance, using a spatial-smoothness based Markov random field prior and training the derivative filters for image restoration (Zhu and Mumford, 1997; Roth and Black, 2005). Example-based restoration has been applied to image and video denoising (Elad and Aharon, 2006; Mairal et al., 2008; Protter and Elad, 2009), image super-resolution (Freeman et al., 2002), shape representation and segmentation (Zhang et al., 2012a,b). We introduce the concept of example-based restoration into low-dose perfusion CT enhancement by learning the prior from the high-dose perfusion maps.

3. Methodology

In this section, we present the new sparse perfusion deconvolution (SPD) framework for CTP quantification. The framework is comprised of two steps: online dictionary learning and sparse perfusion deconvolution.

3.1. Perfusion parameter model

Based on the theoretical model provided in (Østergaard et al., 1996b), in CTP, the amount of contrast in the region is characterized by

$$C_v(t)=\mathit{CBF}{\int }_0^t{C}_a(\tau )R(t-\tau )d\tau ,$$ (1)

where C_v(t) is the tissue enhancement curve (TEC) of tracer at the venous output in the volume of interest (VOI), CBF is the cerebral blood flow, C_a(t) is an arterial input function (AIF) and R(t) is the tissue impulse residue function (IRF), which measures the mass of contrast media remaining in the given vascular network over time. Under this model, at time t = t₀, a unit of contrast agent is injected as a bolus, and R(t = t₀) = 1 indicates that the entire mass of contrast agent is within the vascular network. After a finite duration (t_N) when all contrast has left the vascular network, R(t = t_N) = 0.

To discretize the computation, we assume that C_a(t) and C(t) are measured with N equally spaced time points t₁, t₂, …, t_N with time increment Δt. The convolution is discretized

$$\mathbf{C}=\mathit{CBF}·\mathrm{\Delta }t·C_a·\mathbf{R},$$ (2)

where

$$\mathbf{C}=\left(\begin{array}{c}C(t_1)\\ C(t_2)\\ ⋮\\ C(t_N)\end{array}\right)\mathbf{R}=\left(\begin{array}{c}R(t_1)\\ R(t_2)\\ ⋮\\ R(t_N)\end{array}\right)$$

and

$${\mathbf{C}}_{\mathbf{a}}=\left(\begin{array}{cccc}{C}_a(t_1)& 0& \cdots & 0\\ C_a(t_2)& C_a(t_1)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_a(t_N)& C_a(t_{N-1})& \cdots & C_a(t_1)\end{array}\right)$$

When R(t) is estimated from Eq. (2), CBF can be computed from

$$\mathit{CBF}=R(t=0)$$ (3)

since from the definition of the residue function R(t), R(t = 0) = 1.

3.2. Circulant truncated singular value decomposition

Singular value decomposition is a widely adopted approach to estimate the perfusion parameter maps (Østergaard et al., 1996b; Cenic et al., 1999, 2000), where matrix C_a is factorized into two orthogonal matrices U and V^T and a diagonal matrix S, with n singular values, s_i, i = 1,2, , n in descending order along the diagonal

$${\mathbf{C}}_{\mathbf{a}}={\mathbf{USV}}^{\mathbf{T}}$$ (4)

Eq. (2) can be rewritten as

$$\mathit{CBF}·\mathrm{\Delta }t·\mathbf{R}=\mathbf{V}{\mathbf{S}}^{\mathbf{T}}{\mathbf{U}}^{\mathbf{T}}·\mathbf{C}$$ (5)

Because smaller singular values related to the higher frequency singular values and the reciprocal of these small singular values lead to large weighting coefficients of oscillatory singular vectors, TSVD regularized the solution by truncating small singular values to zero using a threshold λ and therefore remove the corresponding oscillatory terms from the solution. In this paper, we set parameter λ=0.3 (30% of the maximum element in S) based on the experimental analysis in (Fieselmann et al., 2011). Delay and dispersions between the AIF and tissue VOI can lead to inaccurate estimation of perfusion parameters, especially when contrast agents arrive earlier in the tissue than in the chosen AIF. Therefore in this paper block-circulant version of Ca matrix is used instead of linear deconvolution to avoid the causality problem.

3.3. Proposed sparse perfusion deconvolution with online dictionary learning (ODL-SPD)

Sparse representations over trained dictionaries for perfusion parameter maps restoration rest on the assumption that the image priors in the perfusion maps can be learned from images, rather than choosing a prior based on some simplifying assumptions, such as spatial smoothness, non-local similarity, or sparsity in the transform domain. Since the low-dose CTP has high noise level in TEC, it is important to learn the dictionaries from the high-dose (thus low noise level) CTP. Therefore, we implement the sparse and redundant representation in the spirit of Sparseland (Elad and Aharon, 2006). In our model, we estimate perfusion parameters by considering both temporal correlations and example-based restoration using dictionaries learned from high-dose data.

Basic framework

Suppose C(x, y, z, t) ∈ ℝ^N×T is TEC in VOI [x, y, z]^T from a spatial-temporal patch of size $\sqrt{N}\times \sqrt{N}\times 1$ pixels and T time points. R(x, y, z, t) ∈ ℝ^N×T represent the remaining tracer concentration of the voxel [x, y, z] at a given time point t, where x, y and z are the respective row, column and slice coordinates of the spatial-temporal data. The least-square form of Eq. (2) is

$$J_{ls}={\Vert \mathbf{C}-{\mathbf{C}}_{\mathbf{a}}\mathbf{R}\Vert }_2^2$$ (6)

By definition, CBF map can be computed using f = R(t = 0), where f ∈ ℝ^N indicates a vector of patch in the CBF map by stacking the pixels vertically.

Due to the noise in the low-dose CTP data, the solution of Eq. (6) may be severely distorted. To utilize the high-dose repository existent as a prior, we first learn a compact dictionary D ∈ ℝ^N×K from the existing high-dose CBF maps, where K is the number of patches in D and N is the number of pixels in each patch. f is the vector of a newly-input patch which needs to be constrained or refined. Our basic framework assumes any input patch can be approximately represented as a weighted linear combination of the patches in the learned dictionary D. We denote α = [α₁,α₂,…,α_K]^T ∈ ℝ^K as the coefficients or weights. Thus the values of α for the linear combination is found by minimizing the following loss function:

$$J_{\mathit{basic}}={\mu }_1{\Vert \mathbf{C}-{\mathbf{C}}_{\mathbf{a}}\mathbf{R}\Vert }_2^2+{\Vert f-\mathbf{D}\alpha \Vert }_2^2$$ (7)

where μ₁ indicates the importance of the temporal correlation term in the loss function. f and α are computed by solving Eq. (7).

Sparse linear combination

The limitations of Eq. (7) are twofold. First the dictionary D may be overcomplete (K > N) when the number of atoms is larger than the length of f. Thus the system may not have a unique solution. More constraints of the coefficient α are needed. Second, the input patch, including the noises, may be perfectly represented if any linear combination can be used. A more approximate assumption is that the input patch can be approximately represented by a sparse linear combination of the dictionary atoms. Thus in the spirit of Sparseland model, the problem is reformulated as:

$$J={\mu }_1{\Vert \mathbf{C}-{\mathbf{C}}_{\mathbf{a}}\mathbf{R}\Vert }_2^2+{\Vert f-\mathbf{D}\alpha \Vert }_2^{2}s.t.{\Vert \alpha \Vert }_0\le k$$ (8)

where ||·||₀ is the l₀ norm counting the nonzero entries of a vector, k is the pre-defined sparsity number. Such formulation ensures that the number of nonzero elements in α is smaller than k. The value of k depends on specific applications.

Convex relaxation

The constraints in Eq. (8) are not directly tractable because of nonconvexity of l₀ norm. Greedy algorithms can be applied to this NP-hard l₀ norm minimization problem, as in (Fang et al., 2012b), but there is no guarantee to capture the global minima. In the general case, no known procedure can correctly find the sparsest solution more efficiently than exhausting all subsets of the entries for f. Thanks to the recent proof of the sparse representation theorem (Donoho, 2006b), l₁ norm relaxation can be employed to make the problem convex while still preserving the sparsity property. Thus Eq. (8) is reformulated as

$$J={\mu }_1{\Vert \mathbf{C}-{\mathbf{C}}_{\mathbf{a}}\mathbf{R}\Vert }_2^2+{\Vert f-\mathbf{D}\alpha \Vert }_2^2+{\mu }_2{\Vert \alpha \Vert }_1$$ (9)

where μ₁ and μ₂ controls the weight of the temporal term and how sparse α is. Since the deviation from Eq. (8) to (9) relaxes the absolute sparseness constraints of the objective function (l₀ norm to l₁ norm), and converts a NP hard problem to a continuous and convex optimization problem, which can be solved efficiently, it paves the way for a feasible spatio-temporal deconvolution procedure as described later.

Connections to other methods

It is interesting to look in Eq. (9) by adjusting μ₁ and μ₂ into some extreme values.

• If μ₁ is extremely large, the temporal correlation term dominates. Thus SPD is similar to methods that do not model spatial regularization.

• If μ₁ is extremely small, the temporal correlation is no longer a constraint. With proper initialization, SPD becomes the imaging denoising method using learned dictionaries.

• If μ₂ is very large, may have only one non-zero element. Thus SPD becomes the nearest neighbor method.

• If μ₂ is very small, the sparsity constraint no longer exists. A dense linear combination of atoms is used, which is able to perfectly approximate the low-dose perfusion parameter map.

Parameter settings

Eq. (9) has two user tunable parameters μ₁ and μ₂, which are usually crucial to the performance and convergence. It is desirable to have parameters easy to tune and insensitive to different data in one application from a practical view. Fortunately the parameters in our algorithm have a physical meaning and it is straightforward to adjust them. μ₁ controls the weight of the temporal correlation term. A good initialization of CBF map would conform to the temporal correlation model. Thus a small μ₁ is good enough with a warm start. μ₂ controls the sparsity of α. The length of vector α is equal to the number of atoms in the dictionaries. It is usually larger than 200. To generate a sparse coefficient α, a relatively large μ₂ is necessary. Both the parameters are straightforward to tune given their meanings.

Vessel and non-vessel threshold

To further improve the signal-to-noise ratio for different types of tissue, which have different physiological structures and spatial resolution requirements, we apply different regularization parameters to different tissue types. In this paper, we use different parameter settings for vessel and non-vessel voxels. Vessels are identified by setting a threshold on the CBF map, e.g. if vessel threshold is 40 mL/100 g/min, then every voxel with at least 40mL/100 g/min CBF value in the brain is marked as vessel. For vessels, we apply low regularization parameters ${\mu }_1^l$ and ${\mu }_2^l$ because vessels have high-contrast boundaries with respect to neighboring regions. For non-vessel voxels, we apply high regularization parameters ${\mu }_1^h$ and ${\mu }_2^h$ because they are expected to be more spatially coherent.

Dictionary learning

To learn the dictionary D, we use the recently developed online learning algorithm (Mairal et al., 2009a) which solves Eq. (9) by processing one sample (or a mini-batch) at a time and updating the dictionary using block coordinate descent with warm restart. We first learn a dictionary by using randomly sampled patches from the CBF perfusion maps estimated from the high-dose CTP data. Given a set of image patches $Z={\{z_j\}}_{j=1}^N$, each of $\sqrt{N}\times \sqrt{N}\times 1$, we seek the dictionary D that minimizes

$$\underset{\mathbf{D},\mathbf{A}}{argmin}\sum _{j=1}^N{\Vert z_j-\mathbf{D}{\alpha }_j\Vert }_2^2+{\mu }_2{\Vert {\alpha }_j\Vert }_1,j=1,\cdots ,N$$ (10)

where A is a matrix formed by [α₁,α₂,…,α_N]. To solve Eq. (10), we start from an initial dictionary (i.e. the overcomplete DCT dictionary), and CBF parameter map estimated using cTSVD algorithm at high-dose CTP.

Sparse perfusion deconvolution (SPD)

When the dictionary D is known, the CBF perfusion parametric map from the low-dose CTP data can be estimated using our sparse perfusion deconvolution method by minimizing Eq. (9) in an iterative fashion. Our SPD method is divided into two sub-problems: (1) minimization with respect to α with f fixed, (2) update of f with α fixed as a simplified linear inverse problem.

The first step is sparse coding, which is formulated as

$$\underset{\alpha }{argmin}{\Vert f-\mathbf{D}\alpha \Vert }_2^2+{\mu }_2{\Vert \alpha \Vert }_1$$ (11)

Eq. (11) can be solved by LARS-Lasso (Efron et al., 2004).

The second step is to minimize

$$\underset{f}{argmin}{\mu }_1{\Vert \mathbf{C}-{\mathbf{C}}_{\mathbf{a}}\mathbf{R}\Vert }_2^2+{\Vert f-\mathbf{D}\alpha \Vert }_2^2$$ (12)

Because f = R(t = 0), Eq. (12) can be rewritten as

$$\underset{f}{argmin}{\mu }_1{\Vert \mathbf{C}-{\mathbf{C}}_{\mathbf{a}}\mathbf{R}·\mathit{diag}(f)\Vert }_2^2+{\Vert f-\mathbf{D}\alpha \Vert }_2^2$$ (13)

where R is the residue functions normalized by f so that R(t = 0) = 1. Eq. (13) is a quadratic term that has a closed-form solution.

If vec(B) denotes the vector formed by the entries of a matrix B in column major order, and define P = C_aR, then

$$\mathit{vec}(C-C_{a}R·\mathit{diag}(f))=\mathit{vec}(\mathbf{C}-\mathbf{P}·\mathit{diag}(f))=\mathit{vec}(\mathbf{C})-\mathbf{M}f$$ (14)

where M is a TN × N matrix in form of

$$\mathbf{M}=\left(\begin{array}{cccc}{P}_{.,1}& 0& \cdots & 0\\ 0& P_{.,2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & P_{.,N}\end{array}\right)$$

where P_.,i dictates the i^th column of matrix P in its column vector form. Eq. (13) can be transformed into the conventional least square problem

$$\underset{f}{argmin}{\Vert ({\mathbf{I}}_{\mathbf{n}};\mathbf{M})f-(\mathbf{D}\alpha ;\mathit{vec}(\mathbf{C})\Vert }_2^2$$ (15)

Let A = (I_n; M) and B = (Dα; vec(C)), we get

$$f={\mathbf{A}}^{+}\mathbf{B}$$ (16)

where A⁺ is the pseudo-inverse of matrix A, (.;.) denotes a vector or matrix by stacking the arguments vertically.

Two procedures are iteratively employed to obtain f and α. Note that theoretically this iterative algorithm might lead to local minima. However, in our extensive experiments (Section 4), we did not observe this situation yet. We also observe our results are quite stable with respect to the training dataset.

To address the global CBF deconvolution problem, we use a sliding window of size $\sqrt{N}\times \sqrt{N}$ on the specific slice and overlaps the windows by a step size of one. The final global CBF parametric map is generated by averaging the areas that the windows overlap.

4. Experiments

In this section, we describe the results from comparing our online-dictionary-learning sparse perfusion deconvolution (ODL-SPD) with cTSVD and SPD deconvolution using K-SVD learning algorithm (KSVD-SPD) (Fang et al., 2012b). Out of 20 subjects, 10 are used as training data (7 with CTP deficits in the brain and 3 normal), and the rest 10 are used for testing purpose (5 with CTP deficits and 5 normal). A board-certified neuro-radiologist with 12 years experience reviewed CTP data in a blind fashion to determine the type and location of CTP deficits.

4.1. Experiment setup

Data acquisition

CTP was performed during the typical time-period for patients with cerebrovascular disease enrolled in an IRB-approved clinical trial from August 2007 to June 2010, between days 6–8 in asymptomatic patients and on the same day clinical deterioration occurred in symptomatic patients. CTP was performed with a standard scanning protocol at our institution using GE Light speed or Pro-16 scanners (General Electric Medical Systems, Milwaukee, WI) with cine 4i scanning mode and 45 second acquisition at 1 rotation per second using 80 kVp and 190 mA. A scanning volume of 2.0 cm was used consisting of 4 slices at 5.0 mm thickness with its inferior extent selected at the level of the basal ganglia, above the orbits, to minimize radiation exposure to the lenses. Approximately 45 mL of nonionic iodinated contrast was administered intravenously at 5 mL/s using a power injector with a 5 second delay.

Low-dose simulation

Repetitive scanning of the same patient at different radiation doses is unethical. Thereby, Gaussian noise is added to the reconstructed CT images in high-dose CTP to simulate low-dose CTP data at I mA following the practice in (Britten et al., 2004).

The noise model is built on the inverse relationship between the tube current I (mA) and the noise standard deviation σ in CT images

$$\sigma =\frac{K}{\sqrt{I}}$$ (17)

The value K is computed by analyzing the Gaussian noise in the CTP images of 22 patients under I₀=190 mA tube current and the average K value is 103.09 mA^1/2. Assume I is the simulated tube current level in mA, and σ₀ is the noise standard deviation in CTP images scanned under I₀ mA. We can rewrite Eq. (17) as

$$\frac{\sigma }{{\sigma }_0}=\frac{\sqrt{I_0}}{\sqrt{I}}$$ (18)

Because noise distribution is statistically independent, the relationship between σ, σ₀ and the standard deviation of the added Gaussian noise σ_a is

$${\sigma }^2={\sigma }_0^2+{\sigma }_a^2$$ (19)

From Eq. (18) and (19), we can compute the simulated tube current I given added noise standard deviation σ_a

$$I=\frac{I_0·{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_a^2}=\frac{K^2}{\frac{K^2}{I_0}+{\sigma }_a^2}=\frac{K^2·I_0}{K^2+{\sigma }_a^2·I_0}$$ (20)

When σ_a = 25.5, the simulated low-dose I = 15 mA.

Implementation details

We implemented cTSVD, KSVD-SPD and ODL-SPD algorithms in MATLAB and applied them to the clinical CTP data acquired at 190mA (high-dose) and simulated low-dose dataset. All experiments are conducted on a 2.8GHz Intel Core i7 with dual cores MacBook Pro with 4GB memory in MATLAB environment. We download the online dictionary learning for sparse representation code from the authors’ website¹.

For all experiments of SPD, the dictionary used are of size 64 × 256 designed to handle perfusion image patches of 8 × 8 pixels with 256 atoms in the dictionary. In all experiments, the denoising process uses a sparse coding of each patch of size 8 × 8 pixels from noisy image.

Evaluation metrics

In this paper, we use two metrics to evaluate the performance of the deconvolution algorithms. CBF maps computed from CTP data obtained at high tube current of 190 mA were regarded as the reference standard.

Root-mean-square error (RMSE) is a measure of similarity between the CBF at high-dose and low-dose, defined by

$$\mathit{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(f_i-{\widehat{f}}_i)}^2}$$ (21)

where f_i and f̂_i, i = 1,2,…, n are the estimated CBF value at low dose and reference standard CBF value at high dose.

Peak signal-to-noise ratio (PSNR) is widely used in signal and image processing to measure the denoising performance. PSNR is defined as the ratio between the maximum intensity value in the ground truth image I_max and the power of corrupting noise σ (RMSE between the ground truth and enhanced image) that affects representation fidelity. PSNR is usually expressed in the logarithmic decibel scale as

$$\mathit{PSNR}=20{log}_{10}\left(\frac{I_{\mathit{max}}}{\sigma }\right)$$ (22)

4.2. Visual comparisons

Comparison of learned dictionaries

Figure 1 shows the learned dictionary using K-SVD and ODL. Both dictionaries were trained on a dataset of 10,000 8 × 8 patches of high-dose CBF perfusion maps and initialized with the redundant DCT dictionary. We could observe from the two dictionaries that the online learned dictionary capture the variety of patterns in the high-dose CTP data, while the dictionary learned using K-SVD has more redundancy in the atoms located in the upper and left corners of the dictionary. K-SVD algorithm solves the l₀ norm problem using a greedy codebook update step, which may lead to unstable dictionary due to perturbation in the training data. Online dictionary learning solves a relaxed l₁ norm problem which is convex and therefore results in more robust dictionary. This leads to the differences in the two learned dictionaries. Additionally, online dictionary learning updates the dictionary with one training sample (or a small batch) each time, which scales up gracefully to large datasets with millions of training samples.

Figure 1.

Learned dictionaries. Left: K-SVD trained dictionary. Right: Online learned dictionary.

Comparison of CBF perfusion maps

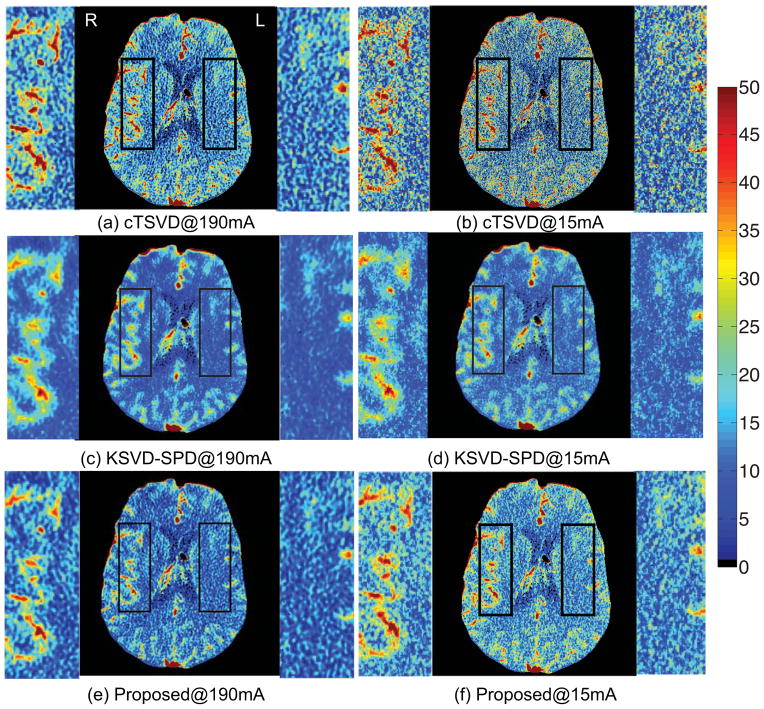
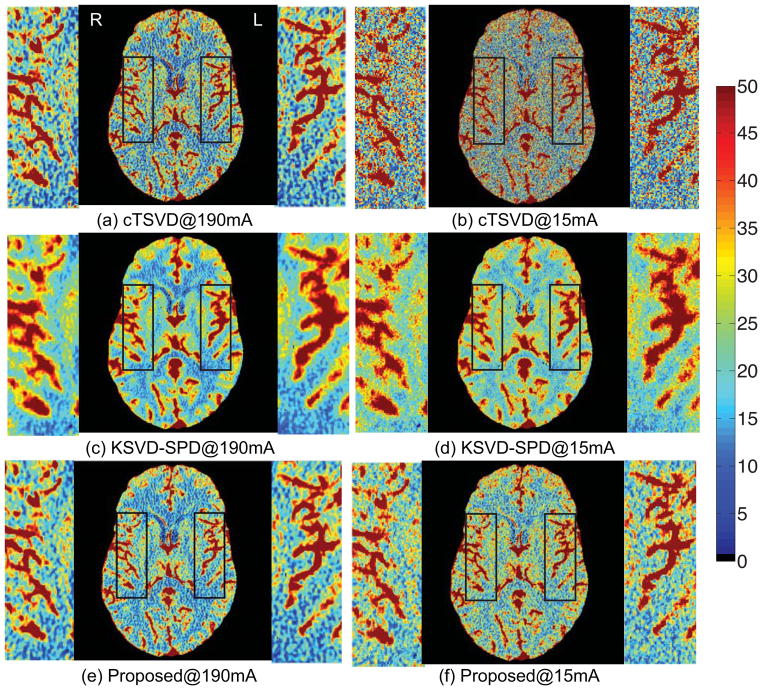
We then compare three deconvolution algorithms by visually observing the estimated CBF perfusion maps of two patients, a patient with left middle cerebral artery (LMCA) perfusion deficit on due to vasospasm in an aneurysmal SAH and a patient with normal CBF map. (Please note that in medical practice, the left and right side of the patient are designated opposite on the image). Low tube current of 15 mA was simulated by adding Gaussian noise with standard deviation of 25.5 (Britten et al., 2004).

As shown in Figs. 2 and 3, variations in the locally smooth regions are reduced significantly by our proposed method, while the boundaries between different tissue types and blood vessels are more visible. The arteries and veins are more evidently defined, while the noise in the white matter is greatly suppressed. While both SPD algorithms suppress noise in the CBF maps, KSVD-SPD smoothes the CBF map too much and the vessels in the CBF maps tend to discontinue and the boundaries of the vessels are less clear-cut. The non-vessel tissue also tends to be under-estimated in the aneurysmal SAH patient and to be overestimated in the normal patient by KSVD-SPD, while our proposed ODL-SPD overcomes these drawbacks with an improved learning and reconstruction algorithm, and different regularization parameter setting for vessel and non-vessel voxels.

Figure 2.

CBF maps and zoomed-in regions of a 35-year-old female with left middle cerebral artery (LMCA) perfusion deficit caused by vasospasm in aneurysmal SAH. LMCA and RMCA are enlarged for comparison. The results given by cTSVD, K-SVD SPD and our online SPD are shown in the 1^st, 2^nd and 3^rd row, respectively, each with CBF map of high-dose (190mA) CTP data on the left and that of low-dose (15mA) on the right.

Figure 3.

CBF maps and zoomed-in regions of a 42-year-old male with normal cerebral blood flow. LMCA and RMCA are enlarged for comparison. The results given by cTSVD, K-SVD SPD and our online SPD are shown in the 1^st, 2^nd and 3^rd row, respectively, each with CBF map of high-dose (190mA) CTP data on the left and that of low-dose (15mA) on the right.

4.3. Quantitative comparisons

To quantitatively compare different methods, we report RMSE and PSNR between the computed perfusion maps and the reference maps of the entire brain region in Table 1 for Fig. 2, Fig. 3 and all test data. Generally cTSVD leads to noisy perfusion maps at low-dose. KSVD-SPD achieves better performance than cTSVD in recovering the high-dose parametric maps, but it over-smooths the texture details in non-vessel structure, especially in patients with CTP deficits. In our proposed method, the robust dictionary and different regularization parameters for vessel and non-vessel structure leads to better performance. It performs the best in terms of both RMSE and PSNR for patients with CTP deficits and normal CTP maps.

Table 1.

Quantitative comparison of RMSE and PSNR (dB) in CBF maps at low-dose are reports using cTSVD, KSVD-SPD and our proposed method. The average value for the patients with CTP deficits, with normal CTP maps and all data are reported. The best performance of each column is highlighted.

Metric	Method	Fig. 2	Fig. 3	Deficit	Normal	All data
RMSE	cTSVD	9.47	12.05	12.72±6.45	11.46±3.28	12.09±4.87
	KSVD-SPD	7.99	9.32	10.05±4.33	8.65±1.98	9.35±3.26
	Proposed	7.23	8.74	9.24±4.62	8.28±2.53	7.32±3.54
PSNR	cTSVD	33.89	34.46	32.95±1.79	31.77±2.30	32.36±2.04
	KSVD-SPD	34.67	36.70	34.71±1.42	34.03±2.31	34.37±1.85
	Proposed	36.23	37.25	35.73±1.48	34.75±2.36	35.24±1.93

4.4. Diagnostic analysis

Comparison of asymmetry

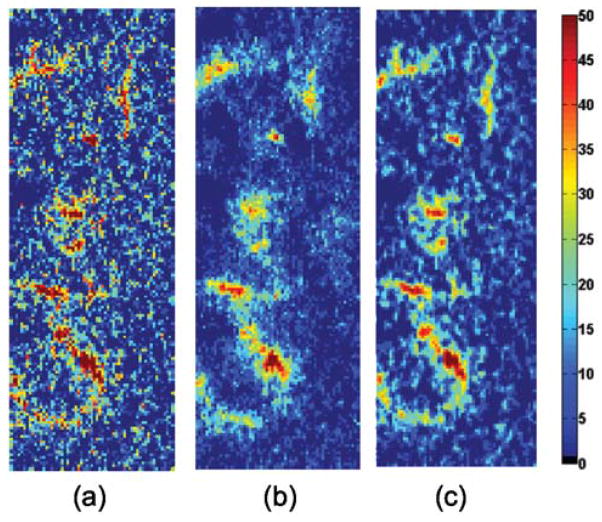
As shown in Fig. 2, the intensity difference of CBF values between LMCA and right middle cerebral artery (RMCA) is more evident in the low-dose CBF map estimated using our method. To visualize the asymmetry in the left and right middle cerebral artery of this patient, we compute the intensity difference maps between LMCA and RMCA for three deconvolution algorithms, namely cTSVD, KSVD-SPD and ODL-SPD, as shown in Fig. 4. We can observe that the intensity different map using cTSVD is too noisy to identify the asymmetry of LMCA and RMCA vessel structures, while KSVD-SPD blurs the details of the vessel structure. Our proposed ODL-SPD generates the different map with better contrast and spatial resolution for diagnosis of asymmetry in LMCA and RMCA.

Figure 4.

Zoomed-in regions of the intensity difference maps between LMCA and RMCA estimated by (a) cTSVD (b) KSVD-SPD and (c) ODL-SPD. Arteries are delineated in red.

Evaluation of ischemic voxels clustering

By aggregating all voxels (within VOI) from the normal hemisphere of the patient data into a single “normal” cluster and the pathologic hemisphere of the ischemia patient data set into an “abnormal” cluster, we have two clusters of n₁ normal voxels and n₂ ischemic voxels. In our case, n₁ = 877 and n₂ = 877. To quantify the separability between normal and ischemic CBF values, we define the distance between these two clusters as:

$$d=\frac{m_1-m_2}{\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}}}$$ (23)

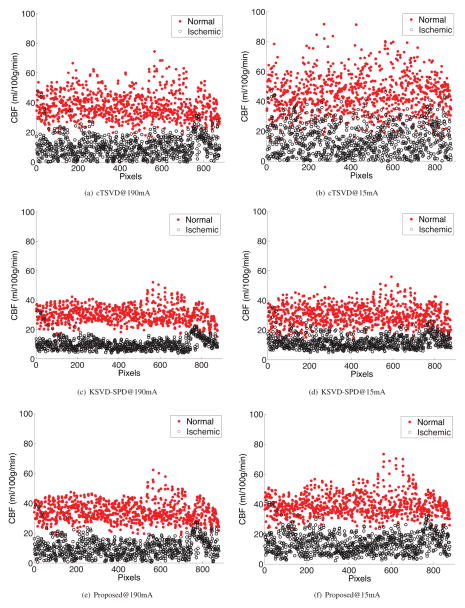
where m₁, m₂ are the means, and σ₁ and σ₂ are the standard deviations of CBF in the normal and ischemic clusters, respectively. We hypothesized that our ODL-SPD algorithm to produce larger distance d as defined in Eq. (23), that is, will more definitely differentiate between normal and ischemic tissues. Fig. 5 shows scatter plots of normal versus abnormal cluster. The x coordinate value of each point if the “number of pixels”–increasing pixel number moves from the top-left to the bottom-right of the region of interest as delineated by a radiologist. It is apparent that the two clusters are more separable in data processed via sparse perfusion deconvolution than cTSVD, as shown in Table 2. Both SPD algorithms perform better than cTSVD at high-dose and low-dose. Although KSVD-SPD achieves better separability between normal and ischemic tissues, it tends to under-estimate the CBF value of normal tissue, as in Fig. 5. At low-dose, ODL-SPD best recovers the CBF values of both normal and ischemic voxels among the three algorithm, and outperforms cTSVD at high-dose by increasing the distance between normal and ischemic voxels.

Figure 5.

Two clusters of normal vs. ischemic voxels from the aneurysmal SAH patient in Fig. 2. The results given by cTSVD, KSVD-SPD and our proposed ODL-SPD are shown in the 1^st, 2^nd and 3^rd row, respectively, each with CBF map of high-dose (190mA) CTP data on the left and that of low-dose (15mA) on the right.

Table 2.

Normalized distance between ischemic and normal tissues

Distance	190 mA	15 mA
cTSVD	72.24	46.55
KSVD-SPD	86.56	68.37
Proposed	81.98	76.63

Comparison of diagnostic accuracy

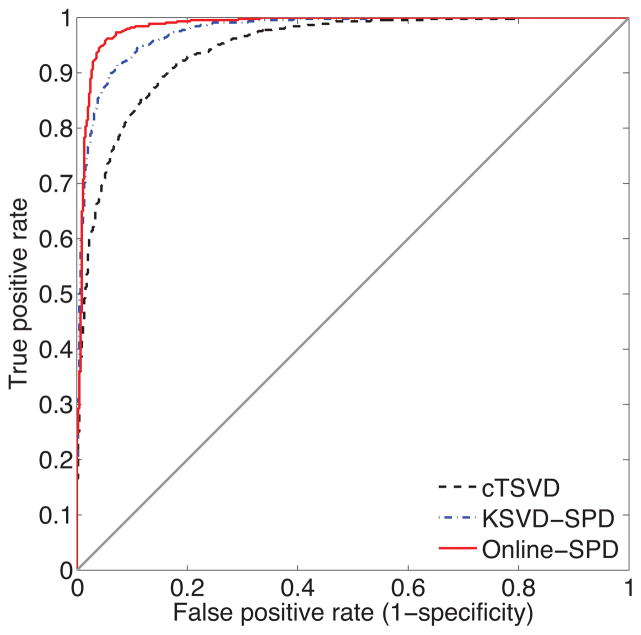
Let us define sensitivity as the proportion of samples with abnormal CBF values, which test positive, and specificity as the proportion of samples with normal CBF values that test negative, at a specific threshold. Fig. 6 is the receiver operator characteristic (ROC) curve drawn based on 877 abnormal samples and 877 normal samples in which we examine a spectrum of thresholds. The plot shows the tradeoff between true positive rate (sensitivity) and false positive rate (1-specificity). The closer the curve is to the upper left corner, the more accurate the test. Fig. 6 shows that ODL-SPD appears to be considerably more accurate than cTSVD and KSVD-SPD, leading to more efficient diagnosis.

Figure 6.

ROC curves generated by cTSVD, KSVD-SPD and ODL-SPD deconvolution algorithms. Area under curve (AUC) of cTSVD is 0.9483, the AUC of KSVD-SPD is 0.9749 and the AUC of online-SPD is 0.9852.

4.5. Parameter influence

Recall that the balance between the temporal convolution model and the dictionary matching is controlled by the parameter μ₁, while the sparsity of the dictionary selection vector α is controlled by parameter μ₂. Table 3 shows the average PSNR at different values of μ₁ and μ₂. Our algorithm consistently achieves similar performance. When ${\mu }_1^h=0.02,{\mu }_1^l=0.01$ and ${\mu }_2^h=0.8,{\mu }_2^l=0.4$, the algorithm provides the best CBF estimation at low-dose in terms of PSNR. Table 4 and 5 shows the parameter influence of vessel threshold and dictionary size.

Table 4.

Parameter influence of vessel threshold

Thresh	10	20	30	40	50	60
PSNR	42.45	42.56	42.67	44.57	44.39	44.36

Table 3.

The influence of parameters μ₁ and μ₂

${\mu }_1^h$	0.005	0.01	0.02	0.08	0.1	0.02	0.02
${\mu }_1^l$	0.01	0.01	0.01	0.01	0.01	0.005	0.02
PSNR	44.30	44.37	44.57	43.68	43.53	44.22	43.80
${\mu }_2^h$	0.8	0.8	0.8	0.8	0.8	0.6	0.9
${\mu }_2^l$	0	0.2	0.4	0.6	0.8	0.4	0.4
PSNR	42.29	44.41	44.57	44.22	43.47	44.39	44.40

Table 5.

Parameter influence of dictionary size

K	64	128	256	512	1024	2048
PSNR	43.47	44.21	44.57	44.33	44.11	44.15

The threshold for two tissue types is set as CBF value of 40 mL/100 g/min, which can best differentiate the vessels from other tissue. The dictionary size is 256 when the best performance is achieved. We therefore use this set of parameters throughout all experiments in Section 4.2 – 4.4.

5. Discussion

We validate the proposed algorithm on clinical dataset with CTP deficits and normal CBF maps. The experimental results show the following facts.

1. This implicitly incorporated image reconstruction constraint benefits the quality of recovered low-dose perfusion maps. Such example-based information improves the robustness and accuracy of low-dose deconvolution algorithm, and demonstrate superior performance than existing computational methods.

2. The sparse linear combination of dictionary atoms learned from high-dose perfusion maps is able to well approximate the input low-dose CTP data. The l₁ norm constraint of the coefficient handles the noise and artifacts at low-dose. Different sparsity regularization parameters are applied to vessels and brain tissue in observation of the different anatomical structures further improves the results.

3. When the number of high-dose perfusion data is huge and comes in sequential fashion, it is infeasible to re-learn the entire dictionary whenever a new training sample becomes available. In this case, online dictionary learning technique is employed so our algorithm can be gracefully scaled-up to contain perfusion map priors from, theoretically, infinite number of training samples.

4. The joint spatio-temporal model overcomes the oscillation in temporal-based models and preserves the spatial image features such as smoothness and boundaries, as well as tissue structures. The proposed spatio-temporal method can be applied to various perfusion maps, such as mean transit time (MTT) and permeability surface product (PS), and different dynamic imaging modalities such as SPECT and MRI, which captures the time sequence images at cine mode. We expect to apply this method to more applications in the future.

We acknowledge the following limitations to this work:

The goal of this work was to enhance parametric maps in low-dose CTP using a model with a “residue” function convolution kernel that relates the input (arterial enhancement) and response (tissue enhancement) (Miles and Griffiths, 2003; Hoeffner et al., 2004; Harrigan et al., 2005). We compared to several existing models including cTSVD and KSVD-SPD, which are based on similar underlying principles but using different approaches to solve the problem. However, we did not assess other models that have been applied to CTP data to calculate perfusion parameters, such as adiabatic approximation to the tissue homogeneity model (AATH) (Lawrence and Lee, 1998; Kershaw and Cheng, 2010). Future studies are needed to determine whether our proposed algorithm regarding the dictionary learning and sparse reconstruction is also effective for these alternative models.

Another limitation is that the analysis of CTP was predominantly performed on CBF maps and not necessarily CBV and MTT maps. CBV and MTT maps provide important and complementary information for detecting and characterizing the ischemic penumbra in stroke patients. The applicability of our proposed deconvolution algorithm to CBV and MTT maps will need to be considered and verified by additional appropriate studies.

Finally, we acknowledge the limited number of patients for evaluation of the proposed deconvolution algorithm in this work. A large-scale validation including evaluation of different cerebrovascular diseases and patient variety is needed to further validate the proposed algorithm for widespread clinical application.

6. Conclusions

In this paper, we proposed a sparsity-based perfusion de-convolution algorithm for enhancing CBF parameter map estimation in low-dose CTP. We take advantage of the complementary parameter map information available in the high-dose CBF maps from the existing database to recover the missing structural information in the low-dose CTP. This is achieved by a spatio-temporal model, which uses a sparse representation approach based on learned dictionaries from the high-dose CBF maps, combined with the temporal convolution model. This framework is validated on clinical dataset with subjects with abnormal and normal CBF maps. Compared to the existing methods, our sparse perfusion deconvolution algorithm exhibits better performance.

The proposed method can be further extended in two directions. First, in clinical diagnosis, infarct core and penumbra usually locate in low-contrast tissues where the delicate tissue texture are important for neuroradiologists in diagnosis and treatment. Therefore, incorporating tissue segmentation into the reconstruction framework is worth investigating as we would learn distinctive dictionaries for tissue types respectively rather than a global dictionary. Second, since the scope of sparsity-based perfusion deconvolution is beyond the cerebral blood flow computation, we plan to apply this proposed method to other parametric maps, such as permeability surface maps, and integrate it into other medical imaging modalities.

1. Dictionaries are from high-dose CTP data for low-dose CBF estimation.

2. Temporal convolution model is combined with spatial dictionary mapping prior.

3. Evaluation on in vivo aneurysmal subarachnoid hemorrhage and normal patients.

4. Outperform existing methods in CBF estimation for low-dose CTP data.

5. Improve the differentiation between ischemic and normal tissues in the brain.