Bacteriophage capsids: Tough nanoshells with complex elastic properties

Abstract

The shell of bacteriophages protects the viral DNA during host-to-host transfer and serves as a high-pressure container storing energy for DNA injection into a host bacterium. Here, we probe the mechanical properties of nanometer-sized bacteriophage φ29 shells by applying point forces. We show that empty shells withstand nanonewton forces while being indented up to 30% of their height. The elastic response varies across the surface, reflecting the arrangement of shell proteins. The measured Young's modulus (≈1.8 GPa) is comparable with that of hard plastic. We also observe fatigue and breakage of capsids after probing them repetitively. These results illustrate the mechanoprotection that viral shells provide and also suggest design principles for nanotechnology.

The protective proteinaceous shells (capsids) of viruses are striking examples of biological materials engineering. These highly regular, self-assembled, nanometer-sized containers are minimalistic in design, but they combine complex passive and active functions. Besides chemical protection, they are involved in the selective packing and the injection of the viral genetic material (1, 2). Bacillus subtilis phage φ29 is a relatively small virus built of only seven different structural polypeptides, including a scaffolding protein directing the assembly. Its capsid assembles as a precursor of 54 × 42 nm (prohead; Fig. 1 A and B) that consists of four proteins, but most of the mechanically coherent shell is made of only one protein (gp8), the presence of one additional component (the fiber protein) being dispensable for structural integrity (3–6). The organization of these proteins within a prohead is known from cryo-electron microscopy (EM) (3, 4, 7–10). A prolate shell is constructed from 235 gp8 subunits form in a T = 3 lattice with 11 pentameric plus 20 hexameric units forming icosahedral end caps and 10 hexameric units forming the cylindrical equatorial region. In one of the end caps, the central pentamer is replaced by the connector complex consisting of a dodecamer of gp10 subunits. The connector complex actively packages a 6.6-μm piece of DNA by using an ATPase (10, 11). When packaged, the DNA is kept under high pressure (≈6 MPa = 60 atm) inside the viral shell (1, 12, 13).

Fig. 1.

Bacteriophage φ29 prohead shape and structure. (A) A 3D cryo-EM reconstruction of an empty prohead. (B) Schematic representation of the protein organization within a prohead as reconstructed by cryo-EM. (C) Low-resolution SFM image of φ29 proheads in buffer (scan area, 2 × 2 μm, 128 × 128 pixels). The proheads were attached to a glass surface by hydrophobic interaction. Topography was recorded by using jumping mode with a loading force of ≈100 pN. (D) Bimodal distribution of the measured heights of the attached objects (n = 93). (E) High-resolution 3D SFM image of a prohead (loading force, ≈120 pN) with the corresponding cross-section profiles along both axes of the prohead.

The structure of many viral capsids is rather well known from scanning-force microscopy (SFM), x-ray crystallography, and EM studies (3, 5, 14–18), but very little is known as yet about their dynamic mechanical properties from direct measurements. Understanding the mechanical properties of such nanometerscale shells is not only important for virus biology but may also provide inspiration for future nanotechnology. Here, we use SFM to directly probe the mechanical strength and elastic response of φ29 capsids. We measured a Young's modulus of ≈1.8 GPa and found evidence for local structure in the mechanical response of the shells. We also studied the breakage and slow disintegration of the viral capsids by deforming them repeatedly with the SFM tip. This method naturally extends to studying other viral shells as well as the mechanical consequences of filling the shells with DNA.

Materials and Methods

Sample Preparation. The proheads used for our experiments were purified from B. subtilis bacteria infected with a φ29 mutant in genes 14 and 16 (ATPase), which results in the formation of stable empty proheads (4). The buffer used for imaging was TMS (50 mM Tris·HCl, pH 7.8/10 mM MgCl₂/100 mM NaCl). The prohead stock solution (6 μg/μl) was diluted 100-fold into the same buffer. A droplet of 20 μl was deposited on a glass disk mounted on the piezo holder. After waiting 20 min for the adsorption of the proheads, the surface was gently rinsed with TMS to remove unbound objects while keeping the surface wet. The glass disks were first cleaned in a solution of 10% KOH and 90% ethanol, dried in a vacuum, and made hydrophobic in vapor of hexamethyldisilazane (Sigma–Aldrich) to attach the proheads.

SFM Measurements. All SFM images were taken with an SFM (Nanotec, Madrid) operated in “jumping mode” in liquid (19). The relevant feature of this mode is that the lateral displacement of the tip occurs always when it is not in contact with the sample so that shear forces are avoided. During imaging with jumping mode, the tip performs a rapid succession of force–distance (FZ) curves, each taken in several milliseconds in a raster scanning fashion. The maximal applied force is well defined because each individual approach is stopped at the cantilever deflection corresponding to the set force. FZ curves were recorded by measuring cantilever deflection (force) as a function of the vertical position of the piezo to which the sample was mounted. The experiments were performed in liquid to investigate the proheads under physiological conditions and to reduce surface-tension forces. The cantilevers that we used (OMCL-RC800PSA, Olympus, Tokyo) had nominal spring constants of 0.05 N/m, which allowed us to apply low loads (<100 pN) on the viral shells. The tip radii of the cantilevers were <20 nm. The spring constant of the cantilevers were calibrated by using a thermal-oscillations method (20), and they were 0.052 ± 0.007 N/m within the used wafer unit.

Results and Discussion

Imaging Proheads. We imaged surface-attached proheads by using jumping-mode SFM, which allowed us to control maximal tip-sample forces accurately (see Materials and Methods) (19). Imaging was first performed at low resolution (128 or 64 pixels per μm) and low maximal force (<100 pN) to determine the prohead position and orientation (Fig. 1C). The distribution of the measured heights of the proheads (Fig. 1D) shows two distinct peaks centered at 42 nm (SD = 2 nm, n = 50) and 54 nm (SD = 2 nm, n = 43). These values are consistent with width (R_s) and height (R_l) of proheads as determined by EM (3, 5). Therefore, about one-half of the shells were deposited on their side, and the other half were deposited standing upright on the surface. For testing their mechanical properties, we have focused on the proheads deposited on their side because the upright shells likely represent two different, hard to distinguish populations (i.e., attached through either the connector end or the opposite end of the capsid). In addition, probing these upright objects led to erratic results.

High-resolution scans of individual proheads showed that they were intact and not measurably perturbed by consecutive imaging at low maximal forces of up to 100 pN (Fig. 1E). When a surface is scanned in contact mode, instead of in jumping mode, lateral forces are exerted on the deposited capsids. We could detach proheads from the surface in contact mode while no evidence of shell rupture (i.e., leftover debris) was observed. These observations show that the binding strength to the surface was smaller than the protein–protein interactions within the proheads. Both results indicate that the surface does not affect the shell significantly. Nevertheless, the proheads were attached firmly enough to not move with respect to background markers after successive scans. Also, features visible on the exterior of the proheads were stationary in consecutive high-resolution images of the same object. They, thus, seemed to be an attribute of the shells (i.e., the gp8 surface topology) and not a scanning artifact. In some images, the connector could be observed in the expected location and with the expected size (≈19 nm), matching EM and x-ray studies (7–9).

Imaging shells with the SFM at different maximal loading force showed the deformability of φ29 shells under uniaxial pressure (Fig. 2A). Shells appeared progressively flattened with higher maximal scan forces and eventually were destroyed. Shells also appeared laterally narrower because of the reduction in the apparent lateral dilation caused by the tip. This dilation is likely due to a combination of vertical and lateral deformation under large load. In Fig. 2 A (image 4) it can be seen that, up to a certain critical force, the induced deformations were reversible; the shell responded elastically. The decrease in measured height of proheads was approximately proportional to force up to a critical force of ≈0.6 nN (Fig. 2B). Above that critical force, the rapid repetitive indentation inherent to the imaging procedure caused them to break apart (Fig. 2 A, image 6). Subsequent low-force images of such broken capsids typically showed that large fragments of virus shell remained intact (Fig. 2 A, image 7).

Fig. 2.

Force dependence of the appearance of proheads. (A) A series of 3D topographical SFM images, each taken with a different maximal loading force. The applied maximal loading force, F_applied, and the maximal measured height, h_max, for images 1–5 are as follows: image 1, F_applied = 120 pN, h_max = 39 nm (corresponding to a slightly deformed shell); image 2, F_max = 270 pN, h_max = 38 nm; image 3, F_max = 450 pN, h_max = 35.5 nm; image 4, F_max = 90 pN, h_max = 40.5 nm (when lowering the maximal force, the shell recovered to its original shape); and image 5, F_max = 550 pN, h_max = 35 nm. For image 6, in the process of taking a topographical image with F_max = 600 pN, the shell was destroyed. Imaging involved thousands of individual tip-sample contacts, which probably started to weaken the structure. In image 7, lowering the loading force again to 90 pN showed that the broken shell consisted of large fragments, with h_max = 27 nm. (B) The dependence of the measured height on applied force. Dashed line indicates a linear regression.

Indenting Shells. The topographical maps of φ29 proheads made in imaging mode at fixed maximal load forces are, for every image, the result of >2,000 tip-sample interactions. To investigate quantitatively the elastic response of the viral shells, we recorded single FZ curves (see Materials and Methods) after positioning the SFM tip above the center of individual proheads. We roughly located the center of a prohead by stopping the cantilever in the middle of a topographical scan of a prohead. We then fine-tuned the tip position by making a profile scan and by redirecting the tip to the middle of the virus cross section. This method made sure that the equatorial region of the prohead was probed and that pushing near the end-caps, where the shell curvature can cause slipping of the tip, was avoided. FZ curves were recorded in two different modes. In the first mode, curves were recorded slowly (≈1 sec) after repositioning the tip to within a few nanometers of the shell center after each contact. This procedure corrected for slow stage drift and allowed us to probe a region repeatedly within the equatorial band (Fig. 3A); the other procedure consisted of recording fast sequences of FZ curves, each taken within 8 msec, to limit thermal drift.** In both kinds of measurements, we obtained an approximately linear response of the proheads to tip forces of up to several nanonewtons. From the slope of the linear sections of the FZ curves, we could, therefore, calculate a spring constant of the prohead (k_shell) by using the equation k_shell = k_c k_eff (k_c - k_eff)^-1, where k_eff is the effective (measured) spring constant due to both cantilever bending and shell deformation acting as two springs in series and k_c is the spring constant of the cantilever.

Fig. 3.

Determining the elastic response of proheads. (A) Two typical FZ curves taken in sequence in slightly different locations on a single shell and a FZ curve taken on the glass surface. The glass curve was shifted along the z axis to match the tip-sample contact points of FZ1 and FZ2 to allow a direct readout of the indentation of the shell because of the applied force. Sudden discontinuities sometimes occurred in the FZ curves, as seen in FZ2 at 1.4 nN. This jump is probably due to a fracture in the shell. (B) Histograms of measured spring constants. In red, 13 intact shells, each measured several times (N_total = 48), are shown. The tip was recentered before each FZ curve. Two rapid series of FZ curves (8 ms per curve) taken at two locations on a prohead (n = 77) are shown in gray.

Modeling Thin Virus Shells. The observed linear behavior is expected from thin-shell mechanics, which predicts a linear elastic response for the indentation of a homogeneous spherical shell up to an indentation amplitude on the order of the shell thickness, h (21). Beyond this regime, nonlinear buckling is predicted because of the coupling of in-plane compression and out-of-plane bending. In general, the linear spring constant k of a homogeneous shell of radius R can depend only on the Young's modulus E, the Poisson ratio σ of the material, and the geometric quantities h and R. In fact, on dimensional grounds, the spring constant must be given by E multiplied by a length. For thin spherical shells, it is expected that k_shell is proportional to Eh²/R (21). We have calculated analytically the deformation of a homogeneous, spherical, and elastic shell that is subject to equal and opposite forces applied at the poles by expanding the shape of the deformed sphere in spherical harmonics. This procedure allowed us to calculate the full elastic energy by standard methods (22, 23). Assuming that the shell is composed of a linear elastic material with a Poisson ratio of 0.3,†† we reproduced the expected Eh²/R scaling of the spring constant for thin shells with a coefficient of ≈4.5 for h/R = 0.1. Thus, the effective spring constant for the total pole-to-pole indentation becomes,

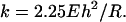[1]

With this expression and the measured k_shell, we can estimate the Young's modulus of the virus shell by taking the values of h and R from EM studies (3).

Mechanically Inhomogeneous Shells. We found, surprisingly, by pushing on different intact proheads on the center area of the equatorial band, that a bimodal distribution emerged for the elastic constant of the shells (Fig. 3B, red bars). The two spring constants were 0.31 N/m (SD = 0.03, n = 18) and 0.16 N/m (SD = 0.04, n = 30), respectively. To rule out the possibility that the soft response could be due to damaged structures, we included only objects in the histogram that were sampled in at least two locations and for which we measured at least one high spring constant after softer ones. Elasticity measurements after irreversible behavior (breakage) were excluded from the histogram as well. Pushing rapidly and up to 100 times on two different locations on a prohead (Fig. 3B, gray bars), we found again a bimodal distribution in the spring constant with similar mean values and SDs as when different objects were sampled and compared.‡‡

The bimodal distribution can be explained by the inhomogeneous structure of the shell on the scale of the subunits (gp8), which is comparable with the size of the tip contact region (≈5 nm) (3, 24, 25). Given these scales, we expect to be able to resolve some local structure of the shells with the SFM. The observed variation of the elastic response can arise either from inhomogeneity of the material (e.g., its thickness) or from variations in local curvature (26); it is harder, for instance, to indent a convex area than a flat one. It may be surprising, however, to find a bimodal distribution of spring constants instead of a broad distribution. Considering the way that a shell deforms under point forces can provide a possible explanation for this phenomenon. Although stress is concentrated near the tip in a local indentation, there is always a dominating (by amplitude) long-wavelength deformation corresponding to a global flattening of the spheroidal shell. This mode averages over local inhomogeneities in the surface. Only if the local elastic response becomes as soft or softer than the response due to the global mode will the local softness be apparent. The overall compliance observed with the SFM in the linear regime can, therefore, be modeled roughly by two springs in series: one spring corresponding to the local mode and the other spring to the global mode. Based on this picture, the highest measured spring constants should reflect primarily the properties of the shell as a whole (the global mode) and, in particular, should be observed whenever the tip is in contact with a locally stiff region. The appearance of a weaker resistance to the tip, however, suggests a soft local area. Thus, the observed bimodal distribution points to the presence of a particularly soft mode of local deformation. Considering the structure of the proheads (Fig. 1B), a plausible candidate for such soft spots could be the central area of the hexagonal regions within the equatorial band, which are weakly curved and of the order of ≈15 nm in diameter. Based on this model, we have used the larger spring constant in the analytical and finite-element analyses of the global shell properties.

Extracting Material Properties. Treating the empty prohead as homogeneous and as a sphere, we obtain from Eq. 1 Young's moduli E of 1.2 or 1.6 GPa, by inserting for R either one of the two radii of the more realistic ellipsoidal shape and by using an h of 1.6 nm. The result underestimates or overestimates E for the short or long radius, respectively. Apart from neglecting the actual prolate shape, this calculation does not take into account the geometrical constraint because of the deposition of the proheads on a flat surface, which could result in an overestimation of the E. Therefore, for comparison, we have modeled our experiments by using finite-element methods.

The finite-element model (CADRE, cadrepro4.2) of the virus shell consisted of 9,000 elements, each of which were 1.6-nm thick with a Poisson ratio of 0.3 and arranged in a hollow geodesic ellipsoid of 20 × 27 nm resting on a surface. A point loading force, perpendicular to the surface, is applied on top of the equatorial region, mimicking the SFM experiments. We again assume that the structure is homogeneous. The modulus E can now be adjusted to match the experimental k_shell,1. This procedure resulted in an estimate of E = 1.8 ± 0.2 GPa, consistent with the analytical result, if one reasonably assumes that the long axis is dominant for the elastic response of the prohead. This value of the Young's modulus is close to the values of hard plastics and similar to values measured for other structural proteins such as actin, tubulin, or collagen (27).

The finite-element analysis also quantifies the stresses for every element of the object. According to our analysis the maximal in-plane stresses at 1 nN applied-point force for a prohead are found to be on the order of 0.3 GPa.§§ Reliably determining maximal stresses at higher forces would require a more sophisticated model incorporating the inhomogeneous features of the prohead. Nevertheless, 0.3 GPa is a lower estimate for the tensile stresses that the empty prohead can still withstand when indented by a force acting from the outside of the structure. The minimal rupture strength of the shells due to internal pressure has been estimated theoretically to be 0.1–0.3 GPa (1, 13, 28, 29, ¶¶). Because indentation reorders the monomers even more than expansion of the shell, it seems that the tensile strength due to internal pressure of the proheads could be >0.3 GPa.

Exploring the Limits of Proheads. To probe the limits of the elasticity and the resilience of the prohead, we applied loads of up to several nanonewtons (Fig. 4A), and we found that proheads still responded linearly to forces of up to 2.8 ± 0.3 nN (n = 11). At these forces, they were indented by 12 ± 3 nm (n = 11). This indentation is a deformation of ≈30% of the total height of a prohead. Nevertheless, proheads would still recover to their normal height after such large deformations, even after pushing repetitively, tens of times, on the same location. Height recovery took place faster than 4 ms, and thus the relaxation time of the proheads was less than that. At forces beyond ≈2.8 nN, there were significant deviations from linearity, with the slope of the FZ curves decreasing (Fig. 4A). This nonlinearity has the opposite sign from the nonlinear response observed when indenting solids, usually modeled by the Hertz model (30, 31). It is expected that a thin shell will undergo a buckling transition in which curvature inverts under the point of pressure and stresses concentrate in a ring of finite radius around the emerging dent (21). The predicted decrease in stiffness is observed qualitatively in our experiments.

Fig. 4.

Pushing the limits of the capsids. (A) Three consecutive FZ curves taken in rapid succession (8 msec) on a prohead. This shell responded linearly to applied forces up to ≈2.5 nN. At higher forces, a softer reaction to applied force was observed. The elastic constant was calculated from the linear region of each curve shown. (B). The change of the measured spring constant with repeated indentations on three different proheads (red, blue, and magenta). The red curve (related to the curves in A) shows a gradual change of the elasticity after ≈30 indentations, whereas the blue curve shows a sudden decrease. Both show that the rigidity of the object is lowered permanently after the decrease (marked by the vertical lines). This decrease was an indication of the destruction of the viral shell. The magenta curve shows how repeated indentation of a prohead can eventually disintegrate it completely. This prohead appeared to be broken at the first scan, and its rigidity decreased further with each consecutive indentation. (C) The magenta and blue curves relate to the magenta and blue curves shown in B. The blue curves display a discrete breakage event in the prohead, which resulted in a permanently lower spring constant of the object. The magenta FZ curves represent the first and last curves of a shell, which disintegrated with every consecutive push.

We also observed irreversible breakage after repeatedly pushing on a prohead (Fig. 4B), presumably because of material fatigue. After such an event, a prohead often still responded linearly to applied force but with a permanently lower elastic constant. Continued pushing on a shell with high force caused severe fracturing of the structure and eventually caused it to fall apart (Fig. 2B, triangles). Severely destroyed shells also started to react in a plastic manner to applied force. An upper limit for the energy dissipated in a small shell rupture can be estimated by calculating the area between two up-curves before and after a rupture event up to the indentation at which the rupture had occurred. For instance, from the blue curves shown in Fig. 4C, using numerical parameters from Purohit et al. (12), it can be estimated that the loss of energy (≈1.3 10^-18 Nm) is about the same as the energy it would cost to dislodge a single monomer from the shell or form a crack of ≈25 nm. Larger breakage events were also observed, which could mean that entire oligomeric forms were removed.

Conclusions. Our results show that one can probe nanoscale shells and quantitatively extract their mechanical properties. We find that the capsid of bacteriophage φ29 is remarkably dynamic yet resilient and tough enough to easily withstand the known packing pressure of DNA (≈60 atmospheres). These capsids, thus, not only provide a chemical shield but also significant mechanical protection for their genetic contents. Viral shells are a remarkable example of nature's solution to a challenging materials engineering problem: they self-assemble to form strong shells of precisely defined geometry (32) by using a minimum amount of different proteins. These biological construction principles suggest possible approaches for man-made nanoscale containers. The method developed here provides a view of viral structural biology, focusing on the mechanics. Important areas to be explored in the future include the effects of packing DNA, the state of the packed DNA inside the shells, and maturation of viral particles.