Abstract
The lateral heterogeneity of cellular membranes plays an important role in many biological functions such as signaling and regulating membrane proteins. This heterogeneity can result from preferential interactions between membrane components or interactions with membrane proteins. One major difficulty in molecular dynamics simulations aimed at studying the membrane heterogeneity is that lipids diffuse slowly and collectively in bilayers, and therefore, it is difficult to reach equilibrium in lateral organization in bilayer mixtures. Here, we propose the use of the replica exchange with solute tempering (REST) approach to accelerate lateral relaxation in heterogeneous bilayers. REST is based on the replica exchange method but tempers only the solute, leaving the temperature of the solvent fixed. Since the number of replicas in REST scales approximately only with the degrees of freedom in the solute, REST enables us to enhance the configuration sampling of lipid bilayers with fewer replicas, in comparison with the temperature replica exchange molecular dynamics simulation (T-REMD) where the number of replicas scales with the degrees of freedom of the entire system. We apply the REST method to a cholesterol and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) bilayer mixture and find that the lateral distribution functions of all molecular pair types converge much faster than in the standard MD simulation. The relative diffusion rate between molecules in REST is, on average, an order of magnitude faster than in the standard MD simulation. Although REST was initially proposed to study protein folding and its efficiency in protein folding is still under debate, we find a unique application of REST to accelerate lateral equilibration in mixed lipid membranes and suggest a promising way to probe membrane lateral heterogeneity through molecular dynamics simulation.
I. Introduction
Molecular dynamics simulations have been used as a powerful tool to study lipid membranes but are limited by the length and time scales of the probing systems. In particular, the lateral diffusion rate of a lipid in a membrane, although varying among different experimental techniques, is in the range 10–9∼10–7 cm2 s–1.1−4 This means that it will take a lipid about hundreds of nanoseconds to microseconds time scale to cover a 1 nm2 area. Furthermore, lipids are observed to move collectively with their neighbors, and therefore, the rate at which a lipid swaps position with its neighbor is even slower.5,6 This poses a serious problem when we simulate lipid bilayers with multiple components, since the lateral organization of different components requires extensive simulation to attain equilibrium7 and common accessible simulation time scales may provide configurations ensemble biased toward the initial conditions.
Temperature replica exchange molecular dynamics (T-REMD) is one of the methods that has been widely used to accelerate equilibration in simulations and achieved numerous success in protein folding.8−10 However, its application to lipid bilayers is rare since the number of replicas scales with the degrees of freedom (DOFs) of the whole system, and lipid membranes usually have many more DOFs than the protein systems, making it computationally prohibitive to use T-REMD to study lipid bilayers.
One promising method to get around the poor scalability of T-REMD with system size is replica exchange with solute tempering (REST), which was initially proposed by Berne and co-workers.11 REST is a specific variation of a generalized Hamiltonian replica exchange method.12 By changing the solute–solute and solute–solvent interactions in the system, REST can enhance the sampling of the solute with significantly fewer replicas. Although REST has been demonstrated to sample the conformational ensemble of the alanine dipeptide successfully, its efficiency in folding larger proteins remains unclear, which impedes a wide adoption of the method.13,14
In this work, we show that REST can be used as an efficient way to accelerate lateral equilibration in a mixed lipid bilayer. We applied constant pressure REST to a 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) bilayer with 50 mol % cholesterol (CHOL). Constant pressure in REST simulation is used because volume expansion at high temperature increases lipids lateral diffusion. By carefully choosing the tempering solute, we managed to simulate the system with only 12 REST replicas, which compares favorably to the requirement for ∼100 replicas with T-REMD at the same replica exchange rate. The relative diffusion rate between molecules in REST is, on average, an order of magnitude faster than the rate in standard MD simulation. We also show that the lateral radial distribution function between all molecular pair types (CHOL–CHOL, CHOL-DPPC, DPPC–DPPC) calculated from separate monolayers converges much faster in REST. Finally, we use REST to obtain the Gibbs free energy profiles between different molecular pair types from the corresponding lateral radial distribution functions.
II. Materials and Methods
1. Replica Exchange with Solute Tempering
Let us start with a brief review of replica exchange with solute tempering (REST).11 REST can be derived from a more general form of replica exchange called Hamiltonian replica exchange.12 In Hamiltonian replica exchange, replica m is simulated with potential energy Em, at temperature Tm (the corresponding inverse temperature will be referred as βm, where βm = 1/kBTm and kB is the Boltzmann constant) and constant pressure Pm. In an isothermal–isobaric ensemble, the probability of configuration Xm with volume Vm in replica m is
| 1 |
where Zm is the corresponding partition function. The exchange between replica m and n can be treated as the change from state i to state f in the generalized ensemble,
| 2 |
and we use T(i → f) to denote the transition probability for i → f. Applying the detailed balance condition
| 3 |
gives the ratio of the transition probabilities
| 4 |
where
| 5 |
If the replicas are simulated at the same temperature T0 and pressure P0 but a different potential energy, eq 5 can be further reduced to
| 6 |
The detailed balance condition guarantees the Boltzmann sampling of all replicas when sufficiently long simulations are performed.
In REST, each replica is simulated at the same temperature (T0) and pressure (P0) but a different potential energy function. We can divide the system potential energy into three terms:
| 7 |
where each term, in order, represents solute–solute, solute–solvent, solvent–solvent interactions. For replica m, we scale its potential energy according to
| 8 |
Following from eq 1, the Boltzmann distribution for replica m becomes
| 9 |
Equation 9 shows that, thermodynamically, we can interpret the solute of the system as if it is simulated at the scaled potential (βm/β0)Ess at temperature T0, or at the original potential Ess at an “effective temperature” Tm. In each REST setup, we should always ensure that there is one replica simulated with Tm = T0. We will refer T0 also as the “target temperature” because it is the temperature of interested for the studied system. Replicas simulated with Tm ≠ T0 are used for the sole purpose of enhancing sampling at T0 and configurations obtained from these additional replicas do not represent any thermodynamic ensembles that have experimental counterparts.
We want to emphasize two points here. First, the definition of solute and solvent in a system is not absolute. The solute can generally present a part of the system whose sampling we want to accelerate, while the solvent is defined as the rest of the system. Second, the potential function of replica m can be of a form different from eq 8. REST is just a specific form of Hamiltonian replica exchange, and there is no restriction in the form of the potential energy function used in each replica in Hamiltonian replica exchange. The advantage of using eq 8 is that there is a physical interpretation associated with it, but this is not required. Therefore, the choice of the prefactor in front of Esw is not unique. We choose (βm/β0)1/2 for the ease of implementation, as suggested by Terakawa et al.15
Following eq 6, the exchange ratio between replica m and n is determined by
| 10 |
It is clear from the above equation that the exchange ratio is independent of solvent–solvent interactions (Eww). Therefore, one can enhance the solute dynamics and simultaneously reduce the number of tempered degrees of freedom, which results in a reduction of the number of required replicas. We want to point out that in our implementation of REST we use eq 6 to calculate exchange rate rather than eq 10 for practical reasons. Specifically, the total potential energy is easily available from the simulation code.
In the following text, we describe how we scale the potential energy function according to eq 8, using separate force field parameters for each replica. In common molecular dynamics force fields, the potential function consists of
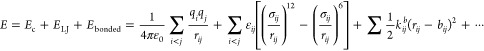 |
11 |
where the first two terms are Coulomb and Lennard-Jones interactions and the third and the following terms are bonded interactions which define the bond length potential, the bond angle potential, the torsion potential, and so forth. The scaling of the potential in replica m descried in eq 8 can be done as follows: (1) for the bonded interactions in the solute, scale the spring constants by (βm/β0), (2) scale the charges in solute by (βm/β0)1/2, and (3) scale εij by βm/β0 if both i and j are in the solute, and by (βm/β0)1/2 if only i or j is in the solute. We scale εij directly because it can be applied to any combination rule. By these, we can scale the potential function as indicated by eq 8.
2. Simulation Details
The system we studied consisted of 144 DPPCs, 144 cholesterols (CHOL), and ∼14k water molecules. Each monolayer in the bilayer was built independently by randomly placing 72 DPPCs and 72 CHOLs on 12 × 12 planar grids. We define the Z axis as the bilayer normal and refer the values of Z > 0 nm and Z < 0 nm as the “upper” and “lower” monolayers. Then, we equilibrated the system for 20 ns at 323 K and 1 atm. The resulting configuration was used as the initial structure for all replicas in REST and the standard MD simulations. We note here that every replica in REST has the same starting configuration as in the MD simulation.
In REST, we chose DPPC molecules as the solute and treated cholesterols and waters together as solvent. The explanation for this choice is provided in the Results section. In total, 12 replicas were used and a 25% exchange rate was achieved between the neighboring replicas. Each replica was simulated at 323 K (T0), while the “effective temperatures” of DPPC were set at 323, 341, 360, 380, 400, 421, 445, 471, 500, 531, 564, and 600 K (Tm). Each replica in REST was simulated for 60 ns, while the MD simulation was conducted for 400 ns.
3. Simulation Parameters
We implemented Hamiltonian replica exchange in Gromacs 4.5.7 software package16,17 to conduct REST. The default Hamiltonian replica exchange in Gromacs is done through thermodynamic integration, and it suffers from a great performance loss if the potential function involving a large portion of the system is altered. Our implementation does not have such issue. The source code will be made available upon request. Systems were simulated under periodic boundary conditions, at constant temperature and pressure. For temperature coupling, DPPC and CHOL molecules were coupled as one group and water molecules as another. Each group was kept at 323 K using the V-rescale algorithm.18 We note here that in REST, each replica is simulated at 323 K and the “heating” of solute is done by reducing the solute–solute and solute–solvent interactions in the force field. The Parrinello–Rahman barostat19 at 1 atm was used and the pressure in the plane of the bilayer was coupled separately from the pressure normal to the bilayer. The temperature and pressure time constants of coupling were 0.1 and 2.0 ps, respectively. A 2 fs time integration step was used. The SPC/E model20 was used for water and the 43A1-S3 force field21 was used for DPPC and CHOL. SETTLE22 was used to constrain water molecules and LINCS23 was used to constrain all other bond lengths in the system. The sixth-order particle mesh Ewald (PME) method24 was used for electrostatic interactions with a Fourier spacing of 0.15 nm. The real space Coulomb interactions and pair-list calculations were set to 1.0 nm. A 1.0/1.6 nm twin-range cutoff scheme was used for VDW interactions and the pair-list was updated every 10 steps.
4. Relative Diffusion Coefficient
To study how molecules diffuse relative to one another, we calculated the relative diffusion coefficient Dij between each pair of molecules i, j. The relative diffusion removes the contribution from collective motions of molecules to the diffusion and should give a better estimate of how fast the system samples various lateral configurations. We define the mean squared relative displacement between molecule i, j in a time interval Δt as
| 12 |
| 13 |
where r⃗i(t) is the position of molecule i at time t and the bracket means an average over different starting times t. Then we linearly fit Rij2(Δt) as a function of Δt for larger Δt. Dij was assigned as 1/4 (two-dimensions) the slope of the curve. We note here that in REST, the relative diffusion rate is an average over temperatures (due to the exchange among replicas, replicas jump in the temperature ladder); however, it should still provide a meaningful description of how fast the simulations sample bilayer lateral configurations in general.
III. Results
A. Choosing the Solute
As mentioned in the methods session, the choice of solute for REST simulations is not absolute. The solute can generally be the part of the system whose dynamics we want to accelerate, while the solvent is the rest of the system. Since in this study we want to accelerate the dynamics of lipid bilayers, it is natural to choose both the DPPC and CHOL as the solute. Before we conduct REST, it is always a good practice to test the system at the highest temperature that we want to simulate in REST. We found that when we simulated the DPPC and CHOL at 600 K (Tm), the CHOL moved out of the monolayers and formed a third layer sandwiched by the DPPC bilayer. A snapshot of the system is shown in Figure 1. A possible explanation of this can be obtained by carefully examining CHOL molecular structures. CHOL has a small hydrophilic alcohol headgroup and a bulky hydrophobic body. At low temperature, the hydrophilic interactions between the CHOL alcohol group and water favors aligning CHOL along the bilayer normal. When the effective temperature of CHOL increases, the entropic effect becomes dominant and CHOL will gain entropically by placing itself in the middle of the bilayer. On the other hand, DPPC has a larger hydrophilic headgroup than CHOL; thus, even at 600 K, it still can anchor itself upright to form the bilayer.
Figure 1.

Snapshot of the system where both DOPC and CHOL molecules are tempered at 600 K. Water is colored blue. The oxygen atom in CHOL and the phosphate atom in DPPC are colored red and gold, respectively. Carbons in CHOL are colored yellow.
Two possible approaches can be taken to handle the above situation. One way is to lower the highest temperature in REST to keep CHOL aligned with the bilayer normal. Another way is to use only DPPC as solute and treat both CHOL and water as solvent. We want to note that we should be able to just conduct REST with both DPPC and CHOL set to 600 K, even though CHOL moved out of the monolayers at this temperature. However, this would be very inefficient. Configurations similar to Figure 1 obtained from high solute temperature replicas will have vanishingly small probabilities in the target temperature replica ensemble (T0 = 323 K) due to the detailed balance condition (eq 6). As a result, those configurations will mostly exchange within the high temperature replicas. Neale et al. has observed such phenomena in another Hamiltonian replica exchange system.25 In this case, high temperature replicas will not enhance the sampling in the target temperature replica but consume computing time. In this work, we take the second approach in which only DPPC is chosen as the tempered solute. Since this reduces the DOFs in the solute, it further decreases the number of replicas required to span our temperature range.
B. Efficiency of REST
1. REST vs T-REMD
By choosing DPPC as solute, we managed to heat DPPC from 323 to 600 K with 12 replicas. The exchange rates between neighboring replicas are 25%, 22%, 24%, 26%, 27%, 22%, 23%, 22%, 22%, 24%, and 22%.
In order to compare the efficiency between REST and T-REMD, we estimate how many replicas we need in our system to conduct T-REMD to maintain a 25% exchange rate between neighboring replicas. The estimation method we used was proposed by Garcia et al.26 Figure 2 shows that if 12 replicas are used in T-REMD, we can only cover the temperature ranging from 323 to 340 K. This would hardly accelerate the simulation as T-REMD usually gains simulation efficiency by increasing the enthalpy barrier crossing rate in high temperature replicas.27,28 Comparatively, REST has a significant advantage over T-REMD as we can heat the DPPC to a much higher temperature with the same number of replicas.
Figure 2.
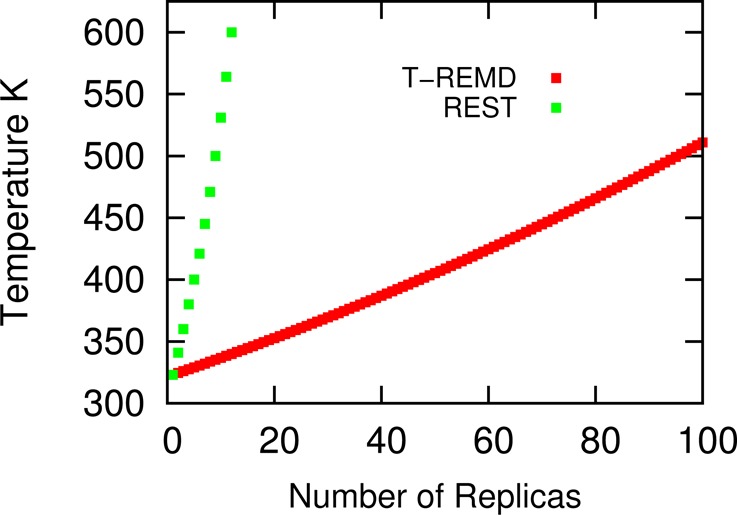
Number of replicas required to obtain a ∼ 25% exchange rate between neighboring replicas in REST and T-REMD (temperature replica exchange).
2. REST vs a Single, Longer, MD Simulation
Below, we compare the sampling efficiency between REST and a single long MD simulation. In our work, we ran REST for 60 ns and standard MD for 400 ns.
2a. Relative Diffusion Coefficient
The equilibrium sampling of lipid bilayers, especially of bilayers with different components, depends on the ability to sample different lateral organizations. The faster the system can explore various lateral configurations, the quicker equilibrium will be reached. Therefore, the lateral diffusion coefficient plays a key role in determining the equilibrium rate. However, lipids usually move collectively in bilayers.5 This collective motion generally does not facilitate the sampling of various lateral configurations but contributes significantly to the lateral diffusion coefficient of each individual molecule. Therefore, we calculated the relative diffusion coefficient between every pairs of molecule as it removes the contribution from collective motion among lipids. Details of the calculation are listed in the methods section.
Three different types (CHOL–CHOL, CHOL–DPPC, DPPC–DPPC) of relative diffusion coefficients are calculated from the MD and REST simulations. Figure 3 shows the probability density of the relative diffusion coefficients. It clearly indicates that in all molecular pair types, molecules in REST diffuse an order of magnitude faster than in standard MD. Also, we observe that the diffusion between CHOL and CHOL is the fastest while the diffusion between DPPC and DPPC is the slowest. This can be understood because geometrically CHOL is more compact than DPPC. Therefore, it diffuses more easily. DPPC, on the other hand, has two acyl tails that are usually entangled with other DPPC, which reduces the diffusion. It is also worth noting that even though we only increase the effective temperature of DPPC, the diffusion of CHOL increases as well. By omitting the CHOL from the tempered solute, we further reduced DOFs in the solute and therefore reduced the number of replicas required for the system. This also suggests that the efficiency of REST may be further optimized by carefully choosing the tempering solute, which is also pointed out in the original paper.14 We note that the total simulation time in REST (60 × 12 = 720 ns) is almost twice as much as the time in MD (400 ns). However, considering an order of magnitude increase in the lipid diffusion, REST is quite efficient.
Figure 3.
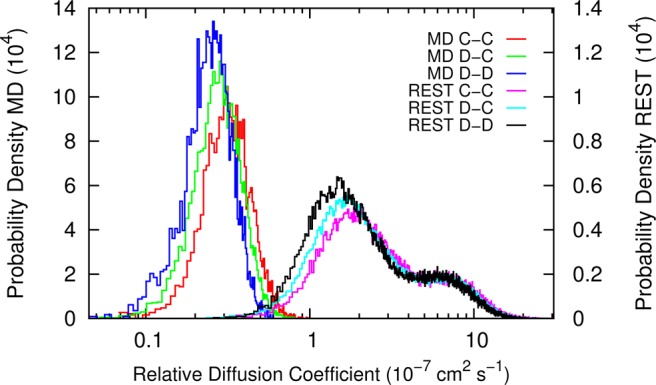
Probability density of all pairwise relative diffusion coefficients between CHOL–CHOL (C–C), DPPC–CHOL (D–C), and DPPC–DPPC (D–D) in MD and REST simulations.
2b. Radial Distribution Function
The radial distribution function (rdf) quantitatively describes the lateral organization of molecules in a bilayer. We define the lateral distance between two molecules as the center of mass (COM) distance between the molecules projected in the x–y plane. As the coupling between separate monolayers is weak, the rdf calculated from the upper and lower monolayers should converge to the same distribution. Therefore, we can judge the convergence of a simulation by the rdf difference calculated from separate monolayers.
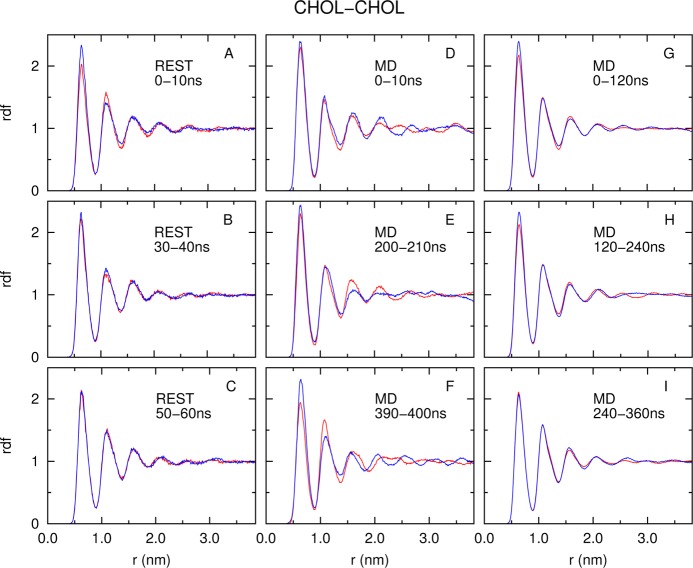
Figure 4 and Supporting Information Figures S1 and S2 show the rdfs among CHOL–CHOL, CHOL–DPPC, and DPPC–DPPC molecular pair types, respectively. The rdfs are calculated from separate monolayers (blue, upper monolayer; red, lower monolayer) from the REST and MD simulations using different block sizes. In all cases, REST shows faster convergence than MD. Taking CHOL–CHOL rdfs (Figure 4) for example, with a 10 ns block size, the rdfs in REST show reasonable convergence between separate monolayers (Figure 4A–C). However, this is not the case for the MD simulation (Figure 4D–F). The rdf difference in MD simulation in the last 10 ns block (Figure 4F) is even larger than the difference in the first 10 ns block (Figure 4D). We reason that as molecules diffuse slowly in the MD simulation, the sampled lateral configurations are highly correlated in time; thus, a larger block size is required to obtain independent configurations. Therefore, we increased the time block size to 120 ns to calculate the rdf from the MD simulation. Figure 4G–I show that rdf converges better when the block size is increased. The converged rdf in MD (Figure 4I) has a very similar shape with the rdf obtained from REST (Figure 4C).
Figure 4.
Lateral radial distribution (rdf) function of CHOL–CHOL center of mass distances calculated from the REST and MD simulations. The time block used to calculate rdf is indicated in each subplot. The blue/red line in each subplot represents the rdf calculated from the upper/lower monolayer, respectively.
Supporting Information Figures S1 and S2 show the rdfs between CHOL-DPPC and DPPC–DPPC pairs, respectively. We observe that the rdf of DPPC–DPPC does not converge as well as the rdf of CHOL–CHOL or CHOL-DPPC. This can be explained from the relative diffusion coefficient. Figure 3 shows that DPPC–DPPC pairs diffuse the slowest in both MD and REST; therefore, we can expect that the rdf of DPPC–DPPC takes the longest time to converge.
To quantitative analyze the convergence rate, we define the rdf difference between separate monolayers (RDFDiff) as
| 14 |
where rdfu(i) and rdfl(i) are the value of the ith bin of rdfs from the upper and lower layer, respectively. N is the total number of bins in the rdf. Figure 5 shows the convergence of rdf as a function of time block size in REST and MD simulations. Error bars are estimated from consecutive blocks with the same block size. Figure 5 shows that the rdf in REST converges an order of magnitude faster than in MD.
Figure 5.
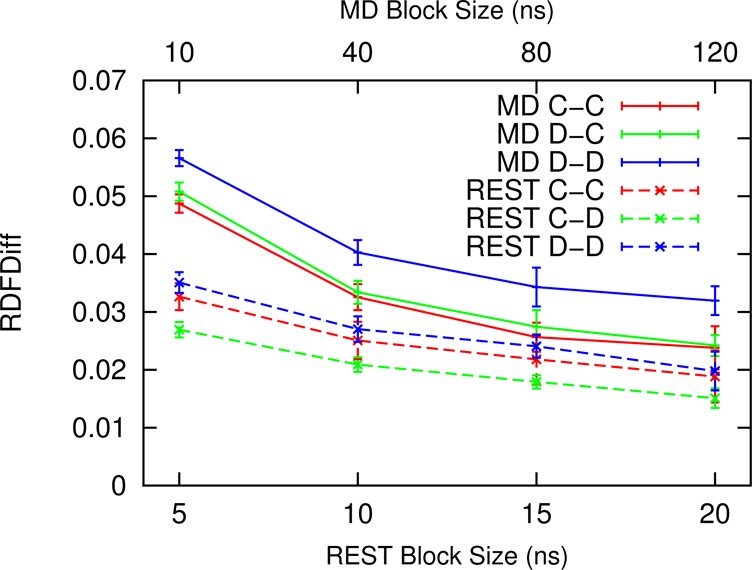
Difference between rdfs calculated from the upper and lower monolayers as a function of block size. Error bars are estimated from consecutive blocks with the same block size.
C. Bilayer Properties
1. Structural Properties
In this session, we compare several bilayer structural properties calculated from the REST and MD simulations. For REST, only the replica simulated with solute temperature at Tm = 323 K is used for analysis, as it represents the system with the original Hamiltonian.
Normally, the area per lipid serves a good indicator on bilayer structural properties. However, since the bilayer we studied has both CHOL and DPPC, we calculated the average area per molecule (AAPM) instead. AAPM is defined as the projected area of the bilayer in the x–y plane divided by the number of molecules in a monolayer. The AAPM are 43.1 ± 0.6 Å2 in REST and 42.8 ± 0.4 Å2 in MD. This is in a good agreement with previous reports.29
Another important bilayer property is the deuterium order parameter (Scd) of the lipid acyl tails. The order parameter of a methylene at position i is defined as
| 15 |
where θi is the angle between a C–D vector of the ith methylene in an acyl chain and the normal of the bilayer (z axis). The angular brackets indicate an ensemble average. Figure 6 shows the |Scd| obtained from the MD and REST simulations. Our calculation suggests that REST and MD simulations have similar bilayer properties, which is a good validation of the REST method.
Figure 6.
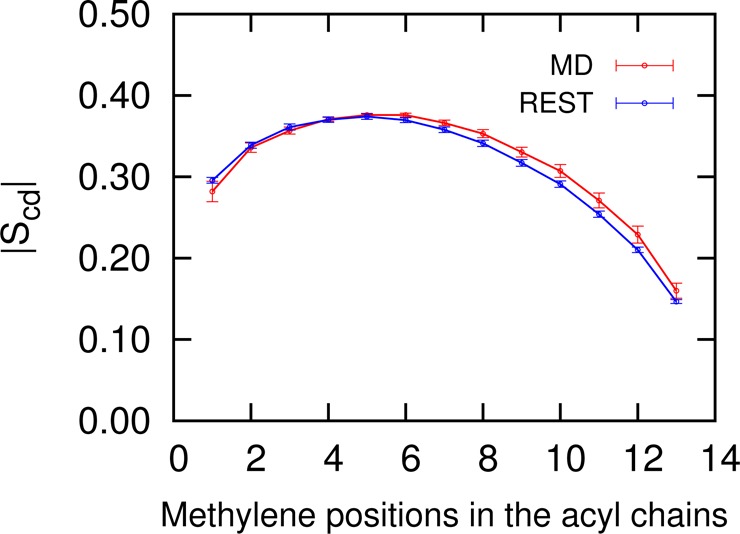
Deuterium order parameters |Scd| of DPPC palmitoyl chains at 323 K calculated from the REST and MD simulations.
CHOL is well-known for its condensing effect on lipid bilayers composed of lipids with saturated acyl tails.30,31 It smooths the lipid liquid/gel phase transition to the lipid disordered/ordered phase transition.32 It is reported that the average value of |Scd| for DPPC at liquid ordered phase and disordered phase are 0.36 and 0.21, respectively.7Supporting Information Figure S3 shows the |Scd| of DPPC at different solute temperatures in REST. At high solute temperatures, the DPPC acyl tails are more flexible and the |Scd| indicates that the bilayer is in the liquid disordered phase. The range of sampled |Scd| in REST suggests that REST works well even when the system experiences the liquid disordered/ordered phase transition.
2. Lateral Free Energy Profile
Based on the high resolution rdf obtained from REST, we calculate the total Gibbs free energy ΔGtotal(r) and excess Gibbs free energy ΔGex(r) profiles between CHOL–CHOL, CHOL–DPPC, and DPPC–DPPC. ΔGtotal(r) and ΔGex(r) are defined as
| 16 |
and
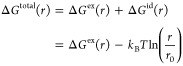 |
17 |
g(r) is the lateral radial distribution function (rdf), and r0 is the reference distance where we set Gtotal(r0) = 0. Gid(r) is the contribution to the Gtotal(r) due to the Jacobian or area effect in the two-dimensional space. Figure 7 shows that ΔGtotal(r) is always above 0. This means that neither CHOL or DPPC tends to aggregate at the 50% CHOL concentration. Andoh et al. reported the CHOL–CHOL Gibbs free energy profile in dilute conditions and found that ΔGtotal(r) drops below zero in the range 1.0 < r < 1.5 nm.33 This difference suggests that CHOL–CHOL Gtotal(r) depends on CHOL concentration. The DPPC–DPPC Gtotal(r) is almost flat when r > 1.0 nm, suggesting a random distribution of DPPC at large distance. Several local minima exist in the CHOL–CHOL ΔGtotal(r), indicating preferential interacting locations for CHOL–CHOL pairs. This supports some phenomenological models, such as the supperlattice model34,35 and umbrella model,36−38 which suggest long-range ordering for CHOL. However, the barriers between the free energy minimums are of the order of kT scale, suggesting that the ordering of cholesterols is sensitive to the temperature. As the derivative of ΔGex(r) is the mean force, the ΔGex(r) we obtained can be used as a reference for various coarse grained models for this system.39,40
Figure 7.
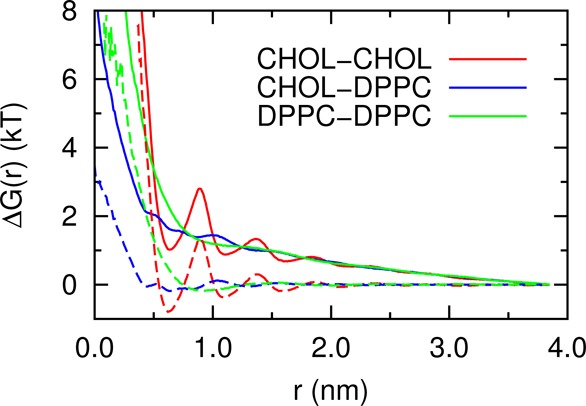
Total free energy ΔGtotal(r) (solid line) and the excess free energy ΔGex(r) (dashed line) profiles between different molecular types as a function of the lateral molecular center of mass distance.
IV. Discussion
To utilize REST efficiently, we need to select the solute appropriately. A general guideline is to choose the part of the system for which we want to accelerate the dynamics as the solute. This flexibility can give REST great power. For example, if we study the lipid–protein interactions and are interested in the affinity of different lipid components to the protein, we can temper the lipids to accelerate their diffusion. On the other hand, if we are interested in how the protein adapt its conformation to the bilayer environment, we can temper the protein instead.
With a good choice of solute, REST can accelerate the dynamics of the system with fewer replicas (compare to T-REMD). However, an inappropriate choice of solute may hurt REST’s efficiency. REST, in essence, is a specific form of Hamiltonian replica exchange. The sole purpose of the replicas with the scaled potentials (Tm ≠ T0) is to sample configurations that are likely to occur in the target temperature ensemble (Tm = T0). Therefore, if we scale the potential in such a way that the system samples configurations with low probability to populate at the target temperature ensemble (configurations such as Figure 1, in our case), REST will be less efficient. However, no matter what the choice of the solute is, we always have one replica in REST that is simulated at the original unscaled potential. Choosing the solute that makes REST efficient may require an intuitive trial and error approach.
In the past, there were several other methods developed by researchers to accelerate lipid dynamics. One popular way is to coarse grain lipid molecules.40−42 Usually, coarse grained systems have fewer degrees of freedom than their atomic counterparts, which results in smoother free energy landscape and faster lipid diffusion. Another method, developed by Tajkhorshid and co-workers, is a membrane mimetic model, which separates the lipid headgroup from its hydrophobic tails. This method facilitates headgroup diffusion while maintaining a hydrophobic core and has been used to study the insertion of peripheral proteins.43,44 Wang et al. also developed a method based on the accelerated molecular dynamics (aMD) method, which accelerates lipid diffusion by adding a boost potential to the original system.45 REST provides an efficient way of accelerating the equilibrium of lipid bilayer systems while simulating at least one copy of an unperturbed potential and maintaining atomistic details.
V. Conclusions
In this work, we applied Replica Exchange with Solute Tempering (REST) to a cholesterol–DPPC bilayer system. In REST, part of the system is chosen as solute and the solute–solute and solute–solvent interactions are scaled such that thermodynamically, the solute is effectively sampling at a different temperature. We found that choosing both cholesterols and DPPCs as solute is not efficient because most of the cholesterols moved out of the monolayers to form a third layer at “high temperature”. Therefore, we chose to temper the DPPC molecules only. Since the number of replicas for REST only scales with the degrees of freedom in the solute, we managed to use 12 replicas to sample DPPC at “temperature” ranging from 323 to 600 K, which, otherwise, would require ∼100 replicas in the traditional temperature replica exchange molecular dynamics (T-REMD). The relative diffusion coefficients between all molecular pair types (CHOL–CHOL, CHOL–DPPC, DPPC–DPPC) in REST are, on average, an order of magnitude larger than in standard MD simulation, indicating a better sampling of lateral structures in REST. We also compare the CHOL–CHOL, CHOL–DPPC, and DPPC–DPPC radial distribution function (rdf) between separate monolayers in the REST and MD simulations. Since the coupling between monolayers is weak, the rdf should converge to the same distribution from different monolayers. Our results show that the rdf converges much faster in the REST than in the MD simulation. Bilayer structural properties such as average area per molecules and deuterium order parameters are similar between the REST and MD simulations. Finally, we obtained the lateral free energy profile between different molecular types from REST, which could be used as a reference to coarse-grained models of the system. The CHOL–CHOL lateral free energy has several local minima and shows a long-range ordering, but the free energy barriers between minima are on the kT scale, indicating the ordering may be sensitive to the temperature. While we see a significant advantage of using REST to accelerate lateral equilibrium in mixed lipid bilayers, we believe that REST, or more generally, Hamiltonian replica exchange will have broader applications. For example, the preferential interactions between different lipids and membrane proteins can be studied by tempering the lipids while leaving the protein and solvent at the target temperature. Also, combined with umbrella sampling, REST can be used to accelerate relaxation on degrees of freedom orthogonal to the reaction coordinate, which is reported as a hurdle in free energy calculations for lipid membranes.25,46,47
Acknowledgments
This work is funded by National Institutes of Health (NIH) grant GM086801. The authors acknowledge Dr. C. Neale, Dr. H. Herce, and Dr. A. Saxena for fruitful discussions and suggestions, and thank Dr. C. Neale for carefully reading the manuscript. This work used the Extreme Science and Engineering Discovery Environment (XSEDE grant No. MCB130178), which is supported by National Science Foundation grant ACI-1053575.
Supporting Information Available
Lateral rdfs of CHOL–DPPC and DPPC–DPPC center of mass distances. Deuterium order parameters of DPPC palmitoyl chains. This material is available free of charge via the Internet at http://pubs.acs.org/.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Wu E.; Jacobson K.; Papahadjopoulos D. Lateral diffusion in phospholipid multibilayers measured by fluorescence recovery after photobleaching. Biochemistry 1977, 16, 3936–3941. [DOI] [PubMed] [Google Scholar]
- Picard F.; Paquet M.-J.; Dufourc É. J.; Auger M. Measurement of the lateral diffusion of dipalmitoylphosphatidylcholine adsorbed on silica beads in the absence and presence of melittin: A 31P two-dimensional exchange solid-state NMR study. Biophys. J. 1998, 74, 857–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scomparin C.; Lecuyer S.; Ferreira M.; Charitat T.; Tinland B. Diffusion in supported lipid bilayers: Influence of substrate and preparation technique on the internal dynamics. Eur. Phys. J. E 2009, 28, 211–220. [DOI] [PubMed] [Google Scholar]
- Poger D.; Mark A. E. Lipid bilayers: The effect of force field on ordering and dynamics. J. Chem. Theory Comput. 2012, 8, 4807–4817. [DOI] [PubMed] [Google Scholar]
- Falck E.; Róg T.; Karttunen M.; Vattulainen I. Lateral diffusion in lipid membranes through collective flows. J. Am. Chem. Soc. 2008, 130, 44–45. [DOI] [PubMed] [Google Scholar]
- Roark M.; Feller S. E. Molecular dynamics simulation study of correlated motions in phospholipid bilayer membranes. J. Phys. Chem. B 2009, 113, 13229–13234. [DOI] [PubMed] [Google Scholar]
- Sodt A. J.; Sandar M. L.; Gawrisch K.; Pastor R. W.; Lyman E. The molecular structure of the liquid-ordered phase of lipid bilayers. J. Am. Chem. Soc. 2014, 136, 725–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita Y.; Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar]
- García A. E.; Sanbonmatsu K. Y. Exploring the energy landscape of a β hairpin in explicit solvent. Proteins Struct. Funct. Bioinfomatics 2001, 42, 345–354. [DOI] [PubMed] [Google Scholar]
- Paschek D.; Hempel S.; García A. E. Computing the stability diagram of the Trp-cage miniprotein. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 17754–17759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu P.; Kim B.; Friesner R. A.; Berne B. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 13749–13754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunishi H.; Watanabe O.; Takada S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J. Chem. Phys. 2002, 116, 9058. [Google Scholar]
- Huang X.; Hagen M.; Kim B.; Friesner R. A.; Zhou R.; Berne B. Replica exchange with solute tempering: Efficiency in large scale systems. J. Phys. Chem. B 2007, 111, 5405–5410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L.; Friesner R. A.; Berne B. Replica exchange with solute scaling: A more efficient version of replica exchange with solute tempering (REST2). J. Phys. Chem. B 2011, 115, 9431–9438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Terakawa T.; Kameda T.; Takada S. On easy implementation of a variant of the replica exchange with solute tempering in GROMACS. J. Comput. Chem. 2011, 32, 1228–1234. [DOI] [PubMed] [Google Scholar]
- Berendsen H.; van der Spoel D.; Van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar]
- Hess B.; Kutzner C.; Van Der Spoel D.; Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101–014101. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182. [Google Scholar]
- Berendsen H.; Grigera J.; Straatsma T. The missing term in effective pair potentials. J. Chem. Phys. 1987, 91, 6269–6271. [Google Scholar]
- Chiu S.; Pandit S.; Scott H.; Jakobsson E. An improved united atom force field for simulation of mixed lipid bilayers. J. Phys. Chem. B 2009, 113, 2748–2763. [DOI] [PubMed] [Google Scholar]
- Miyamoto S.; Kollman P. SETTLE: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
- Hess B.; Bekker H.; Berendsen H.; Fraaije J. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10093. [Google Scholar]
- Neale C.; Madill C.; Rauscher S.; Pomès R. Accelerating convergence in Molecular Dynamics simulations of solutes in lipid membranes by conducting a random walk along the bilayer normal. J. Chem. Theory Comput. 2013, 9, 3686–3703. [DOI] [PubMed] [Google Scholar]
- Garcia A. E.; Herce H.; Paschek D. Simulations of temperature and pressure unfolding of peptides and proteins with replica exchange molecular dynamics. Annu. Rep. Comput. Chem. 2006, 2, 83–95. [Google Scholar]
- Zuckerman D. M.; Lyman E. A second look at canonical sampling of biomolecules using replica exchange simulation. J. Chem. Theory Comput. 2006, 2, 1200–1202. [DOI] [PubMed] [Google Scholar]
- Nymeyer H. How efficient is replica exchange molecular dynamics? An analytic approach. J. Chem. Theory Comput. 2008, 4, 626–636. [DOI] [PubMed] [Google Scholar]
- Falck E.; Patra M.; Karttunen M.; Hyvönen M. T.; Vattulainen I. Lessons of slicing membranes: Interplay of packing, free area, and lateral diffusion in phospholipid/cholesterol bilayers. Biophys. J. 2004, 87, 1076–1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan J.; Mills T. T.; Tristram-Nagle S.; Nagle J. F. Cholesterol perturbs lipid bilayers nonuniversally. Phys. Rev. Lett. 2008, 100, 198103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan J.; Tristram-Nagle S.; Nagle J. F. Effect of cholesterol on structural and mechanical properties of membranes depends on lipid chain saturation. Phys. Rev. E 2009, 80, 021931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMullen T. P.; McElhaney R. N. Physical studies of cholesterol–phospholipid interactions. Curr. Opin. Colloid Interface Sci. 1996, 1, 83–90. [Google Scholar]
- Andoh Y.; Oono K.; Okazaki S.; Hatta I. A molecular dynamics study of the lateral free energy profile of a pair of cholesterol molecules as a function of their distance in phospholipid bilayers. J. Chem. Phys. 2012, 136, 155104. [DOI] [PubMed] [Google Scholar]
- Chong P. Evidence for regular distribution of sterols in liquid crystalline phosphatidylcholine bilayers. Proc. Natl. Acad. Sci. U.S.A. 1994, 91, 10069–10073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F.; Sugar I. P.; Chong P. Cholesterol and ergosterol superlattices in three-component liquid crystalline lipid bilayers as revealed by dehydroergosterol fluorescence. Biophys. J. 1997, 72, 2243–2254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J.; Feigenson G. W. A microscopic interaction model of maximum solubility of cholesterol in lipid bilayers. Biophys. J. 1999, 76, 2142–2157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J. Exploration of molecular interactions in cholesterol superlattices: Effect of multibody interactions. Biophys. J. 2002, 83, 1014–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali M. R.; Cheng K. H.; Huang J. Assess the nature of cholesterol–lipid interactions through the chemical potential of cholesterol in phosphatidylcholine bilayers. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 5372–5377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murtola T.; Falck E.; Karttunen M.; Vattulainen I. Coarse-grained model for phospholipid/cholesterol bilayer employing inverse Monte Carlo with thermodynamic constraints. J. Chem. Phys. 2007, 126, 075101. [DOI] [PubMed] [Google Scholar]
- Izvekov S.; Voth G. A. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 2005, 109, 2469–2473. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [DOI] [PubMed] [Google Scholar]
- Monticelli L.; Kandasamy S. K.; Periole X.; Larson R. G.; Tieleman D. P.; Marrink S.-J. The MARTINI coarse-grained force field: Extension to proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [DOI] [PubMed] [Google Scholar]
- Arcario M. J.; Ohkubo Y. Z.; Tajkhorshid E. Capturing spontaneous partitioning of peripheral proteins using a biphasic membrane mimetic model. J. Phys. Chem. B 2011, 115, 7029–7037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohkubo Y. Z.; Pogorelov T. V.; Arcario M. J.; Christensen G. A.; Tajkhorshid E. Accelerating membrane insertion of peripheral proteins with a novel membrane mimetic model. Biophys. J. 2012, 102, 2130–2139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Markwick P. R.; de Oliveira C. A. F.; McCammon J. A. Enhanced lipid diffusion and mixing in accelerated molecular dynamics. J. Chem. Theory Comput. 2011, 7, 3199–3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale C.; Bennett W. F. D.; Tieleman D. P.; Pomès R. Statistical convergence of equilibrium properties in simulations of molecular solutes embedded in lipid bilayers. J. Chem. Theory Comput. 2011, 7, 4175–4188. [DOI] [PubMed] [Google Scholar]
- Huang K.; García A. E. Free energy of translocating an arginine-rich cell-penetrating peptide across a lipid bilayer suggests pore formation. Biophys. J. 2013, 104, 412–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.