Abstract
Persistent neural firing is of fundamental importance to working memory and other brain functions because it allows information to be held “online” following an input and to be integrated over time. Many models of persistent activity rely on some kind of positive feedback internal to the neural circuit concerned; however, too much feedback causes runaway firing (instability), and too little results in loss of persistence (leak). This parameter sensitivity leads to the hypothesis that the brain uses an error signal (external feedback) to tune the stability of persistent firing by adjusting the amount of internal feedback. We test this hypothesis by manipulating external visual feedback, a putative sensory error signal, in a model system for persistent firing, the goldfish oculomotor neural integrator. Over tens of minutes to hours, electronically controlled visual feedback consistent with a leaky or unstable integrator can drive the integrator progressively more unstable or leaky, respectively. Eye fixation time constants can be reduced >100-fold to <1 s. Normal visual feedback gradually retunes the integrator back to stability. Changes in the phase of the sinusoidal vestibulo-ocular response are consistent with integrator detuning, as are changes in ocular drift following eye position shifts compensating for brief passive head movements during fixations. Corresponding changes in persistent firing of integrator neurons are presented in the accompanying article. The presence, strength, and reversibility of the plasticity demonstrate that, in this system, external visual feedback plays a vital role in gradually tuning the stability of the neural integrator.
The ability to turn transient inputs into persistent changes in activity is a basic requirement for neural systems to be able to combine information from multiple inputs arriving at different times: temporal integration in the broad sense. In awake animals, many areas of the central nervous system have this capability, most notably prefrontal cortex, where items being held in working memory appear to be represented by persistent neural firing during the delay period of temporal association tasks, in the absence of on-going sensory inputs. Single neurons can show persistent firing at multiple different levels, depending on the stimulus and response (1, 2). In many cases, the persistent firing is graded or analog, the rate varying smoothly and continuously with some stimulus or response parameter (3), with stable firing being possible at any rate over a given range. Despite long persistence times of tens of seconds or more, inputs can cause rapid transitions in firing rates within hundreds of milliseconds (4). We still do not know the biophysical mechanisms underlying this nontrivial combination of long persistence times, rapid transitions, and stable firing at multiple or continuously graded rates.
The simplest in vivo system that has so far been found to demonstrate robust graded persistent neural firing with both rapid transitions and long persistence times is the horizontal oculomotor neural integrator in the goldfish (5, 6), composed of only 30-60 neurons (“area I”) on either side of the caudal brainstem. Area I is vital for maintaining stable eye position (fixation) between saccades, and for an effective vestibulo-ocular response (VOR) (5). In this system and other neural integrators (7), changes in persistent firing are proportional to the input, so the firing rate represents the time integral of past inputs, temporal integration in the strict mathematical sense.
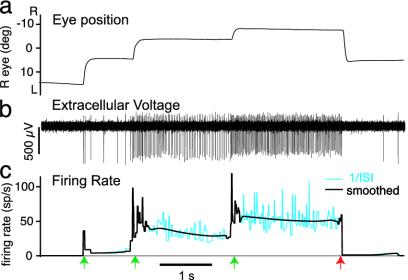
In the dark, in the absence of rapid, online visual feedback, restrained normal goldfish move both eyes horizontally from left to right and then back again in a series of steps or saccades lasting about 100 ms (Fig. 1a) (5). Saccades are separated by fixations, which can last from < 1 s to >10 s, during which the eyes are held almost stationary. This behavior depends on the activity of area I neurons (Fig. 1 b and c) (5), which are excited by transient inputs during a saccade toward the ipsilateral side, resulting in a brief burst of action potentials and increased tonic firing in the next fixation (6, 8). The neurons also receive transient inhibitory inputs during saccades toward the contralateral side, causing a transient dip in their discharge, followed by tonic firing at a lower rate during the next fixation. To a first approximation, the tonic firing rate is proportional to eye position (6) and represents the time integral of velocity-encoding saccadic and vestibular inputs. Online proprioceptive feedback plays a minor role, if any, in generating persistent firing in this system (9-11).
Fig. 1.
Normal eye movements and firing pattern of a generic area I cell. (a) Right horizontal eye position recorded in dark. Fixations were approximately stable between saccades. L, left; R, right. Positions L (R) of midrange were taken to be positive (negative). (b) Action potentials of right-side area I neuron recorded with extracellular electrode. (c) Cyan, instantaneous firing rate (1/interspike interval); black, smoothed progressively more away from saccades (see ref. 25, Methods); green arrows, “ON” direction saccades; red arrow, “OFF” direction saccade.
There are many models of persistent firing and neural integration. The basic problem all of the models have to contend with is the seemingly contradictory requirements of achieving rapid changes in firing in response to transient inputs while maintaining firing at a constant level for extremely long times between inputs. The classical way of achieving this is through recurrent synaptic feedback, tuned extremely precisely to just maintain overall self-excitation (12, 13), although some models make use of other forms of positive feedback within a single cell (14) and/or dendritic bistability (15-18). All of these models can be regarded as involving some form of net positive feedback and therefore require careful choice of parameters, especially if they are to carry out accurate temporal integration. The parameter sensitivity of positive feedback led to the hypothesis that, in real animals, external visual feedback could be used to tune up the oculomotor neural integrator (19).
VOR phase or gain adaptation has been reported to cause leak or instability of the integrator (20, 21). Recently it has been observed that the ability of goldfish to hold their eyes at a constant position between saccades degrades roughly 2-fold when they are left in the dark for an hour (22). After this, fixation performance in the light is improved after an hour in the light. However, it is not clear whether these changes are caused by nonspecific effects, such as altered alertness or optokinetic response gain (23, 24), or whether they reflect tuning of the integrator by visual feedback. Reports of visual deprivation leading to integrator detuning in mammals are summarized in ref. 22.
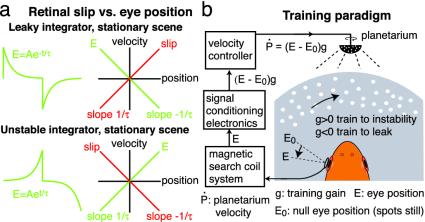
External visual feedback could be used to tune the oculomotor neural integrator as follows. A perfectly stable integrator should hold the eyes still. However, if the integrator's parameters are mistuned, for example, because of insufficient internal positive feedback, so that firing rates decay toward a “null” rate, then the eyes will follow suit, and the retinal image will slip in the opposite direction (Fig. 2a Upper). In the case of simple exponential decay, seen in many models when internal positive feedback is too weak, the visual surround will appear to move with a velocity proportional to eye position, with the proportionality constant equal to 1/(time constant). This pattern of retinal slip vs. eye position (“leaky slip”) could be used to generate a signal to increase positive feedback within the integrator, which would tune it back toward stability. Conversely, if the integrator is unstable, with eye position deviating exponentially away from a null position, as seen in many models when internal positive feedback is too strong, the visual surround will appear to move with a velocity proportional to minus eye position (Fig. 2a Lower). This pattern of slip (“unstable slip”) could generate a signal to decrease positive feedback within the integrator, which would again tune it back toward stability.
Fig. 2.
Simulating leaky and unstable retinal slip. (a) Eye drift and retinal slip of detuned integrator with a stationary visual surround. (Upper) Leaky. (Lower) Unstable. (Left) Integrator output (eye position) E vs. time (green). (Right) Position-velocity (PV) plots of eye drift velocity (green) and apparent motion of visual surround (retinal slip, red) against E. (b) Training paradigm. The fish is positioned horizontally. Horizontal eye position E measured with scleral coil, offset by E0, and amplified by g controls horizontal rotation velocity of planetarium above fish, projecting spots onto wall of tank. This provides visual feedback consistent with a leaky (g > 0) or unstable (g < 0) integrator, which gradually drives the integrator to the opposite condition.
Here we test the hypothesis that external visual feedback tunes the integrator. We reasoned that if visual feedback normally tunes integrator stability, it should be possible to detune it to instability by using an electronically controlled visual stimulus to impose a retinal slip vs. eye-position relationship consistent with the integrator being leaky. This effect could be achieved by rotating the visual surround horizontally with a velocity proportional to eye position (Fig. 2b, “training to instability”; see Supporting Methods, which is published on the PNAS web site). Conversely, rotating the surround with a velocity proportional to minus eye position, imposing unstable slip, should drive the integrator leaky (“training to leak”). Both manipulations simulate the normal pattern of visual feedback, but with an altered gain between retinal slip and eye position.
We report that the goldfish oculomotor neural integrator demonstrates remarkable plasticity when visual feedback is manipulated in this manner and is capable of being trained to instability or leak with an effective time constant reduced to ≈1 or 2 s, respectively, a two-orders-of-magnitude change from control. Conversely, visual feedback from a stationary surround can gradually retune the neural integrator back toward stability. Judging by independent tests of responses to vestibular inputs, fixation instability and leak represent genuine detuning of the neural integrator. This is a clear demonstration of a progressive tuning mechanism for the dynamics of a model biological system for persistent neural activity. Corresponding changes in area I neural responses are described in a companion paper (25).
Methods
Preparation. All experiments (n = 100 fish) were Institutional Animal Care and Use Committee approved and performed in compliance with the National Research Council Guide for the Care and Use of Laboratory Animals. Goldfish [Carassius auratus, 3-5 inches (8-13 cm) tip to peduncle, from a commercial supplier] were acclimated to 20-23°C in a 50-gallon aquarium with daily light exposure. Awake fish were mounted head-fixed horizontally under water in the experimental tank (6, 22) at a temperature of 20-22°C. Eye movements were measured with scleral search coils (26) and were digitized along with planetarium velocity and head position (Digidata and clampex, Axon Instruments, Foster City, CA).
Visual Training. A planetarium above the head was rotated by a velocity-controlled servo motor and projected a random pattern of white dots moving horizontally on a plastic white screen, 15-cm radius, surrounding the animal (Fig. 2b). During training, the voltage output of one eye coil was filtered (50-Hz low pass), offset, amplified, and used as the planetarium velocity drive signal. This amplification or training gain (g) is presented in units of (degree/s of planetarium velocity per degree of eye position) or s-1. The offset E0 (eye position at which spots stationary) was adjusted to achieve roughly symmetrical leftward and rightward movements. Generally the eye providing the command was alternated every 10 or 20 min. Effective training was achieved by starting with a low g, then gradually increasing it (range, ±0.5 to ±5 s-1). If too high a g was imposed when training to leak, the eyes would become trapped in a rapid sawtooth motion on one side, impairing training. A light shield surrounded the apparatus so that the planetarium provided the only source of light. Training was continued for up to 22 h, during which fixation performance was monitored every 20 min or longer by recording for 3-10 min in the dark.
Saccade Detection. When analyzing data, the beginning and end of a saccade were identified as the first and last time points at which the absolute value of acceleration exceeded a threshold (100-500 degrees/s2) after filtering with a 25-ms Gaussian.
Eye Position-Velocity (PV) Plots. Ocular drift during fixations was measured after excluding saccade-related transients in eye position (22). A period ta after every saccade was excluded, to avoid “postsaccadic slide” in eye position and firing rate (6), as was a period tb = 0.1 s before the next saccade; ta ranged from 0.5 to 1.5 s (constant for a given animal, but varied between animals to allow for different slide durations). A straight line was fit by regression through the first tf = 1 s segment of the remainder of the fixation (if at least tf long), to minimize effects of saturation and null-point shifts (see below) which were more pronounced at the ends of fixations. Eye position was the mean position of the fitted segment, and eye velocity was the slope of the regression line. Each fitted segment yielded a single (position, velocity) data point for the PV plot. Finally, standard leastsquares linear regression was performed to obtain the slope k of the best-fit line through all points in the PV plot.
Training Time Course Experiments. Twelve animals were trained to instability by using training gain 0.5 s-1 for 80 min, then 1 s-1 for 80 min. Every 20 min, fixations were assessed in the dark for 3 min, except immediately after training finished, when the assessment period was 10 min (5 × 2-min measurement periods). After this, the fish were split into two groups. One group was left in the light (spots still) and tested in the dark for 3 min every 20 min. The other group was left in the dark. After a total of 380 min, fish kept in the dark were switched to the light recovery protocol. A similar experiment was performed on 10 fish trained to leak, following the same protocol but with negative training gains.
VOR. For vestibular stimulation, the tank, planetarium, field coils, and light shield were mounted on a rate table with a computer-controlled servo motor. Eye position was measured relative to head position. The fish's head was at the center of rotation about a vertical axis, and the angular position of the table was measured with an axial potentiometer. Horizontal sinusoidal vestibular stimulation was carried out at 1/32, 1/16, or 1/8 Hz with 8-32 degrees/s peak head velocity. Peaks or troughs of eye position more than 4° into the opposite half of the oculomotor range to the head were selected for phase-shift analysis (see Supporting Methods). Apparent phase shifts were determined from times of peaks and troughs of the eye position relative to the nearest trough or peak of the head position, respectively.
All data presented are from animals in the dark, unless otherwise stated.
Results
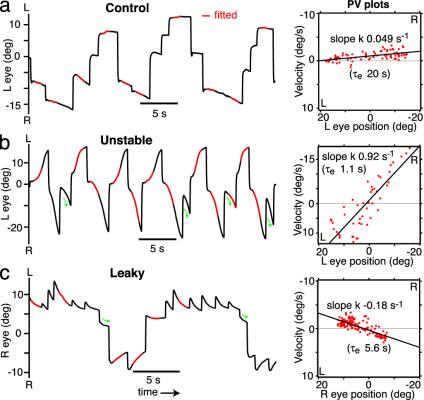
Artificially Imposed Visual Feedback Can Detune Stability of Fixations. In the dark, control animals had approximately stable fixations (Fig. 3a). Over the course of an hour or more of training under a planetarium rotating with velocity proportional to eye position, animals developed pronounced fixation instability when tested in the dark (n = 58 fish). The instability became more extreme the longer the animals were trained or the greater the training gain g. The eyes deviated centrifugally from midpositions at a rate that increased with eccentricity before saturating near the extremes of the oculomotor range (Fig. 3b). Likewise, over the course of an hour or more of training under a planetarium rotating with velocity proportional to minus eye position, animals developed striking fixation leak when tested in the dark (n = 45 fish), with eye position decaying centripetally toward midpositions (Fig. 3c). Again, the leak grew more severe the longer the training or the more negative the training gain. The same animal could be trained first to leak and then to instability, or vice versa (n = 23), indicating that the plasticity process is both bidirectional and reversible. Oculomotor behavior during training, which resembled a more extreme version of the trained behavior, is illustrated in Fig. 7, which is published as supporting information on the PNAS web site.
Fig. 3.
Artificially imposed visual feedback can detune fixations to extreme instability or leak. (Left) Eye movements in dark, control animal. Red, fitted 1-s segments of data; each contributes one point to the PV plot. (Right) Quantification by PV plot least-squares fit line, slope k, effective time constant τe = 1/|k| (5 min of data). (b) Same animal as in a, in dark, after training to instability for 6 h, with gain 2.5 s-1.(Right) PV plot of 3 min of data. (c) Another animal, in dark, after training to leak for 16.5 h, with gain -2 s-1. (Right) PV plot of 14 min of data. Drift depends primarily on eye position, as opposed to previous saccade direction (b and c). Green arrows highlight fixations following saccades toward but not crossing midposition; direction of drift is the same as in the previous fixation. When saccades cross midposition, the direction of drift reverses.
Fixations Can Be Detuned to Extreme Instability or Leak. Integrator performance was assessed from fixations in the dark, by means of PV plots (22), illustrated in Fig. 3 (see Methods), obtained by fitting straight lines to segments of fixations (Left, red). The slope k of the regression line through all of the PV data points, and τe, the effective time constant, defined as 1/|k|, were used as measures of fixation performance. This procedure could be applied across the range of fixation behaviors explored, unlike exponential fitting, which could not be used on control data because the time constant was generally much longer than the fixations.
Control animals had roughly stable fixations in the dark, in the absence of visual feedback, yielding PV plots with nearly horizontal best-fit lines (Fig. 3a Right), with median k -0.004 s-1 (range -0.068 to 0.032 s-1, n = 85 fish), equivalent to median τe = 250 s (range 15 s leaky to 31 s unstable). Following sufficient training to instability, generally 20 min or longer, PV plots developed positive slopes (Figs. 3b and 4a). Similarly, training control animals to leak for 20 min or more resulted in PV plots with negative slopes (Figs. 3c and 4b). In general, the longer an animal was trained (Fig. 4 a and b), and the more extreme the training gain g, the steeper the slope k of the PV plot would become (when the animal was tested in the dark). Over the entire data set, the most positive k value achieved was 0.92 s-1 (τe = 1.1 s). Three animals were trained to k > 0.8 s-1 or τe < 1.25 s, 13 to k > 0.4 s-1 or τe < 2.5 s, and 30 to k > 0.2 s-1 or τe < 5 s. The median k for animals trained to instability for at least an hour with g ≥ 0.5 was 0.23 s-1, equivalent to a τe of 4.3 s (n = 53). The most negative k value achieved was -0.43 s-1 (τe = 2.3 s). Two animals were trained to leak with k < -0.4 s-1 or τe < 2.5 s, and 13 to k < -0.2 s-1 or τe < 5 s. The median k of animals trained to leak for at least an hour with g ≤ -0.5 was -0.13 s-1 (n = 39), corresponding to τe = 7.7 s. These experiments clearly demonstrate that visual feedback can detune fixation stability over a huge dynamic range, with neural PV slopes k changing over two orders of magnitude in either direction from control values.
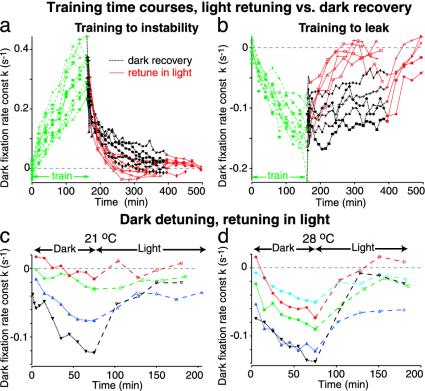
Fig. 4.
Normal visual feedback retunes fixation stability. (a and b) Time course of changes in the slopes k of dark fixation PV plots during and after training. Each line and symbol indicates a specific fish. Dashed green lines, training. Retuning with a stationary surround (solid red lines) is faster than recovery in the dark (dotted black lines). During training and light retuning, k tested during brief periods in dark. (a) Instability training, gain g 0.5 for 80 min, then 1 s-1 for 80 min. (b) Leak training, g -0.5 then -1 s-1.(c) Fixations detune toward leak in the dark and are retuned by a stationary surround. Time course of k for four animals left in the dark at 21°C for 80 min, followed by a lights-on period with a stationary visual surround (k tested during brief periods in dark). Each color and symbol indicates a specific animal. (d) Time course of dark fixation k for same animals (plus one) at 28°C.
Time constants τe extracted from PV plots are a conservative measure of the degree of plasticity. In the case of unstable fixations, the rate of drift frequently began to saturate or even decrease as the eyes approached the edges of the oculomotor range (Fig. 3b). This saturation tended to reduce the slope of the PV plot and increased τe. In the case of leaky fixations, the null point to which the eye position decayed generally shifted in the direction of the preceding saccade (Fig. 3c) (27, 28). This shift had the effect of increasing τe above the time constant obtained by exponential fitting, which was below 1 s in many animals trained to leak (n = 10).
Normal Visual Feedback Retunes the Neural Integrator. We tested whether visual feedback from a stationary visual surround could retune unstable and leaky fixations back to stability. Twelve animals were trained to instability and 10 to leak by following standardized protocols. Each group was split, with half the fish being left in the dark after training, the other half with a stationary surround, except for 3 min in the dark every 20 min to assess integrator performance. The stationary visual surround speeded recovery to stability in both cases (Fig. 4 a and b; P < 0.05, Mann-Whitney U test), indicating that normal visual feedback can retune fixation performance. The difference was less pronounced for animals trained to instability, reflecting the tendency for fixations to become progressively more leaky during long periods in the dark (Fig. 4 c and d) (22).
After instability training, the median half-life of the PV slope k was 43 min in the dark (n = 14 fish; see Supporting Methods), decreasing to 17 min with a stationary surround (n = 12, P < 0.001, Kolmogorov-Smirnov test). After leak training, the median half-life of k was 180 min in the dark (n = 5), which was reduced to 30 min by a stationary surround (n = 14, P < 0.001).
To confirm that visual feedback tunes up fixation stability under normal conditions, we examined dark fixations in animals that had been left in the dark for 80 min and were then placed back in a stationary visual surround, testing for 3 min in the dark every 20 min. In all cases, fixations became gradually leakier in the dark (Fig. 4 c and d), and the stationary surround progressively improved fixation performance, assessed in the dark. These experiments were repeated at two different temperatures, 21°C and 28°C. Detuning in the dark was more pronounced at the higher temperature, but the stationary surround retuned fixations to comparable stability at both temperatures.
Fixation Detuning Is Due to Integrator Detuning. During training, the planetarium velocity was proportional to eye position and, because of the optokinetic response, the eyes generally followed the stimulus. This means that during training to instability the eyes followed unstable trajectories, and during training to leak they followed leaky trajectories (see Fig. 7). Therefore, a key question is whether the detuning and retuning of fixations in the dark reflect changes in the oculomotor neural integrator itself or in some other process, such as training of an independent general-purpose trajectory mimicking or play-back circuit, which learns to anticipate the imposed pattern of drift of the visual surround or to imitate the pattern of eye movements during training. We tested these competing hypotheses by measuring responses to vestibular inputs that were never experienced during training and by attempting to train eye movements to mimic other kinds of surround motion.
In addition to saccadic burst inputs, the oculomotor neural integrator receives vestibular inputs encoding both head velocity and acceleration (29, 30). These are integrated with respect to time into position and velocity signals (5, 31) that are fed forward into the motoneurons to maintain a constant direction of gaze while the head moves. When control goldfish are sinusoidally rotated about a vertical axis in the dark at frequencies between 1/8 and 1/32 Hz, the VOR counterrotates the eyes almost perfectly with a gain close to unity (32). The turning points of the slow phases of the eye position (relative to the head) are in phase with the turning points of minus angular head position (dashed lines, Fig. 5a). A simple model of the integrator is governed by the first-order differential equation
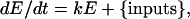 |
[1] |
where E is eye position. The solution has two components: sinusoidal and exponential. The first is the response to continuous sinusoidal inputs; the second is the response to brief saccadic and other transient inputs (see Supporting Mathematical Appendix, which is published as supporting information on the PNAS web site) (33). If the integrator is unstable, the sinusoidal component of E will have a phase lag with respect to head position, whereas with a leaky integrator the sinusoidal component will lead head position. The phase shift φ of the sinusoidal component, in degrees (derived in Supporting Mathematical Appendix) is
 |
[2] |
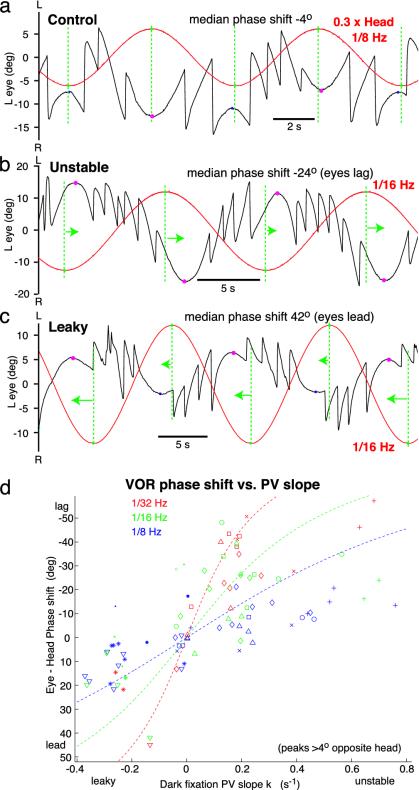
where f is the frequency of rotation. This equation is most accurate at predicting the phase shift of the overall response when the exponential components are small, which occurs when the peaks of eye position are well into the opposite half of the oculomotor range to the head (see Supporting Mathematical Appendix). When such cases were analyzed, animals with pronounced fixation instability showed clear phase lags, as predicted (Fig. 5b, arrows). Animals with very leaky fixations showed clear phase leads, also as predicted (Fig. 5c, arrows). In Fig. 5d, phase shifts are plotted against k for nine animals at various stages of training and retuning, at three test frequencies. The shifts are generally more pronounced at lower frequencies, as expected from Eq. 2. Phase lags grow with increasing instability, and phase leads grow with increasing leak, consistent with integrator detuning.
Fig. 5.
VOR phase shifts are consistent with integrator detuning. (a-c) Black, left eye position; red, head position × 0.3; green vertical lines, extremes of head position; dots mark turning points of eye position slow phases; magenta, selected peaks, >4° into half-range opposite head; arrows indicate phase shift of eyes relative to head. All data were collected in dark. (a) Control, negligible phase shifts. (b) Unstable animal, dark fixation PV slope k = 0.7 s-1. Selected peaks (troughs) lag nearest head trough (peak). (c) Leaky animal, k = -0.13 s-1. Selected peaks (troughs) lead nearest head trough (peak). (d) Scatter plot of median apparent VOR phase shifts (of selected peaks and troughs) vs. k for 9 animals (different symbols). Dashed lines, phase shifts predicted by Eq. 2, for reference.
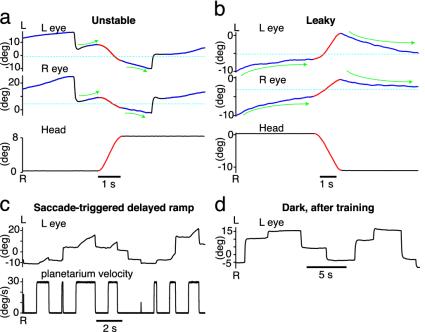
Brief vestibular stimuli were also used to verify that detuning of dark fixations reflected detuning of the neural integrator. The eyes were counterrotated across the null position by means of a transient head movement part-way through a fixation (n = 4 animals). In animals with unstable fixations, forcing the eyes across the midposition by using vestibular input caused them to carry on diverging from this position, but in the opposite direction (Fig. 6a). Likewise, in animals with leaky fixations, forcing the eyes across the midposition caused them to carry on converging exponentially toward this position, but from the opposite direction (Fig. 6b). Across fish, a median of 92% of midfixation null crossings led to the expected direction change (range 89-100%; unstable n = 111, leaky n = 184 crossings). In all cases, PV plots of pre- and postmovement data were qualitatively consistent, having slopes of the same sign (data not shown). Because there were no head movements during training, a general-purpose trajectory mimicker would have no means of learning this midfixation direction switch in response to vestibular stimulation.
Fig. 6.
Training is due to integrator detuning, not general-purpose trajectory prediction. (a and b) Drift reversed after eyes counterrotated by VOR across null position (dashed cyan line) in response to transient head rotation (red). (a) Unstable animal. Eyes drifted away from null position both before and after head movement. (b) Leaky animal. Eyes leaked toward null position both before and after head movement. (c and d) General trajectory prediction was limited. (c) Response during training with saccade-triggered delayed ramps in planetarium position (velocity steps). (d) Response in dark after 2 h of training. Animal failed to mimic target trajectory.
If the brain contained a general-purpose visual surround trajectory-mimicking circuit responsible for the all results above, it ought to be able to learn simple patterns of movement, such as saccade-triggered delayed ramps. Saccades were detected online during the experiment, and after a delay of 1 s the planetarium was rotated with a constant velocity of between 5 and 30 degrees/s until the next saccade (see Supporting Methods). During training, the eyes moved qualitatively in the same manner as the planetarium position (Fig. 6c). In the dark, however, even after many hours of training, there was no obvious “playback” or imitation of this pattern of movement (Fig. 6xd, n = 3 fish). The general-purpose trajectory-mimicking capabilities of goldfish are therefore limited and are unlikely to contribute much to fixation instability and leak.
Discussion
We have shown that, over tens of minutes to hours, the goldfish oculomotor system makes use of visual feedback to tune the stability of its neural integrator. The mechanism and locus of plasticity are yet to be established, although area I, area II (the velocity storage neural integrator), and cerebellum are prime candidates (5, 34). We have not established whether a direct error signal is used or whether the system adjusts itself indirectly by some kind of associative or Hebbian mechanism operating during the training-imposed trajectories, gated by light or the optokinetic response (OKR). The system appears to tune its own stability by using the retinal slip vs. eye position relationship that it itself generates; steeper slopes generally lead to faster training rates (Fig. 4, retuning data). The OKR gain and eye PV relationship may also be involved; animals whose eyes follow the training stimulus better train better (data not shown). The system gradually changes itself so as to progressively reduce the slip vs. position slope (gain) toward zero. A simple alteration to normal visual feedback, such as artificially changing this slip/position gain, can drive the neural integrator to extremes of instability or leak, depending on the sign and magnitude of the imposed gain. This plasticity is bidirectional and is reversed by normal visual feedback from a stationary surround, or by changing the sign of the gain, i.e., training to the opposite condition. Manipulating the slip/position relationship allows us, seemingly, to take control of a slow “external” feedback loop of this self-tuning system and to drive the integrator to either extreme of its dynamic range of tuning.
Our results are a clear demonstration of the tuning of the internal dynamics, or the time constant, of a neural integrator by simple changes to the normal pattern of external sensory feedback. The majority of the oculomotor plasticity literature (34) concerns VOR gain changes, which reflect input/output plasticity, rather than internal changes in integrator stability. VOR phase or gain adaptation can cause fixation drift (20, 21), but in those studies the reported changes were much smaller than those found here, and no clear evidence was presented for exponential instability or leak, or for retuning of fixation stability by normal visual feedback.
Another kind of oculomotor plasticity, postsaccadic slide training (35-38), can be induced by transient postsaccadic rotations of the visual surround, which in some respects resembles the training paradigm used here. However, several lines of evidence rule out postsaccadic slide plasticity as an explanation for our data. First, unlike trained postsaccadic slide, the direction and magnitude of drift after instability or leak training depended primarily on eye position, not the direction of the preceding saccade. When a saccade returned the eyes toward but not across the midposition, the direction of drift was unchanged (Fig. 3, green arrows), but when the eyes crossed the midposition, the direction of drift reversed. Second, drift occurred throughout fixations lasting many seconds, whereas postsaccadic slide is generally limited to a few hundred milliseconds (6). Third, postsaccadic slide plasticity would not lead to the observed phase shifts in sinusoidal VOR responses, or the reversal of drift direction after counterrotation of the eyes across the null position. Unlike the plasticity demonstrated here, postsaccadic slide plasticity does not appear to be caused by internal changes in the integrator itself.
In conclusion, we have demonstrated that the goldfish oculomotor neural integrator is strongly tuned by its visual environment. The integrator time constant can be reduced >100-fold to <1 s in either direction (instability or leak), consistent with highly parameter-sensitive models, such as those depending on some form of positive feedback internal to the integrator.
Supplementary Material
Acknowledgments
We thank Georgi Gamkrelidze, Owen Debowy, Jim Beck, Tom Adelman, Carlos Brody, John Hopfield, and Samuel Wang for comments and help. This work was supported by Lucent Technologies, Princeton University, the National Institutes of Health, the National Science Foundation, and the Wellcome Trust.
Abbreviations: PV, position-velocity; VOR, vestibulo-ocular response.
References
- 1.Fuster, J. M. (2001) Neuron 30, 319-333. [DOI] [PubMed] [Google Scholar]
- 2.Goldman-Rakic, P. S. (1995) Neuron 14, 477-485. [DOI] [PubMed] [Google Scholar]
- 3.Romo, R., Brody, C. D., Hernandez, A. & Lemus, L. (1999) Nature 399, 470-473. [DOI] [PubMed] [Google Scholar]
- 4.Funahashi, S., Bruce, C. J. & Goldman-Rakic, P. S. (1989) J. Neurophysiol. 61, 331-349. [DOI] [PubMed] [Google Scholar]
- 5.Pastor, A. M., de la Cruz, R. R. & Baker, R. (1994) Proc. Natl. Acad. Sci. USA 91, 807-811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Aksay, E., Baker, R., Seung, H. S. & Tank, D. W. (2000) J. Neurophysiol. 84, 1035-1049. [DOI] [PubMed] [Google Scholar]
- 7.Robinson, D. A. (1989) Annu. Rev. Neurosci. 12, 33-45. [DOI] [PubMed] [Google Scholar]
- 8.Pastor, A. M., de la Cruz, R. R. & Baker, R. (1994) J. Neurophysiol. 72, 1383-1393. [DOI] [PubMed] [Google Scholar]
- 9.Gestrin, P. & Sterling, P. (1977) J. Neurophysiol. 40, 573-588. [DOI] [PubMed] [Google Scholar]
- 10.Aksay, E., Gamkrelidze, G., Seung, H. S., Baker, R. & Tank, D. W. (2001) Nat. Neurosci. 4, 184-193. [DOI] [PubMed] [Google Scholar]
- 11.Keller, E. L. & Robinson, D. A. (1971) J. Neurophysiol. 34, 908-919. [DOI] [PubMed] [Google Scholar]
- 12.Kamath, B. Y. & Keller, E. L. (1976) Math. Biosci. 30, 341-352. [Google Scholar]
- 13.Cannon, S. C., Robinson, D. A. & Shamma, S. (1983) Biol. Cybern. 49, 127-136. [DOI] [PubMed] [Google Scholar]
- 14.Durstewitz, D. (2003) J. Neurosci. 23, 5342-5353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goldman, M. S., Levine, J. H., Major, G., Tank, D. W. & Seung, H. S. (2003) Cereb. Cortex 13, 1185-1195. [DOI] [PubMed] [Google Scholar]
- 16.Koulakov, A. A., Raghavachari, S., Kepecs, A. & Lisman, J. E. (2002) Nat. Neurosci. 5, 775-782. [DOI] [PubMed] [Google Scholar]
- 17.Lisman, J. E., Fellous, J.-M. & Wang, X.-J. (1998) Nat. Neurosci. 1, 273-275. [DOI] [PubMed] [Google Scholar]
- 18.Loewenstein, Y. & Sompolinsky, H. (2003) Nat. Neurosci. 6, 961-967. [DOI] [PubMed] [Google Scholar]
- 19.Arnold, D. B. & Robinson, D. A. (1991) Biol. Cybern. 64, 447-454. [DOI] [PubMed] [Google Scholar]
- 20.Tiliket, C., Shelhamer, M., Roberts, D. & Zee, D. S. (1994) Exp. Brain Res. 100, 316-327. [DOI] [PubMed] [Google Scholar]
- 21.Kramer, P. D., Shelhamer, M. & Zee, D. S. (1995) Exp. Brain Res. 106, 318-326. [DOI] [PubMed] [Google Scholar]
- 22.Mensh, B. D., Aksay, E., Lee, D. D., Seung, H. S. & Tank, D. W. (2003) Vision Res. 44, 711-726. [DOI] [PubMed] [Google Scholar]
- 23.Robinson, D. A. (1981) in The Nervous System, Handbook of Physiology, eds. Brookhart, J. M. & Mountcastle, V. B. (Am. Physiol. Soc., Bethesda), Section 1, Vol. 2, pp. 1275-1320. [Google Scholar]
- 24.Marsh, E. & Baker, R. (1997) J. Neurophysiol. 77, 1099-1118. [DOI] [PubMed] [Google Scholar]
- 25.Major, G., Baker, R., Aksay, E., Seung, H. S. & Tank, D. W. (2004) Proc. Natl. Acad. Sci. USA 101, 7745-7750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Robinson, D. A. (1963) IEEE Trans. Biomed. Eng. 10, 137-145. [DOI] [PubMed] [Google Scholar]
- 27.Crawford, J. D. & Vilis, T. (1993) Exp. Brain Res. 96, 443-456. [DOI] [PubMed] [Google Scholar]
- 28.Nakamagoe, K., Iwamoto, Y. & Yoshida, K. (2000) Science 288, 857-859. [DOI] [PubMed] [Google Scholar]
- 29.Hartmann, R. & Klinke, R. (1980) Pflügers Arch. 388, 111-121. [DOI] [PubMed] [Google Scholar]
- 30.Peterson, E. H. (1998) News Physiol. Sci. 13, 194-201. [DOI] [PubMed] [Google Scholar]
- 31.Pastor, A. M., Torres, B., Delgado-Garcia, J. M. & Baker, R. (1991) J. Neurophysiol. 66, 2125-2140. [DOI] [PubMed] [Google Scholar]
- 32.Pastor, A. M., de la Cruz, R. R. & Baker, R. (1992) J. Neurophysiol. 68, 2003-2015. [DOI] [PubMed] [Google Scholar]
- 33.Goldman, M. S., Kaneko, C. R., Major, G., Aksay, E., Tank, D. W. & Seung, H. S. (2002) J. Neurophysiol. 88, 659-665. [DOI] [PubMed] [Google Scholar]
- 34.du Lac, S., Raymond, J. L., Sejnowski, T. J. & Lisberger, S. G. (1995) Annu. Rev. Neurosci. 18, 409-441. [DOI] [PubMed] [Google Scholar]
- 35.Optican, L. M. & Miles, F. A. (1985) J. Neurophysiol. 54, 940-958. [DOI] [PubMed] [Google Scholar]
- 36.Miles, F. A. & Kawano, K. (1986) J. Neurophysiol. 56, 1381-1396. [DOI] [PubMed] [Google Scholar]
- 37.Optican, L. M., Zee, D. S. & Miles, F. A. (1986) Exp. Brain Res. 64, 596-598. [DOI] [PubMed] [Google Scholar]
- 38.Kapoula, Z., Optican, L. M. & Robinson, D. A. (1989) J. Neurophysiol. 61, 879-891. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.