Abstract
In a companion paper, we reported that the goldfish oculomotor neural integrator could be trained to instability or leak by rotating the visual surround with a velocity proportional to +/- horizontal eye position, respectively. Here we analyze changes in the firing rate behavior of neurons in area I in the caudal brainstem, a central component of the oculomotor neural integrator. Persistent firing could be detuned to instability and leak, respectively, along with fixation behavior. Prolonged training could reduce the time constant of persistent firing of some cells by more than an order of magnitude, to <1 s. Normal visual feedback gradually retuned persistent firing of integrator neurons toward stability, along with fixation behavior. In animals with unstable fixations, approximately half of the eye position-related cells had upward or unstable firing rate drift. In animals with leaky fixations, two-thirds of the eye position-related cells showed leaky firing drift. The remaining eye position-related cells, generally those with lower eye position thresholds, showed a more complex pattern of history-dependent/predictive firing rate drift in relation to eye drift. These complex drift cells often showed a drop in maximum persistent firing rate after training to leak. Despite this diversity, firing drift and the degree of instability or leak in firing rates were broadly correlated with fixation performance. The presence, strength, and reversibility of this plasticity demonstrate that, in this system, visual feedback plays a vital role in gradually tuning the time course of persistent neural firing.
We demonstrated in a companion paper (1) how visual feedback with an altered retinal slip vs. eye position gain can be used to detune the goldfish oculomotor neural integrator to extreme instability or leak and how normal visual feedback can retune the integrator to stability. Here we test the hypothesis that visual feedback tunes graded (analog) persistent firing of oculomotor neural integrator neurons themselves.
In the vertebrate oculomotor system, the ability to maintain stable eye position depends on the activity of a central “neural integrator” responsible for transforming velocity-encoding command or sensory signals to position-encoding outputs that feed into extraocular motoneurons. Experiments in primate (2-6) and cat (7-9) indicate that the velocity-to-position neural integrator (VPNI) for horizontal eye movements is localized in part to two bilateral brainstem nuclei, the nucleus prepositus hypoglossi (NPH) and the medial vestibular nucleus (MVN), reviewed in ref. 10. Experiments in goldfish (11, 12) suggest that the horizontal VPNI is localized in part to a bilateral region of the reticulum analogous to the mammalian NPH, termed area I.
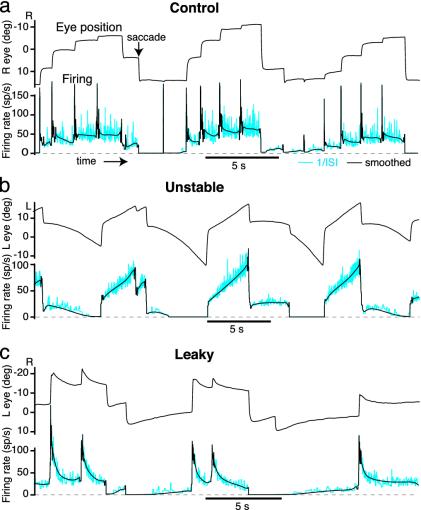
As shown in Fig. 1a, the spontaneous oculomotor behavior of a control head-fixed goldfish consists of a cyclic scanning pattern of sequential saccades and fixations. With each saccade in the temporal direction of the ipsilateral eye, neurons in area I typically show a brief burst, followed by a sustained discharge during the subsequent fixation. Saccades in the nasal direction are followed by a reduced tonic firing level during the subsequent fixation. Above a threshold eye position that can differ for each neuron, firing rate is approximately described by a linear relationship between firing rate and eye position (ref. 12, but see ref. 13). Given the basic correspondence between sustained tonic discharge and fixation, we reasoned that, after training to leak or instability, there would be corresponding changes in the dynamics of neural firing rate. We therefore used extracellular recording methods to monitor the effect of training on the firing properties of area I neurons.
Fig. 1.
Area I persistent firing can be detuned by manipulating retinal slip. (a) Normal pattern of horizontal eye movements and firing of area I neurons in the goldfish oculomotor neural integrator. Between saccades, eye position and firing rate are approximately stable. Instantaneous firing rate [inverse interspike interval (1/ISI)] is shown in cyan; smoothed firing rate is shown in black. (b) Unstable fixations and area I neuron firing in the dark, after training to instability for 22 h with training gain g (ref. 1) between 1 and 2.6 s-1. (c) Leaky fixations and area I neuron firing, in the dark, after training to leak for 22 h with training gain g between -1.9 and -3.3 s-1. R, right; L, left; sp/s, spikes per s; deg, degrees.
In the companion paper (1), we used plots of eye velocity as a function of eye position to quantify oculomotor performance. These position-velocity (PV) plots were first used by Becker and Klein (14) in the study of human oculomotor behavior. A linear PV plot corresponds to an exponential dependence of drift on position with a time constant determined by the inverse slope; positive slopes correspond to an unstable integrator, whereas negative slopes correspond to a leaky integrator. Here, we have extended the PV plot analysis to neural firing rates by plotting neural firing rate drift vs. firing rate. We report that the pronounced behavioral plasticity described in the companion paper (1) is associated with similar changes in the firing patterns of integrator neurons.
Methods
For detailed methods, see ref. 1. All data presented were recorded in the dark.
Electrophysiology. Surgery, recording of extracellular action potentials from single units, spike detection, and area I mapping were as previously described (12, 15). Eye movements, planetarium velocity training signals, head position, and extracellular voltage recordings were simultaneously digitized (Digidata and Clampex, Axon Instruments, Foster City, CA). The extracellular voltage was recorded through a 2-5 MΩ beveled sharp glass electrode containing 2 M NaCl and fast green FCF (Sigma), by using a Neurodata IR-283 amplifier (Cygnus Technology, Delaware Water Gap, PA) with capacitance compensation. The extracellular voltage was amplified 1,000-fold, filtered (high-pass 300 Hz, low-pass 10 kHz, 8-pole Bessel), ac-coupled, and digitized at a 35- to 60-μs sample interval. A systematic grid search for eye position-related neurons 400-1,000 μm below the floor of the fourth ventricle was carried out, starting 400 μm lateral to the midline rhombomere marking (often a blood vessel) midway between the obex and facial lobe (12). Large action potentials were sought by making electrode penetrations at 25-μm intervals in the mediolateral direction, and then eye position-related neurons were searched for by making penetrations at 200-μm intervals, then at smaller intervals, first caudally, then rostrally. The sizes of action potentials and cell types at each location were noted to guide the search. The electrode position was optimized, in most cases, to give spikes from the cell of interest of peak negative amplitude 400-900 μV and spikes from neighboring cells of <300 μV, compared with a background noise of ≈100-200 μV peak to peak. In untrained animals, area I was defined functionally as the region containing predominantly eye position-related neurons with large biphasic (putative somatic) action potentials, crisp transitions in firing rate associated consistently with saccades, and persistent firing during fixations at a rate that depended on eye position (12). The firing patterns of these cells during and after training were noted and used to guide the search for eye position-related neurons in pretrained animals. In the latter experiments, cells with clear eye position sensitivity were sought in the usual location of area I. Recordings of individual position-related neurons frequently lasted many hours.
Firing Rate Analysis. This analysis was performed on all well isolated neurons recorded for at least 2 min, with firing in clear relation to eye position. Of 84 such area I cells (in 28 fish), 7 cells were followed during retuning with a stationary surround, 9 cells were followed during training to the opposite condition, 11 cells were followed as the animal was trained from control to unstable, 11 cells were followed from control to leaky, and 53 cells were followed for at least 20 min across different states of tuning. Custom matlab software (The MathWorks, Natick, MA) was used to detect action potentials off-line with a 2D windowing algorithm (peak negative voltage and average voltage over specified sample points relative to peak). Instantaneous interspike interval as a function of time was calculated from the spike times at the eye position digitization sample interval (3.5-6 ms). This waveform was inverted to give the instantaneous firing rate as a function of time (Fig. 1), which was then smoothed progressively more strongly away from saccades (Supporting Methods, which is published as supporting information on the PNAS web site) (13).
Neural PV Plots. In a temporal integrator described by first-order kinetics (equation 1 in ref. 1), the response to a transient stimulus is an exponential waveform (in figure 2a of ref. 1). This type of response has the fundamental property that poststimulus drift is proportional to the output. Integrator stability can therefore be assessed from the slope of PV plots (1, 14, 15). The output of a neural integrator can also be measured directly from the firing of its constituent neurons. By analogy with eye PV plots, firing rate drift vs. firing rate, or neural PV, plots were used to quantify the stability of neural responses. To maximize the number of points in neural PV plots and corresponding eye PV plots (Figs. 2 and 3), as many consecutive fit intervals as possible of duration tf = 0.3 s were used in each fixation, excluding a period ta = 0.3 s after and tb = 0.1 s before saccades. To reduce sensitivity to outliers, minimum absolute deviation (MAD) lines (16) were fitted through all points on neural PV plots, excluding those with very low spike rates (<0.25 spikes per s) and fixations with no spikes. The average firing rate drift, <fdrift>, was defined as the mean firing rate drift of all nonexcluded points in units of spikes per s2. MAD lines were fitted through all points on corresponding eye PV plots. Linear regression and t tests were used to assess the statistical significance of changes in neural PV slope (17). Smoothing the firing rates less caused no systematic changes in the PV slopes obtained but did increase the scatter in the data.
Fig. 2.
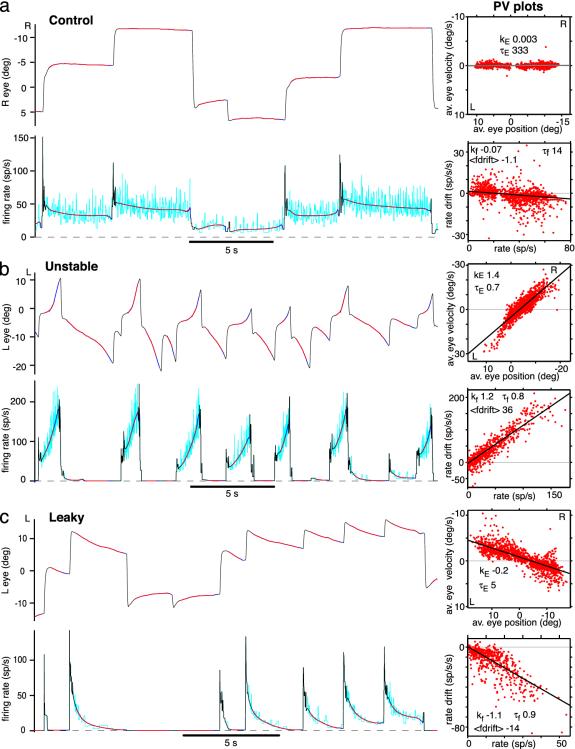
Persistent firing can be detuned to time constants of <1 s. (Left) Ipsilateral eye position and area I cell firing rates. Instantaneous firing rate (inverse interspike interval) is shown in cyan; smoothed firing rate is shown in black and dark blue. (Right) Fitted 300-ms line segments generating PV plots are shown in red (10 min of data). Best-fit line slopes kE and kf and effective time constants τE and τf are shown for eye and neural PV plots, respectively. Mean firing rate drift <fdrift> is shown in spikes per s2 (sp/s/s). (a) Control. (b) Animal with unstable fixations, cell with bidirectional firing rate instability. (c) Animal with leaky fixations, cell with downward firing rate leak and apparent null point shifts. R, right; L, left; sp/s, spikes per s; deg, degrees; av., average.
Fig. 3.
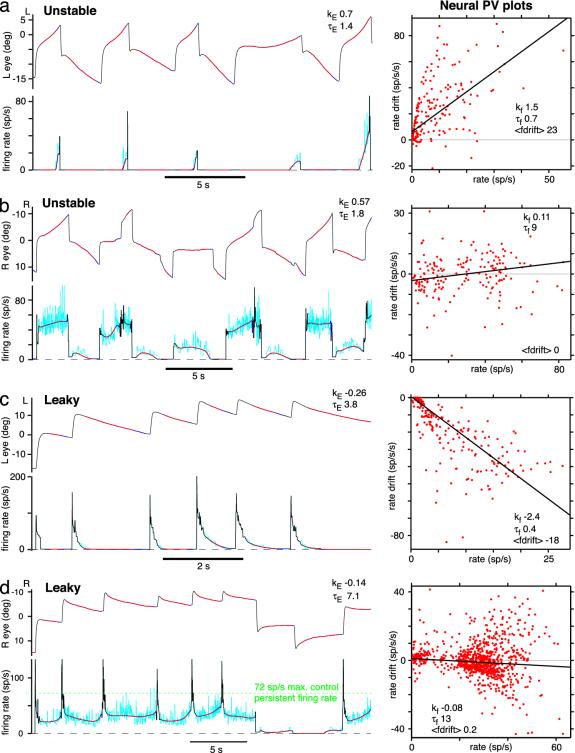
There is unexpected diversity of firing rate drift after training. (Left) Ipsilateral eye position (upper trace) and area I cell firing rate (lower trace). (Right) Neural PV plots (10 min of data). (a) Unstable fixations, high-threshold cell with rapid increase in firing toward left extreme of range. (b) Unstable fixations, low-threshold cell with complex pattern of history-dependent/predictive mildly unstable firing rate drift. (c) Leaky fixations, high-threshold cell with rapid downward leak in firing rate. (d) Leaky fixations, low-threshold cell with nearly stable firing but maximum persistent firing rate reduced from control (green dashed line, 72 spikes per s). L, left; R, right; deg, degrees; sp/s, spikes per s.
Results
Persistent Firing Can Be Detuned to Extreme Instability and Leak. Goldfish eye fixations were trained to instability or leak as described in ref. 1. Horizontal eye position was offset and amplified and used to drive a planetarium positioned above the fish. The planetarium projected spots on the wall of the tank holding the fish. The firing pattern of a typical area I neuron in the dark under control conditions is shown in Fig. 1a. After training to instability (with the planetarium rotating with velocity proportional to eye position), many area I neurons developed an unstable pattern of firing rate drift (Fig. 1b) resembling the instability of the eye fixations. At high rates firing rate would increase, at intermediate rates it was stable, and at low rates it would decrease. Similarly, after training to leak (with planetarium velocity proportional to minus eye position), many area I neurons developed a leaky pattern of firing rate drift, decaying downward from high rates, being stable at intermediate rates, and, in many cases, decaying upward from low rates (Fig. 1c), resembling the leaky eye fixations.
By analogy with eye PV plots (15), firing rate drift vs. firing rate (neural PV) plots were used to quantify the stability of neural responses, as illustrated in Fig. 2 (see Methods). The slope kE of the eye PV best-fit line was used to characterize fixation performance. Persistent firing stability was characterized by the slope kf of the neural PV best-fit line and also by the average firing rate drift, <fdrift>. The latter measure was included because different cells are recruited at different eye position thresholds (12), and so steady up- or downward drift in the rate of a particular cell can contribute to instability or leak of the total population response. Effective time constants were defined as τE = 1/|kE| and τf = 1/|kf|.
A typical area I neuron stable control firing pattern is shown in Fig. 2a. The neural PV plot is nearly flat, with τf = 14.3 s. The firing pattern of an area I neuron in a fish trained to extreme instability is shown in Fig. 2b. Both the eye and the neural PV plots exhibit pronounced instability, with steep positive slopes, giving effective time constants of <1 s for both the eyes and the persistent firing. An area I neuron from a fish trained to extreme leak is shown in Fig. 2c, also with an effective time constant of persistent firing of <1 s. In all, two and five cells were trained to instability with τf < 1 s and τf < 2 s, respectively. Six and nine cells were trained to leak with τf < 1 s and τf < 2 s, respectively.
Neural Firing Rate Drift Patterns Are Diverse. Different area I cells normally have different eye position thresholds, spanning a large fraction of the oculomotor range (12). Neurons from control animals had a median neural PV slope k of -0.11 s-1 f (range, -0.26 to 0.048 s-1; n = 31 cells), corresponding to a leaky median effective time constant of persistent firing τf = 9.1 s (range, 3.9 s leaky to 20.8 s unstable). Higher-threshold cells tended to be leakier. Forty neurons were recorded from area I in fish trained to instability. Some cells had high thresholds, switching on partially through fixations and increasing their firing rates very rapidly as the eyes moved in the ON (ipsilateral) direction (Fig. 3a; n = 7 cells, 17.5%). Neurons with medium thresholds exhibited instability (n = 11 cells, 27.5%), which in some cases was bidirectional, with firing increasing at high rates and decreasing at low rates (Figs. 1b and 2b; n = 3 cells, 8%). Other neurons, with lower thresholds, tended to exhibit more complex firing drift patterns and less overall instability than the eyes (Fig. 3b; n = 22 cells, 55%, of which 9 were followed from control, confirming that they started off as normal area I neurons).
Thirty-two neurons were recorded in area I in fish trained to leak. High-threshold cells exhibited downward leak (Fig. 3c; n = 10 cells, 31%). Lower-threshold cells often showed bidirectional leak, downward at high rates and upward at low rates (Fig. 1c; n = 12 cells, 38%). Many cells in these two groups seemed to exhibit null point shifts, just like the eyes. In other words, the asymptotic rate at which the firing decayed appeared, on average, to shift in the direction of the intervening saccade (n = 13 cells, 41%). A rate that was very leaky after an ON direction saccade would often become approximately stable after one or more additional ON direction saccades (compare rates of 10-20 spikes per s across fixations in Fig. 2c). The remaining cells, which mostly had even lower thresholds, exhibited more complex patterns of drift and were less leaky than the eyes (n = 10 cells, 31%). In half of these, the main change from the control state was a drop in maximum persistent firing rate (Fig. 3d), which may have contributed to leak at extreme eye positions through reduced support to motoneuron firing.
The majority of complex drift patterns were hysteretic/predictive (Fig. 3b and d) often showing more decay preceding a switch to the OFF direction (contralateral) saccades, relative to other fixations with comparable drift velocities. This observation cannot be explained by eye velocity encoding (or the lack of it) by these neurons. Identified area I neurons were followed from control to detuned states (n = 22 cells); generally, those with lower thresholds developed complex drift patterns (n = 15 cells), whereas those with higher thresholds developed simple drift patterns more consistent with the eye movements (n = 7 cells).
Another interesting observation may help to make sense of the complex drift patterns. Under control conditions, approximately half of area I cells (n = 15 of 31 cells), generally those with lower eye position thresholds, demonstrated a phenomenon we term “nonmonotonic persistent firing.” Above a certain firing rate ceiling, persistent firing of these cells stopped increasing with ipsilaterally (ON) directed saccades and, in many cases, even decreased. Although such cells could fire transiently at higher rates during saccadic bursts or during vestibular stimulation, these inputs did not raise the poststimulus persistent firing rate beyond the ceiling level, although the eyes were moved to and held at more extreme positions in the ON direction (see Fig. 5, which is published as supporting information on the PNAS web site). When detuned, such cells almost always showed complex drift. Conversely, cells with monotonic persistent firing (always increasing with eye position in the ipsilateral direction) almost always detuned to simple drift.
It is worth emphasizing that, after training, the persistent firing patterns of both monotonic and nonmonotonic cells were changed from the control state, generally in a manner consistent with the degree of instability or leak exhibited by the fixations.
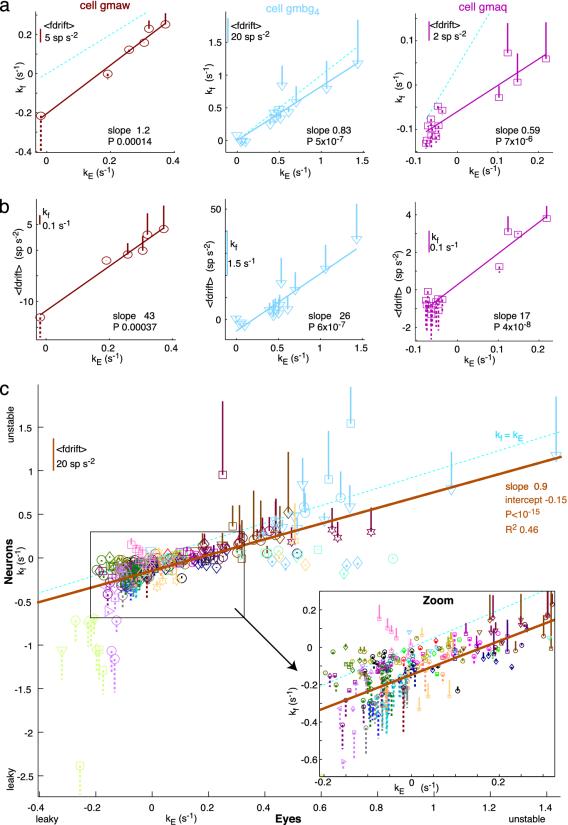
Neural Firing Rate Drift Detunes and Retunes in Line with Fixations. Many recordings were maintained while fixations were detuned or retuned over a range of behaviors (see Methods). Three examples are shown in Fig. 4a and b, all from data taken in the dark. Neural PV slope kf and average firing drift <fdrift> are plotted against eye PV slope kE. The first cell (Fig. 4 a and b Left) was recorded while the fish was detuned from stability to instability. There were strong, significant positive trends in both kf and <fdrift> with kE. Initially, in the control state, the cell was leaky (kf, -0.22 s-1), but as the animal trained to instability, the firing also trained to instability, eventually resulting in a kf of 0.25 s-1.
Fig. 4.
Detuning of persistent firing and fixations are correlated. Trends in neural PV slope kf and mean firing rate drift <fdrift> vs. eye PV slope kE. 3D plots, with one firing measure plotted on the ordinate, another represented by the bar. Solid bar up from point represents positive values; dashed downward bar represents negative values; dashed diagonal cyan lines indicate kE = kf; solid lines indicate linear regression best fits, with slopes and significance (P) noted. (a and b) Single cells. (a) kf vs. kE. (b) <fdrift> vs. kE. (Left) Trained from control to unstable. (Center) Retuned with stationary surround from unstable to stable. (Right) Trained from control to leak, then to instability. All data are from fixations in the dark. (c) Entire data set. Different colors represent different fish, and different symbols represent different cells. kf vs. kE with <fdrift> are shown as bars, as in a. The solid brown line indicates the linear regression fit.
The second cell (Fig. 4 a and b Center; see also Fig. 2b) was recorded in a fish trained to extreme instability then retuned to stability by using a stationary surround. The firing pattern retuned along with the fixations, again resulting in strongly positive, highly significant trends in neural instability and firing drift with eye instability.
The third cell (Fig. 4 a and b Right) was recorded while the animal was trained from stability to leak, then trained to instability. Again, there were strongly positive, significant correlations in both plots.
In all, 15 cells recorded for long periods showed significant trends in neural PV slope kf and/or average firing drift <fdrift> with eye PV slope kE (P < 0.05). Most cells recorded over more than one state of tuning showed a significant change in kf in the same direction as the change in kE (n = 39 of 53 cells, 74%).
Pooling the entire data set of 84 neurons revealed a very striking overall correlation between neural and eye PV slopes, across the range of behaviors explored (Fig. 4c). Generally, kf was more negative than kE. A strong correlation also was seen between average firing drift <fdrift> and kE (data not shown; R2, 0.43; slope, 21 spikes per s; P < 10-15; intercept, -1.5 spikes per s2). Because of recruitment of different cells at different eye position thresholds, a constant component of firing rate drift in a particular neuron could also contribute to instability or leak of fixations, because progressively more of such components of a given sign would be added together by the motoneurons as the eyes moved to more extreme positions. The diversity of firing rate drift patterns at a given state of fixation detuning is reflected by the vertical spread of the data points. Despite this diversity, it is clear that detuning of fixations goes hand in hand with detuning of persistent firing in area I. This was not a foregone conclusion a priori; for example, the plasticity could have occurred entirely downstream of area I, possibly in the motoneurons, or in parallel with and bypassing area I.
Discussion
Despite many years of study, we still do not understand the basic mechanisms generating graded persistent neural firing during working memory in cortex and other brain areas. There are strong arguments for studying a simple in vivo model system exhibiting graded persistent firing, such as the goldfish oculomotor neural integrator.
We have shown that, over tens of minutes to hours, the goldfish oculomotor system makes use of external visual feedback to tune the stability of persistent firing in its neural integrator. This finding is a clear demonstration of continuous tuning by sensory feedback of the dynamics of persistent neural firing in an in vivo model system, rather than just changes in overall activity or selectivity associated with learning (18, 19). Tuning is implicitly predicted by the parameter sensitivity of many models of persistent neural firing, which generally involve some form of net positive feedback internal to the integrator. A negative result, no tuning, would have argued against these parameter-sensitive models. The experimental demonstration that persistence can be smoothly tuned and detuned is an important piece of evidence supporting these models against other possibilities not requiring a tuning mechanism.
Tuning of the time course of graded persistent activity can also occur in higher brain areas during the learning of time prediction tasks (20). The firing rate buildup of many area I neurons in fish with unstable fixations resembles climbing activity seen in cortex or thalamus during time or trajectory prediction (21), suggesting that the goldfish oculomotor neural integrator may also prove to be a model system for time-varying persistent firing. Indeed, the integrator can be regarded as a simple predictive circuit whose purpose is to minimize retinal slip. It does this by generating rapid feedforward preemptive eye movements to compensate for the pattern of world motion expected on the basis of current vestibular inputs, avoiding the feedback delays and oscillations associated with the optokinetic response (22).
There were a number of surprises in this study. Apriori, there was no reason to suspect that we would be able to reduce the persistent firing time constants of some cells to <1 s (in the case of both instability and leak). This result suggests that visual feedback is a powerful tuning mechanism for persistent firing in this system. Second, the wide diversity of neural firing drift patterns in individual fish at all states of tuning was unexpected. Interestingly, many area I cells had roughly stable neural PV plots or had complex history-dependent/predictive firing drift patterns in animals with very detuned fixations, and a few cells even had the opposite pattern of drift to the eyes. Finally, in animals with unstable fixations, no cells active over most of the oculomotor range were found exhibiting symmetrical bidirectional instability (upward drift at high rates and downward drift at low rates), imitating the eye movements. Instead, most low-threshold cells showed complex firing rate drift.
Two recurrent synaptic feedback models, namely the line attractor (23) and the spiking conductance-based model with an outer-product synaptic weight matrix (24), predict that under control conditions all cells in the integrator should have similar neural PV plots over their active ranges and that they should all detune in roughly the same manner when synaptic weights are changed uniformly (24). One would not expect to see the diversity of firing rate drift patterns on different neurons observed here. Nor do published versions of these models demonstrate systematic firing-rate null point shifts in the direction of saccades, where a rate that is leaky in one fixation becomes stable after one or more saccades. Furthermore, cells active over most of the oculomotor range should show bidirectional instability in animals with unstable fixations (the achievement of bidirectionality requires additional tonic inhibition in the case of the conductance-based model). These predictions differ somewhat from the experimental data. Detuned area I firing patterns may be consistent with multiintegrator models with several different time constants (25, 26), which could result from nonuniform detuning of a line attractor or outer-product model. However, taken together with other striking features of area I firing patterns in animals with well tuned integrators, such as nonmonotonic persistent firing (see supporting information) and firing rate-firing rate hysteresis (13), as well as evidence that area I firing rates have unexpectedly long time constants after inactivation of approximately one-third of the cells (E. A., R. B., and D. W. T., unpublished data), the results above suggest that the original line attractor (23) and outer-product weight matrix (24) models may be too simplistic. However, more complex variants of these recurrent synaptic feedback models could be more consistent with the data, for example those involving higher-dimensional attractors, non-outer-product weight matrices or mixed excitatory/inhibitory networks (27).
The diversity of firing rate drifts may also be consistent with models involving other forms of tuned positive feedback, such as multiple single-cell integrators with many coupled bistable dendrites (28), dendritic wave fronts (29, 30), tuned intracellular positive feedback between calcium, calcium-activated conductances and spiking (21), or hybrid cellular-network mechanisms (31, 32).
Although area I is clearly involved in the plasticity of the oculomotor neural integrator, the plasticity may not be restricted to area I. Indeed, the changes in area I neurons could result from plasticity in other areas of the brainstem and/or cerebellum.
In conclusion, we have shown, in this in vivo biological model system, that external sensory feedback can gradually, yet powerfully, detune and retune the time course of analog persistent neural firing.
Supplementary Material
Acknowledgments
We thank Georgi Gamkrelidze, Owen Debowy, Jim Beck, Tom Adelman, Carlos Brody, John Hopfield, and Samuel Wang for comments and help. This work was supported by Lucent Technologies, Princeton University, the National Institutes of Health, the National Science Foundation, and the Wellcome Trust.
Abbreviation: PV, position-velocity.
References
- 1.Major, G., Baker, R., Aksay, E., Mensh, B., Seung, H. S. & Tank, D. W. (2004) Proc. Natl. Acad. Sci. USA 101, 7739-7744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Luschei, E. S. & Fuchs, A. F. (1972) J. Neurophysiol. 35, 444-461. [DOI] [PubMed] [Google Scholar]
- 3.Cannon, S. C. & Robinson, D. A. (1987) J. Neurophysiol. 57, 1383-1409. [DOI] [PubMed] [Google Scholar]
- 4.McFarland, J. L. & Fuchs, A. F. (1992) J. Neurophysiol. 68, 319-332. [DOI] [PubMed] [Google Scholar]
- 5.Kaneko, C. R. S. (1997) J. Neurophysiol. 78, 1753-1768. [DOI] [PubMed] [Google Scholar]
- 6.Goldman, M. S., Kaneko, C. R., Major, G., Aksay, E., Tank, D. W. & Seung, H. S. (2002) J. Neurophysiol. 88, 659-665. [DOI] [PubMed] [Google Scholar]
- 7.Lopez-Barneo, J., Darlot, C., Berthoz, A. & Baker, R. (1982) J. Neurophysiol. 47, 329-352. [DOI] [PubMed] [Google Scholar]
- 8.Cheron, G., Godaux, E., Laune, J. M. & Vanderkelen, B. (1986) J. Physiol. 372, 75-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Delgado-Garcia, J. M., Vidal, P. P., Gomez, C. & Berthoz, A. (1989) Neuroscience 29, 291-307. [DOI] [PubMed] [Google Scholar]
- 10.Moschovakis, A. K. (1997) Front. Biosci. 2, D552-D577. [DOI] [PubMed] [Google Scholar]
- 11.Pastor, A. M., de la Cruz, R. R. & Baker, R. (1994) J. Neurophysiol. 72, 1383-1393. [DOI] [PubMed] [Google Scholar]
- 12.Aksay, E., Baker, R., Seung, H. S. & Tank, D. W. (2000) J. Neurophysiol. 84, 1035-1049. [DOI] [PubMed] [Google Scholar]
- 13.Aksay, E., Major, G., Goldman, M. S., Baker, R., Seung, H. S. & Tank, D. W. (2003) Cereb. Cortex 13, 1173-1184. [DOI] [PubMed] [Google Scholar]
- 14.Becker, W. & Klein, H. M. (1973) Vision Res. 13, 1021-1034. [DOI] [PubMed] [Google Scholar]
- 15.Mensh, B. D., Aksay, E., Lee, D. D., Seung, H. S. & Tank, D. W. (2003) Vision Res. 44, 711-726. [DOI] [PubMed] [Google Scholar]
- 16.Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. (1992) Numerical Recipes in C (Cambridge Univ. Press, New York).
- 17.Edwards, A. E. (1976) An Introduction to Linear Regression and Correlation (Freeman, San Francisco).
- 18.Chen, L. L. & Wise, S. P. (1995) J. Neurophysiol. 73, 1122-1134. [DOI] [PubMed] [Google Scholar]
- 19.Wirth, S., Yanike, M., Frank, L. M., Smith, A. C., Brown, E. N. & Suzuki, W. A. (2003) Science 300, 1578-1581. [DOI] [PubMed] [Google Scholar]
- 20.Komura, Y., Tamura, R., Uwano, T., Nishijo, H., Kaga, K. & Ono, T. (2001) Nature 412, 546-549. [DOI] [PubMed] [Google Scholar]
- 21.Durstewitz, D. (2003) J. Neurosci. 23, 5342-5353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marsh, E. & Baker, R. (1997) J. Neurophysiol. 77, 1099-1118. [DOI] [PubMed] [Google Scholar]
- 23.Seung, H. S. (1996) Proc. Natl. Acad. Sci. USA 93, 13339-13344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Seung, H. S., Lee, D. D., Reis, B. Y. & Tank, D. W. (2000) Neuron 26, 259-271. [DOI] [PubMed] [Google Scholar]
- 25.Crawford, J. D. & Vilis, T. (1993) Exp. Brain. Res. 96, 443-456. [DOI] [PubMed] [Google Scholar]
- 26.Anastasio, T. J. (1998) Biol. Cybern. 79, 377-391. [DOI] [PubMed] [Google Scholar]
- 27.Escudero, M. & Delgado-Garcia, J. M. (1988) Exp. Brain Res. 71, 218-222. [DOI] [PubMed] [Google Scholar]
- 28.Rosen, M. J. (1972) IEEE Trans. Biomed. Eng. BME-19, 362-367. [DOI] [PubMed] [Google Scholar]
- 29.Loewenstein, Y. & Sompolinsky, H. (2003) Nat. Neurosci. 6, 961-967. [DOI] [PubMed] [Google Scholar]
- 30.Wang, S. S. & Major, G. (2003) Nat. Neurosci. 6, 906-908. [DOI] [PubMed] [Google Scholar]
- 31.Koulakov, A. A., Raghavachari, S., Kepecs, A. & Lisman, J. E. (2002) Nat. Neurosci. 5, 775-782. [DOI] [PubMed] [Google Scholar]
- 32.Goldman, M. S., Levine, J. H., Major, G., Tank, D. W. & Seung, H. S. (2003) Cereb. Cortex 13, 1185-1195. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.