Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2014 Oct;24(10):1698–1706. doi: 10.1101/gr.168773.113

Probing the effect of promoters on noise in gene expression using thousands of designed sequences

Eilon Sharon 1,2,5,6, David van Dijk 1,2,5, Yael Kalma 2, Leeat Keren 1,2, Ohad Manor 1, Zohar Yakhini 3,4, Eran Segal 1,2,✉
PMCID: PMC4199362  PMID: 25030889

Abstract

Genetically identical cells exhibit large variability (noise) in gene expression, with important consequences for cellular function. Although the amount of noise decreases with and is thus partly determined by the mean expression level, the extent to which different promoter sequences can deviate away from this trend is not fully known. Here, we present a high-throughput method for measuring promoter-driven noise for thousands of designed synthetic promoters in parallel. We use it to investigate how promoters encode different noise levels and find that the noise levels of promoters with similar mean expression levels can vary more than one order of magnitude, with nucleosome-disfavoring sequences resulting in lower noise and more transcription factor binding sites resulting in higher noise. We propose a kinetic model of gene expression that takes into account the nonspecific DNA binding and one-dimensional sliding along the DNA, which occurs when transcription factors search for their target sites. We show that this assumption can improve the prediction of the mean-independent component of expression noise for our designed promoter sequences, suggesting that a transcription factor target search may affect gene expression noise. Consistent with our findings in designed promoters, we find that binding-site multiplicity in native promoters is associated with higher expression noise. Overall, our results demonstrate that small changes in promoter DNA sequence can tune noise levels in a manner that is predictable and partly decoupled from effects on the mean expression levels. These insights may assist in designing promoters with desired noise levels.

Stochastic cell-to-cell variability in gene expression (noise) can lead to substantial phenotypic differences within a genetically identical cell population grown in the same environment (Blake et al. 2003; Munsky et al. 2012). Therefore, maintaining low or high noise levels for specific genes may provide an evolutionary advantage (Acar et al. 2008; Beaumont et al. 2009; Rainey et al. 2011). Indeed, genome-wide measurements of protein levels reveal that genes exhibit different levels of stochastic noise (Bar-Even et al. 2006; Newman et al. 2006). These measurements display the qualitative trend that is expected from a Poisson process of protein production and degradation (Blake et al. 2003; Bar-Even et al. 2006; Newman et al. 2006) in which noise decreases as mean expression increases (Bar-Even et al. 2006; Newman et al. 2006). However, the measured relationship between noise and mean expression does not quantitatively match a Poisson process (Blake et al. 2003; Bar-Even et al. 2006; Newman et al. 2006), and the results fit better to a model in which genes are transcribed in bursts that partly result from promoters switching between active and inactive transcriptional states (Paulsson 2004; Raser and O’Shea 2004; Friedman et al. 2006; So et al. 2011). In this model, noise is affected by both the rate of transcriptional activation and the size of the transcriptional bursts (the number of mRNA molecules produced at each instance of promoter activation) (Sherman and Cohen 2014) and the number of proteins produced from each mRNA. Therefore, according to this model, promoters can encode different combinations of expression mean and noise by modulating transcriptional bursting, as shown experimentally in several studies (Ozbudak et al. 2002; Choi and Kim 2009; Amit et al. 2011; Hornung et al. 2012; Raveh-Sadka et al. 2012; Dadiani et al. 2013). However, we have a poor understanding of the extent to which promoters regulate noise beyond the level that is dictated by the mean and the sequence features by which such regulation is encoded.

Genome-wide measurements of protein levels (Newman et al. 2006; Stewart-Ornstein et al. 2012) do not isolate the effect of the promoter, since they represent the combined effect of all layers of regulation. In addition, the local chromatin structure of the gene may also affect its level of expression noise (Batenchuk et al. 2011). One way to isolate this effect is to integrate the tested promoter upstream of a reporter gene and within a fixed genomic context. Moreover, since the sequence of native promoters differs by many parameters, mutated versions of native promoters (Hornung et al. 2012), synthetic promoters built by random ligation of several building blocks (Mogno et al. 2010), or designed synthetic promoters (Murphy et al. 2007; Amit et al. 2011; Raveh-Sadka et al. 2012; Carey et al. 2013; Dadiani et al. 2013) are more suitable for studying the rules by which promoter sequence affects noise. Previous such studies show that nucleosome-disfavoring sequences increase expression and reduce noise (Choi and Kim 2009; Raveh-Sadka et al. 2012; Dadiani et al. 2013), whereas an equivalent increase in mean expression that results from the addition of an activator binding site increases noise (Dadiani et al. 2013), and TATA boxes have little effect on noise (Mogno et al. 2010). However, due to the difficulties of constructing synthetic promoters, these studies were done on at most dozens of promoters. Thus, since no effective high-throughput method of measuring promoter-driven noise exists, the effect on noise of much of the possible combinatorial complexity of promoter architecture has not been tested to date.

Here, we study the effect of promoter sequence on noise in gene expression using noise measurements of thousands of fully designed synthetic promoters with systematic changes to the number, location, and spacing of several regulatory elements. For this aim, we devised a novel high-throughput method, which is an extension of our previously developed method (Sharon et al. 2012) that enables us to obtain these thousands of different noise measurements in a single experiment with a high agreement to measurements of isolated strains (Pearson’s R2 = 0.80) and high reproducibility (Pearson’s R2 = 0.78). Notably, we found that promoters with similar mean expression levels in this set can vary by more than one order of magnitude in their noise levels, and that this large variation is similar to the variation found in native promoters (Bar-Even et al. 2006; Carey et al. 2013). By examining the effect of various promoter sequence elements on expression, we find that nucleosome-disfavoring sequences in the promoter increase expression and decrease noise in a manner that correlates with their length, consistent with observations on small sets of promoters (Raveh-Sadka et al. 2012). In addition, we find that larger and more dense clusters of transcriptional activator binding sites yield noisier expression for a given mean expression level. We show that a simple linear model can predict a large part of the variation in noise that is independent of the mean expression, and that fitting two alternative kinetic models to the data, which assume different transcription factor DNA binding schemes, suggests that nonspecific DNA binding and one-dimensional sliding along the DNA of transcription factors may play a role in how promoter sequence affects noise (Li et al. 2009; Hammar et al. 2012). Finally, we show that in native genes, binding-site multiplicity is associated with higher noise.

Our work presents the largest measurement to date of promoter-driven noise and an investigation of how small and systematic changes in the promoter sequence affect single-cell expression. The insights afforded by our work may provide the ability to tune noise with little effect on mean expression and enhance our understanding of how native promoters encode their noise levels. In addition, the method presented in this work, which achieves at least an order of magnitude more data points than previous studies, is scalable to other systems and organisms and should be a useful tool for studying DNA-encoded single-cell gene expression in various systems.

Results

Measuring the noise of thousands of designed promoters

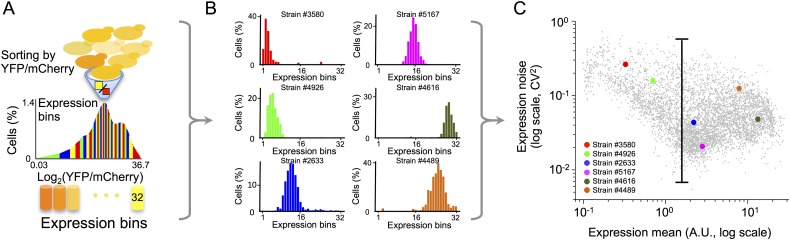
To study the rules by which promoter sequences determine noise, we used a set of 6500 designed synthetic promoters with systematic manipulations to the affinity, location, spacing, and several different regulatory elements. By devising new analysis methods for an experimental approach that we previously developed (Sharon et al. 2012), we extracted accurate noise measurements for each of these promoters. Briefly, a pool of cells containing all 6500 promoters (one promoter per cell with each promoter integrated upstream of a yellow fluorescent protein [YFP]) are first sorted by their YFP expression level into 32 expression bins using fluorescence-activated cell sorting (FACS). Next, the promoters of every expression bin are amplified and sequenced using parallel sequencing. By counting the number of sequencing reads obtained for each strain in every expression bin, we reconstruct the single-cell expression distribution of each promoter and from it, extract both its mean expression and noise (Fig. 1A–C; see Methods). We found that our method is highly reproducible across replicates in terms of mean expression (Pearson’s R2 = 0.99) (Supplemental Fig. S1C), noise (Pearson’s R2 = 0.78) (Supplemental Fig. S1A, measured as the variance divided by the mean squared, also termed the squared coefficient of variation [CV2]), and noise strength (Pearson’s R2 = 0.75) (Supplemental Fig. S1B, measured as the variance divided by the mean, also termed the Fano factor). More importantly, our measurements are highly accurate compared to measurements of 54 isolated strains for mean (Pearson’s R2 = 0.97) (Supplemental Fig. S1F), noise (Pearson’s R2 = 0.80) (Supplemental Fig. S1D), and noise strength (Pearson’s R2 = 0.88) (Supplemental Fig. S1E). Thus, these results show that our approach can measure the noise of thousands of fully designed promoters with an accuracy that approaches that obtained when constructing and measuring each strain individually.

Figure 1.

Figure 1.

Open in a new tab

Measuring the single-cell gene expression distribution of thousands of designed promoter sequences within a single experiment. (A) Cells of the pooled library of 6500 strains are sorted into 32 expression bins. (B) The single-cell expression distribution of each strain is reconstructed by determining the fraction of cells that contain each promoter in every expression bin using parallel sequencing of the promoter region. Shown are single-cell expression distributions of six strains from the library. The mean, noise, and noise strength of each strain are then extracted from these distributions (see Methods). (C) Shown is the mean expression (x-axis) and noise (y-axis) of each of the 6500 different library strains. Colored points correspond to the six strains shown in B. Also shown is a vertical line corresponding to a nearly two orders of magnitude range in noise.

Examining the range of values spanned by our library, we found that the dynamic range of both the mean expression and the noise of our synthetic promoters is similar to that of native promoters, suggesting that our library is highly relevant for native transcriptional regulation (Supplemental Fig. S2). Notably, the noise levels of our synthetic promoters span more than one order of magnitude even at similar mean expression levels (Fig. 1C). Since we designed the library such that many promoters differ by a small number of base pair changes (e.g., changes to a single TFBS location or affinity), these results demonstrate that even small base pair changes may result in large effects on noise.

Promoter sequence features determine the relationship between expression mean and noise

To study the rules by which promoter sequence determines gene expression noise, we examined the effect on noise of systematic changes to the number and length of poly(dT:dA) nucleosome-disfavoring elements and to the number, location, and spacing of transcription factor binding sites (TFBSs). For poly(dT:dA) tracts, we compared the expression of 1268 pairs of promoters that each differ by only a single insertion of a 15-bp tract and found that addition of such tracts results in a significant increase in the mean expression (Supplemental Fig. S3A, Student’s t-test P < 10−170; Supplemental Fig. S3D, median increase of 86% with 95% confidence intervals [CI]: 76%–93%) and a significant decrease in the noise (Supplemental Fig. S3B, Student’s t-test P < 10−26; Supplemental Fig. S3D, median decrease of 60% with 95% CI: 57%–63%) but has a significant though relatively smaller effect on the noise strength (Supplemental Fig. S3C, Student’s t-test P < 10−3; Supplemental Fig. S3D, median decrease of 12% with 95% CI: 7%–16%). Consistent with this effect of poly(dT:dA) tracts, we also found that longer tracts, and separately, more tracts, increase mean expression, decrease noise, and have little effect on noise strength (Fig. 2A; Supplemental Figs. S4, S5). Assuming the promoter ON-OFF switching model (Raser and O’Shea 2004), these results are qualitatively in line with poly(dT:dA) tracts increasing expression mainly through an increase in the promoter on-switching rate (burst frequency) rather than through an increase in promoter transcription rate (which is linearly correlated with burst size) (see Supplemental Material for an investigation of this model).

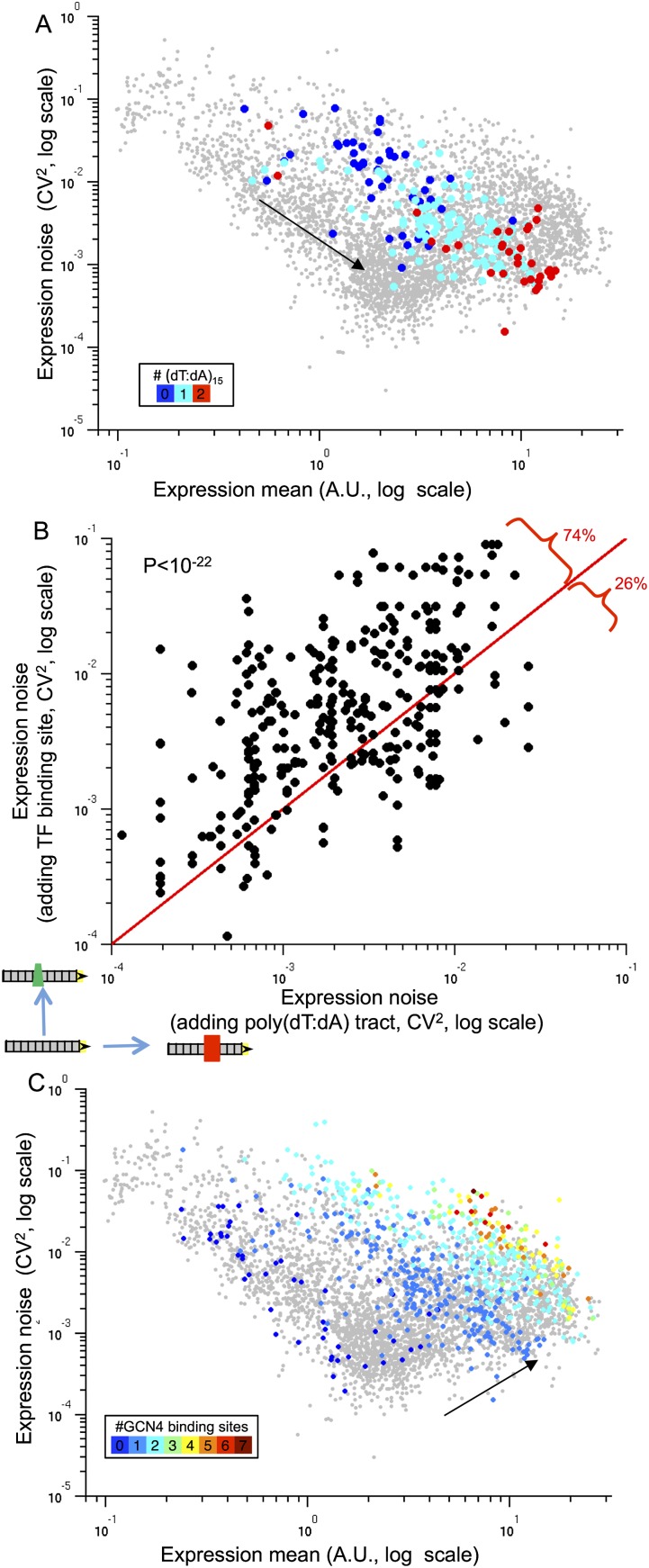
Figure 2.

Figure 2.

Open in a new tab

The effect of nucleosome-disfavoring sequences and number of binding sites on noise. (A) Mean expression and noise of 182 promoters with zero (blue points), one (light blue points), or two (red points) poly(dT:dA) of length 15 bp and a single Gcn4 site. Note that promoters with more poly(dT:dA) tend to have higher expression and lower noise. (B) Shown is a comparison of the effect on expression noise of increasing the mean expression either by adding a TF binding site or by adding a nucleosome-disfavoring sequence. Shown are 417 promoter pairs in which adding a TF binding site or a poly(dT:dA) tract resulted in a similar increase of the mean expression (all promoters were divided into 50 bins according to their log expression values, and promoters that share a bin are considered to have similar expression levels). In 309 (74%) of these 417 promoter pairs, adding a TF site resulted in noisier expression as compared to adding a nucleosome-disfavoring sequence (binomial test P < 10−22). (C) Mean expression and noise of 643 promoters with zero (dark blue points) to seven (dark red points) binding sites of Gcn4 and no other TF. The black arrows (A,C) point in the direction of expression and noise change. Note the general increase in both expression mean and noise that results in the addition of Gcn4 binding sites.

Next, we compared the effect on noise of increasing the mean expression by adding an activator binding site versus adding a poly(dT:dA) tract, because a recent study that we performed on a few strains showed that these two different strategies for increasing the mean expression have opposing effects on noise. Notably, in 309 of 417 (74%) promoters from our library, for which adding a poly(dT:dA) tract resulted in a similar increase in mean expression as did addition of an activator binding site, adding a poly(dT:dA) tract resulted in significantly lower noise (binomial test P < 10−22) (Fig. 2B; Supplemental Fig. S6). These results thus considerably expand the scope of our previous observations (Dadiani et al. 2013) and suggest that nucleosome-disfavoring sequences are an efficient tool for increasing expression while maintaining low noise.

To examine the effect of varying the number and configuration of transcription activator binding sites on noise, we examined a set of 643 promoters that contains 0–7 Gcn4 binding sites in various positions and background sequences. Notably, we found that for a given expression level, promoters that contain more Gcn4 binding sites are noisier (ANOVA test P < 10−19) (Fig. 2C; Supplemental Fig. S7). This result also holds in a set of 443 promoters with up to two binding sites for the transcription activator Leu3 (Supplemental Fig. S8). These results thus suggest that increasing the number of binding sites of transcription activating factors will result in noisier expression.

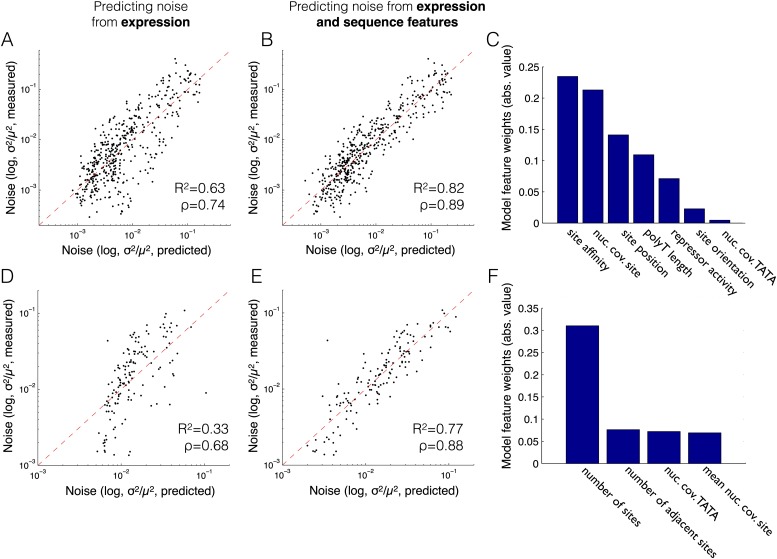
To quantify the effect of promoter sequence features on the mean-independent component of noise, we constructed a linear model that predicts mean expression from promoter sequence features and noise from either mean expression or from both mean expression and promoter sequence features. We applied this model to two sets of promoters, one consisting of 457 promoters with a single Gcn4 binding site in various configurations and another consisting of 128 promoters with multiple Gcn4 binding sites (all combinations of placing 0–7 Gcn4 binding sites in seven predefined positions). We evaluated the performance of our model using a fivefold cross-validation, in which we split the data into five subsets and predicted the expression of each promoter using a model that was trained on the four subsets that did not include the predicted promoter (Fig. 3; Supplemental Figs. S9, S10). Notably, we found that although mean expression alone explains nearly two-thirds (Pearson’s R2 = 0.63; Spearman’s ρ = 0.74) and one-third (Pearson’s R2 = 0.33; Spearman’s ρ = 0.68) of the noise in both promoter sets (Fig. 3A,D), more than half of the remaining noise can be explained by adding only a few sequence features to the model (Pearson’s R2 = 0.82; Spearman’s ρ = 0.89; Pearson’s R2 = 0.77; Spearman’s ρ = 0.88, respectively) (Fig. 3B,E). Examining the set of features used by the model (via their respective standardized weights; see Methods for details), we found that TFBS affinity and multiplicity are the strongest predictors of the mean-independent component of noise (Fig. 3C,F). We note that the latter might be expected because it is the major parameter changing between promoters. Since part of the variation in our data is due to experimental error (Supplemental Fig. S1), the preceding values are likely an underestimation. Overall, these results demonstrate that a simple combination of changes to properties of nucleosome-disfavoring elements and TF binding sites can account for much of the effect of promoter sequence on the mean-independent component of noise.

Figure 3.

Figure 3.

Open in a new tab

A linear model based on promoter sequence features predicts a large fraction of the mean-independent component of the noise. (A,B,D,E) Shown is a comparison of the predicted (x-axis) and measured (y-axis) noise for a model that predicts noise using only mean expression (A,D) and for a model that also incorporates promoter sequence features (B,E). Results are shown for promoters with a single Gcn4 site (A,B) or multiple sites (D,E). The noise of each promoter was predicted using a model that was trained on the four subsets that did not include the promoter, out of five equally sized subsets among which we split the data. Pearson’s R-squared value (R2) and Spearman’s rank correlation coefficient (ρ) are shown in each model plot (A,B,D,E). (C,F) The weights of the sequence features used in the linear models presented in B and E (the weight of the expression mean is not shown). The weights correspond to the absolute value of the relative contribution of each feature to the prediction of the noise component that is independent of the mean.

A kinetic model of transcription factor target search can partly explain the mean-independent expression noise

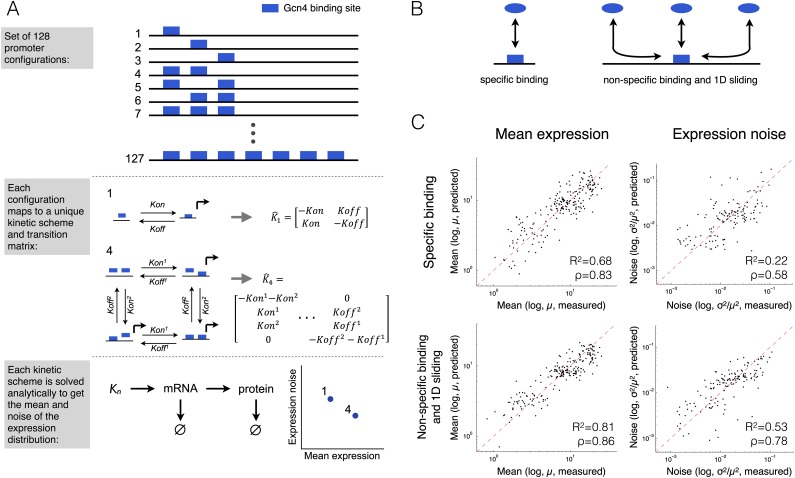
To obtain insights into the mechanism by which noise increases with TFBS number, we explored the possibility that this effect partly results from the way in which TFs search for their target sites. Transcription factors are known to search for their sites through some combination of nonspecific DNA binding via three-dimensional (3D) diffusion and subsequent sliding across the DNA via one-dimensional (1D) diffusion (Hammar et al. 2012; Khazanov et al. 2013). However, the extent to which these mechanisms affect transcriptional regulation is not well understood. A recent study (Hammar et al. 2012) showed that adjacent TFBSs result in slower binding rates to each site, likely because a TF molecule bound to one of the sites may limit the size of the region in which a second TF molecule can slide in search of its target. Based on this observation, we hypothesized that if 1D sliding is indeed a major determinant of TF binding rate, then promoters with multiple sites may have relatively slower TF binding kinetics and therefore slower switching rates between transcriptionally active and inactive states, possibly resulting in noisier expression.

To examine this hypothesis, we modeled a set of promoters with multiple Gcn4 binding sites (all 128 combinations of 0–7 sites at seven predefined positions in two different sequence contexts that differ by their GC content) using two models that differ in their assumptions about how TFs search for their target sites. The first model (denoted 3D model) assumes that TFs search their sites using only 3D-diffusion, whereas the second (denoted 3D+1D model) assumes a combination of 3D-diffusion and 1D-sliding. Therefore, in the second model, the presence of a binding site can affect TF binding to a neighboring site, whereas in the first model, the TF binds directly to each site independently of other neighboring sites. The parameters of both models were the same except for an additional TF sliding distance parameter in the 3D + 1D model (see Methods for details). For both models, we predict mean expression and noise by mapping each binding site configuration to a unique kinetic scheme that is simulated or solved analytically (Fig. 4A, see Methods). We used a fivefold cross-validation scheme to compare the ability of the two models to predict the expression mean and noise (Fig. 4B,C). We estimated their performance both using the coefficient of determination (R2) and the Spearman’s rank correlation coefficient (ρ) of the predictions to the measurements. We found that the performance of the 3D + 1D model on expression mean (R23D+1D = 0.80 ± 0.05; ρ3D+1D = 0.86 ± 0.08) and expression noise (R23D+1D = 0.51 ± 0.15; ρ3D+1D = 0.77 ± 0.9) is significantly better than the performance of the 3D model on expression mean (R23D = 0.68 ± 0.09; ρ3D = 0.83 ± 0.05) and expression noise (R23D = 0.17 ± 0.2; ρ3D = 0.57 ± 1.3) as shown by a Wilcoxon rank sum test on the distributions of R2 values for mean (P < 10−7) and noise (P < 10−6) and on the distributions of Spearman’s correlation (ρ) values for mean (P < 0.05) and noise (P < 10−6). Although additional mechanisms, such as cooperative binding (Giniger and Ptashne 1988; Miller and Widom 2003) and allosteric effects (Amit et al. 2011; Kim et al. 2013) likely have effects, these results suggest TF 1D sliding along the DNA as another mechanism which may affect gene expression noise and could explain the observation that more TF binding sites result in higher noise for the same mean expression level. Consistent with this idea, we found that native promoters (Stewart-Ornstein et al. 2012) with higher affinity to TFs (Basehoar et al. 2004; MacIsaac et al. 2006; Portales-Casamar et al. 2010; Pachkov et al. 2013) or with higher levels of TF binding (Venters et al. 2011) drive noisier gene expression (Supplemental Fig. S13).

Figure 4.

Figure 4.

Open in a new tab

The effect of multiple transcription factor binding sites on noise is largely mediated by 1D sliding of the cognate transcription factor. For each promoter with a different number and configuration of seven possible TFBS (A, top), we constructed a kinetic model. Each of the 127 possible configurations was represented by a unique kinetic scheme and transition matrix (A, middle). The rate parameters of the reactions in the matrix were computed from the free parameters of the model using one of two alternative mappings that assume either that TFs search for their target through 3D diffusion (B, left) or that they do so by a combination of 3D and 1D diffusion (B, right). The transition matrix, together with reactions for transcription, translation, and mRNA and protein degradation, were simulated and solved analytically to obtain the steady-state mean protein abundance and noise (A, bottom). (C) The free parameters of the models were fitted in a leave-one-out cross-validation and the predictions (x-axis) of mean expression and CV2 were compared to the measured (y-axis) (see Supplemental Fig. S12 for a 10-fold cross-validation). The results show that the model that incorporates both 3D and 1D diffusion performs significantly better for both mean expression and noise than the model that assumes only 3D diffusion.

Discussion

In summary, we presented the first large-scale investigation of fully designed systematic changes to promoter sequence features on single-cell gene expression. For this aim, we developed a high-throughput approach that produces highly accurate and reproducible noise measurements for thousands of fully designed sequences in a single experiment. We found that the noise of promoters with similar mean expression can vary more than one order of magnitude, indicating that promoter sequence has a major effect on noise beyond that which is mediated by the promoter’s mean expression level. Specifically, we found that nucleosome-disfavoring sequences increase expression and reduce noise, and promoters with more transcriptional activator binding sites exhibit higher noise. A linear model based on a small number of simple sequence features, in a controlled setting, can predict much of the mean-independent effect of promoter sequence on noise. We note that although our model explains our synthetic designed promoters, further development is required in order to apply similar models in more general settings, i.e., on native promoter sequences. Finally, we fit to our measurements two kinetic models of gene expression—one that assumes only TF three-dimensional diffusion and a second model that assumes also TF one-dimensional sliding along the DNA. The latter is able to better explain our measurements, and therefore suggests that changes in binding kinetics, when sites are clustered and due to one-dimensional sliding of TFs along the DNA, may have an effect on expression noise.

We note that in our experimental system, the sole difference between the strains is their promoter DNA sequence. Therefore, we assume that the differences in mean expression and noise that we measured are a result of changes to the binding kinetics of the transcriptional machinery, in turn affecting the size and the frequency of transcriptional bursts. In other words, we assume that expression mean and noise changes reflect changes in transcriptional bursting mediated by promoter DNA sequence changes. Although we and others (Weinberger et al. 2005; Blake et al. 2006; Raj et al. 2006; Zenklusen et al. 2008; Hornung et al. 2012; Carey et al. 2013; Dadiani et al. 2013) have previously found convincing evidence for the validity of this assumption, further work is necessary to prove if and to what extent transcriptional bursting can have effects on noise at the protein level, since this assumption was only proven for protein bursting (Friedman et al. 2006).

In line with the preceding interpretation of the results and assuming a promoter ON-OFF switching model (Raser and O’Shea 2004), our finding that nucleosome-disfavoring sequences increase expression and reduce noise with significant though much smaller effect on noise strength suggests that these elements may increase expression mainly by increasing the promoter activation frequency (promoter ON switching rate), perhaps by increasing the promoter’s accessibility to transcriptional activators. This result is consistent with previous findings observed with a small set of promoters (Raveh-Sadka et al. 2012; Dadiani et al. 2013).

We also found that other sequence features, such as the affinity, number, and configuration of binding sites, affect the mean-independent component of the noise, and a model based solely on DNA sequence features can predict a large part of the expression mean and noise. This modeling task benefits from the controlled setting of our synthetic promoter library; and although it is beyond the scope of this work, applying such models to native promoters can improve our understanding of transcriptional regulation in native settings.

Another notable finding is that the number and relative spacing of TF binding sites may have large effects on noise. We observed that promoters with larger and denser clusters of sites give a higher noise level for a given mean expression in both our designed promoters. Although such direct observation on native promoters is still difficult due to their higher complexity, we did find evidence for this behavior also in native promoters (Supplemental Fig. S13). In search of a mechanism that can explain this observation, we suggested a novel model of expression regulation that integrates TFs searching for their targets using a combination of 3D diffusion and 1D sliding (Hammar et al. 2012) into the common model of transcription regulation that considers only 3D diffusion of TFs (Gertz et al. 2009). We fitted these kinetic models to expression measurements of promoters with all combinations of seven predefined binding sites in two sequence contexts and found that including 1D sliding significantly improves predicting the expression mean and noise. Therefore, we suggest that slower TF binding kinetics, due to decreased 1D sliding of TFs, may in part explain how the number and configuration of binding sites can affect promoter noise levels. Although it is known that TFs find their targets by a combination of 3D diffusion and 1D sliding along the DNA, the relative contribution of each of these mechanisms to the resulting expression behavior is not well understood. Since homotypic TFBS clustering is a general organization principle of cis-regulatory regions, as suggested by enrichment of such clusters in proximal promoters and distal enhancers and by their conservation between vertebrate and invertebrates (Wunderlich and Mirny 2009; Gotea et al. 2010; Weingarten-Gabbay and Segal 2014), it is important to understand their effect on dynamics of transcription. Our results, combined with our findings in native genes, suggest that competitive binding, as a result of densely clustered binding sites, may be a mechanism that affects the expression noise of native promoters. Since native promoters alone are possibly too diverse to perform a structural investigation on, it will be interesting to conduct a similar study on a library of native and mutated promoters. Although our kinetic modeling scheme is limited in several aspects, because it ignores chromatin effects and other more complex models of transcription initiation, and assumes that transcriptional bursting is in part controlled by DNA sequence and has significant effect on the noise, its ability to fit (in cross-validation) both mean expression and noise better than a model that ignores one-dimensional sliding may suggest that TF 1D diffusion behavior has some non-negligible consequences for transcriptional noise and may be considered in any future models of transcriptional regulation. In other words, although further study is needed to prove the underling mechanisms, our work can stimulate further research in this direction. Our results may also have implications for the understanding of the selective pressure shaping promoter sequences because the organism may benefit from maintaining either low or high noise for specific genes. Evidence of such selection is present in the finding that yeast stress genes are noisier (Bar-Even et al. 2006; Newman et al. 2006).

Our approach has several limitations. First, the quality of our pooled noise measurements is not as accurate as measuring isolated strains. Second, although we analyze a relatively uniform cell population and normalize by our fixed promoter regulated mCherry (red fluorescence) level, our results may include a pathway-specific extrinsic noise component. However, previous work in our laboratory showed that the level of such noise is low (less than the lowest observed noise level) (Carey et al. 2013), and that it accurately agrees with a dual reporter assay that only measures intrinsic noise (Elowitz et al. 2002). Third, we assume that changes in transcriptional bursting can be observed from changes in the protein level noise (i.e., higher noise is bigger bursts). Although this has been suggested in several studies (Elowitz et al. 2002; Cai et al. 2006; Friedman et al. 2006; Pedraza and Paulsson 2008; Hornung et al. 2012) and previous work in our laboratory showed convincing evidence that transcriptional bursting as measured by time-lapse microscopy (Dadiani et al. 2013) can, at least in part, be controlled by promoter sequence, much understanding is still lacking on the validity and significance of this mechanism. We note that our measured protein abundance distributions reflect bursts of both transcription and translation (from the produced mRNAs following the activation of the promoter). Fourth, current data processing filters out promoters deriving multimodal expression distribution. Since none of the isolated strains showed multimodal distributions and almost all of our promoters have at least 75% of their reads within a single distribution peak, we do not expect that this filter removed a considerable number of promoters that derive true multimodal expression distribution; however, removing this filter is advised if the tested promoters may produce such distributions. Fifth, since in our method the promoters are integrated into plasmids in a fixed position, we do not measure the effect of the local chromatin structure on the promoter function (Batenchuk et al. 2011). It would be interesting to investigate this effect by measuring the function of our set of promoters in various genomic contexts. Finally, we note that since the core promoter used by our library is fixed and contains a TATA box, our results are limited to TATA-containing core promoters. Since TATA-containing promoters are associated with higher noise (Tirosh and Barkai 2008; Choi and Kim 2009; Lehner 2010), it will be interesting to examine synthetic promoters in the context of TATA-less promoters. In spite of these limitations, our ability to measure the noise of thousands of sequences within a single experiment paves the way for examining the effect on noise of other promoter sequence features and of other regulatory layers such as post-transcriptional and translational regulation.

Taken together, we presented a method for measuring designed promoter-driven noise in high-throughput and found that promoter sequence has profound effects on gene expression noise, and that many of these effects are independent of the effect mediated by the mean expression level. Aside from the biological insights that our results provide on the extent to which different types of DNA sequence elements affect cell-to-cell expression variability, our experimental framework offers powerful means by which further research in this field may be carried out.

Methods

Promoter library design construction and measurements

The promoter library was designed, constructed, and measured as described in Sharon et al. (2012), except for the differences below. Briefly, a large collection of synthetic promoter reporter gene strains was generated by a pooled ligation of 6500 fully designed DNA oligos (obtained by synthesis on a microarray by Agilent Technologies) (LeProust et al. 2010). The oligos were ligated upstream to a yellow fluorescent protein (YFP) gene with a short (100 bp) core promoter sequence taken from HIS3 gene promoter and into a low copy plasmid that also contains a TEF2 promoter deriving red fluorescent protein (mCherry). The resulting plasmids were then transformed into yeast (S. cerevisiae, strains: Y8205). Next, the pool of cells was grown in amino acid starvation condition (SCD without amino acid except histidine) and sorted according to their YFP expression level into 32 expression bins (mCherry was used for gating one plasmid copy cell and for normalization). The DNA of the promoters in each bin was then amplified and sent to multiplexed parallel sequencing. Each sequencing result was mapped to a specific promoter and expression bin, resulting in a distribution of cells that contain each promoter across all expression bins.

The following differences were applied relative to the description in Sharon et al. (2012). The medium used both for growing the cells and for their sorting was SC-Glu-URA (synthetic complete media with 2% glucose and without uracil) medium without amino acids, except for histidine. In order to achieve expression distributions with high resolution that would allow good assessment of expression noise, the library cells were sorted into 32 bins according to their ratio of YFP and mCherry expression level, thereby normalizing for extrinsic noise effects. Each of the two extreme expression bins contained 2% of the library cells, and each of the remaining 30 bins contained 3.2%. We collected a total of 10,000,000 cells. As previously described, the mapping of cells to bins involves parallel sequencing of the amplified promoter regions. For this purpose, Illumina HiSeq 2000 was used to obtain >30,000,000 mapped reads. The two replicates were separately generated from the ssDNA oligo library and separately measured as described above.

High-throughput measurement of expression mean and variance

For each promoter, the fraction of cells with that promoter in each expression bin was estimated as described in Sharon et al. (2012). Several new computational procedures were then applied to filter and improve the accuracy of the results (see also Supplemental Material). First, strains that were represented by less than 1000 sequencing reads (20% of the library) were filtered. Second, the distribution of each strain across the expression bins was examined, and the peak that contained the largest fraction of cells of each strain was detected. The small fraction of cells outside of the main peak was considered as technical noise and therefore set to zero. Note that this assumes that the distribution is not multimodal, which holds for all of the isolated strains and therefore is most likely for the entire library. Of the strains for which the largest peak contained <75% of the cells, 2.2% were filtered out (Supplemental Fig. S13A). Third, to further reduce the technical noise, a gamma distribution was fitted to the cells' distribution across the bins (using MATLAB [MATLAB and Statistics Toolbox Release 2012b, The MathWorks]). Of the strains for which gamma fitting could explain <80% of the variance of cells' distribution across the bins, 2.4% were filtered out (Supplemental Fig. S13B), and the gamma distribution was used to compute the mean and variance for the rest. Finally, 5.8% of the cells for which the two replicates gave substantially different results (the 2.5% and 5% of smallest/largest ratio of the two replicates' mean and noise values, respectively, of unfiltered data) were filtered out to get the final accurate results for ∼65% of the designed library strains.

Linear model of expression mean and noise with elastic-net regularization

The sets of promoters were used to learn a regularized linear regression model from sequence features that predicts the value of mean expression, noise (CV2), and noise strength (Fano factor). Learning was done using a fivefold cross-validation scheme, whereby model parameter fitting was done only on training data, and the model was evaluated on the held-out test data. The model was regularized using elastic-net (Zou and Hastie 2005), where the value of lambda (the penalty coefficient) was learned using a fivefold internal cross-validation scheme on the training data (i.e., internally partitioning the training data to learning and validation sets) and selecting the value that gave best results on the validation set. The training R2 was calculated as the average R2 achieved using internal cross-validation on the training set.

Kinetic model of gene expression

Gene expression is a function of TF binding to the promoter. Therefore, the way in which TFs find their target has implications for gene expression output. A recent study (Hammar et al. 2012) presented two observations regarding TF search. First, it showed that the proximity of two TFBSs affects the time that it takes the TF to bind them (Kon) in a manner that depends on the distance between the sites. Second, the study showed that a DNA-bound protein increases both the time between binding events (Kon) and the bound TF dissociation (Koff) of a neighboring TFBS. These ideas were used to integrate different mechanisms of TF search in a model of gene expression.

Mean expression and expression noise for the set of all 27 combinations of seven TF binding sites in two sequence contexts (see Supplemental Table S1) was predicted by mapping each promoter configuration to a unique kinetic scheme in which the reactions represent either binding or unbinding events at the promoter. A promoter that has N sites has 2N possible promoter states (each site is either bound or not bound) for which the transitions between them are defined by a transition matrix K, where Kij is the rate of going from state j to state i. Only binding or unbinding events a single site at a time are allowed; all other reaction rates are set to zero. Each promoter state has a transcription rate defined in vector r, where ri is the transcription rate of state i. This system was solved analytically by following the procedure described by Sanchez et al. (2011) and assuming translation to happen instantaneously, i.e., that the mRNA half-life is much shorter than the protein half-life, so that it can be assumed that the number of proteins produced per mRNA follows a geometric distribution with mean (burst size) b. Protein degradation happens with rate delta, but is mostly a result of dilution from cell division due to the high stability of the fluorescent reporter. The described kinetic scheme is solved analytically using the Master equation to obtain the mean protein abundance and noise. Alternatively, the kinetic scheme was solved numerically using stochastic simulations (Gillespie algorithm) (Gillespie 1977). We note that both methods gave similar results (R2 = 0.99) (see Supplemental Fig. S14).

Although the free parameter values of the model can be constrained to a biologically meaningful regime (see Supplemental Material), the values of the free parameters were learned from our measured data. In order to prevent overfitting, a 10-fold cross-validation scheme was used in which the model performance was tested on a held-out subset of the data that was not used for learning.

For each of the two alternative models, a different mapping between the free parameters of the model and the transition matrix K was specified. The 3D diffusion, specific-binding-only model assumes that binding happens only at the specific site. All rates in this model are independent of neighboring sites or bound TFs. The nonspecific binding and 1D diffusion model assumes a general nonspecific binding and unbinding rate and unique binding and unbinding rates for each of the seven binding sites. Therefore, the effective rates of binding and unbinding were computed using the equations presented by Hammar et al. (2012) in which a 1D diffusion coefficient, the nonspecific binding or unbinding rate, and the distance to the neighboring site determine the effective rate of binding or unbinding, respectively. A computation of this rate involves two scenarios: (1) The neighboring site is empty, in which case it is assumed that it “steals” effective binding from the current site; and (2) the neighboring site is bound, in which case it acts as a “roadblock” and decreases the effective rate of both binding and unbinding. See Supplemental Material for the equations used.

Measurement of native S. cerevisiae promoter reporter library

Genomically integrated native promoter reporter strains from Keren et al. (2013) and isolated strains from the library were measured using fluorescence-activated cell sorting (FACS) in SC-Glu-URA (synthetic complete media with 2% glucose and without uracil) medium without amino acids, except for histidine. For each strain a minimum of 20,000 cells were collected.

Data access

Raw and processed data from this study have been submitted to the NCBI Gene Expression Omnibus (GEO; http://www.ncbi.nlm.nih.gov/geo/) under accession number GSE55346. Code used for the library construction and analysis is available in the Supplemental Material and at http://genie.weizmann.ac.il/software/p_noise.html.

Supplementary Material

Supplemental Material
supp_24_10_1698__index.html (1.6KB, html)

Acknowledgments

This work was supported by grants from the European Research Council and the US National Institutes of Health to E.S. E.S. is the incumbent of the Soretta and Henry Shapiro Career Development Chair. We thank Shai Lubliner for help with computational analyses.

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.168773.113.

References

  1. Acar M, Mettetal JT, van Oudenaarden A. 2008. Stochastic switching as a survival strategy in fluctuating environments. Nat Genet 40: 471–475 [DOI] [PubMed] [Google Scholar]
  2. Amit R, Garcia HG, Phillips R, Fraser SE. 2011. Building enhancers from the ground up: a synthetic biology approach. Cell 146: 105–118 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bar-Even A, Paulsson J, Maheshri N, Carmi M, O’Shea E, Pilpel Y, Barkai N. 2006. Noise in protein expression scales with natural protein abundance. Nat Genet 38: 636–643 [DOI] [PubMed] [Google Scholar]
  4. Basehoar AD, Zanton SJ, Pugh BF. 2004. Identification and distinct regulation of yeast TATA box-containing genes. Cell 116: 699–709 [DOI] [PubMed] [Google Scholar]
  5. Batenchuk C, St-Pierre S, Tepliakova L, Adiga S, Szuto A, Kabbani N, Bell JC, Baetz K, Kærn M. 2011. Chromosomal position effects are linked to sir2-mediated variation in transcriptional burst size. Biophys J 100: L56–L58 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beaumont HJE, Gallie J, Kost C, Ferguson GC, Rainey PB. 2009. Experimental evolution of bet hedging. Nature 462: 90–93 [DOI] [PubMed] [Google Scholar]
  7. Blake WJ, Kærn M, Cantor CR, Collins JJ. 2003. Noise in eukaryotic gene expression. Nature 422: 633–637 [DOI] [PubMed] [Google Scholar]
  8. Blake WJ, Balázsi G, Kohanski MA, Isaacs FJ, Murphy KF, Kuang Y, Cantor CR, Walt DR, Collins JJ. 2006. Phenotypic consequences of promoter-mediated transcriptional noise. Mol Cell 24: 853–865 [DOI] [PubMed] [Google Scholar]
  9. Cai L, Friedman N, Xie XS. 2006. Stochastic protein expression in individual cells at the single molecule level. Nature 440: 358–362 [DOI] [PubMed] [Google Scholar]
  10. Carey LB, van Dijk D, Sloot PMA, Kaandorp JA, Segal E. 2013. Promoter sequence determines the relationship between expression level and noise. PLoS Biol 11: e1001528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Choi JK, Kim YJ. 2009. Intrinsic variability of gene expression encoded in nucleosome positioning sequences. Nat Genet 41: 498–503 [DOI] [PubMed] [Google Scholar]
  12. Dadiani M, van Dijk D, Segal B, Field Y, Ben-Artzi G, Raveh-Sadka T, Levo M, Kaplow I, Weinberger A, Segal E. 2013. Two DNA-encoded strategies for increasing expression with opposing effects on promoter dynamics and transcriptional noise. Genome Res 23: 966–976 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Elowitz MB, Levine AJ, Siggia ED, Swain PS. 2002. Stochastic gene expression in a single cell. Science 297: 1183–1186 [DOI] [PubMed] [Google Scholar]
  14. Friedman N, Cai L, Xie XS. 2006. Linking stochastic dynamics to population distribution: an analytical framework of gene expression. Phys Rev Lett 97: 168302. [DOI] [PubMed] [Google Scholar]
  15. Gertz J, Siggia ED, Cohen BA. 2009. Analysis of combinatorial cis-regulation in synthetic and genomic promoters. Nature 457: 215–218 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gillespie DT. 1977. Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81: 2340–2361 [Google Scholar]
  17. Giniger E, Ptashne M. 1988. Cooperative DNA binding of the yeast transcriptional activator GAL4. Proc Natl Acad Sci 85: 382–386 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gotea V, Visel A, Westlund JM, Nobrega MA, Pennacchio LA, Ovcharenko I. 2010. Homotypic clusters of transcription factor binding sites are a key component of human promoters and enhancers. Genome Res 20: 565–577 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hammar P, Leroy P, Mahmutovic A, Marklund EG, Berg OG, Elf J. 2012. The lac repressor displays facilitated diffusion in living cells. Science 336: 1595–1598 [DOI] [PubMed] [Google Scholar]
  20. Hornung G, Bar-Ziv R, Rosin D, Tokuriki N, Tawfik DS, Oren M, Barkai N. 2012. Noise–mean relationship in mutated promoters. Genome Res 22: 2409–2417 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Keren L, Zackay O, Lotan-Pompan M, Barenholz U, Dekel E, Sasson V, Aidelberg G, Bren A, Zeevi D, Weinberger A, et al. 2013. Promoters maintain their relative activity levels under different growth conditions. Mol Syst Biol 9: 701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Khazanov N, Marcovitz A, Levy Y. 2013. Asymmetric DNA-search dynamics by symmetric dimeric proteins. Biochemistry 52: 5335–5344 [DOI] [PubMed] [Google Scholar]
  23. Kim S, Broströmer E, Xing D, Jin J, Chong S, Ge H, Wang S, Gu C, Yang L, Gao YQ, et al. 2013. Probing allostery through DNA. Science 339: 816–819 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lehner B. 2010. Conflict between noise and plasticity in yeast. PLoS Genet 6: e1001185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. LeProust EM, Peck BJ, Spirin K, McCuen HB, Moore B, Namsaraev E, Caruthers MH. 2010. Synthesis of high-quality libraries of long (150mer) oligonucleotides by a novel depurination controlled process. Nucleic Acids Res 38: 2522–2540 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Li GW, Berg OG, Elf J. 2009. Effects of macromolecular crowding and DNA looping on gene regulation kinetics. Nat Phys 5: 294–297 [Google Scholar]
  27. MacIsaac KD, Wang T, Gordon DB, Gifford DK, Stormo GD, Fraenkel E. 2006. An improved map of conserved regulatory sites for Saccharomyces cerevisiae. BMC Bioinformatics 7: 113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Miller JA, Widom J. 2003. Collaborative competition mechanism for gene activation in vivo. Mol Cell Biol 23: 1623–1632 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mogno I, Vallania F, Mitra RD, Cohen BA. 2010. TATA is a modular component of synthetic promoters. Genome Res 20: 1391–1397 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Munsky B, Neuert G, van Oudenaarden A. 2012. Using gene expression noise to understand gene regulation. Science 336: 183–187 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Murphy KF, Balázsi G, Collins JJ. 2007. Combinatorial promoter design for engineering noisy gene expression. Proc Natl Acad Sci 104: 12726–12731 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Newman JRS, Ghaemmaghami S, Ihmels J, Breslow DK, Noble M, DeRisi JL, Weissman JS. 2006. Single-cell proteomic analysis of S. cerevisiae reveals the architecture of biological noise. Nature 441: 840–846 [DOI] [PubMed] [Google Scholar]
  33. Ozbudak EM, Thattai M, Kurtser I, Grossman AD, van Oudenaarden A. 2002. Regulation of noise in the expression of a single gene. Nat Genet 31: 69–73 [DOI] [PubMed] [Google Scholar]
  34. Pachkov M, Balwierz PJ, Arnold P, Ozonov E, van Nimwegen E. 2013. SwissRegulon, a database of genome-wide annotations of regulatory sites: recent updates. Nucleic Acids Res 41: D214–D220 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Paulsson J. 2004. Summing up the noise in gene networks. Nature 427: 415–418 [DOI] [PubMed] [Google Scholar]
  36. Pedraza JM, Paulsson J. 2008. Effects of molecular memory and bursting on fluctuations in gene expression. Science 319: 339–343 [DOI] [PubMed] [Google Scholar]
  37. Portales-Casamar E, Thongjuea S, Kwon AT, Arenillas D, Zhao X, Valen E, Yusuf D, Lenhard B, Wasserman WW, Sandelin A. 2010. JASPAR 2010: the greatly expanded open-access database of transcription factor binding profiles. Nucleic Acids Res 38: D105–D110 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Rainey PB, Beaumont HJE, Ferguson GC, Gallie J, Kost C, Libby E, Zhang XX. 2011. The evolutionary emergence of stochastic phenotype switching in bacteria. Microb Cell Fact (Suppl 1) 10: S14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Raj A, Peskin CS, Tranchina D, Vargas DY, Tyagi S. 2006. Stochastic mRNA synthesis in mammalian cells. PLoS Biol 4: e309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Raser JM, O’Shea EK. 2004. Control of stochasticity in eukaryotic gene expression. Science 304: 1811–1814 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Raveh-Sadka T, Levo M, Shabi U, Shany B, Keren L, Lotan-Pompan M, Zeevi D, Sharon E, Weinberger A, Segal E. 2012. Manipulating nucleosome disfavoring sequences allows fine-tune regulation of gene expression in yeast. Nat Genet 44: 743–750 [DOI] [PubMed] [Google Scholar]
  42. Sanchez A, Garcia HG, Jones D, Phillips R, Kondev J. 2011. Effect of promoter architecture on the cell-to-cell variability in gene expression. PLoS Comput Biol 7: e1001100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sharon E, Kalma Y, Sharp A, Raveh-Sadka T, Levo M, Zeevi D, Keren L, Yakhini Z, Weinberger A, Segal E. 2012. Inferring gene regulatory logic from high-throughput measurements of thousands of systematically designed promoters. Nat Biotechnol 30: 521–530 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Sherman MS, Cohen BA. 2014. A computational framework for analyzing stochasticity in gene expression. PLoS Comput Biol 10: e1003596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. So LH, Ghosh A, Zong C, Sepúlveda LA, Segev R, Golding I. 2011. General properties of transcriptional time series in Escherichia coli. Nat Genet 43: 554–560 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Stewart-Ornstein J, Weissman JS, El-Samad H. 2012. Cellular noise regulons underlie fluctuations in Saccharomyces cerevisiae. Mol Cell 45: 483–493 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tirosh I, Barkai N. 2008. Two strategies for gene regulation by promoter nucleosomes. Genome Res 18: 1084–1091 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Venters BJ, Wachi S, Mavrich TN, Andersen BE, Jena P, Sinnamon AJ, Jain P, Rolleri NS, Jiang C, Hemeryck-Walsh C, et al. 2011. A comprehensive genomic binding map of gene and chromatin regulatory proteins in Saccharomyces. Mol Cell 41: 480–492 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Weinberger LS, Burnett JC, Toettcher JE, Arkin AP, Schaffer DV. 2005. Stochastic gene expression in a lentiviral positive-feedback loop: HIV-1 Tat fluctuations drive phenotypic diversity. Cell 122: 169–182 [DOI] [PubMed] [Google Scholar]
  50. Weingarten-Gabbay S, Segal E. 2014. The grammar of transcriptional regulation. Hum Genet 133: 701–711 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wunderlich Z, Mirny LA. 2009. Different gene regulation strategies revealed by analysis of binding motifs. Trends Genet 25: 434–440 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zenklusen D, Larson DR, Singer RH. 2008. Single-RNA counting reveals alternative modes of gene expression in yeast. Nat Struct Mol Biol 15: 1263–1271 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Zou H, Hastie T. 2005. Regularization and variable selection via the elastic net. Stat Methodol 67: 301–320 [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
supp_24_10_1698__index.html (1.6KB, html)
supp_gr.168773.113_Supplemental_Material.pdf (12.2MB, pdf)
supp_gr.168773.113_Supplemental_scripts.zip (100.2KB, zip)
supp_gr.168773.113_TableS1.txt (23.6KB, txt)
supp_gr.168773.113_TableS2.txt (461B, txt)
supp_gr.168773.113_TableS3.txt (1.3MB, txt)
supp_gr.168773.113_TableS4.txt (1.3MB, txt)
supp_gr.168773.113_TableS5.txt (1.5KB, txt)
supp_gr.168773.113_TableS6.txt (1.5KB, txt)
supp_gr.168773.113_TableS7.txt (511.6KB, txt)

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES