Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Oct 17;4:6663. doi: 10.1038/srep06663

Ranking scientific publications: the effect of nonlinearity

Liyang Yao 1, Tian Wei 1, An Zeng 1,2,a, Ying Fan 1,b, Zengru Di 1
PMCID: PMC4200399  PMID: 25322852

Abstract

Ranking the significance of scientific publications is a long-standing challenge. The network-based analysis is a natural and common approach for evaluating the scientific credit of papers. Although the number of citations has been widely used as a metric to rank papers, recently some iterative processes such as the well-known PageRank algorithm have been applied to the citation networks to address this problem. In this paper, we introduce nonlinearity to the PageRank algorithm when aggregating resources from different nodes to further enhance the effect of important papers. The validation of our method is performed on the data of American Physical Society (APS) journals. The results indicate that the nonlinearity improves the performance of the PageRank algorithm in terms of ranking effectiveness, as well as robustness against malicious manipulations. Although the nonlinearity analysis is based on the PageRank algorithm, it can be easily extended to other iterative ranking algorithms and similar improvements are expected.

Many efforts have been made to accelerate the publication of research findings. As a result, hundreds of new journals have been created in the past decade, and thousands of scientific papers are published everyday. Determining how to measure the scientific influence of these publications is not easy and has been a research focus for a long time1. So far, many metrics have been introduced, but it remains unclear whether these methods rank papers in an objective way2,3,4,5,6. The number of citations, though simple, is a widely used metric to measure the importance of a paper7,8,9. The number of citations is now treated as a common indicator to assess the scientific productions of individuals or institutions as well as the influence of scientists10,11,12. For example, the well-known H index is designed based on the citation number of papers13. Recently, a universal property of citation distributions has been found within several science disciplines, making it possible to design an unbiased indicator for citation performance across disciplines and years14,15. From another aspect, comments are found as early indicators of the future impact of criticized papers in research16. A mechanistic model for the citation dynamics of individual papers has also been developed to predict the future citation evolution17.

To evaluate the scientific impact of a paper, one must consider not only the number of citations that matters but also the means, by which the paper is being cited18,19. This idea is realized by introducing Google's PageRank algorithm to the citation networks to rank papers20. This algorithm takes into account the importance of the citing papers and assigns a high score to a node cited by important papers. The scores of papers are updated in each iteration loop, and the final stable scores are used as the indicator of the significance of the papers. Many variants of the PageRank algorithm were later designed to highlight the prestige in the citation networks of journals21, publications20,22,23 and scientists18,24. The so-called CiteRank, for example, accounts for the strong aging characteristics of citation networks by initially distributing random surfers exponentially with age, in favor of the more recent publications22. Another variant, called DivRank, makes use of a reinforced random walk on the citation network to diversify the papers in the top of the obtained ranking list25.

Malicious activities are common in citation networks, in particular, when researchers manipulate the citations to boost the importance of their papers26,27. One example of the manipulation is to deliberately cite the target papers when researchers or their friends publish new papers. Although, in these cases, the citing papers are usually not extremely outstanding ones, they can still substantially increase the citation number and the PageRank score of the target papers. In PageRank and its variants, the random jump process is used to avoid the sink nodes attracting all scores, so any paper in the network will at least have the score from the random jump process25,28. In each iteration loop of these algorithms, the score of a node equals to the linear summation of the score transferred from neighboring nodes. Therefore, one can always increase the score of the target paper as long as he/she can continue to publish new papers.

In this paper, we argue that the robustness of the iterative ranking algorithms against malicious citations can be improved by introducing nonlinearity to the PageRank algorithm. Specifically, when aggregating the score of the nodes in each step, we introduce a nonlinear operation that favors the nodes with high-score citing papers but punish the nodes with only low-score citing papers. We refer to our method as NonlinearRank in this paper. In fact, the concept of nonlinearity has recently been introduced to design an algorithm to rank the fitness of countries and complexity of products in international trading networks29. Our method was validated in the citation network constructed from the data of American Physical Society (APS) journals30. Simulations indicate that our NonlinearRank algorithm outperforms PageRank in identifying influential papers (examined by real awards, prediction power and spreading ability). Moreover, NonlinearRank is more robust against malicious manipulations.

Results

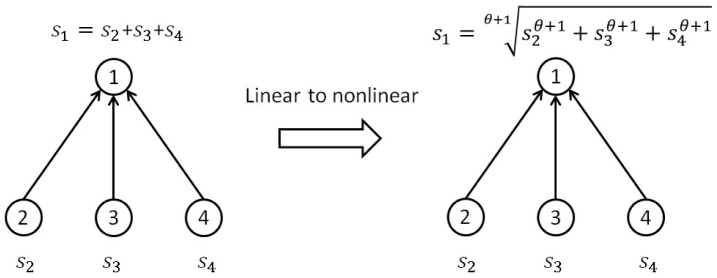
To begin our analysis, we briefly describe the basic concept of the NonlinearRank algorithm. The essential difference between the NonlinearRank and PageRank algorithms is the way a node aggregates the score from its incoming links. The process of these two algorithms is illustrated in Fig. 1. In PageRank, the score of the target node is simply the linear summation of the score distributed from its downstream neighbors (i.e. the papers citing it). However, this procedure is performed in a nonlinear way in NonlinearRank, as shown Fig. 1. The reason to introduce the nonlinearity is twofold. First, the power to the score further separates the contribution of nodes of high score from those of low score, which enables only the papers cited by some high score papers to become important. Second, the root reduces the effect of the number of citations on the final ranking. With this approach, the nodes cited by a large number of low score papers cannot have high score in the end. The power and the root actually work in the same direction: favoring the papers cited by many important ones and punishing the papers cited by a large number of unimportant ones. In fact, Pagerank can be interpreted as a diffusion process on networks. It is simply a combination of random walk and random jump processes, with a parameter c determining the probability of random jump. In NonlinearRank, the random jump process is preserved while the other process is replaced by a non-diffusion iterative process. In each step, the score of a node is equal to the p-norm of the vector consisting of the neighboring nodes' scores (p = θ + 1 in this case). When θ is infinitely large, each node only receives the score from the highest-score neighbor. Unlike the random walk process, the total score of the new iterative process is no longer conservative but smaller than the initial value. However, the nodes' scores will reach a steady state after several steps of iterations (see SI). The detailed description of the NonlinearRank algorithm is presented in the Method section. In the following, we will validate the method from several aspects.

Figure 1. The illustration of the linear and nonlinear aggregation of the score from a node's downstream neighbors.

Figure 1

Open in a new tab

We tested the performance of the NonlinearRank algorithm in the citation network Ga constructed from the articles in the American Physical Society (APS) journals from 1897 to 2009. The citation network is described by an adjacency matrix A in which an element Aij = 1 indicates that the article i is cited by the article j. Because new articles can only cite articles published earlier, Ga should be a directed acyclic network. However, we observe some inconsistent records in the raw data that form some loops in the citation network. After filtering out these problematic data by the information of publishing date, the final citation network used in this paper is a pure acyclic one with 462, 720 nodes (articles) and 4, 620, 025 edges (citations). The analysis of NonlinearRank in this paper is based on this full APS data. We actually investigate as well the performance of NonlinearRank in a subset where the network is constructed by randomly selecting 20% publications in APS data. Even though the advantage of NonlinearRank over PageRank is smaller when the amount of data is reduced, the results are qualitatively similar to that with full data.

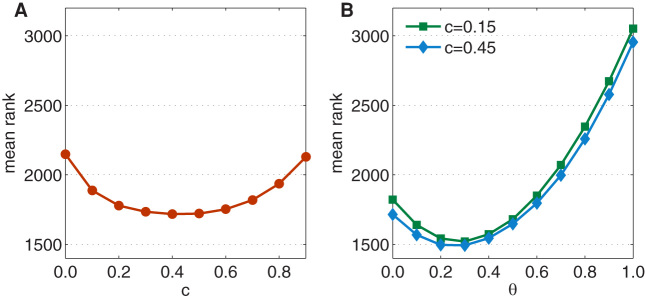
Due to the detailed information of the raw data, we can gain access to the title of each paper, thus being able to determine which papers are recognized by prizes. This information on awards and prizes is very important because it enables us to identify some truly outstanding articles that are commonly accepted as being outstanding by scientists. These papers serve as a benchmark set for us to examine the performance of the PageRank and NonlinearRank in identifying the high quality papers. Here, we picked 39 articles awarded the Nobel Prize in Physics from the year 1950 to 2009 as our benchmark articles (see SI for details). Generally speaking, a good algorithm should assign these prized papers with high ranks. We thus compare the mean rank of these papers in the PageRank and NonlinearRank algorithms, as shown in Fig. 2. One immediate observation from Fig. 2(a) is that there is an optimal parameter c for the random jump in PageRank that results in a minimum mean rank of these prized papers. Interestingly, the optimal parameter c is 0.45 instead of 0.15, which indicates the popular parameter choice in computer science may not serve as an optimal setting for applying PageRank in complex network analysis. This result is consistent with a recent finding in which the optimal c is drawn by the rank-reversal analysis31. To compare the performance of the NonlinearRank to PageRank, we set c = 0.15 and c = 0.45 in two implementations of NonlinearRank and investigated the effect of the parameter θ on the mean rank of the prized papers. We found that the adjustment of θ can lead to a substantial decrease of the mean rank and that the optimal θ in both cases is approximately 0.3.

Figure 2. The dependence of the mean rank of 39 Nobel awarded articles on parameter c and θ in the (A) PageRank and (B) NonlinearRank algorithms, respectively.

Figure 2

Open in a new tab

We further validated the effectiveness of the NonlinearRank method via the spreading process on citation networks. The spreading process in citation networks can be regarded as the propagation of scientific ideas, such as techniques or findings. Each paper in the citation network holds an idea, which will be spread to each paper that cites the initial paper. The papers accepting this idea with a certain probability will further spread it to their downstream papers. The more influential paper should be able to spread its idea more broadly. In fact, the spreading of knowledge and the tracing of the origin of ideas in science are interesting problems and have attracted much attention recently32. Here, we employ the Susceptible-Infected-Removed (SIR) model33 and consider the final coverage given the spreading originating from it as the influence of each paper. We choose the top-L ranked nodes in the NonlinearRank algorithms and study the dependence of their average spreading coverage on θ. We again select two typical parameter settings c = 0.15 and c = 0.45 in Fig. 3. Note that when θ = 0, the NonlinearRank degenerates to the PageRank. We can see in both Fig. 3(A) and (B) that when θ = 0.3 the average spreading coverage of the top ranking nodes is larger than that when θ = 0, indicating NonlinearRank outperforms PageRank in ranking the influence of the nodes. Nevertheless, we observe that the improvement of NonlinearRank to PageRank is smaller when c = 0.45.

Figure 3. The evolution of the average spreading coverage of the top-50 ranked nodes in NonlinearRank with (A) c = 0.15 and (B) c = 0.45.

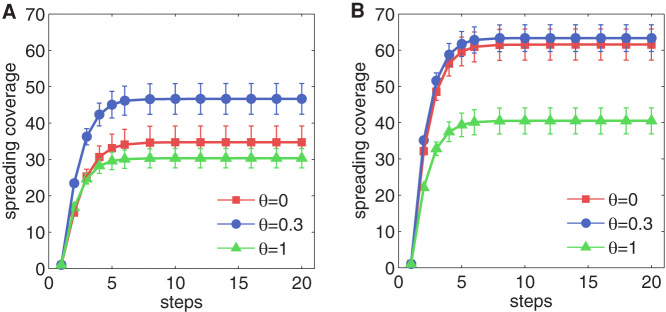
Figure 3

Open in a new tab

The infection rate of the SIR model is set as 0.03. Results are obtained by averaging 100 times of independent realizations.

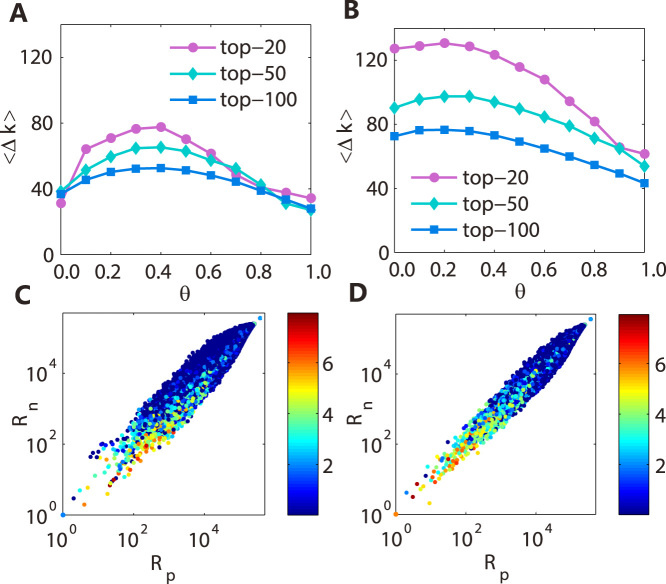
A good ranking algorithm should be effective not only in identifying the influential nodes, but also in predicting the future. Instead of predicting the detailed evolution of the degree of the nodes, here we focus on predicting the most popular nodes. In particular, we pick a testing time t and construct the citation network based on all historical data before t where the PageRank and NonlinearRank algorithms are running. After obtaining the ranking lists, we select the top-L papers and calculate their future degree increment 〈Δk〉 in a future time window [t, t + Δt]. Naturally, if a ranking algorithm is good at identifying the most popular papers in the future, 〈Δk〉 of the top-L papers in [t, t + Δt] will be accordingly large. We tested 40 testing times t from 1960 to 1999 with Δt = 10 years. For clarification, we selected three representative L papers to present in Fig. 4. By examining the dependence of the 〈Δk〉 on θ, we find that there is an optimum of 〈Δk〉 of approximately θ = 0.3. This result indicates that the nonlinearity can indeed improve the prediction ability of the ranking algorithm.

Figure 4.

Figure 4

Open in a new tab

The dependence of the average future degree increment 〈Δk〉 of the top-L papers on θ in NonlinearRank with (A) c = 0.15 and (B) c = 0.45. The results in both (A) and (B) are averaged over 40 testing times t from 1960 to 1999 with the future time window as 10 years. The future degree increment loge(Δk) of papers as a function of Rp and Rn are shown in (C) c = 0.15 and (D) c = 0.45, with t = 2000, Δt = 9 years.

As further support of the proposed approach, we studied Δk of papers as a function of Rp (ranks of papers from PageRank) and Rn (ranks of papers from NonlinearRank) in Fig. 4, where t = 2000 and Δt = 9 years. In this scatter plot, the color of each point corresponds to Δk of this particular article. Obviously, those articles with high Δk are located in the region where Rn is small but Rp is relatively large. This result confirms again that NonlinearRank outperforms PageRank in its prediction performance.

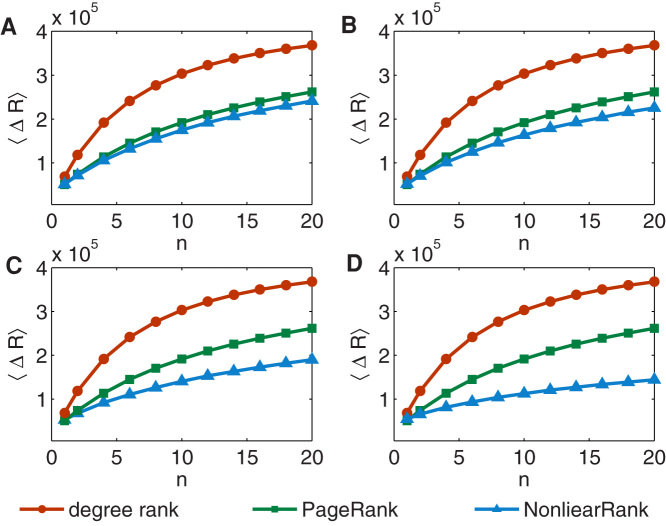
Tolerance of the ranking algorithms against malicious behaviors is crucial, especially when the network structure is subject to manipulations. Here, we consider a common case in a citation network in which some articles deliberately cite one target paper to enhance its ranking. We study the robustness of the ranking algorithms to this situation via the leave-one-out validation. Specifically, we constructed the citation network from the APS data and assumed that it is error-free. A paper with indegree k = 0 is randomly picked and considered as the target paper whose rank is intended to be enhanced. n new papers with m links each are then added to the citation network. All of these new papers will cite the target paper and the rest of their links will randomly connect to other nodes. In the original network, the ranks of the target paper from the PageRank and NonlinearRank are denoted as Rp(Ao) and Rn(Ao), respectively. In the modified network, the corresponding ranks from the PageRank and NonlinearRank are denoted as Rp(Am) and Rn(Am), respectively. The rank change for the PageRank and NonlinearRank results can be calculated as ΔRp = Rp(Ao) − Rp(Am) and ΔRn = Rn(Ao) − Rn(Am). A smaller ΔR indicates a higher robustness against manipulations. The relationship between the average rank change 〈ΔR〉 and n is shown in Fig. 5, where we study the degree rank, PageRank and NonlinearRank methods. As expected, the degree rank is the most sensitive to such a manipulation. PageRank is better than degree rank in resisting the manipulation. Among these three methods, NonlinearRank enjoys the smallest 〈ΔR〉 in different n, indicating the high reliability of the method. Interestingly, the parameter θ is strongly related to the reliability of the NonlinearRank. One can see in Fig. 5 that 〈ΔR〉 generally decreases with θ. Accordingly, we remark that the selection of θ is a trade-off between ranking effectiveness (i.e. identifying the influential papers) and reliability (i.e. suppressing the manipulated low quality papers). A small θ of approximately 0.3 enjoys a high ranking effectiveness but leads to only slightly better ranking reliability than that of the PageRank method. A large θ, although very robust against malicious manipulation, does not have a satisfactory ranking effectiveness. In practice, one can use a smaller value of θ if the ranking effectiveness is the main goal, or a larger value if the resistance to manipulation is a major issue.

Figure 5. The average rank change 〈ΔR〉 of the manipulated papers when different ranking algorithms are used.

Figure 5

Open in a new tab

In this figure, n is the number of new papers added and each new paper has m = 20 links. In both PageRank and NonlinearRank, c = 0.45. θ of NonlinearRank is different in each panel: (A) θ = 0.3, (B) θ = 0.5, (C) θ = 1.0 and (D) θ = 2.0. Results are obtained by averaging 100 times of independent realizations.

Discussion

We proposed an iterative ranking algorithm where the nonlinearity is imposed on the aggregation of scores of the nodes in each step. The basic idea is to further enhance the effect of high score papers while suppressing the effect of the low score papers in the iterations of the algorithm. Extensive simulation results indicated that the proposed NonlinearRank method is able to outperform the well-known PageRank method in identifying the influential papers with respect to real awards, spreading ability and prediction. In particular, the NonlinearRank method can resist the malicious manipulation in the citation networks that aims to enhance the rank of low quality papers. Though the NonlinearRank method aims to rank the influence of individual publication, it may contribute to related research in macroscopic level. For example, a more accurate ranking of papers' quality may help to deepen our understanding of scientists' career patterns35, as well as the scientific production and consumption in different regions36. The application of the NonlinearRank method is not restricted to citation networks. The proposed method can be naturally used in many other real systems, such as designing search engines in the World Wide Web and revealing the leaderships in social networks.

In fact, there are many other nonlinearity formulae that can be used for the iterative algorithms. A possible one is to make the random walk in the PageRank algorithm be preferential towards nodes of different degree or similarity. Such preferences can be further adjusted by nonlinear functions. In addition, the random walk process can be nonlinearly hybridized with the heat conduction process. This hybridization has already been shown to enhance the recommendation performance in user-object bipartite networks34. Similar nonlinear combination in PageRank might be able to improve its effectiveness as well as the diversity in the top of the ranking list.

Finally, even though a very simple malicious manipulation scheme is considered in this paper, we remark that the cases in real systems are more complicated. For example, the malicious papers in citation networks might form many triangles. This malicious manipulation will largely increase the PageRank score of these malicious papers and subsequently enhance the rank of the target low quality paper. Moreover, the malicious papers might deliberately cite a very small number of papers, making most of the PageRank score of these malicious papers to be transferred to the target low quality paper. Under both manipulation schemes above, the ranking from the iterative algorithms might be influenced more significantly than the degree rank. Therefore, the iterative algorithms resistance to these more realistic manipulation approaches requires future investigation.

Methods

Degree rank

The most straightforward method to rank articles is to use their citation numbers. In the citation network, the citation is simply the indegree of nodes as

graphic file with name srep06663-m1.jpg

where Aij is an element in the adjacency matrix of the citation network. The final ranking of nodes will be obtained by sorting ki in a descending order.

PageRank

PageRank is a famous ranking algorithm that forms the basis of the Google™ search engine. In practice, PageRank assigns a score si to denote the attractiveness of the webpage i. Webpage i obtains a higher score if many other important webpages point to it. From the physical perspective, PageRank describes a random walk process on a directed network, where the score si is proportional to the frequency of visits to a particular node i by a random walker. In the PageRank algorithm, the parameter c (0 ≤ c ≤ 1) called return probability is introduced, which represents the probability for a random walker to jump to a random node, and (1 − c) is the probability for the random walker to continue walking through the directed links. In this way, the node i's centrality score at time t (t ≥ 1) is given by

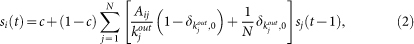graphic file with name srep06663-m2.jpg

where δa,b = 1 when a = b, and δa,b = 0 otherwise. Initially, we assign each node one random walker, namely si(0) = 1 for 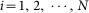Inline graphic. The typical value of the return probability in computer science is approximately 0.1528. The final score of each node is defined as the steady value after the convergence of si(t). The final ranking of nodes in PageRank, denoted as Rp, will be obtained by sorting si in a descending order when si reaches the stable state.

NonlinearRank

NonlinearRank works similarly to PageRank. The only difference is the way it aggregates the score from downstream neighboring nodes. Mathematically, it reads

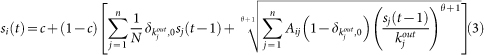graphic file with name srep06663-m3.jpg

where θ is a tunable parameter. We can control the effect of downstream papers through the adjustment of parameter θ, so that only papers cited by high score papers get higher score and the paper cited by plenty of low score papers cannot get high score in the end. Notice that NonlinearRank reduces to PageRank when θ = 0. The final ranking of nodes in NonlinearRank, denoted as Rn, will be obtained by sorting si in a descending order when si reaches the stable state. The basic statistical properties of the NonlinearRank method are presented in the SI.

Author Contributions

A.Z., Y.F. and Z.D. designed the research, L.Y. and T.W. performed the experiments, L.Y., T.W. and A.Z. analysed the data, A.Z., L.Y., Y.F. and Z.D. wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep06663-s1.pdf (73.4KB, pdf)

Acknowledgments

This work is supported by the National Natural Science Foundation of China under Grant Nos. 61374175 and 61174150, and the major project of National Social Science Fund (12&ZD217).

References

  1. Sidiropoulos A. & Manolopoulos Y. Generalized comparison of graph-based ranking algorithms for publications and authors. J. Syst. Software 79, 1679–1700 (2006). [Google Scholar]
  2. Seglen P. O. Why the impact factor of journals should not be used for evaluating research. BMJ 314, 498–502 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Favaloro E. J. Measuring the quality of journals and journal articles: the impact factor tells but a portion of the story. Semin. Thromb. Hemost. 34, 7–25 (2008). [DOI] [PubMed] [Google Scholar]
  4. Maslov S. & Redner S. Promise and pitfalls of extending Google's PageRank algorithm to citation networks. J. Neurosci. 28, 11103–11105 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Adler R., Ewing J. & Taylor P. Citation statistics. Statist. Sci. 24, 1–14 (2009). [Google Scholar]
  6. Frey B. S. & Rost K. Do rankings reflect research quality? J. Appl. Econ. 13, 1–38 (2010). [Google Scholar]
  7. Garfield E. Citation indexes for science A new dimension in documentation through association of ideas. Science 122, 108–111 (1955). [DOI] [PubMed] [Google Scholar]
  8. Garfield E. Citation Indexing: Its Theory And Application In Science, Technology, And Humanities. (John Wiley & Sons Inc., New York, 1979). [Google Scholar]
  9. Amsterdamska O. & Leydesdorff L. Citations: Indicators of significance? Scientometrics 15, 449–471 (1989). [Google Scholar]
  10. Van Raan Anthony F. J. Fatal attraction: Conceptual and methodological problems in the ranking of universities by bibliometric methods. Scientometrics 62, 133–143 (2005). [Google Scholar]
  11. Boyack K. W. & Borner K. Indicator-assisted evaluation and funding of research: Visualizing the influence of grants on the number and citation counts of research papers. J. Am. Soc. Inf. Sci. Technol. 54, 447–461 (2003). [Google Scholar]
  12. Mazloumian A., Eom Y. H., Helbing D., Lozano S. & Fortunato S. How citation boosts promote scientific paradigm shifts and nobel prizes. PLoS ONE 6, e18975 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hirsch J. E. An index to quantify an individual's scientific research output. Proc. Natl. Acad. Sci. U.S.A. 102, 16569–16572 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Radicchi F., Fortunato S. & Castellano C. Universality of citation distributions: Toward an objective measure of scientific impact. Proc. Natl. Acad. Sci. U.S.A. 105, 17268–17272 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Radicchi F. & Castellano C. Rescaling citations of publications in physics. Phys. Rev. E 83, 046116 (2011). [DOI] [PubMed] [Google Scholar]
  16. Radicchi F. In science there is no bad publicity: Papers criticized in comments have high scientific impact. Sci. Rep. 2, 815 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Wang D., Song C. & Barabasi A. L. Quantifying Long-Term Scientific Impact. Science 342, 127–132 (2013). [DOI] [PubMed] [Google Scholar]
  18. Radicchi F., Fortunato S., Markines B. & Vespignani A. Diffusion of scientific credits and the ranking of scientists. Phys. Rev. E 80, 056103 (2009). [DOI] [PubMed] [Google Scholar]
  19. Franceschet M. The difference between popularity and prestige in the sciences and in the social sciences: A bibliometric analysis. J. Informetr. 4, 55–63 (2010). [Google Scholar]
  20. Chen P., Xie H., Maslov S. & Redner S. Finding scientific gems with Google's PageRank algorithm. J. Informetr. 1, 8–15 (2007). [Google Scholar]
  21. Bollen J., Rodriquez M. A. & Van de Sompel H. Journal status. Scientometrics 69, 669–687 (2006). [Google Scholar]
  22. Walker D., Xie H., Yan K. K. & Maslov S. Ranking scientific publications using a model of network traffic. J. Stat. Mech. Theor. Exp. 2007, P06010 (2007). [Google Scholar]
  23. Ma N., Guan J. & Zhao Y. Bringing PageRank to the citation analysis. Inform. Process. Manag. 44, 800–810 (2008). [Google Scholar]
  24. Ding Y., Yan E. & Frazho A. PageRank for ranking authors in co-citation networks. J. Am. Soc. Inf. Sci. Technol. 60, 2229–2243 (2009). [Google Scholar]
  25. Mei Q., Guo J. & Radev D. Divrank: the interplay of prestige and diversity in information networks. Proceedings of the 16th ACM SIGKDD international conference on Knowledge Discovery and Data Mining: KDD'12, Washington, DC. New York: ACM Press. (10.1145/1835804.1835931) (July2010). [Google Scholar]
  26. Smith L. C. Citation analysis. Libr. Trends 30, 83–106 (1981). [Google Scholar]
  27. Zeng A. & Cimini G. Removing spurious interactions in complex networks. Phys. Rev. E 85, 036101 (2012). [DOI] [PubMed] [Google Scholar]
  28. Brin S. & Page L. The anatomy of a large-scale hypertextual Web search engine. Comput. networks ISDN 30, 107–117 (1998). [Google Scholar]
  29. Tacchella A., Cristelli M., Caldarelli G., Gabrielli A. & Pietronero L. A new metrics for countries' fitness and products' complexity. Sci. Rep. 2, 00723 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. APS, Data sets for research. https://publish.aps.org/datasets. (2010). (accessed June 8 2010).
  31. Son S. W., Christensen C., Grassberger P. & Paczuski M. PageRank and rank-reversal dependence on the damping factor. Phys. Rev. E 86, 066104 (2012). [DOI] [PubMed] [Google Scholar]
  32. Gualdi S., Medo M. & Zhang Y. C. Influence, originality and similarity in directed acyclic graphs. Europhys. Lett. 96, 18004 (2011). [Google Scholar]
  33. Kermack W. O. & McKendrick A. G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A 115, 700–721 (1927). [Google Scholar]
  34. Zhou T. et al. Solving the apparent diversity-accuracy dilemma of recommender systems. Proc. Natl. Acad. Sci. U.S.A. 107, 4511–4515 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Deville P. et al. Career on the Move: Geography, Stratification, and Scientific Impact. Sci. Rep. 4, 4770 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zhang Q., Perra N., Goncalves B. Ciulla F. & Vespignani A. Characterizing scientific production and consumption in Physics. Sci. Rep. 3, 1640 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep06663-s1.pdf (73.4KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES