Intrinsic Functional Component Analysis via Sparse Representation on Alzheimer's Disease Neuroimaging Initiative Database

Abstract

Alzheimer's disease (AD) is the most common type of dementia (accounting for 60% to 80%) and is the fifth leading cause of death for those people who are 65 or older. By 2050, one new case of AD in United States is expected to develop every 33 sec. Unfortunately, there is no available effective treatment that can stop or slow the death of neurons that causes AD symptoms. On the other hand, it is widely believed that AD starts before development of the associated symptoms, so its prestages, including mild cognitive impairment (MCI) or even significant memory concern (SMC), have received increasing attention, not only because of their potential as a precursor of AD, but also as a possible predictor of conversion to other neurodegenerative diseases. Although these prestages have been defined clinically, accurate/efficient diagnosis is still challenging. Moreover, brain functional abnormalities behind those alterations and conversions are still unclear. In this article, by developing novel sparse representations of whole-brain resting-state functional magnetic resonance imaging signals and by using the most updated Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset, we successfully identified multiple functional components simultaneously, and which potentially represent those intrinsic functional networks involved in the resting-state activities. Interestingly, these identified functional components contain all the resting-state networks obtained from traditional independent-component analysis. Moreover, by using the features derived from those functional components, it yields high classification accuracy for both AD (94%) and MCI (92%) versus normal controls. Even for SMC we can still have 92% accuracy.

Introduction

Although first identified more than 100 years ago (Graeber et al., 1997), systematic studies of Alzheimer's disease (AD) regarding its causes, associated symptoms, and treatments or interventions have gained great momentum only during recent decades (Thies and Bleiler, 2013). AD is the most common type of dementia (accounting for 60% to 80%) and is the fifth leading cause of death for those people who are 65 or older (Thies and Bleiler, 2013). Today, every 68 sec someone in the United States develops AD and, by 2050, one new case of AD in the United States is expected to develop every 33 sec (Thies and Bleiler, 2013). During the first 10 years of the current century, the proportion of deaths caused by prostate cancer, heart disease, and stroke have decreased by 8%, 16%, and 23%, respectively, whereas the proportion resulting from AD has increased by 68% (Thies and Bleiler, 2013). Unfortunately, there is no available effective treatment that can stop or slow the death of neurons that causes AD symptoms. It is already widely believed that AD starts before development of the associated symptoms, so its prestages, including mild cognitive impairment (MCI) or even earlier stages such as significant memory concern (SMC), have received increasing attention, not only because of their potential as a precursor of AD, but also as a possible predictor of conversion to other neurodegenerative diseases (Petersen et al., 2001). Although these prestages have been defined clinically (Albert et al., 2011; Sperling et al., 2011), accurate/efficient diagnosis and differentiation among different stages, such as early MCI (EMCI), late MCI (LMCI), and SMC, is still challenging.

Although researchers have already found some critical factors related to AD, such as amyloid plaques that are core pathological features of AD, it is difficult to apply this examination on live people directly. Indeed, amyloid positron emission tomography (PET) imaging and the measurement of beta-amyloid (Aβ42) in cerebrospinal fluid can provide an indirect way for measuring fibrillar beta amyloid (Aβ) in the brain. These measures, however, are difficult to be applied in practical clinical applications due to their invasive nature. Moreover, the recent finding that many MCI brains and aged controls exhibit a similar degree of Aβ deposition in postmortem brain tissues might limit the use of Aβ deposition as an effective biomarker (Aizenstein et al., 2008; Price et al., 2009). In the last 10 years, many studies have proposed using magnetic resonance imaging (MRI) to identify brain changes that might help to interpret AD symptoms. Structure-MRI-derived biomarkers include abnormalities of white matter bundles or structural connectivity alterations (Li et al., 2008), local gray matter (GM) atrophy that is often represented as decrease of GM thickness (Wang et al., 2009), and loss of volume with some specific brain tissues/regions, such as in cingulate, hippocampus, and entorhinal cortices (Devanand et al., 2007; Gómez-Isla et al., 1996; Kordower et al., 2001; Mufson et al., 2012; Villain et al., 2010). But these structural changes are often found in the late-disease stage in which the symptoms are relatively obvious. Moreover, they might be insignificant in the very early stage, such as EMCI or SMC, and spatially distributed over many brain areas (Chételat et al., 2002; Convit et al., 2000; Davatzikos et al., 2008; Dickerson et al., 2001).

Recently, researchers started to investigate the merit of resting-state functional MRI (R-fMRI) in studying the potential functional alterations in MCI/AD (Greicius et al., 2004; Maxim et al., 2005; Sorg and Riedl, 2007; Supekar et al., 2008; Wang et al., 2007). For instance, Wang and coworkers (2007) indicated that increased positive correlations often appear within lobes, while decreased positive correlations usually exist between different lobes, such as parietal and prefrontal lobes. Supekar and colleagues (2008) and Zhu and colleagues (2014) adopted different region of interest strategies to study the functional connectivity alterations of the whole brain. Greicius and associates (2004) and Sorg and Riedl (2007) suggested a disruptive resting-state activity existing within the default mode network (DMN) in AD or MCI patients. In general, R-fMRI has obvious advantages compared with the traditional methods due to its capability for reflecting the potential intrinsic functional activities occurring in the brain. It is the only possible way so far to examine the whole-brain functional abnormalities behind the known structural changes in vivo.

From our perspective, there are two major barriers that hamper successfully applying R-fMRI to AD studies. The first challenge is due to the variability and complex nature of fMRI BOLD signals. From the MRI physics point of view, by imaging the blood flow, BOLD contrast can reflect neuron activities since they are coupled. But the signals acquired from fMRI contain multiple sources, including different types of noise, for example, respiration or heart rate. After many years of fMRI studies, there is still much to learn regarding the source of the signals (Heeger and Ress, 2002). From the neuroscience side, it has been widely agreed that a variety of brain regions and networks exhibit strong functional heterogeneity and diversity (Anderson et al., 2013; Duncan, 2010; Fedorenko et al., 2013; Kanwisher, 2010; Pessoa, 2012). That is, the same brain region could participate in multiple functional processes/domains simultaneously and a single functional network might recruit various neuroanatomic areas at different stages as well. Under this situation, the practical fMRI signals extracted from every single voxel tend to reflect a complex functional activity resulting from multiple sources/components within the whole brain. The second barrier is the critical lack of computational modeling strategies with which we can fuse, replicate, and validate fMRI-derived features in independent neuroimaging datasets. Indeed, validation of neuroimaging studies has been challenging for many years due to the lack of ground-truth data. It is even more challenging to validate on separate populations or imaging centers, given the variability in demographics, imaging equipment, scan protocols, image reconstruction algorithms, and even the parameters in the preprocessing pipelines.

To effectively address the just-mentioned fundamental barriers and limitations, in this article, we developed a novel computational framework of sparse representations of whole-brain fMRI signals and applied it on the most recently updated Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset. Inspired by the successes of using sparse coding for imaging and signal representations in machine learning and pattern recognition fields (Wright et al., 2009), the core idea of our proposed framework is to assemble all R-fMRI signals within the whole brain of a single subject into a big data matrix, which is further decomposed into an over-complete dictionary matrix and a coefficient weight matrix via an effective online dictionary learning algorithm (Mairal et al., 2010). The most important characteristic of this framework is that each row of the coefficient weight matrix naturally reflects one spatial overlap pattern of the corresponding dictionary atom in the dictionary matrix, which is represented as a time series in the over-complete basis dictionaries. It turned out that this novel method can effectively uncover multiple functional components corresponding to pairs of time series (one dictionary matrix atom) and spatial pattern (one coefficient weight matrix atom), which potentially represent multiple functional networks/sources. To validate the effectiveness and robustness, we applied our framework on 210 subjects who are from ADNI dataset (until September 2013). Note that even though these subjects were scanned with similar protocols, their R-fMRI data were acquired at different sites and possess varied imaging parameters, including resolution and TR (repetition time). Our results proved that all the known resting-state networks (RSNs) (Smith et al., 2009), including DMN, can be consistently identified from the achieved functional components for all the subjects. Moreover, by using the features derived from those functional components, it yields high classification accuracy for both AD (94%) and MCI (92%) versus normal controls. Even for SMC we can still have 92% accuracy.

Materials and Methods

Overview

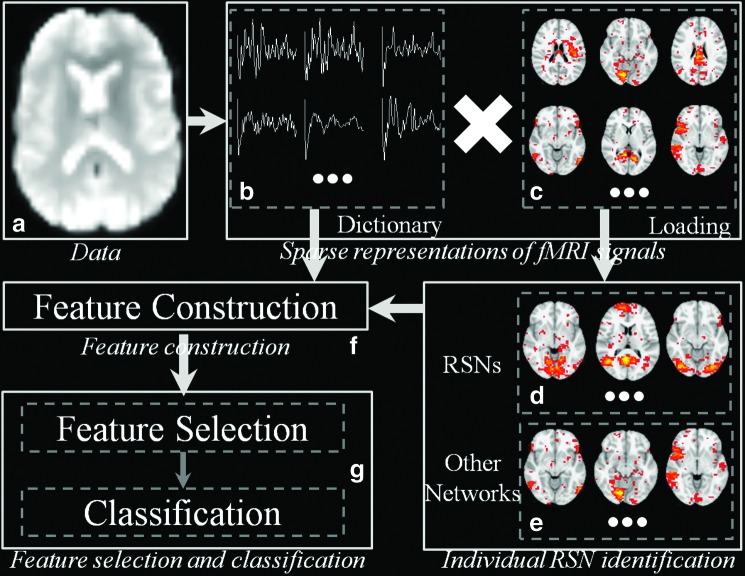
As illustrated in Figure 1, the framework can be divided into three major parts: functional sparse representation (Fig. 1b, c), feature construction (Fig. 1f) based on learned dictionary matrix/coefficient weight matrix, and feature selection/classification (Fig. 1g). First, by using online dictionary learning methods, the whole-brain fMRI BOLD signals are sparsely represented as the product of common dictionary matrix (Fig. 1b) and the corresponding coefficient weight matrix (Fig. 1c). That is, the signals of each voxel can be sparsely and effectively represented as linear combinations of some atomic dictionary components. Through comparing with 10 predefined RSN templates, including visual, DMN, cerebellum, sensorimotor, auditory, executive control, and frontoparietal, we successfully identified highly similar dictionary atoms (Fig. 1d) from others (Fig. 1e) within each subject. Then for those identified dictionary atoms that are highly similar with the RSNs, the likelihood of being RSNs as well as the functional characteristics (e.g., functional connectivity) with other dictionary atoms are explored to construct multiple types of features (Fig. 1f). At last, all the features are fit in the correlation-based feature selection (CFS) algorithm and the ones with the most differentiation power will be preserved. An effective support vector machine (SVM) classifier was employed to solve the classification problem (Fig. 1g). In addition, those highly discriminating features are also analyzed and discussed in the “Results” section (Features with high differentiation power heading).

FIG. 1.

Illustration of the proposed framework. (a) Resting-state functional magnetic resonance imaging data. Here, the input dataset includes 210 subjects from the most recently updated ADNI database until September 2013. (b) Dictionary matrix. (c) Coefficient weight matrix. (d) Ten identified RSNs using ICA templates. (e) Other dictionary atoms. (f) Using dictionary matrix and identified RSNs we constructed six types of features. They are spatial overlapping rate, functional connectivity within RSNs, functional connectivity within dictionary, entropy of functional connectivity, entropy of component distribution within RSNs, and common dictionary distribution. (g) Correlation-based feature selection and support vector machine classifier. ADNI, Alzheimer's Disease Neuroimaging Initiative; ICA, independent-component analysis; RSN, resting-state network. Color images available online at www.liebertpub.com/brain

Data

The dataset used in the preparation of this article was obtained from the ADNI database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical corporations, and nonprofit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether PET, serial MRI, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private companies, and subjects have been recruited from over 50 sites across the United States and Canada. The initial goal of ADNI was to recruit 800 adults but which has been followed by ADNI-GO (2009) and ADNI-2 (2010). To date these three phases have recruited over 1500 subjects, ages from 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or LMCI, and people with early AD. For up-to-date information about ADNI database, see www.adni-info.org

Subject

From ADNI-GO phase the resting-state fMRI (R-fMRI) data were introduced into the ADNI database and enriched through ADNI-2. Because we are aiming to explore the potential functional abnormalities in the whole brain regarding the non-normal aging people, only the subjects with at least one R-fMRI scan until September 2013 are included. And we only consider the R-fMRI scan at first time for each subject since we do not focus on the longitudinal changes of subjects in this article. In addition, besides normal and AD, new cohorts of EMCI, LMCI, and SMC are also considered in this study. In brief, the just-mentioned criteria yield a total of 210 subjects, including 50 normal controls, 34 AD patients, 56 EMCI patients, 44 LMCI patients, and 26 SMC adults.

Imaging data acquisition and data preprocessing

All R-fMRI datasets were acquired on 3.0 Tesla Philips scanners (varied models/systems) at multiple sites. There is a range for imaging resolution in X and Y dimensions, which is from 2.29 to 3.31 mm and the slice thickness is 3.31 mm. TE (echo time) for all subjects is 30 msec and TR is from 2.2 to 3.1 sec. For each subject, there are 140 volumes (time points). Preprocessing steps of the R-fMRI data included brain skull removal, motion correction, spatial smoothing, temporal prewhitening, slice time correction, global drift removal, and band pass filtering (0.01–0.1 Hz) (Zhu et al., 2014).

Sparse representations of fMRI signals

Given a collection of data vectors 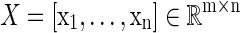, if there exists a linear combination of a small number of d_i that can effectively represent X, then we say that X admits a sparse approximation over dictionary D, where 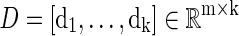. A general form of cost function in sparse dictionary learning is defined as

Where D 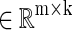is the dictionary and ℓ is the loss function, which is to be small if D can effectively represent the original data X. In general, k will be much less than n.

In this article, for each R-fMRI dataset having n voxels with t time length, we are aiming to learn a neuroscience meaningful and over-complete dictionary 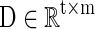(m>t and m<< n) (Mairal et al., 2010) for the sparse representation of whole-brain signals, S. That is, for the R-fMRI signal set 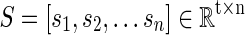, the empirical cost function is rewritten as Equation (2) by considering the average loss of regression of n signals.

For an effective sparse representation using D, the general loss function is further defined in Equation (3) by using a ℓ₁ regularization that yields to a sparse resolution of α_i. Similar to LASSO (Tibshirani, 1996), here λ is a regularization parameter that can be used as a trade-off item between the sparsity level and the regression residual.

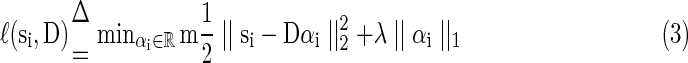Because we are more interested with the fluctuation shapes and patterns of basis fMRI BOLD activities, it is necessary to avoid D having an arbitrarily large number of elements. So the columns 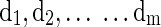in the learned dictionary D are constrained by Equation (4).

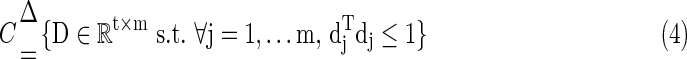Eventually, the whole solution of dictionary learning problem in this article can be rewritten as a matrix factorization with ℓ₁ regulation in Equation (5).

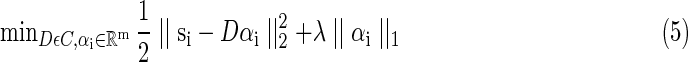Specifically, the sparse learning procedure in this article includes three steps. First, for each single-subject's brain, we extract preprocessed R-fMRI signals of whole brain by using individual brain mask. Then, after normalizing the signal to have zero mean and standard deviation of 1, these signals are reassembled into a big matrix S 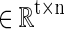, where t is the number of time points (fMRI volume numbers) and n columns represent fMRI signals extracted from n GM voxels. Finally, by applying a publicly available efficient online dictionary learning methods (Mairal et al., 2010), each fMRI signal (each column vector) in S can be modeled as a linear combination of a small size of learned dictionary atoms. For example, a specific signal vector, s_i, can be represented as the product of basis dictionary D and α_i, where α_i is the corresponding coefficient vector in the coefficient weight matrix.

The rationale and advantages behind using sparse representation of fMRI signals have two aspects. (1) As mentioned in the “Introduction” part, from neuroscience perspective, it has been widely agreed that a variety of brain networks and regions exhibit strong functional heterogeneity and diversity (Anderson et al., 2013; Duncan, 2010; Fedorenko et al., 2013; Kanwisher, 2010; Pessoa, 2012). That is, the same brain region could participate in multiple functional processes/domains simultaneously and a single functional network might recruit various neuroanatomic areas at different stages as well. So the practical fMRI signals of every single voxel tend to reflect a complex functional activity resulting from multiple components/sources within the whole brain. Under this case, a natural strategy is to decompose the actual signals back to multiple components that potentially represent the original sources. Here, we adopted the same assumption as previous studies (Lee et al., 2011; Oikonomou et al., 2012) that the components of each voxel's fMRI signal are sparse and the neural integration of those components is linear. (2) Given the fact that it is largely unknown to what extent those multiple interacting functional networks spatially overlap with each other and jointly fulfill the intact brain functions, we do not enforce the statistically independent constraint to the decomposed components like independent component analysis (ICA) (Calhoun et al., 2001) does. Therefore, our framework has more freedom during the sparse learning procedure and eliminates the need for initialization using a predefined model at the most extent.

Individual RSN identification

As described in “Sparse representations of fMRI signals” heading and illustrated in Figure 1, for each atom in the dictionary D, the corresponding coefficient vector α_i of the coefficient weight matrix can be projected back to the volumetric fMRI image space for the interpretation of the spatial patterns. In this way, the spatial patterns of atoms in different subjects can be compared within a template image space to determine their spatial correspondences, as well as to further identify meaningful RSNs within each subject.

In R-fMRI data analysis, a meaningful RSN is identified and examined mainly based on its spatial pattern, since the temporal and frequency characteristics have not been fully understood or quantitatively described. Specifically, in this article, a spatial-pattern-overlapping metric is adopted to identify meaningful RSNs in each subject and defined as

Where X is the spatial pattern of one functional component, T is a specific RSN template, and SOR is the spatial overlapping rate of X and T. For each subject, we first calculated the SORs of all spatial patterns contained in the coefficient weight matrix with a specific RSN template, and sorted them in decreased order. Then the first spatial pattern with the highest SOR (Fig. 1d) was determined as the specific RSN of this subject. Moreover, the corresponding atoms of the spatial patterns were used for feature construction, which will be detailed in the following heading. In this article, we adopted the 10 well-defined and widely known RSNs in Smith and coworkers (2009) as the RSN templates to identify the corresponding RSNs in each subject. More details of the 10 RSN templates are illustrated in “RSN identification” heading.

Feature construction

After the sparse representation of fMRI signals and identification of 10 RSNs, we constructed six types of features that can effectively reflect both spatial and functional characteristics during the resting state. They are SOR, functional connectivity within RSNs (FC-RSNs), functional connectivity within dictionary (FC-D), entropy of functional connectivity (ET-FC), entropy of component distribution within RSNs (ET-CDRSNs), and common dictionary distribution (CDC). Except for the first type of feature (SOR), the other five are directly or indirectly derived from the dictionary matrix.

Spatial overlapping rate

As mentioned in the previous heading (Individual RSN identification), for each subject, by calculating the overlapping rate (Eq. 6) we can identify 10 dictionary atoms for which the corresponding spatial patterns are most similar to the RSN templates. Thus, we have 10 features to depict the similarity between the selected spatial patterns and the template. Since our strategy is to pick the atoms that are most similar to the RSN templates, the overlapping rate could reflect the potential alterations of RSNs in terms of the spatial patterns.

FC-RSNs and FC-D

Because the identified dictionary atoms corresponding to 10 RSNs have intrinsic correspondence across different subjects, for example, DMN, we can easily calculate their functional connectivity represented by a 10×10 symmetric matrix (FC-RSNs). Note that only 45 unique elements can be used for features. Similar to FC-RSNs, in which we only examine the internal relation among 10 RSN-dictionary atoms, we also need to consider the interaction between these RSN-dictionary atoms and other decomposed dictionary atoms (FC-D), even though their functional roles are largely unknown so far. FC-RSNs and FC-D can complement each other because they reflect the functional interactions among dictionary atoms from two different angles. The former one focuses on the interactions within RSN-dictionary atoms, while the latter one focuses on the interactions between RSN-dictionary atoms and non-RSN-dictionary atoms. An essential difference between our FC features and traditional FC features is that instead of calculating the correlation between actual fMRI signals, we explored the relation between dictionary atoms. Because these dictionary atoms are more likely to represent the intrinsic activities of the corresponding spatial regions described in the coefficient matrix, our computed FC features are more grounded from neuroscience point of view.

ET-FC and ET-CDRSNs

Based on the FC-D features, we can construct a histogram representing the overall functional connectivity distribution. Specifically, for each RSN atom (the dictionary atom identified as a correspondence of one RSN) we calculate its functional connectivity with all the other dictionary atoms (except RSN atoms). If the size of dictionary is k, then we could have k-10 functionary connectivity results that are from −1 to +1 for each RSN atom. In this article we adopted 20 bins to cover [−1, +1] with equal distance and count how many dictionary atoms are within each bin, which is followed by the calculation of Shannon entropy, named as ET-FC. Similarly, we can also construct a histogram to reflect the component distribution for each RSN-dictionary atoms. For each voxel involved in a specific RSN-dictionary atom (this voxel belongs to this RSN), we calculate its non-RSN atoms' (dictionary) composition when representing the original fMRI signals. To do this, we focus on the nonzero items of the column corresponding to this voxel in the coefficient weight matrix. This process is repeated for each voxel contained in this RSN. Eventually, this yields a distribution in terms of how many voxels have been used for each dictionary atom and based on which we calculate the Shannon entropy as ET-CDRSNs. In general, the Shannon entropy characterizes the information carried by the distribution itself (e.g., uniformly distributed or not). Hence, ET-FC and ET-CDRSNs depict the distribution of functional connectivity and RSN-related functional complexity from the information theory point of view.

Common dictionary distribution

For each subject, we derive a unique dictionary matrix (Sparse representations of fMRI signals heading) that can be used to represent the original fMRI signals within individual space. One question is whether we can find a set of common dictionary atoms D* that have the capability to represent all the individual dictionary atoms. Here we applied the second-round sparse learning on the individual dictionaries. Specifically, we assemble all the individual dictionaries into one matrix as we did to the fMRI signals in “Sparse representations of fMRI signals” heading. It should be noted that the size of D* is the same as that of D. Adopting the similar procedure as ET-CDRSNs, we can calculate a distribution of how many individual dictionary atoms can be represented for each common dictionary atom. In other words, CDC is trying to explore and extract the most common dictionary atoms that could effectively compose individual dictionaries.

Feature selection and classification

So far we have six types of features and we are aiming to preserve only those features with most differentiation power. At the same time we also need to consider the relevance among different features since sometimes a set of “good” features cannot predict well when only part of them are used. In this article we employed the CFS (Hall and Smith, 1999) algorithm as the feature selection strategy. Briefly, the core idea of CFS is that through a heuristic process it evaluates the merit of a subset of all the features by considering the “goodness” of individual ones along with the intercorrelation among them when predicting. That is, CFS will calculate feature-class and feature-feature correlations at the same time. Given a subset of features, S, with k features, the Merit_s is defined as:

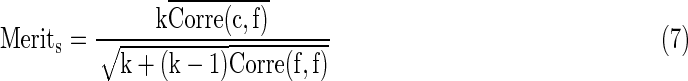Where 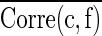and 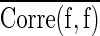represent mean feature-class correlation and average feature-feature intercorrelation, respectively. Here we adopted Pearson correlation coefficient as the measurement for the correlation. Corre(c, f) and Corre(f, f) are defined as Corre(c, f)=cov(c, f)/σ_cσ_f and Corre(f, f)=cov(f_i, f_j)/σ_fi σ_fj, where f_i and f_j are two different features, cov(.) is the covariance, and σ is the standard deviation. Once we obtained the most discriminative features following CFS procedure; an SVM classifier (Chang and Lin, 2001) was employed for solving the classification problem. Specifically, for each group, a 10-fold cross-validation was adopted to evaluate the performance of classifiers with different parameters. The major parameters include type of SVM (C-SVC and nu-SVC), kernel function type (linear, polynomial, radial basis function, and sigmoid), and penalty parameter C (ranges from 2⁻¹⁰ to 2¹⁰, interval is 2^0.1). For each of all combinations of those parameters, we used 10-fold cross-validation to obtain the classification accuracy, respectively. Then, the parameter sets with highest classification accuracy are obtained. In total, we have trained five classifiers (NC/AD, NC/SMC, NC/EMCI, NC/LMCI, and NC/EMCI+LMCI). The detailed classification results including sensitivity (proportion of patients correctly predicted) and specificity (proportion of healthy controls correctly predicted) are showed in “Classification results based on sparse representation features” heading.

Results

RSN identification

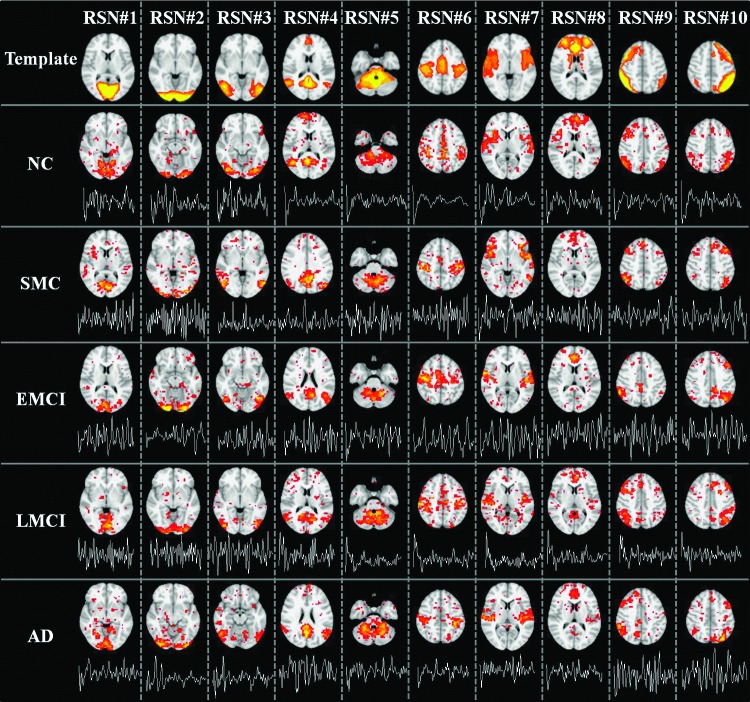
As described in “Individual RSN identification” heading, we adopted 10 well-defined RSN templates provided in http://fsl.fmrib.ox.ac.uk/analysis/brainmap+rsns/ (Smith et al., 2009) to identify the corresponding 10 RSNs in each subject. The first row of Figure 2 shows the most informative slice as the spatial pattern of each RSN template. In brief, RSNs#1, #2, and #3 are located in the “visual” cortex, and include medial (BA 17), occipital pole, and lateral visual areas (BAs 18/19), respectively. RSN #4 is known as the “default mode network” (DMN) (Raichle et al., 2001), which mainly includes anterior (BAs 12/32) and posterior cingulate cortex (BA 29), the medial prefrontal gyrus (BAs 9/10/11), and bilateral supramarginal gyrus (BA 39). RSN #5 is located in cerebellum. RSN #6 is known as the “sensorimotor” network, which mainly includes pre- and postcentral gyrus (BAs 1/2/3/4), and the supplementary motor area (BA 6). RSN #7, known as the “auditory” system, encompasses the Heschl's gyrus, lateral superior temporal gyrus, and posterior insular cortex. RSN #8 includes anterior cingulate and paracingulate regions and is known as “executive control” network. RSNs #9 and #10 show networks that have strong lateralization in the right (RSN #9) and left (RSN #10) hemispheres, covering the middle frontal and orbital (BAs 6/9/10) and superior parietal areas (BAs 7/40). More details of the 10 RSNs are referred to Smith and coworkers (2009).

FIG. 2.

Ten well-matched RSNs identified from sparse representation. The first row showed the 10 RSN templates. For each template, the most informative slice, which is superimposed on the MNI152 template image, was shown as the spatial pattern. Rows 2 to 6 show the identified RSNs of a randomly selected subject of five groups (NC, SMC, EMCI, LMCI, and AD), respectively. In each subfigure, the most informative slice, superimposed on the MNI152 template image, was shown as the spatial pattern of a specific RSN. The time series of corresponding atom was also shown below each spatial pattern of the RSN. All 10 RSNs were matched by calculating and sorting the overlapping rate with the corresponding RSN templates (first row) provided in http://fsl.fmrib.ox.ac.uk/analysis/brainmap+rsns/ (Smith et al., 2009). The RSN templates shown in first row were thresholded at z=3. The color scale of spatial maps in sparse representation ranges from 0.1 to 10. AD, Alzheimer's disease; EMCI, early mild cognitive impairment; LMCI, late mild cognitive impairment; SMC, significant memory concern. Color images available online at www.liebertpub.com/brain

As illustrated in “Imaging data acquisition and data preprocessing” and “Sparse representations of fMRI signals” headings, since the time points t=140 for each subject, we set the dictionary size m>140 based on our experience to learn an over-complete (m>t) dictionary D and corresponding coefficient weight matrix α for each subject. Afterward, 10 RSNs were identified for each subject in all five groups (NC, SMC, EMCI, LMCI, and AD) via the method in “Individual RSN identification” heading. Note that to evaluate the impact of parameter selection, different combinations of parameters were explored to verify whether reproducible and consistent results can be achieved. Specifically, the dictionary learning and sparse representation pipeline was applied to subjects of NC group with different combinations of parameters since we expect to exclude the possible effect of diseased group. To make fair and easy comparison, first, λ is fixed, and we change the dictionary size from 200 to 600 (interval is 100). The mean overlap rate of all identified RSNs in all subjects is 0.38, 0.30, 0.31, 0.24, and 0.23. Second, m is fixed and λ changes from 1.0 to 2.0 (interval is 0.5). The mean overlap rate of all identified RSNs in all subjects is 0.31, 0.31, and 0.24. From the comparison, we can see that although the parameter alteration will cause slight spatial variation for the derived RSNs, the overall spatial overlap rate is reasonably stable. In this article, we chose m=200 and λ=1.5 with better spatial overlap rate of RSN in NC group. Rows 2 to 6 of Figure 2 show the 10 identified well-matched RSNs of a randomly selected subject in each of the five groups, respectively. In each subfigure, the most informative slice, superimposed on the MNI152 template image, was shown as the spatial pattern of a specific RSN. The time series of corresponding atom was also shown below each spatial pattern. Quantitatively, the mean overlap rate of all 10 RSNs is 0.38 (0.24 to 0.52) for all subjects in NC group, 0.37 (0.25 to 0.49) for SMC group, 0.37 (0.25 to 0.48) for EMCI group, 0.34 (0.23 to 0.44) for LMCI group, and 0.34 (0.24 to 0.46) for AD group. More detailed results are shown in Table 1. We can see that for some specific RSNs (e.g., RSN #4 representing DMN), the mean overlap rate is different across the five groups and the trend is decreasing along with the disease progression (from 0.52 in NC to 0.46 in AD for RSN #4, as detailed in Table 1), demonstrating that the overlap rate might be an effective feature to differentiate subjects between two groups.

Table 1.

The Mean Overlap Rate of All RSNs in Sparse Representation of Each Group

	NC	SMC	EMCI	LMCI	AD	All
RSN #1	0.46±0.09	0.44±0.12	0.45±0.11	0.42±0.13	0.39±0.12	0.43±0.12
RSN #2	0.37±0.07	0.37±0.07	0.36±0.09	0.32±0.09	0.33±0.09	0.35±0.08
RSN #3	0.40±0.09	0.40±0.11	0.38±0.11	0.37±0.12	0.38±0.12	0.39±0.11
RSN #4	0.52±0.08	0.49±0.08	0.48±0.12	0.44±0.14	0.46±0.14	0.48±0.12
RSN #5	0.41±0.07	0.39±0.08	0.39±0.10	0.34±0.11	0.37±0.11	0.38±0.09
RSN #6	0.40±0.09	0.41±0.10	0.41±0.11	0.40±0.15	0.37±0.12	0.40±0.11
RSN #7	0.37±0.07	0.37±0.09	0.38±0.10	0.35±0.11	0.33±0.11	0.36±0.10
RSN #8	0.32±0.07	0.33±0.08	0.33±0.07	0.30±0.10	0.30±0.08	0.32±0.08
RSN #9	0.24±0.03	0.25±0.05	0.25±0.05	0.23±0.04	0.24±0.04	0.24±0.05
RSN #10	0.29±0.07	0.27±0.08	0.28±0.07	0.27±0.08	0.28±0.07	0.28±0.07

Each overlap rate is represented as mean±standard deviation.

AD, Alzheimer's disease; EMCI, early mild cognitive impairment; LMCI, late mild cognitive impairment; SMC, significant memory concern.

Classification results based on sparse representation features

In this section, we constructed six types of features (SOR, FC-RSNs, FC-D, ET-FC, ET-CDRSNs, and CDC) containing both spatial and functional characteristics of R-fMRI data illustrated in “Feature construction” heading, and performed classification based on these features. For the feature construction, it should be noted that, in “Individual RSN identification” heading, we calculated the SORs of all spatial patterns of atoms with a specific RSN template, and sorted them in decreasing order. It is highly possible that first several spatial patterns may have similar high SOR with a specific RSN template. As a consequence, for each RSN, we considered top five spatial patterns with highest SOR and adopted the corresponding atoms to measure functional characteristics and construct features. Our rationale of considering top five spatial patterns for each RSN is twofold. (1) There might be intrinsic functional characteristics missed to differentiate normal controls from patients if we only chose top one spatial pattern merely based on SOR criterion. (2) The potential feature redundancy problem of introducing top five spatial patterns for each RSN can be effectively solved in the feature selection step via CFS. Finally, the numbers of features in each type are listed as following: 10 for SOR; 45×5=225 for FC-RSNs; 10×5=50 for FC-D, ET-FC, and ET-CDRSNs, respectively; and 200 for CDC. The total number of features is 585 for each subject. CFS was then adopted on all 585 features of subjects in each group pair (NC/AD, NC/SMC, NC/EMCI, NC/LMCI, and NC/EMCI+LMCI) to perform feature selection. Finally 10-fold cross-validation was performed for classification of each group pair via SVM.

We summarized the number of features before and after CFS and the corresponding classification results in Table 2. If we trained classifiers and performed classification using all 585 features, then the classification accuracy is not satisfied for all five group pairs (40.38% to 67.00%). After CFS, 5 to 30 features survived for the five group pairs detailed in Table 2. We can see that with the most relevant and discriminative features, the classification accuracy substantially improved for all five group pairs (80.00% to 94.12%). Moreover, we removed the eight subjects in EMCI group with different TR (not 3 sec) to exclude the potential effect of the scan parameters, and performed the feature selection and classification. The classification accuracy is 79.59%, specificity is 72.00%, and sensitivity is 87.50%. The results did not change much compared with the results in Table 2. We will interpret those features with high differentiation power in detail in the following heading.

Table 2.

Summary of the Feature Number and the Classification Accuracy Using Either All Features or Features After Correlation-Based Feature Selection for Each Group Pair

	NC-SMC	NC-EMCI	NC-LMCI	NC-EMCI+LMCI	NC-AD
All features
Feature no.	585	585	585	585	585
Accuracy	40.38%	62.00%	45.45%	67.00%	44.12%
Specificity	42.31%	64.00%	36.36%	52.00%	35.29%
Sensitivity	38.46%	60.00%	54.55%	82.00%	52.94%
Features after CFS
Feature no.	22	8	5	30	11
Accuracy	92.31%	80.00%	80.68%	92.00%	94.12%
Specificity	96.15%	76.00%	79.55%	90.00%	94.12%
Sensitivity	88.46%	84.00%	81.82%	94.00%	94.12%

CFS, correlation-based feature selection.

Features with high differentiation power

As illustrated in “Classification results based on sparse representation features” heading, we adopted CFS to obtain the features with high differentiation power for each group pair. Table 3 summarized the detailed feature numbers in six feature types after CFS for each group pair. We discuss the features with high differentiation in each of the five group pairs in detail as follows.

Table 3.

Summary of Number of Features After Correlation-Based Feature Selection in Six Feature Types for Each Group Pair

		Feature types
	Total	SOR	FC-RSNs	FC-D	ET-FC	ET-CDRSNs	CDC
NC-SMC	22	0	13	2	1	3	3
NC-EMCI	8	1	2	1	1	1	2
NC-LMCI	5	0	2	2	0	1	0
NC-EMCI+LMCI	30	1	17	4	2	3	3
NC-AD	11	3	3	0	1	1	3

FC-RSNs, functional connectivity within resting-state networks; SOR, spatial overlapping rate.

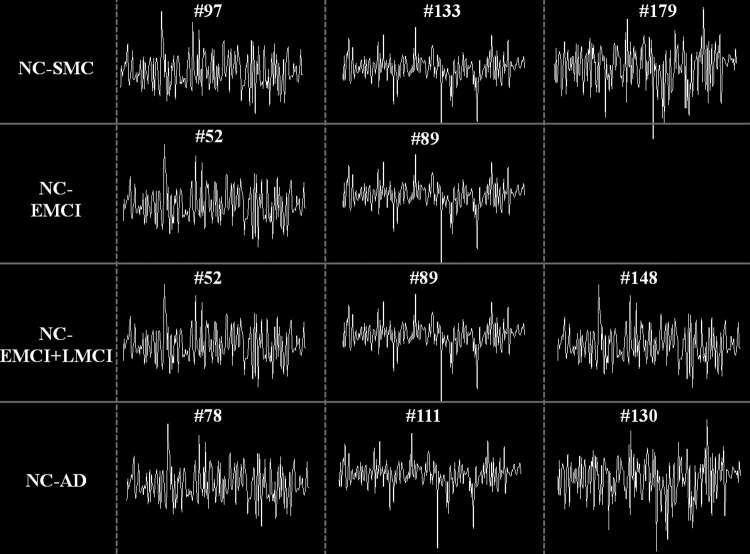
For NC-SMC group, there are 22 features in total after CFS. Specifically, there is no feature in SOR type. For FC-RSNs type, there are 13 features, including the functional connectivity between RSNs #4–#10, #5–#8, #1–#3, #3–#6, #3–#7, #7–#8, #1–#8, #3–#4, #4–#7, #1–#4, and #4–#5. The RSN IDs can be referred to Figure 2. This result indicates that there are widespread functional connectivity alterations among RSNs in SMC. For FC-D type, there are two features related to RSNs #1 and #8. There is one feature in ET-FC that corresponds to RSN #8. For ET-CDRSNs type, there are three features related to RSNs #1 and #5. For CDC, there are three features representing the common atoms #97, #133, and #179. The time series of these common atoms with high differentiation power are shown in Figure 3.

FIG. 3.

Time series of the common atoms with high differentiation power in each group pair. There are 140 time points. The index of the common atoms in the learned dictionary for each subject is shown above the time series of the atoms.

For NC-EMCI group, there are eight features in total after CFS. There is one feature in SOR type corresponding to RSN #1. For FC-RSNs type, there are two features corresponding to the functional connectivity between RSNs #3–#5 and #5–#6. For FC-D type, there is one feature corresponding to RSN #4. For ET-FC type, there is one feature corresponding to RSN #1. For ET-CDRSNs type, one feature corresponds to RSN #3. For CDC, two features correspond to atoms #52 and #89 (Fig. 3).

For NC-LMCI group, there are five features in total. There is no feature in SOR, ET-FC, or CDC type. For FC-RSNs type, there are two features corresponding to the functional connectivity between RSNs #1–#4 and #4–#5. For FC-D type, there are two features corresponding to RSNs #2 and #4. There is one feature in ET-CDRSNs corresponding to RSN #10. We can see that RSN #4, known as DMN, has discriminative functional characteristics in differentiating LMCI from NC.

For NC-EMCI+LMCI group, there are 30 features in total after CFS. There is one feature in SOR corresponding to RSN #2. For FC-RSNs, there are 17 features corresponding to the functional connectivity between RSNs #2–#8, #5–#10, #7–#10, #2–#9, #4–#7, #1–#6, #3–#5, #4–#5, #4–#7, #6–#8, #1–#4, #1–#10, #2–#4, #3–#10, #5–#6, and #6–#9. This result is in agreement with our previous results that show that there are widespread functional connectivity alterations among RSNs in MCI (Jiang et al., 2013). For FC-D type, there are four features related to RSNs #4, #6, and #7. For ET-FC, there are two features corresponding to RSNs #4 and #3. There are three features in ET-CDRSNs corresponding to RSNs #2, #3, and #4. For CDC type, there are three features corresponding to atoms #52, #89, and #148 (Fig. 3). We can also see that RSN #4, known as DMN, has discriminative functional characteristics in differentiating MCI from NC. It should be noted that the performance of NC/EMCI+LMCI group classification is better than NC/EMCI and NC/LMCI. Although we cannot compare the classification results of the three groups directly since the classifiers of the three groups were trained separately based on different and specific features of the three groups after feature selection, from theoretical perspective, one possible explanation is that after feature selection, more features that have relevant and discriminative power for classification were retained in the NC/EMCI+LMCI group than those in NC/EMCI and NC/LMCI groups.

For NC-AD group, there are 11 features in total after CFS. There are three features in SOR type corresponding to RSNs #1, #2, and #4. For FC-RSNs, there are three features corresponding to the functional connectivity between RSNs #3–#8, #4–#8, and #7–#9. There is no feature in FC-D type. For ET-FC type, there is one feature corresponding to RSN #1. For ET-CDRSNs type, there is one feature corresponding to RSN #10. For CDC type, there are three features corresponding to atoms #78, #111, and #130 (Fig. 3).

Discussion and Conclusions

In this article, we have presented a novel computational framework to represent whole-brain R-fMRI signals via sparse learning. The core idea is to assemble all the fMRI signals within the whole brain of one subject into a big data matrix, which is factorized into an over-complete dictionary basis matrix and a coefficient weight matrix via an online dictionary learning algorithm. Then, we designed a computational method to quantitatively characterize 10 RSNs from the extracted functional components by estimating the SOR. And last, we constructed six types of features derived from the previous sparse representation and successfully applied them for feature selection/classification on 210 subjects from the ADNI database. The results showed more than 90% classification accuracy on AD, MCI, and SMC from normal controls. Moreover, these six types of features also displayed high differentiation power between EMCI and LMCI with around 80% accuracy. One of the essential differences between our proposed framework and traditional fMRI analysis (Greicius et al., 2004; Maxim et al., 2005; Sorg and Riedl, 2007; Supekar et al., 2008; Wang et al., 2007) on AD/MCI is that, instead of estimating functional connectivity on the original fMRI signals, we recovered the complex/hybrid-source fMRI signals into multiple components that potentially reflect different functional networks corresponding to those back-stage brain activities. Based on our results, these latent functional networks reflect some intrinsic brain activities that are difficult to be observed from the fMRI signals directly. Note that we do not enforce the statistically independent constraint during the factorization like ICA does. This means that our framework has more freedom during the sparse learning stage and on eliminating the need for initialization using a predefined model at the most extent.

Another contribution of this article is that we purposely construct six types of new features based on the sparse representation results. For example, SORs reflect the possible alterations of RSNs in terms of the spatial patterns comparing to the normal RSN templates; FC-RSNs/FC-D characterize the functional interactions within/outside RSNs; ET-FC and ET-CDRSNs depict the distribution of functional connectivity and RSN-related functional complexity from the information theory point of view; CDC does the second round of sparse learning of the individual dictionaries. Through this way, it can successfully extract the most common dictionary atoms composing individual dictionaries. The high classification accuracy illustrated in “Classification results based on sparse representation features” heading and Table 2 proves the effectiveness of all these features. Moreover, we also compared our classification results with a recently published method (Jie et al., 2014) using the same dataset. The difference is that, in the work of Jie and colleagues (2014), they adopted a graph-kernel-based approach to construct the features. The comparison result is summarized in Table 4 and the advantages of using sparse-representation-derived features are obvious.

Table 4.

Comparison of the Classification Accuracy with Graph-Kernel-Based Method

	Classification accuracy of proposed method	Classification accuracy of graph-kernel method (Jie et al., 2014)
NC-SMC	92.31%	71.05%
NC-EMCI	80.00%	65.09%
NC-LMCI	80.68%	60.22%
NC-EMCI+LMCI	92.00%	66.44%
NC-AD	94.12%	61.9%

Meanwhile, the work and methods in this article can be further expanded and enhanced in the following aspects in the future. First, at the current stage, we have adopted the dictionary size at 200 and λ at 1.5 based on experiment evaluation. To further refine our framework, we need to systematically evaluate the relation of these parameters to the components extracted from the sparse representation. Although how to choose the “best” parameters is still an open question in machine learning field, we can introduce some prior knowledge or constraints from neuroscience point of view. Second, we can introduce and integrate more meaningful functional and structural features into our framework to improve the classification power of our method (e.g., to handle the subtle difference among the subtypes of MCI and achieve satisfactory classification accuracy). In this article, we only focused on the quantitative characterization of spatial patterns of 10 well-known RSNs in “Individual RSN identification” heading. It should be pointed out that there are many other potentially important and meaningful dictionary network components that should be examined and characterized in the future. For instance, Figure 1e shows other spatial distributions that do not match the known RSN templates. However, it is unclear whether their spatial patterns correspond to some potential functional networks activated during the resting state. On the other hand, we could do more analysis in the temporal domain (dictionary matrix) to explore the dynamic interactions among different dictionary atoms at different frequency scales. Another thing we can do is to introduce structural information and combine with current-derived spatial patterns. For example, we can predict dense individualized and common connectivity-based cortical landmarks (DICCCOLs) (Zhu et al., 2012) on these 210 subjects and examine whether there exists a consistent overlap between DICCCOLs and a specific spatial pattern. Finally, it should be also noted that, in this article, we focus on the presentation of the methodologies that using dictionary-learning-based method for AD classification based on the R-fMRI scan at first time for each subject. In the future work, we will apply our method to other applications, for example, the MCI conversion prediction and studies of longitudinal changes of subjects.

Acknowledgments

D.Z. and X.J. were supported by NSF CAREER Award (IIS-1149260), NIH R01 DA-033393, NIH R01 AG-042599, and NSF BME-1302089. X.Z. was supported by the China Government Scholarship and the Doctorate Foundation of Northwestern Polytechnical University. Data used in this article were funded by the ADNI (U01AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2_0012). ADNI is funded by the NIA, NIBIB, and through generous contributions from the following: Alzheimer's Association; Alzheimer's Drug Discovery Foundation; BioClinica, Inc.; Biogen Idec, Inc.; Bristol-Myers Squibb Company; Eisai, Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; GE Healthcare; Innogenetics, N.V.; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Medpace, Inc.; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Novartis Pharmaceuticals Corporation; Pfizer, Inc.; Piramal Imaging; Servier; Synarc, Inc.; and Takeda Pharmaceutical Company. The CIHR is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the FNIH (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Disease Cooperative Study at UCSD. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.

Author Disclosure Statement

No competing financial interests exist.