The effect of local bending on gating of MscL using a representative volume element and finite element simulation

Abstract

Many physiological processes such as cell division, endocytosis and exocytosis cause severe local curvature of the cell membrane. Local curvature has been shown experimentally to modulate numerous mechanosensitive (MS) ion channels. In order to quantify the effects of local curvature we introduced a coarse grain representative volume element for the bacterial mechanosensitive ion channel of large conductance (MscL) using continuum elasticity. Our model is designed to be consistent with the channel conformation in the closed and open states to capture its major continuum rheological behavior in response to the local membrane curvature. Herein we show that change in the local curvature of the lipid bilayer can modulate MscL activity considerably by changing both bilayer thickness and lateral pressure profile. Intriguingly, although bending in any direction results in almost the same free-energy cost, inward (cytoplasmic) bending favors channel opening, whereas outward (periplasmic) bending facilitates closing of the narrowest part of the MscL pore. This quantitative study using MscL as a model channel may have wide reaching consequences for the effect of local curvature on the physiological function of other types of prokaryotic and eukaryotic membrane proteins.

Introduction

Studies of membrane proteins have implicated a direct link between the lipid environment and the structure and function of some of these proteins.¹ Many of the membrane proteins such as mechanosensitive (MS) ion channels are coupled to the lipid bilayer due to hydrophobic forces.^2-7 Thus, any mechanical stimuli on the lipid bilayer are expected to cause a force induced conformational change in the embedded protein as well. However, the physical basis of force transduction in mechanosensitive ion channels has not been quantitatively elucidated.

One of the most studied physiological mechanotransduction mechanism in bacteria is found in the form of the multiple mechanosensitive channels including the mechanosensitive channels of small and large conductance, MscS and MscL.^3,7,8 In addition to these channels, the small antibiotic peptide gramicidin A also shows stretch sensitivity and can be either activated or inactivated by tension. These processes are reliant on bilayer thickness.⁹

To date, owing from the results obtained from various molecular and nanoscale approaches (e.g., MD, EPR and FRET) the structure and function of MscL reconstituted in the lipid are well characterized.^3,4,10-14 However, due to the “multi time scale and length scale” property of the full gating process, the underlying mechanism has not quantitatively been clarified. MscL is gated directly by the membrane tension in the lipid bilayer.^3,15,16 Thus, we aim to introduce a representative volume element (RVE) for gating of MscL which is designed to be consistent with the channel structure (in the resting and open states) to capture some of the continuum rheological behavior of this important family of bacterial channels during gating. This is a major distinction of this work to introduce and employ a coarse grain model, which is relatively simple to use and has an acceptable similarity to the reality of the channel and its surrounding at the molecular level.

Materials and Methods

To proceed with the continuum (coarse grain) study of gating of MS channels, the lipid bilayer has been considered as a three layer sandwich plate,¹⁷ in which the upper and lower plates represent the head groups and the core is representing the tails of the lipid bilayer (Fig. 1A). This enabled us to capture the phenomenological details of the lipid bilayer deformation during suction and bending of the membrane. (Moreover, using ANSYS APDL (Classic) software,¹⁸ a funnel shape representative volume element (RVE) with minimum thickness of 5Å(equal to the diameter of each transmembrane helix) has been introduced as a continuum model of MscL. The geometry of the RVE pore is based on the MscL pore conformation in the detergent obtained using HOLE program¹⁹ (Fig. 1B). Similar to the other coarse grain models,^20,21 in our continuum (FE) model the less important factors have been overlooked to facilitate exploring the major conformational responses of the lipid bilayer and the embedded MS channel to external perturbations during the whole gating process. Moreover, the proposed three-dimensional FE model is able to simulate the overall fiexural behavior of MscL and its surrounding lipid bilayer subjected to the non-uniform distributed loads. The bilayer and MscL were fully meshed using eight-node linear brick Solid185 elements using ANSYS APDL software. The mesh refinement must satisfy the need for a fine mesh to give an accurate stress distribution in a reasonable analysis time. The optimal solution is to use a finer mesh in areas of high stress, respectively in the contact zones of the MscL and the lipid pore, then in the remaining areas (Fig. 1A).

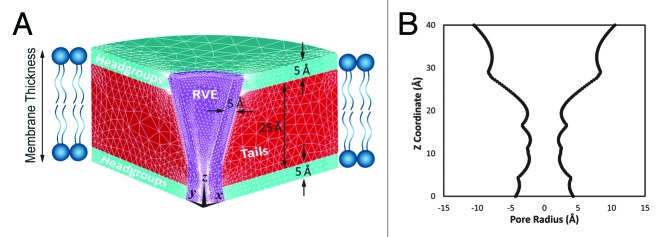
Figure 1. (A) A section of 3D axisymmetric FE model of the lipid bilayer and the incorporated MscL. The upper and lower layers represent the head groups and the core illustrates the tails of lipid bilayer. The thickness of the representative volume element (RVE) is 5 Å. (B) The initial RVE conformation is based on the resting conformation of MscL in detergent which may be determined using HOLE program employing a spherical probe.¹⁹

In nano- and molecular-mechanics (MM), usually an RVE will be used to facilitate the calculations and continuum mechanic description of a structure.^22-25 However, first, it is important to define how the proper equivalent mechanical properties of the proposed RVE can be determined based on physical behavior of the target structure. In the case of MscL, we modeled the initial shape of the RVE based on the MscL crystal structure in the detergent. Then the MscL model was embedded in the lipid membrane to see how the protein structure deforms due to the intrinsic pressure profile of the lipid bilayer. After the first equilibrium position (closed state of MscL in the lipid bilayer), a tension (15 mN/m above the midpoint activation threshold of MscL⁴) was exerted on the lipid bilayer. Hence, the actual tension is a superimposition of the prestress in the bilayer, and the tension developed in the membrane resulted from the applied suction through the micropipette.⁴ This is followed by an extensive parametric study using our calibrated FE model to find out for what equivalent mechanical properties of RVE, the pore shape is fit to the closed and open states of MscL obtained from MD simulation.²⁶ In our FE model, Young’s modulus and Poisson’s ration of the lipid bilayer are assumed to be 15 MPa and 0.5, respectively.²⁷ The Poisson’s ratio of the RVE is also assumed to be 0.5.

Results and Discussions

To find the most appropriate mechanical properties for the MscL RVE, a wide range of Young’s modulus, E, (10 MPa to 70 MPa) was considered on our set of parametric FE simulations. The corresponding equilibrium shape of the channel model under the effect of the intrinsic pressure of the lipid bilayer (before applying tension on the bilayer) has demonstrated for 4 typical values of the elasticity modulus (Fig. 2A). The intrinsic pressure profile in the bilayers is because of the amphipathic nature of the lipids composing it. In fact, the hydrophilic headgroups are packed together to prevent the exposure of the hydrophobic tails to water (solvent),²⁸ while maintaining a nearly constant volume (Poisson’s ratio for both lipid and MscL is close to 0.5) due to attractive dispersion forces and entropic repulsion between the lipid tails.

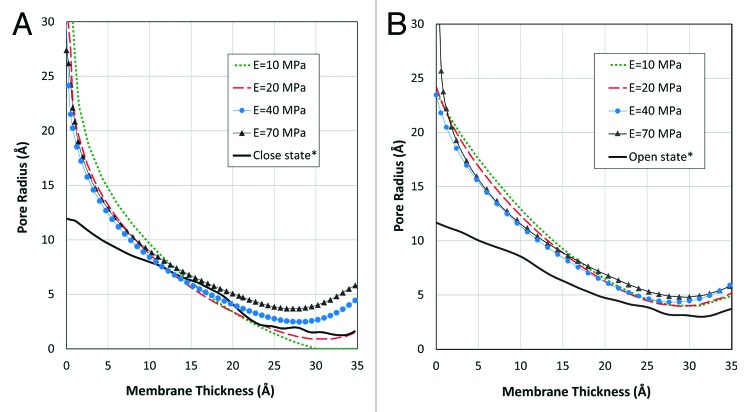
Figure 2. (A) The effect of internal pressure of the lipid bilayer on RVE of MscL for different Young’s moduli after reconstitution of MscL in lipid bilayer. The pore shape across the membrane deforms to minimize the strain energy of the lipid and the channel. The shape of the deformed pore may be compared with the closed pore conformation (black line signed by *) obtained from MD simulations²⁶ to find the most appropriate elastic module for the MscL RVE. (B) Deformation of the MscL RVE for different Young’s moduli after applying tension (15 mN/m, higher than MscL midpoint activation threshold^40,41) on the lipid bilayer. After the application of this tension the pore conformation across the membrane deforms to minimize the strain energy of the system. The shape of the deformed pore can be compared with the open pore conformation of MscL (black line signed by *) obtained from MD simulations²⁶ to acquire the most appropriate elastic modulus for the MscL RVE.

According to Figure 2A, E = 10 MPa is clearly too soft to be used as the equivalent elastic modulus for our protein as it resulted in the radius of zero in the narrowest part of the channel pore. Among all the feasible values for the Young’s modulus of the RVE, the Young’s modulus of 40 MPa and 50 MPa seem to be the best candidates as their corresponding channel conformation are closer to the MD results in the resting state of the channel. However, this is not the only case. We should also consider the shape of the pore after applying tension on the lipid bilayer, and check for what value of E the RVE deformed shape is the closest to the open channel structure obtained from the MD simulation²⁶ (Fig. 2B). The applied tension was assumed to be 15 mN/m, which is above the midpoint activation of MscL (~12 mN/m).⁴ It is represented that again 40 MPa and 50 MPa are the best candidates to model the open state as well (Fig. 2B). To acquire the most appropriate value, the mean value of the error square of the deviation of each FE profiles from the MD results (in 10 equally distributed points in all over the channel pore) has been presented in Figure 3 in two steps: (i): after channel reconstitution in the lipid bilayer and (ii): after applying tension on the lipid bilayer. Based on our FE computations, E = 40 MPa is the best equivalent value for the RVE elasticity modulus according to the first step (after MscL reconstitution in the lipid bilayer), while with a little difference from E = 40 MPa, the FE result corresponding to E = 50 MPa appears to be the best value in the second step (after applying tension on the lipid bilayer). However, as both steps are equally important in describing the channel gating behavior, in overall (the unbroken line in Figure 3), E = 40 MPa is the most appropriate value for the elastic modulus of the RVE (Fig. 3). More importantly, if one focuses on the area near the channel effective pore by considering a weight function in which the square of deviation in this area has a bigger weighting factor, then E = 40 MPa would conclusively be the best value.

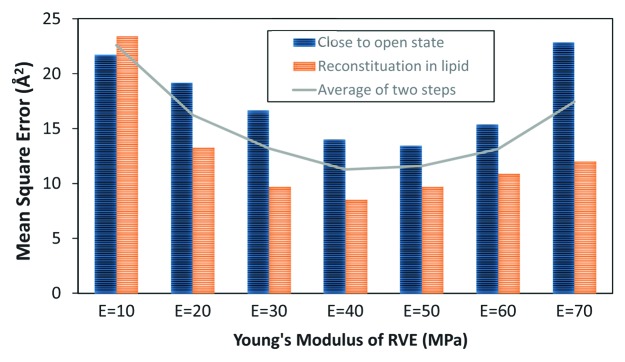
Figure 3. The mean square error of the RVE conformation deviation from its molecular conformation²⁶ across the membrane in the closed and open states of MscL; Mean Square Error is defined as $(MSE)=\frac{1}{n}{{\displaystyle {\sum }_{i=1}^n(R}}_i-R_i{(}^2$ Where ^R_i is the orientation of an alternative point across the pore and R_i is the orientation of the corresponding point on the relevant MD graph of the pore.²⁶n is the total number of points (nodes) which are distributed equally through the bilayer thickness (z coordinate) which was sufficient to be taken as 15. The unbroken line shows the sum of mean squares in the two (closed and open) states. E = 40 MPa would be the most appropriate value for the RVE Young’s modulus with respect to both closed and open conformations.

In addition to physiological processes such as cell division, endocytosis and exocytosis, asymmetric incorporation of chlorpromazine (CPZ) and/or lysophosphatidylcholine (LPC) may change membrane curvature ¹⁶, inducing greater pressure in the polar regions of one leaflet ²⁹ (Fig. 4A). The latter one leads to a strong interaction amid the phosphate groups of the upper part of the membrane and therefore changes its initial curvature. A number of studies have been performed to address the effect of asymmetrical incorporation of amphipaths into the lipid bilayer and thus their effects on gating of MS channels using various approaches such as patch clamp electrophysiology,^13,16,30,31 and Molecular Dynamics simulation (MD).³² Some experimental approaches confirmed that the curvature causes modulation of channels.^30,31,33,34 However, the mechanism by which these molecules affect channel gating has not been elucidated.

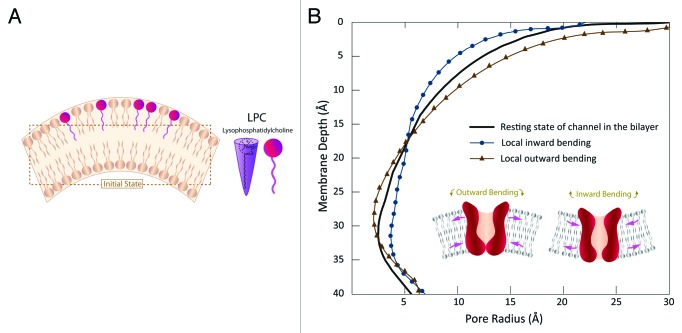
Figure 4. (A) Curvature change caused by asymmetrical incorporation of lyso-phosphatidylcholine (LPC) in the outer leaflets of the bilayer. (B) Influence of outward and inward bending on the channel conformation along the bilayer thickness. Inward bending results in a considerable opening in the narrowest part of the channel, whereas the outward bending shrinks the channel in this area. The total areal change of the channel in the both cases is very similar.

Herein, using benefit of our FE model, we can calculate the stress and strain fields developed in the channel area due to the local bending of lipid bilayer. The lipid bilayer thickness, h, was assumed to be 35 Ǻ with the Young’s modulus and Poisson’s ratio being 15 MPa and 0.5, respectively. Assuming a local radius of curvatureR = 25 nm, the curvature value, C, would be C = 1/R = 1/(25nm) or 0.04 nm^-1. This value is in the range of curvature of the bilayer available in the literature.^1,31 Thus, the effect of a local curvature of 0.04 nm^-1 in the lipid bilayer on the channel pore configuration has been represented (Fig. 4B).

Interestingly, our computational results have demonstrated that bending direction is crucial in gating of MscL. In other words, when the lipid bilayer experienced an inward bending, the effective pore radius of MscL increased from 2.4 Ǻ to 3.7 Ǻ. However, the outward bending of the lipid bilayer resulted in reducing the channel pore in this area, and consequently less space for ions to pass through the channel. These results complements and expands the experimental results obtained from the patch clamp recording of bacterial MS channels in conjunction with incorporation of amphipaths such as LPC, CPZ into lipid bilayer.^16,30,35 For example, MscL of Escherichia coli embedded in bilayers composed of asymmetric amounts of single-tailed and double-tailed lipids has been shown to gate spontaneously, even in the absence of membrane tension.³ Moreover, anionic and neutral amphipaths preferentially insert into the outer half of the bilayer and produce crenation. Cationic amphipaths insert into the negatively charged inner half of the bilayer and lead to cup formation.³⁶ Intriguingly, the effect of curvature direction is not limited to the prokaryotic MS channels. However, based on our computational results, we predict that the response of different channels to different curvature directions varies depending on the channel structure. We also need to consider that only local curvature direction could modulate the channel, while change in the direction of the global curvature of the membrane (such as applying negative and positive pressures on a patched membrane) cannot cause a considerable change in the pressure profile of the membrane. This is simply because the curvature in both directions is much bigger than the size of the channel and thus the moment resulted from the change in the global curvature of the patch (i.e., > 100 nm) is not, per se, enough to modulate an MS channel like MscL. Thus, activation and inactivation of TREK-1 in a cell-attached patch in the zero voltage³⁰ is unlikely to be because of the curvature change in the whole patch due to applying positive and negative pressures. Different patch clamp results by Brohawn et al. also showed that TRAAK and TREK1 channels are activated by both positive and negative pipette pressure.³⁷

Another important aspect of study is about the way one judges about gating energy needed for opening of the channel. Our result indicates that both inward and outward bending result in a similar membrane tension, T, and areal change, ∆A, and thus a similar gating energy, ∆ G = T∆A, with ∆ G being the gating energy.³⁸ However, we showed that formation of outward curvature is not favorable for opening MscL. Only inward curvature can make a bigger effective pore for passing the ions through the channel, whereas outward curvature reduces the radius of the pore in the narrowest part of MscL (Fig. 4B).

Furthermore, according to our computational results, after the channel protein was reconstituted in the lipid bilayer, the pressure profile of the lipid bilayer altered to a different equilibrium state (Fig. 5). In a lipid bilayer at equilibrium, the summation of forces should be zero. In other words, the contracting influence of the headgroups must be balanced by the tendency of the lipid tails to maximize their entropy by occupying a greater volume, since the net tension in a free bilayer is zero. However, some researchers³⁹ believe that the consequent pressure profile after channel reconstitution may not still be enough to fully open the channel, but it confidently facilitates the channel opening as the free gating energy is reduced.³⁹ Nevertheless, it has been claimed previously in other works¹⁷ that 10% change in the pressure profile leads to channel activation. Consequently, according to Figure 5, it can be seen that the local curvature can easily cause the required pressure difference for activating the MS channels. More interestingly, for both upward and downward concavity, the change in the pressure profile in comparison with the resting mode is approximately 15% (Fig. 5). Therefore, it can be concluded that the existence of local curvatures and their variation as well as their concavity direction dramatically changes the stress profile through the thickness of bilayer. Furthermore, in agreement with the previous experiments,² because of the hydrophobic coupling between the lipid bilayer and proteins, the bilayer thickness varied by 5 Å (14%) as MscL was embedded in the lipid bilayer (Fig. 5).

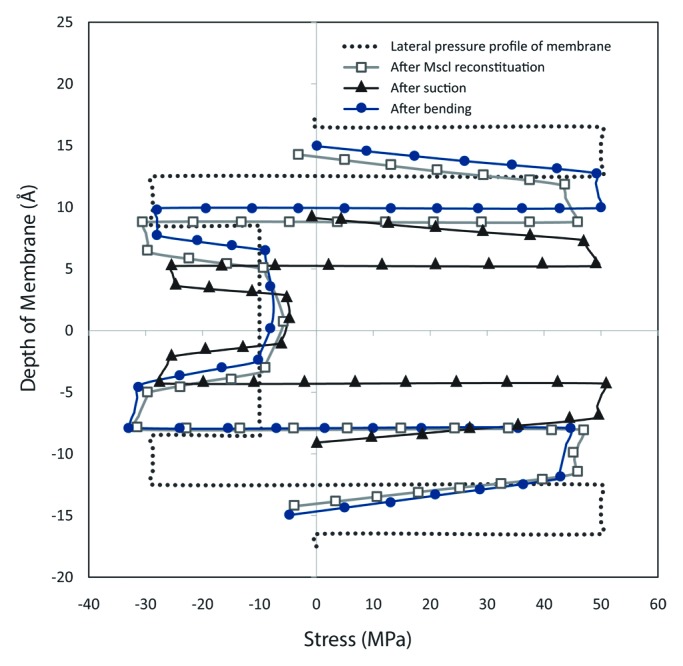
Figure 5. Lateral pressure profile of the membrane after the MscL reconstitution, applying a bilayer tension and local curvature; the dotted line demonstrates the intrinsic lateral pressure in the lipid bilayer; the blue line with square markers shows the change in the bilayer pressure profile as a result of reconstitution of the channel in the membrane. After application of tension, the pressure profile still remains symmetric (black line with triangle markers); however the bilayer thickness decreases around the channel area as a result of Poisson’s effect. The red line with circle markers illustrates the asymmetric pressure profile across the lipid bilayer after application of bending.

Conclusion

To suppress the limitations of molecular dynamics simulations, using benefit of finite element (FE) modeling, a representative volume element (RVE) has been introduced for MscL to get insights about gating of MS channels due to local membrane bending. The most important advantage of our FE computational model is its higher speed in comparison to other approaches such as Molecular Dynamics (MD) simulations. Moreover, without compromising the accuracy, our model has the capability to investigate the effect of the various force regimes on the function of MscL channel and lipid bilayers such as stress strain distribution field, conformational change in both channel and lipid bilayer during gating, and MscL sensitivity to change in the membrane local curvature. Thus, developing such a straight forward model allows us to study the gating of MS channel under different force regimes and geometrical conditions. As such, this computational model facilitates studying the effects of local and nonlocal curvatures of lipid bilayers on the conformational changes of MS channels.

The RVE model was designed to be consistent to the channel conformation in three conditions including channel structure in detergent as well as the channel conformation in the closed and open states. Based on our computational results, local curvature has a considerable effect on stress profile of the lipid bilayer and thus modulation of the MS channel reconstituted in a lipid bilayer. In addition, local curvature considerably changes the lipid bilayer thickness due to existence of hydrophobic forces between MscL and lipid bilayer. Our results confirms and expand the experimental works has been done previously on this subject. For instance, the lateral pressure profiles and surface tensions observed in this study can quantitatively confirm the experimental observations that asymmetric incorporation of lysolipids into different leafiets of a bilayer patch in a patch-clamp setting led to activation of MscL. Interestingly, we indicated that MscL respond differently to different local curvature directions. Inward (cytoplasmic) curvature has shown to be more effective in opening of the MscL, while the effective channel pore (the narrowest part of the channel) reduces due to outward (periplasmic) bending and thus facilitate inactivation of the channel. The proposed model has also far-reaching biophysical implications such as studying the impact of cytoplasmic and periplasmic physiological stimuli or osmotic gradients on modulation of MS channels.

10.4161/chan.29572