Coiling of elastic rods on rigid substrates

Significance

The deployment of a rodlike structure onto a moving substrate is commonly found in a variety engineering applications, from the fabrication of nanotube serpentines to the laying of submarine cables and pipelines. Predictively understanding the resulting coiling patterns is challenging given the nonlinear geometry of deposition. In this paper, we combine precision model experiments with computer simulations of a rescaled analogue system and explore the mechanics of coiling. In particular, the natural curvature of the rod is found to dramatically affect the coiling process. We have introduced a computational framework that is widely used in computer animation into engineering, as a predictive tool for the mechanics of filamentary structures.

Abstract

We investigate the deployment of a thin elastic rod onto a rigid substrate and study the resulting coiling patterns. In our approach, we combine precision model experiments, scaling analyses, and computer simulations toward developing predictive understanding of the coiling process. Both cases of deposition onto static and moving substrates are considered. We construct phase diagrams for the possible coiling patterns and characterize them as a function of the geometric and material properties of the rod, as well as the height and relative speeds of deployment. The modes selected and their characteristic length scales are found to arise from a complex interplay between gravitational, bending, and twisting energies of the rod, coupled to the geometric nonlinearities intrinsic to the large deformations. We give particular emphasis to the first sinusoidal mode of instability, which we find to be consistent with a Hopf bifurcation, and analyze the meandering wavelength and amplitude. Throughout, we systematically vary natural curvature of the rod as a control parameter, which has a qualitative and quantitative effect on the pattern formation, above a critical value that we determine. The universality conferred by the prominent role of geometry in the deformation modes of the rod suggests using the gained understanding as design guidelines, in the original applications that motivated the study.

The laying of the first transatlantic telegraph cable (1) opened the path for fast long-distance communication. Nowadays, submarine fiber-optic cables, a crucial backbone of the international communications (e.g., the Internet) infrastructure, are typically installed from a cable-laying vessel that, as it sails, pays out the cable from a spool downward onto the seabed. The portion of suspended cable between the vessel and the contact point with the seabed takes the form of a catenary (2). Similar procedures can also be used to deploy pipelines (3), an historical example of which is the then highly classified Operation PLUTO (Pipe-Lines Under the Ocean) (4), which provided fuel supplies across the English Channel at the end of World War II. One of the major challenges in the laying process of these cables and pipelines is the accurate control between the translation speed of the ship, $v_b$, and the pay-out rate of the cable, v. A mismatch between the two may lead to mechanical failure due to excessive tension (if $v_b>v$) or buckling (if $v_b<v$), which for the case of communication cables can cause the formation of loops and tangles, resulting in undesirable signal attenuation (5, 6). At the microscale, deployment of nanowires onto a substrate has been used to print stretchable electronic components (7), and both periodic serpentines and coils have been fabricated by the flow-directed deposition of carbon nanotubes onto a patterned substrate (8).

The common thread between these engineering systems is the geometry of deployment of the filamentary structure with a kinematic mismatch between the deposition rate and the translational speed. Moreover, the suspended catenary can be treated as a thin rod (9) given that the diameter of the cable, pipe, or filament can be orders of magnitude smaller than any other length scales in the system. The process of pattern formation for an elastic rod coiling on a substrate, also known as the elastic sewing machine (10), has been previously studied both numerically (11) and experimentally (10, 12). However, a systematic study and a predictive understanding of the underlying mechanisms that determine the coiling modes and set the length scale of the patterns remain remote. Moreover, there is a need for high-fidelity numerical tools that can capture the intricate geometric nonlinearities of the coiling process.

Here, we conduct a hybrid experimental and numerical investigation of the coiling of a thin elastic rod onto a moving substrate and characterize the resulting patterns. We perform precision experiments at the desktop scale (Fig. 1A), where a custom-fabricated rod is deposited onto a conveyor belt. As the relative difference between the speeds of the injector and the belt is varied, we observe a variety of oscillatory coiling patterns that include sinusoidal meanders (Fig. 1B and Movie S1), alternating loops (Fig. 1C and Movie S2), and translated coiling (Fig. 1D and Movie S3). Our model experiments explore the scale invariance of the geometric nonlinearities in the mechanics of thin elastic rods (9), thereby enabling a systematic exploration of parameter space. In parallel, we perform numerical simulations, using the discrete elastic rods (DER) method (9, 13, 14) that is introduced from computer graphics into the engineering community, and find good quantitative agreement with experiments.

Fig. 1.

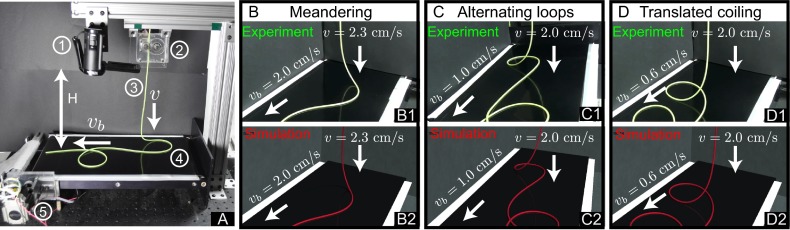
(A) Photograph of the experimental apparatus. The thin elastic rod (3) is deposited by an injector (2) onto a conveyor belt (4), which is driven by a stepper motor (5). The patterns that form on the belt are recorded by a digital video camera (1). (B–D) Representative coiling patterns at different values of the control parameters: Upper, from experiments (in green); and Lower, from DER simulations (in red). (B) Sinusoidal meanders ($v_b=2.0\hspace{0.17em}\mathrm{cm}/\mathrm{s}$, $v=2.3\hspace{0.17em}\mathrm{cm}/\mathrm{s}$) (Movie S1). (C) Alternating loops ($v_b=1.0\hspace{0.17em}\mathrm{cm}/\mathrm{s}$, $v=2.0\hspace{0.17em}\mathrm{cm}/\mathrm{s}$) (Movie S2). (D) Translated coils ($v_b=0.6\hspace{0.17em}\mathrm{cm}/\mathrm{s}$, $v=2.0\hspace{0.17em}\mathrm{cm}/\mathrm{s}$) (Movie S3). Material properties of the rod are $r_0=0.16\hspace{0.17em}\mathrm{cm}$, $\rho =1.18\hspace{0.17em}\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$, $E=1.3\hspace{0.17em}\mathrm{MPa}$ (i.e., $L_{gb}=3.3\hspace{0.17em}\mathrm{cm}$), with a deployment height of $H=50\hspace{0.5em}\mathrm{cm}$.

Our investigation emphasizes (i) geometry, (ii) universality, and (iii) the significance of natural curvature. The patterns resulting from coiling of an elastic rod in our experiments have a striking resemblance to those found when deploying a viscous thread onto a moving belt (14–19) (known as the viscous sewing machine) and in electrospinning of polystyrene fibers (20). As such, (i) this similarity across various systems reinforces that geometry is at the heart of the observed phenomenon, whereas the constitutive description plays second fiddle. A fundamental challenge in this class of problems lies in the geometric nonlinearities that arise in the postbuckling regime, even though the material remains in the linear regime and small-strain elasticity is maintained (9). Furthermore, (ii) as we investigate the first mode of instability, from straight to meandering patterns, we observe that the onset is consistent with a Hopf bifurcation (21). Finally, (iii) we find that the natural curvature of the rod is a pivotal control parameter. This is important given that in the engineering systems mentioned above, natural curvature may develop from the spooling of the cables and pipes for storage and transport (22). Together, the experiments and numerics enable us to identify the physical ingredients and predictively understand the characteristic length scales that underlie the coiling process.

Physical and Numerical Experiments

Desktop-Scale Physical Experiments.

A photograph of our experimental apparatus is presented in Fig. 1A; an elastomeric rod is deployed at a controlled injection speed, v, onto a conveyor belt that is moving with speed $v_b$. The rod is custom fabricated from a silicone-based rubber [vinylpolysiloxane (VPS)], using a protocol (22–24) that accurately prescribes the circular cross-sectional radius, $r_0=1.6\hspace{0.5em}\text{mm}$; density, $\rho =1.02\hspace{0.5em}\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$ or $\rho =1.18\hspace{0.5em}\mathrm{g}/\mathrm{c}{\mathrm{m}}^3$; Young’s modulus, $E=0.18\hspace{0.17em}\mathrm{MPa}$ or $E=1.3\hspace{0.17em}\mathrm{MPa}$; Poisson’s ratio $\nu \approx 0.5$; and natural curvature, $0<{\kappa }_n<0.4\hspace{0.5em}{\text{cm}}^{-1}$. A variety of coiling patterns can be attained when the rod comes in contact with the belt and the process is imaged by a digital camera. The possible coiling states include meandering (sinusoidal patterns, Fig. 1 B1 and Movie S1), alternating loops (Fig. 1 C1 and Movie S2), translated coiling (coiling only to one side, Fig. 1 D1 and Movie S3), and stretched coiling (coils separated by a long catenary, see Fig. 3B). See Materials and Methods for additional details on the experiments.

Fig. 3.

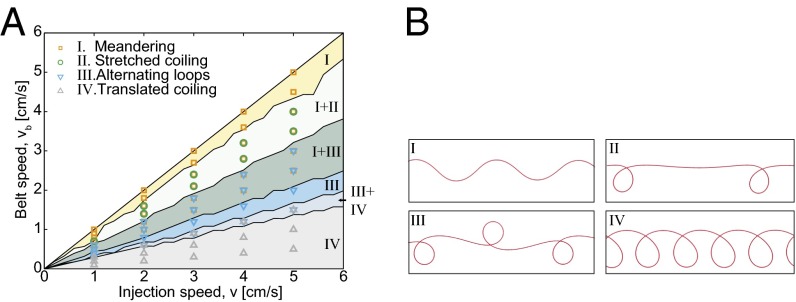
Dynamic coiling. (A) Phase diagram of coiling patterns in the $\left(v,v_b\right)$ parameter space, for a rod with $L_{gb}=3.3\hspace{0.5em}\mathrm{cm}$, deployed from height $\overline{H}=15$. Data points correspond to experiments. Shaded regions correspond to DER simulations (only the data for the phase boundaries are shown for the numerics). The study is focused in $v>v_b$, the region where nonlinear coiling patterns are observed. (B) Representative snapshots (from simulations) of the trace left on the belt for the various coiling regimes: I, meandering, $\left(v,v_b\right)=\left(2.3,\hspace{0.5em}2.0\right)\hspace{0.17em}\mathrm{cm}/\mathrm{s}$; II, stretched coiling, $\left(v,v_b\right)=\left(4.5,\hspace{0.17em}3.0\right)\mathrm{cm}/\mathrm{s}$; III, alternating loops, $\left(v,v_b\right)=\left(2.0,\hspace{0.5em}1.0\right)\hspace{0.17em}\mathrm{cm}/\mathrm{s}$; and IV, translated coiling, $\left(v,v_b\right)=\left(2.0,\hspace{0.17em}0.6\right)\hspace{0.17em}\mathrm{cm}/\mathrm{s}$.

Numerics from the Graphics Community.

Hand in hand with the physical experiments, we conduct numerical simulations using the DER method (13, 14), which was originally developed to serve the visual special effects and animated feature film industries’ pursuit of visually dramatic (i.e., nonlinear, finite deformations) dynamics of hair, fur, and other rod-like structures. DER is based on discrete differential geometry (DDG), a budding field of mathematics that is particularly well suited for the formulation of robust, efficient, and geometrically nonlinear numerical treatments of elasticity (25). This method supports arbitrary (i.e., curved) undeformed configurations, arbitrary cross sections (i.e., noncircular), and dynamics. A direct comparison between simulations and experiments is provided in Movies S1–S3, with no fitting parameter; all control, geometric, and material parameters are measured independently.

Physical Ingredients

We assume that due to its slenderness and the geometry of the setup, the rod is inextensible. The configuration of a Kirchhoff elastic rod (9, 26) is succinctly represented by an adapted framed curve $\left\{\gamma \left(s\right),\theta \left(s\right)\right\}$, where $\gamma \left(s\right)$ is an arc-length parameterized curve in ${\mathrm{ℝ}}^3$ describing the rod’s centerline, and $\theta \left(s\right)$ describes the angular evolution of the tangent-aligned orthonormal material directors $\left\{{\gamma }^{\prime }\left(s\right),{\mathbf{m}}_1\left(s\right),{\mathbf{m}}_2\left(s\right)\right\}$ relative to a natural, twist-free reference frame (27). The prime refers to differentiation with respect to arc length; e.g., ${\gamma }^{\prime }\left(s\right)=d\gamma /ds$. Upon deformation of the rod, the local strains are captured by the twist, ${\theta }^{\prime }\left(s\right)$, and curvature, $\kappa \left(s\right)=\Vert {\gamma }^{″}\left(s\right)\Vert$.

The energy stored in the deformation of the rod is expressed in terms of inertial, gravitational, and elastic contributions per unit length,

$${\mathrm{ℰ}}_{\text{total}}={\mathrm{ℰ}}_i+{\mathrm{ℰ}}_g+{\mathrm{ℰ}}_e.$$ [1]

The elastic energy term can itself have bending and twisting components, ${\mathrm{ℰ}}_e={\mathrm{ℰ}}_b+{\mathrm{ℰ}}_t$, depending on the specific deformation mode. The inertial term is ${\mathrm{ℰ}}_i=\pi \rho r_0^2{v}^2$, and the remaining, geometry-dependent, terms are elaborated later when needed. Depending on the relative magnitude of the various energies, the following coiling regimes can be identified (12): (i) elastic $\left({\mathrm{ℰ}}_e\gg {\mathrm{ℰ}}_g\sim {\mathrm{ℰ}}_i\right)$, (ii) gravitational $\left({\mathrm{ℰ}}_g\sim {\mathrm{ℰ}}_e\gg {\mathrm{ℰ}}_i\right)$, and (iii) inertial $\left({\mathrm{ℰ}}_i\sim {\mathrm{ℰ}}_e\gg {\mathrm{ℰ}}_g\right)$. Given the properties of our rod and slow injection speeds, $0.5 \text{cm}/\text{s}<v<6.0 \text{cm}/\text{s}$, the ratio between inertial and gravitational energies, yields a Froude number, $\text{Fr}=v^2/\left[gR\right]$ (R is the typical radius of curvature of deformation of the rod) that lies within ${10}^{-4}<\text{Fr}<{10}^{-2}$. Inertial effects can therefore be neglected.

Gravito-Bending Length.

We now identify the primary characteristic length scale of our system. We first consider the case of a planar, twist-free deformation $\left({\mathrm{ℰ}}_t=0\right)$ of a straight rod $\left({\kappa }_n=0\right)$ that is deformed into a configuration with curvature κ. The corresponding bending energy is ${\mathrm{ℰ}}_b=EI{\kappa }^2/2$, where $I=\pi r_0^4/4$ is the area moment of inertia. Taking the radius of curvature, $R={\kappa }^{-1}$, as the relevant length scale for height, the gravitational energy is ${\mathrm{ℰ}}_g=\pi \rho g{r}_0^{2}R$. Balancing the bending and gravitational energies yields the characteristic length,

$$L_{gb}={\left(\frac{r_0^{2}E}{8\rho g}\right)}^{1/3}.$$ [2]

This gravito-bending length (28) will be shown to be crucial in setting the various features of the coiling patterns. Hereafter, an overbar represents nondimensionalization of length by $L_{gb}$ and time by $L_{gb}/v$; e.g., ${\overline{\kappa }}_n={\kappa }_n{L}_{gb}$ denotes the dimensionless natural curvature.

Static Coiling

We start our investigation by deploying the rod onto a steady substrate (belt speed $v_b=0$), which leads to nearly circular coiling (Fig. 2 A and B, SI Appendix, and Movies S4 and S5).

Fig. 2.

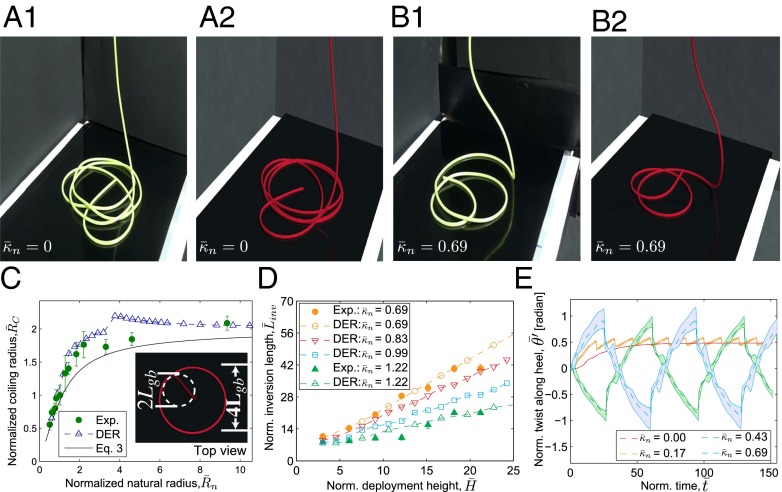
Static coiling (belt is stopped, $v_b=0$, and speed of injection is $v=2\mathrm{cm}/\mathrm{s}$). (A) Coiling of a straight rod (${\overline{\kappa }}_n=0$, $L_{gb}=3.3\hspace{0.5em}\mathrm{cm}$) (Movie S4). (B) Coiling of a curved rod (${\overline{\kappa }}_n=0.69$, $L_{gb}=3.3\hspace{0.5em}\mathrm{cm}$) with an imminent reversal in coiling direction (Movie S5). A1 and B1 are from experiments. A2 and B2 are from simulations. (C) Normalized radius of coiling, ${\overline{R}}_C$, vs. the normalized natural radius of the rod, ${\overline{R}}_n=1/{\overline{\kappa }}_n$. Solid line is the scaling prediction from Eq. 3. Deployment height is fixed at $\overline{H}$ = 15. (Inset) Top view of the coil from DER simulations. For reference, the dashed circle has diameter $2L_{gb}$. (D) Normalized inversion length, ${\overline{L}}_{\text{inv}}$, as a function of normalized deployment height, $\overline{H}$, at different values of ${\overline{\kappa }}_n$. (E) Time series of twist, ${\overline{\theta }}^{\prime }\left(\overline{t}\right)$, of the suspended heel $\left(0<s<s_c\right)$. The dashed line represents the average value within $0<s<s_c$ and the thin solid lines correspond to the minima and maxima within this interval. All other values of ${\overline{\theta }}^{\prime }$ are within the shaded region. The curves with ${\overline{\kappa }}_n=\left\{0,\hspace{0.17em}0.17\right\}$ correspond to the regime in A. The curves with ${\overline{\kappa }}_n=\left\{0.43,\hspace{0.17em}0.69\right\}$ correspond to the regime in B, exhibiting torsional buckling and coiling inversions.

The Role of Natural Curvature.

In Fig. 2C, we plot the dimensionless coiling radius as a function of the dimensionless natural radius of the rod, ${\overline{R}}_n={\overline{\kappa }}_n^{-1}$, finding excellent quantitative agreement between experiments and simulations. For low values of the natural radius, the coiling radius first scales as ${\overline{R}}_C\sim {\overline{R}}_n$, but then levels off and eventually asymptotes to ${\overline{R}}_C\sim 2$, for nearly straight rods.

Above, for a straight rod $\left({\overline{\kappa }}_n=0\right)$, we showed that the balance between bending and gravitational energies results in the characteristic length scale $L_{gb}$, which we now find to set the coiling radius. Toward interpreting the results in Fig. 2C, we extend the previous scaling analysis to consider a rod with natural curvature: When deformed to coil at radius ${\overline{R}}_C={\overline{\kappa }}_C^{-1}$, the bending energy scales as ${\mathrm{ℰ}}_b\sim \left(EI/2\right){\left({\kappa }_C-{\kappa }_n\right)}^2$. Balancing this with the gravitational energy, ${\mathrm{ℰ}}_b\sim {\mathrm{ℰ}}_g$ yields

$${\overline{\kappa }}_C{\left({\overline{\kappa }}_C-{\overline{\kappa }}_n\right)}^2=c^3.$$ [3]

The constant c can be estimated by noting that, for a straight rod, the radius of curvature of its suspended portion at the contact point with the substrate (Fig. 2C, Inset) is of order $L_{gb}$, because it is also set by the balance ${\mathrm{ℰ}}_b\sim {\mathrm{ℰ}}_g$. By inspection, the dashed circle in Fig. 2C, Inset has radius $L_{gb}$, and together with the above observation that the normalized radius of coiling for ${\overline{\kappa }}_n=0$ is ${\overline{R}}_C=2$, we deduce that $c=0.5$. Replacing this value of c in Eq. 3 yields the solid line in Fig. 2C, which is in good agreement with both experiments and simulations.

The Interplay Between Natural Curvature and Twist.

In Fig. 2 A and B we present snapshots of static coiling, using both a straight rod (Fig. 2A, ${\overline{\kappa }}_n=0$) and a naturally curved rod (Fig. 2B, ${\overline{\kappa }}_n=0.69$), finding that, in both experiments and simulations, the two cases are qualitatively distinct. For straight rods, the coiling orientation is set once by the breaking of symmetry during the initial contact, whereas for naturally curved rods, the orientation reverses periodically. The scenario can be contrasted with the perversion in helix handedness exhibited by naturally curved tendrils in climbing plants (29). In Fig. 2D, we plot the normalized inversion length, ${\overline{L}}_{\text{inv}}$ (i.e., the length of rod deployed between subsequent reversals), as a function of normalized deployment height, $\overline{H}$, and find the inversion length to scale as ${\overline{L}}_{\text{inv}}\sim \overline{H}$, with a slope monotonic in ${\overline{R}}_n$.

Given the good agreement between experiments and simulations found thus far, we now use the DER simulations to access quantities numerically that are challenging or impossible to obtain from the experiments. In Fig. 2E we plot simulated data for the time series (time is normalized by $L_{gb}/v$) of the normalized distribution of twist, ${\overline{\theta }}^{\prime }={\theta }^{\prime }{L}_{gb}$, along the suspended heel (between the injector, at $s=0$, and the contact point with the substrate, at $s=s_c$). Both the minimum and maximum values of ${\overline{\theta }}^{\prime }$ (thin solid lines) and the average values (dashed line) are reported for different natural curvatures. The relatively narrow band that includes all values of ${\overline{\theta }}^{\prime }$ (between the minima and maxima; shaded region of each curve), demonstrates that twist is nearly uniform along the heel. For rods with significant natural curvature (e.g., ${\overline{\kappa }}_n=\left\{0.43,0.69\right\}$), the twist increases monotonically over time until a critical value, ${\overline{\theta }}_c\prime$. At this moment, an inversion event occurs as a result of torsional buckling of the rod. After this coiling reversal, twist decreases and builds up again in the opposite direction until $-{\overline{\theta }}_c\prime$ is reached, and the process repeats periodically. By contrast, for rods with small or no natural curvature (e.g., ${\overline{\kappa }}_n=\left\{\mathrm{0,0.17}\right\}$), the twist asymptotes to a constant, lower than ${\overline{\theta }}_c\prime$, and no inversions occur.

To gain further insight into the nature of these two regimes we note that, by geometry, every deposited loop introduces a total twist of $2\pi$ that must be distributed along the rod (SI Appendix). Naturally curved rods prefer to twist along their heel; twisting along the deposited loop is costly in bending energy, due to the attendant misalignment between natural and actual curvature orientations. Rods with low or no natural curvature also begin by twisting along their heel (similar to their curved counterparts). Eventually, however, the accumulated twisting force along the heel overcomes the bending resistance along the deposited loop. As a result, twist begins to accumulate continuously in the deposited loop, rather than in the suspended heel (SI Appendix, Fig. S3).

Coiling Inversion and the Critical Value of Twist.

We now seek to understand the finding that the coiling inversion occurs at a critical twist, ${\overline{\theta }}_c\prime$. For this, in addition to the gravitational and bending contributions in Eq. 1, we also need to include the twist energy per unit length, ${\mathrm{ℰ}}_t=\left(G\pi r_0^4/4\right){\theta }^{\prime }{\left(s\right)}^2/2$, where $G=E/3$ is the shear modulus of the incompressible material $\left(\nu =0.5\right)$. There is a stationary energetic cost (in gravity and elasticity) for inversion to occur; to overcome this cost, a critical amount of twisting energy $\left(G\pi r_0^4/4\right){\theta }_c^{\prime 2}H$ must accumulate in the heel. In the case of naturally curved rods, the twisting energy of the heel increases at a nearly constant rate (SI Appendix, Fig. S1B), and after a length ${\overline{L}}_{\text{inv}}$ is deposited, the critical value is reached, as shown in Fig. 2E, leading to a coiling inversion.

The dependence of the inversion length on $\overline{H}$ and ${\overline{\kappa }}_n$ (Fig. 2D) can now be understood as follows. If N loops are deposited between inversion events, this increases the mean dimensionless twist by ${\overline{\theta }}_c\prime =N2\pi /\overline{H}$ (SI Appendix), while consuming a rod segment of length ${\overline{L}}_{\text{inv}}=N2\pi {\overline{R}}_C$. Eliminating N gives ${\overline{L}}_{\text{inv}}={\overline{\theta }}_c\prime {\overline{R}}_C\overline{H}$. This is consistent with the linear dependence of ${\overline{L}}_{\text{inv}}$ on deposition height (and the coiling radius in the ${\overline{R}}_C\sim {\overline{R}}_n$ regime) shown in Fig. 2D.

Dynamic Coiling

We proceed by investigating the dynamic coiling regime, where the rod is deployed at a controlled injection speed, v, onto a substrate that is now made to move, by switching on the conveyor belt in our apparatus with a speed, $v_b$. We focus on the regime where the injection speed is larger than the belt speed, $v>v_b$, because sliding and stick-slip dynamics are observed for $v<v_b$, which is beyond the scope of this study. Depending on the relative difference between v and $v_b$, we observe a variety of nonlinear patterns.

Phase Diagrams.

In Fig. 3A we present the phase diagram constructed from a systematic exploration of the $\left(v,v_b\right)$ parameter space for the case of a naturally straight rod, both experimentally (data points) and numerically (shaded regions). The phase boundaries delineating each of the regions with different patterns can be approximated by straight lines that pass through the origin. This suggests that the pattern formation process is governed by the dimensionless speed mismatch between the injector and the belt, $\mathit{ϵ}=\left(v-v_b\right)/v$, a geometric control parameter that can also be regarded as the dimensionless length of excess rod injected onto the belt. When $\mathit{ϵ}=0$ (i.e., $v=v_b$), the deployment results in a straight-line pattern on the belt, and the suspended heel acquires a steady catenary shape. In the limit of $\mathit{ϵ}\to 1$ (i.e., $v_b\to 0$), we recover the static coiling scenario studied above. Nonlinear patterns are observed within the range $0<\mathit{ϵ}<1$. Some of the regions of parameters space exhibit multistability. As such, to ensure that every possible pattern in the simulations is realized, we approached each $\left(v,v_b\right)$ point from two directions. First, keeping v constant, we stepped up $v_b$ in increments of $\mathrm{\Delta }{v}_b\le v/20$ from $v_b=0$ to $v_b=v$. Then, we stepped down $v_b$ along the same range and with the same increment.

We have also constructed the $\left({\overline{\kappa }}_n,\mathit{ϵ}\right)$ phase diagram (SI Appendix, Fig. S5A) and found that the meandering regime can be expanded significantly with increasing ${\overline{\kappa }}_n$. In the discussion of the pattern formation process, thus far, we have neglected the effect of the height of the injector. This is motivated by a more detailed analysis that is presented in SI Appendix, where we also constructed the $\left(\overline{H},\mathit{ϵ}\right)$ phase diagram for a straight rod (SI Appendix, Fig. S5B), finding that $\overline{H}$ has a negligible (logarithmic) effect on the patterns.

The Straight-to-Meandering Transition.

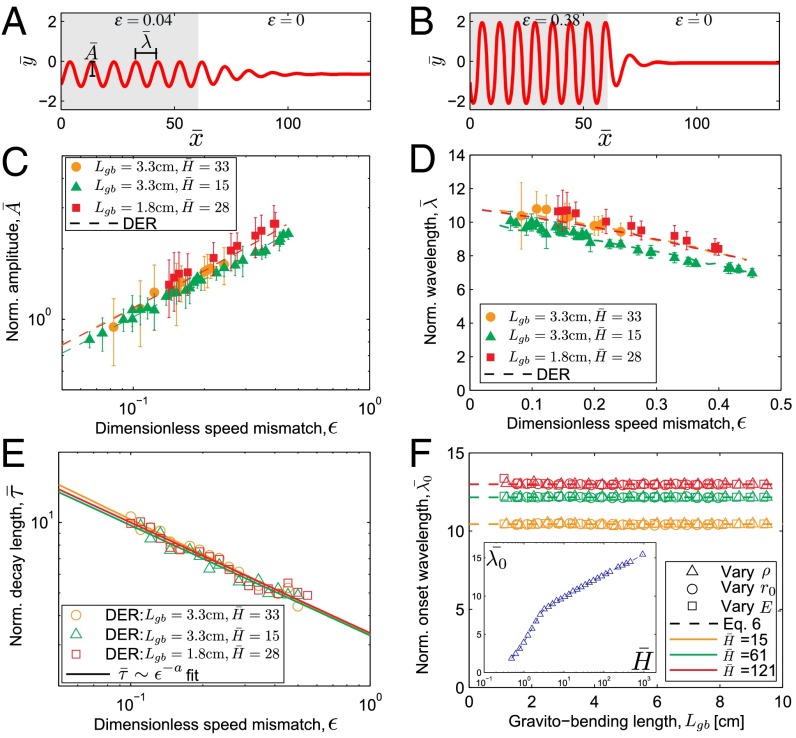
We now give special focus to the first mode of instability above $\mathit{ϵ}=0$, the meandering pattern (Fig. 1B and Movie S1), where the rod prescribes a sinusoidal trajectory on the belt. In Fig. 4 A and B (for $0<\overline{x}<60$) we present two representative examples of simulated steady states of the trace of the rod on the belt at $\mathit{ϵ}=0.04$ and $\mathit{ϵ}=0.38$, respectively. The dimensionless steady-state peak-to-peak amplitude, $\overline{A}$, and wavelength, $\overline{\lambda }$ are plotted in Fig. 4 C and D, as a function of the control parameter ε, for two rods with $L_{gb}=\left\{3.3,1.8\right\}$ cm deployed from different heights, $H=\left\{\mathrm{110,50}\right\}\hspace{0.5em}\mathrm{cm}$. In both experiments and simulations, the dimensionless amplitude is found to scale as

$$\overline{A}={\overline{A}}_0{\mathit{ϵ}}^{1/2},$$ [4]

and the dimensionless wavelength $\overline{\lambda }\left(\mathit{ϵ}\right)$ scales linearly with ε, with a finite value at the onset of the instability, ${\overline{\lambda }}_0=\overline{\lambda }\left(0\right)$. We show below that ${\overline{A}}_0$ and ${\overline{\lambda }}_0$ can be directly related to the physical properties of the rod and the geometry of the system.

Fig. 4.

Quantification of the sinusoidal meandering regime. (A and B) Simulated traces of the meandering patterns for (A) $\mathit{ϵ}=0.04$ and (B) $\mathit{ϵ}=0.38$. At $\overline{x}=60$ ($\overline{x}$ oriented along the direction of travel of the belt), the speed mismatch is instantaneously switched to $\mathit{ϵ}=0$ in both cases, resulting in a decay to a straight pattern. (C) Dimensionless meandering amplitude, $\overline{A}$, vs. ε. (D) Dimensionless meandering wavelength, $\overline{\lambda }$, vs. ε. Both experimental (data points) and simulated (dashed line) data are shown for the values of $L_{gb}$ and $\overline{H}$ presented in Inset. (E) Dimensionless decay length, $\overline{\tau }$, as a function of ε, obtained from the DER simulations. The solid lines are fits to $\overline{\tau }\sim {\mathit{ϵ}}^{-a}$ with exponents $a=\left\{0.49\pm 0.05,0.47\pm 0.06,\hspace{0.5em}\mathrm{and}\hspace{0.5em}0.47\pm 0.05\right\}$ for the datasets with $\left(L_{gb},\overline{H}\right)=\left\{\left(3.3\hspace{0.17em}\text{cm},\hspace{0.17em}33\right),\left(3.3\hspace{0.17em}\text{cm},\hspace{0.17em}15\right),\hspace{0.5em}\mathrm{and}\hspace{0.5em}\left(1.8\hspace{0.17em}\text{cm},\hspace{0.17em}28\right)\right\}$, respectively. (F) Simulated data for dimensionless onset wavelength, ${\overline{\lambda }}_0$, as a function of $L_{gb}$. To vary $L_{gb}$, we start with the parameters of an experimental rod ($r_0=0.16\hspace{0.17em}\text{cm}$, $\rho =1.18\hspace{0.17em}\text{g}/{\text{cm}}^3$, $E=1.3\hspace{0.17em}\text{MPa}$). Then, while keeping two of the three parameters (E, ρ, and $r_0$) fixed, the third is varied over a range spanning up to three orders of magnitude. Inset shows simulated ${\overline{\lambda }}_0$ as a function of $\overline{H}$, at fixed $L_{gb}=3.3\hspace{0.5em}\text{cm}$.

We now investigate these dependences of the amplitude and wavelength of the sinusoidal meandering patterns, on the dimensionless speed mismatch, ε. We start by assuming that the rod is inextensible, such that the arc length of a single period, l, can then be related to its wavelength by $\mathit{ϵ}=\left(l-\lambda \right)/l$, which combined with Eq. 4 yields

$$\overline{\lambda }={\overline{A}}_0\left(C_1\mathit{ϵ}+C_2\right),$$ [5]

where $C_1=-2.48$ and $C_2=3.20$ are known numerical coefficients that can be calculated exactly (SI Appendix). Eq. 5 recovers the finite value ${\overline{\lambda }}_0={\overline{A}}_0{C}_2$ at the onset of instability and the predicted linear dependence is in excellent agreement with experiments and simulations (Fig. 4D). In SI Appendix, the accuracy of this comparison is quantified further against the simulated data.

Our DER simulation tool also supports dynamics and can therefore capture transients caused by step variations of the control parameter, ε. These are, however, challenging to be systematically studied experimentally due to the excessive length of rod required. As such, and ensured by the excellent agreement between the experiments and numerics presented in Fig. 4 C and D, we use DER to quantify these transient dynamics. For example, in Fig. 4 A and B, the control parameter was instantaneously switched from the meandering states, $\mathit{ϵ}=0.04$ and $\mathit{ϵ}=0.38$, respectively, down to $\mathit{ϵ}=0$, at which we expect a catenary straight-line pattern with $\overline{A}=0$. The decay length between the oscillatory and the steady states is considerably slower for the case with a step decrease $\mathit{ϵ}=0.04\to 0$ than that for $\mathit{ϵ}=0.38\to 0$. We fit the local maxima and minima of the trace of the rod on the belt with $\overline{\left|y\right|}=\overline{A}\exp \left(-{\overline{x}}^{\prime }/\overline{\tau }\right)$, where $\overline{A}$ is the dimensionless amplitude before the switch, and $\overline{x^{\prime }}=\overline{x}-60$ is the dimensionless distance along the belt from the location at which the switch to $\mathit{ϵ}=0$ is performed. This enables quantification of the dimensionless characteristic decay length of the transient, $\overline{\tau }$, between the two steady states. In Fig. 4C, we plot $\overline{\tau }$ as a function of the initial value of ε, before the switch to $\mathit{ϵ}=0$, finding a behavior consistent with the power-law dependence $\overline{\tau }\sim {\mathit{ϵ}}^{-1/2}$, which is significant of the “critical slowing down” (30) that is commonly found in dynamical systems near bifurcations.

Together, these observations on the meandering patterns combined—square root dependence of the amplitude on the control parameter, a finite onset wavelength, and critical slowing down at the onset of the instability—suggest that the meandering instability in our rod deployment pattern formation process is consistent with a Hopf bifurcation, which marks the transition from a stable to an oscillatory state in many other nonlinear systems. Moreover, it is interesting to note that the meandering instability for a viscous thread falling onto a moving belt has been shown to also arise through a Hopf bifurcation (17, 18), pointing to universality features and emphasizing the prominence of geometry in these two systems.

Meandering Length Scales.

It remains to establish how the meandering amplitude and wavelength depend on the physical parameters of the problem: the gravito-bending length, $L_{gb}$, and the height of deployment, H. For this purpose, we have performed a series of DER simulations in the meandering regime for rods with gravito-bending lengths in the range $1.0\text{cm}<L_{gb}<10.0\hspace{0.17em}\text{cm}$ (set by varying the density $0.05\hspace{0.17em}\text{g}/{\text{cm}}^3<\rho <25\hspace{0.17em}\text{g}/{\text{cm}}^3$, radius of rod $0.07\hspace{0.17em}\text{cm}<r_0<0.6\hspace{0.17em}\text{cm}$, and Young’s modulus $0.05\hspace{0.17em}\text{MPa}<E<30\hspace{0.17em}\text{MPa}$) from the deployment heights $\overline{H}=\left\{15,61,121\right\}$.

In Fig. 4F we plot the values of dimensionless onset wavelength, ${\overline{\lambda }}_0$, as a function of $L_{gb}$, finding ${\overline{\lambda }}_0$ to stay constant against $L_{gb}$, and an increase in ${\overline{\lambda }}_0$ with increasing $\overline{H}$. Furthermore, Fig. 4F, Inset shows that ${\overline{\lambda }}_0$ scales logarithmically with $\overline{H}$ for $\overline{H}\gg 1$. Combined, these two findings indicate that ${\overline{\lambda }}_0=D_1\log \left(\overline{H}\right)+\beta$, where $D_1$ and β are numerical constants (derivation in SI Appendix), and using Eq. 5 we find

$$\overline{\lambda }=\frac{C_1\mathit{ϵ}+C_2}{C_2}\left[D_1\log \left(\overline{H}\right)+\beta \right].$$ [6]

Note that the ability of Eq. 6 to describe the $\overline{\lambda }\left(\overline{H}\right)$ data breaks down when the deployment height is of the same order as or lower than $L_{gb}$, as seen in Fig. 4F, Inset for $\overline{H}\mathrm{\lesssim }8$. The reason for this discrepancy is that in this limit, bending dominates over gravity, and our initial assumption of a balance between the two is no longer valid. Fitting the simulation data to Eq. 6 yields $D_1=1.22\pm 0.01$ and $\beta =7.14\pm 0.02$. Finally, combining Eq. 6 with Eqs. 4 and 5 allows us to predict the amplitude and wavelength, over arbitrary values of ε in the meandering regime, for rods with a wide range of mechanical properties and deployment heights. This prediction agrees with our observations from experiments and simulations, summarized in Fig. 4 C, D, and F.

The Effect of Natural Curvature.

In the dynamic coiling regime $\left(v_b>0\right)$ thus far, we have considered only a naturally straight rod. We return to the effect of natural curvature ${\kappa }_n$, which was found to qualitatively and quantitatively affect static coiling $\left(v_b=0\right)$. In Fig. 5 A and B, we plot the normalized meandering length scales, ${\overline{A}}_0$ and ${\overline{\lambda }}_0$, respectively (from which all other quantities including the dependence on ε can be calculated), as a function of ${\overline{R}}_n=1/{\overline{\kappa }}_n$, for both experiments and simulations. In this section, we fix both $\overline{H}=15$ and $L_{gb}=3.3\hspace{0.5em}\text{cm}$, unless stated otherwise, and consider rods with ${\overline{R}}_n>1$, given that below this limit (highly curved rods) the coiling patterns can be 3D, which go beyond the scope of our study.

Fig. 5.

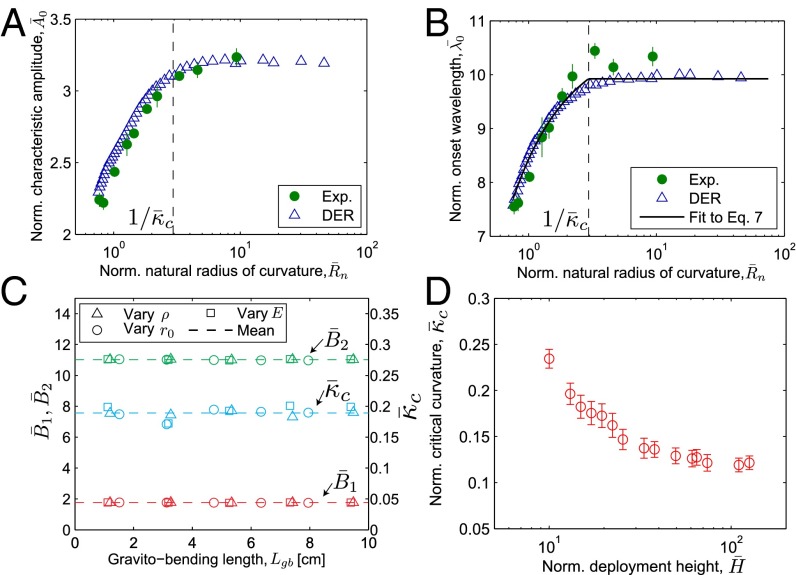
Effect of natural curvature of the rod on meandering. (A and B) Normalized characteristic amplitude, ${\overline{A}}_0$ (defined in Eq. 4) (A), and normalized onset wavelength, ${\overline{\lambda }}_0$ (B), as a function of ${\overline{R}}_n$. In A and B, the rod has gravito-bending length, $L_{gb}=3.3\hspace{0.5em}\text{cm}$, and is deployed from a height of $\overline{H}=15$. (C) Simulation data for the dependence of the parameters ${\overline{B}}_1$, ${\overline{B}}_2$, and ${\overline{\kappa }}_c$, defined in Eq. 7, as a function of $L_{gb}$ (varied in the same way as in Fig. 4F) at $\overline{H}=15$. (D) Variation in the normalized critical curvature, ${\overline{\kappa }}_c$, as a function of $\overline{H}$ at a fixed $L_{gb}=3.3\hspace{0.5em}\mathrm{cm}$.

Whereas the amplitude and wavelength are left unmodified for lower values of ${\overline{\kappa }}_n$, for high values of curvature, ${\overline{A}}_0$ and ${\overline{\lambda }}_0$ decrease linearly with ${\overline{\kappa }}_n$. This points to a threshold critical curvature, ${\overline{\kappa }}_c$, below which the effect of curvature can be neglected. The dependence of ${\overline{\lambda }}_0$ on ${\overline{\kappa }}_n$ can therefore be described as

$${\overline{\lambda }}_0\left({\overline{\kappa }}_n\right)=\{\begin{array}{ll}{\overline{\lambda }}_0\left(0\right),\hfill & \text{for}\hspace{0.5em}{\overline{\kappa }}_n<{\overline{\kappa }}_c\hfill \\ -{\overline{B}}_1^2{\overline{\kappa }}_n+{\overline{B}}_2,\hfill & \text{for}\hspace{0.5em}{\overline{\kappa }}_n>{\overline{\kappa }}_c,\hfill \end{array}$$ [7]

where ${\overline{\lambda }}_0\left(0\right)$ is the dimensionless onset wavelength for a naturally straight rod, and ${\overline{B}}_1$ and ${\overline{B}}_2$ are two numerical constants. Owing to continuity between the two piecewise regimes of ${\overline{\lambda }}_0\left({\overline{\kappa }}_n\right)$ in Eq. 7, we require ${\overline{\lambda }}_0\left(0\right)=-{\overline{B_1}}^2{\overline{\kappa }}_c+{\overline{B}}_2$ and obtain the critical curvature

$${\overline{\kappa }}_c=\frac{{\overline{B}}_2-{\overline{\lambda }}_0\left(0\right)}{{\overline{B}}_1^2}.$$ [8]

Following a similar procedure to that used above to produce Fig. 4F, in Fig. 5C we find that at a fixed dimensionless height $\overline{H}=15$, the parameters $\left\{{\overline{B}}_1,{\overline{B}}_2,{\overline{\kappa }}_c\right\}$ stay constant against $L_{gb}$ with fitted values of ${\overline{B}}_1=1.76\pm 0.01$, ${\overline{B}}_2=11.2\pm 0.01$, and ${\overline{\kappa }}_c=0.189\pm 0.004$. We have numerically evaluated $\left\{{\overline{B}}_1,{\overline{B}}_2,{\overline{\kappa }}_c\right\}$ as functions of $L_{gb}$ at different heights and observed similar trends (data for $\overline{H}=\left\{61,121\right\}$ is shown in SI Appendix). Even if ${\overline{\kappa }}_c$ is constant with $L_{gb}$, it does, however, have a weak dependence on the dimensionless deployment height, $\overline{H}$, as shown in the results of Fig. 5D (DER simulations with $L_{gb}=3.3\text{cm}$). Combined, Eqs. 7 and 8, along with the data in Fig. 5 C and D, allow us to estimate the critical natural curvature of rods over a wide range of physical parameters and deployment conditions.

Conclusions

We have explored a rescaled analog system to study the geometrically nonlinear coiling during deployment of a thin elastic rod onto a substrate. We combined precision model experiments, computer simulations, and scaling analyses to predictively understand the physical parameters that determine the coiling patterns. We focused on static coiling; established the radius of coiling as a function of the gravito-bending length, $L_{gb}$, and natural curvature; and studied the meandering mode of instability in the dynamic regime. The amplitude and wavelength of the meandering patterns were found to be set directly by $L_{gb}$. We gave particular emphasis to the natural curvature of the rod, which both qualitatively and quantitatively affects the coiling patterns. The preponderance of $L_{gb}$ is further emphasized by the fact that it also sets the value of critical natural curvature, ${\kappa }_c$, below which a rod can be considered naturally straight. We have also effectively identified the conditions under which twist does and does not affect the coiling behavior. In the static coiling regime, for example, twist is an important ingredient for inversions, but only when it interacts with sufficient natural curvature. On the other hand, twist does not play a role in the meandering patterns.

Our dimensionless formulation suggests that the problem is geometry dominated, conferring a universality of our findings across engineering applications of diverse spatial scales, from the microscopic (e.g., serpentine nanotubes) to the macroscopic (e.g., transoceanic cables and pipelines). Having generated phase diagrams for the control parameters, it becomes possible to target specific patterns. For example, meandering modes could be excited during the deployment of wires in a textile or pipelines onto the seabed, thereby conferring resilience under strain due to stretching of fabric or seismic activity, respectively. Because wires, cables, and pipelines are often manufactured, stored, and transported in spools that impart permanent curvature, our quantitative analysis could help predict the threshold spool radius beyond which these rodlike structures cannot be considered naturally straight. Understanding the participation of twist in static coiling and meandering could inform the design of application-specific rodlike structures, whose elastic response to twist and bending could be tuned separately; e.g., rotating joints could reduce twist effects, allowing small radii spools to deposit without static coiling inversion. Finally, considering additional practical ingredients such as fluid loading and complex topographies is a possible direction of future study that can now be readily tackled by further augmenting the framework that we have introduced.

Materials and Methods

Rapid Prototyping of Rod Samples.

The rods used in the experiments were cast with silicone-based rubber (vinylpolysiloxane, Elite Double 8 and 32; Zhermack), using PVC tubes as molds. To impart natural curvature to the rod, the tubes were first wrapped around cylindrical objects with the desired radii. The fluid mixture of polymer and catalyst was injected into each tube, which was carefully cut after the curing process to extract the soft elastic rod. For the fabrication of a straight rod, the mold was attached to a rigid straight bar. Two types of rods were used. The first had radius $r_0=0.16\hspace{0.5em}\text{cm}$, density $\rho =1.18\hspace{0.17em}\text{g}/{\text{cm}}^3$, and Young’s modulus $E=1.3\hspace{0.17em}\text{MPa}$. This gives a gravito-bending length, $L_{gb}=3.3\hspace{0.17em}\text{cm}$. The second type had $r_0=0.16\hspace{0.17em}\text{cm}$, $\rho =1.02\hspace{0.17em}\text{g}/{\text{cm}}^3$, and $E=0.18\hspace{0.17em}\text{MPa}$, resulting in $L_{gb}=1.8\hspace{0.17em}\text{cm}$.

Experimental Setup.

The apparatus was composed of a conveyor belt with a vinyl surface and an injection system to deploy the rod, both of which were driven using stepper motors (MDrive). For consistency, we ensured that the rod was aligned at the injector $\left(s=0\right)$ in a way that the orientation of its natural curvature was fixed throughout injection. A digital video camera was used to capture the motion of the rod on the belt. One column of pixels from each frame was retained, and a stack of such columns was processed to obtain the pattern formed by the rod on the belt.

Discrete Elastic Rods Simulation.

Our DER code represents the rod by a piecewise linear centerline, along with a per-segment material frame represented by its angular deviation from a reference frame (13, 14). See SI Appendix for more details. We implemented a simple contact model by applying Dirichlet boundary conditions (pinned nodes) at the points of rod–substrate contact. However, the edges (an edge connects two consecutive nodes) on the deposited rod that are within a certain arc length from the contact point can rotate about the rod centerline. We take this distance to be $\alpha L_{gb}$ and observe that as long as $5\le \alpha \le 50$, it has negligible influence on our quantities of interest, e.g., the coiling radius, the meandering amplitude, and the wavelength. In our numerical experiments, we used $\alpha =5$. We neglect self-contact of the rod on the substrate. The quantitative agreements between experiments and numerics throughout the paper support this assumption. The source code of our numerical tool is available for download (more details in SI Appendix).