Fully automated detection of diabetic macular edema and dry age-related macular degeneration from optical coherence tomography images

Abstract

We present a novel fully automated algorithm for the detection of retinal diseases via optical coherence tomography (OCT) imaging. Our algorithm utilizes multiscale histograms of oriented gradient descriptors as feature vectors of a support vector machine based classifier. The spectral domain OCT data sets used for cross-validation consisted of volumetric scans acquired from 45 subjects: 15 normal subjects, 15 patients with dry age-related macular degeneration (AMD), and 15 patients with diabetic macular edema (DME). Our classifier correctly identified 100% of cases with AMD, 100% cases with DME, and 86.67% cases of normal subjects. This algorithm is a potentially impactful tool for the remote diagnosis of ophthalmic diseases.

1. Introduction

Optical Coherence Tomography (OCT) is widely used in ophthalmology for viewing the morphology of the retina, which is important for disease detection and assessing the response to treatment. Currently, the diagnosis of retinal diseases such as age-related macular degeneration (AMD) and diabetic retinopathy (the leading causes of blindness in elderly [1] and working-age Americans [2], respectively) is based primarily on clinical examination and the subjective analysis of OCT images by trained ophthalmologists. To speed up the diagnostic process and enable remote identification of diseases, automated analysis of OCT images has remained an active field of research since the early days of OCT imaging [3].

Over the past two decades, the application of image processing and computer vision to OCT image interpretation has mostly focused on the development of automated retinal layer segmentation methods [4–18]. Segmented layer thicknesses are compared to the corresponding thickness measurements from normative databases to help identify retinal diseases [19–22]. Aside from measuring retinal layer thicknesses, a few papers have focused on segmenting the fluid regions seen in retinal OCT images such as edema or cystic structures, which are often observed in advanced stages of diseases such as diabetic macular edema (DME) and wet (exudative) age-related macular degeneration [23, 24]. Despite recent advances in the development of multi-platform automated layer segmentation software, for the case of “real-world” clinical OCT images (as opposed to experimental images attained through long imaging sessions) of severely diseased eyes with significant pathology, applications are currently limited to a few boundaries [25] or to the detection of retinal diseases in early stages before the appearance of severe pathology [26].

A relatively small number of algorithms have been developed for the automatic detection of ocular diseases with less emphasis on the direct comparison of retinal layer thicknesses. One method used texture and morphological features from OCT images of the choroid to differentiate between three image classes using decision trees. The accuracy of this algorithm for the detection of (1) neovascular AMD or exudations secondary to diabetic or thrombotic edema; (2) diffuse macular edema without blood and exudations or ischemia of the inner retinal layers; and (3) scaring fibrovascular tissue was 0.73, 0.83, and 0.69, respectively [27]. Another very recent work performed binary classification to differentiate between normal eyes and eyes with advanced AMD using kernel principal component analysis model ensembles, with a recognition rate of 92% for each class [28]. Using a similar data set from advanced AMD and normal subjects, a method based on a Bayesian network classifier achieved an area under curve classification performance of 0.94 [29]. Finally, a recent method measured inner retinal layer thicknesses and speckle patterns and utilized a support vector machine (SVM) classifier to differentiate between normal eyes and eyes with glaucoma [30]. Additionally, we recently introduced an SVM-based classification method for differentiating wild-type from rhodopsin knockout mice utilizing their volumetric OCT scans with 100% accuracy [31].

A very exciting work in this field, which is the closest to what we propose in this paper, is a method by Liu and colleagues. In their work, the authors used multiscale Local Binary Pattern (LBP) features to perform multiclass classification of retinal OCT images for the detection of macular pathologies [32]. While this method shows excellent results, it was limited, in that it requires manual input to select a single fovea-centered good-quality OCT image (signal strength of 8 or above in a Cirrus system) per volume, and detects diseases within the entire eye using only that image.

Here, we present an alternative fully automated method that detects retinal diseases within eyes. This method uses Histogram of Oriented Gradients (HOG) descriptors [33] and SVMs [34] to classify each image within a spectral domain (SD)-OCT volume as normal, containing dry AMD, or containing DME. Our algorithm analyzes every image in each SD-OCT volume to detect retinal diseases and requires no human input. Section 2 introduces our classification method, Section 3 demonstrates the accuracy and generalizability of our classifier through leave-three-out cross-validation, and Section 4 outlines conclusions and future directions.

2. Methods

This section introduces our method for detecting retinal diseases by classifying SD-OCT images. The core steps are outlined in Fig. 1 and described in detail in the following subsections.

Fig. 1.

Overview of the algorithm for classifying SD-OCT volumes.

2.1 Image denoising

SD-OCT images are corrupted by speckle noise, so it is beneficial to denoise them to reduce the effect of noise on the classification results. B-scan averaging or other special scanning patterns [35, 36] reduces noise but decreases the image acquisition speed. Thus, to improve the quality of our captured images, we denoise individual B-scans in the SD-OCT volume using the sparsity-based block matching and 3D-filtering (BM3D) denoising method that is freely available online [37]. Each B-scan is resized to 248 rows by 256 columns for consistent and non-excessive feature vector dimensionality using the MATLAB command imresize and then denoised with BM3D.

2.2 Retinal curvature flattening

SD-OCT images of the retina have a natural curvature (which is further distorted due to the common practices in OCT image acquisition and display [38]) that varies both between patients and within each SD-OCT volume. Following [5], to reduce the effects of the perceived retinal curvature when classifying SD-OCT images, we flatten the retinal curvature in each image.

To flatten the retinal curvature in each SD-OCT image, we first calculate a pilot estimate of the retinal pigment epithelium (RPE) layer. From our prior knowledge that the RPE is one of the most hyper-reflective layers within a retinal SD-OCT image, we assign the outermost of the two highest local maxima in each column of the denoised image as the estimated RPE location. Next, we calculate the convex hull around the pilot RPE points, and use the lower border of the convex hull as an estimate of the lower boundary of the retina. We remove outliers by applying a [1 × 3] median filter (MATLAB notation) to this estimate. To create the roughly flattened image, we fit a second-order polynomial to the estimated retinal lower boundary points and shift each column up or down so that these points lie on a horizontal line. Figure 2 demonstrates this flattening, where Fig. 2(b) is the version of Fig. 2(a) with the retinal curvature flattened.

Fig. 2.

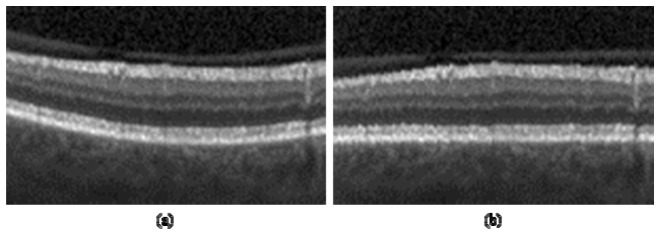
Retinal curvature flattening. (a) SD-OCT image. (b) Image with retinal curvature flattened.

2.3 Image cropping

To focus on the region of the retina that contains morphological structures with sufficient variation between disease classes, we crop each SD-OCT image before extracting the feature vector. In the lateral direction, each image is cropped to the center 150 columns. In the axial direction, each image is cropped to 45 pixels, 40 above and 5 below the mean lower boundary of the retina.

2.4 Feature vector extraction

To effectively describe the shape and appearance of morphological structures within each image, we use HOG descriptors. The HOG descriptor algorithm divides the image into connected regions, called cells, and the shape of local objects is described by counting the strength and orientation of the spatial gradients in each cell. In summary, the image is divided into small spatial cells, and a 1-D histogram of the directions of the spatial gradients, weighted by the gradient magnitudes, is calculated for each cell. To encourage the descriptors to be invariant to factors such as illumination and shadowing, these gradient values are contrast-normalized over larger overlapping spatial blocks. The descriptor vector v for each block is normalized using the L2-Hys method from [33], v→v/(||v||²₂ + ε ²)^1/2 where ε is a small constant, followed by limiting the maximum value of v to 0.2 and then renormalizing. The feature vector for each image consists of the collected normalized histograms from all the blocks. Figure 3 displays a visualization of the HOG descriptors, with Fig. 3(a) as the original SD-OCT image, Fig. 3(b) as the denoised, flattened, and cropped image, and Fig. 3(c) as a visualization of the HOG descriptors for each block.

Fig. 3.

HOG descriptor visualization. (a) Original SD-OCT image. (b) Denoised, flattened, and cropped image. (c) HOG descriptor visualization for each block.

In our implementation, we use the MATLAB command extractHOGFeatures with a [4 × 4] cell size, [2 × 2] cells per block, a block overlap of [1 × 1] cells, unsigned gradients, and 9 orientation histogram bins. Furthermore, to consider structures at multiple scale levels, we extract HOG feature vectors at four levels of the multiscale Gaussian lowpass image pyramid and concatenate them into a single feature vector for each image. The image pyramid is calculated using the MATLAB command impyramid, which uses the separable kernel W(m,n) = w(m)w(n) with w = [(1/4)-(a/2),1/4,a,1/4,(1/4)-(a/2)] from [39] with a = 0.375.

2.5 Image classification

For multiclass classification of each SD-OCT image, we train separate SVMs in a one-versus-one fashion. In our experiments, we have three classes: Normal, AMD, and DME. We train a multiclass classifier, composed of three linear SVMs, to classify Normal vs. AMD, Normal vs. DME, and AMD vs. DME. Our classifier is implemented in MATLAB using the functions svmtrain and svmclassify.

To classify an image, the extracted feature vector is classified using all three SVMs, and the class that receives the most votes is chosen as the classification for the image. An entire SD-OCT volume is classified as the mode of the individual image classification results.

2.6 SD-OCT data sets

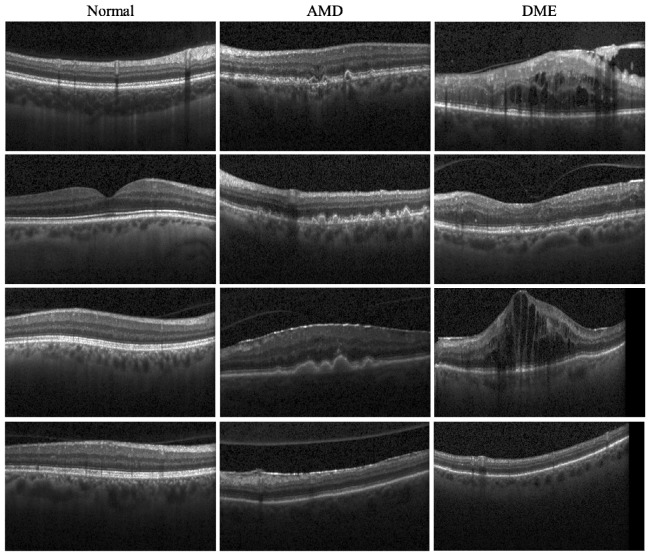
The SD-OCT data sets used for cross-validation consisted of volumetric scans acquired from 45 patients: 15 normal patients, 15 patients with dry AMD, and 15 patients with DME. All SD-OCT volumes were acquired in Institutional Review Board-approved protocols using Spectralis SD-OCT (Heidelberg Engineering Inc., Heidelberg, Germany) imaging at Duke University, Harvard University, and the University of Michigan. Table 1 shows the scanning protocol for these subjects. Figure 4 displays example images from SD-OCT volumes of each of our three classes, demonstrating varying degrees of pathology and the intraclass variability displayed in our data sets.

Table 1. SD-OCT scanning protocol for the study subjects.

Type	Axial Resolution (µm)	Lateral Resolution (µm)	Azimuthal Resolution (µm)	Scan Dimensions (mm × mm)	A-scans	B-scans
Normal	3.87	12	63	6.1 × 6.1	512	97
Normal	3.87	12	62	5.9 × 6.0	512	97
Normal	3.87	12	63	6.1 × 6.1	512	97
Normal	3.87	12	63	6.1 × 6.1	512	97
Normal	3.87	11	59	5.6 × 5.7	512	97
Normal	3.87	11	60	5.8 × 5.8	512	97
Normal	3.87	11	58	5.6 × 5.6	512	97
Normal	3.87	12	61	5.9 × 5.9	512	97
Normal	3.87	11	61	5.8 × 5.9	512	97
Normal	3.87	12	62	6.0 × 6.0	512	97
Normal	3.87	12	129	6.2 × 6.3	512	49
Normal	3.87	12	64	6.1 × 6.2	512	97
Normal	3.87	11	60	5.8 × 5.8	512	97
Normal	3.87	12	64	6.1 × 6.2	512	97
Normal	3.87	12	62	5.9 × 6.0	512	97
AMD	3.87	11	120	5.8 × 5.9	512	49
AMD	3.87	11	120	5.8 × 5.9	512	49
AMD	3.87	6	124	6.0 × 4.6	1024	37
AMD	3.87	11	122	5.8 × 4.5	512	37
AMD	3.87	12	122	5.9 × 4.5	512	37
AMD	3.87	11	122	5.8 × 4.5	512	37
AMD	3.87	6	62	5.9 × 4.5	1024	73
AMD	3.87	11	119	5.7 × 4.4	512	37
AMD	3.87	6	60	5.8 × 4.4	1024	73
AMD	3.87	6	62	5.9 × 4.5	1024	73
AMD	3.87	11	122	5.8 × 4.5	512	37
AMD	3.87	11	122	5.8 × 4.5	512	37
AMD	3.87	11	122	5.8 × 4.5	512	37
AMD	3.87	6	59	5.7 × 4.3	1024	73
AMD	3.87	11	122	5.8 × 4.5	1024	37
DME	3.87	11	120	8.7 × 7.3	768	61
DME	3.87	12	120	8.8 × 7.3	768	61
DME	3.87	12	120	8.7 × 7.3	768	61
DME	3.87	12	232	8.7 × 7.2	768	31
DME	3.87	12	121	8.9 × 7.4	768	61
DME	3.87	12	126	9.1 × 7.6	768	61
DME	3.87	12	120	8.7 × 7.3	768	61
DME	3.87	11	118	8.6 × 7.2	768	61
DME	3.87	12	118	8.7 × 7.2	768	61
DME	3.87	11	60	5.8 × 5.8	512	97
DME	3.87	12	66	6.3 × 6.4	512	97
DME	3.87	11	61	5.8 × 5.9	512	97
DME	3.87	12	62	6.0 × 6.0	512	97
DME	3.87	12	62	5.9 × 6.0	512	97
DME	3.87	11	61	5.8 × 5.9	512	97

Fig. 4.

Example SD-OCT images from normal (column 1), AMD (column 2), and DME (column 3) data sets. Note that the third and fourth rows are from the same subjects. The first three rows show the hallmark B-scans from each disease group. The B-scans in the fourth row of the diseased eyes show that classification based on a single B-scan may not be reliable (e.g. the DME B-scan in the fourth row maybe mistaken for a case of dry-AMD).

During the cross-validation, 65 images from 2 AMD patients and 3 DME patients that were unrepresentative of their classes were excluded when training the classifier. This does not limit the fully-automated property of the proposed method, because all images were used for testing. To facilitate comparison and future studies by other groups, we have made all the images used in the study available at: http://www.duke.edu/~sf59/Srinivasan_BOE_2014_dataset.htm .

3. Results

To assess the performance of our classification algorithm and its ability to generalize to an independent data set, we used leave-three-out cross-validation to efficiently utilize all data sets and to avoid bias in our results by excluding any data. Using our data set of 45 SD-OCT volumes, we performed 45 experiments. In each experiment, the multiclass classifier was trained on 42 volumes, excluding one volume from each class, and tested on the three volumes that were excluded from training. This process results in each of the 45 SD-OCT volumes being classified once, each using 42 of the other volumes as training data. The cross-validation results can be seen in Table 2.

Table 2. Fraction of volumes correctly classified during cross-validation.

Class	Fraction of Volumes Correctly Classified
Normal	13/15 = 86.67%
AMD	15/15 = 100%
DME	15/15 = 100%

The fully automated algorithm was coded in MATLAB (The MathWorks, Natick, MA) and tested on a 4-core desktop computer with a Windows-7 64-bit operating system, Core i7-4770 CPU at 3.4 GHz (Intel, Santa Clara, CA), and 12 GB of RAM. When utilizing the proposed [45 × 150] pixels cropped region, the average computation time was 0.25 seconds per image (averaged over 1000 trials per image). The SVM training process took 57.23 seconds per set of three one-versus-one classifiers. Note that the SVM training is a one-time process and in practice does not add to the overall computation time for the image classification. When using smaller [30 × 100] or larger [60 × 200] fields-of-view, the classification time was 0.19 seconds and 0.29 seconds, respectively. The training time for the former and latter cases was 54.15 and 65.78 seconds, respectively.

4. Conclusion

This paper presented a novel method for the detection of retinal diseases using OCT. This method was successfully tested for the detection of DME and dry AMD. The proposed method does not rely on the segmentation of inner retinal layers, but rather utilizes an easy to implement classification method based on HOG descriptors and SVM classifiers. This is a potentially important feature when dealing with diseases that significantly alter inner retinal layers and, thus, complicate the layer boundary segmentation task. Moreover, our algorithm achieved perfect sensitivity and high specificity in the detection of retinal diseases despite utilizing images captured with different scanning protocols, which is often the case in real-world clinical practice.

Our algorithm is relatively robust with respect to the analysis field-of-view defined by the cropped area in Section 2.1. While our results report the more conservative and large [45 × 150] region, we could achieve similar performance for a 50% smaller in each direction field-of-view of [30 × 100] region on each B-scan. Using a smaller field-of-view is beneficial as it reduces the memory requirements compared to the larger field-of-view case. However, there is a possibility that in some cases, a smaller field-of-view analysis window would miss the pathology appearing in the more peripheral regions. Similarly to the above cases, when we increased the analysis field-of-view to a very large [60 × 200] region, we misclassified only two subjects. However, the misclassified cases were one DME subject and one Normal subject. We should note that the memory requirements of the very large field-of-view case were significantly higher than the previous cases, and it could not be executed on PC computers with less than 12GB of RAM memory. An uncropped ([248 × 256]) field-of-view case could not be run on our test computer due to heavy memory requirements.

Noting that we used the exact same algorithmic parameters for all subjects in our study, one of the exciting characteristics of our algorithm is its robustness with respect to the imaging parameters, including resolution. As explained in Section 2.1, we resize all input images to a fixed image size. Thus, although our input data was captured with different scanning protocols, resulting in different pixel pitch and resolutions as illustrated in Table 1, we used the exact same algorithmic parameters, including crop size, for all images in our data set. Indeed, it is foreseeable that in a certain study, images could be captured by a significantly different imaging protocol as compared to the common clinical protocols used in this paper. In such cases, the cropping parameters might need to be adjusted to provide a similar pixel pitch as in this study; however, the investigation of such cases is out of the scope of this paper.

In Section 2.2, we used a second order polynomial approximation of the retina curvature. Such an approximation is computationally attractive due to its simplicity and relative robustness to image and vessel shadow artifacts, as compared to more complex models. However, while this model has experimentally proven to be adequate for our classification method, it is indeed a very rough approximation of the true anatomy of the eye. Indeed, many retinal layer segmentation algorithms, especially those using graph cuts based on Dijkstra’s shortest path, should utilize more complex models and techniques to better approximate the retinal curvature to achieve the desired flattening accuracy [12].

Additionally, in Section 2.2, to attain a roughly flattened retina, we shifted the columns by integer values. In some cases, such integer shifts can produce slight retinal layer discontinuities in the flattened image, as seen in Fig. 3(c). If desired, more visually appealing flattened images can be attained by using interpolation to achieve subpixel column shifts. Since the interpolation will slightly increase the computational cost, it might be best reserved for use in cases where the axial resolution of the OCT system is critically low, as in the case of time-domain OCT systems, where interpolation might improve the classification accuracy.

The analysis of a single B-scan is often not sufficient for the diagnosis of retinal diseases. For example, one criterion for the characterization of intermediate dry-AMD, as defined in the Age-Related Eye Disease Study (AREDS), is finding 50 distinct medium-sized drusen [40]. These drusen can appear on several B-scans, requiring multi-frame analysis. Thus, we advocate utilizing several B-scans for the detection of retinal diseases. In our study, we experimentally found out that if 33% or more of the images in the volume are classified as AMD/DME, we achieved the best diseases detection rate. It is reasonable to assume that such detection rate should be lowered for studies of the very early stages of AMD and DME or other diseases such as macular hole, which have a more localized pathologic manifestation.

This fully automated technique is a potentially valuable tool for remote diagnosis applications. Thus, part of our ongoing work is to extend the application of this algorithm to other retinal diseases such as macular hole, macular telangiectasia, macular toxicity, and central serous chorioretinopathy. However, we emphasize that the independent application of this algorithm is not the most appropriate method for the detection of all diseases with retinal manifestations. For example, the detection of the earliest stages of diabetic retinopathy [26] or glaucoma [16] is expected to be significantly more accurate when using layer segmentation methods. We expect that the most efficient fully automated remote diagnostic system for ophthalmic diseases would incorporate both of these approaches. The development of such a comprehensive method is part of our ongoing work.