Automatic detection of bioresorbable vascular scaffold struts in intravascular optical coherence tomography pullback runs

Abstract

Bioresorbable vascular scaffolds (BVS) have gained significant interest in both the technical and clinical communities as a possible alternative to metallic stents. For accurate BVS analysis, intravascular optical coherence tomography (IVOCT) is currently the most suitable imaging technique due to its high resolution and the translucency of polymeric BVS struts for near infrared light. However, given the large number of struts in an IVOCT pullback run, quantitative analysis is only feasible when struts are detected automatically. In this paper, we present an automated method to detect and measure BVS struts based on their black cores in IVOCT images. Validated using 3 baseline and 3 follow-up data sets, the method detected 93.7% of 4691 BVS struts correctly with 1.8% false positives. In total, the Dice’s coefficient for BVS strut areas was 0.84. It concludes that this method can detect BVS struts accurately and robustly for tissue coverage measurement, malapposition detection, strut distribution analysis or 3D scaffold reconstruction.

1. Introduction

In coronary artery disease (CAD), plaques build up in the vessels and obstruct the oxygen-rich blood supply to the heart muscle, which can cause angina or eventually a heart attack. Nowadays, stenting after angioplasty is one of the main treatment options for CAD. Stents are tiny tube-like devices that are usually made of metal meshes, designed to support the vessel wall to prevent the acute vessel recoil after the plain-old balloon angioplasty [1]. The first introduced stent was the bare metal stent (BMS), with a known risk of neointimal hyperplasia (NIH) which re-narrows of the vessel lumen [2]. The drug-eluting stent (DES) emerged as an alternative to the BMS. It can alleviate NIH significantly, but later, multiple risk factors became evident, such as late stent thrombosis and late acquired malapposition [3, 4]. As a result, a new concept of the temporary stent or scaffold was proposed. Such a device is designed to offer temporary radial strength to avoid the acute vessel closure as a consequence of the acute vessel recoil, and at a later stage, it will be fully absorbed, leading to restoration of lumen patency and vascular flow [5, 6]. A series of temporary vascular stents, termed “Bioresorbable Vascular Scaffold (BVS),” have been developed and undergone extensive clinical evaluation in the past ten years [4, 7–10]. ABSORB BVS (Abbott Vascular, Santa Clara, California, US) is one of first developed temporary scaffolds which have been used for clinical treatment. It consists of a backbone of poly-L-lactide coated with poly-D,L-lactide which contains and controls the release of the antiproliferative drug everolimus (Novartis, Basel, Switzerland) [11]. The thickness of backbone with coated drug layer is 158 µm. ABSORB BVS will be fully absorbed approximately two years after implantation and has exhibited strong positive clinical and angiographic results [12].

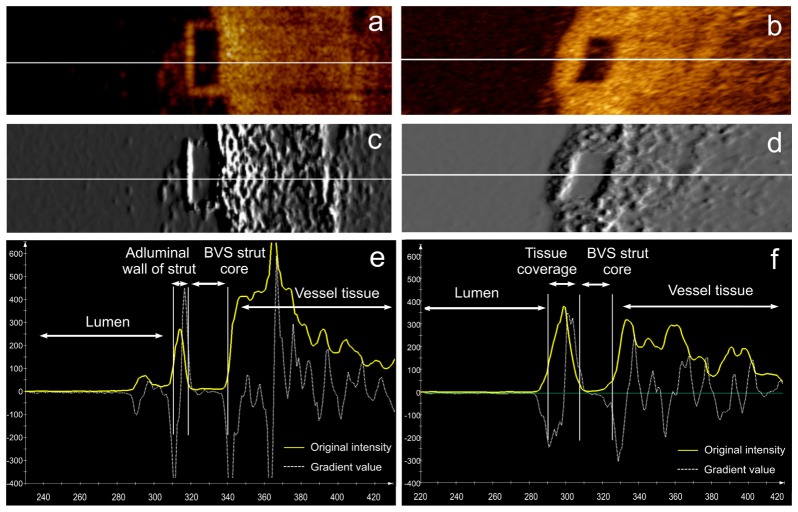
Intravascular optical coherence tomography (IVOCT) is being increasingly used during BVS studies and clinical trials for accurate BVS analysis to assess the rate of bioresorption and to inspect the response of vessel walls [13]. As a relatively new optical signal acquisition technique, IVOCT imaging has a radial resolution of about 10 µm which is ten times higher than its comparable technique: intravascular ultrasound (IVUS). IVOCT has a limited penetration of 3 mm, but it provides a better signal-to-noise ratio than IVUS within the limitation. Furthermore, IVOCT imaging is particularly suitable for BVS struts as they are made of translucent polymers [12]. The transmitted light can readily pass through them and backscattering originates from the difference in refractive index between a strut and its environment (flush fluid or tissue), which results in bright boundaries. Besides, if a strut contains a big fracture which appears as a scattering center, it looks similar to confluent struts [14]. An IVOCT image with newly implanted BVS struts in two different coordinate systems is shown in Fig. 1. There are different BVS strut shapes; however, struts having bright boundaries and box-shape black cores account for 100% of the shapes at baseline, more than 82% at 28 days and 80% at 24 months of all the struts [15]. Therefore in this paper we will focus on the box-shape type of BVS struts. The strut area is measured based on its black core. The bright boundary is not included since when a strut is covered by tissue, its boundary cannot be precisely defined, while for a newly implanted strut, its thickness will be overestimated by measuring the distance between the leading-edges of its adluminal wall and abluminal wall [12].

Fig. 1.

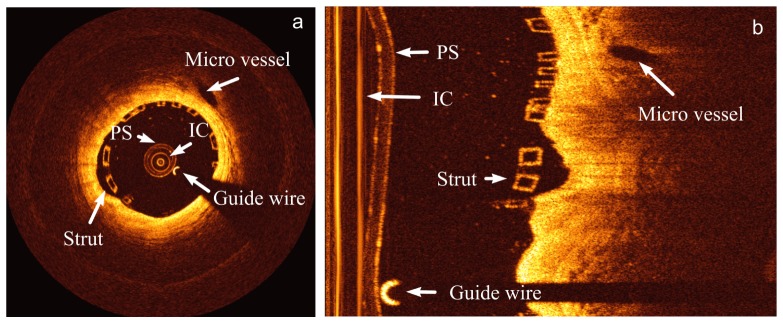
A baseline IVOCT image in (a) the Cartesian coordinate system and (b) the polar coordinate system. In both images, the imaging catheter (IC), the protective sheath (PS), the guide wire, a micro vessel and a BVS strut are marked.

Many automated metallic stent strut detection methods [16–19] have been published. However, to the best of our knowledge, current BVS analyses in IVOCT images still rely on the labor intensive manual delineation of struts. Given the large number of struts in a pullback run, quantitative analysis is feasible only when struts can be detected automatically. In this paper, we present an automated method to detect BVS struts and to measure their black core areas in IVOCT pullback runs.

2. Method

To detect struts accurately, a-priori information of the input IVOCT data set type (baseline or follow-up) is requested, as the presented algorithm has two slightly different strategies for baseline and follow-up images with respect to some different parameters, false positive filters and the region of interest (ROI). However, in this section, the described procedures are implicitly used for both strategies, unless stated differently in context. As Fig. 2 shows, both strategies contain five main steps: 1) Pre-processing. The bright components in the lumen including the imaging catheter, the guide wire and the protective sheath should be detected and masked; 2) Image transformation. The lumen contour and center are detected so that we can transform Cartesian IVOCT images into new polar images based on the lumen center. In the new polar images, the shapes of BVS struts are usually more rectangular than these in the original polar images; 3) Candidate strut detection. In the new polar images, short candidate segments describing black cores are detected and later clustered as candidate struts; 4) False positive removal. These are removed using a series of false positive filters; 5) Strut contour refining. The strut contours are refined to be smooth and accurate for area measurement and center calculation. In the following subsections, each step of the method is described in more detail.

Fig. 2.

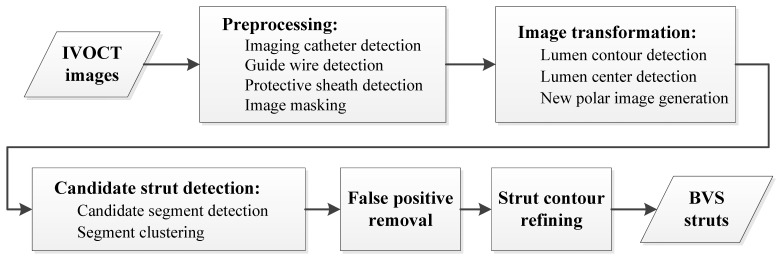
The flow chart of the BVS strut detection method.

2.1 Preprocessing

Bright components inside the lumen, including the imaging catheter, the guide wire and the protective sheath, were masked to improve the further processing. The imaging catheter center is the center of Cartesian images, and as Fig. 1(a) shows, the imaging catheter produces a series of very bright concentric circles, which appear as vertical lines in the polar images as presented in Fig. 1(b). After a proper Z-offset correction, the imaging catheter is located in the same position in the whole pullback run and hence can be detected in the minimum image of the entire pullback run by checking the intensity sum of every column [20]. If a guide wire is used during the image acquisition, it blocks the light signal and consequently generates a black shadow behind it. According to its intensity profile, the guide wire and its shadow were detected using a previously developed method [21].

The imaging catheter is always covered by a protective sheath which appears as a ring with a certain width dependent on the manufacturer and catheter type. During the image acquisition, the imaging catheter moves sideways inside the protective sheath, thus the protective sheath position varies during the pullback and therefore must be detected frame by frame. First, a ROI was defined for the detection. It started from the outer wall of the imaging catheter and was wide enough to cover the protective sheath. As the protective sheath diameter and the image resolution are known, a proper width of the ROI can be computed. Next, the Prewitt compass edge filter with a kernel sensitive to vertical edges [22] was applied to the image, so that the outer (bright-to-dark) edge of the protective sheath was represent by strong negative values. The gradient image was used as a cost matrix to which Dijkstra’s algorithm [23] was applied to detect the minimum cost path dynamically. This path is the outer boundary of the protective sheath. An example of the detection results of the imaging catheter, the protective sheath and the guide wire shadow region is given in Fig. 3(a). To avoid creating new dark to bright edges that may influence the lumen contour detection, the image region inside the protective sheath was masked using the background intensity value. It was computed based on a fixed percentile of the histogram of the entire image sequence. An example of the preprocessed image is presented in Fig. 3(b).

Fig. 3.

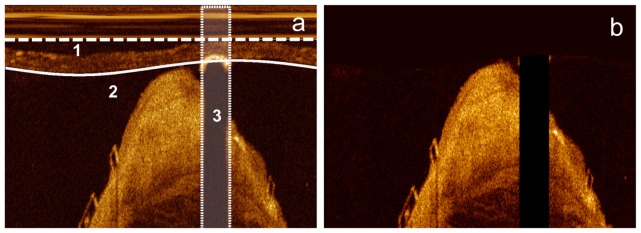
The detected imaging catheter (dashed straight line “1”), protective sheath (solid curve “2”) and guide wire shadow region (area “3”) are given in figure (a). The masked image is given in figure (b). Inside the protective sheath, it is masked with the background intensity value, while the guide wire shadow region is masked as 0.

2.2 Image transformation

Our BVS strut detection is applied to polar images. However, the box-shape BVS struts are usually distorted like parallelograms in the original polar images, since they are converted from Cartesian images based on the catheter center instead of the stent contour center. To improve the BVS strut appearance, new polar images should be created from Cartesian images based on the stent contour center. As lumen contour is similar to the stent contour in most of the cases, its center was used as an approximation of the stent contour center.

The lumen boundary was detected in the original polar images. First, the images were denoised using a median filter [24] to smooth the lumen boundary. Next, a gradient image was generated by applying the Prewitt compass edge filter with the kernel for vertical edges to the smoothed image. Two examples are given in Figs. 4(a) and 4(b). In the gradient image, the lumen boundary is represented by strong negative values and hence Dijkstra’s minimum cost path detected in it was treated as the lumen boundary as Figs. 4(c) and 4(d) demonstrate. The detected lumen boundary was converted into the Cartesian coordinates system and its center was detected using a distance transformation method presented in [25]. Based on the lumen center, a Cartesian image can be transformed into a new polar image like Fig. 4(e). Compared with the original polar images, the shapes of most BVS strut are more rectangular. However, in some cases, the lumen contour is highly irregular, so that BVS struts are still not rectangular after the image transformation as Fig. 4(f) shows. They have irregular shapes and different thickness in the vertical direction. The proposed method contains procedures to detect these irregular struts in the further steps, but in the worst situation, these struts cannot be detected.

Fig. 4.

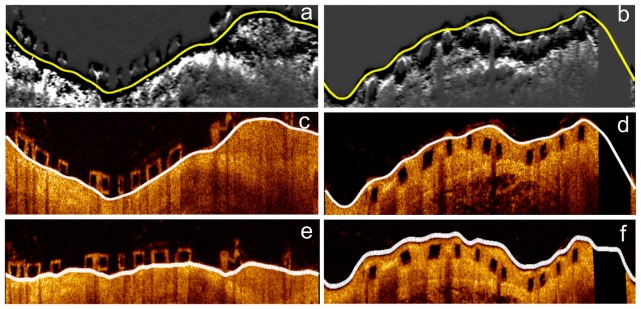
The gradient images of a baseline image and a follow-up image are given in figures (a) and (b). They are used for lumen detection. Yellow curves indicate the detected minimal cost paths. In figures (c) and (d), the original polar images are presented with lumen contours (white curves). The new polar images transformed based on the lumen center are shown in figures (e) and (f) in which most of the BVS struts are more rectangular than in original polar images.

2.3 Candidate strut detection

In the new transformed polar images, candidate BVS struts were detected. As mentioned in the beginning, the presented method has two different strategies to detect baseline and follow-up struts, separately. There are three main differences between them:

• 1. Different ROI for strut detection. For baseline data sets, the struts are usually aligned with the lumen boundary or malapposed, which means most of the struts are inside the lumen contour as Fig. 4(e) demonstrates. However, the lumen detection may be affected by confluent struts or struts placed inside the tissue, so that the detected lumen contour may follow the front wall of these struts instead of the back wall. To cover all the baseline struts, the detected lumen contour needs to be extended with an offset equal to BVS strut thickness. The ROI of baseline strut detection is between this extended contour and the previously detected protective sheath contour. In contrast, in the follow-up data sets, most of the BVS struts are outside the lumen contour as Fig. 4(f) shows, but when some struts are not covered by tissue, the detected lumen contour could pass behind them mistakenly. To include all the follow-up struts, we need to shrink the lumen contour to the lumen center direction with an offset equal to BVS strut thickness. Therefore, the ROI for follow-up strut detection is between the shrunken lumen contour and the image boundary.
• 2. Different thickness threshold. After implantation, BVS struts start to be degenerated and covered by healing tissue. Hence, the boundaries of the follow-up struts are less sharp than newly implanted struts. Consequently, the method uses a slightly bigger thickness threshold to detect follow-up struts than the newly implanted struts. This parameter is set based on the image resolution and will be described later in this section.
• 3. Different degree of the boundary completeness. The boundary of a newly implanted strut usually contains many small gaps as Fig. 4(c) shows. Because a baseline strut is not covered by tissue, its box-shape boundary is mostly created by the backscattering at the strut surfaces which could be affected by the strut position and orientation. Parts of the boundary could be blurred or even missing. Moreover, the residual blood and other artifacts also can affect the completeness of the box-structure. At follow-up stage, struts are usually covered by tissue which helps to generate bright boundaries as Fig. 4(d) shows. Compared with the newly implanted struts, the follow-up struts have a more complete box-shape boundary and hence the method is stricter with regard to their boundary shape and completeness.

In the ROI, we first detected the candidate line segments between the front and back walls of BVS struts scan-line by scan-line and later clustered these segments into candidate struts. To detect candidate segments, both original and gradient images were used. Again, the Prewitt compass edge filter for vertical edges was applied to generate gradient images in which dark-to-bright edges are represented by negative values and bright-tot-dark edges are positive values. The intensity profile and the gradient profile of a scan-line that passes through a BVS strut are given in Fig. 5. According to these profiles, one can state that the BVS region starts with a relatively high intensity (front wall) followed by a certain low intensity region (black core) and it ends with another relatively high intensity (back wall). As a result, candidate segments constituting BVS struts were detected with four main rules:

Fig. 5.

Figures (a) and (b) show a scan-line (white line) passing through a BVS strut in a baseline image and a follow up image, respectively. The corresponding gradient images are presented in figures (c) and (d). The intensity profile (yellow curve) and the gradient profile (white curve) are given in figures (e) and (f). A BVS strut always has low intensity values in the black core region and strong gradient values along the boundary.

• 1. It has low intensity black core region. In this method, the low black core intensity threshold was calculated based on a fixed percentile of the histogram of the pullback run.
• 2. It has a strong positive gradient value in the beginning and a strong negative gradient value in the end. Both the gradient value thresholds were computed according to fixed percentiles of the histogram of the gradient images.
• 3. It has a reasonable length. Segment length represents the strut thickness in scan-line direction. Ideally, the thickness of BVS struts in a pullback run should be the same in each scan-line. However, BVS struts could still appear distorted after the image transformation in section 2.2, since the lumen is not always circular. Moreover, the strut boundary thickness can be influenced by the distance and orientation of the struts. Struts close to the imaging catheter or uncovered by tissue usually are characterized by a wider boundary. Therefore, the thickness of the strut cores in a single pullback run can be different from the standard thickness. In our approach, a range of acceptable thicknesses of BVS strut cores was set based on the standard thickness.
• 4. Candidate segments should not be overlaid in the same scan-line. In case the noise has stronger edge than real struts, the algorithm allows more than one candidate segment in the same scan-line. However, when two candidate segments were found overlaid in the same scan-line, only the one having the highest intensity sum of the front and back walls was selected. If they both had the same intensity sum, the longest one was saved.

For example, the candidate segment results for Figs. 6(a) and 6(b) are presented in Figs. 6(c) and 6(d), which still contain some false candidate segments. They are generated due to the residual blood, micro-vessels, plaques and weak signal region deep in the tissue.

Fig. 6.

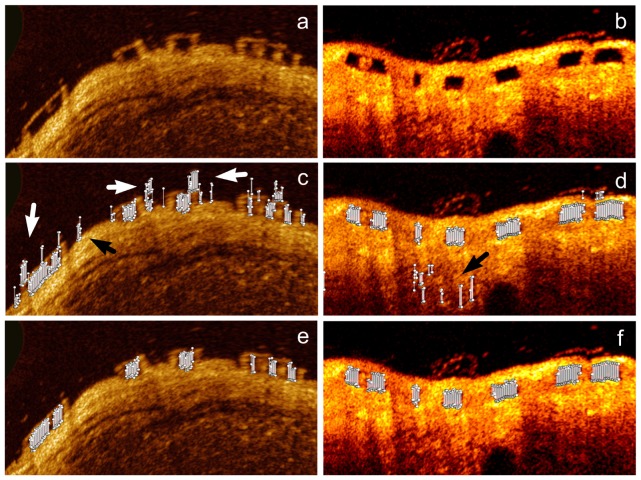
Figure (a) shows a new polar baseline image that is transformed based on the center of a highly irregular lumen contour. The BVS struts in figure (a) still appear distorted and their thickness in the vertical direction is very different. Figure (b) demonstrates a follow-up image transformed based on the center of a circular lumen contour. The BVS struts are less distorted than these in figure (a). The detected candidate line segments (short white lines) are presented in both figures (c) and (d). Both white and black arrows point out the candidate segments caused by residual blood or noise in tissue. These candidates will be clustered as false candidate strut during the clustering. After the false positive removal, only real struts are left as figures (e) and (f) shows.

After having obtained the BVS candidate segments, a clustering method was applied to merge these segments into candidate struts. As Figs. 6(c) and 6(d) show, the candidate segments belonging to the same BVS strut are connected, while the false positives are usually randomly distributed. In this method, the segments were clustered according to their position. It started from the first un-clustered candidate segment and searched for the next segment close to it. A candidate segment can be added to the cluster if it is connected with the last segment in the cluster. The searching continues until no more segments can be attached. Next, we checked if a cluster has top and bottom boundaries as BVS struts should have box-shape boundaries. The follow-up BVS strut boundary is usually complete due to the tissue coverage so that only clusters having both top and bottom edges were saved. In baseline data sets, the BVS strut could have an incomplete box-structure, so that the method allows a cluster to miss its top or bottom boundaries.

2.4 False positive removal

During the clustering, many false candidate struts were generated from false candidate segments as presented in Figs. 6 (c) and 6(d). Therefore, a series of false positive filters were applied to the clustering results to remove them. First, the strut size was used for filtering. A BVS strut should contain a certain number of candidate segments. Small clusters are usually caused by random noise or artifacts in the images. In our research, clusters containing less than 3 candidate segments were removed as false positives. A second filter was applied to search for overlaid struts in each scan-line, because there should be at most one strut in any radial direction, but some false positives can share parts of the boundary with real struts. As a result, when two clusters were overlaid in the radial direction, only the one with complete box-structure was saved. If both clusters had complete box-structures, the bigger cluster was kept.

The third filter is only applicable for follow-up data sets. After the first two filters, a few false positives may still exist in the deep tissue region which contains much random noise due to the weak signal. Compared with the true positives, these false positives were commonly located deeper in the tissue; therefore, a filter was applied to remove outliers based on the thickness of tissue coverage (the distance between struts and the lumen boundary) for each candidate strut, so that a candidate strut having a very different thickness of tissue coverage with the majority was considered as a false positive, since the thickness of tissue coverage changes smoothly in the follow-up data sets. After the previous filtering, the majority of current results should be true positives. Therefore, the median coverage thickness was computed for outlier detection. To be accurate, the clusters in the neighboring frames were used to estimate the median coverage thickness as well. This filter also removed most of the false positives caused by micro vessels and plaques. However, it is not applicable for baseline data sets, as the malapposed struts could have very different distances to the lumen boundary. Examples of the false positive removal results are given in Figs. 6(e) and 6(f).

2.5 Strut contour refining

After false positive removal, the main bodies of the strut black cores were detected. As the candidate segments were always selected with the strongest boundary intensity, the detected adluminal and abluminal walls of BVS struts were usually rough. Besides, the original boundary could be fluctuating because of the noise, inside fractures and low image quality. Examples of the unsmoothed BVS strut contours are shown in Fig. 7(a). Therefore, the front wall and back wall of each detected strut were smoothed using a median filter. Any outliers were replaced by the interpolated point between the nearest neighboring points. The smoothing results are show in Fig. 7(b).

Fig. 7.

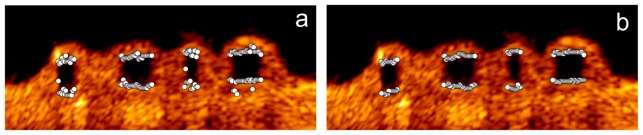
The original boundaries of clusters formed by white points in figure (a) and the smoothed boundaries in figure (b).

The main bodies of the strut cores were formed by line segments with a range of acceptable thickness. However, an irregular shape strut could contain sharp tips in one or both ends as Fig. 8(a) shows. The core regions in the sharp tips have smaller thickness than the acceptable thickness and usually contain more noise than the main body. As a result, the sharp tip regions might be missed during the detection. To recover these tip regions, a post-processing was applied. First, the adluminal and abluminal boundaries were fitted into lines using the least-square error method and the fitted lines specify the ROI for tip refining. Due to the irregular lumen contour, a long BVS strut could be curved, so its front and back walls cannot be fitted into one single line. To be accurate, we fitted two separated lines for the top and bottom boundary of the struts containing more than 20 candidate segments as Fig. 8(b) presents. Next, along the fitted lines, the adluminal and abluminal walls for the missed sharp tip regions were recovered by searching continuous boundaries in the Prewitt edge filtered polar images. The searching ended when the fitted line met the top or bottom edges. The recovered boundary can be seen in Fig. 8(c). In the end, a spline contour was generated for each BVS strut based on the refined boundary as Fig. 8(d) shows. At the same time, the center of each BVS strut was calculated.

Fig. 8.

Figure (a) shows the smoothed boundaries of a cluster in yellow dots. In figure (b), two white lines are fitted to the top part of the strut boundary and two light blue lines are fitted to the bottom part of the strut boundary. Along the fitted lines, the missed boundaries in the sharp tip regions are recovered as figure (c) demonstrated and the final refined strut contour is generated as (d) presents.

3. Validation and results

The automatic BVS strut detection and measurement method was developed using the MeVisLab toolbox (Fraunhofer MeVis, Bremen, Germany) together with in-house developed C++ modules. For validation purposes, 6 pullback runs were used which were acquired using a C7-XR FD-OCT intravascular imaging system together with a C7 Imaging catheter (St. Jude Medical Inc., St. Paul, MN, USA). The automated pullback speed was 20 mm/s with a data frame rate of 100 frames per second. All the pullback runs are in the original 16-bit polar format and each contains 271 frames. Three pullback runs were acquired at baseline, while the other three at 6 to 24 months, respectively. In both baseline and follow-up groups, one pullback run contains no guide wire and the other two contain a standard 0.014 inch steerable guide wire. Temporary blood flushing was performed with a contrast infusion. All the stents are the ABSORB 1.1 bioresorbable vascular scaffold (Abbott Vascular, Santa Clara, CA, USA). Overtime struts are absorbed. According to the trails for the ABSROB BVS [15], there is about 9% reduction of struts in IVOCT images over 6 months and 35% reduction over 24 months. Already due to the difference in position of the IVOCT catheter for the same scaffold at the same time point, there could be a difference in the number of struts. In our study, the baseline and follow up data sets are from different patients and therefore the number of struts is different. Part of the BVS struts could become undetectable after 24 months, but every visible strut in the 6 in-vivo IVOCT pullback runs were used for validation purposes, including struts without box-shape and the struts partly blocked by guide wire shadows.

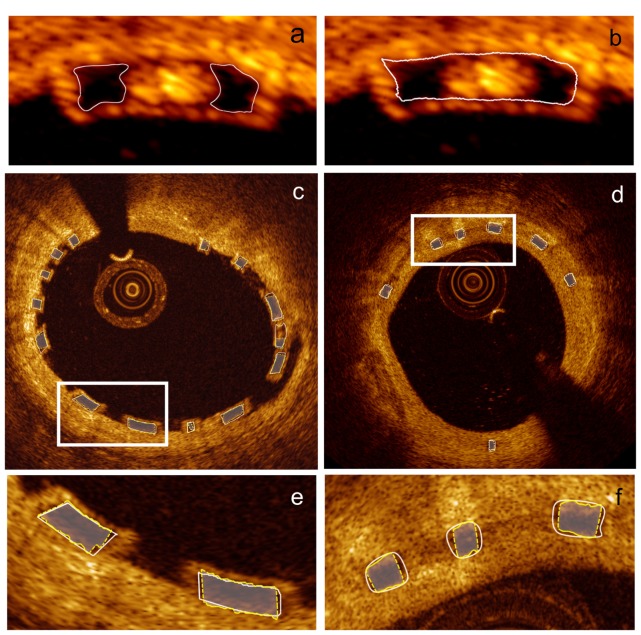
To generate the ground truth, one observer manually drew all 4691 black cores of BVS struts in the 6 pullback runs, 2183 cores from the baseline group and 2508 from the follow-up group. A second independent observer manually drew all the struts in a subset containing one baseline data set and one follow-up data set. The second observer drew one contour for a strut with big fractures. These struts contain more than one black core, and have similar appearance as confluent struts. Therefore, the ground truth from the second observer contains some bright regions between black cores compared with that from the first observer as Figs. 9(a) and 9(b) shows. For incomplete struts, both observers marked the contour based on experience. In total, 726 newly implanted struts and 795 follow-up struts were marked by the second observer. In the same subset, the first observer marked 783 baseline cores and 819 follow-up strut cores. The agreements for BVS strut were given in Sensitivity and the core area agreements were computed using the Dice’s coefficient. The inter-observer agreement of the BVS struts was 98.8% for baseline struts and 99.6% for follow-up struts. The strut area similarity was both 0.83 in the baseline group and the follow-up group. The area difference is mainly because the first observer did not include the bright region caused by big fractures.

Fig. 9.

Figure (a) shows two black cores marked by the first observer and they were marked as a big strut by the second observer as figure (b) presents. A comparison of the ground truth (solid white contours) from the second observer and the algorithmic results (dashed yellow contour with white translucent mask) in a baseline image is presented in figure (c) and another comparison of the ground truth from the first observer and the algorithmic results in a follow-up image is given in figure (d). The enlarged images of the white rectangle regions are given in figures (e) and (f).

During the evaluation, if a detected strut overlays the area of a ground truth, it was counted as a true positive. Otherwise, it is a false positive. The accuracy of black core area was measured by Dice’s coefficient as well. According to the first observer, on average, the method correctly detected 90.0 ± 3.2% struts with 3.1 ± 0.7% false positives in every baseline data set and the Precision was 97.0 ± 0.1%. The Dice’s coefficient for the BVS strut area was 0.83 ± 0.02. If we measure only the area of the correctly detected struts, the Dice’s coefficient was 0.86 ± 0.01. For the follow-up group, the method detected 96.6 ± 2.0% struts correctly with only 0.8 ± 0.8% false positives and the Precision was 99.2 ± 0.1%. The Dice’s coefficient for the strut area was 0.85 ± 0.02. For only the true positive struts, the number was 0.86 ± 0.01. According to the second observer, the method successfully detected 90.8% of baseline struts with 4.3% false positives and the Precision was 95.9%. 92.6% of follow-up struts were detected with 2.2% false positives and the Precision was 97.7%. The Dice’s coefficient for baseline and follow-up strut areas was 0.76 and 0.75, separately. Counting only true positive areas, the Dice’s coefficient was 0.79 and 0.77. Some examples of the ground truth from both observers and algorithmic results are given in Figs. 9(c)–9(f). The strut detection and the area measurement performance for each individual pullback run are presented in Table 1 and Table 2, separately.

Table 1. The strut detection results of the presented method for each validation data set. For each data set, the number of frames containing struts (Frame No.), the numbers of struts in the ground truth (GT), the percentages of true positive (TP) and false positive (FP) are given.

Strut status	Data set	Frame No. (with struts)	No. of GT	TP (%)	FP (%)
Baseline	1	89	630	85.5	3.8
	2	94	770	92.2	3.3
	3	93	783	92.5	2.0
Follow-up	4	97	868	93.7	0.0
	5	91	819	98.0	0.6
	6	97	821	90.4	1.8
Total	-	561	4691	93.7	1.8

Table 2. The strut area measurement performance of the present method in each validation data set. The area of the ground truth (GT) and the Dice’s coefficient between the ground truth and the algorithmic results are given for all struts and only successfully detected struts.

Strut status	Data set	Area of all struts		Area of only true positives
		GT area (mm2)	Dice	GT area (mm2)	Dice
Baseline	1	16.4	0.81	15.0	0.86
	2	14.3	0.82	13.7	0.85
	3	15.9	0.85	15.4	0.87
Follow-up	4	20.1	0.87	19.9	0.88
	5	19.8	0.83	19.0	0.85
	6	18.3	0.84	18.0	0.85
Total	-	104.8	0.84	101.0	0.86

The center position error of the correctly detected strut was computed as well. The average distance error of the strut centers was 17.0 ± 22.5 µm for newly implanted struts, 13.9 ± 11.1 µm for follow-up struts and 15.3 ± 21.0 µm for all struts. The median distance errors for two groups were both 11.1 µm.

4. Discussion

According to the validation results, the algorithm successfully detected 96.6 ± 2.0% follow-up struts with only 0.8 ± 0.8% false positives and 90.0 ± 3.2% newly implanted struts with 3.1 ± 0.7% false positives. The strut center error was 15.3 ± 21.0 µm. Generally, the presented method is accurate and robust under different image circumstances. The performance for the follow-up group is slightly better than the baseline group, because follow-up BVS struts have more complete box-shape boundaries due to the tissue coverage. Backscattering on the interface between struts and tissue creates strong bright boundaries. By checking the boundary completeness during the clustering, the algorithm can easily remove most of the false positive from the follow-up pullback runs. In contrast, the contour of newly implanted struts can be influenced by noise in the lumen, such as residual blood, and hence contains many gaps. The algorithm keeps the clusters that have mild incomplete boundaries to avoid removing too many true positives, but fails to keep the real struts having severe incomplete boundaries. On the other hand, it also leaves more false positives in the results than the follow-up data set. Most of these false positives can be later removed by the filters, but still a few could leave as they are difficult to distinguish. Actually, most of the final false positives are from the baseline group. Similarly, the strut area performance in the follow-up pullback runs (0.85 ± 0.02) is also better than in the baseline pullback runs (0.83 ± 0.02).

When a BVS strut fractures, it generates bright scattering regions that separate the strut into several black cores as Fig. 9(a) shows. In this case, the first observer marked each cores separately, while the second observer drew one big contour for all the cores including the bright fractures as Fig. 9(b) presents. Hence, the manual results from the second observer contain fewer struts but more strut areas than those from the first observer, and the false positive rate according the second observer is 3.2% and the Dice’s coefficient for the strut area is 0.75. However, if we count only the agreed areas between two observers, 95.1% and 96.9% of these areas were correctly detected for baseline and follow-up groups, separately. It suggests that the algorithmic results have a good agreement with the black core regions from both observers. The area errors in the baseline data sets are largely caused by incomplete boundaries, because the strut areas may be overestimated or underestimated. The area errors for follow-up struts are mainly due to the blurred boundary edges, because struts are slowly bioresorbed after implantation. Tissue coverage also weakens the sharpness of strut boundaries. As this method prefers strong edges when detecting struts, the final follow-up strut contours could be distorted.

The strut detection also replies on the proper preprocessing. The imaging catheter, the guide wire and the protective sheath should be removed to facilitate the lumen detection. Besides, these bright components also can negatively impact the baseline strut detection. The lumen center is used as an approximation of the stent contour center. After transforming the Cartesian image to a new polar image based on the lumen center, we could get more rectangular strut contours. However, when the lumen contour is highly irregular, the BVS strut in the transformed polar image could be still distorted like a parallelogram and in many cases, the strut edges are not straight. Therefore, the thickness and the shape of these struts could vary a lot during in the pullback run. To handle this situation, the presented method allows a range of acceptable thickness instead of only the standard thickness to detect as many candidate segments as possible, and in the end, refines irregular strut contours to be more accurate. In a rare case, a strut can be highly distorted in the new polar image and therefore, cannot be detected by this method.

Most of the parameters used in the presented method are related to the image size and image resolution, while the remaining three parameters were set based on the histogram of the original images or the gradient images. These parameters are the minimum intensity threshold for strut boundary, the minimum absolute gradient threshold for edges and the maximum intensity threshold for black core regions. One data set from each group was used for parameter tuning. The same parameter setting was applied to all the pullback runs during the validation.

The presented method also has limitations. The BVS struts can have four different appearances: preserved box, open box, dissolved black box and dissolved bright box [15]. This method can only detect the majority of the cases, being the preserved box, which has a closed high intensity boundary and a low intensity core. All other three types cannot be detected. It also has limitations to handle struts with an incomplete boundary. Moreover, in a few cases, BVS struts can be overlaid after the implantation, but our method cannot detect the overlapping BVS struts, because a false positive filter checks all the overlapping results in radial direction. Only one of these struts could be left in the results. This research is based on the ABSORB 1.1 BVS struts; hence our results cannot be directly generalized to other type of BVS struts which may have different appearance with ABSORB 1.1 BVS after implantation and during the follow up.

5. Conclusion and future work

In conclusion, with the ongoing development of BVS technology, automated BVS strut detection methods become important as they can simplify and speed the quantitative analysis for both clinical research and medical care. In this paper, we implemented an automatic method to detect and measure BVS struts based on the black core region in both baseline and follow-up IVOCT image sequences. The validation results suggest that the proposed algorithm is very accurate and robust, which could be a helpful tool for tissue coverage thickness measurement, strut distribution analysis, 3D visualization, BVS bioresorption validation and vascular response research. In future, we plan to improve the current detection method and to detect BVS struts without box-shape contours.