Close encounters with DNA

Abstract

Over the past ten years, the all-atom molecular dynamics method has grown in the scale of both systems and processes amenable to it and in its ability to make quantitative predictions about the behavior of experimental systems. The field of computational DNA research is no exception, witnessing a dramatic increase in the size of systems simulated with atomic resolution, the duration of individual simulations and the realism of the simulation outcomes. In this topical review, we describe the hallmark physical properties of DNA from the perspective of all-atom simulations. We demonstrate the amazing ability of such simulations to reveal the microscopic physical origins of experimentally observed phenomena and we review the frustrating limitations associated with imperfections of present atomic force fields and inadequate sampling. The review is focused on the following four physical properties of DNA: effective electric charge, response to an external mechanical force, interaction with other DNA molecules and behavior in an external electric field.

1. Introduction

After water and oxygen, DNA is, very likely, the most famous molecule of life known to mankind. This is not surprising, as we all know that an eye-catching, double-helical molecule of DNA carries instructions to manufacture and assemble all the components of a living organism. The wealth of information encoded in a DNA molecule often overshadows its unusual physical properties. For example, the force-extension dependence of double-stranded DNA has a well-defined plasticity plateau that is associated with melting or conformational change of its two strands.

Despite being highly negatively charged, DNA molecules can attract one another and form a condensed state. The direction of DNA motion in an external electric field can reverse upon changing the concentration of the surrounding electrolyte. DNA nucleotides are usually sequenced using methods that rely on the electrophoretic motion of DNA, a physical process of little direct biological relevance. Even the biological role of DNA as storage for genetic information is affected by its sequence-specific physical properties [1–3].

Despite the large number of theoretical and experimental studies, the nature of the microscopic processes that give rise to the above phenomena remain highly debated. With the advent of massively parallel supercomputers it has become possible to characterize these processes directly, through all-atom molecular dynamics (MD) simulations. In this topical review, we present an up-close perspective of the major physical properties of DNA. Because the all-atom MD method explicitly describes the trajectory of every atom in the system with femtosecond resolution, it has the potential to give unparalleled insight into an experimental system. The primary use of the MD method is to suggest a physically plausible explanation or justification of an experimental measurement by animating an equivalent system in silico. Equipped with a physically correct description of interatomic interactions and adequate computational power, the MD method should be able to predict the physical behavior of any biological system. Despite ever-increasing availability of massive parallel computing platforms, making quantitative predictions using MD remains challenging, in part due to imperfections of the inter-atom interaction models.

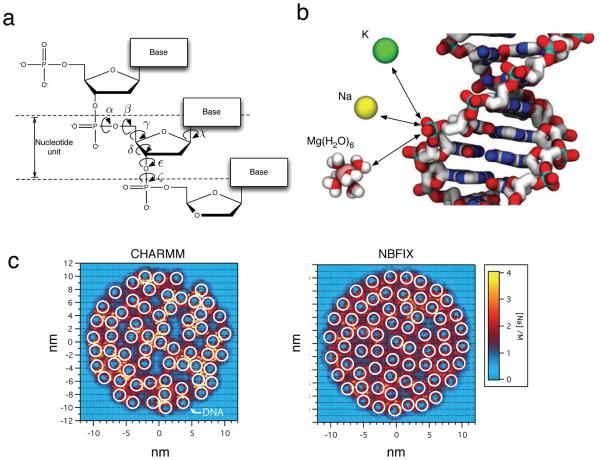
Before we proceed, let’s review the basic chemical structure of DNA, Figure 1. A molecule of DNA is a polymer made up of many DNA nucleotides linearly arranged into a polymer chain. Single-stranded DNA (ssDNA) is made of one such chain, whereas in double-stranded DNA, two ssDNA molecules are arranged into a DNA double helix through non-covalent interactions. The basic unit of DNA structure—a DNA nucleotide—has three major groups: backbone, sugar and base. The backbone is negatively charged under physiological conditions and has a direction (5′-to-3′) determined by the order of the atoms forming the backbone. The sugar group links the backbone to the base. The chemical difference between DNA and RNA is the presence of an extra hydroxyl (OH) moiety in the sugar group, which strongly alters the properties of the molecule. The DNA base carries genetic information and typically comes in the one following four types: adenine (A), cytosine (C), guanine (G) and thymine (T). The complementary hydrogen bond paring of A with T and G with C governs the nucleotide sequence-specific assembly of two single strands into a double helix. The most familiar conformation of a DNA duplex is the so-called B-form duplex shown in Figure 1, but DNA can also adopt a similar but more compact conformation known as an A-form duplex. Except where specified, discussion about double-stranded DNA pertains to B-form DNA.

Figure 1.

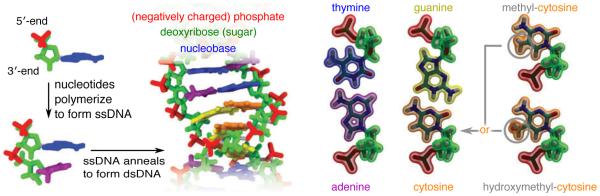
Chemical model of DNA. DNA is a polymer composed of nucleotides, each having a negatively charged phosphate, a deoxyribose sugar ring and one of the four nucleobases: adenine, thymine, guanine, cytosine. Two single DNA strands form a double helix held together through non-covalent interactions. In addition to the four types of DNA nucleotides, chemical modification of DNA occurs frequently and includes methylation and hydroxymethylation.

Chemical modification of DNA bases is common. The most abundant variation is the addition of a methyl group to cytosine, transforming it into a methylated cytosine—a carrier of epigenetic information (derived from the history of an organism). Modifications are possible, including hydroxymethylation and other derivatives [4]. Under physiological conditions, each DNA nucleotide carries a charge of one electron. A single DNA strand is much more flexible than a double helix. The following discussion implicitly assumes that DNA is in an aqueous environment at pH 7.0.

The rest of the review is organized as following. After a brief description of the history and the present state of all-atom modeling of DNA, we describe the application of the MD method to the study of equilibrium properties of DNA, including its charge and mechanical properties, the behavior of DNA under an external force, the interaction between DNA molecules and finally the motion of DNA in an external electric field. Where possible, we begin our description of the physical phenomena with a brief review of conventional theoretic models.

2. Historical perspective on DNA modeling and simulation

The year 1952 witnessed the publication of the first solid evidence that DNA is the genetic material [5]. Just one year later in 1953, the basepaired double-helical structure of DNA was proposed [6]. In that same year, Hermann Staudinger received a Nobel Prize for his work in 1922 demonstrating that polymers are composed of long chains of covalently bonded atoms, and Paul Flory—later a Nobel laureate for his work in theoretical polymer chemistry—published his seminal book “Principles of Polymer Chemistry”. Thus, a theoretical framework for discussing polymers was available for the study of DNA, including the widely employed freely-jointed and worm-like chain models [7–9], see Section 5.1. No time was wasted; in that same year, the worm-like chain (WLC) model was used to analyze the angular dependence of the intensity of scattered light to suggest a surprisingly accurate measure of the flexibility of DNA [10, 11]. Other early theoretical studies of DNA focused on the thermodynamic transition of denaturation using a variety of approaches [12–15]. One perhaps iconic approach was an adaptation of the one-dimensional Ising model (originally developed to describe magnetization), whereby the likelihood of a given basepair’s unpairing depends on the paired status of its nearest neighbors in a DNA helix [12].

By 1975, it was known that DNA was a rather rigid polymer, yet it could form compact structures like chromatin [16], sparking a debate about kinked versus smoothly bent DNA. In the earliest atomic-modeling studies that employed computation, models of kinked and bent DNA were produced by performing least-squares searches of toy potentials linking rigid groups of atoms [17, 18]. Soon after, Levitt borrowed atomic interaction potentials from protein and RNA refinement studies to relax the full set of atomic coordinates of a DNA molecule that was bent and twisted by varying amounts [19]. Although both solvent and electrostatics were absent in the calculations and the calculations probed only the local energy minima, the study correctly determined the 10.5 basepairs-per-turn pitch of a DNA helix in solution, departing from the 10 basepairs-per-turn pitch observed in the solid-state Watson-Crick structure.

The first room-temperature computations involving DNA were performed by Clementi and Corongiu in 1979 and 1980 [20,21]. These Monte Carlo (MC) simulations, performed using a model optimized to reproduce energies of ab initio calculations, revealed the structure of water molecules around fixed DNA helices and nucleotides. In the MC method, atomic coordinates were propagated according to Boltzmann statistics, so equilibrium, but not dynamical, properties of the system could be studied. In the beginning of 1983, Levitt, borrowing again the methods developed for the study of proteins, reported an MD simulation that showed asymmetric bending and twisting motions of duplex DNA in the absence of solvent [22]. This was followed only a few months later by a similar MD report by the Karplus group [23]. Finally in 1985, the Kollman group performed the first MD simulation of a DNA fragment in electrolyte solution [24].

Beveridge et al. comprehensively reviewed the following decade of MD studies of DNA [25, 26]. At that time, simulations were rapidly approaching the nanosecond timescale [27]. Nevertheless, most simulations from that era described DNA using implicit solvent and truncated electrostatics. In 1995, it was noted that the outcome of a simulation could qualitatively depend on the method used to describe the dielectric environment of a charged polymer [28]. The Kollman group (1995) demonstrated that simulations of DNA using the particle mesh Ewald (PME) method, which effciently calculates long-range electrostatic interactions in Fourier space, are more accurate than the simulations performed using truncated electrostatics [29]. Although accurate representation of electrostatics is essential for modeling of a highly charged molecule such as DNA, the community was at first slow to adopt the particle mesh Ewald method due to the high computational cost [30]. At that time, several “second-generation” all-atom force fields with explicit solvent were released, including AMBER-94 and CHARMM22 [31]. Around the same time, National Science Foundation supercomputers became more accessible to researchers and the major MD codes AMBER and CHARMM were parallelized.

Prompted by these methodological advances, longer and more accurate studies of DNA structure and dynamics were performed. Of particular note, Cheatham and Kollman (1996) observed a spontaneous transition of DNA from A-form to a more stable B-form during the first multi-nanosecond simulation of explicitly solvated DNA, indicating good accuracy for the AMBER force field [32]. Shortly thereafter Young, Ravishanker and Beveridge reported the first 5-nanosecond trajectory of B-DNA [33], which revealed substantial fluctuation of the DNA structure, in agreement with with x-ray crystallography and NMR. The latter study was one among several that found that MD simulations employing the CHARMM or AMBER force field could reproduce the crystal and NMR structures [30], which was an important test of the force fields. The sequence-specificity of DNA structures began to be investigated including comparisons of twist, roll, and tilt obtained for different basepair stacks [34]. More dramatically, the intrinsic curvature of A-tract DNA was observed [33] (see Section 5.1 for details). Back in 1986, it had been recognized from crystal structures that water may considerably affect the conformation of DNA (A-form vs. B-form) [35]. Feig and Pettitt (1998) reviewed molecular dynamics simulations that investigated the structure and properties of water surrounding DNA [36]. Another question of outstanding importance was the location and dynamics of ions, which were believed to bind DNA tightly [37]. A number of studies investigated whether and where the ions would bind to DNA [38] and began to characterize the ion atmosphere [39–41]. Around the same time, the generalized Born method [42] was introduced to implicit solvent simulations with AMBER [43] and CHARMM [44] parameters for more accurate estimation of the electrostatic solvation energy.

From 1995 to 2000, the era of quantitative MD simulations of DNA began to emerge, starting with free energy perturbation simulations of ligand binding [30, 34]. The structural and intramolecular character of DNA was investigated through free energy simulations of base pairing, stacking, and DNA stretching [30]. In particular, MacKerell and Lee (1999) used umbrella sampling MD simulations and atomic force microscopy to study stretch-induced melting of short DNA fragments [45]. Near-quantitative agreement was obtained between simulation and experiment, indicating good overall performance of the CHARMM22 force-field. It must be cautioned that the AFM results were not in complete agreement with the seminal study of stretching long (48.5 kbp) λ-phage DNA using an optical trap [46], perhaps because different DNA constructs were employed [45]. Nevertheless, the simulation represented the first, to our knowledge, quantitative comparison of mechanical DNA properties observed in experiment and in simulation.

In the new millennium, there have been a few general reviews of DNA simulations [54–56]. However, the field has grown such an extent that there have been very many special-topic reviews on a wide range of subjects. For example, the base stacking interactions were reviewed from a quantum mechanics (QM) perspective [47]. Another recent review that included QM and MD descriptions of DNA focused on the backbone rather than bases [57]. Work continued toward understanding the relationship between DNA and the solvent [58, 59], however, it was only recently found that the standard parameterization of cation–phosphate interaction had considerable problems [60]. Advances in computing permitted the mechanical properties of DNA to be examined in more detail [61–64]. Finally, there were many investigations of DNA association with other molecules, including small molecules such as anti-cancer drugs [65,66], sequence-specific DNA binding proteins [65,67], non-specific DNA binding proteins such as the nucleosome [68] and synthetic structures such as carbon nanotubes [69] and silicon nitride nanopores [70].

In recent years, MD simulations of DNA have moved toward large systems and long durations. The first microsecond simulation of B-DNA was performed by the Orozco group in 2007 [71], which revealed the limitations of the AMBER-99 force field and a new parameterization of the all-atom model that addressed the problem. Meanwhile, a number of impressive developments have happened in the related field of RNA systems simulations. An all-atom model of one of the smallest viruses—the satellite tobacco mosaic virus—was simulated for ~ 50 ns, which included 60 copies of the coat protein, a 1063-nucleotide single-stranded RNA molecule and the electrolyte solution, about 1 million atoms in total [72]. Even larger RNA systems have since been simulated. Atomic simulations of the ribosome, an enormous protein synthesis factory predominantly composed of RNA, were recently reviewed by Sanbomatsu [73]. The simulations examined the conformational changes in the ribosome, the effects of point mutations and quantified the kinetics and free energy barriers of conformational transitions using a 3 million atom model and the aggregate simulation time of ~2 μs.

Large-scale MD simulations of DNA systems have only recently matched the scale of the largest RNA simulations, perhaps because of the lack of atomic-scale structures of large DNA assemblies. Matching the setup of DNA array experiments of Rau and Parsegian [74], Yoo and Aksimentiev simulated the structure, dynamics, ionic atmosphere and intermolecular forces of a DNA array [60]. The outcome of these simulations revealed the limitations of the standard ion-DNA interactions and a method to fine-tune the parameters to achieve quantitative agreement with experiments (see Section 3.3). Another example was a simulation of end-to-end self-assembly of a large number (~450) of duplex DNA [75]. One of the current frontiers of DNA simulations are DNA origami and related self-assembled nanostructures [76–78]. The first atomic-resolution simulation of DNA origami was reported very recently [50], revealing the situ structure of several DNA origami designs as well as their local and global mechanical properties.

The above discussion has focused predominantly on fully-atomic simulation of DNA. By employing a less detailed, “coarse-grained” (CG) model the timescale accessible to simulations of DNA can be significantly extended [79–81]. In the past five years, many CG models of DNA have been developed to reproduce various properties of double-stranded DNA [82–92]. Most available CG models employ a few interaction sites to represent each nucleotide, but CG models can span an enormous range of scales, from the near-atomic [91] to the meso and macroscopic [52]. An excellent review of available CG DNA models can be found in the recent article from the de Pablo group [82].

Parameters describing the interactions of coarse-grained models are usually obtained by fitting against experimental data, such as the nearest neighbor DNA melting parameters [93], or by reproducing structural parameters from atomic resolution simulations. In analogy to the atomic force fields, which are optimized against a mix of finer quantum calculations and experimental data, it is our belief that the most accurate general purpose CG models of DNA will be obtained through a combination of all-atom simulations and single molecule experiment. A recent application of such an approach is a CG model of single-stranded thymine homopolymers specifically developed to match both the all-atom simulations and single-molecule fluorescence resonance energy transfer measurements [94].

Finally, the coarsest biologically relevant description of DNA ignores its physical form altogether, representing each nucleotide with one of four letters, A-C-G-T. In the field of genomics, computers play an instrumental role in organizing, sorting, search and comparing the genomes of different species and individuals. Since this field lies largely outside of our expertise, we merely mention computational genomics as an important and exciting area of computational modeling the biological function of DNA.

3. All-atom force fields for DNA simulations

The MD method approximates the quantum mechanics of chemical bonds using classical equations of motion. Such an approximation requires a set of functions and parameters— the molecular force field—to describe the interactions between the atoms. In general, biomolecular force fields can be categorized according to the level of description of the surrounding media (gas phase, implicit solvent, explicit solvent), functional form of the force-field, and crucially the method used to obtain the parameters.

Prominent early efforts in force field development for DNA were undertaken in the Karplus [23] and Kollman [95–97] groups, eventually leading to the CHARMM and AMBER parameter sets. The functional forms of those force fields are similar to those found today: harmonic terms on the bonds, angles and improper dihedral angles; a periodic term for each dihedral angle; and Lennard-Jones and Coulomb terms between non-bonded atoms. Below we briefly review the formulations of the all-atom MD method and describe recent advances in this area.

3.1. General formulation of the all-atom MD method

In the MD method, point particles represent atoms. The atomic force field (discussed below) provides all atoms with predefined physical parameters such as partial charges and van der Waals interaction parameters. The connectivity (or covalent bonds) among atoms are given a priori. For computational effciency, the physical parameters remain same during the a given simulation, with a few exceptions such as alchemical free energy simulations [98, 99]. Next-generation force fields may include a dynamic description of molecular properties such as polarizability [100, 101]. For example, a polarizable CHARMM force field based on a classical Drude oscillator model with a complete description of DNA, water, and ions was published recently [102, 103]. This model was optimized using several different levels of computations: quantum calculations for base-cation interactions and backbone torsions; thermodynamic osmotic pressure calculation for cation-phosphate interactions; hydration free energy calculation for DNA-water interactions.

Covalently bonded atoms interact with each other through bonded potentials, while the other atom pairs interact through nonbonded potentials:

$$\mathit{U}\mathrm{(}{\mathrm{r}}^{\mathit{N}}\mathrm{)}\mathrm{=}{\mathit{U}}_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d}}\mathrm{(}{\mathrm{r}}^{\mathit{N}}\mathrm{)}\mathrm{+}{\mathit{U}}_{\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d}}\mathrm{(}{\mathrm{r}}^{\mathit{N}}\mathrm{)}$$ (1)

where r^N denotes the coordinates of N atoms in a system. Bonded interactions model quantum mechanical behavior of covalently connected atoms by means of harmonic bond, angle and improper dihedral angle restraints, and periodic dihedral angle potentials:

$$U_{\mathrm{bonded}}=\sum _{\mathrm{bonds}}{K}_b{(b-b_0)}^2+\sum _{\mathrm{angles}}{K}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\mathrm{torsions}}{K}_{\chi }\{1+\cos (n\chi -\delta )\}+\sum _{\mathrm{impropers}}{K}_{\varphi }{(\varphi -{\varphi }_0)}^2$$

where K_b and b₀ are the force constant and equilibrium distance of the bond, respectively; Kθ and θ₀, the force constant and equilibrium value of the angle, respectively; K_χ, n, and δ, the force constant, multiplicity and phase of the dihedral, respectively; K_ϕ and ϕ₀, the force constant and equilibrium value of the improper dihedral angle [104]. The nonbonded potential usually applies to atom pairs separated by more than two covalent bonds and consists of Lennard-Jones (LJ) potential for van der Waals interactions and Coulomb potential for electrostatic interactions:

$$U_{\mathrm{nonbonded}}=\sum _{nonbond}\left\{4{∊}_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]+\frac{q_i{q}_j}{∊r_{ij}}\right\},$$ (3)

where ∈_ij is the well depth; σ_ij, the finite distance at which the LJ potential is zero; r_ij, the interatomic distance; q_i,j, atomic charges for atom i and j. The bonded parameters are empirically calibrated based on the quantum mechanical calculations of small molecules, whereas the nonbonded parameters are mainly derived from quantum chemistry calculations (e.g., partial charges) and empirical matching of thermodynamic data (e.g., hydration free energy).

Intramolecular and intermolecular nonbonded forces dominate the tertiary structure of a molecule and molecular binding, respectively. Thus, accurate description of the nonbonded forces is essential. In the 1980s and 1990s, the Coulomb interactions, when included, were truncated at a relatively short distance (~ 1 nm). Furthermore, since solvent was prohibitively expensive to treat explicitly, the early Karplus and Kollman force fields treated it implicitly with the approximation that the dielectric constant depended on the distance between charged two atoms [105,106]. This practice occurred apparently without physical justification, but nevertheless provided reasonable results [26]. Usually the charge of the DNA was significantly reduced to represent the effect of counterions in accordance with Manning counterion condensation theory (see Section 4.1.2 for details) [26,106].

Presently, the most practical and accurate treatment of long-range interactions takes advantage of the periodic boundary conditions employed in most modern MD simulations by using the Ewald summation method, which effciently computes both short-and long-range electrostatic interactions in crystal systems. Cheatham et al. have demonstrated the importance of using the Ewald method for DNA simulations by showing that B-form DNA conformations were stable only when the Ewald method was used [29]. Optimized versions of the Ewald method [107] permit highly parallelized MD simulations to be effciently performed.

3.2. Recent updates to the second-generation force fields

An all-atom empirical force field for DNA is a set of bonded (Eq. 2) and nonbonded (Eq. 3) parameters optimized utilizing quantum mechanics calculations and thermodynamics data. Although there exist several all-atom force fields, the CHARMM [108] and AMBER [109] force fields are two most popular choices for the simulations of DNA. Steady advances in cluster computing continue to increase the size and duration of MD simulations, outpacing force field development. More often than not, simulations today greatly exceed the duration and complexity of the simulations that were originally used to develop and validate the force fields. It is, therefore, perhaps unsurprising that the force fields require frequent updates to keep up with the opportunities offered by modern supercomputing systems.

3.2.1. Backbone

Since the original development of the “second generation” DNA force fields about 20 years ago [108,109], both the AMBER and CHARMM force fields have been updated several times. The majority of the updates focused on refinements of the bonded parameters, in particular the torsional potentials, using quantum mechanics calculations to improve the description of intra-helical conformations [56, 110]. The large number of updates reffects the complexity of the backbone torsional motions in DNA, see Figure 3a. specific updates of the torsional potentials include refinements of χ and γ to improve the balance of A- and B-form DNA populations [111], α and γ to improve the stability of B-form DNA conformations in long simulations (> 10 ns) [112,113], and ∈ and ζ to improve sequence-dependent distributions of B-DNA subpopulations [114]. Thus, six torsion angles along the DNA backbone are required to describe the conformation of a nucleotide unit, whereas a peptide bond requires only two. The structure and fluctuations of the backbone are essential for proper description of protein recognition [57].

Figure 3.

Intra-DNA and DNA-ion interactions. (a) Schematic illustration of the chemical structure of DNA. Seven torsion angles are required to describe the conformation of a nucleotide unit. (b) DNA-cation interactions. The phosphate groups of the DNA backbone strongly interact with cations because of electrostatic attraction. The accuracy of these opposite-charge interactions is essential for simulations of DNA–ion and ion-mediated DNA–DNA interactions [60]. Magnesium is shown in a Mg(H₂O)₆ complex to emphasize its pervasive ability to coordinate water molecules. See Section 4.2.2 for a detailed discussion of Mg²⁺ parameterization. Bulk water and DNA hydrogen atoms are omitted for clarity. (c) Custom NBFIX corrections improve accuracy of DNA array simulations. The panels show representative configurations of 64 dsDNA molecules (white circles) confined in a cylindrical volume (not shown). The color indicates the local density of cations. Left. The artificially strong attractions between cations and DNA phosphate results in erroneous clustering of DNA. Right. Using custom parameters to describe cation–DNA phosphate interactions recovers hexagonal packing of DNA helices [60], in agreement with experiments [74].

Compared to the canonical helical conformations of dsDNA, noncanonical conformations (e.g., loops, bulges, and kinks or single-stranded DNA) are harder to validate due to significantly larger torsional spaces [115]. It has been suggested recently that conventional AMBER and CHARMM force fields cannot properly describe non-canonical conformations of DNA [116]. This criticism prompted development of AMBER force field variants, e.g., ff11 and ff12 [117,118]. Readers interested in the detailed history of DNA force field development are referred to recent reviews on this subject [56, 110].

3.2.2. Ions

It has been a common practice to use the AMBER force field together with parameters for inorganic ions, e.g., Na, K, Mg, Ca, developed by Åqvist et al. about 25 years ago [119]. Similarly, ion parameters developed more than 20 years ago are commonly used with the CHARMM force field [120]. While parametrized to match the ion solvation energy, the default sets of ion parameters in both AMBER and CHARMM overestimate the interaction energy of cation–anion pairs as well as the energy of select ion–charged group interactions. When used in a simulation, such inaccurate parameterization leads to the formation of artificial ion clusters [121, 122]. Updates to the default ion parameters were put forward by the Cheatham group for the AMBER force field (Cheatham ion parameters) [123,124] and the Roux group for the CHARMM force field (Roux ion parameters) [122]. The ion parameters were developed in the absence of biomolecules and in principle one could employ the either the Cheatham or Roux ion parameters in simulations using either force field. However, the Cheatham and Roux ion parameters have not been thoroughly validated outside the contexts of the AMBER and CHARMM force fields, respectively.

Even the updated parameters were found to produce considerable artifacts in simulations of dense DNA systems [60]. Such high density DNA systems are commonplace in biological systems and in nanotechnological applications of DNA. For example, in a fully packed bacteriophage (a virus infecting bacteria), the inter-DNA distance is < 30 Å [125, 126] and hence the molar concentration of the bare DNA charge is higher than 1 M. The DNA charges must be neutralized by a similar amount of opposite charge counterions, which include both inorganic, such as those shown in Figure 3b, and more complex organic compounds, such as biogenic polyamines or histone tails. Therefore, an accurate parameterization of inter-DNA and DNA–ion interactions is as important as the parametrization of intra-DNA interactions for proper description of high density DNA systems.

Figure 3c illustrates some of the problems with conventional parameters. When 64 dsDNA molecules were simulated in a cylindrical well permeable to ions, the DNA molecules formed clusters mediated by exaggerated binding of ions to the DNA phosphate groups [60]. The pressure required to keep the DNA molecules confined to the cylindrical well was an order of magnitude less than in experiment [74]. Yoo and Aksimentiev introduced custom corrections to the vdW parameters (NBFIX) describing the interaction of a specific cation (Li, Na, K, or Mg) with a phosphate oxygen to bring the simulated osmotic pressure of the binary mixture into accordance with the experiments of acetate (a proxy for phosphate)–cation solutions [127]. Using such corrections considerably improved the realism of DNA array simulations. specifically, the simulations could reproduce the hexagonal packing of the DNA helices; the average inter-DNA distance, and the dependence of the internal DNA pressure on the inter-DNA distance, all in agreement with the corresponding experimental measurements [74]. Additional validation of the NBFIX corrections was obtained by simulating competitive binding of two cation species to DNA [128], which quantitatively reproduced ion counting experiments [129] (see Section 4.2).

A detailed discussion of the parameterization strategies for accurate description of divalent ions in the context of nucleic acid simulations is given in Section 4.2.2.

3.2.3. Base-stacking

As the computational capabilities of modern computer systems keeps on increasing, so does the appetite for simulations of ever more realistic biological systems involving DNA, which often feature non-canonical conformations of DNA and DNA–protein assemblies. One of the major problems in describing such conformations is the strength of base stacking interactions of DNA nucleotides. For example, a recent study has quantitatively investigated the end-to-end association of short duplex DNA fragments using free energy and brute-force simulations [75], see Section 6.4. The magnitude of the end-to-end attraction was found to be considerably larger than the corresponding experimental estimates [130,131].

Base stacking interactions have been the subject of extensive quantum mechanics (QM) studies [47]. Acceptable agreement was found for the quantum gas-phase enthalpies and the AMBER-99 force field, but the atomic radii in the force field were noted to be larger than expected from state-of-the-art QM calculations (in the direction normal to the base). It is important to note that the latter was a recent discovery enabled by simulations employing a basis set with a higher-level description of electron correlations than previously possible. The results of the advanced QM calculations were taken into account by the Garcia group in a recent modification of the AMBER-99 force field that eliminated unrealistic aggregation of nucleotides at low concentrations [132]. Using this sequence-independent correction to the base stacking interaction permitted a more realistic simulation of folding of one RNA molecule [132]. However, the correction has not yet been validated for a variety of RNA and DNA structures.

3.2.4. Best practices

At the time of writing this review, the latest and probably the most recommended force field choices for the simulations of canonical B-DNA duplexes [56, 110] is AMBER ff99bsc0 [113] and CHARMM36 [114]. Simulations of ssDNA are best performed using the CHARMM36 force field, as the AMBER parameterization was found to enforce the helical conformation of dsDNA on single DNA strands [115]. We strongly recommend using the NBFIX corrections to describe ion–phosphate interactions [60]. Additional improvement of accuracy could be expected from the base stacking corrections [132], however such corrections have not yet been validated in combination with other recent force field updates. A combination of several recent force field updates might be required for accurate simulations of non-canonical nucleic acids, such as Holliday junctions, ribozyme, DNA/RNA hairpins, or synthetic DNA nanostructures. We strongly urge early adopters to always test new force field modifications before employing them in long term and computationally expensive projects.

4. Electrostatics and ion atmosphere

4.1. Theoretical background

What is the charge of DNA? While a simple answer might be −e per nucleotide under standard conditions, we often speak of effective charges due to the complex electrostatics of the molecule in solution. There are various ways to measure charge and therefore various ways to define effective charges. Perhaps the most basic way to measure charge is to place a charged probe at some distance from the molecule and measure the force. If we make the charge of the probe small enough, then we can make the measurement with only negligible effects on the subject of the measurement, allowing us to calculate the force on a probe of charge q from the electric potential ϕ by F = −qVϕ. For measuring DNA–ion interactions, the charge of the probe may need to be much smaller than e, the charge of a proton, but for the moment let’s not consider the complication of actually making experimental measurements of the charge this way. We will soon find that determining the effective charge of DNA from the potential at some distance away from it or vice-versa is complex even in theory.

Within organisms, DNA is most commonly in its stiff double-helical B-form, which is about 2.5 nm in diameter and has a persistence length at least 20 times greater [133]. Therefore, DNA is often modeled as an infinitely long rod, with varying levels of detail in its charge distribution. Below we model DNA as a uniformly charged cylinder, allowing for easy calculation, but neglecting the complexity of the ion distribution near the DNA. In the B-form double helix, each basepair typically represents a 0.34 nm step along the helical axis, although the length of the step varies a bit with the DNA sequence. Therefore, DNA has a standard charge density of Q/L = −2e/0.34 nm. To compute the electrostatic potential, we can employ Gauss’s law from elementary electrostatics, which tells us that the charge inside any closed surface can be related to the potential at the surface by

$${\mathit{Q}}_{\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d}}\mathrm{=}\mathrm{-}{\mathit{\epsilon }}_{\mathrm{0}}{{\displaystyle \oint }}_{\mathrm{closed\; surface}}\mathrm{\cdot }\mathrm{\nabla }\mathit{ɸ}$$ (4)

Computing ϕ from Gauss’s law for a uniformly charged cylinder is a standard textbook problem, and is calculated by integrating over a closed surface with the form of a “can”–a capped cylinder of radius r sharing its axis with the axis of the uniformly charged cylinder. We obtain the solution

$$\mathit{ɸ}\mathrm{(}\mathit{r}\mathrm{)}\mathrm{=}\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{\mathit{\epsilon }}_{\mathrm{0}}}\frac{\mathit{Q}}{\mathit{L}}\ln \mathrm{(}\mathit{r}\mathrm{/}{\mathit{r}}_{\mathrm{0}}\mathrm{)}$$ (5)

where r is the distance between the uniformly charged cylinder and the point at which we are evaluating ϕ, t0 is the electric constant, Q/L is the linear charge density of the DNA, and r0 is an arbitrary distance where ϕ(r₀) = 0.

This calculation, however, was performed in a vacuum. In water, the Qenclosed of Gauss’s law must include also the charges of the water molecules. Although water molecules are neutral on the whole, they have an electric dipole moment whose orientation becomes biased by an electric field. When placing our imaginary “can” into water, the surface of the can severs the dipoles, leaving unbalanced charges within the surface. At low fields, water can be treated as a homogeneous isotropic linearly polarizable medium, and the effect water polarization can be captured by a scalar dielectric constant. Eq. 5 becomes

$$\mathit{ɸ}\mathrm{(}\mathit{r}\mathrm{)}\mathrm{=}\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{\mathit{\epsilon }}_{\mathrm{0}}{\mathit{\epsilon }}_{\mathrm{r}}}\frac{\mathit{Q}}{\mathit{L}}\ln \mathrm{(}\mathit{r}\mathrm{/}{\mathit{r}}_{\mathrm{0}}\mathrm{)}$$ (6)

where ∈_r is the relative permittivity, or dielectric constant, of the water. Note that we must be careful with the assumption of a uniform dielectric constant since high electric fields and water structuring can modify the dielectric constant of the water near ions or DNA [134].

Here is an example where we can illustrate the idea of an effective charge, Suppose we let Q_eff = Q/∈_r. This substitution is not often made, but it serves as an example. The advantage of this substitution is that the equation for the potential in water regains the simple form it had for the vacuum. However, we must keep in mind that the effective charge is not an intrinsic property of the DNA, but depends also on the solvent. Moreover, under the conditions where the dielectric properties of water can no longer be described by a single scalar value, Q_eff will also cease to be constant. Introducing an effective charge can be useful for simplifying a complex theory; however, in all cases, as in this case, we must be wary about its range of validity.

DNA is invariably suspended in an aqueous electrolyte solution containing many small mobile ions, such as Na⁺,K⁺, Cl⁻, or ions of higher valencies such as Mg²⁺. The high charge of DNA therefore causes a complex rearrangement of these mobile ions, making the form of ϕ calculated above invalid. A large amount of literature has been focused on understanding the interaction between nucleic acids and ions due to the importance of the phenomenon in processes necessary for life including protein–nucleic acid binding, gene expression, and chromosome packaging as well as in biotechnology applications. Here, we briefly describe some pertinent research in the field to examine the use of effective charges for DNA.

4.1.1. Poisson-Boltzmann theory

A number of analytical and computational techniques exist in the literature to study the interaction between DNA and ions, each with varying levels of complexity and range of applicability. Due to its simplicity, Poisson-Boltzmann (PB) theory is almost invariably the starting point for such studies. A good description of PB and related mean field theories is given by Grosberg et al. [135]. In a simple derivation, PB theory begins with the Poisson equation with a scalar permittivity, ∇²ϕ = −ρ/(∈₀∈_r), where ϕ is the electric potential, ρ is the charge density, ∈₀ is the electric constant, and ∈_r is the dielectric constant (relative permittivity) of the medium. We then assume that small mobile ions rearrange themselves in accord with Boltzmann statistics. We treat the ions as point particles so that their energy is simply E = qϕ, where q is the charge of ion. In doing this, we have considered interactions of the ions only through the average potential ϕ and are neglecting interactions such as steric repulsion between nearby ions and hydration effects. Let’s suppose that we have a net-neutral univalent electrolyte like KCl in an aqueous solution. Then the Poisson-Boltzmann equation is

$${\mathrm{\nabla }}^{\mathrm{2}}\mathit{ɸ}\mathrm{=}\mathrm{-}\frac{\mathit{e}{\mathit{c}}_{\mathrm{0}}}{{\mathit{\epsilon }}_{\mathrm{0}}{\mathit{\epsilon }}_{\mathit{r}}}\mathrm{[}\exp \mathrm{(}\mathrm{-}\mathit{e}\mathit{ɸ}\mathit{\beta }\mathrm{)}\mathrm{-}\exp \mathrm{(}\mathit{e}\mathit{ɸ}\mathit{\beta }\mathrm{)}\mathrm{]}$$ (7)

where β =1/kBT is the inverse of the thermal energy, c0 is the bulk concentration of the ions (the concentration where ϕ = 0) and the first and second exponential terms represent the charge densities of the cations and anions, respectively. Despite the fact that the PB equation neglects ion correlations (being a mean field theory) and steric repulsion between ions at small separations, it contains much of the physics necessary to understand the interaction between DNA and ions. Recent updates to the PB formalism allows the inclusion of steric interactions [136,137].

If we are working in a region where the potential is small (eϕβ « 1), then we can linearize the PB equation by expanding the exponentials by exp(x) ~ 1 + x. With the linear PB equation the following potential is obtained for a uniformly charged cylinder [138],

$$\mathit{ɸ}\mathrm{(}\mathit{r}\mathrm{)}\mathrm{=}\frac{\mathrm{2}\mathit{\xi }{\mathit{r}}_{\mathrm{D}\mathrm{H}}}{\mathit{e}\mathit{\beta }\mathit{\alpha }}\frac{{\mathit{K}}_{\mathrm{0}}\mathrm{(}\mathit{r}\mathrm{/}{\mathit{r}}_{\mathrm{D}\mathrm{H}}\mathrm{)}}{{\mathit{K}}_{\mathrm{1}}\mathrm{(}\mathit{\alpha }\mathrm{/}{\mathit{r}}_{\mathrm{D}\mathrm{H}}\mathrm{)}}$$ (8)

where K₀ and K₁ are modified Bessel functions [139], a is the radius of the DNA, ${\mathit{r}}_{\mathrm{D}\mathrm{H}}\mathrm{=}\sqrt{{\mathit{\epsilon }}_{\mathrm{0}}{\mathit{\epsilon }}_{\mathrm{r}}}\mathrm{/}\mathrm{(}\mathrm{8}\mathit{\pi }{\mathit{e}}^{\mathrm{2}}{\mathit{c}}_{\mathrm{0}}\mathit{\beta }\mathrm{)}$ is the Debye-Hückel screening length, and $\mathit{\xi }\mathrm{=}\mathrm{|}\mathit{Q}\mathrm{/}\mathit{L}\mathrm{|}\mathit{e}\mathit{\beta }\mathrm{/}\mathrm{(}\mathrm{4}\mathit{\pi }{\mathit{\epsilon }}_{\mathrm{0}}{\mathit{\epsilon }}_{\mathrm{r}}\mathrm{)}$.

4.1.2. Ion condensation

Eq. 8 might be the end of the story for describing interactions between ions and DNA for dilute electrolytes (the c₀ → 0 limit). However, when the charge density of the uniformly charged cylinder Q/L becomes sufficiently high so that ξ > 1, nonlinear effects in the PB equation lead to a change in character of the solutions [135]. A certain fraction of the counterions, 1 − 1/ξ, become intimately associated with the uniformly charged cylinder—in a phenomenon referred to as counterion condensation [37]. Note that this use of the word “condensation” refers a loose association and does not imply physical contact between the ions and DNA. This phenomenon is especially interesting because it applies to the B-form DNA double helix in water at room temperature: using the formulas above we find that ξ =4.2 and that 76% of the counterions are condensed.

What is the nature of this condensation? Originally, Manning demonstrated that the free energy of a point charge interacting with a line charge is infinite if the line charge density exceeds a certain threshhold. The critical charge density turns out to be ~ 25% of the DNA charge for monovalent electrolyte [37]. The divergence of the free energy only occurs for the model where the point charge can approach the line charge arbitrarily close. Nevertheless, something akin to counterion condensation emerges simply from the nonlinear PB equation as detailed above for more realistic systems like a finite-sized cylinder. However, in realistic models of DNA, counterion condensation cannot be thought of as binding of ions to specific sites on the DNA [129], as x-ray scattering shows no discrete structure. Manning [140] speaks of the condensed ions as a liquid and emphasizes that the number of condensed ions is determined only by electrostatics [141, 142].

Mathematically, condensation can be manifested as counterions that remain at finite distances from the DNA as the bulk ion concentration is reduced to zero. Beyond the Debye-Hüuckel screening length rDH, interactions between charged bodies decrease rapidly; therefore, rDH can be thought as the characteristic length scale for electrostatic interaction in the solution. As c₀ is reduced, r_DH grows; however, the radius that contains the condensed fraction of ions grows more slowly, ${\mathit{R}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}\mathrm{~}\sqrt{{\mathit{r}}_{\mathrm{D}\mathrm{H}}}$ [138]. In a sense, therefore, the DNA holds the condensed ions more and more tightly as the bulk ion concentration is reduced, since the radius enclosing the condensed ions relative to the characteristic length scale decreases: ${\mathit{R}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}\mathrm{/}{\mathit{r}}_{\mathrm{D}\mathrm{H}}\mathrm{~}\mathrm{1}\mathrm{/}\sqrt{{\mathit{r}}_{\mathrm{D}\mathrm{H}}}$. Larger fractions of the counterions do not have this behavior and the relative radius enclosing them, R_cond/r_DH, remains finite as c₀ → 0 [138].

Here is where introducing an effective charge, Q_eff , can be useful. Let the effective charge of the DNA be its bare charge minus the charge of the condensed counterions, Q_eff = Q − Q(1 − 1/ξ)= Q/ξ. At distances beyond the radius confining the condensed ions, $\mathit{r}\mathrm{»}{\mathit{R}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}}\mathrm{\approx }\sqrt{\mathrm{2}\mathit{\alpha }{\mathit{r}}_{\mathrm{D}\mathrm{H}}}\exp \mathrm{[}\mathrm{(}\mathit{\xi }\mathrm{-}\mathrm{2}\mathrm{)}\mathrm{/}\mathrm{(}\mathrm{2}\mathit{\xi }\mathrm{-}\mathrm{2}\mathrm{)}\mathrm{]}$, we can approximate the potential in a dilute electrolyte [138] by

$$\mathit{ɸ}\mathrm{(}\mathit{r}\mathrm{)}\mathrm{=}\frac{\mathrm{2}{\mathit{\xi }}_{\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{f}}{\mathit{r}}_{\mathrm{D}\mathrm{H}}}{\mathit{e}\mathit{\beta }\mathit{\alpha }}\frac{{\mathit{K}}_{\mathrm{0}}\mathrm{(}\mathit{r}\mathrm{/}{\mathit{r}}_{\mathrm{D}\mathrm{H}}\mathrm{)}}{{\mathit{K}}_{\mathrm{1}}\mathrm{(}\mathit{\alpha }\mathrm{/}{\mathit{r}}_{\mathrm{D}\mathrm{H}}\mathrm{)}}$$ (9)

Eq. 9 is nearly identical to the formula obtained from the linearized PB equation (Eq. 8). The only difference is that ξ is replaced by ξ_eff, which differs from ξ only in that the bare charge Q has been replaced with the effective charge Q_eff. Thus, under restricted conditions, we can think of the DNA and its condensed counterions as a single entity with a charge density of Q_eff/L.

We have continually used an infinite uniformly charged cylinder as a model for DNA. We might worry that the theory of counterion condensation would fail for a more realistic DNA model, for example, having a molecule of finite length or using a helical charge distribution. As it turns out,the condensed fraction 1 − 1/ξ and the critical value of the charge density where condensation occurs is fairly universal. Being due to long-range electrostatic effects, the condensed fraction and critical charge density do not depend on the local details of the DNA’s charge distribution—the same results have been found for discrete charges in a double helical arrangement [143]. As for the assumption of infinite length, the calculations presented above hold when the DNA is significantly longer than rDH [144]. Note, that we must be careful about this criterion, since we are working the dilute (rDH → ∞) limit. Most importantly, a number of experiments and simulations show evidence of a sharp change in a variety of observables near the critical value ξ = 1 [145].

Thus far, we have considered the dilute limit. Can the above considerations be extended to sizeable ion concentrations? Gauss’s law (Eq. 4) relates the potential of a closed surface to the quantity of charge inside the surface. Suppose that you place a cylinder around a DNA double helix and measure the charge of the mobile ions inside as function of the cylinder’s diameter. The charge of the DNA should be completely screened at a suffciently large distance; therefore, for a large diameter cylinder the charge of the mobile ions within should exactly cancel the DNA charge. A cylinder of a suffciently small diameter contains no ions. For intermediate diameters, one might expect the charge of the ions within the cylinder to monotonically increase, approaching the total charge of the DNA, which is exactly what PB theory predicts. This prediction, however, is wrong. At high bulk ion concentrations (2.5 M), Monte Carlo simulations using explicit ions and implicit solvent showed a rise in the ion charge beyond that needed to neutralize the DNA [146]. This effect is known as overneutralization or charge inversion and could be produced by several physical mechanisms [135,147].

4.2. Simulations of ion atmosphere around DNA helices

DNA is a polyanion with a large local charge density; when we assume a cylinder of 1-nm radius for a DNA double helix, the local DNA charge density is about 1.5 M. For charge neutrality, a similar number of counterions is expected around DNA [37], and this diffuse layer of counterions is called the “ion atmosphere” [148]. The physiologically relevant ions (e.g., Na⁺,K⁺, Mg²⁺, Ca²⁺, and polyamines) bind DNA competitively, playing an important role in DNA stability, structure, and function [149]. In the following subsections, we discuss the recent experimental and simulation studies on the ion atmosphere and technical issues on the simulations of divalent cations.

4.2.1. Experimental and simulation studies of the ion atmosphere

Experimental ion detection is still technically challenging and details of the counterion distributions around DNA remain elusive. Currently, small-angle x-ray scattering is the most widely used experimental method for studying the counterion atmosphere. For example, using this method, Pollack and coworkers directly demonstrated the existence of the counterion atmosphere around DNA [150] and the competition of cations with different valences [151, 152]. However, the SAXS technique can only provide a qualitative description of the counterion distribution. Recently, Herschlag and coworkers developed a novel technique, buffer equilibration and atomic emission spectroscopy (BE–AES), that enables direct counting of ionic species condensed to DNA [129]. The quantitative ion counts from the BE–AES method can complement the qualitative spatial distribution data from SAXS, providing a more detailed view of the ion atmosphere.

The microscopic structure and dynamics of the ion atmosphere around DNA are dificult to examine experimentally, but can be studied using the MD method. Pioneering studies utilizing explicit solvent and the Ewald summation technique for long-range electrostatics have been performed since the mid 1990s. Young and coworkers reported that counterions could be found in high concentration within the DNA grooves, but weren’t “stuck” to the DNA [38]. Ordered Na⁺ sites were observed in the major and minor grooves of DNA [40]. Early simulations suggested that the minor groove of AT DNA narrowed upon Na⁺ binding, but later studies disagreed [154, 155]. We caution that minor groove binding sites may be artifacts of the force fields employed at the time. The ion-binding sites on the DNA required ~ 50 ns to be fully sampled, while the overall ion atmosphere and DNA conformation relaxed much more quickly around ~ 5 ns [156]. Because water also plays an important role on DNA structure in aqueous solutions [41], the orientation and density of water molecules around DNA, especially the minor groove, were scrutinized in the above studies.

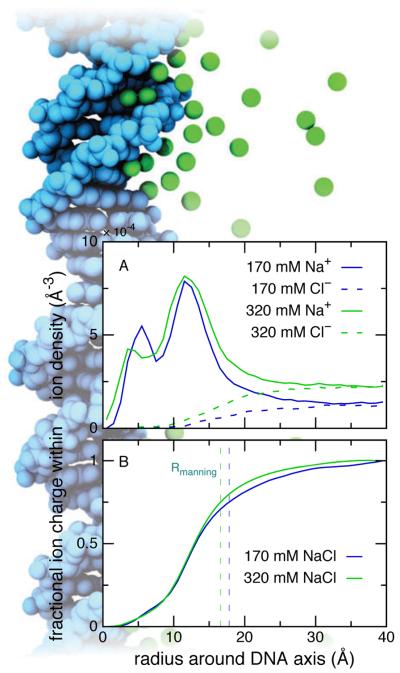
Figure 4 illustrates the distributions of ions around a poly(dA)·poly(dT) DNA duplex in 170 and 320 mM NaCl electrolytes obtained in previously reported MD simulations [153]. Na⁺ ions are found in both grooves of the DNA with the highest concentration just outside the DNA phosphate groups. Further away, the concentration of Na⁺ ions rapidly decays while that of Cl⁻ ions rises to the bulk concentration at about 30 ÅA from the DNA helical axis. The Na⁺ ions tended to dwell for ~ 250-ps intervals around the phosphates and near a nitrogen atom of the adenine base in the major groove. Thus, the ions were found to be highly mobile and only loosely associated with the DNA. The Manning radius, defined to be the radius at which 75% charge neutralization occurred, was found to be about 16–17 Å and only weakly depended on the ion concentration in the range of 170–320 mM. However, the radius was found to be significantly larger for low ion concentration solutions; at 30 mM the radius was about 33 Å [153].

Figure 4.

Typical distribution of monovalent ions around duplex DNA. (A) Density of Na⁺ (solid) and Cl⁻ (dashed) ions as a function of distance from the axis of a DNA molecule corresponding to bulk ion concentrations of 170 (blue) and 320 (green) mM. (B) Charge of ions within the specified distance from the DNA axis, normalized by the DNA charge. Colors are as in (A). The Manning radius is indicated for each ion concentration as a vertical dashed line. The ion distributions were taken from trajectories reported in Ref 153. The background shows the DNA molecule (cyan) surrounded by ions (green) superimposed from several snapshots of an MD trajectory. The molecular image is arranged to scale with the data so that the axis of the DNA corresponds to the zero mark of the graph’s x-axis.

4.2.2. The roles of divalent ions

Divalent cations, such as Mg²⁺ and Ca²⁺, can have a dramatic effect on the structure and function of DNA and RNA [157]. According to their function, they can be described as “coordinating” and “diffuse” cations. The “coordinating” divalent cations are found at active sites of enzymes where they catylize chemical reactions [157]. Such divalent cations are essential for the activities of many tRNA and ribozyme molecules [157–159], as well as ATP-dependent biological motors, and can be often resolved in crystal structures [157]. The function of “diffuse” divalent cations is to reduce the internal stress in DNA or RNA structures by partially neutralizing the negative charge of the phosphate groups [160–162].

Developing a single set of parameters capable of describing the two functional roles of divalent cations remains a major challenge. The catalytic ability of divalent ions is largely due to their +2 charge, which can impart strong electrostatic forces on nearby negatively charged moieties such as water oxygen or anions. Simulations employing a polarizable force field demonstrated that the dipole moments of waters in the first solvation shell of Ca²⁺ and Mg²⁺ were respectively increased by 20% and 40% [163], an effect that is dificult to capture using non-polarizable force fields. The physical size of a divalent cation dramatically effects its properties. For example, the water exchange rates in the first and second solvation shells are significantly different for Mg²⁺ (~10 μs) and Ca²⁺ (<ns) [164,165]. The difference cannot be explained by considering the individual interactions between an ion and a water molecule. Rather, water packing in the first solvation shell determines the slow kinetics for Mg²⁺, which has exactly six water molecules (vs. 7–8 for Ca²⁺) that fit perfectly in a stable octahedral conformation that prevents other water molecules from intervening [164].

Thus, accurate description of divalent ions by MD requires realistic treatment of the polarizability and kinetics of surrounding water. The most straightforward approach is to employ a polarizable force field to allow the atomic dipole moments respond to the electric field of a divalent cation during a simulation. Several groups have already used developing versions of polarizable force fields and obtained significantly improved agreement with experiment [163, 164, 166, 167]. However, a general purpose polarizable force field capable of describing large nucleic acid systems and long time scale (>100 ns) processes is presently not available.

Several approaches have been proposed to improve the realism of divalent cation simulations within the framework of standard CHARMM and AMBER force fields. Allnér et al. optimized the Lennard-Jones parameters of Mg²⁺ and Ca²⁺ so that they can be used directly with the CHARMM and AMBER force fields [168]. By performing a series of binding free energy calculations between Mg²⁺/Ca²⁺ and water/phosphate molecules, they demonstrated that the new parameter sets can reproduce water kinetics in the first solvation shell better than the standard force fields. Saxena and Sept proposed a novel multi-site model of Mg²⁺/Ca²⁺, in which these divalent cations are modeled as six dummy atoms in an octahedron conformation [169]. These two recent studies primarily focused on reproducing the structure and kinetics of the first solvation shell of Mg²⁺ and Ca²⁺ ions. However, proper coordination of the first solvation shell does not guarantee correct description of long-ranged interactions between Mg²⁺ or Ca²⁺ and other molecules such as DNA. Furthermore, the very long exchange time of water in the first solvation shell of Mg²⁺ (~ 10μs [164]) suggests that the coordination chemistry of a typical Mg²⁺ ions should remain unchanged during a typical MD simulation. For example, if a coordinating Mg²⁺ ion is initially in direct contact with a DNA phosphate oxygen, it will remain bound to the DNA for the duration of the simulation. Thus, the coordination state of each crystallographically resolved Mg²⁺ ion must be carefully considered at the setup stage of an MD simulation [157].

When a fully solvated Mg²⁺ ion approaches DNA, it is unclear whether it will retain its six coordinating water molecules or some of them will be exchanged for phosphate oxygens. Several lines of evidence suggest that the vast majority of Mg²⁺ ions will remain forming a Mg²⁺-hexahydrate complex (Mg²⁺(H2O)6) shown in Figure 3b. First, measurements using fluorescence and thermal melting methods indicated that tertiary structure of an RNA pseudoknot does not have directly bound Mg²⁺ [170]. Second, measurements of DNA pressure and inter-DNA spacing in a DNA array system in the presence of Mg²⁺ and Ca²⁺ have shown that Ca²⁺ lowers the DNA array pressure slightly more effciently than Mg²⁺ does [74]. If (meta)-stable Mg²⁺–DNA complexation were possible, Mg²⁺ would bridge neighboring DNA helices better than Ca²⁺ do, which would result in a lower internal pressure compared to Ca²⁺. Third, if a Mg²⁺ ion directly bridges the phosphate groups of two DNA helices, the inter-helical distance would be about 22–24 Å, which is inconsistent with experimentally measured distances of at least 25 Å, even at extremely high external pressure (~ 50 bar) [74]. Fourth, if specific direct binding of Mg²⁺ to DNA phosphates were energetically favorable they would be crystallographically resolved. Finally, a MgCl2 solution does not contain Mg²⁺–Cl⁻ pairs according to Raman spectroscopy [164].

Yoo and Aksimentiev proposed a model, in which a Mg(H2O)6 complex is treated as a stable molecular complex [60]. Such an approach is reminiscent of using cobalt hexamine, Co(NH4)6, a molecule having the same geometry as Mg(H2O)6, as an analog for Mg²⁺ in single-molecule experiments [171]. Achieving quantitative agreement between simulated [60] and measured [74] DNA array data was only possible by increasing the dipole moments of water molecules forming the Mg(H2O)6 complex to the values observed using a polarizable model [163]. The biggest limitation of the magnesium hexahydrate model is that it requires, a priori, a different treatment of chemical moieties that bind Mg²⁺ directly or indirectly. Extension of the model to Ca²⁺ is not straightforward, as the first solvation shell of Ca²⁺ is not as stable as Mg²⁺ , and hence, restraining 7–8 water molecules around Ca²⁺ may cause artifacts. One possible solution to the above problems is to dynamically reassign parameters for water molecules as they move in and out of the first solvation shell of a divalent cation.

4.2.3. Competitive binding

Physiological ionic solutions usually contain various cation species. Of the monovalent ions, K⁺ is more prevalent than Na⁺ and interacts with DNA differently; K⁺ does not enter the minor groove of DNA [155,172,173] and K⁺ ions diffuse about the DNA surface significantly more quickly than Na⁺ [172,173].

Early simulations employing high concentrations of Mg²⁺ ions demonstrated that the DNA conformation shifted towards the A-form [174]. Later simulations showed that Mg²⁺ binds to the DNA backbone and G·C basepairs preferentially, and that a DNA molecule was more rigid in Mg²⁺ electrolyte than in Na⁺ [175]. However, both of the above Mg²⁺-containing studies were performed before the availability of the NBFIX parameters needed for accurate representation of Mg²⁺–DNA interactions, which were previously far too strong.

By utilizing the new NBFIX-enabled parameterization, Yoo and Aksimentiev could quantitatively describe the ionic atmosphere of DNA surrounded by two competiting cation species [128]. Figure 5 illustrates the ion atmosphere in one such system containing a mixture of Na⁺ and Mg²⁺ ions. In a 100 ns MD trajectory, Na⁺ was found to bind predominantly to the minor grooves while Mg²⁺ was found to bind to the minor and major grooves with equal affinity Figure 5a,b. Due to the stronger binding affinity of Mg²⁺, the local concentration of Mg²⁺ near DNA is about twice that of Na⁺ , although the bulk concentration of Na⁺ is about an order of magnitude higher than that of Mg²⁺, Figure 5c. Chloride is completely excluded near the DNA due to electrostatic repulsions. Overall, all ion concentrations converge to their bulk values at around 30 Å from the center of the DNA, Figure 5c. By integrating the ion concentration profiles in Figure 5c, we could evaluate the excess ion counts for each species, Figure 5d. The comparison between the computed and experimental ion count data shows quantitative agreements, indicating that the NBFIX parameters provide a realistic description of ion atmosphere [128]. For the competition between Na⁺ and K⁺, it was found that K⁺ prefers the major groove while Na⁺ prefers the minor groove. For the Na⁺ and Li⁺, both cations prefer binding to the minor groove. For all data set, quantitative reproduction of the experimental data [129] was demonstrated.

Figure 5.

Competitive binding of Mg²⁺ and Na⁺ to dsDNA. (a) A representative configuration of ions near a 24-bp duplex. The two DNA strands are shown in black and gray; Na⁺ and Cl⁻ ions are shown as yellow and green spheres. The first solvation shell of each Mg²⁺ (pink) ion is explicitly shown. (b) Volumetric representations of DNA (gray), Mg²⁺ (blue), and Na⁺ (green) obtained by averaging a ~100 ns trajectory. The density maps are shown as isosurfaces of 0.5 and 0.02 Åatom number density for DNA and ions, respectively. (c) Ion concentration as a function of the radial distance from the DNA axis. Data in panels a-c correspond to bulk ion concentrations of ~5-mM Mg²⁺ , ~40-mM Na⁺, and ~50-mM Cl⁻. (d) Simulated excess number of Mg²⁺ (red), Na⁺ (blue), and Cl⁻ (green) ions as a function of Na⁺ concentration at the background of 5 mM Mg²⁺. For comparison, experimental data [129] are shown in black. Reprinted with permission from Ref. 128. Copyright 2012 American Chemical Society.

4.2.4. Multivalent electrolytes

Multivalent (valence of 3 or greater) polyamines, including spermine, spermidine and histone tails, play an essential role in genome compaction [176,177]. Spermine (+4) was found to compete with Na⁺ for binding DNA in the minor groove [178–182]. Other polymanines, putrescine (+2) and spermidine (+3) were found to bind DNA much like spermine with putrescine also binding somewhat in the major groove [179]. All three of these natural polyamines displaced water in the first hydration layer of the DNA [178, 180]. All-atom MD simulations of DNA with tetramethylammonium (+4) demonstrated that this polyamine can enter either groove of the DNA. However, small-angle neutron scattering experiments indicated that tetramethylammonium does not penetrate the deeply within the grooves [181], providing further evidence that the polyamine–phosphate interactions are not well described by current force fields.

Theoretical developments beyond mean-field treatments have resulted in the prediction of charge inversion of DNA. The strongly correlated liquid theory of Shklovskii [183, 184] predicted that higher valency counterions could result in DNA of net positive charge due to counterion condensation. MD simulations have been applied to investigate such possibility [182]. An effectively infinite fragment of DNA was placed at the center of a nanochannel and surrounded by electrolyte containing various concentrations of Na⁺, Mg²⁺, spermidine (3+) and spermine (4+) cations. The systems were simulated using the MD method until the ion distributions around the DNA reached equilibrium. The possibility of charge inversion was examined using Gauss’s law, Eq. 4. The total charge of DNA and the surrounding electrolyte enclosed within a cylinder co-axial with the DNA was plotted against the radius of the cylinder. For monovalent electrolytes, the effective electric charge of DNA and the surrounding cations monotonically increased reaching zero at large distances, indicating the absence of charge inversion. For some multivalent electrolytes, the charge could become positive, indicating overscreening or charge inversions. The study further investigated the relationship of such electric charge inversion with the inversion of the electrophoretic mobility of DNA, finding that the two phenomena have different physical origins as discussed in Section 7.3.4.

5. DNA mechanics

5.1. Equilibrium conformations

Why do two complementary DNA strands form a double helix? An obvious answer is that the complementary hydrogen bonding of the DNA nucleotides from the two strands. However, DNA hybridization is a balancing act, requiring all the forces involved (hydrogen bonding, basestacking, electrostatics and solvation) to have the right magnitude.

All-atom MD simulations should be able, in principle, to answer exactly that question, as the magnitude of the force applied to every atom of the simulation system is known at every step of a simulation. Nevertheless, studies reporting the average forces acting on individual components of biomolecules are rare as they require averaging the instantaneous forces as frequently as every simulation time step to provide statistically meaningful estimates of the average force [185]. Even when such averaging is done, extracting the contributions from forces of different origins is difficult, in particular when the electrostatic interactions are not calculated in pairwise fashion, which is typically the case when the PME method is used.

The force experienced by DNA nucleotides in a double helix from the solvent (water and ions) surrounding the DNA can be surprisingly strong. Figure 6 illustrates the forces experienced by individual nucleotides from the solvent in MD simulations performed by Luan and Aksimentiev. In these simulations, a 20 base-pair fragment of dsDNA (poly(dA)·poly(dT)) molecule was solvated in 0.1 M KCl electrolyte with and without 4 M urea added, Figure 6a. The 5′-end and the 3′-end of each DNA strand were covalently linked through the periodic boundary of the simulation system, forming an effectively infinite molecule. The simulations were performed using an older AMBER parameter set [109] and a custom version of NAMD [185]. The force between each nucleotide in the DNA and the entire electrolyte was calculated at every time step. For each atom of a nucleotide, the vdW and electrostatic forces exerted by the atoms of the electrolyte within 12 Å of that atom were recorded. The long-range Coulomb forces from the electrolyte atoms outside the 12 Å cutoff were extracted from the PME calculation. The total force on a nucleotide was then computed as a sum of the forces on the individual atoms of that nucleotide. The forces shown in Figure 6 were averaged over MD trajectories tens of nanoseconds in duration. To verify the accuracy of the force calculation, the total force on a nucleotide from all other nucleotides of the DNA fragment was calculated. The latter force balanced the force on the same nucleotide from the surrounding electrolyte, as expected.

Figure 6.

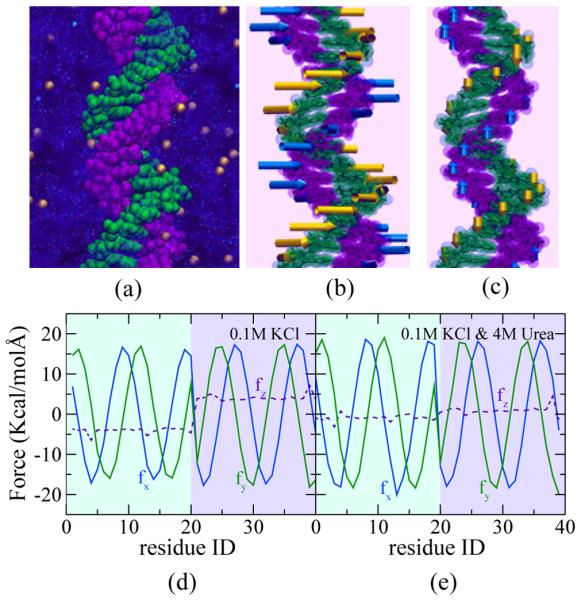
MD simulations of the solvent force on dsDNA. (a) Simulation set-up. A fragment of dsDNA (green and purple) is surrounded by an aqueous solution of K⁺ (gold) and Cl⁻ (cyan) ions. Bonds connecting atoms in each urea molecule are shown as lines; water molecules are not shown. (b,c) Schematic representation of the lateral (panel b) and vertical (panel c) mechanical forces (represented by arrows) on each nucleotide in 0.1 M KCl. (d) Cartesian components of the force acting on each nucleotide of the DNA at 0.1 M KCl. (e) Same as in panel d, but in the presence of 4 M urea. In panels d and e, nucleotides that belong to the one strand of dsDNA are numbered from 1 to 20 and to the other strand from 21 to 40; the force along the z-axis is shown using dashed lines.

Figure 6b and c respectively illustrate the lateral (normal to the DNA axis) and vertical (along the DNA axis) forces from the solvent on individual nucleotides of dsDNA. Each arrow points along the direction of the force and the length of the arrows represents the magnitude of the force. Figure 6d,e plot the cartesian components of the forces. It is interesting to notice that the lateral force on each nucleotide is directed tangential to the DNA helix, applying a torque that intertwines the two DNA strands into a double helix. The vertical forces on both strands are in the opposite directions and push the two strands towards each other. The addition of 4 M urea to the 0.1 M KCl electrolyte considerably reduced the vertical forces, causing a wider minor groove of dsDNA. MD simulations of that kind might provide a mechanical account of urea’s action as a denaturant of dsDNA.

In the above example, the DNA was linked to itself and hence was unable to change its conformation. However, if the bonds across the boundaries were removed, the DNA would lose its rod-like appearance and exhibit some degree of bending. Depending on the nucleotide sequence, fragments of dsDNA may exhibit different conformations, such as B-DNA or A-DNA. While interactions between nucleotides forming a DNA double helix are expected to affect the conformation, the interactions between dsDNA and the surrounding electrolyte also contribute. Melting-temperature measurements suggest that the dsDNA structure is more stable in electrolytes with high ion strengths.

The local bending of dsDNA is highly dependent on the DNA sequence. For example, dsDNA is more likely to bend at the AT step. The network of hydrogen bonds formed by water molecules on DNA surface varies in accord with the DNA sequence. For a poly(dA)·poly(dT) fragment, a water “spine” is formed in the minor groove of the dsDNA, bridging the N3 and O2 atoms in neighboring basepairs. When a sequence contains 4–6 dA nucleotides repeated with helical periodicity, the DNA curves on average toward the minor groove by ~ 10–20° per turn. These so-called A-tracts have been recently reviewed in outstanding detail [186]. The molecular mechanisms that underlie A-tract curvature are a challenge to determine because there are many possible causes, including solvent interactions, ion-binding, anomalous stacking or base-pairing. It is tempting to attempt to describe A-tract curvature using a nearest neighbor model, such as the model that accurately describes the free energy of DNA hybridization as a sum of energies associated with pairs of stacked basepairs [93]. However, it was shown using MD simulation that the conformation of a CG basepair stack depended on the sequence context in the DNA [187]. Thus, it appears that the sequence-dependent attributes of DNA mechanics cannot be fully described by a nearest neighbor model, at least if we assume that the MD result was not due to artifacts in the force field.

At the length scale greatly exceeding the helical pitch of dsDNA, polymer models can provide an adequate description of dsDNA’s equilibrium conformations. The wormlike chain (WLC) model mathematically represents a polymer of length l by a continuous set of unit-length tangent vectors $\mathit{t}\mathrm{(}\mathit{s}\mathrm{)}\mathrm{\to }$ parameterized by the distance along the contour s ∈ (0,l). The polymer is assumed to behave like a cylindrically symmetric beam with a mechanical rigidity described by an elastic modulus. Thus local bending of the polymer requires an energy du proportional to $\frac{\mathrm{\partial }\mathit{t}\mathrm{\to }}{\mathrm{\partial }\mathit{s}}{\mathrm{|}}^{\mathrm{2}}$. In thermodynamic equilibrium $\frac{\mathrm{\partial }\overrightarrow{\mathit{t}}\mathrm{(}\mathit{s}\mathrm{)}}{\mathrm{\partial }\mathit{s}}$ should sample from the Boltzmann distribution and it can be shown by integrating over all possible polymer configurations that the expected value for $\mathrm{⟨}\mathit{t}\mathrm{(}\overrightarrow{\mathit{s}}\mathrm{)}\mathrm{\cdot }\mathit{t}\mathrm{(}\overrightarrow{\mathrm{0}}\mathrm{)}\mathrm{⟩}\mathrm{=}{\mathit{e}}^{\mathrm{-}\mathit{s}\mathrm{/}{\mathit{L}}_{\mathit{p}\mathrm{[9].}}}$. Thus, the tangent vector of a polymer is expected to be correlated for a characteristic contour length of Lp, the persistence length. For DNA, a range of values for Lp have been obtained, centered around 45–50 nm by fitting the WLC model to a wide variety of experimental measurements [188]. Finally, it is worth noting that the WLC model has been extended to incorporate elastic stretching as well as twisting [189–191].

5.2. Mechanical stretching

The mechanical properties of dsDNA have been the subject of extensive study [46, 63, 192–197] because of their fundamental importance to gene regulation processes in biological cells. The first single-molecule measurements of the elastic properties of DNA were performed nearly twenty years ago and revealed that dsDNA can be mechanically melted to form ssDNA [46]. At low forces (below 20 pN) stretching of dsDNA is accurately described by the WLC model, which captures the entropy-driven contraction of dsDNA.

Single-molecule manipulation experiments revealed a characteristic plateau in the force-extension curve of dsDNA that signifies a highly cooperative transition from a canonical B-DNA structure to an overstretched S-DNA conformation, the so-called B-to-S transition [193]. Despite extensive experimental and theoretical studies, the nature of the B-to-S transition remains controversial [194]. Molecular dynamics (MD) simulations revealed that stretching DNA with a force transforms the canonical B-DNA structure into a ladder-like conformation [193,195]. However, subsequent thermodynamic analysis of DNA stretching suggested that the “B–S” plateau indicates a melting transition, i.e., separation of the two DNA strands that occurs at the beginning of (and throughout) the plateau [196]. Furthermore, both theory [197] and experiment [198] suggest that depending on the twist of the DNA helix, i.e., the number of basepairs per turn of the helix, several DNA conformations may coexist during the transition.

A single strand of DNA behaves differently under applied force. Typically, the force-extension curve of ssDNA does not exhibit an overstretching plateau [199]. However, a plateau reminiscent of that observed in stretching dsDNA can be observed for homopolymeric (such as poly(dA)) single-stranded DNA [200] and RNA [201] (for example, poly(A)), suggesting that basestacking in such molecules may enforce a helical secondary structure. In general, single-molecule stretching of ssDNA can be challenging to interpret because of a large number of secondary structures that a long random-sequence ssDNA may form during the measurement [94].

5.2.1. Steered molecular dynamics

Complementing experimental studies of DNA mechanics, stretching of DNA has been studied using MD simulations. Perhaps the most straightforward way to model single-molecule stretching is to apply a constant force to one end of the DNA while holding the other end fixed. Despite its simplicity, this method is seldom used. Although a large enough force is guaranteed to produce pronounced stretching, it is almost always irreversible and requires force magnitudes that greatly exceed those applied in experiment. A small force, in contrast, will produce only modest elastic deformation. For an activated process, which typically describes forced unfolding of a biomolecule, the likelihood of observing structural transition is an exponential function of the applied force. Hence, it is very dificult to “dial in” the right magnitude of the force to observe the stretching process that maximizes the realism of the simulation given the limited duration of the MD trajectory.

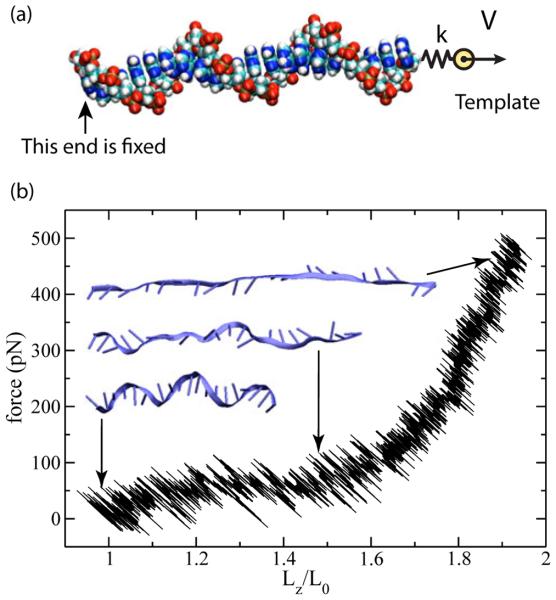
In contrast, the steered molecular dynamics (SMD) approach [202], guarantees the observation of a deformation process of a prescribed magnitude within the available simulation time. Figure 7a illustrates this method using a fragment of ssDNA. In this simulation, a homopolymer of 20 adenosine nucleotides was stretched in a 0.1 M NaCl solution. The coordinates of the O3′ atom at the 3′-end were fixed whereas the O5′ atom at the 5′-end was subject to a harmonic potential (spring constant k = 10 pN/Å) mimicking the action of a virtual spring. The other end of the virtual spring was pulled at a constant velocity of 2 Å/ns. At any time during the simulation, the force applied to the 5′-end of the DNA could be computed from the extension of the spring. The extension of the ssDNA was obtained as the distance between the terminal O5′ and O3′ atoms.

Figure 7.

SMD simulation of ssDNA stretching. (a) Setup of the simulations. A single DNA strand (vdW spheres) is placed in electrolyte solution (not shown). One end of the DNA is fixed in space; the other end is coupled through a harmonic potential of the spring constant k to a template particle. Moving the template with a constant velocity V stretches the DNA. The difference between the coordinates of the template and the end of the DNA reports the applied force. (b) The force-extension dependence of a a poly(dA)₂₀ fragment simulated using SMD. The inset shows three representative conformations of ssDNA corresponding to different amounts of stretching (L = L₀, 1.5L₀ and 1.9L₀), respectively. L₀ denotes the extension of a single DNA strand in a DNA double helix.

Starting from the initial conformation of a B-form DNA (Figure 7b), the DNA strand was stretched by about twofold in 30 ns. In apparent agreement with experiment [200], the simulation revealed a force-extension plateau, Figure 7b. In the plateau region, the base stacking was observed to have breaks, as illustrated by the inset to Figure 7b (at L = 1.5 L₀). At that stage of the stretching process, ssDNA lost its helical structure, however many consecutive bases remained stacked. When overstretched (L = 1.9 L₀), the backbone of the ssDNA was nearly straight. The stacking of neighboring bases in this stretched ssDNA was weak and could transiently form and break.

While it is tempting to describe the above simulation as successful, it actually illustrates several potential pitfalls of the MD method. First of all, the force field used for the above simulation (AMBER-94) poorly describes the conformation of ssDNA [115], which probably explains helical base stacking in partially stretched ssDNA. Second, the force plateau could also be observed in simulated stretching of poly(dT) strands, which was not observed in experiment [200]. Finally, the magnitude of the forces required to stretch ssDNA is significantly greater than the magnitude of the forces applied in experiment. This is perhaps the largest drawback of the SMD method and is a direct consequence of the short (in comparison to experiment) simulation timescale.

In general, ssDNA exhibits dynamics on timescales that are long compared to the all-atom MD timescale. Thus, the timescale of end-to-end collisions for a 20 nt dT fragment was experimentally measured to be 800 ns [203]. It is therefore difficult to sample ssDNA conformations adequately in atomic resolution simulations, especially when the solvent is represented explicitly. For many applications, the need to enhance sampling efficiency warrants the use of coarse-grained representations of DNA. Most coarse-grained DNA models have been optimized to represent the properties of double-stranded DNA [82–92], with only a few models capable of reproducing physical properties of ssDNA [82,94,204].

5.2.2. Anisotropic pressure control

As an alternative to SMD-type simulations of short dsDNA fragments [156, 193, 195, 205, 206], Luan and Aksimentiev suggested an anisotropic pressure-control method to stretch an effectively infinite DNA molecule [207]. Figure 8a illustrates a typical setup of such a simulation. A fragment of dsDNA, containing two helical turns, is submerged in 1 M KCl electrolyte. In each strand of the DNA helix, the backbone of the first nucleotide is covalently linked to the backbone of the last nucleotide over the periodic boundary of the system. This simulation set-up avoids the effect of free ends and is particularly suited for simulations of dsDNA stretching at a constant twist.

Figure 8.

Stretching DNA using anisotropic pressure control. (a) Simulation set-up. A fragment of a DNA helix (orange and blue) is placed in a rectangular box of water (semi-transparent surface) and surrounded by potassium (tan) and chloride (cyan) ions. The strands of DNA are linked to themselves across the periodic boundary. The lateral pressures (P_xx,P_yy) are maintained at 1 bar, while the longitudinal (along the DNA helical axis) pressure (P_zz) is set to a negative value to stretch DNA. (b) A DNA overstretching processs, simulated using anisotropic pressure control. (Top) Densities of the bulk water and electrolyte away from DNA versus simulation time. (Bottom) The length of the DNA fragment versus simulation time. (c) Simulated force-extension dependences of torsionally constrained and nicked dsDNA molecules. The figures are adapted from Luan and Aksimentiev, Ref. 207, with permission. Copyright 2008 by the American Physical Society.

To stretch DNA, simulations are performed under anisotropic pressure conditions maintained using the Nosé-Hoover Langevin piston pressure control [208]. While the P_xx and P_yy components of the pressure tensor are kept at 1 bar, the P_zz component is set to a negative value stretching the system in the z direction until the total internal stress in the simulated system balances the applied pressure Pzz. During this process, the cross-sectional area of the simulation system decreases as the water density remains constant, Figure 8b. A typical process of dsDNA overstretching is illustrated at the bottom panel of Figure 8b. Repeating such simulations at different negative values of Pzz yields the dependence of stress vs. strain.

Assuming the pressure in bulk water is isotropic, the zz component of the water stress tensor ${\mathit{P}}_{\mathrm{z}\mathrm{z}}^{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}\mathrm{\approx }{\mathit{P}}_{\mathrm{X}\mathrm{X}}\mathrm{\approx }\mathrm{1\; bar.}$. From the balance of the applied external pressure P_zz and the internal stress in DNA and water, the tensile force inside DNA can be written as

$$\mathit{F}\mathrm{=}\mathrm{-}\mathrm{(}{\mathit{P}}_{\mathrm{z}\mathrm{z}}\mathit{S}\mathrm{-}{\mathit{P}}_{\mathrm{z}\mathrm{z}}^{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}\mathrm{(}\mathit{S}\mathrm{-}{\mathit{S}}_{\mathrm{D}\mathrm{N}\mathrm{A}}\mathrm{)}\mathrm{)}$$ (10)

where S and S_DNA are the cross-sectional areas of the simulation system and DNA, respectively, in the x–y plane. Because the product of ${\mathit{P}}_{\mathrm{z}\mathrm{z}}^{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\mathit{S}}_{\mathrm{D}\mathrm{N}\mathrm{A}}$ is less than 0.5 pN, Eq. 10 to compute the tensile force in DNA can be simplified as,

$$\mathit{F}\mathrm{=}\mathrm{-}\mathrm{(}{\mathit{P}}_{\mathrm{z}\mathrm{z}}\mathrm{-}\mathrm{1}\mathrm{)}\mathrm{\times }\mathit{S}$$ (11)

Thus, the force-extension dependence of a DNA molecule can be computed from the stress-strain relation of the entire system.

Figure 8c shows the force-extension curves obtained using the anisotropic pressure control method for torsionally constrained poly(dA₁₀dC₁₁)·poly(dT₁₀dG₁₁) and nicked poly(dC₂₁)·poly(dG₂₁) dsDNA. Each force-extension curve shown in Figure 8c has three characteristic regions: elastic, transition, and overstretched. The force required to initiate the overstretching transition is in good qualitative agreement with experiment. When torsionally unrestrained, λ-DNA exhibits an overstretching plateau at a tension of about 70 pN and that the tension slightly increases in the plateau region [193, 199]. For torsionally constrained DNA, experiment has shown a significantly higher yield force of about 110 pN [198]. Direct quantitative comparison, however, is difficult because of the heterogeneous sequence of λ-DNA. A detailed analysis of the sequence effects can be found in Ref. 207.

5.3. Twisting dsDNA

A DNA molecule can be bent, stretched along its helical axis, or twisted about this axis. Measurements of the extension of a double-stranded DNA molecule under low applied force (< 10 pN) probes the mechanical bending of DNA [209]. At higher force (but still below the overstretching transition), the same measurements can characterize elastic stretching along the helical axis [209]. Such experiments are usually performed using optical traps which allow the DNA to relax torsionally. In biological cells, torsional stress in DNA was shown to regulate gene expression [210, 211].

Usually, the term flexibility refers to a polymer’s ability to bend, which is quantified by its persistence length. For a generic dsDNA molecule, the persistence length is ~ 45-50 nm [63,188] or about 20 times its diameter (2.5 nm), which makes DNA fairly stiff for a natural polymer. In direct analogy to the persistence length, one can define a torsional persistence length for dsDNA that represents the characteristic length scale along which a DNA molecule’s twist is correlated. This length is similar to the persistence length, but varies considerably in the literature from 36–75 nm [188,212,213].

Analysis of the crystal structures suggests that the intrinsic twist of a DNA helix depends on its nucleotide sequence and can range from 31° for an AG step to 40° for a TA step [214, 215]. Here we follow the usual convention that the first letter is on the 5′-end of one strand, and we note that some sequences are “palindromes” (e.g. AA with TT). The standard deviation of the twist is similar for different basepair steps, ranging from 3.9° for an AA step to 6.5° for a CA step, suggesting a mild dependence of the torsional persistence length on the DNA sequence. The sequence-dependent average twist and twist moduli were obtained from MD simulations of DNA fragments [212] using the AMBER force-field [109] without the parmbsc0 refinement. The results of the MD simulations were in overall agreement with the results of the crystal structure survey [215] with some discrepancies, primarily for GG steps. CG steps were found to be the most conformationally flexible, and AT steps the least. Overall, the study demonstrated significant sequence-specific coupling between various coordinates used to describe basepair steps.

A more recent simulation study employed the newer AMBER-99 force-field and a much larger, systematic set of sequences to examine the flexibility of specific base-steps [216]. Despite reporting on overall flexibility, which included contributions from both twist and bending, the results of the study were consistent with previous observations, assessing the TA, CG and CA (but not AT, GC, and AC) steps as the most flexible. The authors emphasized a correlation between the flexibility of a step and the absence of water molecules in the minor groove that bridge the base pairs forming the step.

Simulations of longer DNA molecules have also been performed. Mazur has studied many DNA properties through simulations employing an all-atom MD method that permits the integration timestep to be increased from 1-2 to 10 fs by treating groups of DNA atoms rigidly [217]. That method enabled long-timescale (> 160 ns) simulations of short (< 2 turns) DNA fragments that revealed a torsional persistence length of 120 nm for AMBER-98 [218]. In contrast however, Noy and Golestanian [219] more recently found the torsional persistence length to be 80 nm from simulations of relatively long (3-5 turns) random sequence DNA molecules using the AMBER-99 force field with the parmbsc0 correction. The disagreement resulted in a debate between the two groups [220, 221], which may partially be attributed to the rather different simulation protocols employed.

A number of elastic models were developed that incorporated twisting and bending of DNA [189–191]. In general, elastic deformations of DNA may be coupled and some elastic responses may be asymmetric. In particular, twist–bend coupling and asymmetric bending were included in an elastic model that ignored stretching [222]. By contrast, single-molecule experiments demonstrated that stretching and twisting are counterintuitively coupled at low force (under 30 pN) with the DNA twisting more when stretched [223]. This led to a refinement of the extensible worm-like chain model that incorporates twist and twist–stretch coupling [224].

Presently, MD simulations cannot reproduce the experimentally observed stretch-twist coupling. Figure 9 illustrates our analysis of the MD simulations reported in Ref. 128. In those simulations, performed using the CHARMM force field [225], a 24-bp dsDNA was free to both rotate and extend. To compute the twist, we defined the orientation of each base pair, fv, according to the standard reference frame [226], Figure 9a. For two consecutive base pairs n and n+1, the twist is arccos $\mathrm{(}\frac{{\overrightarrow{\mathit{v}}}_{\mathrm{n}}\mathrm{\cdot }{\overrightarrow{\mathit{v}}}_{\mathrm{n}\mathrm{+}\mathrm{1}}}{\mathrm{\left|}{\overrightarrow{\mathit{v}}}_{\mathrm{n}}\mathrm{\right|}\mathrm{\left|}{\overrightarrow{\mathit{v}}}_{\mathrm{n}\mathrm{+}\mathrm{1}}\mathrm{\right|}}\mathrm{)}$. The rise is computed as the average distance between the plane of N9, N1, and C6 atoms of the base pair n and those three atoms of the base pair n + 1. Figure 9 shows a scatter plot of the instantaneous twist versus instantaneous raise computed from a 50 ns MD trajectory at a mixture of 50 mM NaCl and 50 mM KCl. A linear regression fit to the scatter plot reveals a weak anticorrelation of the twist with extension, which is opposite to the dependence observed in single molecule experiments [223, 227, 228].

Figure 9.

MD simulation of twist-stretching coupling. (A) Definition of a base pair geometry. The orientation of a base pair is characterized using a plane passing through atoms N9, N1, and C6, and a vector, $\overrightarrow{\mathit{v}}$, connecting atoms N9 and N1. (B) Scatter plot of instantaneous versus instantaneous rise from a 50 ns simulation of dsDNA. The red line shows a linear fit to the scatter plot, indicating slight (R² =0.12) anticorrelation of twist and rise.

When DNA is twisted enough, linear elastic models fail to describe its properties. This was demonstrated in MD simulations where a three-turn DNA molecule was twisted by −0.22 to +0.39 turns [229]. Initially, the DNA had uniform twist, but by the ends of a 10-ns simulation it was slightly undertwisted or extremely overtwised; the DNA conformation included a mixture of B-DNA and locally denatured DNA accommodating the overall twist. The MD simulations also indicated that counterions were able to access the minor groove more easily in overwound than underwound DNA.

5.4. DNA looping

Because cells can suppress expression of genes by looping DNA, the behavior of DNA in small loops has long been of interest. Under thermal fluctuations or applied force, DNA bends away from its equilibrium curvature. For moderate bending, the wormlike chain model (WLC) describes this bending very well with a 45–50 nm persistence length. Early simulations were not long enough to allow accurate determination of the persistence length of DNA. However, the studies from Mazur [218] and from Noy and Golestanian [219] reported persistence lengths of 65-85 nm for AMBER-98 and 43–51 nm for AMBER-99bsc0, respectively.

The likelihood of DNA having complementary single-stranded overhangs to form a loop [230], or to cyclize, depends on both the bending and twisting properties of DNA. As a function of DNA length, this likelihood has a peak around 400 bp, where the DNA is neither too long (so that the ends cannot find each other), nor too short (so that the DNA is unable to bend into a loop). This assay has been used to unambiguously distinguish intrinsic sequence-dependent curvature from isotropic flexibility [230]. For DNA molecules shorter than 500 bp, the likelihood of DNA cyclization was found to fluctuate periodically with respect to the length of the DNA fragment [63].

Under high curvature, the WLC model must break down, however, there is much disagreement with respect to the critical curvature where the model loses its validity. It was experimentally observed that very short DNA fragments (~ 100 bp) could form circles more readily than predicted by the elastic models of DNA [213], suggesting strong bending or kinking. Similar results were observed from atomic force microscope images [1] and from the interference of x-ray scattering off gold nanoparticles tethered to either end of a short DNA molecule [231]. Other experiments rigorously defended the validity of the WLC model for short DNA [63,64,232,233]. The controversy continues as DNA was seen to be highly flexible in recent melting experiments of curved DNA [234] and in single-molecule experiments where the looping of 100-bp DNA fragments was monitored by fluorescence [3]. It is interesting to note that most experimental studies that reported sharp bending of DNA employed either divalent electrolytes or high concentrations of monovalent electrolyte [1, 3, 234]. In the nucleus, counterions with valence > 2 strongly screen electrostatic interactions, so studies of DNA bending at elevated concentrations of monovalent electrolyte may still be biologically relevant.

All-atom simulations demonstrated spontaneous kinking of initially well-formed 94-bp DNA minicircles with two different linking numbers that were expected to flank the torsionally relaxed state [235]. The kinks broke stacking interactions with bending of 90–120° towards the minor groove. A more recent study involved shorter simulations (10–30 ns) of homopolymeric DNA minicircles under various degrees of torsional strain [236]. In that study, kinks and duplex melting were observed in torsionally strained DNA, but not in the simulations of relaxed DNA, perhaps because of the short durations of these simulations (10 ns).

Given that the atomic models employed (AMBER-94/99) significantly overestimate the base-stacking interaction free-energy [132], the above studies appear to suggest that DNA is likely to be kinked in 94-bp circles. However, caution should be taken in jumping to this conclusion; the force field likely enhances the free energy required to form a kink, but it also may enhance the free energy needed to form continuous curves. Whether a DNA circle kinks in MD simulation depends on the relative magnitude of these free energies. This discussion then begs the question of whether the AMBER force field overestimates the bending rigidity of unkinked DNA. Unfortunately, both experiments and all-atom MD simulation are locked in debates that pertain to the likelihood of looping of short DNA sequences.

5.5. Nucleosomes

Sharply bent DNA structures naturally occur in nucleosomes—the storage units of eukaryotic genomes. In a typical nucleosome, a 150-bp long DNA segment wraps almost twice around a protein core called a histone octamer complex. The interaction of DNA with the histone proteins is thought to play a critical role in gene regulation [237]. When the existence of nucleosomes was first established, the DNA in nucleosomes was expected to be kinked (e.g., [16]). However, subsequent crystallographic studies revealed that DNA can wrap around a histone octamer without disrupting its basepairing pattern [237]. Interested readers are referred to a recent review on this subject (Ref. 237).

For a eukaryotic gene to be transcribed, nucleosomal DNA must be unwrapped from the histone core. Not surprisingly, a number of single-molecule techniques have been applied to study the internal mechanics of nucleosomes [238–241]. Despite extensive efforts, the structural details of the unwrapping process remain elusive. Several research groups have used computer simulations to study the structure and dynamics of nucleosomes. Until recently, all-atom MD studies of nucleosomes have been tempered by the relatively large size of the simulation system. By far a more serious obstacle is the slow dynamics of unstructured parts of the histone proteins (so-called histone tails), which strongly interact with DNA because of their polybasic nature. Consequently, coarse-grained approaches have historically prevailed [242–244]. However, several all-atom MD simulations of nucleosomes have been reported already [49,245]. For example, Biswas et al. reported a 100-ns simulation that characterized interactions of histone tails with dsDNA [49].

A potentially interesting approach is to use the SMD method to simulate forced unwrapping of nucleosomal DNA [245]. If performed properly, such a simulation could provide a structural interpretation of the single-molecule pulling experiments [238–241]. In the simulation featured in Figure 10, unwrapping of dsDNA was produced by increasing the length of a virtual spring whose ends were anchored at the centers of mass of the terminal 10-bp fragments of the DNA. Initially, the equilibrium length of the spring was increased at a rate of 1 nm/ns, which was reduced to 0.2 nm/ns after 18 ns. While pulling the ends of the nucleosomal DNA apart, we observed symmetric unwrapping of the DNA conformation until approximately 40 ns, Figure 10d. After 44 ns, local melting of dsDNA was initiated, Figure 10e. Thereafter, only the propagation of DNA melting, not DNA unwrapping, was observed. Such a disappointing outcome is perhaps not surprising, asthe SMD force exceeded 100 pN at the moment of the DNA melting Figure 10f. This simulation indicates that a significantly slower SMD pulling will be required to properly reproduce experimental unwrapping of nucleosomes.

Figure 10.

SMD simulation of nucleosomal DNA unwrapping. (a–e) Representative conformations of a partially unwrapped nucleosome at several instances of the SMD trajectory. To realize the SMD protocol, a harmonic spring potential was applied between the centers of mass of the terminal fragments (10 bp) of DNA. The equilibrium length of the spring was increased at a rate of v to unwrap the nucleosome. The inset in panel e illustrates local melting of DNA produced by the excessive SMD force (~100 pN). (f) SMD force as a function of the simulation time. Note that the pulling rate was reduced by a factor of 5 at t ~ 18 ns to facilitate structural relaxation.

6. DNA–DNA interactions

Direct, physical interactions between DNA molecules are central to many fundamental biological processes and underpin emerging DNA nanotechnology. Below we describe the surprising range of DNA–DNA forces that sensitively depend on the properties of the interacting molecules, e.g., their mutual orientation, as well as the properties of the environment, e.g., electrolyte concentration. The discussion below does not cover DNA–DNA forces mediated by proteins.

6.1. DNA hybridization

The most fundamental DNA–DNA interaction is hybridization, which is the formation of a double helix by non-covalent self-assembly of two ssDNA molecules carrying complementary nucleotide sequence [6]. Despite tremendous interest in this fundamental problem, fully atomistic simulations of DNA hybridization remains a challenging problem because sampling of conformational space of ssDNA is beyond current computational power. For example, single-molecule experiments have shown that hybridization of a ~10-bp DNA molecule at mM concentration would require a millisecond-timescale to observe [246]. Instead, all-atom MD simulations have focused on the observation of single base binding-unbinding events [247] or folding of short hairpins (about 4 bps) [132, 248–251]. Currently, the most practical solution for simulations of DNA/RNA hairpin folding is the replica exchange MD (REMD) technique, which enhances sampling of a thermodynamic ensemble by accelerating energy barrier crossing using coordinate-swapping among ~100 replicas each held at different temperature [132,249,251].

6.2. Side-by-side repulsion of duplex DNA

DNA molecules carry a high negative charge and hence electrostatically repel one another unless the DNA charge is compensated by polycationic condensing agents, such as cobalt hexamine (4+), spermidine (3+), spermine (4+), polylysine or polyarginine [74, 176, 252–254]. While the effective charge of a macromolecule can be theoretically determined from the force between a point charge and the macromolecule, in practice such forces are difficult to measure. Computational methods offer this capability (Section 4.2.4), but their validation requires connection to experimental observables.

A related, experimentally attainable approach is to determine the effective force between charged macromolecules. Quantitative measurement of the force between DNA molecules as a function of inter-DNA distance was not possible until Parsegian and coworkers developed, about 30 years ago, a method to condense DNA using osmotic pressure of polyethylene glycol (PEG) polymer [74, 255]. In that seminal work, the authors found that condensed DNA arranged in a hexagonal lattice pattern. The study established that inter-DNA forces are generally repulsive in the presence of monovalent and divalent cations. The only two exceptions are manganese (Mn²⁺) and cadmium (Cd²⁺) ions that can induce DNA condensation in a specific temperature range [256], see Section 6.3. Furthermore, they observed that the inter-DNA repulsions decays exponentially at short distances regardless of cation types and argued that “hydration forces”, not electrostatic forces, are at the origin of the cation-independent repulsion [74].

In principle, the force between two DNA molecules can be estimated from the non-linear Poisson-Boltzmann (NLPB) equation (Section 4.1.1). The PB equation is nonlinear so the ionic densities surrounding two DNA molecules in isolation do not add trivially when the molecules are brought into proximity. Therefore, one can expect that the effective charge of DNA determined by measuring the interaction with a point charge may not describe the interaction between two or more DNA molecules. Nevertheless, it is useful to consider an effective charge for the purpose of modeling these interactions. Additionally, an effective charge highlights deviations between the behavior of real DNA and that predicted by idealized models. As we shall see, the effective charge of DNA as determined through DNA–DNA interactions can depend on the ionic strength and the DNA–DNA separation. One should, however, keep in mind that the NLPB equation neglects many effects including hydration, finite ion size, correlations in the ion atmosphere and local dielectric response of the medium [257–259].

Prior to the availability of the ion–phosphate NBFIX parameters, several all-atom MD simulations quantified the repulsion between parallel dsDNA molecules [48,260,261]. The studies demonstrated significant repulsion with forces around 5-10 pN/turn between parallel DNA molecules having center of mass separations between 25 and 30 Å around physiological KCl or NaCl concentrations. Replacing potassium ions with sodium ions was found to decrease the repulsion [260], in qualitative agreement with experimental measurements of DNA condensation under osmotic pressure [262].

Using the NBFIX corrections for ion-phosphate interactions (described in Section 3.2.2), all-atom MD simulations could quantitatively reproduce the experimental inter-DNA distance and the osmotic pressure in DNA arrays [60]. In an MD simulation, various ionic species of the same valence differ from one another solely by their mass, the vdW radius and the well-depth of the vdW potential. A custom NBFIX correction for a particular ion–phosphate pair selectively increases the vdW radius just for that pair interaction. For monovalent ions, the adjustment needed to bring simulation into agreement with experiment was larger for smaller ions. Potassium ions, which have the largest vdW radius of common ions, needed the smallest adjustment. Hence the results from the previous studies performed without the NBFIX corrections are likely to be the most accurate in the case of KCl electrolytes.

In the dilute regime, repulsive DNA–DNA interactions can be experimentally studied by several means. For example, small angle x-ray scattering experiments can provide an average measure of the pairwise interaction potential between particles in a solution, and demonstrate overall repulsion of long DNA fragments in mono-and divalent electrolyte. Similarly, forces involved in packaging viral capsids have been related to DNA–DNA repulsion [263]. Another system for the study pairwise DNA interactions can be created by twisting a long DNA molecule tethered to a magnetic bead and a stationary surface, whereupon the DNA will buckle forming a twisted loop called a plectonemic supercoil, Figure 11. The two halves of the plectonemic loop are wrapped closely around one another even when DNA–DNA interaction is repulsive. As the DNA molecule continues to be twisted, DNA is transfered from the tether region to the plectoneme, which grows in an ion-concentration dependent manner. Given a functional form, the strength of the electrostatic interaction can be inferred from the rate of plectonemic growth.

Figure 11.

Schematic representing the experimental protocol used to produce plectonemic supercoils [48]. DNA is tethered to a stationary surface and a magnetic bead. A constant tension is applied to the DNA as it is twisted. At some critical number of twists, the DNA buckles to form a plectoneme (red curve). MD simulations quantified the interactions between the two halves of the plectoneme by averaging the force needed to restrain two effectively infinite DNA fragments about various separations. A typical simulation system is shown below the drawing of the experimental setup. Water is shown a transparent molecular surface. Ions (green and cyan) and DNA atoms (grey, red backbone) are shown as vdW spheres. A small spring is drawn between the DNA, representing the method used to obtain the force of the interaction.

In a collaborative study of experimentalists and modelers, DNA–DNA interactions within a plectoneme were modeled as that of uniformly charged cylinders interacting through a potential obtained from the linearized PB equation scaled by a charge reduction factor (CRF) [48]. The CRF was used as an adjustable parameter to fit theoretical predictions to experimental data, yielding a value of 0.42 for the CRF in 1:1 electrolyte over a wide range of concentrations. All-atom MD simulations verified that a CRF of 0.42 improved the linearized PB prediction of the force between parallel dsDNA molecules. This CRF contrasts with that from Manning counterion condensation theory, demonstrating that the effective charge of DNA depends on the process it is used to describe with.

6.3. Side-by-side attraction

In all kingdoms of life, the genome is highly condensed for efficient and safe storage and gene regulation. The simplest life forms where such compaction is observed are DNA viruses such as bacteriophages. When the genome of a bacteriophage is fully packed inside its capsid, the inter-DNA distances is less than 30 Å and the nucleotide concentration easily exceeds 1 M. Eukaryotic genomes are also densely packed inside the nucleus. For example, the 3 billion base pair long human genome is packed inside a nucleus roughly 10 μm in diameter. Simple estimation of nucleotide concentration, assuming only DNA exists inside the nucleus, gives about 10 mM concentration; considering non-DNA biomolecules such as histone and transcription factor proteins, one can easily imagine that the effective concentration of DNA inside the nucleus significantly exceeds 10 mM. Therefore, DNA condensation has been the focus of intense research for several decades owing to its immense importance in biological and biomedical processes.

Polyvalent counterions (or polycations) play a critical role in stabilizing DNA condensates, providing electrostatic screening for the highly charged naked DNA and even facilitating attraction of like-charged DNA under certain conditions. A notable example is polybasic peptides in eukaryote cells that condense the eukaryotic genome. Histone tails and, especially, H1 histones are rich in basic residues such as lysine and arginine so that they can stabilize highly condensed chromatin fibers. Protamine, which is a relatively short polybasic polypeptide, is also known to condense genome in sperm cells. Moreover, non-peptide biogenic polyamines such as putrescine, spermidine, and spermine are abundant in eukaryotic cells, indicating potential roles in genome condensation [264, 265].

Inspired by the biologically abundant polyamines and their potential importance in biological functions, in vitro studies of condensed DNA phases by biogenic polyamines have been performed by several groups. Long strands of duplex DNA (more than 400 bp) pack into dense toroids or rod-like structures within which they are assembled into a highly organised hexagonal lattice [266]. Short strands of DNA form liquid crystalline aggregates in the presence of multivalent electrolytes such as spermine and spermidine [253, 267]. Most in vitro studies have shown that the electrostatic forces between DNA chains in bulk solutions containing mono-or divalent electrolytes are purely repulsive [74, 268]. To induce condensation, a counterion valence of Z≥3 is required [176, 267]. Recent experiments involving small-angle x-ray scattering demonstrated that short duplexes of DNA containing 20 base pairs could attract each other in divalent solutions exceeding a threshold value of counterion concentration [130]. However, the same group revealed that the DNA association observed in the presence of divalent cations was caused by end-to-end stacking of short DNA oligomers [130, 131]. Subsequent experiments demonstrated that such association was inhibited by the presence of short T4 loops at the ends of the DNA [131]. Thus, experimental data convincingly indicates that DNA condensation at physiological temperature can occur only in the presence of polycations with at least +3 valence. The only two DNA-condensing divalent cations are Mn²⁺ and Cd²⁺ [256]. Because Mn²⁺ or Cd²⁺ can induce DNA condensation only in a certain temperature range (30 to 60° C), the Mn²⁺-or Cd²⁺-induced condensation is usually attributed to an entropic contribution of water [256]. However, the detailed mechanism is not yet known.

The microscopic mechanism of DNA condensation is a subject of a debate. The two main forces implicated in the mechanism arise from hydration and electrostatics. Experimental studies by Rau et al. [252] suggested that the reconfiguration of water between the macromolecular surfaces as a possible mechanism for DNA compaction. The concept was developed from direct measurement of the osmotic stress as a function of the separation between parallel DNA helices. Multivalent ions bound to DNA appeared to reconfigure the water between the DNA surfaces to create long range attractive hydration forces. The authors observed that the B-form DNA molecules condensed by multivalent cations assembled into well-defined lattices of lattice spacing greater than the diameter of a double helix. Measurements of the forces between dsDNA that were pushed together from a self-assembled state revealed an exponentially increasing repulsion of a 1.3 to 1.5 Å decay length. The decay length was found to be insensitive to the ionic strength and to the valence of the cationic species. These findings could not be explained by direct bridging of neighboring DNA molecules by cationic ligands or by the electrostatic double layer theory. Hence the authors conjectured that an alternate mechanism involving a disruption of the water structure between neighboring DNA molecules was at play in DNA condensation.

The other competing theory of DNA condensation is based on counterion fluctuations and correlation effects due to multivalent couterions. Bloomfield et. al. [269] proposed that the phenomenon of DNA lateral condensation originates from correlations in the counterion environment of homogeneously charged cylinders (representing DNA in this theory). When the counterion distribution has a quasi-two-dimensional character, i.e. the counterions are localized within a thin layer close to the cylinder surface, the problem can be reduced to the interaction between layers of adsorbed but mobile counterions neutralizing surfaces of similar charge density. The electrostatic repulsion between counterions can produce layers of alternating positive and negative charge near the surface. Two such opposing surfaces adjust complementarily to one another to minimize their total energy, resulting in a mutual attraction of the surfaces.

A similar theory proposed by Shklovski [270] suggested that counterions at the surface of the cylinders can exhibit quasi-crystalline ordering. Since dsDNA has a rigid rod-like structure, a bundle of such parallel rods can serve as a background for counterions to form a Wigner crystal. The binding energy of the bundle originates from the correlations of counterion motion. This simple picture, however ignores the discrete nature of the DNA charge. The same year Kornyshev and Leikin [271] proposed an electrostatic zipper model for DNA aggregation. The authors showed that binding of counterions to the grooves of DNA creates an axial separation of positive and negative charges. The attraction between a negatively charged strand and the positively charged grooves of the neighboring molecule creates an electrostatic zipper running along the whole length of the molecule. Divalent cations such as Ca²⁺ and Mg²⁺, which have high affinity to phosphates, do not induce DNA condensation within the electrostatic zipper model because of weak charge separation. However, ions that preferentially bind to the grooves and not to the DNA backbone, such as Mn²⁺, enhance DNA condensation.

While the implications of these theories cannot be directly tested by experiments, all-atom MD simulations might provide an insight into the molecular mechanism of attraction. Dai et. al. [272] investigated the interaction between two parallel duplex DNA molecules in the presence of multivalent counterions, putrescine, spermidine, spermine and cobalt hexamine. The inter-DNA potential obtained from umbrella sampling techniques showed that with increasing valence of the counterions and smaller ligand size, the interaction becomes more attractive. The attractive force was associated with the formation of short-lived ion-bridges, i.e. multivalent ions simultaneously bound to two DNA molecules. There was no evidence for long-range persistent two-dimensional ordering of counterions at the surface of the DNA as suggested by the counterion correlation theory. Using all-atom MD simulations, Luan and Aksimentiev demonstrated that monovalent and divalent electrolytes can include attraction between two parallel DNA fragments [261]. The simulations suggested that, although a mutual attraction between DNA double helices in NaCl electrolyte is possible, the attractive potential well is too shallow to allow for condensation. Although these two studies elucidated general aspects on cation-induced DNA–DNA interactions, they could not reproduce the experimental data quantitatively due to artificially strong cation–DNA interactions as described in Section 3.2.2. For example, in both reports, the free energy minima were at ~23–24 Å, which is about 5 Å shorter than that in spermine-induced DNA condensate.

Using the improved parameterization of cation-phosphate interactions, one can compute the interaction free energy between two parallel DNA helices, similar to the method used in Refs. 261, 272. The outcome of such simulations is significantly more consistent with experimental data [74, 176]. Figure 12a illustrates the simulation setup with two parallel DNA helices submerged in a solution of spermine(4+) and NaCl. Figure 12b shows the interaction free energy computed as a function of DNA-DNA distance using the conventional umbrella sampling technique. Consistent with experiment [74], inter-DNA forces are always repulsive at all ranges of DNA–DNA distance in the presence of Na⁺ and Mg²⁺ although Mg²⁺ lowers the inter-DNA repulsion significantly. At sub-mM spermine concentrations, long-range inter-DNA attraction develops, indicated by the free energy minimum near A, which is quantitatively 28 Åconsistent with experiment [176].

Figure 12.

Interaction free energy of two parallel DNA helices. (a) Simulation setup contains two parallel DNA helices (G₂₀ ·C₂₀), which are effectively infinite under periodic boundary condition. The DNA helices are shown using a cartoon representation; Na⁺, Cl⁻, and spermine ions are shown as vdW spheres. Water is not shown for clarity. (b) The free energy of two DNA helices versus the DNA–DNA distance. The simulations were performed for the following three onic conditions: [Na⁺] = 200 mM (red); [Na⁺] = 200 mM, [Mg²⁺] = 20 mM (black); [Na⁺] = 200 mM, [spermine] < 1 mM (blue). Consistent with experimental data [74, 176], attraction is observed only in the presence of polyamine. Data are taken from Yoo and Aksimentiev (unpublished).

6.4. End-to-end attraction of duplex DNA

Recently, the Clark and Bellini groups studied liquid crystal phases formed by dense solutions of short (8 bp) duplex DNA fragments [273–275]. Surprisingly, the researchers observed particular kinds of liquid crystal phases that could be formed only by elongated molecules characterized by energetically favorable axial alignment. The only explanation for the results was that the short duplex DNA fragments were aggregating end-to-end into long rod-like structures. From the concentration dependence of the phase transitions, the authors estimated a standard binding free energy of the end-to-end interaction to be between −2.3 and −4.7 kcal/mol [273]. Experimental evidence supporting end-to-end attraction was independently obtained through small-angle x-ray scattering [131]. End-to-end attraction of DNA was an unexpected discovery that may have implications in for a variety of systems, as outlined in Figure 13C. In particular, end-to-end attraction of duplex DNA could play an important role in guiding the initial steps in the repair of double-stranded DNA breakage, a serious form of DNA damage [276].

Figure 13.

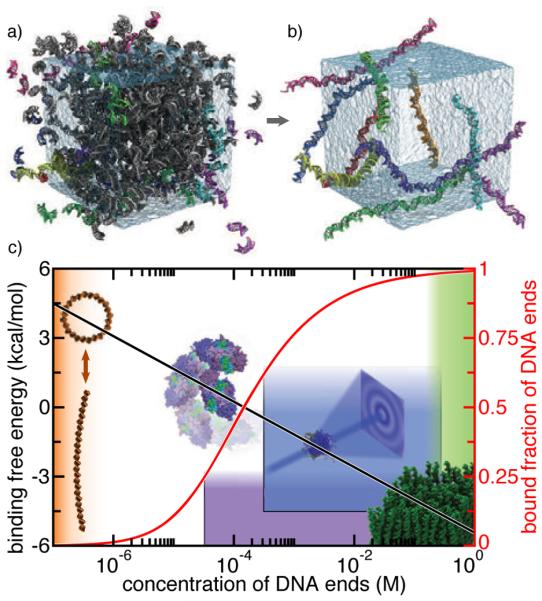
End-to-end association of duplex DNA fragments. (A) Simulation system containing a solution of 458 DNA fragments near the density of the experimentally determined isotropic–nematic phase transition [273]. Most DNA fragments are shown in grey. Those fragments that formed the ten largest end-to-end chains at the end of the simulation are shown in color. The simulation used periodic boundary conditions, lasted 260 ns and included about 1,500,000 atoms. Water in the simulation unit cell is shown as a semitransparent molecular surface. (B) The ten largest end-to-end chains at the end of the simulation. The kinetic association and dissociation rates enabled estimation of the standard binding free energy of the end-to-end interaction. (C) End-to-end attraction in different DNA systems. The effective binding free energy (black) and the fraction of bound DNA ends (red) are plotted against the reference concentration of DNA ends. Images illustrate four DNA systems in which the end-to-end attraction may or may not play a role. From top left to bottom right: blunt-ended DNA circles (orange); repair of DNA during non-homologous end joining [276] (purple); small-angle x-ray scattering experiments [130] (blue); DNA aggregation into liquid crystal phases [273] (green). Figures adapted with permission from Ref. 75.

The magnitude and mechanism of end-to-end attraction was investigated using a variety of all-atom MD methods [75]. In 40 out of 40 simulations, two axially aligned duplex DNA fragments rapidly collapsed to an end-to-end bound complex. Strikingly, DNA with terminal phosphates were found to stack with a continuous conformation of the backbone that resembled B-DNA. The bound complexes were stable in subsequent simulations (without axial restraints) for hundreds of nanoseconds. Using steered MD, select complexes were ruptured and an upper bound of the end-to-end free energy was estimated. Maffeo and co-workers also employed umbrella sampling simulations, the gold standard of methods for obtaining free energy, within thermodynamic cycle adapted from Woo and Roux [277] to estimate the standard binding free energy of end-to-end assembly at −5.4 ± 1 kcal/mol. To our knowledge, this was the largest system to which the method had been applied.

Since the magnitude of the free energy was quite large compared to experimental estimates [273], the researchers verified the free-energy calculations through a brute-force simulation of a massive system containing ~ 450 initially separated DNA fragments, see Figure 13A. The DNA fragments spontaneously associated end-to-end forming long chains during the 250 ns simulation, see Figure 13B. The trajectory allowed the association rate kon to be evaluated. During the simulation, only one end-to-end junction ruptured, allowing for a very rough estimation of the dissociation rate k_off. The logarithm of the ratio of those rates is the standard binding free energy, which was found to lie between −4.4 and −7.6 kcal/mol, consistent with the prior estimate. Since that study was performed, the Garcia group published a correction to the force-field that reduces the strength of the stacking interaction [132], so the magnitude of the free energy obtained in the above study could have been overestimated.

More recently, the Sciortino group employed coarse-grained simulations to validate a theoretical model that, given a stacking free energy, provides a link between the concentration of short DNA duplexes and the degree of the end-to-end polymerization, which can in turn be related to the liquid crystal phase of DNA solution [278]. The theory was then use to estimate the range of end-to-end stacking free energies compatible with the experimentally observed liquid crystal phase transitions, finding the end-to-end association free energy in the range of −0.4 and −2.4 kcal/mol.

7. DNA in electric field

As a highly charged molecule, DNA moves in an external electric field. This phenomenon, electrophoresis, has many important applications in biotechnology and forensic. For example, gel or capillary electrophoresis is a key step of the Sanger’s method of sequencing DNA [279]. The electrophoretic motion of DNA through nanopores and nanochannels is essential to many emerging methods of DNA characterization, in particular the so-called nanopore sequencing [280–282]. From a purely scientific point of view, the motion of DNA in electric field is a particularly interesting subject as it permits validation and further improvement of various theoretical models of polyelectrolyte solutions.

7.1. Free-solution electrophoresis

The movement of an object, such as DNA, under the influence of an electric field is described by its electrophoretic mobility μ:

$$\mathit{\mu }\mathrm{=}\frac{\mathit{v}}{\mathit{E}}$$ (12)

where E is the electric field and v is the measured velocity. In free-solution electrophoresis, however, the behaviour of μ for DNA can be puzzling. In particular, μ of DNA, which might reasonably be expected to be proportional to the number of bases N, is actually independent of N for large N [283, 284]. Moreover, under certain conditions μ(N) displays a maximum before lowering slightly to its large-N value [283].

How can this counterintuitive result be understood? Authors sometimes turn to the Einstein relation between μ and the diffusion constant D:

$$\mathit{\mu }\mathrm{=}\frac{\mathit{Q}\mathit{D}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}$$ (13)

where Q is the electric charge of DNA. However, for a long polymer the diffusion constant scales as D(N) ~ 1/N^ν, where ν is 1/2 or 3/5, depending upon whether excluded volume effects are important. For shorter DNA (N < 250), ν was found to be approximately 0.68 [285]. Since Q ~ N and μ is independent of N, Eq. 13 cannot be correct [285].

Combined with measurements of the diffusivity of DNA [284, 285], one may be tempted to salvage Eq. 13 by assigning DNA an effective charge [286]. Based on the above scaling argument, such a construction would scale as Q_eff (N) ~ N^1−ν. However, this obscures the reasons for the failure of Eq. 13. As pointed out by Hoagland et al. [283], the Einstein relation neglects the very important effect of counterions surrounding the DNA. An applied electric field acts on these counterions as well; since they are by definition of the opposite charge of DNA, an electroosmotic flow is set up which acts against the motion of DNA.

The effects of the electroosmotic flow are significant. It leads not only to a lower Q_eff of DNA, but qualitatively changes the behaviour of DNA motion in an electric field. The counterion motion effectively screens hydrodynamic interactions between monomers [287]. Thus, the fact that a long strand of DNA is a single, covalently bonded polymer is irrelevant to its motion, and the mobility μ is independent of the polymer length. The DNA coil is transparent to the motion of counterions and is hence described as “free-draining” [288]. For diffusive motion, on the other hand, hydrodynamic forces between monomers are not screened, leading to the failure of Eq. 13 [285].

The independence of DNA mobility on N led to the so-called local force picture. In the local force picture, DNA is thought of as chain of segments, each with an effective charge qk and friction coeffcient ξk. The segments do not exert force on each other, and thus the velocity of the DNA is given by v = NkqkE/Nkξk = qkE/ξk, independent of the number of segments Nk. However, this picture can be misleading: As pointed out by Vivoy [289], the local force picture implicitly assumes that the background fluid is at rest.

7.2. Sieved electrophoresis

Since in free-solution electrophoresis the DNA mobility μ is independent of the DNA length, free-solution electrophoresis cannot generally be used for mass fractionation, and therefore is not useful for DNA sequencing applications [290]. In the presence of a sieving matrix, however, DNA mobility once again depends on the DNA length. The sieving matrix may be a gel such as polyacrylamide or agarose, or a polymer such as polydimethylacyrylamide (for an exhaustive review of sieving media, see Klepárník and Boc̆ek [291]).

A sieving matrix can be thought of as a network of pores of typical size b. DNA with a radius of gyration R_g « b must radically deform to electrophorese through such a network, forming (at low fields) a random chain. The motion of such DNA is called “reptation”, akin to the motion of an entangled polymer described by de Gennes [292], and is described mathematically by various reptation models, such as Biased Reptation (BRM) and Biased Reptation with Fluctuations (BRF) models [289, 293]. In these models, DNA is confined to a tube (made of connected pores) and undergoes biased diffusional motion in that tube.

Why does sieving work? Because it breaks the scaling between friction and driving forces. In its “tortured” (snake-like) conformation, the effective force on DNA F_eff ~ R_x, where R_x is the vector between the two DNA ends projected in the field direction. In weak fields, DNA behaves as a gaussian chain, and therefore R_x ~ N^1/2 [289, 293]. Meanwhile, the friction still scales as ξ ~ N, and so the velocity in the tube ν_curv = F_eff/ξ ~ N^−1/2. Projecting this velocity along the field direction yields the familiar result ν ~ N⁻¹.

At low field, the DNA indeed forms a Gaussian chain, to a good approximation. As the field increases, however, the DNA tends to orient along the field direction. In a strong field, the DNA is fully oriented, and mass fractionation is no longer possible because the effective force on DNA no longer scales as N^1/2, but as N, thus making the mobility μ independent of N. The same breakdown occurs as N increases, limiting the effective read length of sieving-based DNA sequencing techniques to ~ 1000 bp.

7.3. Nanopore electrophoresis

Over the last decade, DNA electrophoresis through a nanometer-sized pore (nanopore) has been extensively studied [294–296]. The device used in experiment usually contains two fluid chambers separated by a thin (tens of nanometers) membrane containing a nanopore. The membrane and nanopore may be biological [294, 297], such as a protein pore in a lipid membrane, or synthetic [298–300], such as a solid-state nanopore drilled in a thin silicon-nitride or silicon-oxide film. The confined geometry of a nanopore facilitates detection and identification of individual biological molecules [301]. Nanopores have been suggested as promising systems for realizing low-cost and high-throughput sequencing of DNA [280,281,302].

In nanopore electrophoresis, DNA is transported from one side of the membrane to the other by a transmembrane electric potential. The translocation events are detected and characterized by measuring the blockades of transmembrane ionic current [303,304]. If the size of the pore constriction is comparable to the diameter of the DNA molecule, the ionic current can be sensitive to the DNA’s nucleotide sequence [305, 306]. Other mechanisms for DNA sequence readout using nanopores have been suggested, including electron tunneling current and local electrostatic potential measurements [307–310]. In general, DNA translocation through nanopores is a found to occur more slowly than one might naïvely expect based on its charge and the magnitude of the electric field [311]. Thus, quantitative characterization of the force experienced by DNA in a nanopore is critical to understanding the microscopic mechanics of the DNA transport.

7.3.1. effective driving force on DNA in a nanopore

The effective force on DNA in a nanopore was measured directly by trapping one end of the DNA molecule with optical tweezers while the other end of the molecule was subject to an electric field in a nanopore [312]. The measurements revealed scaling of the effective force F with the electrostatic field E, i.e., F = Q_eff E, where the scaling factor Q_eff , also known as the DNA’s effective charge, was found to be about 25% of the DNA’s bare charge Q. However, the interpretation of these measurements was ambiguous. On the one hand, the measurements are in perfect agreement with the Manning condensation theory [37] that predicts a 76% reduction of the DNA charge arising from the electrostatic field of counterions that condense near the DNA surface. Such interpretation neglects solvent as a possible source of the effective screening and assumes that the fraction q^* of the DNA charge that is not screened by the electrostatic field of the condensed counterions is the effective charge that determines the effective force. On the other hand, theoretical and experimental studies of DNA electrophoresis suggested that hydrodynamic drag is an important factor influencing DNA transport [285,313]. The importance of hydrodynamic interactions between DNA and the solvent inside a solid-state nanopore was pointed out by S. Ghosal [314, 315].

To determine the microscopic origin of the effective driving force acting on DNA in a nanopore, Luan and Aksimentiev performed all-atom MD simulations of a mechanically tethered DNA molecule subject to an electric field in a nanopore. [316]. Figure 14a illustrates a typical setup of the MD simulation: a DNA fragment subject to an electric field is confined in a cylindrical channel, cut from a Si₃N₄ crystal. Mimicking the action of optical tweezers, a harmonic potential (a virtual spring of a spring constant k) is attached to the center of mass of the DNA fragment. Subject to the applied electric field, the DNA initially drifts opposite the field direction, Figure 14b, until the force of the restraining potential balances the effective driving force of the electric field. Repeating the simulations at several values of the applied potential reveals the dependence of the effective electrophoretic force on the electric field strength, Figure 14c. For the particular nanopore geometry considered in the study, the simulations revealed a linear dependence of the effective forces F on the applied electirc fields E. The effective DNA charge determined as the ratio of F to E was found to be ~25% of the nominal DNA charge, in apparent agreement with the Manning condensation theory. As shown below, such an agreement was coincidental.

Figure 14.

MD simulation of the effective force on DNA in a nanopore. (a) Simulation setup. Two strands of DNA are colored in purple and blue; K⁺ (tan) and Cl⁻ (cyan) ions are shown as spheres; water (green) is shown as a semitransparent surface. A mechanical tether force is applied to the DNA via a harmonic potential (a virtual spring). One end of the spring is fixed in space whereas the other end is attached to the center of mass of the DNA fragment. A uniform external electric field E is applied to the whole system. The DNA molecule is made effectively infinite by connecting the backbone to its image across the periodic boundary. (b) The restraining force versus the simulation time for several values of the applied electric field. The color of the lines corresponds to the color of the symbols in panel c. (c) The average effective force acting on DNA versus the nominal force of the electrostatic field QE, where Q is the nominal electrical charge of DNA. Figures were adapted from Ref. 316 with permission. Copyright 2008 by the American Physical Society.

Recent works [207, 315, 317] have clearly shown the prominent role of the electroosmotic flow in determining the effective force on DNA in a nanopore. Experimentally, measurements of the force on DNA in nanopores of different size showed that the effective charge is actually a decreasing function of pore radius [317]. Thus, the effective charge of DNA in a pore should also decrease as the pore radius increases. The following relationship was predicted theoretically by Ghosal [315] by solving the coupled Poisson and Stokes equations:

$${\mathit{Q}}_{\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{f}}\mathrm{=}{\mathit{F}}_{\mathrm{m}\mathrm{e}\mathrm{c}\mathrm{h}}\mathrm{/}\mathit{E}\mathrm{=}\mathrm{2}\mathit{\pi }\mathit{\epsilon }\mathit{L}\frac{\mathrm{ɸ}\mathrm{(}\mathit{\alpha }\mathrm{)}\mathrm{-}\mathrm{ɸ}\mathrm{(}\mathit{R}\mathrm{)}}{\ln \mathrm{(}\mathit{R}\mathrm{/}\mathit{\alpha }\mathrm{)}}$$ (14)

where L is the membrane thickness, ∈ is the dielectric constant of an electrolyte, a and R are respectively the radii of the DNA and nanopore, and Φ(a) and Φ(R) are ζ-potentials at DNA and pore surfaces, respectively. Finding potentials Φ(a) and Φ(R) numerically by solving the Poisson-Boltzmann equation, the experimental results [317] could be quantitatively reproduced using Eq. 14 with a constant offset.

Complementing the theoretical and experimental studies, MD simulations have elucidated the contribution of the electroosmotic flow to the effective force experienced by DNA in a nanopore [316]. Figure 15 illustrates the local velocity of water in a 3 nm diameter nanopore for three simulations setups. The first setup, Figure 15a, directly measures the effective electrophoretic force F_elec by balancing it with a tether force F_teth, just like in Figure 14a. Although the DNA fragment remains stationary, ionic current flows through the nanopore, dragging water molecules along. The resulting water flow has a parabolic profile, reaching zero at the surface of the DNA and the nanopore, Figure 15d (circles). In this particular simulation, the tether (spring) force is 118 pN and the applied electric field is 8 mV/Å In the absence of electric field, Figure 15b, DNA is pulled by a mechanical force of the tether with a velocity of 7 nm/ns; the pulling force (~118 pN) is balanced by the hydrodynamic friction. The flow profile (diamonds in Figure 15d) has a maximum of ~ 7 nm/ns at the DNA surface, implying no-slip flow. Subject to the electric field of 8 mV/Å and in the absence of the restraining force of the tether, the DNA moves in the direction opposite to the direction of the field with an average velocity of −7 nm/ns. The solvent flow (triangles in Figure 15d) has the same velocity near the DNA surface as the DNA fragment.

Figure 15.

Electroosmotic screening of the DNA charge. (a) A stationary DNA fragment is subject to a restraining force Fteth and an electrophoretic force Felec. (b) The DNA fragment is displaced through the nanopore with a constant velocity by a mechanical pulling force F_mech. (c) The DNA fragment is displaced through the nanopore by an electrophoretic force F_elec. (d) Water velocity as a function of radial position, calculated from all-atom MD simulations corresponding to the setups shown in panels a–c. The DNA surface is located at approximately 11 Å; the surface of the nanochannel is located at ~30 Å. A superposition (blue stars) of the flow profiles observed in mechanical pulling (cyan diamonds; panel b) and electrophoresis (black triangles; panel c) simulations reproduces the flow profile observed in the simulations of the effective electrophoretic force (red circles; panel a). Positive values of the water velocity corresponds to the upward direction in panels a–c. The data were taken from Ref. 316.

The results of the above simulations indicate that a stationary DNA subject to simultaneous action of mechanical and electric forces can be considered as a superposition of the electrophoretic motion (ν = μ E) and mechanical pulling (ν = F/ξ). Indeed, the superposition of the flow profiles produced by the electrically and mechanically driven motions of DNA (stars in Figure 15d) reproduces the flow profile observed when DNA is held stationary by the simultaneous action of the electrophoretic and tether forces. From the relation of superposition

$$\mathit{F}\mathrm{=}\mathit{\xi }\mathit{\mu }\mathit{E}$$ (15)

where ξ is the friction coeffcient and μ is the electrophoretic mobility [316]. This relation was directly verified by MD simulations of the DNA’s electrophoretic and mechanical motion through nanochannels of different radii and different surface roughnesses [207]. Note that the above expression was previously derived [287] for DNA electrophoresis in a gel. Importantly, it allows for a more satisfying and illuminating expression for the effective charge of DNA:

$${\mathit{Q}}_{\mathrm{e}\mathrm{f}\mathrm{f}\mathrm{f}}\mathrm{=}\mathit{\xi }\mathit{\mu }$$ (16)

The two seemingly different expressions for the effective charge of DNA, Eq. 14 and Eq. 16, are consistent with each other, given that the friction coeffcient ξ and the electrophoretic mobility μ, derived from electrohydrodynamics equations [315,317], are

$$\mathit{\xi }\mathrm{=}\frac{\mathrm{2}\mathit{\pi }\mathit{\eta }\mathit{L}}{\ln \mathrm{(}\mathit{R}\mathrm{/}\mathit{\alpha }\mathrm{)}}$$ (17)

$$\mathit{\mu }\mathrm{=}\mathit{\epsilon }\frac{\mathrm{ɸ}\mathrm{(}\mathit{\alpha }\mathrm{)}\mathrm{-}\mathrm{ɸ}\mathrm{(}\mathit{R}\mathrm{)}}{\mathit{\eta }}$$ (18)

where η is the viscosity of the electrolyte. With explicit expressions for ξ and μ, the equivalence of Eq. 14 and Eq. 16 becomes obvious.

7.3.2. DNA translocation through charged nanopore

The effect of the hydrodynamic flow on the effective charge of DNA is even more dramatic in a charged nanopore because of the additional electroosmotic flow that develops near the charged nanopore surface. Luan and Aksimentiev have showed that the surface charge density can regulate the electrophoretic mobility of DNA [318]: lowering the surface charge reduces the effective electrophoretic force and hence the electrophoretic mobility. When the surface charge density is positive, the induced electroosmotic flow near the pore surface moves in the same direction as DNA, increasing the effective force on and the translocation velocity of DNA, in comparison to an uncharged pore, see Figure 16. When the surface charge density is negative, the induced electroosmotic flow near the pore surface acts against the electrophoretic force, reducing the DNA translocation speed. Further decreasing the surface charge density can even reverse the direction of the electrophoretic force, Figure 16. Consequently, the effective electrophoretic charge of DNA is also a function of the nanopore surface charge density [318]. Because the nanopore surface serves as a boundary of the hydrodynamic flow, other surface properties, such as roughness and hydrophobicity, can affect the flow profile and thereby the effective charge of DNA in a nanopore.

Figure 16.

The effective force acting on a DNA fragment in a solid-state nanochannel of surface charge density σ. The force was measured using a setup similar to that shown in Figure 14a. The data were taken from Ref. 318.

7.3.3. Slowing down DNA transport in LiCl

DNA translocation experiments in the Cees Dekker group at TU Delft revealed an unexpected phenomenon: the size, not the charge, of cations was found to affect the DNA translocation velocity through a nanopore [319]. specifically, the transport of DNA was found to be slower when DNA was surrounded my smaller monovalent cations (at the same cation concentration). Such a phenomenon could not be explained by continuum modeling as the size of cations is not taken into account by the theory.

MD simulations illustrated in Figure 17 determined the microscopic origin of this phenomenon [319]. A the same bulk ion concentration, the instantaneous number of Li⁺ , Na⁺, or K⁺ ions bound to the surface of DNA was found to be the same. Consequently the total charge of the surrounding solvent is the same regardless of the ion type and hence the force driving the electro-osmotic flow. However, the duration of the transient bound state between cations and DNA was found to sensitively depend on the type of cations: the bound state formed by Li⁺ lasted, on average, longer than the bound state formed by Na⁺ and the latter were found to be longer than the bound state formed by K⁺. Using a simplified model, Figure 17b, its was demonstrated that such a change in bond strength could indeed affect the force transmitted from ion to DNA, producing better effective neutralization of the DNA charge and hence reducing the velocity of DNA transport through a nanopore.

Figure 17.

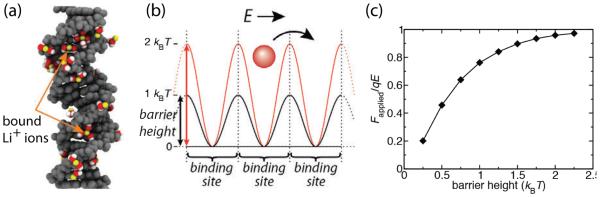
The type of monovalent ions affect the translocation velocity of DNA. (a) A snapshot from an MD simulations illustrating binding of Li⁺ ions to dsDNA. DNA is shown in gray, lithium is shown in yellow, and water is shown in red and white. Only those water molecules involved in the lithium-DNA bonds are shown. (b) A toy model describing ion binding to DNA. Red and black lines schematically represent 1D potentials describing affinity of two different cations to DNA. The depth of the free-energy minima are the same and so is the instantaneous number of ions bound to DNA. The barrier for hopping between the adjacent sites along DNA varies with the ion size and so is the strength of the bond. (c) The barrier height (the strength of the cation-DNA bond) affects the effective charge of DNA. The effect of water flow is neglected in this model. Adapted with permission from Ref. [319]. Copyright 2012 American Chemical Society.

7.3.4. Electrophoretic charge inversion

Motion of a charged object in electric field in vacuum can serve as a measure of the object’s electric charge. In the case of DNA in electrolyte solution, interpretation of such measurements is not straightforward. At the very least, measurements of the direction of the electrophoretic motion can be used to detect the inversion of the DNA’s effective charge. Indeed, by measuring the electrophoretic mobility of DNA, Besteman et al. concluded that charge inversion could occur when DNA was surrounded by spermine ([C10N4H30]⁴⁺) and cobalt sepulchrate ([CoC12H30N8]³⁺) counterions, and not by two other types of trivalent cations [320]. Strictly speaking, the above experiments have only shown the inversion of the effective electrophoretic charge of DNA.

Using the MD method, Luan and Aksimentiev [182] demonstrated inversion of the electrophoretic mobility of dsDNA in the presence of spermine(4+) and spermidine(3+) counterions, Figure 18. These simulations were already described in Section 4.2.4 when inversion of the DNA’s electrical charge was discussed. When the amount of spermidine molecules was just enough to neutralize the DNA charge, the DNA was observed to move in the direction opposite to the direction of the electric field, Figure 18. By increasing the number of spermidine cations the direction of the electrophoretic motion could be reversed. The study has also unequivocally shown that inversion of the DNA’s electric charge (measured using the Gauss law, Section 4.2.4) is not equivalent to inversion of the DNA’s electrophoretic charge (indicated by the direction of the DNA’s motion) [182]. The electric charge inversion is related to the ionic screening within the plane perpendicular to the DNA duplex and thus is insensitive to the action of an external electric field directed parallel to the DNA helical axis. Inversion of the DNA’s electrophoretic charge is conditioned by both direct binding of counterions to DNA and the electroosmotic effect, which in turn depends on the boundary condition for the electroosmotic flow.

Figure 18.

Reversal of the electrophoretic motion of DNA in a multivalent electrolyte. (a) Setup of MD simulations. The two strands of a DNA duplex are shown using a molecular surface representation, spermidine molecules directly bound to the grove of DNA are shown using vdW spheres, spermidine molecules dissolved in solution are shown using a ball-and-stick model. Subject to electric field, the DNA molecule moves through the nanochannel (gray molecular surface). (b) Center-of-mass displacement of the DNA duplex versus simulation time at three different concentrations of spermidine counterions. The data were taken from Ref. 182.

8. Concluding remarks

The steady advancement of scientific computing leaves no doubt that atomistic MD simulations will play a major role in the future development of the nucleic acids research field. Although several challenges lie ahead with regard to improvement of the molecular force field and sampling of the conformational space, it has already become clear that MD simulations can not only compliment experiment but make testable predictions and lead development in the field. Exciting opportunities await in combining single-molecule experiment with atomistic simulations to uncover the physical mechanisms that biological cells use to store, transcribe, duplicate and repair DNA. Atomistic simulations will allow exploration of DNA nanostructures for a variety of applications, from advanced materials to drug delivery. For the physics community, atomistic simulations of DNA are expected to firmly link theory to experiment, leaving no room for interpretation.

Figure 2.

Nucleic acid systems that represent the range of scales amenable to various computational and theoretical methods. From left to right, generally increasing in number of nucleotides: (a) Base-stacking interactions can be studied through quantum mechanics calculations, and reveal asymmetric van der Waals radii [47]. Adapted with permission from Ref. 47. The all-atom MD method with explicit or implicit solvent provides a balance between computational speed and descriptive detail. This method can be used to study systems ranging from a few nucleotides to (b) several turns of DNA [48] to (c) hundreds nucleotides as in the nucleosome [49]. (d) A large multi-layer, curved DNA origami construct described by MD simulation with explicit solvent [50]. Coarse-grained simulations can describe DNA with a wide range of detail, from near atomic (e.g. to describe (e) a plectoneme [51]) to many nucleotides per site (e.g. to describe (f) the packaging of a virus [52]). The two dominant polymer models of DNA are (g) the wormlike chain (WLC) model [9], and the freely jointed chain (FJC) model [7, 8]. The WLC model describes DNA under tension better than FJC, but FJC is convenient for very coarse descriptions of DNA, (h) such as at the level of chromatin [53]. Panels adapted with permission from (a) Ref. 47, (b) Ref. 48, (d) Ref. 50, (e) Ref. 51, (f) Ref. 52, and (h) Ref. 53.