How much information can be obtained from tracking the position of the leading edge in a scratch assay?

Abstract

Moving cell fronts are an essential feature of wound healing, development and disease. The rate at which a cell front moves is driven, in part, by the cell motility, quantified in terms of the cell diffusivity D, and the cell proliferation rate λ. Scratch assays are a commonly reported procedure used to investigate the motion of cell fronts where an initial cell monolayer is scratched, and the motion of the front is monitored over a short period of time, often less than 24 h. The simplest way of quantifying a scratch assay is to monitor the progression of the leading edge. Use of leading edge data is very convenient because, unlike other methods, it is non-destructive and does not require labelling, tracking or counting individual cells among the population. In this work, we study short-time leading edge data in a scratch assay using a discrete mathematical model and automated image analysis with the aim of investigating whether such data allow us to reliably identify D and λ. Using a naive calibration approach where we simply scan the relevant region of the (D, λ) parameter space, we show that there are many choices of D and λ for which our model produces indistinguishable short-time leading edge data. Therefore, without due care, it is impossible to estimate D and λ from this kind of data. To address this, we present a modified approach accounting for the fact that cell motility occurs over a much shorter time scale than proliferation. Using this information, we divide the duration of the experiment into two periods, and we estimate D using data from the first period, whereas we estimate λ using data from the second period. We confirm the accuracy of our approach using in silico data and a new set of in vitro data, which shows that our method recovers estimates of D and λ that are consistent with previously reported values except that that our approach is fast, inexpensive, non-destructive and avoids the need for cell labelling and cell counting.

1. Introduction

Moving cell fronts are key features of tissue repair [1] and tumour spreading [2]. The rate at which the front of a population of cells moves is influenced by the rate at which individual cells within the population migrate and proliferate [3]. Random, undirected cell migration is typically quantified in terms of the cell diffusivity D, whereas cell proliferation is quantified in terms of the proliferation rate λ. Developing methods to estimate D and λ from experimental observations is important so that we can assess the effectiveness of intervention strategies which often aim at influencing either D or λ [4,5]. For example, drugs such as mitomycin-C, which inhibit proliferation [4], are used to reduce tumour spreading [5], whereas steroid treatment, which stimulates cell migration [6], is often studied with the aim of enhancing wound healing.

Scratch assays [7–10], also known as scrape or wound-healing assays [9,10], are routinely used to investigate the motion of cell fronts by creating a scratch in a cell monolayer and observing the motion of the cell front. Images of the front are captured over a period of time that is typically less than 24 h [7,11,12]. Use of short-time-scale experimental data is very common because it avoids the need for replenishing the nutrients in the assay. There are various ways that data from a scratch assay are reported and analysed. The most common method is to present a qualitative, visual comparison between a control assay and another assay where some treatment has been applied. This kind of data is often presented without any attempt to estimate D or λ. For example, Teppo et al. [9] presented scratch assay data showing that hypoxia increased the rate at which the fronts of cancer cells moved, but they did not determine how the hypoxic conditions affected D and/or λ.

Another approach to analyse scratch assays is to use a mathematical model, such as the Fisher–Kolmogorov equation [13] or an extension of this reaction–diffusion equation [14–17] (electronic supplementary material). Some previous studies have focused on matching the experimental front speed with the long-time asymptotic travelling wave speed of the Fisher–Kolmogorov equation, 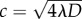[18–20]. Unfortunately, this approach is of little practical use for most experiments which are conducted over short time scales where no such travelling wave forms [7,11,12]. Another way of analysing scratch assays is to generate cell density profiles which can be matched to numerical solutions of a reaction–diffusion equation [3,21,22]. Unfortunately, this approach is expensive and time consuming because it requires some kind of direct or indirect cell counting technique to construct the density profiles. Other mathematical models have been used to interpret scratch assays, such as mechanistic [23] and biased continuum models [24]. However, the experimental procedures required to parametrize these models are time consuming because they involved individual cell counting [23] or individual cell tracking [24].

The simplest and most cost-effective measurement that can be made to characterize a scratch assay is to record the location of the cell front as a function of time [8,11,25]. The widespread availability of automatic edge detection algorithms [26,27] means that it is straightforward to obtain this information. Given that most scratch assays are conducted for short time periods, here we seek to determine whether it is possible to reliably estimate D and λ from short-time leading edge data alone without constructing cell density profiles [3,21,22]. To explore this question, we use automatic edge detection algorithms to analyse a discrete model of collective cell spreading driven by cell migration and cell proliferation [28]. While such models have been used to analyse various types of in vitro assays previously [21,29], these studies have not focused on short-time leading edge data. Our work shows that great care must be taken when interpreting short-time leading edge data because the most straightforward model calibration approach indicates that there are many choices of D and λ which lead to indistinguishable leading edge data. To overcome this, we develop a novel method by dividing the leading edge time-series data into two intervals allowing us to estimate D from the first time interval, and then we separately estimate λ using the second time interval. We test the method using both in silico and in vitro data showing that we recover estimates of D and λ that are consistent with previously reported results obtained using far more complicated experimental procedures.

This article is organized in the following way. In §2, we describe a discrete model for simulating the motion of cell fronts. Section 2 describes the image analysis and experimental procedure. Data in §3 show that a straightforward model calibration procedure implies that there are many choices of D and λ that match short-time leading edge data. As a result, we also describe, in §3, a modified method that leads to unique estimates of D and λ, and we validate our results using both in silico and in vitro data. Finally, in §4, we discuss our results and outline options for extending the work.

2. Material and methods

2.1. Experimental method

The experimental method has been presented previously [3]. Briefly, murine fibroblast 3T3 cells [30] were grown in T175 cm² tissue culture flasks and 1 μl of cell suspension was placed into the well, with diameter 15.6 mm, of a tissue culture plate. The tissue culture plate was incubated at 37°C and 5% CO₂ until the population became confluent. A scratch was made in the monolayer using a P1000 pipette tip (Lab Advantage, Australia). Images were recorded at t = 0, 3, 6, 9, 12 and 24 h, and a schematic illustration of the assay at t = 0 is given in figure 1a.

Figure 1.

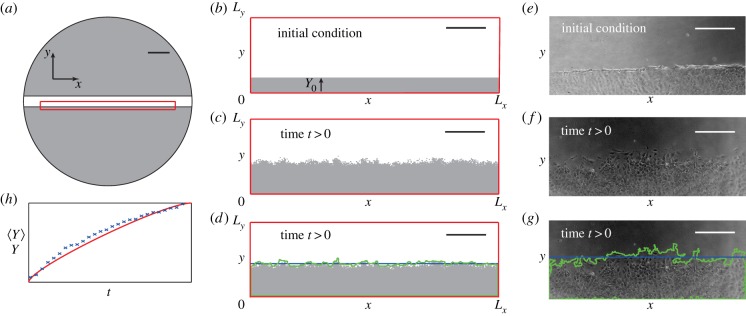
Schematic illustrating the initial scratch in the cell monolayer, simulation and leading edge data. (a) Monolayer of cells (grey) immediately after the scratch (white) has been made. The red rectangle indicates the spatial region which we simulate. (b) The initial confluent cell monolayer (grey) has height Y₀ and the width L_x, corresponding to the width of the red rectangle in (a). The height of the domain L_y is chosen to be sufficiently large that the agents in the simulation never touch this boundary within the 24 h period of the simulation. (c) Simulation after time t. (d) The simulation results are analysed using the image analysis tools to detect the leading edge (green) which is used to estimate the average position of the leading edge (blue). Scale bars in (a–d) are 2 mm. (e) Typical experimental image immediately after a scratch has been made. To illustrate the edge detection algorithm, we show in (f) an experimental image and in (g) the detected leading edge (green) and the average position of the front (blue). Scale bars in (e–g) are 400 µm. (h) Typical temporal evolution of the position of the leading edge for experimental data (blue crosses) and averaged simulation data (red).

2.2. Mathematical model

We consider a lattice-based random walk model on a two-dimensional square lattice, with lattice spacing Δ [28,31]. Each site may be occupied by, at most, one agent, and each simulation contains a total of Z(t) agents which have the ability to move and proliferate, with probability 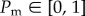and 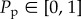, respectively, during each time step of duration τ. We make the standard assumption that P_m and P_p are constants, which are related to D and λ by

2.1

which means that we can view the parameters (P_m, P_p) as being interchangeable with (D, λ). During each time step Z(t), agents are chosen, at random, one at a time, and given the opportunity to move [28]. An agent at (x,y) will attempt to step to (x ± Δ, y) or (x, y ± Δ), with the target site chosen with equal probability. After Z(t) potential motility events have been attempted, an additional Z(t) agents are selected, at random, one at a time, and given the opportunity to proliferate. A proliferative agent at (x,y) will attempt to place a daughter agent at (x ± Δ, y) or (x, y ± Δ), with the target site chosen with equal probability. Potential motility and proliferation events will only succeed if the target site is vacant, otherwise the event is aborted. Implicitly, this means that individual agents in crowded regions will be relatively immobile and unable to proliferate, whereas uncrowded agents will behave differently and will have a greater opportunity to move and proliferate. The continuum-limit description of this model is a generalization of the Fisher–Kolmogorov equation in two dimensions [28] (electronic supplementary material). This description is valid only when the ratio P_p/P_m is sufficiently small [28,32].

We apply this model to mimic the geometry of the scratch assay. In all results, we set Δ = 25 µm, corresponding to a typical cell diameter [3,33]. The simulation domain, shown in figure 1b, is 0 ≤ x ≤ L_x and 0 ≤ y ≤ L_y. We choose L_x = 12.5 mm so that our domain captures almost the entire population within the well without directly simulating the curved boundaries. Although it is possible to simulate such curved geometries [3,33], we neglect these details here because our experimental data, described in §3.3, focus on several rectangular subregions within the well, away from the circular boundary. We choose L_y = 3.75 mm which is sufficient to ensure that agents in simulations never reach the boundary, y = 3.75 mm, during the 24 h simulation period. Symmetry conditions are applied along the lines x = 0, x = L_x, y = 0 and y = L_y. To match our experimental conditions, agents are initially placed on the lattice so that the region y < Y₀ is confluent. All simulation data are presented for a particular choice of τ, and we re-simulated all results with smaller values of τ to ensure our results are insensitive to τ.

The results in this work could have been generated using a lattice-free model [34,35]. Instead, we chose a lattice-based model because lattice-free models with crowding effects are far more computationally expensive [34,35]. Furthermore, our recent work showed that lattice-based and lattice-free models produce equivalent data at the leading edge [34,35] which means that there is no advantage in using a lattice-free model here if we are focusing on leading edge data.

2.3. Image analysis

We use Matlab's Image Processing Toolbox to estimate the position of the leading edge from the experimental and modelling images. The experimental image is imported and converted to greyscale using imread and rgb2gray, respectively. The simulation data are converted from a matrix representing occupied and vacant sites into a greyscale image using mat2gray. Henceforth, the procedure for analysing the experimental images and simulation data is identical. Edges are detected using edge with the Canny method [36] and a threshold between 0.04 and 0.1. Detected edges weaker than the threshold are ignored. Remaining edges are dilated, using imdilate, by a stretching element, defined using strel, with a square element of size seven. Any remaining vacant spaces are filled, using imfill, after which the dilation was reversed by eroding the image with the stretching element, defined previously, using imerode. The edges within the image were smoothed using medfilt2, and the area enclosed by the leading edge estimated using regionprops. For illustrative purposes, this algorithm was applied to the simulation data in figure 1c and the detected edge is superimposed in figure 1d. To estimate the vertical position of the leading edge, Y, we use

2.2

where A is the area enclosed by the detected leading edge. The average position of the leading edge, Y, is superimposed in figure 1d. To estimate how Y changes with time, we repeat the process at many time points and subtract the initial position to give a measure of the net displacement of the leading edge as a function of time. Schematic results in figure 1h indicate how the net displacement of the leading edge evolves with time for a representative set of experimental and averaged simulation data. We acknowledge that the edge detection could have been performed with ImageJ rather than Matlab. For this work, we chose to use Matlab because our previous comparison of Matlab and ImageJ edge detection algorithms showed that Matlab allows greater flexibility in the choice and control of threshold and dilation parameters [26].

3. Results

In this work, we will generate, and refer to, two distinct types of data: experimental data and averaged simulation data. The differences between these types of data can be described as follows:

• — Experimental data. Describes the position of the leading edge as a function of time obtained from a single experiment. Furthermore, we consider two different ways of generating experimental data:

  • (i) In vitro experimental data. Corresponds to data from experimental images.
  • (ii) In silico experimental data. Corresponds to data from discrete simulation images.

• — Averaged simulation data. Describes the average position of the leading edge, where the average has been constructed using data from many identically prepared realizations of the discrete model, that is, simulations performed with an identical algorithm, initial condition and parameters.

We construct the averaged simulation data using

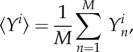3.1

where 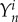is the position of the leading edge, at time step i, in the nth identically prepared realization and M is the total number of identically prepared realizations. To measure the differences between different sets of experimental data and averaged simulation data, we define

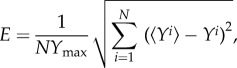3.2

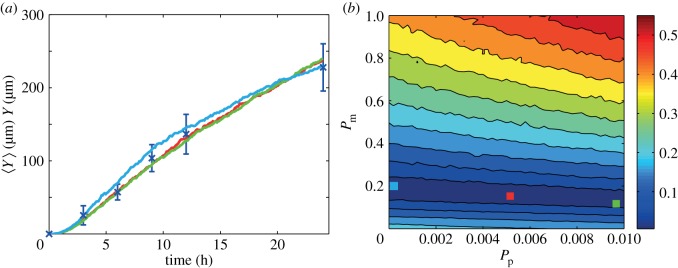
where 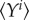is the position of the leading edge, at time step i, using averaged simulation data, Yⁱ is the position of the leading edge, at time step i, using experimental data, N is the number of time steps and Y_max is the maximum value of Yⁱ, for i = 1, 2, 3, …, N.

3.1. Naive parameter recovery

To explore whether it is possible to reliably estimate D and λ from short-time leading edge data, we first analyse a representative set of in silico experimental data corresponding to (P_m, P_p) = (0.5, 5 × 10⁻³), with Δ = 25 µm, which is reported in figure 2a. We note that it is difficult to draw specific conclusions by a simple visual inspection of this dataset, with the exception that it appears that the front speed is not constant over this time interval. To analyse this data, we generate a suite of averaged simulation data, sampling 2601 equally spaced parameter combinations within the region P_m ∈ [0, 1], P_p ∈ [0, 0.01], and we present a contour plot of E, given by equation (3.2), in figure 2b. We expect that if there is a unique choice of D and λ that matches the data in figure 2a, we would see a unique minimum on the E surface. Instead, we observe a relatively large, flat region, within which E takes on small, indistinguishable, values. This region extends right across this portion of the parameter space, indicating that there are many combinations of D and λ which match the experimental data equally well. To demonstrate that our observations for this parameter set hold more generally, we repeated the process focusing on in silico experimental data with a higher proliferation rate and found similar results (electronic supplementary material).

Figure 2.

Comparison of in silico experimental data and averaged simulation data. (a) Leading edge in silico experimental data correspond to (P_m, P_p) = (0.5, 5 × 10⁻³) (blue crosses). Data are presented at every 20th time step. (b) Contour plot of E (equation (3.2)) measuring the difference between the in silico experimental data and averaged simulation data within the region P_m ∈ [0, 1], P_p ∈ [0, 0.01]. Simulation parameters are M = 10, Y₀ = 750 µm, Δ = 25 µm and τ = 0.09191 h, with a final time of 24 h. The contour plot of E was generated by considering 2601 different parameter combinations; 51 equally spaced values of P_m, and 51 equally spaced values of P_p. The light blue, green and red coloured squares in (b) correspond to three different parameter combinations: (P_m, P_p) = (0.6, 1.4 × 10⁻³), (0.46, 8.8 × 10⁻³) and (0.5, 5 × 10⁻³), respectively. Averaged simulation data from these three different parameter combinations are superimposed in (a), showing that all three parameter combinations lead to indistinguishable short-time leading edge data. All averaged simulation data are insensitive to τ.

To demonstrate the redundancy in the short-time leading edge data, we choose three different combinations of (P_m, P_p), highlighted in figure 2b, and we superimpose the corresponding averaged leading edge data on the experimental data in figure 2a. Comparing these datasets confirms that there are several parameter combinations which give indistinguishable short-time leading edge data. Furthermore, we found that any parameter combination within the dark blue region in figure 2b also gives averaged simulation data that matches the experimental data (not shown). These results indicate that short-time leading edge information should be treated with care because a standard model calibration procedure may not provide useful information.

3.2. Parameter recovery accounting for the separation of time scales

Our results in §3.1 imply that additional information needs to be incorporated into our parameter estimation procedure if we are to infer useful information from short-time leading edge data. Here, we make use of the fact that there is a large separation of time scales between cell proliferation processes and cell motility processes. Typical estimates of the cell doubling time are approximately 15–30 h [3,19], whereas the time scale of cell motility events is approximately 10–20 min [37]. This separation of time scales implies that the first part of the leading edge time-series data will be dominated by the influence of cell motility, and we can make use of this information by dividing our time-series data into two intervals: (i) t < T and (ii) t > T, where T is a time interval during which the motion of the leading edge is dominated by cell motility. Intuitively, we expect that T ought to be chosen to be much less than the cell doubling time, and we will discuss this choice in §3.3.

To make use of this separation of time scales, we estimate P_m and P_p iteratively as follows:

• — Step 1. Estimate P_m by considering experimental data for t < T, we set P_p = 0 and systematically vary P_m so that our averaged simulation data match the experimental data.

• — Step 2. Estimate P_p by considering experimental data for t > T, we set P_m to be the value found previously, and we systematically vary P_p so that our averaged simulation data match the experimental data.

• — Step 3. Re-estimate P_m by considering experimental data for t < T, we set P_p to be the value found in step 2, and we systematically vary P_m so that our averaged simulation data match the experimental data. Repeat steps 2 and 3 until both P_m and P_p converge.

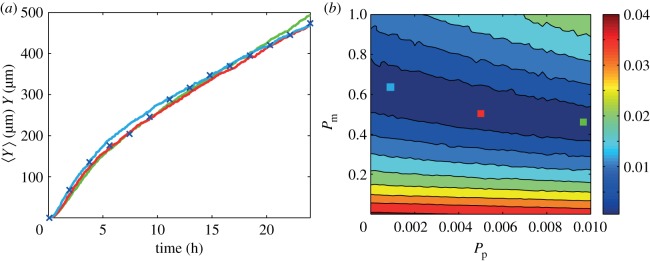
We now apply this method to in silico experimental data and then examine in vitro data in §3.3. Figure 3a shows same in silico experimental data presented previously in figure 2a. The results from estimating P_m using the iterative procedure are given in figure 3b and show that by choosing T = 3 h and focusing on the interval P_m ∈ [0, 1], we observe a relatively well-defined minimum in the plot of E indicating that we have P_m ≈ 0.48. The results from estimating P_p are given in figure 3c and show that with T = 3 h and P_m = 0.48, we observe a well-defined minimum in E indicating that we have P_p ≈ 5.6 × 10⁻³. We note that it took two iterations for P_m and P_p to converge. These parameter estimates are a great improvement on the results in §3.1 where we found it was impossible to distinguish between many different parameter combinations. We note that our parameter estimates do not precisely coincide with the expected values of P_m = 0.50 and P_p = 5 × 10⁻³, and there are two potential explanations for this. First, our in silico experimental data correspond to one realization of the discrete model which might not be representative of the expected behaviour we would observe when considering many identically prepared realizations. Second, when we generated the averaged simulation data, we only used a modest value of M = 10, and we expect that our estimate could be improved by increasing M. To further illustrate the robustness of our approach, we also applied it to data generated using several different parameter combinations, including some for larger proliferation rates, and we found that this method also gave reliable parameter estimates for these additional cases (electronic supplementary material).

Figure 3.

Parameter recovery for in silico experimental data using the iterative separation of time scales approach. (a) In silico experimental data, at every 20th time step, with (P_m, P_p) = (0.5, 5 × 10⁻³) (blue crosses). The vertical line represents T = 3 h. (b) Observing the minimum value of E (equation (3.2)) measuring the difference between the in silico experimental data and averaged simulation data for t < 3 h suggests that P_m is approximately 0.48. The averaged simulation data correspond to 51 equally spaced values of P_m in the interval P_m ∈ [0, 1], and P_p = 0. (c) E (equation (3.2)) measuring the difference between the in silico experimental data and averaged simulation data for 3 < t < 24 h. The averaged simulation data correspond to 51 equally spaced values of P_p in the interval P_p ∈ [0, 0.01] and P_m = 0.48, giving P_p ≈ 5.6 × 10⁻³. Simulation data were generated with M = 10, Y₀ = 750 μm, Δ = 25 μm and τ = 0.09191 h, with a final time of 24 h. P_m and P_p required two iterations to converge. All averaged simulation data are insensitive to τ.

Once we have obtained estimates of P_m and P_p, it is possible to re-examine the suitability of our choice of T. Our estimate of P_p indicates that the average time taken for an isolated agent to undergo a proliferation event is approximately 18 h, whereas our estimate of P_m indicates that the average time taken for an isolated agent to undergo a motility event is approximately 30 min. These time scales give a physical explanation for why our choice of T = 3 h is sufficient, because agents have plenty of opportunity to undergo motility events during the first 3 h of the simulation, whereas there is hardly any opportunity for proliferation to occur during this interval. To further demonstrate the robustness of our results, we repeated the process of estimating P_p and P_m using the data in figure 3a and found that we obtained excellent estimates of the parameters regardless of whether we chose T = 2, 3 or 4 h.

3.3. In vitro data

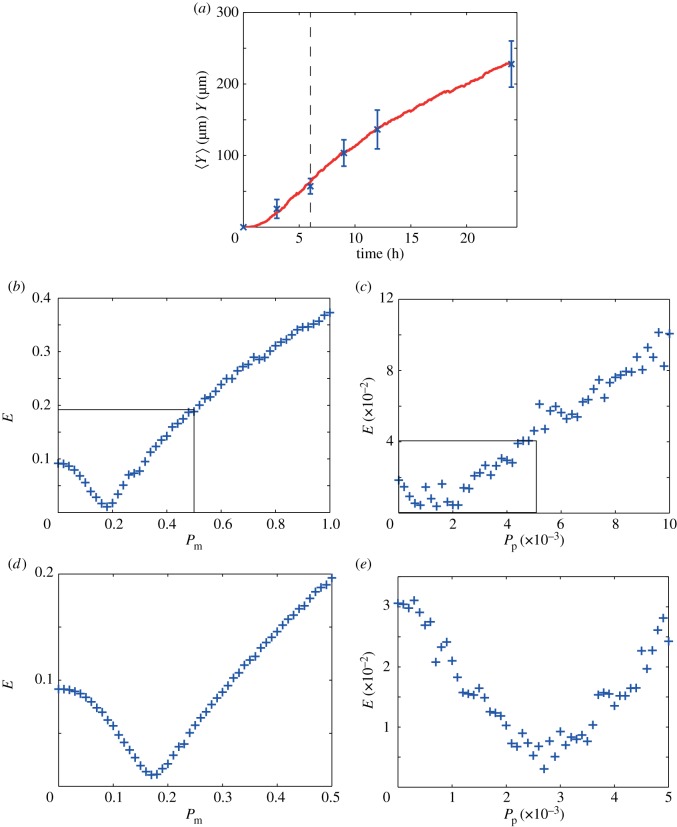
We obtained in vitro experimental data for a scratch assay using 3T3 fibroblast cells as described in §2.1. At each time point, we took four different images, at different spatial locations, in the scratch assay. The field of view in each image is approximately 2 mm wide and 0.8 mm high. The spatial location of the four sets of images is approximately evenly spaced along the edge of the scratch within the red rectangle in figure 1a. One set of such images, at t = 0, 12 and 24 h, is presented in figure 4a–c. An example of the results from the edge detection algorithm, applied to the image at t = 12 h, is illustrated in figure 4d–f. Results summarizing the average position of the leading edge as a function of time are given in figure 5a, and the original dataset from the four sets of images at all time points is given in the electronic supplementary material.

Figure 4.

Time evolution of a scratch assay with 3T3 fibroblast cells. Experimental images are shown at: (a) 0, (b) 12 and (c) 24 h. To illustrate the application of the edge detection algorithm, we show in (d) the image at 12 h and in (e) we superimpose the detected leading edge (red). (f) Detected leading edge (red) and the average position of the front (blue). Scale bar corresponds to 200 µm.

Figure 5.

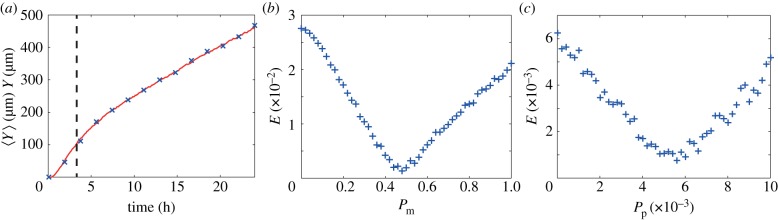
Comparison of in vitro experimental data and averaged simulation data. (a) Leading edge in vitro data (blue crosses) are presented with the error bars indicating 1 s.d. from the mean. (b) Contour plot of E (equation (3.2)) measuring the difference between the in vitro data and the averaged simulation data in the region P_m ∈ [0, 1], P_p ∈ [0, 0.01]. Simulation parameters are M = 10, Y₀ = 750 µm, Δ = 25 µm and τ = 0.09191 h, with a final time of 24 h. The contour plot of E was generated by considering 2601 different parameter combinations; 51 equally spaced values of P_m and 51 equally spaced values of P_p. The red, green and light blue coloured squares in (b) correspond to three different parameter combinations: (P_m, P_p) = (0.16, 5.4 × 10⁻³), (0.14, 9.6 × 10⁻³) and (0.2, 2 × 10⁻⁴), respectively. Averaged simulation data from these three different combinations are superimposed in (a), showing that all three parameter combinations lead to indistinguishable short-time leading edge data. All averaged simulation data are insensitive to τ.

We first apply the naive parameter recovery method, described in §3.1, where we consider the difference between our in vitro experimental data were averaged simulation data using the entire time series of leading edge data. The averaged simulation data were generated using 2601 equally spaced parameter combinations within the region P_m ∈ [0, 1], P_p ∈ [0, 0.01]. Results in figure 5b show a contour plot of E, defined by equation (3.2), which confirms that there is a large region within the parameter space for which the short-time leading edge data are indistinguishable. To confirm that multiple parameter combinations match the in vitro experimental data, we consider three distinct parameter pairs, highlighted in figure 5b, and superimpose the corresponding averaged simulation data in figure 5a.

We now apply the approach described in §3.2 to our in vitro data choosing T = 6 h. Results in figure 6a show the averaged experimental data. A plot of E, given in figure 6b, constructed using 51 equally spaced values of P_m in the interval P_m ∈ [0, 1], with P_p = 0, indicates that the optimal value of P_m is approximately 0.18. A plot of E, given in figure 6c, constructed using 51 equally spaced values of P_p in the interval P_p ∈ [0, 0.01], with P_m = 0.18, indicates that the proliferation parameter lies within the subinterval P_p ∈ [0, 5 × 10⁻³]. We now refine our parameter estimates by repeating the process and increasing the number of realizations used to generate the averaged simulation data from M = 10 to M = 50. Furthermore, we now focus our attention on the subintervals P_m ∈ [0, 0.5] and P_p ∈ [0, 5 × 10⁻³], highlighted by the rectangles superimposed on figure 6b,c. By repeating the parameter estimation process, we obtained the refined results shown in figure 6e,f, indicating that the optimal parameter pair is (P_m, P_p) = (0.17, 2.7 × 10⁻³), or (D, λ) ≈ (300 µm² h⁻¹, 0.03 h⁻¹). To quantify the uncertainty in our estimates, we repeated the same process using the mean experimental data ±1 sample standard deviation of the experimental data. This gave P_m = 0.17 (0.14−0.20) and P_p = 2.7 × 10⁻³ (1.6 × 10⁻³ − 3.5 × 10⁻³), where the ranges in the parentheses indicate an estimate of the uncertainty. Our estimates of P_m and P_p were obtained using just one iteration.

Figure 6.

Parameter recovery for in vitro data using the separation of time scales approach. (a) In vitro data (blue crosses) showing the average position of the leading edge with the error bars denoting 1 s.d. from the mean (see the supplementary material for the original dataset). The vertical line indicates T = 6 h. (b) Plot of E (equation (3.2)) measuring the difference between the in vitro experimental data and averaged simulation data for t < T with P_p = 0. The plot of E was generated by considering 51 equally spaced values of P_m within the interval P_m ∈ [0, 1] and indicates that P_m is approximately 0.18. (c) Plot of E measuring the difference between the in vitro experimental data and the averaged simulation data for t > T with P_m = 0.18. The plot of E, generated using 51 equally spaced values of within the interval P_p ∈ [0, 0.01], indicates that the true value of P_p lies in the subinterval P_p ∈ [0, 5 × 10⁻³]. (d) Plot of E measuring the difference between the in vitro experimental data and the averaged simulation data for t < T with P_p = 0. The plot of E, generated using 51 equally spaced values of P_m within the subinterval P_m ∈ [0, 0.5], indicates that an improved estimate is P_m ≈ 0.17. (e) Plot of E measuring the difference between the in vitro experimental data and the averaged simulation data for t > T with P_m = 0.17. The plot of E, generated using 51 equally spaced values of P_p within the subinterval P_p ∈ [0, 5 × 10⁻³], indicates that the true value of P_p is approximately 2.7 × 10⁻³. Averaged simulation data showing the position of the leading edge with P_m = 0.17 and P_p = 2.7 × 10⁻³ are superimposed on the in vitro experimental data in (a). All simulation data correspond to Y₀ = 750 µm, Δ = 25 µm and τ = 0.09191 h. Results in (b,c) correspond to M = 10, while results in (d,e) correspond to M = 50. Our estimates of P_m and P_p required one iteration to converge. All averaged simulation data are insensitive to τ.

To explore whether our results are sensitive to our choice of T, we repeated the process using T = 9 h and found that this also gave (P_m, P_p) = (0.17, 2.7 × 10⁻³), or (D, λ) ≈ (300 µm² h⁻¹, 0.03 h⁻¹), indicating that our results are relatively insensitive to T. The reason for this insensitivity can be explained by considering the time scales implied by our parameter estimates. Our estimate of λ indicates that the average time required for an isolated cell to proliferate is approximately 34 h. In comparison, our estimate of D indicates that the average time taken for an isolated cell to undergo a motility event is approximately 30 min. This indicates that that either T = 6 or 9 h is appropriate because either of these time scales is sufficiently small relative to the proliferation time scale is well as being sufficiently large compared with the motility time scale. Averaged simulation data produced using (P_m, P_p) = (0.17, 2.7 × 10⁻³) are superimposed in figure 6a, confirming that the simulated leading edge data match the measurements. We note that our parameter estimates are consistent with Tremel et al.'s [22] previously reported estimates. However, we would also like to point out that our estimates of D and λ were obtained simply and inexpensively, using only short-time leading edge data, whereas Tremel's results were obtained by constructing cell density profiles and tracking individual cells, both of which are time consuming and expensive.

4. Discussion and conclusion

Moving cell fronts [7–10] play a key role in development, disease and tissue repair. The rate at which the cell front moves depends both on the motility and proliferation of individual cells within the population. Mathematical models can be used to interpret scratch assays, with some previous studies focusing exclusively on matching experimental estimates of the front speed with the long-time asymptotic wave speed of the travelling wave solution of the Fisher–Kolmogorov equation, 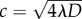[14]. This approach suffers from two limitations. First, travelling wave solutions require a large amount of time to develop, whereas most scratch assays are performed for short-time intervals. Second, even if large-time experimental data are available, this approach determines the product, λD, and not the values of λ and D separately [19,20]. Other methods for interpreting scratch assays have involved calibrating the numerical solution of a reaction–diffusion equation to observed cell density profiles [3,21,22] to provide estimates of λ and D. Unfortunately, this approach is expensive and time consuming since it requires either a direct or indirect method for counting individual cells to construct the cell density profiles.

In this work, we describe a different approach for analysing scratch assays relying only on determining short-time leading edge data. Our method can be implemented either for new experimental images or, retrospectively, using previously published images. The simplicity of our approach derives from the fact that we do not require any analysis or counting of individual cells. Using a discrete model of cell motility and cell proliferation, we show that care ought to be exercised when analysing short-time leading edge data because a straightforward model calibration procedure, whereby we match the entire time history of the position of the leading edge, reveals that there are many parameter combinations for which the short-time leading edge data from the model are equivalent. To overcome this, we make use of the fact that cell migration takes place on a short time scale compared with cell proliferation, and we introduce a new iterative method where we analyse the leading edge time-series data in two steps. First, we analyse the interval t < T, setting P_p = 0 in the model, to provide an estimate of P_m. Second, we analyse the time interval t > T, using our previously determined estimate of P_m, to provide an estimate of P_p. These two steps can be applied iteratively until our estimates converge to within some tolerance. Our approach relies on estimating some time, T, which is sufficiently large compared with the time scale of cell migration, yet is sufficiently small compared with the time scale of proliferation. We confirm our approach using both in silico and in vitro data, and we note that our estimates of D and λ for the in vitro data are consistent with previously published values for the same cell line in a similar experiment [22].

As we demonstrate, once the data have been analysed to produce an estimate of D and λ, we can test the sensitivity of our estimates to our choice of T. For our in silico data, we found that we obtained similar results regardless of whether we chose T = 2, 3 or 4 h. Similarly, for our in vitro data, where we had less experimental data points from which to choose T, we found that we obtained the same values for D and λ regardless of whether we chose T = 6 or 9 h.

Our parameter estimates for the in vitro data indicate that care should be taken when interpreting leading edge data with the long-time asymptotic wave speed expression for the Fisher–Kolmogorov equation [18–20]. Our parameter estimates for the in vitro data correspond to (D, λ) ≈ (300 µm² h⁻¹, 0.03 h⁻¹). While it is possible to use these parameters to estimate the speed of the travelling wave solution of the Fisher–Kolmogorov equation [18–20], this result is valid only in the long-time limit, t → ∞. As our experimental results have been reported over a time interval which is less than the doubling time, we expect that it is inappropriate to use such a result because there has been insufficient time for the travelling wave to form. Indeed, comparing the slope of the data in figure 5a with 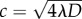, evaluated using our parameter estimates, confirms that these approaches give different estimates of the front speed.

Our approach of combining simulation data with automated leading edge analysis can be extended in several ways. One important point, not considered here, is that certain cells, such as melanoma [33] and glioma cells [37], exhibit significant cell-to-cell adhesion. To incorporate cell-to-cell adhesion, we could consider a different discrete model with an additional parameter controlling the adhesion strength [37]. Under these conditions, it would be interesting to explore whether the three parameters governing cell migration, cell proliferation and the strength of adhesion could be uniquely determined by short-time leading edge data. Alternatively, we could apply our model to scratch assays performed on different substrates [19,20] to analyse the effect of cell-to-substrate adhesion. Another approach may be to apply our model to narrow wounds, where cell proliferation is negligible or absent [38]. A further application of our model would be to analyse a series of scratch assays where we considered some control assay relative to a set of other assays where a chemical inhibitor or promotor has been applied. Our approach could be used to determine precisely how D and/or λ varies as a function of the concentration of the chemical, and therefore play a role in the design of intervention strategies aimed at manipulating the movement of cell fronts.