Reinitiation enhances reliable transcriptional responses in eukaryotes

Abstract

Gene transcription is a noisy process carried out by the transcription machinery recruited to the promoter. Noise reduction is a fundamental requirement for reliable transcriptional responses which in turn are crucial for signal transduction. Compared with the relatively simple transcription initiation in prokaryotes, eukaryotic transcription is more complex partially owing to its additional reinitiation mechanism. By theoretical analysis, we showed that reinitiation reduces noise in eukaryotic transcription independent of the transcription level. Besides, a higher reinitiation rate enables a stable scaffold complex an advantage in noise reduction. Finally, we showed that the coupling between scaffold formation and transcription can further reduce transcription noise independent of the transcription level. Furthermore, compared with the reinitiation mechanism, the noise reduction effect of the coupling can be of more significance in the case that the transcription level is low and the intrinsic noise dominates. Our results uncover a mechanistic route which eukaryotes may use to facilitate a more reliable response in the noisy transcription process.

1. Introduction

Transcription, or the synthesis of RNA from a DNA template, is one of the most important steps in gene expression. Given that gene expression plays a central role in almost all life processes, its reliability and precision are important to the functions of almost all living organisms and cells. Contrary to this perception, gene expression in single cells is an inherently stochastic process owing to the low number of present gene copies and the stochastic nature of the involved biochemical reactions. Mathematical modelling for stochastic gene expression began decades ago [1–3] to understand the noise and its regulation. In these pioneering works, based on simplified models, the authors analysed the protein distributions and the mechanisms for translation bursts, etc. However, owing to severe restrictions in the available experimental methods in those days, these insightful theoretical works could not be quantitatively verified by experiments and thus had not received much attention at that time. In recent years, this topic has gained renewed interests owing to rapid advances in experimental techniques that can now directly observe the real-time fluctuations of transcripts and proteins in individual live cells. In particular, the origins, consequences and control of noise have been investigated extensively, both theoretically and experimentally [4,5]. Many studies have revealed that transcriptional noise is an important source of the fluctuations in protein abundance [6]. On the other hand, some recent experimental studies have suggested that fluctuations in the chromatin state are a major source of noise in gene transcription/expression [7–9]. Therefore, it is of significance to understand how various types of promoter complexity, determined mainly by promoter states and the transitions between them, influence the amount of noise in the process of gene transcription.

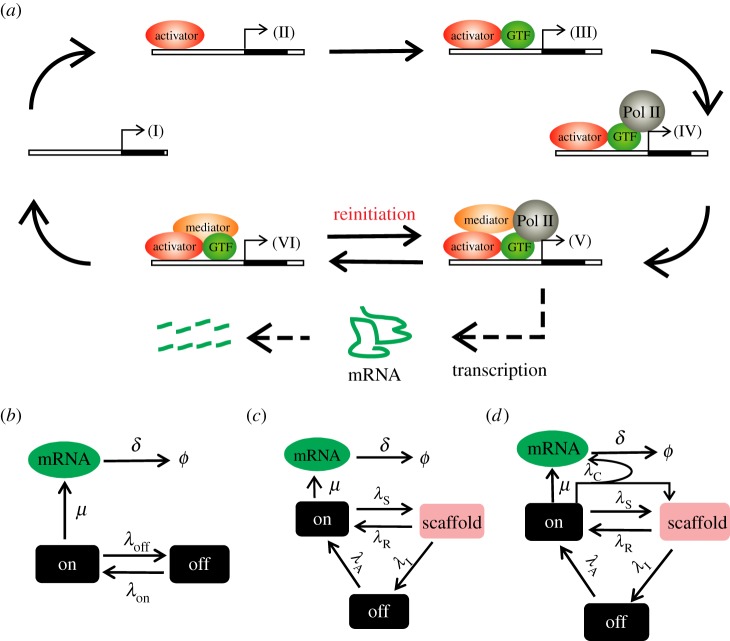
Although the general principles of transcription are conserved across species, the detailed transcriptional processes are highly gene specific [10]. In particular, the eukaryotic transcription machinery is more complex than the prokaryotic one [11,12] in many aspects such as RNA polymerase and promoter activation, which may lead to different noise properties in prokaryotic and eukaryotic transcriptions [13–15]. In particular, the transcription reinitiation, addressed by in vitro studies [16], is expected to play a fundamental role in eukaryotic transcription, and in many cases is a specific target of regulation [17]. In figure 1a [18], a general RNA polymerase II (Pol II)-mediated transcription process is summarized, which is described as a cyclic process and termed as a transcription cycle. In figure 1, the transition steps from (I) to (IV), namely the activation of the promoter from the inactive state is defined as initiation, whereas the process from (VI) to (V), namely the activation of the promoter from the intermediate scaffold is defined as reinitiation. Reinitiation has already been recognized and investigated as an important mechanism in early in vitro transcription studies [19,20]. Compared with transcription initiation in prokaryotes and eukaryotes, reinitiation, which is expected to occur predominantly in eukaryotes, can bypass some rate-limiting transition steps such as the binding of TFIID, so that it has a higher rate than transcription from initiation, and thus can facilitate high levels of transcription. Besides, the reinitiation scaffold also introduces novel regulatory mechanisms in eukaryotic transcription [19].

Figure 1.

Schematic illustration of transcription modelling. (a) Simplified sketch of polymerase II (Pol II)-mediated transcription (see [21] for details). First, the activator binds to the DNA at a specific promoter, then some general transcription factors (GTFs) bind before the recruitment of Pol II, which is followed by the association of the mediator. When mRNA production initiates, Pol II is released from the transcription complex, forming a scaffold which is capable of reinitiation until the whole complex falls off the DNA and finishes a transcription cycle. (b–d) General stochastic models for gene activation and transcription. Panel (b) is the two-state model: an active state (V, VI), which is capable of mRNA production, and an inactive state (I, II, III, IV). Panel (c) is a three-state model: an active state (V), an inactive state (I, II, III, IV) and the reinitiation scaffold (VI), where the mRNA production and the reinitiation scaffold formation are independent events. Panel (d) is another three-state model that takes the transcription coupling into account, which incorporates a new elementary reaction of simultaneous mRNA production and reinitiation scaffold formation. The rate constant for each step is indicated in the model. (Online version in colour.)

Although some in vivo experimental evidence is in conflict with the current reinitiation model in some aspects, investigation of the reinitiation mechanism established by in vitro studies can still help to deepen our understanding of a fundamental aspect of eukaryotic transcription. The conflict around the in vivo experimental evidence means that reinitiation is currently a controversial phenomenon, but also provides fascinating challenges for future in vitro transcription studies to bridge the in vivo and in vitro gap, which may include biochemical elucidation of possible new mechanisms, factors and conditions. As many studies have indicated, the slow transition between different promoter states is an important source of the noise in gene expression. The reinitiation mechanism, which mainly influences the transition between promoter states, is naturally expected to have an important influence on the transcriptional noise. Given that the impact of promoter states on the transcriptional/translational noise has been studied extensively [9,21–25], analysis on the reinitiation mechanism is not available yet. In this paper, we first proposed a new transcription model that incorporates the transcription reinitiation mechanism in eukaryotes, then by deriving the corresponding master equations and analysing the noise intensity in the mRNA abundance, we obtain two important conclusions (i) compared with a non-reinitiation model at the same transcription level, the reinitiation model always has a lower transcription noise intensity, and a higher reinitiation rate can not only reduce the transcription noise intensity independent of the transcription level, but also enables a more stable scaffold advantageous for noise reduction and (ii) the coupling between the scaffold formation and the mRNA transcription can further reduce the transcription noise intensity without influencing the transcription level. In summary, these results constitute a possible novel mechanism that may be used by eukaryotic cells to enable a reliable (or a low-noise) transcription in contrast to the prokaryotic cells. In addition to theoretical analysis, these conclusions are also supported by the stochastic simulations based on the Gillespie algorithm [26].

2. Model and methods

The real transcription process is rather complicated and may include thousands of factors and transition steps. To analyse such complex dynamics, it is necessary to formulate a simplified model that can properly summarize the essential events of the process. As introduced in the §1, the transcription models contain two central processes in general: the dynamic transitions between different states of the promoter, and the transcription of mRNA molecules. Other processes are implicitly included in effective rate constants. In a widely used transcription model known as the two-state model or random telegraph model (figure 1b) [1,3,14,27], the promoter has two states: an inactive state (‘off’ in figure 1b, corresponding to the states (I)–(IV) in figure 1a) and an active one (‘on’ in figure 1b, corresponding to the states (V)–(VI) in figure 1a). The promoter randomly switches between these two states, and when it is in the active state, mRNA is transcribed randomly with a certain rate. The mRNA molecules are degraded linearly after synthesis.

To begin our theoretical analysis, we first develop a new transcription model that incorporates the transcription reinitiation mechanism. To avoid complicated mathematics, we here adopt a minimum model (figure 1c), in which the promoter has three states: an inactive state (‘off’ in figure 1a, corresponding to the states (I)–(IV) in figure 1a), an active state (‘on’ in figure 1c, corresponding to (V) in figure 1a), and a reinitiation scaffold state (figure 1a (VI)). In this new model, the active and inactive states are similar to those in the two-state model, whereas the reinitiation scaffold is a new state, which can either return rapidly to the active state or further transit to the inactive state.

Let P_A, P_I and P_S represent the active state, the inactive state and the scaffold state of the promoter, M is the mRNA molecules and is the outcome of the mRNA degradation. The biochemical reactions of this model with the standard notation can be introduced as follows

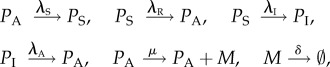where λ_S is the rate of scaffold formation, λ_A (λ_I) is the rate of gene activation (inactivation), λ_R is the reinitiation rate, μ is the transcription rate and δ is the mRNA degradation rate.

Let 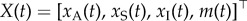, with x_A(t), x_S(t), x_I(t)∈ {0, 1} being the numbers of active, scaffold and inactive promoters, respectively, and 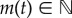the number of mRNA molecules at time t. Let 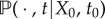be the probability distribution of X(t) for a given initial value X(t₀) = X₀. Now, for each 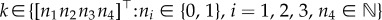, we can derive the master equation for mRNA transcription as follows [28,29]

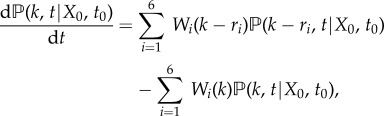2.1

where

with W_i(X(t)) being the rate of the ith reaction, and

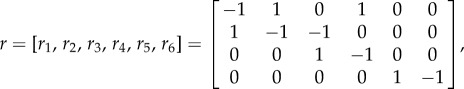with the jth element of r_i being the number change of the jth molecules due to reaction i.

Let denote the expectation of a random variable. From the theory in [29], we can obtain the following exact ordinary differential equations for the mean 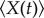, and the covariance 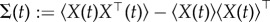from the master equation

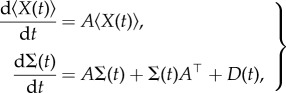where

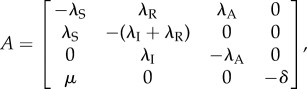and

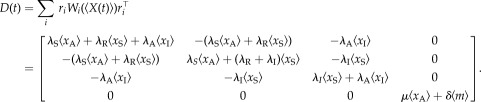At the stationary state, by setting 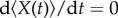and 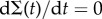, we can solve 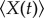and Σ(t), among which the mean and variance of the mRNA molecules are relevant to our analysis.

There are many kinds of noise indices, such as the Fano factor (the variance over the average), which equals one for Poisson distributions, the normalized variance (the variance over the squared average) and the coefficient of variation (the standard deviation over the average). In the following analysis, we adopt the normalized variance as the noise intensity. It should be noted that generally our results are not sensitive to the choice of metric of noise. Because the normalized variance is the squared coefficient of variation, they have the same monotonicity, and all the results are qualitatively true if we use the coefficient of variation as the metric. In addition, most of the results are obtained under a constant transcription level, so they are also qualitatively true for the Fano factor.

3. Results

By solving the set of equations for 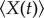and Σ(t) at the stationary state, we can analytically obtain the mean 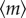and variance 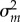in mRNA abundance [29] (see the electronic supplementary material) as follows

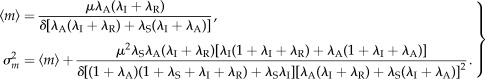3.1

Then, the stationary noise intensity 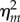, defined as the normalized variance in mRNA, 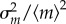, is given as follows:

3.2

3.3

Here, the first term in (3.2) is always referred to as ‘intrinsic noise’, whereas the second term ‘extrinsic noise’ in [6] indicates their deemed sources. From this result, it can be seen that the noise intensity increases with the mRNA degradation rate δ. However, this influence is qualitatively independent of other factors and not relevant to the topic of this paper. Thus, hereafter, we assume that all the parameters are normalized by the mRNA degradation rate δ (i.e. δ = 1, which is also assumed in the electronic supplementary material).

3.1. The influence of the reinitiation rate

By substituting 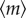into 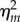with proper rearrangement of (3.2) (see the electronic supplementary material), we have

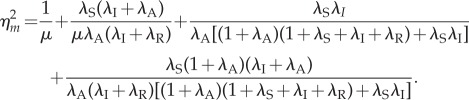It is clear that 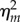is a decreasing function of the reinitiation rate λ_R. Hence, a higher reinitiation rate always results in a lower noise intensity independent of the other parameters. However, this observation is a little trivial given that a high reinitiation rate can increase the population and thus naturally reduces the relative fluctuations by some well-known results. To show that the noise reduction effect of reinitiation is more than such a trivial one, in the following we further compare our model with a non-reinitiation model at the same transcription level. For this purpose, we construct an equivalent model without reinitiation. By ‘equivalent’, we mean that these two models not only have the same transcription level, but also have the same states as well as the same parameters wherever possible. To obtain such a model, we apply a minimum modification to the model in figure 1c in the following way. We set the reinitiation rate λ_R = 0, and decrease λ_S, so that its transcription level is the same as that in the reinitiation model, and keep all the other states and parameters unchanged. In this way, we obtain an equivalent model without reinitiation but with a more stable active state, so that it has the same transcription level with the reinitiation model. This modification also coincides with the usual modelling strategy that assimilates the reinitiation scaffold into an active state. The noise intensity in this non-reinitiation model, denoted as 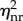, can be obtained by setting λ_R as 0 and the new λ_S as λ_Sλ_I/(λ_I + λ_R) in (3.2) (see the electronic supplementary material):

3.4

Here, the first term 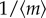is the same as that in (3.2) because they are of the same transcription level. Thus, we need to compare only the second terms in (3.2) and (3.4). After calculation, we have

where

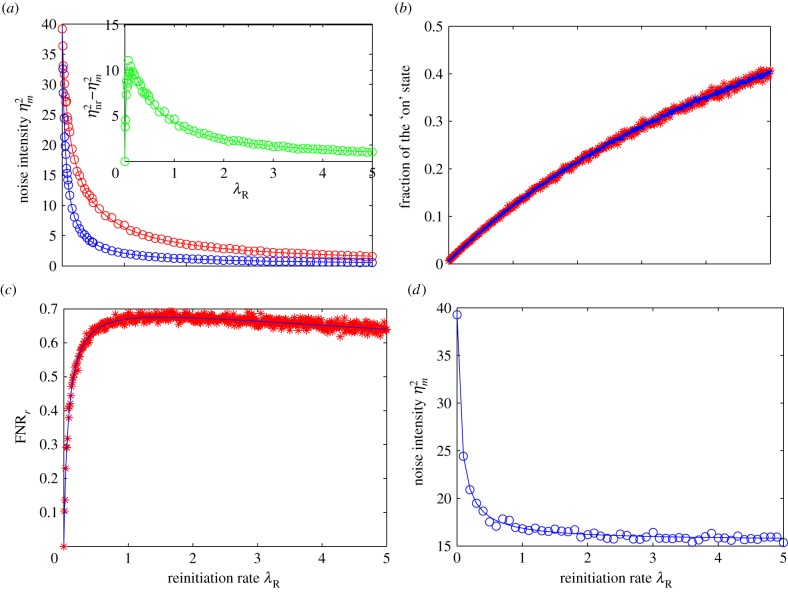
This indicates that reinitiation can reduce the transcription noise intensity independent of the transcription level as shown in figure 2a. From figure 2b, we can see that at each transcription level, the average fractional ‘on’ state in the reinitiation model is no higher than that in the equivalent non-reinitiation model, but its distribution is narrower than that in the equivalent non-reinitiation model. This implies that the noise reduction effect of a higher reinitiation rate is really not caused by increasing the average fraction of time the promoter spends in the active state, but may be at least partially owing to the reduction in the fluctuations of this fraction. This also implies that ignoring the reinitiation mechanism in the modelling can overestimate the noise. On the other hand, because 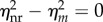when λ_R = 0 or λ_R → +∞, there is an optimal value of λ_R such that 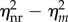reaches its maximum (figure 2a, inset). Considering transcription modelling, this means that the influence of reinitiation on the transcriptional noise can be negligible when the reinitiation rate is too low or too high. In those cases, we can use a non-reinitiation model to approximate the reinitation model without significantly overestimating the noise level. It should be noted from the inset of figure 2a that the amount of noise reduction by reinitiation reaches its maximum when the reinitiation rate is slightly higher than the initiation rate, and then slowly decreases. Many studies have shown that the reinitiation rates are about threefold higher than the initiation rates [30], which is near the optimal value. In our simulation, 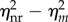reaches its maximum 10.0575 when λ_R = 1.2λ_A = 0.12. When λ_R = 3λ_A = 0.3, this amount is 8.5035, which is not far from the maximum. This may imply that in many real eukaryotic transcriptions, the influence of reinitiation is not negligible.

Figure 2.

The influence of the reinitiation rate. The parameters are set as λ_S = 5, λ_I = 0.05, λ_R ranges from 0 to 5, λ_A = 0.1, and μ = 10. The meaning of each parameter is indicated in figure 1, and all of them are normalized by the mRNA degradation rate δ. In (a,d), the solid lines are theoretical values, whereas the circles give the simulation values. (a) The blue line (circles) shows the noise intensity under different reinitiation rates, whereas the red line (circles) shows the noise intensity in an equivalent model without reinitiation; the inset (green line/circles) shows the difference of the noise intensity between these two models (b). The simulation results for the fraction of the ‘on’ state, plotted for both the reinitiation model (blue) and its equivalent non-reinitiation model (red) with respect to the reinitiation rate; (c) the quantitative contribution of reinitiation, FNR_r, with respect to the reinitiation rate, where the blue solid line is the theoretical plot, and the red stars are simulation results; (d) the influence of the reinitiation rate on the transcription noise intensity at a constant transcription level. When the reinitiation rate increases, the stability of the active state is decreased to keep the transcription level constant.

To quantify the contribution of reinitiation to the noise reduction of eukaryotic transcription, we introduce an index, namely the fraction of noise reduced by reinitiation as follows

Figure 2c plots the quantitative contribution of reinitiation with respect to the reinitiation rate. From this plot, FNR_r increases quickly at the beginning, reaches a maximum of more than 0.6 for λ_R between 5λ_A(=0.5) and 10λ_A(=1), and then slowly drops. Although the optimal value of the reinitiation rate becomes larger when using this new index, the real reinitiation rate still lies near the optimal value.

Another interesting observation on FNR_r is that at a constant transcription level (e.g. we increase λ_I and μ, so that a constant transcription level is maintained),

This means that in a promoter with a large inactivate rate λ_I and a high transcription rate μ, the quantitative contribution of reinitiation in noise reduction will drop. Because a very-bursting promoter has a very long ‘off’ period, a very short ‘on’ period and a high transcription rate, corresponding to large λ_I and μ, this observation indicates that the contribution of reinitiation in a very-bursting promoter is relatively small.

Next, we investigate the influence of varying the reinitiation rate at a constant transcription level. In this procedure, we increase the reinitiation rate and reduce the stability of the active state to maintain a constant transcription level. That is, we let λ_S depend on λ_R in such way that 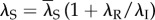. By this setting, we make the transcription level

independent of the reinitiation rate. In this case, the noise intensity

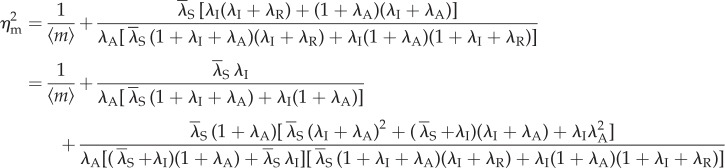monotonically decreases with the reinitiation rate λ_R as shown in figure 2d. Thus, increasing the reinitiation rate can monotonically reduce the noise intensity at a constant transcription level.

In reference [31], by a more complicated transcription model and numerical techniques, Wang et al. showed that a higher reinitiation rate is a necessary condition for reliable transcription responses. In this study, from the viewpoint of noise reduction, we provided further evidence for the advantages of a higher reinitiation rate in the fidelity of signal transduction via gene expression.

Currently, it is possible to test the noise reduction role of reinitiation in vitro. For example, we can construct two synthetic promoters from one wild-type promoter: one reinitiation promoter and one non-reinitiation promoter, working as a control. Suppose that by varying the concentrations of some specific transcription factors (TFs), we can adjust the reinitiation rate in the reinitiation promoter and the stability of the active state in the non-reinitiation promoter. Keep the environments for these two promoters identical except the concentrations of these specific TFs and measure the noise intensities at different transcription levels for these two promoters. Then, by comparing the reinitiation and non-reinitiation noise intensity at each same transcription level, we can determine the contribution by reinitiation.

3.2. The influence of scaffold stability

In addition to the reinitiation rate, the reinitiation scaffold also plays an important role in the regulation of transcription. For example, Wang et al. [31] showed that a stable reinitiation scaffold is among the necessary conditions for reliable transcriptional responses. Now, we further analyse the effect of the scaffold stability on the transcription noise. Here, as in [31], we consider the scaffold as a platform where reinitiation occurs and understand its stability as the time it stays on the promoter, which is determined by the rate that it falls off the promoter, but not the rate of reinitiation. By a proper rearrangement of (3.2), we have

where

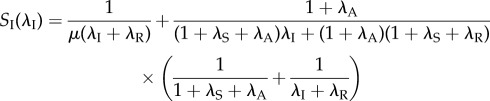is a decreasing function of λ_I (see the electronic supplementary material). Because the scaffold stability is determined by its inactivation rate λ_I, i.e. a higher scaffold stability corresponds to a smaller inactivation rate λ_I, the qualitative influence of the scaffold stability on the transcription noise intensity depends on the relation between the initiation rate λ_A and the reinitiation rate λ_R. Mathematically, if λ_A − λ_R>(or < )0, then a higher scaffold stability results in a higher (or lower) noise intensity in mRNA abundance. This can be explained as the competition between the two paths, initiation and reinitiation, in their respective contributions to mRNA synthesis. The change in scaffold stability can redistribute the relative contributions of these two paths in mRNA synthesis, and the result depends on their relative effectiveness. It should also be noted that in the critical case when the initiation rate and reinitiation rate are identical, i.e. λ_A = λ_R, the transcription noise intensity is not influenced by the scaffold stability. Intuitively, one may think that this property comes from the influence of scaffold stability on the transcription level. For example, when λ_R > λ_A, increasing the scaffold stability also increases the transcription level, thus reduces the relative fluctuations in mRNA output. Although this explanation looks reasonable, we show in the following that this property still holds when the transcription level is fixed. To see this, we vary the parameters λ_I and λ_S at the same time, so that the transcription level is kept constant. Here, we decrease λ_I and increase λ_S, so that the scaffold becomes more stable while the active state becomes more unstable, and at the same time, let λ_I and λ_S satisfy a certain relation, so that the trade-off between them makes the transcription level unchanged. Precisely, given a constant k, let

3.5

so that the transcription level 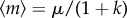is constant. Substituting (3.5) into (3.2), and noting that 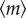is constant, we obtain

where

is a decreasing function of λ_I.

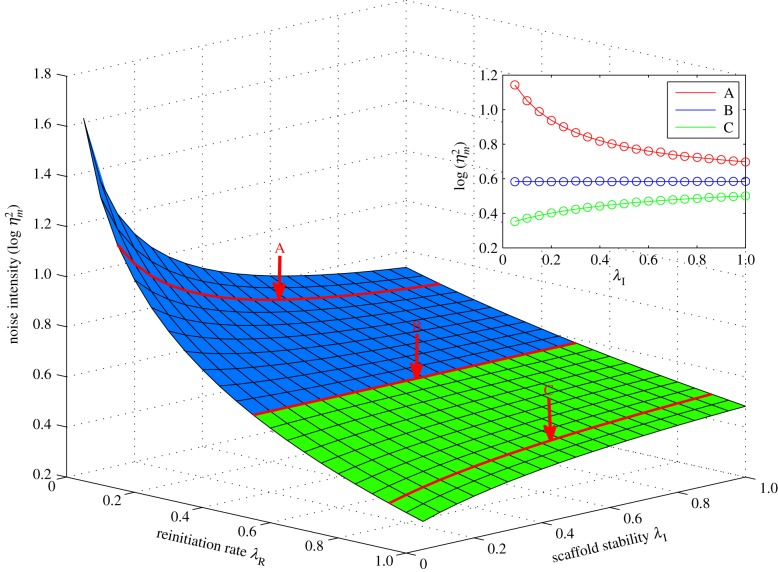
In real eukaryotic transcription, the reinitiation rate is always much higher than the initiation rate; as we have mentioned before, many in vitro studies have shown that the reinitiation rates at some promoters are at least threefold higher than the initiation rates [30]. Thus, a more stable scaffold can enable a larger contribution of the reinitiation path to mRNA synthesis, and results in a lower noise intensity (figure 3). Hence, through theoretical analysis, we revealed another role that high scaffold stability plays in eukaryotic transcription, namely the noise reduction. These results suggest that a highly stable reinitiation scaffold is advantageous for low-noise transcription independent of the transcription level, thereby facilitating high fidelity in the transduction of upstream signals. Furthermore, the above analysis also indicates that the reinitiation scaffold plays a special role and in general can be considered as neither an active nor an inactive state. It is the ‘intermediate form’ between the active and inactive states that can exhibit different types of behaviour depending on the reinitiation rate. When the reinitiation rate is higher than the initiation rate (the case in eukaryotes), it behaves more like an active state, and when the reinitiation rate is low, or even zero (the case in prokaryotes), it behaves more like an inactive state. This also provides a potential method to determine whether a state should be assimilated into an active state or an inactive one when simplifying models.

Figure 3.

The influence of transcription scaffold stability. The parameters are set as λ_S = 5, λ_A = 0.5, μ = 10 and λ_I (λ_R) ranges from 0.05 (0) to 1. (Inset) Three sectional curves with different values of the reinitiation rate (A: λ_R = 0.1, B: λ_R = 0.5 and C: λ_R = 0.9). The solid curves show the theoretical values, whereas the circles show the simulation results.

3.3. Transcription coupling further reduces noise

So far, we showed that reinitiation can reduce the transcription noise independent of the transcription level. This property is of particular interest, because, in many cases, the average transcription output may carry some important information that should not be changed. For example, in the process of signal transduction, for a given input signal, the average of the output may correspond to the faithfully transcribed signal. In such a case, we do not expect the average output to be changed when reducing the fluctuations. Generally, an ideal noise reduction mechanism is to reduce the noise without affecting other aspects of the biological process, or having minimum effects on unrelated aspects. Besides the reinitiation mechanism that has been revealed in §3.2, the so-called multi-step mechanism that can be observed at transcription in higher eukaryotes [32] is also a similar mechanism, which has been proved to reduce the noise intensity in eukaryotic transcription without influencing the transcription level under some circumstances [22]. Here, we further reveal another novel mechanism, termed transcription coupling, that accompanies the transcription reinitiation and has a least interference feature on the original dynamics. In the model of figure 1c, when the gene is in the active state, the mRNA production and the scaffold complex formation are considered as independent events. However, experimental evidence indicates that they are concurrent, or at least partially coupled. Many studies have used models that incorporate the mRNA synthesis and scaffold formation into one elementary reaction. For example, see [5,13] and the review paper [33] for similar models. This direct coupling between the two processes of gene activation and mRNA synthesis violates the independent assumption, although its influence on the transcription noise has not been revealed yet. To investigate this transcription coupling, we modify our model of figure 1c to take it into account (figure 1d). To be more general, we add an elementary reaction, with rate λ_C, to the model in figure 1c which combines the mRNA synthesis and scaffold formation. Hereafter, the preceding model of figure 1c is referred to as the independent model, whereas the modified model of figure 1d is referred to as the coupling model. Obviously, the independent model corresponds to the extreme case of the coupling model when λ_C = 0. By a similar analysis as that in §3.2 (see the electronic supplementary material), we obtain the stationary transcription noise intensity in the coupling model as follows

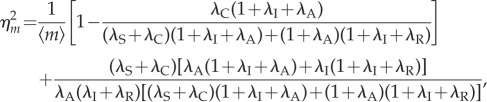3.6

where

3.7

is the average number of mRNA molecules.

To understand the changes induced by this coupling, we investigate the coupling model with different values of coupling strength λ_C while keeping the transcription level constant. For that purpose, we keep λ_S + λ_C = λ_SC and μ + λ_C = μ_C as constant. Obviously, when λ_C = 0, the coupling model becomes the independent model with the same transcription level, and the coupling strength achieves its maximum when λ_C is maximum, that is, 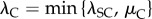. From (3.6), the noise intensity now becomes

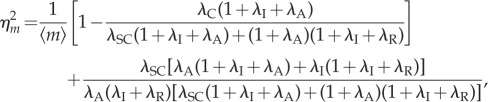3.8

with

3.9

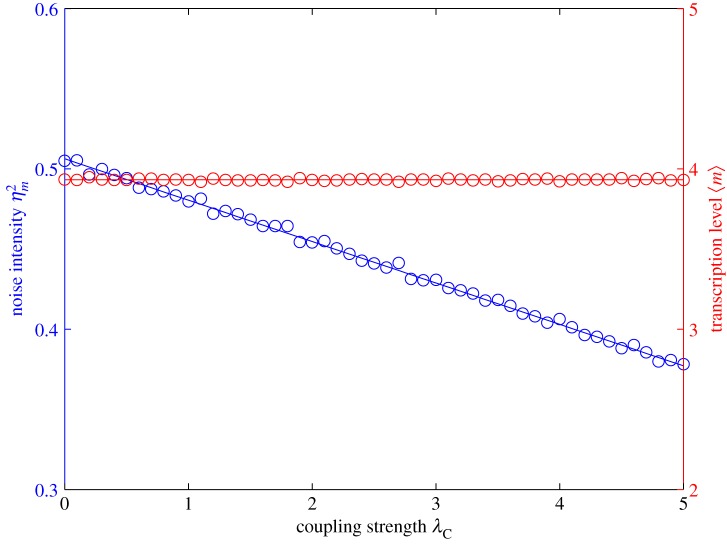
It can be seen that 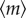does not depend on the coupling strength λ_C, whereas the noise intensity 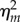monotonically decreases with the increasing of λ_C, as shown in figure 4. Compared with the independent model at the same transcription level, the amount of noise reduced by the coupling model with coupling strength λ_C is

Figure 4.

The influence of transcription coupling at a constant transcription level. The parameters are set as λ_R = 4, λ_I = 0.05, λ_A = 0.2 and λ_S = 5−λ_C and μ = 10−λ_C are adopted to keep the transcription level constant while varying the coupling strength λ_C from 0 to 5. The blue line (circles) shows the transcription noise intensity, whereas the red line (circles) shows the transcription level.

Besides the noise reduction, this coupling has several other properties that may be advantageous. First, like the reinitation mechanism and the multi-step mechanism, it does not influence the transcription level. This is different from some other regulatory mechanisms such as negative feedback. Although negative feedback also reduces the noise intensity, it suppresses the transcription level at the same time, and in general, it needs a long loop that is costly in energy and fundamentally limited in accuracy [34]. Second, we found that all the qualitative properties discussed above are conserved under this coupling (see the electronic supplementary material). That is, a higher reinitiation rate can still result in a lower noise intensity in transcription, and the influence of the scaffold stability on the noise intensity still depends on the competition between the initiation and reinitiation paths in the same way.

By a burst model approximation [21,35], which characterizes mRNA production as random quantal bursts with random time intervals (see the electronic supplementary material), we can provide an explanation for the noise reduction by the coupling. It can be analytically demonstrated that the coupling can reduce the fluctuations in the burst size (see the electronic supplementary material). This explanation becomes more obvious in the extreme case where the reinitiation rate is 0 and λ_C = λ_S = μ. In this case, the burst size for the independent model in each transcription cycle is random, whereas for the coupling model, it is 1. As to the multi-step mechanism, the burst model approximation can show that it reduces noise by decreasing the fluctuations in the time intervals between successive mRNA bursts [21,36].

By comparing the coupling mechanism with the multi-step mechanism, we observed that they are similar in one aspect and complementary in the other. On the one hand, both mechanisms do not depend on feedback and do not change the transcription level as well as many other qualitative properties. Hence, they are direct, highly efficient and less interfering noise reduction mechanisms. On the other hand, the multi-step mechanism mainly reduces the fluctuations in the burst frequency, whereas the transcription coupling mainly reduces the fluctuations in the burst size. Hence, the two mechanisms reduce different aspects of the noise. Given that both the burst size and frequency can carry information and are equally modulated in eukaryotic transcription [37–39], it is very likely that eukaryotes may use these less interfering, fine-tuning mechanisms separately to selectively reduce the fluctuations in the burst size or frequency depending on which one carries more important information. Besides, the two mechanisms can also work cooperatively to achieve more precise regulation of transcriptional responses. Note that the less interfering feature of the multi-step mechanism also indicates that our theoretical results, although obtained by a minimum model, can also qualitatively hold true for a more general multi-state model, for example, by dividing the ‘off’ state in figure 1c or d into multiple ‘off’ states as in [22].

Furthermore, comparing with the reinitiation mechanism and the multi-step mechanism, the coupling has another advantage which may be more significant under certain circumstances. That is, the multi-step and reinitiation mechanisms can only reduce the extrinsic noise, which is independent of the transcription level, so the amount of noise that is reduced by them is also independent of the transcription level. Thus, when the transcription level is very low and the intrinsic noise dominates, their noise reduction effect becomes inconsequential. Unfortunately, concerning the fact that the number of copies of gene and mRNA is very small in single cells, such a case is not rare in reality. As to the coupling, the amount of noise that it reduces increases when the transcription level decreases and the intrinsic noise dominates. In such cases, the coupling may be more significant in noise reduction compared with both the reinitiation mechanism and the multi-step mechanism.

4. Conclusion and discussion

Transcription in single cells is a rather complicated noisy process, involving numerous factors and transition steps. To understand the process and its regulation, various models at different simplified levels that represent essential events and capture fundamental characteristics of the process have been proposed and analysed.

Reinitiation is an important mechanism in eukaryotic transcription that has been receiving attention from experimentalists for many decades [19]. Although currently there are some conflicts between the in vitro and in vivo evidence concerning this phenomenon, both experiments and model analysis have suggested that reinitiation may play an important role in the regulation of eukaryotic transcription [19,31]. However, concerning the stochastic transcription process in individual cells, how reinitiation may influence the transcription noise still has not been revealed yet. To theoretically answer this question, we extended the widely used random telegraph model to a minimum three-state model to incorporate the reinitiation mechanism. By solving the stationary mean and variance in mRNA abundance from some differential equations obtained by the chemical master equation, we analysed the influence of reinitiation on the transcription noise intensity.

Our results suggest that reinitiation can affect many aspects of the noise properties of eukaryotic transcription, and hence plays an important role in generating reliable transcriptional responses in eukaryotes. First, reinitiation provides a shortcut for more effective mRNA production with a lower noise intensity through a high reinitiation rate and a stable scaffold complex. Besides the intuitively obvious fact that a higher reinitiation rate can maintain a larger mRNA population, which naturally reduces the relative fluctuations, we clearly demonstrated the noise reduction effect of the reinitiation mechanism independent of the transcription level by comparing the reinitiation model with an equivalent non-reinitiation model. Even at the same transcription level, the transcription model with a higher reinitiation rate always has a lower transcription noise intensity than that with a lower one. Furthermore, the fact that the reinitiation rate in an eukaryotic cell is always much higher than the initiation rate enables a stable reinitiation scaffold to be advantageous for noise reduction. All these imply that reinitiation may provide an important way or mechanism to facilitate reliable signal transduction in eukaryotic cells. Then, we analysed another novel mechanism that accompanies reinitiation, namely the transcription coupling, and showed that it can further reduce the transcription noise. Compared with most of other well-studied mechanisms, the coupling mechanism is unique in the sense that it is less interfering, because it does not change the transcription level and many other qualitative properties. Besides, it neither increases the number of reaction steps nor requires a long feedback loop. These are advantageous from the viewpoint of energy cost and efficiency. Furthermore, it has a special advantage that the amount of noise that it reduces increases when the transcription level decreases and the intrinsic noise dominates. Therefore, it should be especially useful for achieving more precise transcriptional responses in single cells where the number of copies of gene and mRNA molecules are very low. In summary, our result reveals a mechanistic route that may be used in some eukaryotes to enhance more reliable transcriptional responses.

As there are other existing works concerning multi-state promoters, it is helpful to make some comparison. In [24,25], the authors proposed a reversible four-state circle model of the promoter and showed that if a TF can influence the transition rates between the active and inactive states in both forward and backward directions but (approximately) keep their ratio, then this TF can regulate the noise intensity independent of the transcription level, which is regulated independently by another TF. Intuitively, such model can be decomposed into the ‘product’ of two independent random graph models, each of which is regulated by one TF. Thus, the results can also be decomposed into elementary facts for random graph models: regulating the transition rate in one direction can regulate the transcription level, while regulating them in both directions, but maintaining their ratio can regulate the noise independent of the transcription level. Different from such an ‘outer’ extension approach of the random graph model which considers the ‘products’ of the random graph model rather than modifying it, our model uses an ‘inner’ extension approach by introducing a scaffold complex into the random graph model. It is elementary by itself and cannot be further decomposed. Besides our model, other ‘inner’ extensions of the random graph model also exist. For example, the so-called multi-step models, which have been proposed based on some experimental observations [10,40] that the promoter activation may contain a series of rate-limiting steps. In [22], Zhang et al. considered the effect of multi-step progress in promoter activation on the transcription noise intensity. They reached the conclusion that a reversible promoter activation can result in a larger noise intensity in the mRNA abundance. However, they considered only irreversible promoter inactivation rather than the reinitiation mechanism considered here. From this point of view, some parts of our work can be seen as a compensation of this result in [22]. In [23], Innocentini et al. proposed a three-state model by introducing an intermediate state with a medium transcription rate to a two-state model and showed that it can significantly reduce the noise when the occupancy probability of the intermediate state increases at a fixed transcription level. Obviously, their intermediate state should at least be an active state, otherwise, high occupancy of this state will lead to a very low transcription level, which can be more noisy. Thus, the transcription reinitiation scaffold introduced in our model is totally different from their intermediate state because it has no transcriptional competence. Furthermore, in our model, the noise reduction cannot be explained by the occupancy probability of the scaffold. Because we consider one promoter, this probability is identical to the stationary mean 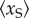. Now, we show that in our model, the noise reduction is independent of 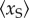when the transcription level is fixed. First, in the reinitiation model, the scaffold occupancy probability

In the equivalent non-reinitiation model, where the reinitiation rate is set to 0, whereas λ_S is replaced with λ_Sλ_I/(λ_I + λ_R), the scaffold occupancy probability

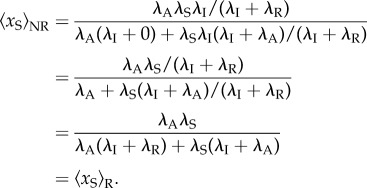Thus, these two models have the same occupancy probability of the scaffold. Second, we show that at a constant transcription level, 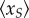is independent of the reinitiation rate. By letting λ_S depending on λ_R such that 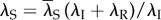, we show that

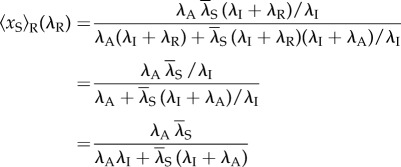is independent of λ_R, thus the occupancy probability of the scaffold is unchanged when we vary the reinitiation rate while fixing the transcription level. All these further indicate that our mechanism is completely new compared with that in [23]. Finally, and most importantly, the transcription coupling of our model has not been contained in the above-mentioned models.

Although our analysis uses only a minimum model, the results are qualitatively correct for a more general multi-state model such as those proposed in [22]. Yet, concerning the fact that the real transcription process is rather complicated and new experimental findings are coming out, we will focus on more realistic models in our future research.

Funding statement

This research is supported by the Aihara Innovative Mathematical Modelling Project, the Japan Society for the Promotion of Science (JSPS) through the ‘Funding Programme for World-Leading Innovative R&D on Science and Technology (FIRST Programme)’ initiated by the Council for Science and Technology Policy (CSTP). This study was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB13000000). It is also supported by National Programme on Key Basic Research Project (no. 2014CB910504), the Knowledge Innovation Programme of the Chinese Academy of Sciences (no. KSCX2-EW-R-01), 863 project (no. 2012AA020406), NSFC (nos. 61134013, 91029301, 11326035) and Platform for Dynamic Approaches to Living System from MEXT, Japan.