Network-based vaccination improves prospects for disease control in wild chimpanzees

Abstract

Many endangered wildlife populations are vulnerable to infectious diseases for which vaccines exist; yet, pragmatic considerations often preclude large-scale vaccination efforts. These barriers could be reduced by focusing on individuals with the highest contact rates. However, the question then becomes whether targeted vaccination is sufficient to prevent large outbreaks. To evaluate the efficacy of targeted wildlife vaccinations, we simulate pathogen transmission and control on monthly association networks informed by behavioural data from a wild chimpanzee community (Kanyawara N = 37, Kibale National Park, Uganda). Despite considerable variation across monthly networks, our simulations indicate that targeting the most connected individuals can prevent large outbreaks with up to 35% fewer vaccines than random vaccination. Transmission heterogeneities might be attributed to biological differences among individuals (e.g. sex, age, dominance and family size). Thus, we also evaluate the effectiveness of a trait-based vaccination strategy, as trait data are often easier to collect than interaction data. Our simulations indicate that a trait-based strategy can prevent large outbreaks with up to 18% fewer vaccines than random vaccination, demonstrating that individual traits can serve as effective estimates of connectivity. Overall, these results suggest that fine-scale behavioural data can help optimize pathogen control efforts for endangered wildlife.

1. Introduction

Vaccines exist for many infectious diseases that threaten wildlife populations (e.g. [1,2]), yet immunization is rarely implemented as a conservation strategy. This is partly due to logistical difficulties in administering vaccines to large enough portions of wildlife populations to substantially drive down transmission. In particular, models based on homogeneous mixing typically indicate that a majority of individuals must be vaccinated to eliminate most pathogens [3]. Further, because vaccination is economically costly, logistically difficult and can carry its own risks [4], high coverage levels can be infeasible or undesirable, particularly when dealing with endangered animals. For many wildlife species, individuals vary in contact rates (e.g. [5]). Thus, vaccination efforts focused on animals with the highest contact rates might lower the level of coverage needed to curb large outbreaks (i.e. achieve a high level of herd immunity), relative to vaccinating randomly selected individuals [6,7].

A major challenge to developing wildlife pathogen control strategies is that data on infection and pathogen transmission are notoriously difficult to obtain for wild animals. Collecting biological samples can require risky immobilizations and epidemics often sweep through populations quickly, leaving researchers with inadequate time to ascertain the infection status of more than a few animals [8]. Given these obstacles, behavioural association data can provide useful estimates for transmission pathways when infection data are not available [9]. Network epidemiology (which represents individuals as nodes and interactions allowing for pathogen transmission as edges) uses association data and infectious disease models to predict the dynamics of pathogen transmission for populations with heterogeneous contact rates [6,9,10]. While traditionally applied to human–pathogen systems, network analysis tools have recently gained traction among ecologists studying wildlife disease dynamics [11–13]. Here, we present how network epidemiology can be used to develop efficient vaccination strategies for a social wildlife species.

Great apes have experienced considerable declines from infectious diseases such as Ebola and respiratory viruses [14,15]. Apes also demonstrate substantial heterogeneity in individual contact rates that can induce tremendous individual variation in the risk of acquiring or spreading infections [16–18]. While network data are not always available for wildlife populations, easily measured demographic and behavioural traits (e.g. sex, age, dominance and family size) might correlate with connectivity. For example, previous work on the Kanyawara chimpanzee community showed individuals with large families (i.e. adult females and juveniles) that range in the core area of the Kanyawara territory were consistently more central to the social network than other community members [19]. Thus, when detailed network data are not available to explicitly identify the most central individuals, immunizing animals with high-risk social traits may be an alternative approach to preventing large outbreaks with less coverage than random vaccination.

We investigated how contact heterogeneity within the Kanyawara chimpanzee community affects the spread and control of directly transmitted pathogens using network epidemiology and empirically derived contact networks. Specifically, we simulated pathogen spread on a series of nine monthly contact networks (n = 37 chimpanzees) to assess how final outbreak sizes were affected by (i) the network position of the index case (first individual to be infected), (ii) the timing of the initial case (across months that differed in connectivity), and (iii) pathogen contagiousness. Our simulations used estimated values of the basic reproductive number (R₀) reported in the human literature for a range of low to highly infectious pathogens that show potential for infecting wild apes [1,3]. We then identified key traits of individuals likely to initiate large outbreaks (similar to high-risk groups identified for human diseases such as HIV, e.g. [20]), and we compared the effectiveness of a random (null) vaccination strategy to two network-based strategies: (i) vaccinations focusing on the most central individuals and (ii) vaccinations targeting individuals with high-risk social traits. We predicted that final outbreak size would increase with index case centrality and that infections starting in core-ranging adult females and juveniles with large families would lead to the largest outbreaks. We also expected the centrality-based vaccinations to require the least coverage to mitigate outbreaks; however, given that detailed network data are not available for many wildlife populations, trait-based vaccinations might be the most logistically feasible to implement in the field.

2. Material and methods

2.1. Field data collection

Over a nine-month period (December 2009–August 2010), we collected behavioural contact data on the habituated, wild Kanyawara chimpanzee community (n = 48) in Kibale National Park, Uganda. Further information on the study site and community is provided in the electronic supplementary material, text S1. Chimpanzees have dynamic, fission–fusion societies, where individuals within communities break off into smaller parties of variable size and composition over periods of hours to months [21]. Each morning, we randomly selected a focal chimpanzee from a party (i.e. individuals within a 50 m radius) to follow. At 15 min intervals, we scanned the focal animal's party to record party member identities based on individuals within a 50 m radius, a common criterion for estimating chimpanzee party sizes [22]. At the 15 min intervals, we also recorded pairs of individuals that were within 5 m of each other. Our total sample size was 37 individuals (adults: 12 males and 12 females; juveniles: seven males and six females), excluding dependent offspring (less than 4 years old). On average, we followed each chimpanzee as a focal subject for 27.79 (±3.6) h, comprising a total of 1028 focal observation hours and 4114 fifteen-minute scans. Our analysis included 306 212 pairwise party associations and 14 673 pairwise 5 m associations. Data are available upon request. See Rushmore et al. [19] for full data collection details.

2.2. Quantifying contact networks

We created monthly contact networks at two spatial scales (proximity networks and party networks) across nine months, in which nodes represented chimpanzees. Proximity networks were considered a proxy for pathogen transmission by direct contact or respiratory droplets, whereas party networks were a proxy for pathogens spread via fomites or fecal oral transmission. Because many pathogens require close contact for transmission, results in the main text pertain to proximity networks unless otherwise stated. Party network results are in the electronic supplementary material, figures S2–S4.

To quantify party association indices (PAIs) used to weight party network edges, we determined the number of scans in which chimpanzees A and B were observed in the same party relative to the total number of scans in which either A or B was observed in any party:

2.1

where S_AB represents scans in which A and B were observed in the same party, S_A represents scans where A was observed in a party without B, and S_B represents scans where B was observed in a party without A. To quantify 5 m association indices (5 mAIs) used to weight edges of proximity networks, we calculated the probabilities that individuals A and B would be both within the same party and within 5 m of each other:

2.2

where S_AB5 represents scans in which A and B were observed within 5 m of each other. Thus, this index, which could range from 0 to 1, represents the overall proportion of time that individuals A and B were within 5 m of each other.

A major challenge in quantifying contact networks for wildlife is that it is often difficult to observe all study subjects within a given time frame. In our monthly networks, 1.72% of the monthly pairwise interactions were undefined because neither individual A nor B was observed within the given month, making it impossible to directly quantify the amount of time the two individuals spent together. To circumvent this issue, we used a Bayesian logistic mixed effects model (with pairwise predictor variables of age, sex, relatedness, difference in rank, difference in family size and number of females in estrus in a given month) to predict the missing pairwise association indices. The model details are described in Rushmore et al. [19].

When simulating pathogen transmission on contact networks, it is important to assess host interactions at a time scale that reflects the transmission dynamics of real-world pathogens. Notably, aggregating the contact data across the entire study period would overestimate the connectedness of the community during a time frame in which a pathogen is likely to spread. Close-contact diseases occurring in chimpanzees and humans typically have an infectious period that ranges from several days to a month (e.g. influenza: 2–3 days, Ebola: 4–11 days, measles: 6–7 days, Streptococcus spp.: 14–30 days [3,23,24]) and published reports of respiratory disease outbreaks in wild chimpanzee communities indicate that epidemics often last two weeks to two months [25,26]. Previous work on our study system (with the same behavioural interaction dataset) demonstrated that the inter-individual associations in two-week versus month-long time steps were significantly correlated for both the proximity and party networks [19]. Thus, here we use only the monthly association networks when simulating pathogen transmission and control. Importantly, the networks were highly dynamic across months, changing in both overall connectivity and topology in ways that might determine temporal variation in the probability of pathogen invasion and final outbreak size.

2.3. Individual trait data

For each individual, we recorded age, sex, dominance rank and family size, following Rushmore et al. [19]. Adult male chimpanzees tend to follow a linear hierarchy, which is not the case for eastern chimpanzee adult females [27]. In the Kanyawara community however, adult females that occupy the territory core tend to be higher ranking than those occupying the territory edges [28]. Adult females and their juveniles typically travel in family units, but not adult males or females without juveniles [29]. We considered large families to be a mother with two or more juveniles (electronic supplementary material, table S1).

2.4. Calculating centrality measures

We used UCINET [30] to calculate the weighted degree centrality (the sum of a node's edge weights [31]) for each individual in each month. We selected weighted degree as a centrality metric because it generally performs better than alternative centrality measures (unweighted degree, betweenness, closeness, farness and eigenvector centrality) for predicting individual risk of infection [32] and predicting outbreak size given the centrality of the index case [9]. Additionally, Salathé et al. [9] showed through simulations on empirical human contact networks that vaccination strategies based on weighted degree centrality were more effective in mitigating outbreak spread than strategies based on other centrality metrics.

2.5. Simulating pathogen transmission on observed networks

We simulated pathogen transmission on observed contact networks using bond percolation, a computationally tractable approach to estimate the final outbreak size of a stochastic, network-based susceptible–infected–recovered (SIR) model [6,33]. In a bond percolation model, the probability of pathogen transmission (T) along an edge connecting nodes i and j, given that one of the nodes is infected, is related to the contact rate between individuals (c_ij), the pathogen transmission rate (β) and the infectious period (τ) as follows [33]:

2.3

In our case of weighted networks, we parametrized c_ij using pairwise association indices from monthly networks. We assumed that for a given pathogen, the transmission rates and infectious periods were the same across all transmission events and individuals.

In each simulation, the bond percolation method simplified the observed network by removing edges (with probability 1 − T) that would not lead to transmission events. The remaining graph represented transmission events, where nodes connected to the index case represented individuals that became infected during the simulation. Therefore, the size of the component (i.e. connected network) with the index case represented the final outbreak size. Unlike methods that reproduce temporal outbreak dynamics, such as chain-binomial models [34], bond percolation does not track temporal changes in individual infection status, and hence substantially reduces computational time. To check the validity of our models, we simulated time-series pathogen transmission for a subset of parameter combinations using the chain-binomial method, which yielded identical results to our percolation-based simulations (electronic supplementary material, figure S1).

The basic reproductive number depends on the probability of transmission (T_ij) and network connectivity. The following three equations demonstrate how we calculated the basic reproductive number (and the associated values of βτ) in the context of our study population. First, for each individual in each monthly network, we set R_0(i,m) for an individual (i) in a given month (m) to the sum of the transmission probabilities between individuals i and j in the network:

2.4

We then set R_0(m) for a monthly network to the mean of R_0(i,m) for all 37 individuals in that monthly network:

2.5

The average R₀ 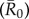across networks was then equivalent to the mean of R_0(m) for all nine monthly networks at a given spatial scale (i.e. proximity versus party networks):

2.6

Averaging R₀ across monthly networks allowed us to measure the effect of network structure (month) on outbreak size for a given level of pathogen contagiousness, where i and j were the indices of the 37 individuals (electronic supplementary material, table S1). Thus, our final definition for 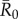(equation (2.6)) represents the mean number of secondary infections that arise from a randomly infected index case, averaged across all nine monthly networks. We calculated pathogen transmission rate (β) such that the resulting 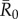values matched estimates for infectious pathogens reported in the human literature showing potential for infecting wild apes. Specifically, we used values of 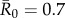(representing pathogens with low contagiousness in which the average index case does not consistently infect at least one other individual), 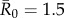(mildly contagious pathogens, such as influenza [35,36]), 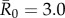(moderately contagious pathogens, such as Ebola [37,38]), and 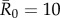(highly contagious pathogens, such as measles [3]) to simulate pathogen transmission on each of the nine monthly contact networks. Given that we used consistent 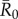values in simulations for each month, differences observed in outbreak size across months arise from changes in network structure. Notably, the referenced R₀ values were calculated for a small number of human populations and should be extrapolated to other human and great ape populations with caution. Estimates of R₀ are not readily available for most wildlife pathogens, and we are not aware of any published reports of R₀ for these diseases in wild primates. Nevertheless, while the 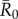for the referenced diseases might vary slightly in our study population, their respective ranks as pathogens with low, mild, moderate and high levels of contagiousness should be consistent. Further information regarding our definition of 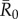, which differs slightly from another definition often used in network epidemiology, is in the electronic supplementary material, text S2.

To examine the effect of index case centrality, month of initial case and pathogen infectiousness (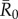 = 0.7, 1.5, 3.0, 10.0) on outbreak size (the cumulative number of individuals infected during an outbreak), we ran 1000 simulations per unique combination of these three parameters at two spatial scales (i.e. proximity networks and party networks), resulting in 2 664 000 simulations. All simulations and subsequent analyses were run in R v. 2.15 [39]; code is available from J. Rushmore upon request.

2.6. Parametrizing trait-based vaccination strategies

To determine which individuals were associated with larger outbreaks, we used permutation-based regressions with 30 000 permutations per test (electronic supplementary material, text S2). Rushmore et al. [19] showed that the most important predictors for individual centrality in the chimpanzee community examined here were family size and range location (core versus edge area of the community territory) for adult female and juvenile groups, and dominance rank for males. Thus, we placed individuals in trait-based groups (i.e. based on the individual's rank and family size; electronic supplementary material, table S1) and verified that our classification scheme predicted outbreak sizes using permutation-based regression tests (electronic supplementary material, text S2). For each 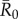value, we examined relationships between mean outbreak size and the trait-based group of the index case while controlling for month. To account for multiple comparisons across 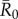values, we applied a Bonferroni correction and considered relationships where p < 0.013 (i.e. p < 0.05/4) to be significant.

2.7. Simulating vaccination strategies

Using bond percolation as described above, we simulated vaccination strategies on observed monthly networks with the assumption that vaccination conferred full protection to treated individuals. For each strategy, we ran 5000 simulations per unique combination of month, 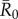, and coverage level (which varied sequentially from 1 to 37 individuals).

3. Results

3.1. Effects of network heterogeneity on outbreak size

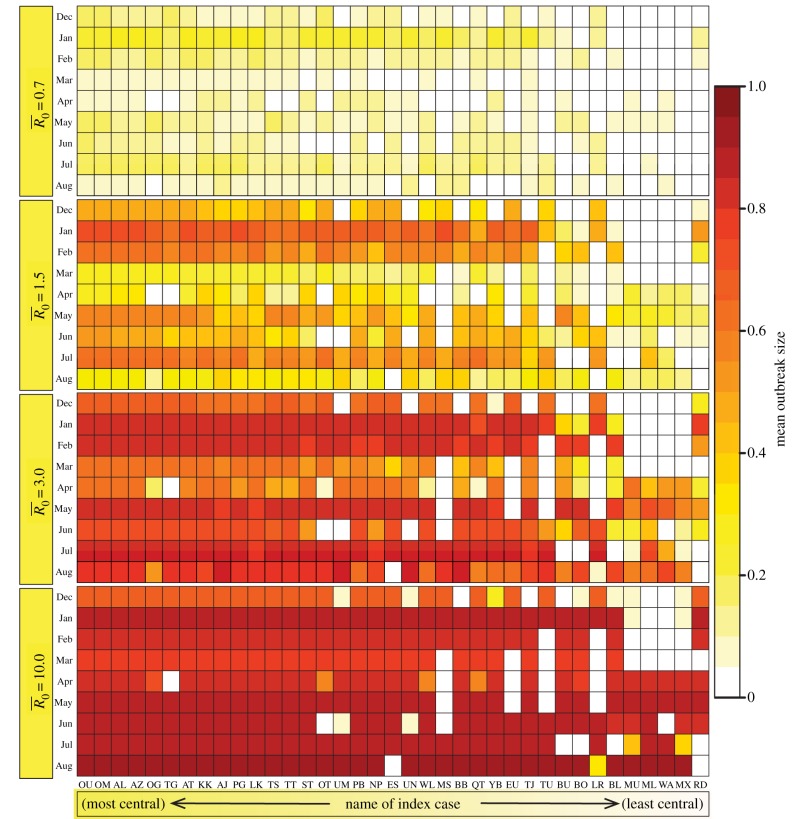
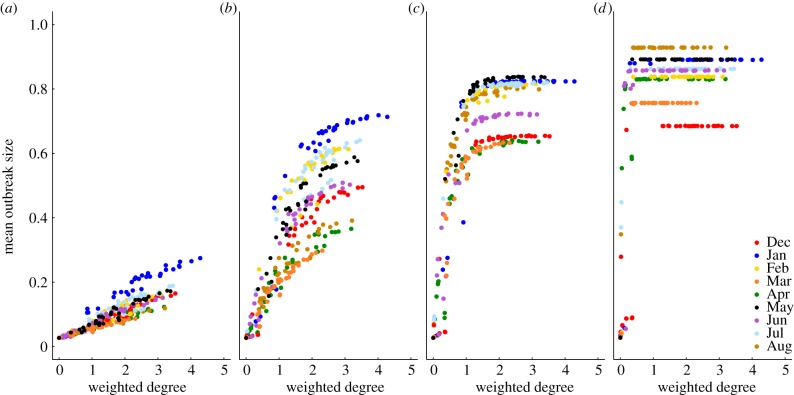
The network position of the index case, the month of initial infection and pathogen contagiousness strongly affected mean outbreak size for the chimpanzee community in our simulations. Within a given monthly network, mean outbreak size generally increased with index case centrality across all 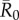values (figures 1 and 2). Notably, when 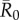was low, index case centrality showed a nearly linear relationship with mean outbreak size; however, when 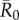was moderate or high, this relationship became saturating. In particular, when 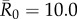, mean outbreak size levelled off as the outbreak approached the size of the largest component (i.e. fully connected network including the index case) for a given month (figure 2).

Figure 1.

Mean outbreak size as a function of index case, month of initial case and pathogen contagiousness 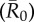. The colour of each cell shows the average proportion of the chimpanzee community (n = 37) that was infected across the 1000 replicates per unique combination of parameters. The x-axis shows the identities of the index cases, ordered from highest to lowest mean weighted degree centrality (i.e. averaged across months).

Figure 2.

Mean outbreak size increases with the weighted degree centrality of the index case. Mean outbreak sizes are shown (as proportions of the community) against weighted degree centrality of the index case for proximity networks. Panels show different levels of pathogen infectiousness (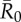 = (a) 0.7, (b) 1.5, (c) 3.0 and (d) 10.0), and data point colours represent different monthly networks. Thus, there are 37 data points (representing each possible index case) for each month within a given value of 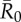. Estrous females were present during Jan (n = 1 estrous female), Apr (n = 1), May (n = 1), Jun (n = 1), Jul (n = 2) and Aug (n = 2).

Across months, mean outbreak size varied considerably and generally increased with monthly network density (i.e. mean edge weight; electronic supplementary material, figure S2). This relationship was strongest for low to moderate 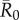values, as high 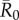values had large outbreak sizes for most months (electronic supplementary material, figure S2). Notably, months with higher levels of network connectivity allowed less contagious pathogens 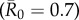to invade and affect up to 30% of the community provided that the infection started with a highly central index case, whereas months with low network connectivity could result in no outbreaks of even highly contagious pathogens 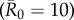if the infection started in a less central index case (figure 1). Additionally, the mean outbreak size linked to an index case varied across months, as a less central individual in one month could be a moderately central individual in another month (figure 1). The dynamic nature of the contact structure might thus appear as an obstacle to efficient network-based vaccinations. However, for our study system, an index case's average weighted degree centrality (i.e. averaged over the study period) strongly predicted outbreak size; thus, vaccination based on average weighted degree should be robust to monthly network variation.

Time-series chain-binomial models (which were run for a subset of network months and index cases: Material and methods) revealed that outbreaks parametrized with infectious periods and 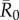values for low to highly infectious pathogens lasted less than a month (electronic supplementary material, figure S1). This finding suggests that the one-month static networks used in our simulations should capture host interactions at a temporal scale that reflects realistic pathogen transmission. Additionally, pathogen simulation results were consistent across proximity (5 m) and party (50 m) networks, with the exception of a positive relationship between mean outbreak size and the number of estrous females in a given month for party networks (electronic supplementary material, figure S4), but not for proximity networks (figure 2).

3.2. Parametrizing vaccination strategies

As compared to a random (null) vaccination strategy, we investigated the efficacy of two network-based vaccination approaches: (i) targeting individuals from high to low average weighted degree centrality and (ii) targeting individuals based on social traits that predict high centrality. To this end, we first verified that our trait-based classifications accurately predicted outbreak sizes (figure 3). Results showed that for adult females and juveniles, infections starting in core-ranging individuals with large families (hereafter, CR-L) led to significantly larger outbreaks across all 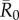values than infections starting in core-ranging individuals with small families (CR-S) or edge-ranging (ER) individuals (figure 3). Infections starting in ER individuals led to significantly smaller outbreaks than for any other trait-based group, making ER individuals poor targets for vaccination (figure 3). For low 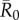values, high rank (HM) adult male index cases tended to cause larger outbreaks than mid- (MM) or low-ranking (LM) adult males but this pattern was not consistent across 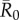values, and differences were never significant. Thus, we collapsed HM, MM and LM into a single adult male group (M) and found that infections originating in CR-L individuals, but not CR-S individuals, generally caused significantly larger outbreaks than infections starting in adult males (figure 3).

Figure 3.

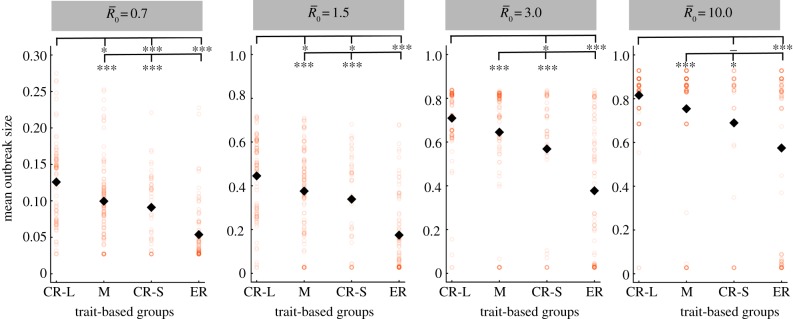
Mean outbreak size for index case trait-based groups across different values of pathogen infectiousness 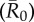. Mean outbreak size is shown as a proportion of the whole community, and trait-based groups are abbreviated as follows: CR-L, core-ranging individuals with large families; M, adult males; CR-S, core-ranging individuals with small families; ER, edge-ranging individuals. Open circles show outbreak size averaged across 1000 simulations per unique combination of monthly network and index case for a given 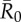. Black diamonds mark the mean outbreak size averaged across each trait-based group. Note the different y-axis scale for the first panel 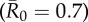. Significant relationships are indicated after Bonferroni correction as follows: ⁻p < 0.013, *p < 0.01, **p < 0.001, ***p < 0.0001. (Online version in colour.)

Given these findings, we parametrized the trait-based vaccination strategy to preferentially vaccinate in the following order: CR-L, M, CR-S, ER. Thus, for each simulation, individuals were first immunized randomly within the CR-L group. Once all individuals in this group were vaccinated, individuals in the M group were randomly immunized, and so on until the predetermined coverage level was reached. To ensure that collapsing the adult male categories did not influence results, we also simulated vaccinations with the following order: CR-L, HM, MM, LM, CR-S, ER. The main text and figures present results for a single male category; however, results for both scenarios are shown in table 1.

Table 1.

Comparison of coverage thresholds across vaccination strategies and pathogen contagiousness. For each vaccination strategy, the coverage threshold is provided as a percentage of the community, with the number of individuals vaccinated in parentheses, for (A) the mean outbreak size to affect less than 10% of the community (minimum coverage threshold) and (B) an outbreak to affect less than 10% of the community in at least 95% of the simulations (conservative coverage threshold). The table shows results for trait-based simulations using a single adult male category (M). Results were identical for simulations using this category M or three adult male categories (HM, MM, LM; see Results), except for a few instances, denoted by superscripts (*) and (**) in which simulations using HM, MM and LM categories required vaccinating one less or one more individual, respectively.

control strategy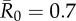
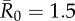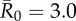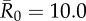(A) minimum coverage threshold
centrality-based	0% (0)	24.3% (9)	40.5% (15)	56.8% (21)
trait-based	0% (0)	29.7% (11)	43.2% (16)*	59.5% (22)
random	0% (0)	35.1% (13)	51.4% (19)	64.9% (24)
(B) conservative coverage threshold
centrality-based	29.7% (11)	51.4% (19)	59.5% (22)	81.1% (30)
trait-based	37.8% (14)*	54.1% (20)*	64.9% (24)	81.1% (30)**
random	46.0% (17)	64.9% (24)	75.7% (28)	86.5% (32)

3.3. Evaluation of vaccination strategies

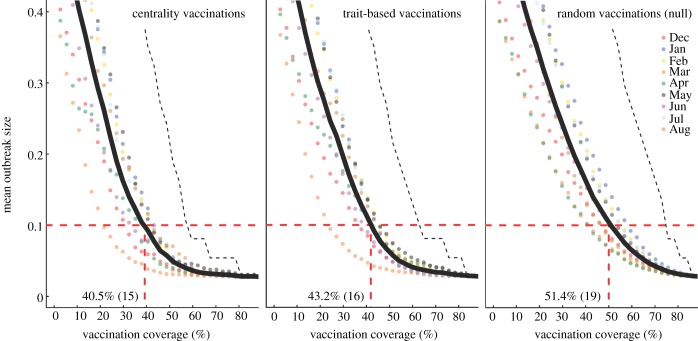
We evaluated vaccination strategies in two ways: (i) to assess coverage needed to protect against the central outbreak tendency (hereafter, the minimum coverage threshold approach), we determined the coverage required to constrain the mean outbreak size to less than 10% of the community and (ii) to assess coverage needed to protect against rare outbreak events (hereafter, the conservative coverage threshold approach), we determined the coverage required to reduce at least 95% of the simulated outbreaks to less than 10% of the community. Constraining outbreaks to 30% of the community (instead of 10%) showed qualitatively similar results for both approaches (electronic supplementary material, table S2). Results based on the minimum coverage threshold showed that pathogens with mild and moderate 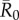values required randomly vaccinating between 35 and 50% of the community, and highly contagious pathogens required randomly vaccinating roughly 65% of the community (table 1 and figure 4). By the conservative coverage threshold, pathogens with low to intermediate 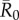values required randomly vaccinating up to 75% of the community, with 86% coverage required for a highly contagious pathogen (table 1 and figure 5).

Figure 4.

Evaluation of vaccination strategies by minimum coverage threshold. Mean outbreak sizes (as proportions of the community) are shown for varying levels of vaccination coverage (as percentages of the community) when 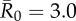. Coloured dots show mean outbreak size by month, and thick black lines show mean outbreak size averaged across months. Red dotted lines indicate the minimum coverage threshold (with the number of chimpanzees in parentheses) required to constrain outbreaks to less than 10% of the community. Black dotted lines show upper 95% CIs, which are equivalent to the conservative coverage thresholds depicted in figure 5. For all coverage levels and vaccination strategies, the lower 5% of simulations had a mean outbreak size of 2.7%, indicating that only the index case was infected.

Figure 5.

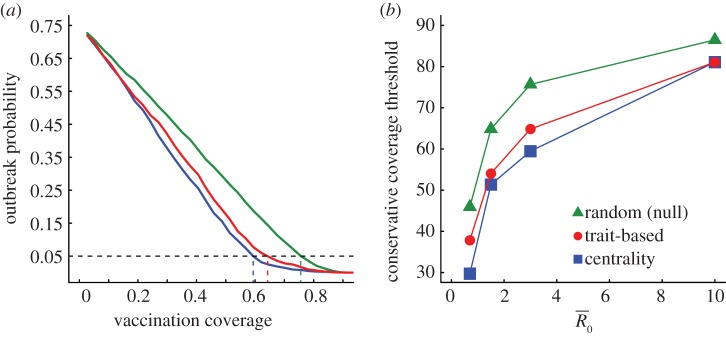
Evaluation of vaccination strategies by the conservative coverage threshold. Panel (a) shows the outbreak probability (i.e. the proportion of simulations resulting in an outbreak, defined as at least 10% of the community being infected) for centrality-based vaccinations, trait-based vaccinations and random vaccinations at varying levels of coverage (shown as a proportion of the community) when 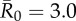. Vertical lines below 0.05 outbreak probability mark the conservative coverage threshold, at which no more than 5% of the simulations result in outbreaks. Panel (b) shows this conservative coverage threshold as a percentage for each vaccination strategy and 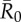combination. (Online version in colour.)

Across all 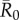values, network-based strategies consistently required less coverage than random vaccinations to achieve the same level of protection. These network-based strategies offered the greatest advantage for pathogens with low to moderate infectiousness (figures 4, 5 and table 1; electronic supplementary material, figure S3 and table S2). While centrality- and trait-based strategies occasionally performed equivalently, centrality-based vaccinations typically required less coverage (figure 5 and table 1; electronic supplementary material, figure S3 and table S2). The conservative coverage threshold showed that as compared to random vaccinations, the number of individuals requiring vaccination was reduced by up to 18% with the trait-based strategy and by up to 35% with the centrality-based approach. Lastly, by preventing immunized individuals from contributing to disease spread (i.e. effectively removing immunized nodes and adjacent edges), each vaccination strategy uniquely changed the underlying network for a given month. Thus, responses to the three vaccination strategies differed across months. For example, when 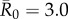, April required twice as much coverage as March with network-based strategies, whereas the two months required equal coverage with random vaccinations (figure 4). Nonetheless, network-based vaccinations were considerably more effective than random control when averaged across months.

4. Discussion

Our study supports the hypothesis that contact heterogeneity predicts outbreak probability and thus is crucially important to consider for wildlife vaccination programmes. Outbreaks were largest when the index case had high centrality, and these individuals were generally core-ranging females or juveniles with a large family. Compared to random vaccination, targeted vaccinations based on weighted degree centrality or high-risk traits reduced the number of chimpanzees requiring vaccination by up to 35% and 18%, respectively. Thus, our simulations show that targeting individuals with high contact rates effectively reduces the level of vaccination coverage required to prevent large outbreaks and could help make wildlife vaccination a more tractable management tool.

Models that assume homogeneous mixing show that outbreak size is larger for high R₀ values than for R₀ values close to one [3]; however, our analysis showed this was not always the case when accounting for heterogeneous contact rates. We observed that outbreaks of pathogens with low infectiousness could affect up to 30% of the community if introduced via highly connected individuals during a well-connected month, whereas an extremely infectious pathogen was unlikely to spread to anyone when starting in a peripheral index case during a sparsely connected month. These findings lend support to a growing body of literature indicating that contact structure can play a fundamental role in pathogen emergence and evolution (e.g. [40,41]). For example, a pathogen that infects a highly central index case during a well-connected month could establish a long chain of transmission (e.g. as compared to infections starting in less central individuals), which could result in the pathogen becoming more contagious through selection [42]. Although a growing number of studies have used temporal contact variation to predict disease outbreaks for human populations (e.g. [43]), few studies have demonstrated these dynamics for endangered wildlife species.

Interestingly, Carne et al. [44] built a network by aggregating several years of wild chimpanzee contact data (Budongo, Uganda) and found that the network structure (i.e. clustering and path length) was robust to removal of the most central individuals; this may suggest that vaccinating central chimpanzees would offer only a slight advantage over random vaccinations. However, by breaking the contact structure into monthly networks (which better reflect the transmission of close-contact pathogens presented here: Material and methods) and simulating disease spread with various levels of transmissibility, our simulations indicate that network-based vaccinations can indeed offer benefits over random vaccinations for wild chimpanzees. Given that many pathogens spread through chimpanzee populations in less than a month (both in our temporal simulations and in observed outbreaks [25]), prophylactic vaccination is likely a more effective intervention option than treating sick individuals in the midst of an epidemic. Owing to herd immunity, our results predict that even the least effective (random) strategy would not require vaccinating the entire community to prevent an outbreak. Of the random and network-based strategies we tested, the most effective method was prophylactically vaccinating individuals based on weighted degree centrality. While a community's network could theoretically change from year to year, there is evidence of long-term stability in association patterns (of the order of 5–10 years) for the chimpanzee community examined here [21].

Further, our results suggest that strategic control strategies are feasible even without detailed interaction data. In these cases, immunizations targeting host traits associated with high contact rates could offer a more practical approach than centrality-based vaccinations. In this study community (n = 37), the impacts of trait-based control on the total number of animals requiring vaccination were somewhat modest; however, we expect that trait-based immunizations could substantially decrease the number of animals requiring vaccination for larger communities (such as the Ngogo chimpanzee community, n ∼ 150, in Kibale National Park, Uganda [45]) or for large populations of other wildlife species. Moreover, because many vaccines are administered to wildlife via hypodermic dart, there is always some expense and risk associated with immunizing endangered animals. For example, the darted animals could experience wounds, falls or adverse effects from the vaccine, and veterinarians or researchers could experience counterattacks or loss of trust from habituated animals. Thus, even moderate coverage reductions offer a valuable conservation advantage.

We recognize there are limitations of our study, including our ability to generalize findings to other habituated chimpanzee communities. A goal of future great ape studies might be to identify traits associated with centrality to shed light on inter-site differences, which could provide crucial information for designing vaccination strategies across populations. Second, our simulations revealed that the benefits of network-based immunizations over random vaccination could be minimal for highly contagious pathogens (where extremely high coverage is needed to protect populations from outbreaks). Third, we lack the detailed ecological data needed to determine the cause(s) of monthly differences in network connectivity (and thus outbreak size) in the proximity networks (but see the electronic supplementary material for evidence of an effect from the number of estrous females in party networks). Nevertheless, targeted vaccinations showed marked improvements over random control when averaged across months. Fourth, as is common among network epidemiology papers, our study assumes our definition of contact (i.e. proximity) corresponds to opportunities for pathogen transmission. While this assumption holds for many pathogens, it is not universal. Lastly, our models assumed that vaccinated individuals received full protection and that infected individuals had equal-length infectious periods. Future work aimed at relaxing these assumptions could help clarify the role that individual immunity plays in pathogen transmission dynamics and could further improve disease control efforts.

Despite some controversial cases (e.g. [46]), vaccination campaigns aimed at wildlife reservoirs [47,48] and endangered wildlife hosts [49,50] have successfully controlled some diseases. In particular, recent work on rabies in Ethiopian wolves showed that low vaccination coverage (informed by demographic and metapopulation distribution data) can effectively curtail large outbreaks and reduce the likelihood of host extinction [2]. Our finding that network-based vaccinations require less coverage than random vaccinations should apply broadly to other social wildlife species. New technologies, such as proximity-logging collars, have made collecting fine-scale association data more feasible than ever, even for elusive or nocturnal wildlife [51]. Thus, our methods for developing and assessing network-based control could readily be adapted to other host systems. Further, because index case centrality was highly associated with outbreak size, our results indicate that contact rates generate useful predictions for which individuals to vaccinate, even in lieu of mechanistic modelling. Overall, we argue that incorporating temporal contact variation into epidemiological models can help optimize disease control efforts across a range of host systems and could aid in the success of future wildlife vaccination campaigns.

The University of Georgia Institutional Animal Care and Use Committee approved our protocols (A2009-10062).

Funding statement

This research was supported by the US Fish and Wildlife Service Awards (96200-9-G250) and (96200-1-G183) to S.A., R.M.S. and J.R. Additional support to J.R. came from the Morris Animal Foundation (D10ZO-401), Fulbright, Margot Marsh Biodiversity Foundation, ARCS Foundation, Graduate Women in Science and the Primate Action Fund. D.C. was supported by NSF (DEB-0749097) to L.A.M.