Joint Model for a Diagnostic Test without a Gold Standard in the Presence of a Dependent Terminal Event

Abstract

Breast cancer patients after breast conservation therapy often develop ipsilateral breast tumor relapse (IBTR), whose classification (true local recurrence versus new ipsilateral primary tumor) is subject to error and there is no available gold standard. Some patients may die due to breast cancer before IBTR develops. Because this terminal event may be related to the individual patient’s unobserved disease status and time to IBTR, the terminal mechanism is non-ignorable. This article presents a joint analysis framework to model the binomial regression with misclassified binary outcome and the correlated time to IBTR, subject to a dependent terminal event and in the absence of a gold standard. Shared random effects are used to link together two survival times. The proposed approach is evaluated by a simulation study and is applied to a breast cancer dataset consisting of 4,477 breast cancer patients. The proposed joint model can be conveniently fit using adaptive Gaussian quadrature tools implemented in SAS procedure NLMIXED.

1 Introduction

The misclassification of a binary disease status in biomedical research due to imperfect sensitivity and specificity of a diagnostic test can have important ramifications for patient management. However, relative to a large body of methods on covariate measurement error, research on error- “contaminated outcomes,” such as a misclassified diagnostic status, has been quite limited [1, 2]. When the interest is in predicting a binary misclassified disease status from a group of covariates, Neuhaus [3] and Neuhaus[4] have clearly demonstrated that a naive analysis that ignores the misclassification leads to biased results in a variety of settings. Most available methods require the use of a gold standard, which can provide estimates of the sensitivity and specificity of the imperfect measure, and then incorporate these external estimates into the likelihood to obtain corrected effect estimates [5–8]. Or, if an internal validation subsample allowing comparison of an imperfect measure with the gold standard is available, a variety of techniques, e.g., those based on likelihood or on weighted estimating equations, have been proposed [9–12].

However, a gold standard or validation subsample may be unavailable, impractical [13, 14], expensive, time consuming, or unethical to perform on all subjects and is commonly difficult to obtain in clinical studies [15]. In the absence of a gold standard/validation subsample, few methods have been proposed for obtaining the accuracy of a single diagnostic test as most methods exploit the information contained in a battery of correlated imperfect diagnostic tests [16, 17]. For a single misclassified binary endpoint, early research by Rindskopf and Rindskopf [18] and Formann [19] utilized a latent class analysis that allows for the estimation of the characteristics of indicators when an accurate diagnosis was unavailable. Duffy et al [20] presented assumption-dependent corrections to odds ratios when the disease was misclassified; however, this approach requires a priori knowledge of the relationship in order to apply a correction factor. Moreover, Joseph et al [21] used a Bayesian approach to estimating diagnostic error for a single diagnostic test by specifying priors for disease prevalence, sensitivity, and specificity, but determining which priors to use may not be straightforward in all applications.

In light of a single imperfect diagnostic test for disease status, adjustment for potential bias due to misclassification requires information on the misclassification structure [22]. Nagelkerke et al [23] suggested modeling the unobserved true disease classification as a logistic function of an instrumental variable, which is considered as an additional parameter serving to increase the outcome degrees of freedom. This instrumental variable framework can be extended whereby survival information is used to inform the disease classification. In oncology research, time to a survival event such as tumor relapse is likely informative for diagnosis, and its utilization in a model conditional on true disease status is conceptually analogous to conditioning on an instrumental variable. But before the disease status and the time to tumor relapse are observed, the follow-up of some patients could be stopped by a terminal event such as disease-related death, or dropout due to adverse event or severe adverse event. Because this terminal event may be related to the individual patient’s unobserved disease status and time to tumor relapse, the terminal mechanism is non-ignorable. The dependent terminal event time is often termed “dependent censoring” or “informative censoring”. It has been shown in the joint modeling literature that ignoring the dependent censoring leads to biased estimates [24, 25]. However, to the best of our knowledge, there is no literature investigating the impact of ignoring the dependent censoring in the framework of binomial regression with misclassified binary outcome and a correlated survival time.

The goal of this article is to develop a joint analysis framework to model the binomial regression with misclassified binary outcome and the correlated time to IBTR, subject to a dependent terminal event and in the absence of a gold standard. The proposed model is applied to a data set on breast cancer relapse diagnosis after breast conservation therapy (BCT). The article proceeds as follows. Section 2 describes a motivating dataset. Section 3 formulates the joint statistical methodology. Section 4 presents results of a simulation study. Section 5 provides results of the motivating dataset analysis and comparisons with previously published findings. Section 6 gives a discussion.

2 Motivating Data

Tumor relapse after breast conservation therapy (BCT) for primary breast cancer has significant morbidity and mortality. Approximately 8–20% of patients undergoing BCT for primary breast cancer will experience ipsilateral breast tumor relapse (IBTR), defined as the relapse of the tumor in the treated breast [26, 27]. It is important to accurately classify true local recurrence (TR) from a new ipsilateral primary tumor (NP), as treatment regimens are markedly different for the two conditions. The TR diagnosis is consistent with regrowth of malignant cells that are not removed by the initial surgery, while the NP diagnosis is consistent with a de novo case of malignancy arising from mammary epithelial cells of the residual breast tissue. The correct classification of IBTR status has significant implications in therapeutic decision-making and patient management; for example, patients experiencing a TR usually benefit from a more aggressive hormone therapy, chemotherapy, and/or additional radiotherapy while NP patients often only require milder treatment. Currently, only imperfect histological test criteria are available to classify IBTR patients as TR or NP, for which there is no gold standard test. Statistically speaking, the binary diagnostic classification based on tumor histology suffers from misclassification.

The data from this study include 4,477 patients with invasive breast cancer who underwent BCT between 1970 and 2010 at The University of Texas MD Anderson Cancer Center. A total of 397 patients later developed IBTR as a first relapse and the remainder (4,080) did not develop IBTR (censored for relapse process). The data have been described elsewhere in detail [17, 28–30] and will now be presented in the context of the current study. Relevant variables collected include patient characteristics (age, race, family history of breast cancer, and other cancer history), contra lateral breast cancer (the occurrence of a second independent primary cancer in the other breast, location, histology, stage, size, estrogen receptor [ER] status), treatment characteristics (surgery, radiation), and patient status at last follow-up. IBTR status was classified as being either NP or TR using a single test based on tumor location and histologic subtype. Specifically, IBTR was defined as TR if the tumor was located within 3 cm of the primary tumor bed and its histologic subtype was consistent with that of the primary tumor; otherwise, IBTR was defined as NP [28–30]. Among the 397 patients with IBTR, 201 (50.6%) and 196 (49.4%) were classified as TR and NP, respectively. However, because of the inherent uncertainties of the clinical and pathologic criteria used for classification, this diagnostic test to classify IBTR was subject to misclassification.

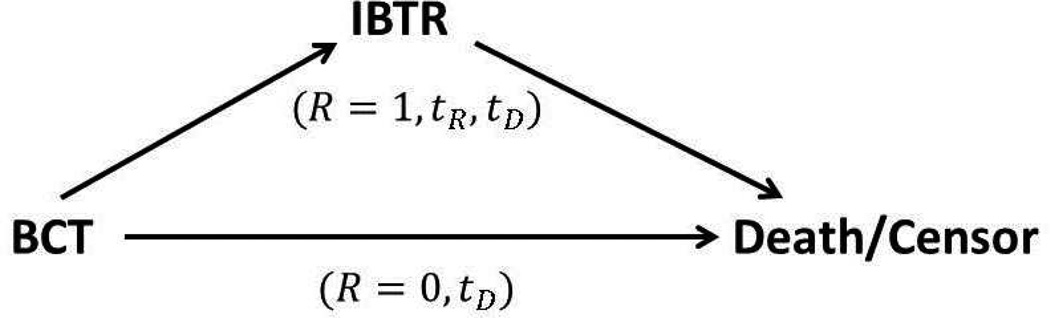
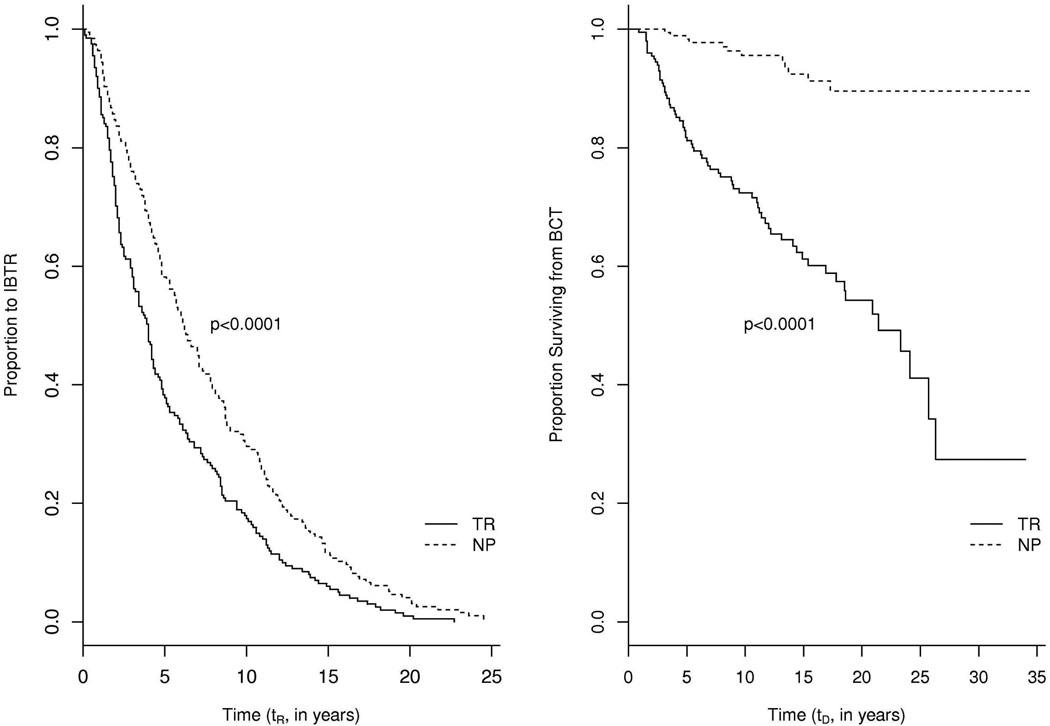
Figure 1 displays the data structures of the patients with or without IBTR, where R is an indicator of IBTR occurrence (1 if IBTR occurs, 0 otherwise), t_R is time from BCT to IBTR (referred to as time to IBTR), and t_D is time from BCT to breast cancer related death or censoring (referred to as time to death). While all patients have observed t_D, the patients with IBTR (R = 1) have one additional observable time t_R. Two interesting features of this patient dataset are: (1) the IBTR status is strongly correlated with both time to IBTR and time to death for the patients with IBTR; (2) the occurrence of IBTR is strongly correlated with time to death for all patients. To visualize the first correlation, Figure 2 displays the Kaplan-Meier curves showing differences in time to IBTR (t_R, left panels) and time to death (t_D, right panels) for patients with IBTR (R = 1, sample size N = 397) and classified as either NP or TR. The left panel indicates that TR patients have shorter time to IBTR than NP patients (log rank test p-value< 0.0001), while the right panel indicates that TR patients have shorter time to death than NP patients (log rank test p-value< 0.0001).

Figure 1.

Data structures of patients with or without IBTR. R is an indicator of IBTR occurrence (1 if IBTR occurs, 0 otherwise), t_R is time from BCT to IBTR, and t_D is time from BCT to death or censoring. BCT, breast conservation therapy; IBTR, ipsilateral breast tumor relapse.

Figure 2.

Kaplan-Meier curves for time from BCT to IBTR (left panel), time from BCT to death (right panel) in those who had IBTR (R = 1, sample size N = 397). P-values are from log rank tests. BCT, breast conservation therapy; IBTR, ipsilateral breast tumor relapse.

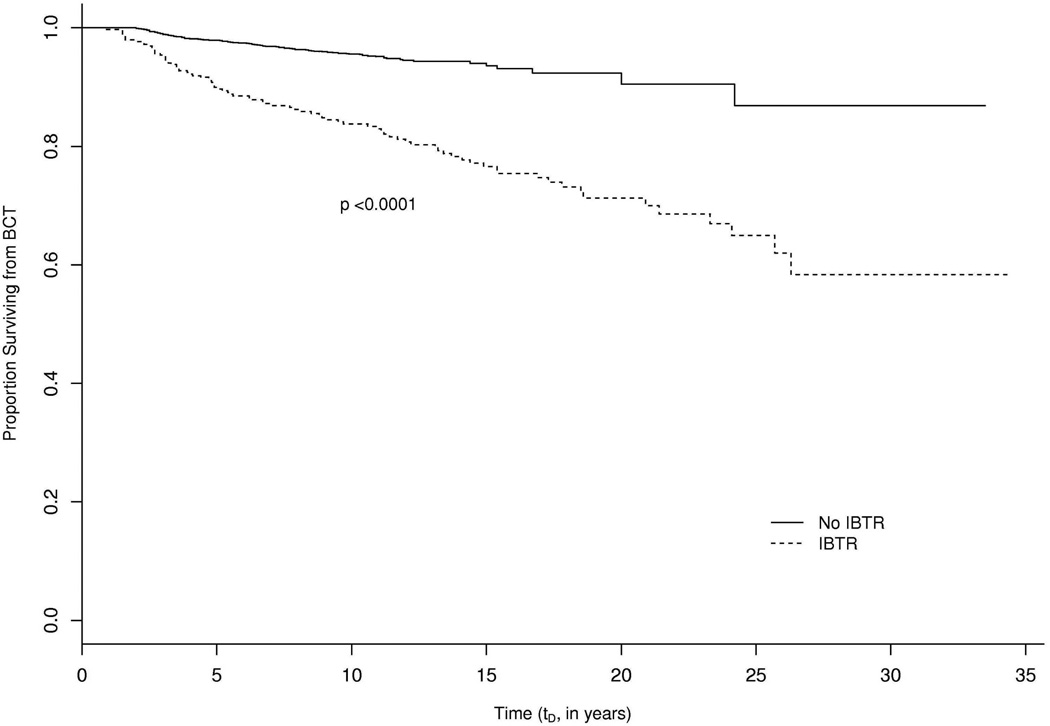
Among a total of 4,477 patients, 251 died of beast cancer. The occurrence of IBTR is likely informative for the time to breast cancer death. To visualize this correlation, Figure 3 displays the Kaplan-Meier curves showing differences in time to death for patients with or without IBTR. The patients with IBTR have shorter time to death than the ones without IBTR (log rank test p< 0.0001). Hence, the breast cancer related death is likely to be dependent terminal event. The purpose of this article is to develop a joint model of a misclassified binary outcome and time to relapse with dependent terminal event in order to (1) estimate the sensitivity and specificity of the diagnostic test, (2) quantify covariate effects on the probability of IBTR being NP and on the hazards of IBTR and the terminal event.

Figure 3.

Kaplan-Meier curves for time from BCT to death of all patients, sample size N = 4,477, with associated log rank test p-value. BCT, breast conservation therapy.

3 Statistical models and likelihood inference

3.1 Model and notation

In this section, a joint modeling framework for a single diagnostic test for IBTR status is formulated. Suppose R is an indicator of IBTR occurrence (1 if IBTR occurs, 0 otherwise). Let t_R be the time to IBTR and t_D = min(C,D), the minimum of an independent censoring time C and a dependent terminal event time D (e.g., breast cancer related death), respectively, both measured from the BCT. Let t_D denote time to death. Let δ (1 if breast cancer death is observed, 0 otherwise) be the censoring indicator. Let t = min(t_R, t_D). Thus, t = t_R and R = 1 for the patients with IBTR and t = t_D and R = 0 for the patients without IBTR. Suppose y (1 if NP, 0 if TR) is the unobserved true IBTR status. Let z (1 if NP, 0 if TR) be the observed outcome from the error-prone diagnostic test. Let p and q be the sensitivity and specificity of the test given the true IBTR status y, i.e., p = p(z = 1|y = 1) and q = p(z = 0|y = 0). Hence, the sensitivity and specificity are the probabilities of correctly classify NP and TR patients, respectively.

Denote x_P, x_R, and x_D as covariate vectors for the probability of IBTR being NP, time to IBTR, and time to death, respectively. Three covariate vectors can be the same or different. The following assumptions are made: (a) the sensitivity p and specificity q do not depend on covariates (non-differential assumption); (b) the times to IBTR and breast cancer death for the same patient are correlated through a shared frailty $u~N(0,{\sigma }_u^2)$; (c) the diagnostic test results, time to IBTR, and time to death are independent conditional on the frailty u and covariate vectors. The binomial regression model for the probability that the IBTR being NP is

$$\pi ({\mathit{x}}_P)=P(y=1|{\mathit{x}}_P)=g^{-1}({\mathit{x}}_P\mathit{\alpha }),$$ (1)

where α is the corresponding vector of regression coefficients, and g⁻¹ is the inverse of a link function (e.g., probit, logit, complementary log-log). Specifically, the logit link function is used in this article. The likelihood of observing outcome z for one patient is f(z|x_P) = [πp + π̅q̅]^z [πp̅ + π̅q]^z̅, where the overhead bar denotes 1 minus the variable (e.g., π̅ = 1 − π).

The hazard of breast cancer death is modeled by

$$\lambda (t_D)={\lambda }_0(t_D)\text{exp}({\mathit{x}}_D\mathit{\eta }+u),$$ (2)

where λ₀(t_D) is the baseline hazard, with corresponding survival function being $S(t_D)=\text{exp}[-\text{exp}({\mathit{x}}_D\mathit{\eta }+u){\int }_0^{t_D}{\lambda }_0(t)dt]$. The hazard function of time to IBTR t_R is

$$r^N(t)=r_0(t)\text{exp}({\mathit{x}}_R\mathit{\beta }+\gamma u),$$ (3)

where the superscript N denotes NP status, r₀(t) is baseline hazard for IBTR. The corresponding survival function $S^N(t)=\text{exp}[-\text{exp}({\mathit{x}}_R\mathit{\beta }+\gamma u){\int }_0^t{r}_0(x)dx]$, The hazard for TR patients is r^T (t) = r₀(t) exp(x_Rβ + ζ + γu), where ζ describes the additional hazard of being TR patients compared with NP patients and the superscript T denotes TR status. The hazard functions of IBTR and death are linked together via the shared random effect u and the parameter γ measures the association between two models. The likelihood of the relapse process is

$$L_1(\mathit{\theta }|u)={\left\{{[\pi p{r}^N(t)S^N(t)+\mathrm{\pi ̅}\mathrm{q̅}{r}^T(t)S^T(t)]}^z{[\pi \mathrm{p̅}{r}^N(t)S^N(t)+\mathrm{\pi ̅}q{r}^T(t)S^T(t)]}^{\mathrm{z̅}}\right\}}^R·{\{[\pi S^N(t)+\mathrm{\pi ̅}{S}^T(t)]\}}^{1-R},$$ (4)

where the unknown parameter vector θ=(α, β, η, σ_u, ζ, γ, p, q). The likelihood of the death process is

$$L_2(\mathit{\theta }|u)={[\lambda (t_D)]}^{\delta }S(t_D).$$ (5)

Thus, the marginal likelihood for one patient is

$$L(\mathit{\theta })=\int L(\mathit{\theta }|u)f(u)du=\int L_1(\mathit{\theta }|u)L_2(\mathit{\theta }|u)f(u)du.$$ (6)

The proposed model, L (θ), is referred to as joint model. In addition the reduced model refers to the analysis of maximizing L₁(θ|u) and L₂(θ|u) separately by assuming the time to IBTR is independent of time to death (i.e., γ = 0).

3.2 Maximum likelihood estimation

The marginal likelihood function in (6) involves an integral with respect to random effects u and this integral cannot be evaluated analytically. Numerical integration such as Laplace approximation [31], Gaussian quadrature [32], can be used for estimation. Liu et al [33] pointed out that both methods generally perform well, with the Laplace approximation being much faster in high dimensional random effects settings. However, Laplace approximation is not yet available in commercial software packages for fitting nonlinear mixed effects models, while Gaussian quadrature can be conveniently implemented in SAS procedure NLMIXED. Thus, adaptive Gaussian quadrature is adopted to approximate the integral in model (6). In numerical analysis, a quadrature rule is an approximation of the definite integral by a weighted sum of function values at specified points within the domain of integration. Moreover, the adaptive Gaussian quadrature method accounts for the shape of the likelihood when placing quadrature points and provides a better approximation than the non-adaptive Gaussian quadrature with equally spaced points [34]. In addition to accurate parameter estimates and available standard error estimates, this estimation approach possesses the advantage of easy implementation because SAS procedure NLMIXED requires inputting the likelihood (conditional on random effects) explicitly and the approximation of the marginal likelihood can be directly maximized.

However, with the unspecified baseline hazard functions r₀(t) and λ₀(t_D), there are non-parametric terms (i.e., baseline hazard functions) in the likelihood functions L₁(θ|u) in (4) and L₂(θ|u) in (5). Hence, the adaptive Gaussian quadrature method is not directly applicable. Instead, a piecewise constant function to approximate the baseline hazard function r₀(t) and λ₀(t_D) is used. It has been shown that survival models with a piecewise constant baseline hazard with 8 to 10 intervals yield good estimators for both fixed effects and frailty [35, 36], although fixed cut points need to be specified a priori. It is more flexible than the a priori choices of parametric baseline hazard distribution (e.g., Weibull distribution) and it retains enough model structure [32]. Piecewise constant baseline hazard function has been widely used in the literature [32, 37, 38]. Given a set of fixed time points τ_D = (τ_D0, …, τ_Dm) with the constraint 0 = τ_D0 < τ_D1 < .… < τ_Dm, and the baseline hazard vector g_D = (g_D0, g_D1, …, g_D−1) for the time to death t_D, the piecewise constant baseline hazard function is defined as ${\lambda }_0(t_D)={\sum }_{l=0}^{m-1}{g}_{D1}{I}_l(t_D)$, with indicator function I_l(t_D) = 1 if τ_l ≤ t_D < τ_l+1 and 0 otherwise. Similarly, the piecewise constant baseline hazard function r₀(t) for time to IBTR can be defined based on a fixed time points vector τ_R and a baseline hazard vector g_R. The marginal likelihood L(θ) in model (6) can be approximated by replacing r₀(t) and λ₀(t_D) by their piecewise constant counterparts. The resulting parametric likelihood is maximized by SAS procedure NLMIXED. An example of SAS code for fitting the proposed model with piecewise constant baseline hazard functions is presented in the Appendix.

4 Simulation studies

This section presents results from a simulation study of two settings to compare the performance of the proposed joint model and reduced model. The simulated data structure is similar to but simpler than the motivating dataset. In each setting, 3,000 datasets are generated with sample size N = 500 using the following algorithm.

1. Simulate y from a Bernoulli distribution with π generated from logit(π) = x_Pα in model (1) with α = (−2, 3, 4) and x_P = (1, x₁, x₂) with x₁ ~ N(0, 1) and x₂ ~ Bernoulli(0.3).

2. Simulate the frailty $u~N(0,{\sigma }_u^2)$ with ${\sigma }_u^2=3$.

3. Set the baseline hazard function for the time to death as λ₀(t) = t^−0.5 in model (2) and set η = (0.5, 0.5) and x_D = (x₁, x₂). Simulate S_D from uniform(0, 1) and generate uncensored time D for the terminal event, subject to independent censoring time C. Obtain t_D = min(C, D) and the censoring indicator δ.

4. Set the baseline hazard function for the time to relapse as r₀(t) = 1.5t^−0.5 in model (3) and set β = (0.5, 0.5), x_D = (x₁, x₂), and ζ = 3. Set γ = 0 for setting I and set γ = 0.5 for setting II. Conditional on y, simulate S^N and S^T from uniform (0, 1) and generate t_R for the relapse process. If t_R ≤ t_D, set R = 1 and simulate z with sensitivity p and specificity q. If t_R > t_D, set R = 0 and IBTR is not observed.

5. Repeat steps 1 to 4 until all patients are generated.

In setting I, the terminal event is independent of the relapse process subject to misclassification (i.e., γ = 0) and the reduced model is the true model. In setting II, the terminal event is dependent on the relapse process subject to misclassification (i.e., γ = 0.5), which is likely a reasonable estimate for the application of interest, considering Figure 3. So in setting II, the proposed joint model is the true model. The simulation results presented in Tables 1 and 2 report the bias, standard error (SE) of parameter estimates, mean of standard error estimates (SEM), and coverage probability (CP) of 95% confidence interval for each parameter of interest under the joint and reduced models defined in Section 3.

Table 1.

Simulation results of fitting the proposed joint model and the reduced model for setting I in which the terminal event is independent on the relapse process subject to misclassification.

	Joint Model				Reduced Model
Parameter	Bias	SE	SEM	CP	Bias	SE	SEM	CP
For the probability of IBTR being NP
α0 = −2	−0.082	0.319	0.312	0.952	−0.056	0.316	0.306	0.952
α1 = 3	0.102	0.433	0.419	0.947	0.083	0.427	0.414	0.946
α2 = 4	0.117	0.624	0.608	0.947	0.094	0.624	0.603	0.946
p = 0.8	0.006	0.056	0.055	0.921	0.002	0.056	0.055	0.933
q = 0.9	−0.000	0.020	0.020	0.940	0.000	0.021	0.020	0.939
For the time to IBTR
β1 = 0.5	0.014	0.091	0.091	0.946	0.003	0.088	0.085	0.938
β2 = 0.5	0.012	0.185	0.183	0.950	0.003	0.181	0.175	0.941
ζ = 3	0.108	0.266	0.278	0.953	0.031	0.238	0.233	0.945
For the time to terminal event
η1 = 0.5	0.075	0.128	0.121	0.950	0.004	0.071	0.069	0.944
η2 = 0.5	0.076	0.188	0.190	0.959	0.002	0.139	0.138	0.950
γ = 0	0.079	1.044	1.863	0.998

Table 2.

Simulation results of fitting the proposed joint model and the reduced model for setting II in which the terminal event is dependent on the relapse process subject to misclassification.

	Joint Model				Reduced Model
Parameter	Bias	SE	SEM	CP	Bias	SE	SEM	CP
For the probability of IBTR being NP
α0 = −2	−0.015	0.355	0.338	0.915	0.061	0.345	0.358	0.926
α1 = 3	0.047	0.459	0.461	0.926	−0.097	0.459	0.476	0.915
α2 = 4	0.036	0.644	0.660	0.940	−0.118	0.651	0.688	0.935
p = 0.8	0.009	0.072	0.069	0.916	−0.008	0.073	0.074	0.942
q = 0.9	0.001	0.022	0.022	0.940	0.002	0.022	0.022	0.940
For the time to IBTR
β1 = 0.5	0.003	0.124	0.117	0.946	−0.112	0.099	0.093	0.752
β2 = 0.5	−0.004	0.251	0.235	0.936	−0.105	0.211	0.203	0.903
ζ = 3	0.053	0.378	0.355	0.936	−0.316	0.262	0.262	0.769
For the time to terminal event
η1 = 0.5	0.026	0.139	0.149	0.958	−0.207	0.066	0.065	0.122
η2 = 0.5	0.012	0.261	0.264	0.953	−0.215	0.142	0.135	0.645
γ = 0.5	0.026	0.262	0.262	0.880

Table 1 suggests that setting I with no correlation (i.e., γ = 0), the reduced model gives reasonable parameter estimates, i.e., the bias is negligible, SE is close to SEM, and the confidence interval coverage probabilities are reasonably close to 0.95 nominal level. In comparison, the joint model generates comparable results with slightly larger bias, SE, and SEM. Under model over parameterization, the estimate of γ from the joint model is correctly close to zero, although the standard error estimate is slightly inflated.

Table 2 suggests that in setting II with some correlation (i.e., γ = 0.5), the joint model provides less biased estimates of covariate effects on time to IBTR (β) and time to terminal event (η) than the reduced model. Although the standard errors of the parameter estimates are similar for the parameters predicting the probability of IBTR (α), when events are assumed to be independent, the standard errors of covariate effects related to the two event processes (i.e., β and η) are drastically underestimated, as would be expected under the incorrect assumption of independence of event times. Correspondingly, the estimated coverage probabilities are nearer to the 0.95 nominal level for the joint model versus the reduced model. For parameters related to the times to IBTR and terminal event (i.e., β and η), the coverage probabilities produced by the reduced model are extremely inaccurate. Further, the parameter estimate of ζ, which represents the additional log hazard of being TR versus NP, is highly negatively biased when fitting the reduced model, since the dependency of the events cannot be accurately measured by assuming independent likelihoods. In comparison, the true value of ζ in simulation is adequately recovered by the joint model.

The proposed joint modeling framework is a shared random effects model, in which two survival models share a function of the random effects. This model has been widely used in joint model literature. Another alternative is multivariate random effects survival models, which assume two survival processes are linked by a vector of two correlated random effects. Specifically, models (2) and (3) are expressed as λ (t_D) = λ₀(t_D) exp(x_Dη+u₁) and r^N(t) = r₀(t) exp(x_Rβ+u₂), respectively, where u = (u₁, u₂)′ ~ N (0, Σ) with Σ being denoted as $(({\sigma }_1^2,\rho {\sigma }_1{\sigma }_2),(\rho {\sigma }_1{\sigma }_2,{\sigma }_2^2))$. However, this model is unidentifiable in this context because each breast cancer patient can possibly have only one IBTR occurrence and one breast cancer death. There is insufficient information to identify parameters in the multivariate random effects correlation matrix. Nevertheless, it is essential to assess the robustness of the proposed joint model under random effects structure misspecification. We simulate 1, 000 datasets from the multivariate random effects survival model with ${\sigma }_1^2=1,{\sigma }_2^2=2$, and ρ = 0.636 and all other parameters identical to setting II. Table 3 compares the simulation results from the joint and reduced models. The results indicate that the proposed joint model provides reasonable results to all parameters with relatively small bias, SEM being close to SE, and CP being around the nominal value. In contrast, the reduced model gives biased estimates and low CP, especially for α, β, η, and ζ, although the estimation results for the sensitivity p and specificity q are reasonably good.

Table 3.

Simulation results of fitting the proposed joint model and the reduced model where data are simulated from the multivariate random effects survival model.

	Joint Model				Reduced Model
Parameter	Bias	SE	SEM	CP	Bias	SE	SEM	CP
For the probability of IBTR being NP
α0 = −2	−0.062	0.436	0.389	0.906	0.117	0.411	0.380	0.872
α1 = 3	0.092	0.560	0.514	0.918	−0.115	0.547	0.503	0.875
α2 = 4	0.140	0.794	0.728	0.928	−0.162	0.744	0.719	0.896
p = 0.8	0.008	0.069	0.066	0.908	−0.004	0.070	0.069	0.931
q = 0.9	0.001	0.022	0.022	0.942	0.000	0.023	0.022	0.929
For the time to IBTR
β1 = 0.5	−0.002	0.135	0.122	0.930	−0.122	0.093	0.092	0.721
β2 = 0.5	0.012	0.260	0.241	0.935	−0.118	0.21	0.196	0.883
ζ = 3	−0.005	0.428	0.400	0.917	−0.526	0.26	0.253	0.442
For the time to terminal event
η1 = 0.5	0.010	0.111	0.114	0.954	−0.111	0.071	0.066	0.608
η2 = 0.5	0.015	0.195	0.197	0.960	−0.112	0.134	0.136	0.875

The simulation study suggests that the joint model provides results comparable to the reduced model under the independent terminal event (setting I). Under the dependent terminal mechanism (setting II), the joint model provides more accurate estimates for the regression parameters of the probability of IBTR and two survival times than the reduced model. Moreover, when the random effects structure is misspecified, the proposed joint model still provides accurate estimates for all parameters of interest while the reduced model gives biased estimates to most parameters.

5 Real Data Analysis

In this section, the methods are applied to the breast cancer patient dataset (n = 4,477). The terminal event is defined as the breast cancer related death (251 patients), all other terminal events (e.g., death unrelated to breast cancer, censoring) are treated as independent censoring. The following 3 covariates are considered: x₁ represents age at breast cancer diagnosis (mean: 55.4 years; SD: 12.1 years); x₂ represents whether a distant recurrence developed in organs other than breasts (e.g., bones, lung, brain, liver; prevalence: 7.5%); x₃ represents primary tumor stage (1 if more aggressive stage II or higher and 0 otherwise; prevalence: 23.1%) [39]. Let x_P = (1, x₁, x₂, x₃) and x_R = x_D = (x₁, x₃).

We use the adaptive Gaussian quadrature estimation method. To specify the baseline hazard functions λ₀(t_D) and r₀(t), we divide the time to IBTR and time to breast cancer death into M₁ and M₂ intervals by every 1/M₁th and 1/M₂th quantiles, respectively. We adopt M₁ = M₂ = 4 in this article. We have also explored other selections of M₁ and M₂ and the results are very similar. For model selection and comparison, the A kaike information criterion (AIC) [40] and Bayesian information criterion (BIC) are computed [41]. The joint model performs significantly better than the reduced model with smaller AIC (7, 578. 0 v.s. 7, 632.6) and BIC (7, 687.0 v.s. 7, 728.7).

Table 4 provides the means, SE, p values, and 95% confidence interval (CI) of the parameters from the proposed joint model (6). Covariate interpretation is as follows. The odds ratio of the IBTR being NP for the patients who developed distant recurrence is 0.012 (i.e., exp(−4.435); 95% CI: [4.273e − 4, 0.329]) versus the patients who did not develop distant recurrence. The covariates age at diagnosis and tumor stage are not statistically significant. These findings are consistent with the results of previous studies [28–30]. The sensitivity and specificity estimates of the diagnostic test are 0.648 (95% CI: [0.494, 0.802]) and 0.873 (95% CI: [0.757, 0.988]), respectively. Thus, this diagnostic test is more likely to correctly classify TR patients than NP patients. Because TR patients tend to have shorter time from BCT to IBTR and need more aggressive treatment than NP patients, the misclassification of TR patients into NP is likely to be more costly than vice versa.

Table 4.

The maximum likelihood estimates (MLE), standard errors (SE), p-values, and 95% confidence interval (CI) of the parameters from the proposed joint model.

	MLE	SE	P	95% CI
For the probability of IBRT being NP
intercept	4.298	2.511	0.087	[−0.626, 9.222]
Age	−0.006	0.031	0.855	[−0.066, 0.055]
Distant	−4.435	1.695	0.009	[−7.758, −1.111]
Stage	−0.730	0.898	0.417	[−2.490, 1.031]
p	0.648	0.079		[0.494, 0.802]
q	0.873	0.059		[0.757, 0.988]
For the time to IBTR
Age	−0.053	0.006	< 0.001	[−0.065, −0.041]
Stage	−0.015	0.171	0.928	[−0.350, 0.319]
ζ	1.826	0.350	< 0.001	[1.140, 2.511]
For the time to breast cancer death
Age	−0.027	0.006	< 0.001	[−0.039, −0.015]
Stage	1.088	0.149	< 0.001	[0.796, 1.380]
γ	0.532	0.144	< 0.001	[0.249, 0.815]
${\sigma }_u^2$	1.592	0.433

The covariate effects on time to IBTR are interpreted as follows. The hazard rate of IBTR is 0.588 (i.e., exp(−0.53); 95% CI: [0.522, 0.664]) for every 10-year increase in the covariate age at breast cancer diagnosis. The TR status significantly increases the hazard of IBTR, with an hazard rate of 6.209 (i.e., exp(1.826); 95% CI: [3.127, 12.317]) compared with NP patients. This large difference in hazard between TR and NP statuses is visually identifiable by the Kaplan-Meier curves (Figure 2) and has also been reported previously [28, 29, 42]. Finally, the hazard rate of breast cancer death is 0.763 (i.e., exp(−0.27); 95% CI: [0.677, 0.861]) for every 10-year increase in age at breast cancer diagnosis. The hazard rate of breast cancer death is 2.968 (i.e., exp(1.088); 95% CI: [2.217, 3.975]) for the patients with higher tumor stage as compared with the ones with lower tumor stage. For model association, note that γ̂ is significantly larger than zero (mean: 0.532, p < 0.001, 95% CI: [0.249, 0.815]), indicating that patients with larger hazard of breast cancer death tend to have IBTR earlier. The statistical significance of γ̂ also suggests that the time to death is strongly correlated to the time to relapse, which justifies the need of joint modeling.

6 Discussion

This article presents a joint analysis method to model the binomial regression with a single misclassified binary outcome and the correlated time to IBTR, subject to a dependent terminal event and in the absence of a gold standard. The models of time to IBTR and time to the terminal event are linked together via shared random effects. The simulation study shows that when the terminal event is independent of the relapse process, the proposed joint model provides comparable results to the reduced model. However, when there exists a dependent terminal event, the joint model provides accurate estimates of all parameters while the reduced model gives severely biased estimates for the regression parameters for the probability of NP at IBTR, and the two survival times. The analysis of the breast cancer dataset indicates that the target diagnostic test has higher specificity than sensitivity (i.e., more likely to correctly classify TR patients than NP patients). This is preferable because TR patients tend to have shorter time to IBTR and need more aggressive treatment than NP patients and the misclassification of TR patients into NP is likely to be more costly than vice versa. Further, our analysis results provide useful information in identifying and quantifying the covariate effects on the probability of IBTR status and survival times. From the analysis results, we found that the sensitivity and specificity of the diagnostic test, which uses only clinical and pathological criteria, are low. A more accurate diagnostic test using the molecular criteria should be developed in the future, as pointed out by Huang et al [28]. The proposed method can be broadly applied to many studies with similar data structure consisting of misclassified binary outcome and a dependent terminal event. The proposed joint model can be conveniently fit using adaptive Gaussian quadrature tools implemented in SAS procedure NLMIXED and can be easily accessible to, modified, and extended by applied researchers.

The difficulty of estimating diagnostic accuracy without a gold standard has been discussed in the literature. For example, Albert and Dodd [43] showed that the estimation of diagnostic accuracy and prevalence is sensitive to the choice of dependence structure for studies with multiple diagnostic tests. They hence recommended collecting gold standard information on a fraction of subjects if possible, doing a sensitivity analysis using very different methods for accounting for multiple test dependence, and taking a large number of tests. However, there is only a single imperfect diagnostic test in this article. It requires information on the misclassification structure to make the model identifiable [22]. The covariates in x in modeling IBTR status in model (1) are instrumental variables and they make the sensitivity and specificity parameters identifiable when their number of different possible realizations is sufficient [23]. Moreover, the survival information included in the proposed model is an important determinant of IBTR status. This is manifested by the clear dichotomy in the Kaplan-Meier curves displayed in Figure 2. The detailed discussion of the identifiability, modeling, and parameter estimation of multiple conditional dependent diagnostic tests can be found in some recent literature, e.g., Dendukuri and Joseph [44], Georgiadis et al [45], and Jones et al [46].

The joint modeling strategy has several limitations that can be addressed in future research. One limitation is the non-differential assumption, i.e., the sensitivity and specificity do not depend on the covariates. This assumption has been relaxed in some statistical literature [47]. We will explore this extension in the future research. In addition, this article only considers a single type terminal event. In the presence of multiple failure types, e.g., death due to breast cancer and other causes, the proposed joint model can be extended to accommodate competing risks survival data. One alternative to the proposed joint model is the models based on pattern mixture modeling (PMM) which stratifies the subjects into subgroups by their censoring patterns, and then models the stratified subgroups separately, e.g., Hogan and Laird [48, 49], Molenberghs and Verbeke [50], Zhang et al [51]. We would like to investigate the application of the PMM model to the proposed joint modeling framework. Another issue is the normality assumption of random effects in our joint model. Some researchers [52, 53] have reported that the statistical inference of joint models is generally robust to the departure from the normality assumption. It is of interest to investigate our joint model’s performance when the underlying random effects distribution is symmetric non-normal or even asymmetric. Moreover, the random effects variance is assumed to be homogeneous (same for all individuals). However, the random effects variance may depend on subject-specific characteristics and is thus heterogeneous. Ignoring the heterogeneity can result in biased estimates [54, 55]. As a future direction, we would address the non-normal and heterogeneous random effects issues in the proposed joint modeling framework.

Appendix

/* Invoke proc nlmixed using adaptive Gaussian Quadrature */
proc nlmixed data=piecewise hess maxit=8000 MAXFUNC=8000;
     /* define the array */
    * piecewise constant function for death
    array r_D{3} r_D1-r_D3;
    * cut points for the intervals of death event
    array tau_D{4} tau_D1-tau_D4;
    * piecewise constant function for IBTR
    array r_R{3} r_R1-r_R3;
    * cut points for the intervals of IBTR
    array tau_R{4} tau_R1-tau_R4;
    * initialize parameters
    parms se=0.7, sp=0.7, sigma2_u=1.5, zeta=2, gamma=0.3,
        r_D1=0.5, r_D2=0.5, r_D3=0.3, r_R1=0.8, r_R2=0.8, r_R3=0.6;
    * set boundaries for parameters
    bounds 1>se>0, 1>sp>0, sigma2_u>0, r_D1 r_D2 r_D3 r_R1 r_R2 r_R3 >0;
    * specify the cut points for the intervals
    tau_R[1]=0; tau_R[2]=2.5; tau_R[3]=8; tau_R[4]=20;
    tau_D[1]=0; tau_D[2]=2.5; tau_D[3]=8; tau_D[4]=20;
     *Calculate the cumulative hazard for relapse and death processes;
    G_D=0; G_R=0; G_DR=0;
    do i=1 to 3;
        if i<IndicatorD then G_D=G_D+r_D[i]*(tau_D[i+1]-tau_D[i]);
if i<IndicatorR then G_R=G_R+r_R[i]*(tau_R[i+1]-tau_R[i]);
if i<IndicatorDR then G_DR=G_R+r_R[i]*(tau_R[i+1]-tau_R[i]);
if i=IndicatorD then G_D=G_D+(T_D-tau_D[i])*r_D[i];
if i=IndicatorR then G_R=G_R+(T_R-tau_R[i])*r_R[i];
if i=IndicatorDR then G_DR=G_R+(T_D-tau_R[i])*r_R[i];
        end;
    eta_p=alpha0+alpha1*x1;
    eta_D=eta1*x1+u;
    eta_TR=beta1*x1+gamma*u+zeta;
    eta_NP=beta1*x1+gamma*u;
    pi=exp(eta_p)/(1+exp(eta_p));
    lambda_tD=r_D[IndicatorD]*exp(eta_D);
    r_TR=r_R[IndicatorR]*exp(eta_TR);
    r_NP=r_R[IndicatorR]*exp(eta_NP);
    S_D=exp(−exp(eta_D)*G_D);
    S_TR= exp(−exp(eta_TR)*G_R);
    S_NP= exp(−exp(eta_NP)*G_R);
    S_TRD= exp(−exp(eta_TR)*G_DR);
    S_NPD= exp(−exp(eta_NP)*G_DR);
     *Calculate the log likelihood;
    if R eq 1 then do;
        if z eq 1 then ll=log(pi*se*r_NP*S_NP+(1-pi)*(1-sp)*r_TR*S_TR)+delta*log(lambda_tD)+log(S_D);
        if z eq 0 then ll=log(pi*(1-se)*r_NP*S_NP+(1-pi)*sp*r_TR*S_TR)+delta*log(lambda_tD)+log(S_D);
        end;
    if R eq 0 then ll=log(pi*S_NPD+(1-pi)*S_TRD)+delta*log(lambda_tD)+log(S_D);
     *specify random effect;
    random u~normal(0,sigma2_u) subject=id;
    model z~general(ll);
run;