Abstract
Classical rate theories often fail in cases where the observable(s) or order parameter(s) used is a poor reaction coordinate or the observed signal is deteriorated by noise, such that no clear separation between reactants and products is possible. Here, we present a general spectral two-state rate theory for ergodic dynamical systems in thermal equilibrium that explicitly takes into account how the system is observed. The theory allows the systematic estimation errors made by standard rate theories to be understood and quantified. We also elucidate the connection of spectral rate theory with the popular Markov state modeling approach for molecular simulation studies. An optimal rate estimator is formulated that gives robust and unbiased results even for poor reaction coordinates and can be applied to both computer simulations and single-molecule experiments. No definition of a dividing surface is required. Another result of the theory is a model-free definition of the reaction coordinate quality. The reaction coordinate quality can be bounded from below by the directly computable observation quality, thus providing a measure allowing the reaction coordinate quality to be optimized by tuning the experimental setup. Additionally, the respective partial probability distributions can be obtained for the reactant and product states along the observed order parameter, even when these strongly overlap. The effects of both filtering (averaging) and uncorrelated noise are also examined. The approach is demonstrated on numerical examples and experimental single-molecule force-probe data of the p5ab RNA hairpin and the apo-myoglobin protein at low pH, focusing here on the case of two-state kinetics.
I. INTRODUCTION
The description of complex molecular motion through simple kinetic rate theories has been a central concern of statistical physics. A common approach, first-order rate theory, treats the relaxation kinetics among distinct regions of configuration space by single-exponential relaxation. Recently, there has been interest in estimating such rates from trajectories of single molecules, resulting from the recent maturation of measurement techniques able to collect extensive traces of single-molecule extensions or fluorescence measurements [1,2]. When the available observable is a good reaction coordinate, in that it allows the slowly converting states to be clearly separated [see Fig. 2(I), left], classical rate theories apply and the robust estimation of transition rates is straightforward using a variety of means [3]. However, in the case in which the slowly converting states overlap in the observed signal [see Fig. 2(III), left], either due to the fact that the molecular order parameter used is a poorly separates them or there is large noise of the measurement (see the discussion in Refs. [4,5]), a satisfactory theoretical description is missing and many estimators break down.
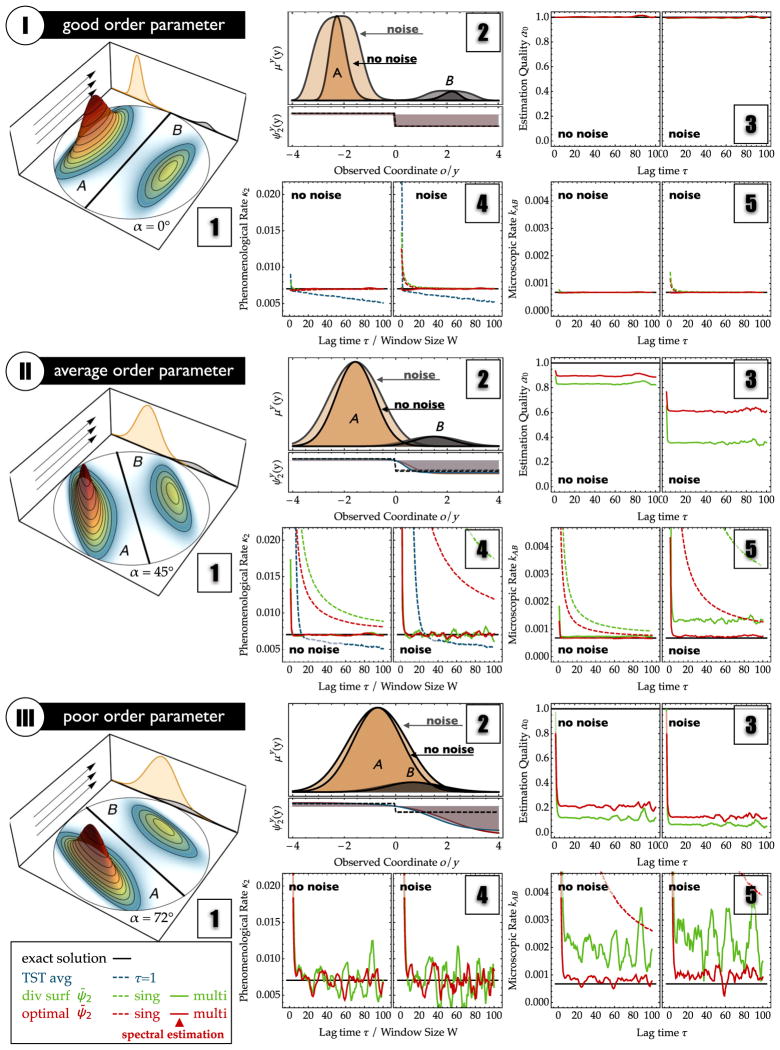
FIG. 2.
Estimation results using overdamped Langevin dynamics in a two-dimensional two-well potential that is projected onto different observables: (I) perfect projection, (II) average-quality projection, (III) poor projection. Results are compared without noise (left half of panels) and with additional measurement noise (right half of panels). (1) Full state space with indicated direction of the used order parameter. (2) Top: Stationary density μy(y) in the observable of the two partial densities of states A (orange) and B (gray). Results with noise are shaded lighter and are more spread out. Bottom: Second eigenvector without noise (solid, blue), with noise (solid, red), and dividing surface (black, dashed line). (3) Estimation quality α from spectral estimation (OQ, red line), and from exponential fitting to the number correlation function using a diving surface at y = 0 (green line). (4) Estimated relaxation rate κ2: TST with averaging window of size W (indicated in the x axis). Dividing surface at o = 0 with single-τ (dashed green line) and multi-τ (solid green line) estimators. Estimates from a MSM-derived second eigenvector ψ̃2 with a single-τ estimate (normal MSM, dashed red line) and multi-τ estimate (spectral estimation, solid red line). The black line is the reference solution, obtained from a direct MSM estimate for τ = 50 in row 1. (5) The transition rates kAB from state A to B. The coloring is identical to panels (4).
Most two-state rate theories and estimators are based on dividing the observed coordinate into a reactant and a product substate and then in some way counting transition events that cross the dividing surface. Transition state theory (TST) measures the instantaneous flux across this surface, which is known to overestimate the rate due to the counting of unproductive recrossings over the dividing surface on short time scales [6].
Reactive flux theory [7] copes with this by counting a transition event only if it has succeeded to stay on the product side after a sufficiently long lag time τ. Reactive flux theory involves derivatives of autocorrelation functions that are numerically unreliable to evaluate [8]. In practice, one therefore typically estimates the relaxation rate via integration or by performing an exponential fit to the tail of a suitable correlation function, such as the number correlation function of reactants or the autocorrelation function of the experimentally measured signal [3,9,10]. In order to split this relaxation rate into a forward and backward rate constant, a clear definition of the reactant and product substates is needed, which is difficult to achieve when these substates overlap in the observed signal.
Markov state models (MSMs) have recently become a popular approach to producing a simplified statistical model of complex molecular dynamics from molecular simulations. While applicable only when the discretization of state space succeeds in separating the metastable conformations, these models can be regarded as steps towards a multistate rate theory. MSMs use a transition matrix describing the probability that a system initially found in a substate i is found in substate j a lag time τ later. When the state division allows the metastable states of the system to be distinguished [11–14], the transition matrix with a sufficiently large choice of τ can be used to derive a phenomenological transition rate matrix that accurately describes the interstate dynamics [15]. This is explicitly done for the two-state case in Ref. [8]. It was shown in Refs. [14,16] that by increasing the number of substates used to partition state space, and hence using multiple dividing surfaces instead of a single one, these rate estimates become more precise. In the limit of infinitely many discretization substates, the eigenfunctions of the dynamical propagator in full phase space are exactly recovered, and the rate estimates become exact even for τ → 0+ [17]. In practice, however, a finite choice of τ is necessary in order to have a small systematic estimation error, especially if “uninteresting” degrees of freedom such as momenta or solvent coordinates are discarded. An alternative way of estimating transition rates is by using a state definition that is incomplete and treats the transition region implicitly via committor functions that may better approximate the eigenfunctions of the dynamical propagator in this region [18–20].
The quality of the rate estimates in all of the above approaches relies on the ability to separate the slowly converting states in terms of some dividing surface or state definition. These approaches often break down in practice when the available observables do not permit such a separation, i.e., when kinetically distinct states overlap in the histogram of the observed quantity. However, such a scenario may often arise in single-molecule experiments where the available order parameter depends on what is experimentally observable and may not necessarily be a good indicator of the slow kinetics. Moreover, consequences of the measurement process may increase the overlap between states, for example, by bead diffusion in optical tweezer experiments or by shot noise in single-molecule fluorescence measurements. In favorable situations, the signal quality can be improved by binning the data to a coarser time scale (often simply referred to as “filtering”), thus reducing the fluctuations from fast processes and shot noise. However, the usefulness of such filtering is limited because the time window used needs to be much shorter than the time scales of interest—otherwise the kinetics will be distorted. In general, one has to deal with a situation where overlap between the slowly converting states is present, both theoretically and practically.
Hidden Markov models (HMMs) [21–23] and related likelihood methods [24] are able to estimate transition rates even in such situations, and recently have been successful in distinguishing overlapping states in molecules with complex kinetics [25,26]. However, HMMs need a probability model of the measurement process to be defined, which can lead to biased estimates when this model is not adequate for the data analyzed. A recent approach, the signal pair-correlation analysis (PCA) [27], provides rate estimates without an explicit probability model, and instead requires the definition of indicator functions on which the measured signal can uniquely be assigned to one of the kinetically separated states. While this is often easier to achieve than finding an appropriate dividing surface, there is a trade-off between using only data that are clearly resolved to be in one state or the other (thus minimizing the estimation bias) while avoiding discarding too much data (thus minimizing the statistical error). Despite these slight limitations, both HMMs and PCA are practically very useful to identify and quantify hidden kinetics in the data. Yet, both are algorithmic approaches rather than a rate theory.
The recent success of single-molecule experiments and the desire for a robust rate estimation procedure that yields viable rate estimates even when highly overlapping states indicate clearly that the observed signal is a poor reaction coordinate highlights the need for a general and robust two-state rate theory for observed dynamics. Here, we make an attempt towards such a general rate theory for stochastic dynamics that are observed on a possibly poor reaction coordinate—often because the probed molecular order parameter is a poor choice, or because the measurement device creates overlap by noise broadening the signal.
Our approach requires only mild assumptions to hold for the dynamics of the observed system. First, the dynamical law governing the time evolution of the system in its full phase space—including all positions and velocities of the entire measured construct and the surrounding solvent—is assumed to be a time-stationary Markov process. We also require that the system obeys microscopic detailed balance in the full phase space and supports a unique stationary distribution. These mild criteria are easily satisfied by a great number of physical systems of interest in biophysics and chemistry.
When projected onto some measured observable, the dynamics of the system are no longer Markovian. In addition, the observed dynamics may be contaminated with measurement noise. As a result, the resulting signal may not be easily separable into kinetically distinct states by a simple dividing surface, something that is often required for existing rate estimation procedures to work well.
Our framework allows us to (i) evaluate the quality of existing estimators and propose optimal estimators for the slowest relaxation rate, (ii) provide a model-free definition of the reaction coordinate quality (RCQ) and the observation quality (OQ) of the signal, and (iii) derive an optimal estimator for the transition rates between the slowly converting states, as well as their stationary probability densities, even if these strongly overlap in the observation.
The present rate theory is exclusively concerned with the systematic error in estimating rates and proposes “optimal” methods that minimize this systematic rate estimation error. Therefore, all statements are strictly valid only in the data-rich regime. Explicit treatment of the statistical error in the data-poor regime is beyond the scope of the present work, but it is briefly discussed at the end of the paper and in the Supplemental Material [28].
II. FULL-SPACE DYNAMICS
We consider a dynamical system that follows a stationary and time-continuous Markov process xt in its full (and generally large and continuous) phase space Ω. xt is assumed to be ergodic with a unique stationary density μ(x). In order to be independent of specific dynamical models, we use the general transition density pτ(xt, xt+τ); i.e., the conditional probability density that, given the system is at point xt ∈ Ω at time t, it will be found at point xt+τ ∈ Ω a lag time τ later. At this point, we will also assume that the dynamics obey microscopic detailed balance, i.e.,
| (1) |
which is true for systems that are not driven by external forces. In this case, μ(x) is a Boltzmann distribution in terms of the system’s Hamiltonian. In some dynamical models, e.g., Langevin dynamics, Eq. (1) does not hold, but rather some generalized form of it does hold [29]. In this case, the present theory also applies (see comment below), but in the interest of the simplicity of the equations, we assume Eq. (1) subsequently.
For a two-state rate theory, we are interested in the slowest relaxation processes, and hence rewrite the transition density as a sum of relaxation processes (each associated with a different intrinsic rate) by expanding in terms of the eigenvalues λi and eigenfunctions ψi of the corresponding transfer operator [14,16]:
| (2) |
Here,
| (3) |
are eigenvalues of the propagator that decay exponentially with lag time τ. We order relaxation rates according to κ1 < κ2 ≤ κ3 ≤ ···, and thus, λ1(τ) > λ2(τ) ≥ λ3(τ) ≥ ···. The first term is special in that it is the only stationary process: κ1 = 0, λ1(τ) = 1, ψ1(x) = 1; thus, the first term of the sum is identical to μ(x). All other terms can be assigned a finite relaxation rate κi or a corresponding relaxation time scale , which are our quantities of interest. The eigenfunctions ψi are independent of τ and determine the structure of the relaxation process occurring with rate κi. The sign structure of ψi(x) determines between which substates the corresponding relaxation process is switching and is thus useful for identifying metastable sets, i.e., sets of states that are long lived and interconvert only by rare events [30,14]. The eigenfunctions are chosen to obey the normalization conditions
| (4) |
and integration always runs over the full space of the integrated variable if not indicated otherwise. At a given time scale τ of interest, fast processes with κ ≫ τ−1 (and, correspondingly, ti ≪ τ) will have effectively vanished, and we are typically left with relatively few slowly relaxing processes.
Finally, we define the μ-reweighted eigenfunctions,
| (5) |
such that the normalization condition of the eigenfunctions can be conveniently written as
| (6) |
Finally, the correlation density cτ(xt, xt+τ), i.e., the joint probability density of finding the system at xt at time t and at xt+τ at time t + τ, is related to the transition density pt by
| (7) |
III. OBSERVED DYNAMICS AND TWO-STATE SPECTRAL RATE THEORY
Consider the case that we are only interested in a single relaxation process—the slowest. Below, we sketch a rate theory for this case. Details of the derivation can be found in the Supplemental Material [28]. Based on the definitions above, the correlation density can then written as
| (8) |
where, if detailed balance (1) holds, the correlation density for the fast decaying processes (which are not of interest here) is given by Eq. (2):
| (9) |
If detailed balance does not hold on the full phase space, but rather some generalized form of it, the spectrum may have complex eigenvalues. Even in this case, the fast part of the dynamics can be bounded by e−κ3τ, and, therefore, Eq. (8) and the subsequent theory hold. See also the discussion in Ref. [16].
A. Exact rate
κ2 is often termed the phenomenological rate because it governs the dominant relaxation rate of any observed signal in which the slowest relaxation process is apparent. The exact rate of interest κ2 can, theoretically, be recovered as follows: If we know the exact corresponding eigenfunction ψ2(x), it follows from Eqs. (2) and (4) that its autocorrelation function evaluates to
| (10) |
where 〈·〉t denotes the time average, which here is identical to the ensemble average due to the ergodicity property of the dynamics.
The correlation function 〈ψ2(0)ψ2(τ)〉t yields the exact eigenvalue λ2(τ) and thus also an exact rate estimate κ̂2 = −τ−1 ln λ2(τ) = κ2, independently of the choice of τ.
B. Projected dynamics without measurement noise
Suppose we observe the dynamics of an order parameter y ∈ ℝ that is a function of the configuration x. Examples are the distance between two groups of the molecule or a more complex observable, such as the Förster resonance transfer efficiency associated with a given configuration. See Fig. 1 for an illustration. We first assume that no additional measurement noise is present. The analysis of a molecular dynamics simulation where a given order parameter is monitored is one example of such a scenario. Now, it is no longer possible to compute the rate via Eq. (10) or some direct approximation of Eq. (10), since the full configuration space Ω in which the eigenfunction ψ2 exists can no longer be recovered once the dynamics has been projected onto an order parameter. Instead, we are forced to work with functions of the observable y. While the theory is valid for multidimensional observables y, the equations below assume y ∈ ℝ for simplicity.
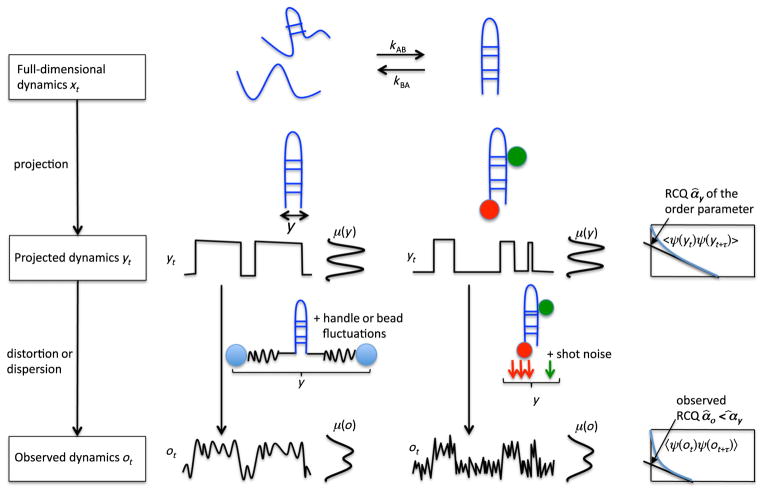
FIG. 1.
Illustration of the observed dynamics for which a rate theory is formulated here. Top row: The full-dimensional dynamics x(t) in phase space Ω. These dynamics are assumed to be Markovian, ergodic, and reversible as is often found for physical systems in thermal equilibrium. Furthermore, the theory here is formulated for two-state kinetics, i.e., the system has two metastable states exchanging at rates kAB and kBA, giving rise to a relaxation rate of κ2 = kAB + kBA. Middle row: One order parameter y(x) of the system is observed, such as the distance between two groups of a molecule, or the Förster Resonance Energy Transfer (FRET) efficiency between two fluorescent groups. The projection of the full-space dynamics x(t) onto the order parameter y generates a time series y(t) that, however, may not be directly observable. The projection also acts on functions of state space, such as the stationary distribution of configurations in full state space that is projected onto a density in the observable μ(y). The reaction coordinate quality α̂y measures how well the order parameter y resolves the slow transition. It is 1 when A and B are perfectly separated and 0 when they completely overlap. Bottom row: The experimental device used may distort or disperse the signal, for example, by adding noise. The resulting observed signal o(t) is distorted and the observable density μo(o) is smoothed. α̂o measures the observation quality (OQ) of the observed signal, and it is shown in the Supplemental Material [28] that α̂o ≤ α̂y holds.
We have two options for deriving the relevant rate equations for the present scenario. As a first option, we note that a projection that is free of noise can be regarded as a function y(x): Ω → ℝ. Thus, any function ψ̃2(y) of elements in observable space ℝ that aims at approximating the dominant eigenfunction ψ2 can also be regarded as a function in full space Ω via ψ̃2(y) = ψ̃2(y(x)). When following this idea, one can use the variational principle of conformation dynamics [31] (see also the discrete-state treatment in Ref. [20]), in order to derive the rate equations for the observed space dynamics. See Supplemental Material [28] for details.
However, since we aim to include the possibility of stochastic measurement noise in a second step, we derive a more general approach (see Supplemental Material [28]), which is summarized subsequently. Consider the function χp(y|x) that denotes the output probability density with which each configuration of the full state space x ∈ Ω yields a measured value y ∈ ℝ. In the case of simply projecting x values without noise to specific y values, χ has the simple form:
| (11) |
This allows the correlation density in the observable space to be written as
| (12) |
where we have used superscript y to indicate the projection of a full configuration space function onto the order parameter: μy(y) is the observed stationary density that can be estimated from a sufficiently long recorded trajectory by histogramming the values of y. Mathematically, the observed stationary density is given by
| (13) |
are the projected eigenfunctions:
| (14) |
In order to arrive at an expression for the rate κ2, we propose a trial function in observation space ψ̃2(y), which we require to be normalized by
| (15) |
and evaluate its autocorrelation function as
| (16) |
where
| (17) |
In contrast to Eq. (10), both ψ̃2 and live on the observable space ℝ. In the special case that ψ2(x) is constant in all variables other than y(x), the projection is lossless [ and for all x], and using the choice , we recover , and thus the exact rate estimate via Eq. (10). In general, however, the eigenfunction ψ2(x) does vary in variables other than y, and, therefore, ψ̃2 can at best approximate the full-space eigenfunction via ψ̃2(y(x)) ≈ ψ2(x).
C. Observed dynamics with measurement noise
Suppose that an experiment is conducted in which each actual order parameter value y(x) ∈ ℝ is measured with additional noise, yielding the observed value o ∈ ℝ. In time-binned single-molecule fluorescence experiments, such noise may come from photon-counting shot noise for a given binning time interval. In optical tweezer experiments, such noise may come from bead diffusion and handle elasticity, assuming that bead and handle dynamics are faster than the kinetics of the molecule of interest. See Fig. 1 for an illustration. Note that we treat the situation of uncorrelated noise only. In situations where the experimental configuration changes the kinetics, e.g., when the optical bead diffusion is slow, thus exhibiting transition rates different from the isolated molecule, our analysis always reports the rate of the overall observed system. The task of correcting the measured rates so as to estimate the rates of the pure molecule is beyond the scope of this work and can, for example, be attempted via dynamical deconvolution [32,33] or other approaches [34].
As before, the probability of observing a measurement value o ∈ ℝ given that the true configuration was x ∈ Ω can be given by an output probability:
| (18) |
which convolves the projection from x to the value of the order parameter χp(y|x), with the subsequent dispersion of the signal by noise χd(o|y). Despite the fact that dispersion operates by a different physical process than projection, the same analysis as above applies. We define the projected and dispersed stationary density and eigenfunctions:
| (19) |
| (20) |
which are “smeared out” by noise compared to the purely projected density and eigenfunctions . As above, the autocorrelation function of a probe function ψ̃2(o) is given by
| (21) |
with
| (22) |
The observation process including noise is a more general process than the observation process excluding noise; therefore—unless the distinction is important—we will generally refer to the observation as o subsequently, whether or not noise is included in the observation.
D. Filtered dynamics
The effect of measurement noise may be reduced by filtering (averaging) the observed signal o(t) → ō(t), for example, by averaging the signal value over a time window of length W. Note that this operation will introduce memory of length W into the signal and will impair the estimation of all rates which are close to W−1. Figure 1 of the Supplemental Material [28] illustrates the effect of filtering on the estimation quality of rates in a simple example. To make sure that the filter used does not impair the rate estimates, we recommend that the filter length be at least a factor of 10 smaller than the time scales of interest, . The filtered signal ō(t) can then be used as input to the various rate estimators discussed in this paper, but the theory of systematic errors given in the subsequent section may no longer apply because filtering destroys the Markovianity of the original dynamic process in the full state space. A more extensive treatment of filtering is given in the Supplemental Material [28].
E. Direct rate estimate
In all of the above cases, the autocorrelation function of the trial function ψ̃2 does not yield the exact eigenvalue λ2(τ), but some approximation λ̃2(τ). For , which can readily be achieved for clear two-state processes where a time-scale separation exists (κ2 ≪ κ3), the terms involving the fast processes disappear:
| (23) |
This suggests that the true rate κ2, as well as the prefactor αo may serve as a basis to measure the observation quality, could be recovered from large τ decay of an appropriately good trial function even from the observed signal. We elaborate this concept in subsequent sections. Note that in experiments the relaxation rates κ2, κ3, etc, are initially unknown and, hence, the validity of Eq. (23) can be checked only a posteriori, e.g., by the fact that estimates based on Eq. (23) are independent of the lag time τ.
IV. EXISTING RATE ESTIMATORS
Many commonly used rate estimators consist of two steps: (1) they (explicitly or implicitly) calculate an autocorrelation function λ̃2(τ) of some function ψ̃2 and (2) transform λ̃2(τ) into a rate estimate κ̃2. In order to derive an optimal estimator, it is important to understand how the systematic error of the estimated rate depends on each of the two steps. Therefore, we now recast existing rate estimators in the formalism of spectral rate theory. The Supplemental Material [28] contains a detailed derivation of the subsequent results.
Many rate estimators operate by defining a single dividing surface which splits the state space into reactants A and products B. Calling hA(o) the indicator function which is 1 for set A and 0 for set B, one may define the normalized fluctuation autocorrelation function of state A [35]:
| (24) |
which can also be interpreted as an autocorrelation function λ̃2(t) for the step function . Here, πA = 〈hA〉μ is the stationary probability of state A, and πB = 1 − πA the stationary probability of state B. Other rate estimates choose ψ̃2 to be the signal ot itself or the committor function between two predefined subsets of the o coordinate [19]. We show that none of these choices is optimal, and the optimal choice of ψ̃2 will be derived in the subsequent section.
Existing rate estimators largely differ in step (2), i.e., how they transform λ̃2(t) into a rate estimate κ̃2. This procedure then determines the functional form of the systematic estimation error. We subsequently list bounds for these errors (see Supplemental Material [28] for the derivation). The prefactor α in the equations below refers to either αp (purely projected dynamics) or αo (dynamics with noise), whichever is appropriate.
A. Reactive flux rate
Chandler, Montgomery, and Berne [7,36] considered the reactive flux correlation function as a rate estimator: . Its error is
| (25) |
which becomes 0 for the perfect choice of ψ̃2 = ψ2 that leads to α = 1, but can be very large otherwise.
B. Transition state theory rate
The transition state theory rate, which measures the instantaneous flux across the dividing surface between A and B, is often estimated by the trajectory length divided by the number of crossings of the dividing surface. Its simplicity makes it a widely popular choice for practical use in experiments and theory (despite its tendency to produce biased estimates, as we discuss later).
In order to arrive at an expression for the estimation error, the TST rate can be expressed as the short-time limit of the reactive flux [7], κ̂2,TST = limτ→0+ κ̃2,rf(τ), such that the error in the rate is given by
| (26) |
which is always an overestimate of the true rate and of the reactive flux rate.
C. Integrating the correlation function
Another means of estimating the rate is via the integral of the correlation function, [see, e.g., Eq. (3.6) of Ref. [7]], with the error
| (27) |
in the special case that κ3 ≫ κ2 (time scale separation); the error is approximately given by κ2(1 − α)/α. Thus, the error of this estimator becomes zero for α = 1, which is the case only for a reaction coordinate with no noise and no further projection (e.g., by using a dividing surface). The error may be very large in other cases (α < 1).
D. Single-τ rate estimators
A simple rate estimator takes the value of the autocorrelation function of some function ψ̃2 at a single value of τ and transforms it into a rate estimate by virtue of Eq. (23).
We call these estimators single-τ estimators. Ignoring statistical uncertainties, they yield a rate estimate of the form
| (28) |
Quantitatively, the error can be bounded by the expression (see derivation in the Supplemental Material [28])
| (29) |
The error becomes identical to this bound for systems with a strong time-scale separation, κ3 ≫ κ2. Equation (29) decays relatively slowly in time (with τ−1; see Fig. 2 for a two-state example). It is shown below that methods that estimate rates from counting the number of transitions across a dividing surface, such as MSMs, are single-τ estimators and are thus subject to the error given by Eq. (29).
The systematic error of single-τ estimators results from the fact that Eq. (28) effectively attempts to fit the tail of a multiexponential decay λ̃2(τ) by a single exponential with the constraint λ̃2(0) = 1. Unfortunately, the ability to improve these estimators by simply increasing τ is limited because the statistical uncertainty of estimating Eq. (23) quickly grows with increasing τ [37].
E. Multi-τ rate estimators
To avoid the error given by Eq. (29), it is advisable to estimate the rate by evaluating the autocorrelation function λ̃2(τ) at multiple values of τ. This can be done, e.g., by performing an exponential fit to the tail of the λ̃2(τ), thus avoiding the constraint λ̃2(0) = 1 [3,10]. The corresponding estimation error κ̂2,multi − κ2 is bounded by
| (30) |
where τ1 is the first lag time from the series (τ1,....., τm) used for fitting, and the constant c also depends on the lag times and the fitting algorithm used. The Supplemental Material [28] shows that, for several fitting algorithms, such as a least-squares procedure at the time points (τ, 2τ,....., mτ), c is such that
| (31) |
Thus, the multi-τ estimator is never worse (and generally better) than the single-τ estimator (see the Supplemental Material [28]). The main advantage of multi-τ estimators is that their convergence rate is exponential in τ when the time-scale separation κ3 − κ2 is not vanishing [compare to Eq. (29)]. Thus, multi-τ estimators are better when the time-scale separation between the slowest and the other relaxation rates in the system is larger.
In the absence of statistical error, all of the above rate estimation methods are seen to yield an overestimation of the rate, κ̃2 ≥ κ2.
V. OPTIMAL CHOICE OF ψ̃2
It was shown above that multi-τ estimators are the best choice for converting an autocorrelation function into a rate estimate. However, what is the best possible choice ψ̂2 = ψ̃2,optimal given a specific observed time series ot? In other words, which function should the observed dynamics be projected upon in order to obtain an optimal rate estimator? Following Eq. (29), the optimal choice ψ̂2 is the one that maximizes the parameter α, as this will minimize the systematic error from a direct rate estimation by virtue of Eq. (29) and also minimize the systematic error involved in estimating κ2 from an exponential fit to Eq. (23). We are thus seeking the solution of
| (32) |
for some τ > 0, subject to the normalization in Eq. (15). Here, arg maxψ̃2 α denotes the function that maximizes α over the space of functions ψ̃2(o). If the system has two-state kinetics, i.e., only ψ1(x) = 1 and ψ2(x) are present as dominant eigenfunctions, the problem (32) s solved by the projected eigenfunction:
| (33) |
How can the best possible ψ̂2 be determined from the observed time series? For a sufficiently large set of n basis functions, γ = {γ1(o),....., γn(o)}, the optimal eigenfunction ψ̂2 is approximated by a linear combination , with coefficients c = {c1,....., cn}. When γ is chosen to be an orthogonal basis set, ψ̂2 = arg maxψ̃2 α can be approximated by the Ritz method [31,38]. An easy way to do this approximation in practice is to perform a fine discretization of the observable o by histogram windows. Using a binning with bin boundaries b1,....., bn+1, and the corresponding indicator functions
| (34) |
the above optimization problem is solved by estimating the transition probability matrix with elements
| (35) |
and calculating c as the second eigenvector
| (36) |
where λ2 < 1 is the second-largest eigenvalue of T. If the system has two-state kinetics, i.e., only ψ1(x) = 1 and ψ2(x) are present as dominant eigenfunctions, the estimate ψ̂2 is independent of the choice of τ in Eq. (35). Thus, in real systems, τ should be chosen to be at least a multiple of [e.g., , as indicated by a constant rate κ2 estimate using a multi-τ estimator (Eq. (30)]. Note that a given optimal ψ̂2(o) can still be used with single-τ and multi-τ rate estimators that would produce different estimates for κ2.
Note that ψ̂2, according to the procedure described here, is optimal only for the case when the observed signal is obtained by projecting the high-dimensional data onto the observable, but is no longer optimal in the presence of noise, and especially large noise. In order to choose ψ̂2 optimal when noise is present, a generalized Hermitian eigenvalue problem must be solved instead of Eq. (36), which includes a mixing matrix whose elements quantify how much the observable bins are mixed due to measurement noise. Since this approach is not very straightforward and in most practical cases leads only to small improvements, we do not pursue this approach further here. Rather, we note that it is often practical to reduce the noise level by carefully filtering the recorded data, provided that the filter length is much shorter than the time scales of interest.
VI. REACTION COORDINATE QUALITY, ESTIMATION QUALITY, AND OBSERVATION QUALITY
Evaluating the suitability of a given observable for capturing the slow kinetics is of great general interest. Although there is not a unique way of quantifying this suitability of the observable, the term reaction coordinate quality (RCQ) is often used. Previous studies have proposed ways to measure the RCQ that are based on comparing the observed dynamics to specific dynamical models or testing the ability of the observable to model the committor or splitting probability between two chosen end states A and B [4,5,39]. These metrics are either valid only for specific models of dynamics or themselves require a sufficiently good separation of A and B by definition, restricting their applicability to observables with rather good RCQs.
The prefactor α̂y (see also Fig. 1) is a measure between 0 and 1, quantifying the relative amplitude of the slowest relaxation in the autocorrelation function after projection of the full-space dynamics onto the molecular observable employed. The value α̂y depends only on the observable itself and is free of modeling choices and of the way rates are estimated from the signal. Therefore, we propose that αy is the RCQ.
However, αy is not directly measurable: for a given observation, both the projection of the full-space dynamics and the measurement noise compromise the quality of the signal, and these effects cannot be easily separated. In addition, the actual prefactor that is obtained in a given estimate of the signal autocorrelation function αo depends on the way the data are analyzed, namely, the functional form ψ̃2(o) used to compute the autocorrelation function λ̃2(τ). Therefore, αo is just an estimation quality.
Fortunately, the ambiguity of the estimation quality is eliminated for the optimal choice ψ̃2 = ψ̂2 [Eq. (32)], which maximizes αo. In this case, we denote this prefactor α̂o, where α̂o = αo(ψ̂2) ≥ αo(ψ̃2). Since α̂o depends only on the observed signal, and not on the method of analyzing it, we term it observation quality (OQ). The OQ is a very important quantity because, by virtue of Eqs. (29) and (30), α̂o quantifies how large the error in our rate estimate can be for the optimal choice ψ̃2 = ψ̂2.
Our definitions of RCQ and OQ are very general, as they make no assumptions about the class of dynamics in the observed coordinate and do not depend on any subjective choices, such as the choice of two reaction end states A and B in terms of the observable o. Through the derivation above, it has also been shown that α̂o measures the fraction of amplitude by which the slowest process is observable, which is exactly the property one would expect from a measure of the RCQ: α̂0 is 1 for a perfect reaction coordinate with no noise and 0 if the slowest process is exactly orthogonal to the observable, or has been completely obfuscated by noise.
While the OQ is the quantity that can be computed from the signal, an analyst is typically interested in the RCQ α̂y that is due to the choice of the molecular order parameter. Unless a quantitative model of the dispersion function χd(o|y) is known, the RCQ α̂y before adding noise cannot be recovered (see also Fig. 1 for an illustration). However, we can still quantitatively relate α̂y and α̂o, and thereby show that even the OQ is very useful. For this, we derive a theory of observation quality. While the detailed derivation is found in the Supplemental Material [28], we summarize the most important results here.
- When observing the order parameter y without noise and projecting the observation onto the optimal indicator function , the RCQ can be expressed as the weighted norm of the projected eigenfunction, expressed by the scalar product:
(37) Unless the projection perfectly preserves the structure of the full-space eigenfunction ψ2, we have α̂y < 1. Thus, almost every observable attains a suboptimal RCQ.
- When additional noise is present, the OQ can be expressed as the weighted norm of the projected and noise-distorted eigenfunction:
(38) -
The RCQ α̂y is determined by the projection onto the selected molecular order parameter alone, and the OQ α̂o including measurement noise are related by
(39) i.e., adding noise means that the OQ is smaller than the RCQ.
The inequality (39) implies that we can use the OQ α̂o in order to optimize both the experimental setup and the order parameter used. For example, in an optical tweezer measurement, we can change laser power and handle length so as to maximize α̂o, thus making α̂o and α̂y more similar and reducing the effect of noise on the measurement quality. On the other hand, since α̂o is a lower bound for α̂y, we can also use it to ensure a minimal projection quality: When the measurement setup itself is kept constant, we can compare the measurements of different constructs (e.g., different FRET labeling positions or different attachment sites in a tweezer experiment). The best value α̂o corresponds to the provably best construct.
Finally, α̂o can be determined by fitting the autocorrelation function of ψ̂2, as described in the spectral-estimation procedure described below. Figures 2–5 show estimates of the OQ of different observed dynamics (via spectral estimation) and of the estimation quality using other rate estimators.
FIG. 5.
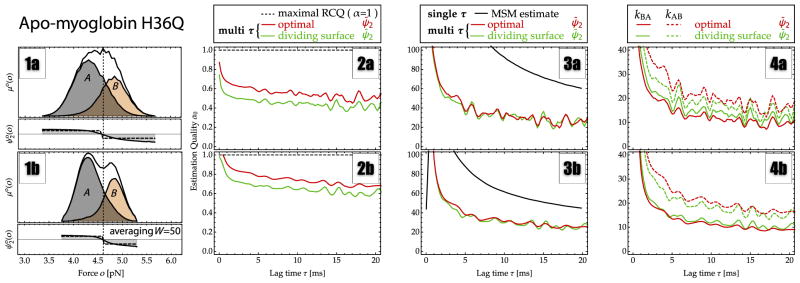
Estimates for rates and estimation qualities from passive-mode single-molecule force-probe experiments of apo-myoglobin. All panels report the estimation results, showing the direct Markov model estimate (black line), a fit to the fluctuation autocorrelation function using a dividing surface at the histogram maximum (minimum between two maxima for filtering) o = 4.6 pN (green line), and spectral estimation (red line). (1a),(1b) The stationary probability of observing a given force value (solid black line). The partial probabilities of states A (gray) and B (orange) obtained by spectral estimation show that there is very little overlap between the states. (2a),(2b) The estimation quality αo, coinciding with the OQ α̂o, for spectral estimation. (3a),(3b) Estimated relaxation rate κ2. (4a),(4b) Estimated microscopic transition rates kAB (dashed line) and kBA (solid line).
VII. MARKOV (STATE) MODELS
MSMs have recently gained popularity in the modeling of stochastic dynamics from molecular simulations [40,14,41,15,12]. MSMs can be understood as a way of implicitly performing rate estimates via discretizing state space into small substates. Let us consider aMSM obtained by finely discretizing the observed space y into bins and estimating a transition matrix T(τ) among these bins. We have seen that this procedure approximately solves the optimization problem of Eq. (32), and the leading eigenvector of T(τ) approximates the projection of the true second eigenfunction available for the given observable o. Reference [15] has suggested to use the implied time scale t̂2 = −τ/ln[λ̂2(τ)] as an estimate for the system’s slowest relaxation time scale, and at the same time for a test of which choice of τ leads to a MSM with a small approximation error. These implied time scales correspond to the inverse relaxation rates, and therefore, the MSM rate estimate is described by Eq. (28) with the choice ψ̃2 = ψ̂2. A sufficiently finely-discretized MSM thus serves as an optimal single-τ rate estimator as its estimation quality approaches the true OQ α̂o for the observed signal that is being discretized. However, when this signal has a poor OQ α̂o since it is poorly separating the slowly converting states, there is a substantial rate estimator error according to Eq. (29) that decays slowly with τ−1. This likely explains the slow convergence of implied time scales shown in recent MSM simulation studies [12–15,42].
VIII. ESTIMATING STATE DENSITIES AND MICROSCOPIC TRANSITION RATES
When the rate κ2 is exactly known, the microscopic transition rates between the two interchanging states, kAB and kBA, could be calculated from the equations
| (40) |
| (41) |
and B:
| (42) |
| (43) |
with and being the partial densities of states A and B in the observable o, respectively.
Here, we attempt to estimate both the partial densities and and from these the microscopic transition rates via Eqs. (40) and (41). The difficulty is that the projections of A and B can significantly overlap in o, due to both the way the order parameter used projects the molecular configurations onto the observable and the noise broadening of the measurement device. This reveals a fundamental weakness of dividing-surface approaches. Although a dividing-surface estimator can estimate the rate κ2 for sufficiently large τ without bias via Eq. (30), it cannot distinguish between substates on one side of the barrier, and thus assumes the partial densities and to be given by cutting the full density μo(o) at the dividing surface. When the true partial densities overlap, this estimate can be far off [compare the curves in Figs. 2(II5) and 2(III5)]. Consequently, incorrect estimates for the microscopic rates kAB and kBA are obtained when Eqs. (40) and (41) are used with πA and πB computed from the total densities “left” and “right” of the dividing surface.
Hidden Markov models approach this problem by proposing a specific functional form of and for example, a Gaussian distribution, and then estimating the parameters of this distribution with an optimization algorithm [21,23]. This approach is very powerful when the true functional form of the partial densities is known, but will give biased estimates when the wrong functional form is used.
Here, we propose a nonparametric solution that can estimate the form of the partial densities and and the microscopic transition rates k̂AB and k̂BA in most cases without bias. For this, we employ the theory of Perron cluster cluster analysis (PCCA+) [17,30]—which is based on PCCA theory [30,44]—which allows for a way to split the state space into substates and at the same time maintain optimal approximations to the exact eigenfunctions (here, ψ2): The state assignment must be fuzzy; i.e., instead of choosing a dividing surface that uniquely assigns points o to either A or B, we have fuzzy membership functions χA(o) and χB(o) with the property χA(o) + χB(o) = 1. These membership functions can be calculated after ψ2 is known.
In order to compute the membership χA and χB, the memberships of two points of the observable o must be fixed. The simplest choice is to propose two observable values that are pure, i.e., that have a membership of 1 to A and B each. Such an approach is also proposed by the signal-pair correlation analysis approach [27] where the pure values need to be defined by the user. However, at this point of our analysis, an optimal choice can be made, because the eigenfunction has been approximated. Thus, we propose to follow the approach of Ref [43] and choose the o values, where achieves a minimum and a maximum, respectively, as purely belonging to A and B. Typically, these are the states that are on the left and right boundaries of the histogram in o. This approach will start to give a biased estimate only when the overlap of the A and B densities is so large that not even these extreme points are pure [see Fig. 2(III), last row, for such an example].
Let ψ̂2 be the second eigenvector of the Markov model T(τ) of the finely binned observable [Eq. (36)]. Then, ψ̂2 is a discrete approximation to the projected eigenfunction . Following the derivation given in the Supplemental Material [28], the fuzzy membership functions on the discretized observable space are given by
| (44) |
| (45) |
where the subscripts i and j denote the discrete state index. Note that the extreme values maxjψ̂2,j and minjψ̂2,j may have large statistical uncertainties when a fine and regular binning is used to discretize the observation. In order to avoid the situation in which our estimates are dominated by statistical fluctuations, we choose the outermost discretization bins such that at least 0.05% of the total collected data are in each of them. The exact choice of this value appears to be irrelevant; as shown in the Supplemental Material [28], any choice between 0.005% and 5% of the data yields similar results. Since we are restricted to the projected eigenfunction ψ̂2, we can determine the optimal choice χ̂A(o) and χ̂B(o) from ψ̂2(o).
Together with the estimated stationary density μo(o), which can, e.g., be obtained by computing a histogram from sufficiently long equilibrium trajectories, the probability of being in A and B is thus given by
| (46) |
| (47) |
These probabilities can be used to split κ̂2 into microscopic transition rates kAB and kBA:
| (48) |
| (49) |
Note that the assignment of labels A and B to parts of state space is arbitrary. Equation (48) is the transition rate from A to B as defined by Eqs. (44) and (45), and Eq. (49) is the corresponding transition rate from B to A.
IX. SPECTRAL-ESTIMATION PROCEDURE
The optimal estimator for κ2 is thus one that fits the exponential decay of λ̂2(τ) while minimizing the fitting error Eq. (30). As analyzed above, the systematic fitting error is minimized by any multi-τ estimator. In order to obtain a numerically robust fit, especially in the case when statistical noise is present, it is optimal to fit to an autocorrelation function λ̃2(τ), where the relevant slowest decay has maximum amplitude α̂0. This is approximately achieved by constructing a fine-discretization MSM on the observed coordinate (see Sec. V). Thus, the optimal estimator of κ2 proceeds as outlined in points (1)–(4) below. The full spectral-estimation algorithm (1)–(6) additionally provides estimates for the microscopic rates kAB, kBA, and for the partial densities μA and μB.
Obtain a fine discretization of the observed coordinate o into n bins, say, [oi, oi+1], for i ∈ 1,....., n. When using an equidistant binning, make sure to increase the outermost states to a size to cover a significant part (e.g., 0.05%) of the total population.
Construct a row-stochastic transition matrix T(τ) for different values of τ. The estimation of transition matrices from data has been described in detail Ref. [14]. A simple way of estimating T(τ) is the following: (i) for all pairs i, j of bins, let cij(τ) be the number of times the trajectory has been in bin i at time t and in bin j at time t + τ, summed over all time origins t, and (ii) estimate the elements of T(τ) by Tij(τ) = cij(τ)/Σkcik(τ). A numerically superior approach is to use a reversible transition matrix estimator [14].
-
Calculate the discrete stationary probability μ and the discrete eigenvector ψ̂2 by solving the eigenvalue equations:
(50) (51) denotes the transpose of the transition matrix. The ith element of the vectors μ and ψ̂2 approximates the stationary density μ(o) and ψ̂2 on the respective point . Functions μo(o) and can be obtained by some interpolation method.
Estimate the relaxation rate κ̂2 and the OQ α̂ via an exponential fit of αe−κ2τ to the tail of λ̂2(τ) = 〈ψ̂2(t)ψ̂2(t + τ)〉t.
Calculate the partial densities μA and μB from Eqs. (46) and (47) using transition matrix eigenvectors estimated at a lag time τmin at which the rate estimate κ̂2 is converged.
Calculate the microscopic transition rates kAB and kBA from Eqs. (48) and (49).
Note that this estimator is optimal in terms of minimizing the systematic error. When dealing with real data, the finite quantity of data may set restrictions of how fine a discretization is suitable and how large a lag time τ will yield reasonable signal to noise. For a discussion of this issue, refer to, e.g., Ref. [37].
X. ILLUSTRATIVE TWO-STATE EXAMPLE
To illustrate the theory and the concepts of this paper, we compare the behavior of different order parameters, measurement noise, and different estimators in Fig. 2. The full-space model here is a two-dimensional model system using overdamped Langevin dynamics in a bistable potential. This choice was made because the exact properties of this system are known and the quality of different estimates can thus be assessed. The potential is chosen such that the eigenfunction associated with the slow process ψ2(x) varies in x1 and is constant in x2, such that the choice o = x1 represents a perfect projection and the choice o = x2 represents the worst situation in which the slow process is invisible.
Figure 2 shows three scenarios using
y = x1 (perfect order parameter—projection angle 0°),
(average order parameter— projection angle 45°),
(poor order parameter—projection angle 72°).
Additionally, we compare the results when the order parameter y is traced without noise [left half of panels (3)–(5)] and when measurement noise is added [right half of panels (3)–(5)]. Here, noise consists of adding a uniformly distributed random number from the interval [−1, 1] to the signal, such that the noise amplitude is roughly 25% of the signal amplitude.
Figure 2, panels (2), show the apparent stationary density in the observable y, μy(y), or in the noisy observable o, μo(o), as a black solid line. The partial densities of substates A (orange) and B (gray), which comprise the total stationary density, are shown as well. The lower part of the figure shows the observed eigenfunction associated with the two-state transition process ( or ) as a black solid line with gray background. For comparison, the results in the case of noise are shown in the background with lighter colors. It is apparent that when the quality of the observation is reduced, either by choosing a poor order parameter or by adding experimental noise, the overlap of the partial densities increases and the continuous projected eigenfunction becomes smoother and, thus, increasingly deviates from the dividing surface model, which is a step function switching at the dividing surface (dashed line).
Figure 2, panels (3), show the estimation qualities or observation qualities in these different scenarios. The fact that the green and red lines are approximately constant after τ = 5 (when the fast processes have relaxed) shows that the OQ can be reliably estimated at these lag time ranges using either the dividing-surface or the spectral-estimation approach. The red line (spectral estimation) corresponds to the OQ, which varies between 1 (perfect order parameter I) and 0.15 (poor order parameter III with additional measurement noise). It is seen that the OQ given by the spectral estimator can be much larger than the suboptimal estimation quality of the dividing-surface estimator that uses a fit to the number correlation function Eq. (24) (green line). This is especially apparent in the case of an intermediate-quality order parameter [Fig. 2(II3)].
Figure 2, panels (4), show the estimate of the relaxation rate κ2 obtained for the three scenarios where each panel compares five different rate estimators with the exact result (black solid line). (1) Direct counting of transitions from time-filtered data (TST estimate, blue line). For this estimator, the x axis denotes the length of the averaging window W, ranging from 1 to 100 frames. (2),(3) The dividing-surface estimates using either a single-τ estimator (28) (dashed green line) or the multi-τ estimator (solid green line). (4),(5) The single-τ MSM estimate (dashed red line) and the multi-τ MSM estimate (spectral estimation, solid red line). For the single-τ and the exact estimators. the x axis indicates the used lag time τ in the estimation where, for the multi-τ estimators (i.e., dividing surface and spectral estimation), the x axis specifies τ, which is the start of the time range [τ, τ + 10] used for an exponential fit.
In the case of a perfect order parameter (I), all estimators yield the correct rate at lag times τ > 5 time steps (where the fast processes with rates κ3 or greater have disappeared). Only in the case of TST (blue line), with increasing size W of the filtering window, the estimated rate tends to be too slow because an increased number of short forward-and-backward transition events become smeared out by the filtering window, therefore systematically underestimating the rate. For the perfect order parameter I, the noise has little effect on the estimate because the partial densities of states A and B are still well separated.
For the average-quality and poor order parameters, the MSM estimate breaks down dramatically, providing a strongly overestimated rate for 0 < τ < 100 time steps. Figures 2(II4) and 2(III4) show the typical behavior of the τ−1 convergence of the MSM estimate predicted by the theory [Eq. (29)]. Clearly, the MSM estimate will converge to the true value for very large values of τ, but, especially for the situation of a poor order parameter, the minimal τ required to obtain a small estimation error is larger than the time scale of the slowest process, thus rendering a reliable estimation impossible.
It is seen that the magnitude of the error for a given value of τ increases when either adding noise [left half of panels (4) of Fig. 2 versus right half] or decreasing the quality of the order parameter [Figs. 2(II4) versus Figs. 2(III4)]. This is because, in this sequence, the OQ deteriorates, as predicted by the theory of reaction coordinate qualities (see above), and, hence, the prefactor of the MSM error increases [see Eq. (29)].
As predicted by Eq. (31), the multi-τ estimators (dividing-surface and spectral estimates, red and green solid lines) are always better than the single-τ estimates (red and green dashed lines). As predicted by Eq. (30), both the dividing-surface and spectral estimates of κ̂2 converge when the fast processes have died out (here, at approximately τ > 5 time steps). Also, Figs. 2(II4) and 2(III4) show that the spectral estimate is more stable than the dividing-surface estimate; i.e., it exhibits weaker fluctuations around the true value κ2. This is because the spectral estimate uses the OQ α̂o as the estimation quality, which is larger than the estimation quality of other estimators, and thus the exponential tail of the autocorrelation function can be fitted using a larger amplitude of the process relaxation with rate κ2, achieving a better signal-to-noise ratio.
Figure 2, panels (5), show the microscopic rate kAB that quantifies the rate at which rare transition events between the large (orange) state A and the smaller (gray) state B occur. The solid lines indicate the estimates from Eq. (48), using either the partial densities from the dividing surface (green) or PCCA+ (spectral estimate, red). Corresponding rates computed from a MSM using the different projections are shown in dashed lines. As expected, the partial densities from the dividing-surface estimate are significantly biased as soon as the states overlap in the observable, due to either choosing a poor order parameter or experimental noise. As a result, the dividing-surface estimates for the microscopic rates kAB and kBA are biased for all of these cases [Figs. 2(II5) and 2(III5)]. The spectral estimate gives an unbiased estimate for average overlap [Fig. 2(II5)]. For strong overlap, even the spectral estimator has a small bias because no pair of observable states can be found that is uniquely assignable to states A and B. Still, the spectral estimator yields good results even in the poor order parameter case [Fig. 2(III5)]. As it is for the relaxation rate (κ2) estimate, the spectral estimator exhibits less fluctuations here because the larger estimation quality yields a better signal-to-noise ratio.
XI. APPLICATIONS TO OPTICAL TWEEZER DATA
In order to illustrate the performance of spectral estimation on real data, it is applied to optical tweezer measurements of the extension fluctuations of two biomolecules examined in a recent optical force spectroscopy study: the p5ab RNA hairpin [45] and the H36Q mutant of sperm whale apo-myoglobin at low pH [46]. The p5ab hairpin forms a stem-loop structure with a bulge under native conditions [Fig. 3(1)] and zips and unzips repeatedly under the conditions used to collect data [Fig. 3(2a)], while apo-myoglobin [crystal structure shown in Fig. 3(4)] hops between unfolded and molten globule states at the experimental pH of 5 [Fig. 3(5a)] [46].
FIG. 3.
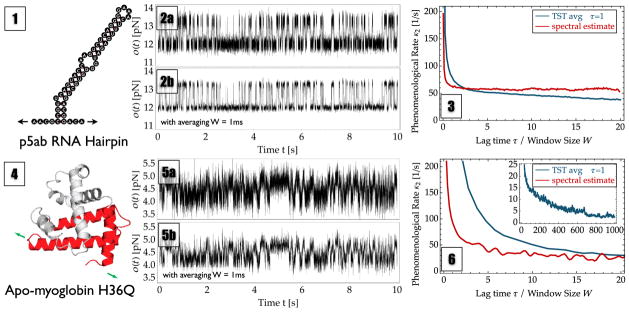
Probed systems by optical tweezer experiments. Top: RNA hairpin p5ab. Bottom: H36Q mutant of sperm whale apomyoglobin. Panels (1) and (4) show schematic views of the probed system in its native secondary or tertiary structure including the direction of the pulling force (green and black arrows). Panels (2) and (5) show the traces used for analysis. Row (a) reports the results when directly analyzing the measured 50 kHz data, while row (b) reports the results when analyzing data that has been binned to 1 kHz to reduce the noise amplitude. Panels (3) and (6) show the estimated phenomenological rates κ̂2 for TPT (blue line) using different averaging window sizes W (x axis) and spectral estimation (red line) for different lag times τ (x axis). For apo-myoglobin, the inset displays the behavior of TST at large window sizes W, where the rate is systematically underestimated.
Experimental force trajectory data were generously provided by the authors of Refs. [45,46]. Experimental details are given therein, but we briefly summarize aspects of the apparatus and experimental data collection procedure relevant to our analysis.
The instrument used to collect both data sets was a dual-beam counterpropagating optical trap [47]. The molecule of interest was tethered to polystyrene beads by means of dsDNA handles, with one bead suctioned onto a pipette and the other held in the optical trap. A piezoactuator controlled the position of the trap and allowed position resolution to within 0.5 nm, with the instrument operated in passive (equilibrium) mode such that the trap was stationary relative to the pipette during data collection. The force on the bead held in the optical trap was recorded at 50 kHz, with each recorded force trajectory 60 s in duration.
It is common practice to estimate rates in such data by directly counting the number of transitions across some user-defined dividing surface and dividing by the total trajectory length. Often, this procedure is applied after filtering the data with a time-running average. The results of this common procedure (effectively a TST estimate or a MSM estimate with τ = 1) are shown in Figs. 3(3) and 3(6) (blue line) using various averaging window sizes W and compared to the optimal estimator (spectral estimation) for a range of estimation lag times τ. Although the TST estimate shows less fluctuations, the spectral-estimation result converges much faster and provides a more stable result in terms of the varying parameter (lag time τ/window size W). TST also tends to underestimate the true rate for large window sizes W. Moreover, the TST estimate never shows any plateau, thereby making it impossible to decide which rate estimate should be used.
XII. RNA HAIRPIN ANALYSIS
Figure 4 compares the results of several rate estimators for optical tweezer measurement of the p5ab RNA hairpin extension fluctuations. A sketch of the RNA molecule and the experimental trajectory analyzed can be found in Figs. 3(1) and 3(2), top. The trajectory exhibits a two-state-like behavior with state lifetimes on the order of tens of milliseconds. Figure 4(1a) shows the stationary probability density of measured pulling forces, exhibiting two nearly separated peaks. Figure 4(2a) shows the estimation quality αo (OQ α̂o for the spectral estimator), which is approximately constant at lag times τ > 5 ms, indicating a reliable estimate for this quantity at lag times greater than 5 ms. An optimum value of α̂o ≈ 0.96 (spectral estimator) is found while the best possible dividing surface results in αo ≈ 0.94. These values indicate that the present reaction coordinate is well suited to separate the slowly interconverting states and that different approaches, including a Markov model, a dividing-surface estimate, and a spectral estimate, should yield good results.
FIG. 4.
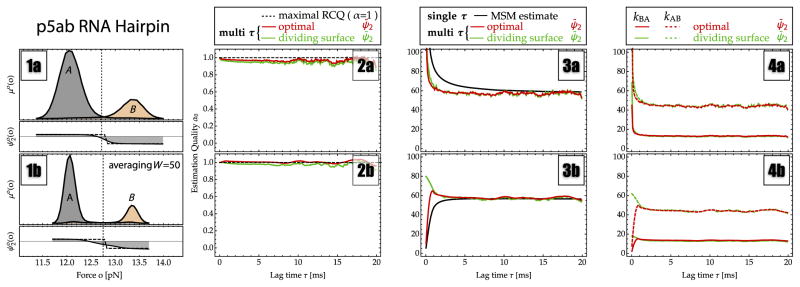
Estimates for rates and estimation qualities from passive-mode single-molecule force-probe experiments of the p5ab RNA hairpin. All panels report the estimation results, showing the direct MSM estimate (black line), a fit to the fluctuation autocorrelation function using a dividing surface at o = 12.80 pN (green line), and spectral estimation (red line). (1a),(1b) The stationary probability of observing a given force value (solid black line). The partial probabilities of states A (gray) and B (orange) obtained by spectral estimation show that there is very little overlap between the states. (2a),(2b) The estimation quality αo, coinciding with the OQ α̂o for spectral estimation. (3a),(3b) Estimated relaxation rate κ2. (4a),(4b) Estimated microscopic transition rates: the folding rate kAB (dashed line) and the unfolding rate kBA (solid line).
Figure 4(3a) compares the estimates of the relaxation rate κ2 using the direct MSM estimate (black), a fit to the fluctuation autocorrelation function using a dividing surface at the histogram minimum o = 12.80 pN (green), and spectral estimation (red). For the multi-τ estimators (dividing-surface and spectral estimations), the lag time τ specifies the start of the time range [τ, τ + 2.5 ms] that was used for an exponential fit. All estimators agree on a relaxation rate of about κ̂2 ≈ 58 s−1, corresponding to a time scale of about 17 ms. The MSM estimate is strongly biased for short lag times, exhibiting the slow τ−1 convergence predicted by the theory for single-τ estimators [Eq. (29)]. It converges to an estimate within 10% of the value from multi-τ estimates after a lag time of about 10 ms. The dividing-surface and spectral estimators behave almost identically and converge after about τ = 5 ms. According to the error theory of multi-τ estimators [Eq. (30)], this indicates that there are additional, faster kinetics in the data, the slowest of which have time scales of 2–3 ms. In agreement with the theory [Eq. (31)], the multi-τ estimators (dividing-surface and spectral estimates) converge faster than the single-τ estimate (MSM).
As indicated in Fig. 4(1a), the substates estimated from PCCA+ are almost perfectly separated and can be well distinguished by a dividing surface at the histogram minimum o = 12.80 pN. Consequently, both the dividing-surface estimate and the spectral estimate yield almost identical estimates of the microscopic transition rates— the folding rate being kAB ≈ 45 s−1 and the unfolding rate being kBA ≈ 15 s−1 [Fig. 4(4)]. In summary, the two-state kinetics of p5ab can be well estimated by various different rate estimators because the slowly converting states are well separated in the experimental observable.
Figure 4, panels (1b)–(4b), show estimation results for data that have been filtered by averaging over 50 frames (1 ms). This averaging further reduces the already small overlap between substates A and B, while the filter length is much below the time scale of A–B interconversion. Therefore, filtering has a positive result on the analysis: The effective OQ α̂o increases and is now approximately equal to 1 according to spectral estimation. The estimation results are largely identical to the case with noise. In Fig. 4(3b), the error made by the Markov model estimate has become smaller because the error prefactor reported in Eq. (29), ln αo, has become smaller. Note that, in contrast to the unfiltered data analysis, some of the rate estimates (MSM and spectral estimate) underestimate the rate for small lag times τ. This is not in contradiction with our theory, which predicts an overestimation of the rate for Markovian processes. By using the filter, one has effectively introduced memory into the signal, and the present theory will apply only at a lag time τ that is a sufficiently large multiple of the filter length, such that the introduced memory effects have vanished.
XIII. APO-MYOGLOBIN ANALYSIS
Figure 5 shows estimation results for an optical tweezer experiment that probes the extension fluctuations of apomyoglobin [46]. Figure 3(4) shows a sketch of the experimental pulling coordinate (green arrows) depicted at the crystal structure of apo-myoglobin. Figure 3(5) shows the trajectory that was analyzed. Out of the trajectories reported in [46], here we have chosen one where the two slowest-converting states have a large overlap. While the trajectory indicates that there are at least two kinetically separated states, the stationary probability density of measured pulling forces [Fig. 5(1a)] does not exhibit a clear separation between these states in the measured pulling force. This is also indicated by Fig. 5(2a), which shows that the optimal OQ has a value of α̂o ≈ 0.5 (spectral estimator) at τ = 15 ms while the best possible dividing-surface results yield only an estimation quality of αo ≈ 0.4 at τ = 15 ms. Thus, the quality of the apo-myoglobin data is similar to that of the two-state model with intermediate-quality order parameter and noise [Fig. 2(IIb)]. These data thus represent a harder test for rate estimators than the p5ab hairpin and should show differences between different rate estimators.
Figures 5(3a), 5(3b), 5(4a), and 5(4b) compare the estimates of κ2 from the direct MSM estimate (black), a fit to the fluctuation autocorrelation function using a dividing surface at the local histogram maximum (minimum between two maxima with filtering) of the binned data at o = 4.6 pN (green), and spectral estimation (red). For the multi-τ estimators (dividing-surface and spectral estimations), the lag time τ specifies the start of a time range [τ, τ + 2.5 ms] that was used for an exponential fit.
Figure 5(3a) shows again that the MSM estimate of κ2 exhibits the slow τ−1 convergence predicted by the theory [Eq. (29)] and does not yield a converged estimate using lag times of up to 20 ms. Since the MSM estimate still significantly overestimates the rate at τ = 50 ms when the relaxation process itself has almost entirely decayed, this estimator is not useful to analyze the apo-myoglobin data. In contrast, both the dividing-surface multi-τ approach and the spectral estimator do yield a converged estimate of κ̂2 ≈ 26 s−1, corresponding to a time scale of about 38 ms [Fig. 5(3a)]. In Ref. [46], a hidden Markov model with Gaussian output functions was used and the rate was estimated to be κ̂2 ≈ 46 s−1, corresponding to a time scale of approximately 21 ms. These differences are consistent with our theory, which shows that rate estimation errors lead to a systematic overestimation of the rate (and underestimation of the time scale). Figure 5(1a) shows the possible reason why the Gaussian HMM in Ref. [46] yields a rate overestimate: the partial probabilities are clearly not Gaussians. Following our theory, the smallest rate estimates the best estimates, which here are provided by the multi-τ estimators using either dividing-surface or spectral-estimation approaches.
In agreement with the theory [Eq. (31)], the multi-τ estimators (dividing-surface and spectral estimates) converge faster than the single-τ estimate (MSM). A double-exponential fit to the spectral estimation autocorrelation function yields an estimate of κ3 ≈ 100 s−1, corresponding to a time scale of 10 ms. Thus, there is a time-scale separation of a factor of about 4 between the slowest and the next-slowest process, indicating that, when viewed at sufficiently large time scales (> 20 ms), the dynamics can be considered to be effectively two state. However, since the presence of faster processes is clearly visible in the data, it may be worthwhile to investigate further substates of the A and B states with multistate approaches, such as hidden Markov models [23] or pair correlation analysis [27]. Such an analysis is beyond the scope of the present paper on two-state rate theory.
As indicated in Fig. 5(1a), the substates A and B estimated from PCCA+ do strongly overlap. Thus, even though the dividing-surface estimator can recover the true relaxation rate κ2, the estimated microscopic rates kAB and kBA depend on the choice of the position of the dividing surface. Figure 5(4a) shows the estimates of the dividing-surface multi-τ estimator, evaluated to kAB ≈ 12 s−1 and kBA ≈ 15 s−1. In contrast, the spectral estimator yields estimates of kAB ≈ 16 s−1 and kBA ≈ 10 s−1. Even though it is not strongly different, the dividing-surface approach suggests a reversed dominant direction of the process.
As for the two-state model results shown in Fig. 2, the spectral estimate is numerically more stable in τ compared to the dividing-surface estimate as a result of achieving a better signal-to-noise ratio. Clearly, in the dividing-surface approach, it is possible to pick a dividing-surface position that yields the same estimates for kAB and kBA, as for the spectral estimator. However, the dividing-surface estimator itself does not provide any information that is the correct choice, and, therefore, this theoretical possibility is of no practical use. Figure 2 in the Supplemental Material [28] compares the estimation results of κ2, kAB, and kBA for different choices of the dividing surface. In contrast to the dividing-surface approach, the spectral estimator assumes only that the extreme values of o are pure, which is a much weaker requirement than assuming that an appropriate dividing surface exists (see theory), and hence provides more reliable rate estimates.
Figures 5(1b)–5(4b) show the effect of filtering the data on the estimation results. Here, the data were averaged over a window length of 1 ms, corresponding to an averaging of 50 data points of the original 50 kHz data. Figure 5(1b) indicates that this filtering enhances the separation of states, and the apparent OQ increases to about α̂0 ≈ 0.7 (spectral estimate) while the dividing-surface estimation quality is α0 ≈ 0.6. The relaxation rate κ2 is still estimated to have κ̂2 ≈ 26 s−1, and the estimate becomes more robust for both the dividing-surface and the spectral estimates [Fig. 5(3b)]. The MSM estimate slightly improves but is still significantly too high. Figure 5(4b) shows that the dividing-surface derived-rate estimates kAB and kBA have improved and are now similar to the spectral-estimation results, while the spectral estimate itself remains at kAB ≈ 16 s−1 and kBA ≈ 10 s−1, independent of the filtering, which is in support of the reliability of the spectral estimate.
XIV. SUMMARY
We have described a rate theory for observed two-state dynamical systems. The underlying system is assumed to be ergodic, reversible, and Markovian in full phase space, as fulfilled by most physical systems in thermal equilibrium. The observation process takes into account that the system is not fully observed, but rather one order parameter is traced (the extension to multiple or multidimensional order parameters is straightforward). During the observation process, the observed order parameter may be additionally distorted or dispersed, for example, by experimental noise. Such observed dynamical systems occur frequently in the molecular sciences and appear in both the analysis of molecular simulations as well as of single-molecule experiments.
The presented rate theory for observed two-state dynamics is a generalization to classical two-state rate theories in two ways. First, most available rate theories assume that the system of interest is either fully observable or the relevant indicators of the slowest kinetic process can be observed without projection error or noise. Second, most classical rate theories are built on specific dynamical models, such as Langevin or Smoluchowski dynamics. The present theory explicitly allows the two kinetic states to overlap in the observed signal (either due to using a poor order parameter or to noise broadening), and does not require a specific dynamical model, but rather works purely based on the spectral properties of a reversible ergodic Markov propagator—hence, the name spectral rate theory.
Given the spectral rate theory, the systematic errors of available rate estimators can be quantified and compared. For example, the relatively large systematic estimation error in the implied time scales or implied rates of Markov state models is explained. Additionally, the theory provides a measure for the observation quality α̂o of the observed signal, which is independent of any specific dynamical model and also does not need the definition of an A or B state and bounds the error in rates estimated from the observed signal. α̂o includes effects of the order parameter measured as well as the effect of the experimental construct on the signal quality, such as experimental noise. It is shown that α̂o is a lower bound to the true reaction coordinate quality due to choosing the order parameter, and can thus be used as an indicator to improve both the quality of the experimental setup and the choice of the order parameter.
The theory suggests steps to be taken to construct an optimal rate estimator which minimizes the systematic error in the estimation of rates from an observed dynamical system. We propose such an estimator and refer to it as a spectral estimator. It provides rather direct and optimal estimates for the following three types of quantities:
The observation quality (OQ) α̂o of the observed signal.
The dominant relaxation rate κ2, as well as the microscopic transition rates kAB and kBA, even if A and B strongly overlap in the observable.
The partial probability densities, and hence projections of the states A and B in the observable, and , as well as their total probabilities, πA and πB. This information is also obtained if A and B strongly overlap in the observable.
Other rate estimators that rely on fitting the exponential tail of a time-correlation function calculated from the experimental recorded trajectories can also estimate κ2 without systematic error. However, the spectral estimator is unique in also being able to estimate kAB, kBA, , and the OQ in the presence of states that overlap in the observable order parameter.
XV. DISCUSSION
The present study concentrates on systematic rate estimation errors that are expected in the data-rich regime. We expect that taking the statistical error into consideration will make the spectral estimator described here even more preferable over more direct approaches such as fitting the number autocorrelation function of a dividing surface. This intuition comes from the fact that the spectral estimator maximizes the amplitude α with which the slow relaxation of interest is involved in the autocorrelation function. In the presence of statistical uncertainty, this will effectively maximize the signal-to-noise ratio in the autocorrelation function and thus lead to an advantage over fitting autocorrelation functions that were obtained differently.
Consideration of the statistical error will also aid in selecting an appropriate τ that balances systematic and statistical error in rate estimates. τ-dependent fluctuations of the sort observed in Fig. 2(III5) might also be suppressed by averaging over multiple choices of τ in a manner that incorporates the statistical error estimates in weighting.
The presented idea of building an optimal estimator for a single relaxation rate upon the transition matrix estimate of the projected slowest eigenfunction ψ̂2 is extensible to multiple relaxation rates, and this will be pursued in future studies.
Acknowledgments
The authors thank Susan Marqusee and Phillip J. Elms (UC Berkeley) for sharing the single-molecule force-probe data. F. N. and J.-H. P. acknowledge funding from the DFG center Matheon. F. N. acknowledges funding from ERC starting grant “pcCell” and DFG Grant No. 825/2. J. D. C. acknowledges funding from a QB3-Berkeley grant during part of this work. We are grateful to Christof Schütte, Attila Szabo, Sergio Bacallado, Vijay Pande, and Heidrun Prantel for enlightening discussions and support.
References
- 1.Greenleaf WJ, Woodside MT, Block SM. High- Resolution, Single-Molecule Measurements of Biomolecular Motion. Annu Rev Biophys Biomol Struct. 2007;36:171. doi: 10.1146/annurev.biophys.36.101106.101451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lapidus LJ, Eaton WA, Hofrichter J. Measuring the Rate of Intramolecular Contact Formation in Polypeptides. Proc Natl Acad Sci USA. 2000;97:7220. doi: 10.1073/pnas.97.13.7220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhou HX. Rate Theories for Biologists. Q Rev Biophys. 2010;43:219. doi: 10.1017/S0033583510000120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dudko OK, Graham TGW, Best RB. Locating the Barrier for Folding of Single Molecules under an External Force. Phys Rev Lett. 2011;107:208301. doi: 10.1103/PhysRevLett.107.208301. [DOI] [PubMed] [Google Scholar]
- 5.Morrison G, Hyeon C, Hinczewski M, Thirumalai D. Compaction and Tensile Forces Determine the Accuracy of Folding Landscape Parameters from Single Molecule Pulling Experiments. Phys Rev Lett. 2011;106:138102. doi: 10.1103/PhysRevLett.106.138102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Eyring H. The Activated Complex in Chemical Reactions. J Chem Phys. 1935;3:107. [Google Scholar]
- 7.Chandler D. Statistical Mechanics of Isomerization Dynamics in Liquids and the Transition State Approximation. J Chem Phys. 1978;68:2959. [Google Scholar]
- 8.Chodera JD, Elms PJ, Swope WC, Prinz J-H, Marqusee S, Bustamante C, Noé F, Pande VS. A Robust Approach to Estimating Rates from Time-Correlation Functions. arXiv:1108.2304 [Google Scholar]
- 9.Elson EL, Magde D. Fluorescence Correlation Spectroscopy. I. Conceptual Basis and Theory. Biopolymers. 1974;13:1. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 10.Skinner JL, Wolynes PG. Relaxation Processes and Chemical Kinetics. J Chem Phys. 1978;69:2143. [Google Scholar]
- 11.Chodera JD, Swope WC, Pitera JW, Dill KA. Long-Time Protein Folding Dynamics from Short-Time Molecular Dynamics Simulations. Multiscale Model Simul. 2006;5:1214. [Google Scholar]
- 12.Chodera JD, Dill KA, Singhal N, Pande VS, Swope WC, Pitera JW. Automatic Discovery of Metastable States for the Construction of Markov Models of Macromolecular Conformational Dynamics. J Chem Phys. 2007;126:155101. doi: 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- 13.Noé F, Horenko I, Schütte C, Smith JC. Hierarchical Analysis of Conformational Dynamics in Biomolecules: Transition Networks of Metastable States. J Chem Phys. 2007;126:155102. doi: 10.1063/1.2714539. [DOI] [PubMed] [Google Scholar]
- 14.Prinz JH, Wu H, Sarich M, Keller B, Fischbach M, Held M, Chodera JD, Schütte C, Noé F. Markov Models of Molecular Kinetics: Generation and Validation. J Chem Phys. 2011;134:174105. doi: 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- 15.Swope WC, Pitera JW, Suits F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations: 1. Theory. J Phys Chem B. 2004;108:6571. [Google Scholar]
- 16.Sarich M, Noé F, Schütte C. On the Approximation Quality of Markov State Models. SIAM Multiscale Model Simul. 2010;8:1154. [Google Scholar]
- 17.Kube S, Weber M. A Coarse-Graining Method for the Identification of Transition Rates between Molecular Conformations. J Chem Phys. 2007;126:024103. doi: 10.1063/1.2404953. [DOI] [PubMed] [Google Scholar]
- 18.Buchete NV, Hummer G. Coarse Master Equations for Peptide Folding Dynamics. J Phys Chem B. 2008;112:6057. doi: 10.1021/jp0761665. [DOI] [PubMed] [Google Scholar]
- 19.Schütte C, Noé F, Lu J, Sarich M, Vanden-Eijnden E. Markov State Models Based on Milestoning. J Chem Phys. 2011;134:204105. doi: 10.1063/1.3590108. [DOI] [PubMed] [Google Scholar]
- 20.Buchner GS, Murphy RD, Buchete NV, Kubelka J. Dynamics of Protein Folding: Probing the Kinetic Network of Folding-Unfolding Transitions with Experiment and Theory. Biochim Biophys Acta. 2011;1814:1001. doi: 10.1016/j.bbapap.2010.09.013. [DOI] [PubMed] [Google Scholar]
- 21.Rabiner LR. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Proc IEEE. 1989;77:257. [Google Scholar]
- 22.McKinney SA, Joo C, Ha T. Analysis of Single-Molecule FRET Trajectories Using Hidden Markov Modeling. Biophys J. 2006;91:1941. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chodera JD, Elms P, Noé F, Keller B, Kaiser CM, Ewall-Wice A, Marqusee S, Bustamante C, Hinrichs NS. Bayesian Hidden Markov Model Analysis of Single-Molecule Force Spectroscopy: Characterizing Kinetics under Measurement Uncertainty. arXiv:1108.1430 [Google Scholar]
- 24.Gopich IV, Szabo A. Decoding the Pattern of Photon Colors in Single-Molecule FRET. J Phys Chem B. 2009;113:10 965. doi: 10.1021/jp903671p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stigler J, Ziegler F, Gieseke A, Gebhardt JCM, Rief M. The Complex Folding Network of Single Calmodulin Molecules. Science. 2011;334:512. doi: 10.1126/science.1207598. [DOI] [PubMed] [Google Scholar]
- 26.Pirchi M, Ziv G, Riven I, Cohen SS, Zohar N, Barak Y, Haran G. Single-Molecule Fluorescence Spectroscopy Maps the Folding Landscape of a Large Protein. Nat Commun. 2011;2:493. doi: 10.1038/ncomms1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hoffmann A, Woodside MT. Signal-Pair Correlation Analysis of Single-Molecule Trajectories. Angew Chem Int Ed Engl. 2011;50:12643. doi: 10.1002/anie.201104033. [DOI] [PubMed] [Google Scholar]
- 28.See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevX.4.011020 for detailed derivations of the theory summarized in this paper, and for additional data on Apomyoglobin.
- 29.Barra F, Clerc M, Tirapegui E. Detailed Balance in Nonequilibrium Systems. Dyn Stab Syst. 1997;12:61. [Google Scholar]
- 30.Schütte C, Fischer A, Huisinga W, Deuflhard P. A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo. J Comput Phys. 1999;151:146. [Google Scholar]
- 31.Noé F, Nüske F. A Variational Approach to Modeling Slow Processes in Stochastic Dynamical Systems. SIAM Multiscale Model Simul. 2013;11:635. [Google Scholar]
- 32.Hinczewski M, von Hansen Y, Netz RR. Deconvolution of Dynamic Mechanical Networks. Proc Natl Acad Sci USA. 2010;107:21493. doi: 10.1073/pnas.1010476107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.von Hansen Y, Mehlich A, Pelz B, Rief M, Netz RR. Auto- and Cross-Power Spectral Analysis of Dual Trap Optical Tweezer Experiments Using Bayesian Inference. Rev Sci Instrum. 2012;83:095116. doi: 10.1063/1.4753917. [DOI] [PubMed] [Google Scholar]
- 34.Hinczewski M, Gebhardt JCM, Rief M, Thirumalai D. From Mechanical Folding Trajectories to Intrinsic Energy Landscapes of Biopolymers. Proc Natl Acad Sci USA. 2013;110:4500. doi: 10.1073/pnas.1214051110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Onsager L. Reciprocal Relations in Irreversible Processes II. Phys Rev. 1931;38:2265. [Google Scholar]
- 36.Montgomery JA, Chandler D, Berne BJ. Trajectory Analysis of a Kinetic Theory for Isomerization Dynamics in Condensed Phases. J Chem Phys. 1979;70:4056. [Google Scholar]
- 37.Zwanzig R, Ailawadi NK. Statistical Error Due to Finite Time Averaging in Computer Experiments. Phys Rev. 1969;182:280. [Google Scholar]
- 38.Ritz W. Über Eine Neue Methode zur Lösung Gewisser Variationsprobleme der Mathematischen Physik. J Reine Angew Math. 1909;135:1. [Google Scholar]
- 39.Peters B. Using the Histogram Test to Quantify Reaction Coordinate Error. J Chem Phys. 2006;125:241101. doi: 10.1063/1.2409924. [DOI] [PubMed] [Google Scholar]
- 40.Noé F, Schütte C, Vanden-Eijnden E, Reich L, Weikl TR. Constructing the Full Ensemble of Folding Pathways from Short Off-Equilibrium Simulations. Proc Natl Acad Sci USA. 2009;106:19011. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Voelz VA, Bowman GR, Beauchamp K, Pande VS. Molecular Simulation of Ab Initio Protein Folding for a Millisecond Folder NTL9. J Am Chem Soc. 2010;132:1526. doi: 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bowman GR, Beauchamp KA, Boxer G, Pande VS. Progress and Challenges in the Automated Construction of Markov State Models for Full Protein Systems. J Chem Phys. 2009;131:124101. doi: 10.1063/1.3216567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Deuflhard P, Weber M. Robust Perron Cluster Analysis in Conformation Dynamics. Zuse Institute Berlin Report No 03–09. 2003 [Google Scholar]
- 44.Deuflhard P, Huisinga W, Fischer A, Schütte C. Identification of Almost-Invariant Aggregates in Reversibly Nearly Uncoupled Markov Chains. Linear Algebra Appl. 2000;315:39. [Google Scholar]
- 45.Elms PJ, Chodera JD, Bustamante C, Marqusee S. Limitations of Constant-Force-Feedback Experiments. Biophys J. 2012;103:1490. doi: 10.1016/j.bpj.2012.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Elms PJ, Chodera JD, Bustamante C, Marqusee S. The Molten Globule State is Unusually Deformable under Mechanical Force. Proc Natl Acad Sci USA. 2012;109:3796. doi: 10.1073/pnas.1115519109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bustamante CJ, Smith SB. Light-Force Sensor and Method for Measuring Axial Optical-Trap Forces from Changes in Light Momentum along an Optic Axis. 7133132. US Patent No. 2006