Structural adaptations to diverse fighting styles in sexually selected weapons

Significance

Animal weapons are among nature’s most diverse structures. Intuitively, species have different types of weapons because they fight in different ways, yet no studies have directly tested whether weapons perform better at the animals’ own style of fighting than they do at others. We constructed biomechanical models of the horns of different rhinoceros beetle species to evaluate the functional performance of horns in response to both species-typical and species-atypical fighting loads. We found that horns are both stronger and stiffer in response to species-typical fighting loads, which suggests selection for improved performance under different fighting styles played an important role in the diversification of weapon form.

Abstract

The shapes of sexually selected weapons differ widely among species, but the drivers of this diversity remain poorly understood. Existing explanations suggest weapon shapes reflect structural adaptations to different fighting styles, yet explicit tests of this hypothesis are lacking. We constructed finite element models of the horns of different rhinoceros beetle species to test whether functional specializations for increased performance under species-specific fighting styles could have contributed to the diversification of weapon form. We find that horns are both stronger and stiffer in response to species-typical fighting loads and that they perform more poorly under atypical fighting loads, which suggests weapons are structurally adapted to meet the functional demands of fighting. Our research establishes a critical link between weapon form and function, revealing one way male–male competition can drive the diversification of animal weapons.

Sexually selected traits are renowned for their extreme size and diversity (1, 2). Some sexual traits, such as elaborate feathers in birds of paradise and widowbirds, are used as ornaments to attract choosy females, whereas others, such as giant elk antlers and stag beetle mandibles, are used as weapons in male–male battles over access to females. Numerous empirical (3–9) and theoretical (10–15) studies have shown how female choice can drive the diversification of male ornaments. Surprisingly few studies, however, have examined whether male–male competition drives the diversification of weapons, and the mechanisms responsible for weapon divergence remain largely unexplored (16). As a consequence, although sexually selected weapons are just as diverse as ornaments, it is not clear why this should be so.

The most intuitive explanation for weapon diversity is that weapons are adapted to species-specific fighting styles. Specifically, differences either in the way males fight or in where they fight may favor corresponding changes in weapon shape (16). This hypothesis has been explored most thoroughly for the horns and antlers of ungulates (17–20). For example, males in species with short, smooth horns tend to be stabbers; males with robust, curved horns typically ram opponents; and males with long, reaching horns wrestle or fence (18, 19). Although these broad comparative patterns provide evidence that different fighting styles have contributed to the divergence of weapon forms, all the studies are correlative. Explicit tests of the functional performance of weapons in response to forces incurred during fights are still lacking, and no studies have tested whether animal weapons perform better at their own style of fighting than they do at others. Thus, although functional specialization of weapons for diverse styles of fighting remains the most intuitive and widely cited driver of weapon diversity, it has yet to be directly tested for any type of animal weapon.

Rhinoceros beetles (Coleoptera: Dynastinae) are ideal for studying weapon diversity for three reasons. First, species vary in the number, size, and shape of their horns, with species wielding long pitchforks, robust pincers, or thin spears, to name just a few of the diverse horn types (16, 21) (Figs. 1 and 2). Second, horns are used as weapons during combat with rival males over access to females. There is no evidence that females choose males on the basis of the shape or size of their horns (22–25), so horn morphology is expected to reflect differences in how horns are used during fights without conflicting selective pressures from female choice. Third, species fight on a variety of substrates (e.g., on broad tree trunks, on narrow shoots, or inside tunnels) and use their horns in different ways, which may select for qualitatively different fighting structures (16, 23, 24).

Fig. 1.

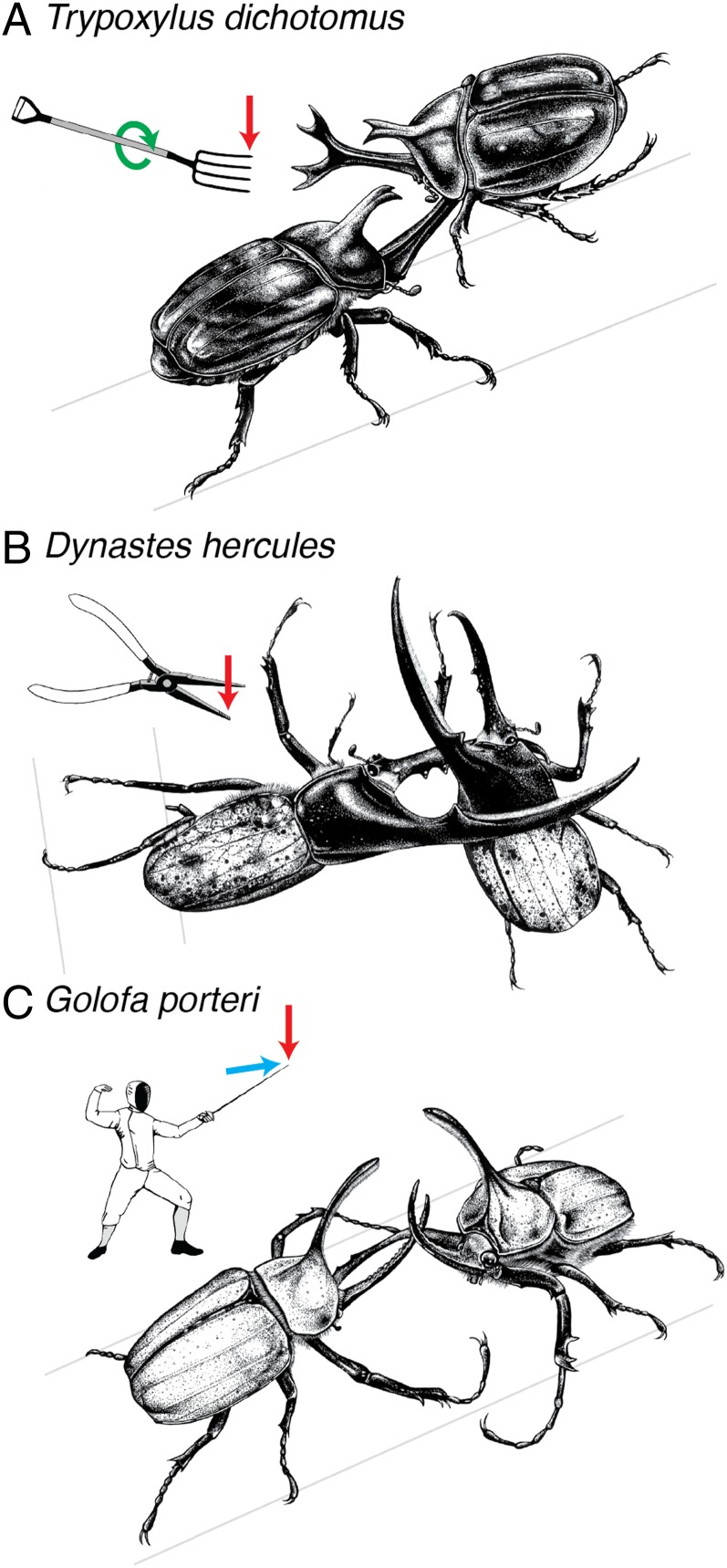
Variation in horn morphology and fighting styles in rhinoceros beetles. (A) Trypoxylus dichotomus males have a long, forked head horn that is used like a pitchfork to lift and twist opponents off tree trunks during fights. (B) Dynastes hercules males have a long head horn and long thoracic horn that are used together similar to pliers to lift, squeeze, and then toss opponents to the ground. (C) Golofa porteri males have a long, slender head horn that is used similar to a fencing sword to both lift opponents off narrow shoots and push them sideways off balance. Vectors represent the typical forces experienced by horns during fights: vertical bending (red), lateral bending (blue), twisting (green). Illustrations by David J. Tuss.

Fig. 2.

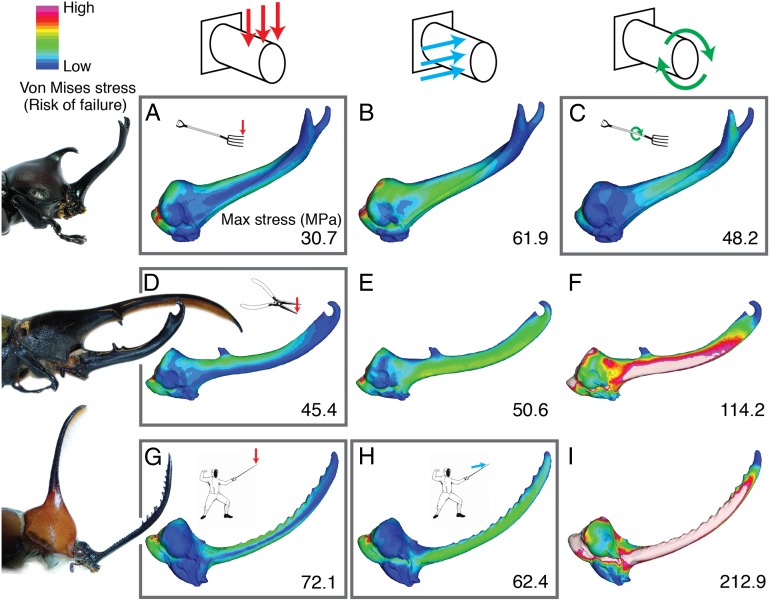
Horns are stronger under species-specific fighting loads. Von Mises stress distributions and maximum stress values from finite element models of Trypoxylus (A–C), Dynastes (D–F), and Golofa (G–I) horns under vertical bending (A, D, G), lateral bending (B, E, H), and twisting (C, F, I) loads. Typical fighting loads for each species are outlined in gray; atypical fighting loads are not outlined. In all three species, maximum Von Mises stresses in the horn are higher (warmer colors) under atypical loading conditions, indicating a higher likelihood of breaking. Contour plots are scaled to 80 MPa maximum stress. The high stresses at the base of the horn are artifacts from constraining the models and are not included in calculating the maximum stress values in the horn.

Here, we perform a functional analysis of rhinoceros beetle horns to test whether horns are structurally suited for diverse fighting styles. Specifically, we compare the mechanical performance of various beetle horn morphologies using finite element analysis, a standard and powerful engineering analysis technique used to predict how complex structures deform, and ultimately fail, in response to applied loads (26). We test whether beetle horns are adapted to meet the functional demands of fighting by constructing finite element models of the head horns of three rhinoceros beetle species and loading the model horns in ways that mimic the forces incurred during both species-typical and species-atypical fights.

Results and Discussion

The three species investigated in this study, Trypoxylus dichotomus, Golofa porteri, and Dynastes hercules, have very different horn morphologies and distinct fighting styles. In all three species, males insert their head horn underneath an opponent to pry him from the substrate, but the specific maneuvers used, and therefore the forces the horns experience, are different (Fig. 1). The head horns of Trypoxylus males are long and forked and function like a pitchfork, prying and twisting opponents off the trunks and branches of trees (24, 27). The head horns of Dynastes males are long and work together with a long thoracic horn like the pincer arms of pliers to lift and squeeze opponents off of trees and toss them to the ground (22). The head horns of Golofa males are long and slender and are used as a fencing sword to both lift opponents and push them sideways off balance in chaotic scrambles for control of narrow shoots (28). Because of their distinctive fighting styles, head horns in these species are bent vertically and twisted (Trypoxylus), bent vertically only (Dynastes), or bent vertically and laterally (Golofa) during fights, which makes it possible to analyze the structural performance of horns in response to fighting loads that are both typical and atypical for each species.

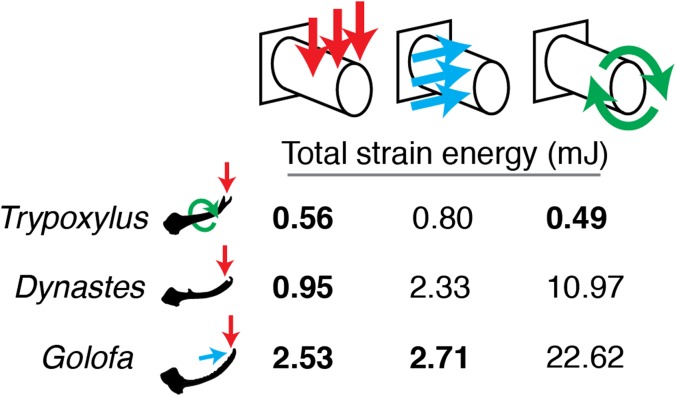
The results from the finite element models indicate that horns performed best when loaded under conditions that mimic species-typical fights, and more poorly when loaded under atypical fighting conditions. We assessed two measures of horn performance: strength and stiffness (Materials and Methods). Horn strength was evaluated by comparing model stress, and horn stiffness was evaluated by comparing total strain energies. In all three species, horns had significantly lower stresses, and thus were less likely to break, under typical fighting loads (Fig. 2). Horns also had significantly lower strain energies while transmitting forces under typical fighting loads (Fig. 3), which indicates that they deformed less, and thus were more effective at transmitting forces to dislodge an opponent, when deployed in a fashion typical of fights for each species. These findings are consistent with the hypothesis that horns are structurally adapted to meet the functional demands of species-specific fighting. We expect that selection for improved fighting performance is the most important agent of selection on horn morphology, but future studies that compare the performance of additional horn types and evaluate the relationships between horn morphology and fighting style in a phylogenic framework (18, 19, 29) are needed to fully understand the diversification of weapon form.

Fig. 3.

Horns are stiffer under species-specific fighting loads. In all three species, total strain energies from finite element models were lower under typical loading conditions (bold) compared with atypical loading conditions (not bold), indicating that horns are stiffer and thus more effective at transmitting forces to dislodge opponents during species-specific fights.

One aspect of horn morphology that likely explains variation in performance is cross-sectional shape. Given that the object of fights is to dislodge opponents (23, 24, 27), an optimal horn should resist deflection in response to typical fighting loads. The resistance of a beam to bending is directly related to the structure’s second moment of area, or how its mass is distributed about the neutral bending axis (30). Structures that are bent predictably in a single direction (e.g., pliers, Dynastes horns) are the most resistant to bending when the mass is distributed far from the bending axis, such that elliptical cross-sections are ideal (20, 30). In contrast, structures that are bent unpredictably from many different directions (e.g., fencing swords, Golofa horns) perform best with circular cross-sections, as circular cross-sections distribute mass equally around all possible bending axes (20, 30).

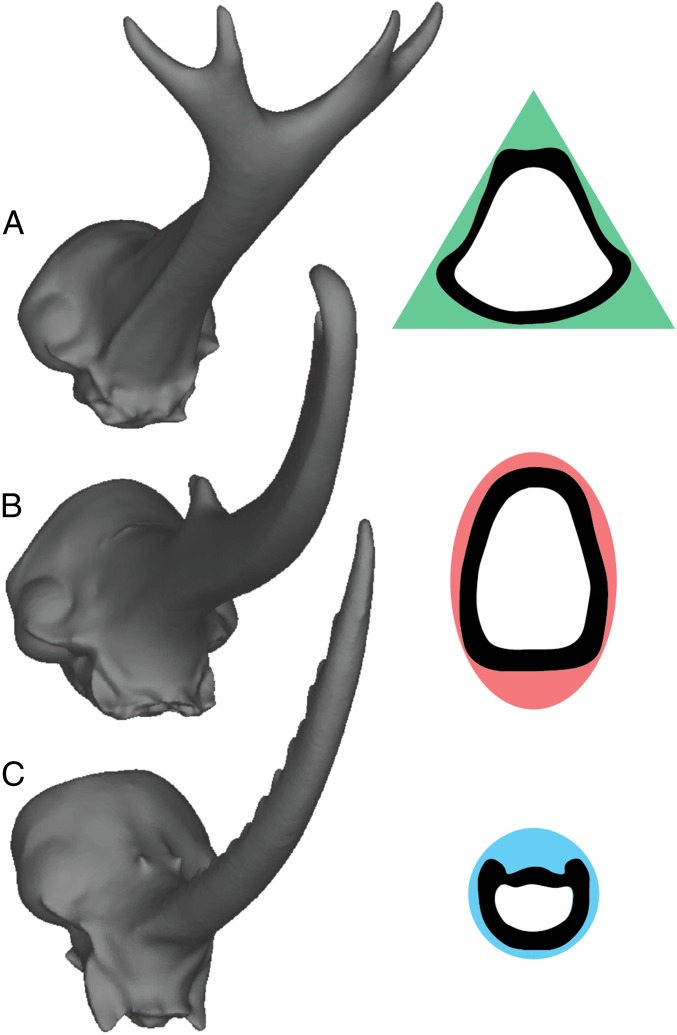
Biological structures that are both bent and twisted should benefit from noncircular cross-sections (such as the triangular cross-sections of sedge petioles or the U-shaped cross-sections of feather rachises), as these shapes allow the structures to twist before being bent out of shape (31). Because triangular cross-sections have both a high second moment of area (which confers high flexural stiffness) and a high polar moment of area (which confers high torsional stiffness) (30), triangular cross-sections may be ideal for structures that must resist bending and twisting (e.g., Trypoxylus horns). Thus, if variation in performance among the three species reflects differences in their resistance to bending and twisting, we predict Trypoxylus horns will have triangular-shaped cross-sections; Dynastes horns, elliptical cross-sections; and Golofa horns, circular cross-sections. Transverse sections from our microcomputed tomography (micro-CT) scans of the three beetle horns confirm these predictions (Fig. 4), suggesting that relatively simple shape changes can have large effects on horn performance, and that differences in cross-sectional morphologies alone may explain much of the variation we observed among species. Cross-sectional shape is, of course, just one aspect of overall horn morphology, and future studies will be necessary to understand how other horn attributes (e.g., horn curvature, teeth along the horn shaft, or forks at the tip) affect mechanical performance during combat. Finite element analysis promises to be an important tool in these endeavors. In particular, we expect that studies that assess additional measures of performance (e.g., stability or grip during combat) and that evaluate the functional significance of specific horn attributes by digitally manipulating horn shape (32–34) will be especially informative in explaining differences in the overall morphology of beetle horns.

Fig. 4.

Variation in horn performance is attributed to different cross-sectional morphologies. 3D finite element models and outlines from transverse micro-CT slices from the middle of each horn. The cross-sectional morphology of horns is triangular in Trypoxylus (A), elliptical in Dynastes (B), and circular in Golofa (C), as predicted if horns are adapted to resist deflection under their typical fighting loads.

Recent improvements in 3D imaging have now made it possible for evolutionary biologists to use mature engineering technology to rigorously test the form and function of complex biological structures. We capitalized on these new applications of standard engineering tools to answer old questions about biological diversity. Using finite element analysis, we were able to expose the weapon from one species to the forces typical of fights of other species and to test the functional performance of weapons for the first time, to our knowledge, in any animal. Our finding that the horns of different rhinoceros beetle species are both stronger and stiffer in response to species-typical fighting loads illustrates the critical link between weapon form and function and suggests that variation in weapon shape reflects a history of selection for improved performance during species-typical fights. More broadly, the findings highlight the potential for male–male competition to drive the divergence of animal weapons, which are among nature’s most elaborate body forms.

Materials and Methods

Model Construction.

Finite element models were based on high-resolution 3D reconstructions of the head horns of three rhinoceros beetle species (Trypoxylus dichotomus, Golofa porteri, and Dynastes hercules) created from micro-CT scans (Movie S1). The specimens were scanned with a SkyScan 1173 micro-CT scanner at 70 kV and 110 μA. The spatial resolution of the files was 20.0 μm for Trypoxylus and 26.6 μm for Golofa and Dynastes.

We simplified the initial reconstructions using Geomagic (Geomagic, Inc.) to remove extraneous morphological details. Specifically, we corrected artificial holes and surface irregularities and deleted the antennae, maxillary and labial palps, and apodemes and tentoria inside the head capsule that significantly increased the geometric complexity (and thus the computational demands) of the models but were unlikely to affect the results of the loading experiments on the horn. The simplified models were then imported into Mimics (Materialise) to be cleaned and edited further (e.g., by improving the aspect ratios and reducing the number of the triangular surface elements) to generate the final solid element models. There were 44,459 nodes and 178,755 elements in the final Trypoxylus model, 44,032 nodes and 192,133 elements in the Golofa model, and 63,832 nodes and 259,918 elements in the Dynastes model. The final models were then imported into Strand7 (Strand7 Pty Ltd) for linear static finite element analysis.

We compared the results of finite element models consisting of four- versus 10-noded tetrahedral elements. The difference in mean stress values was less than 10%, which indicates that our models were robust (35). Because of the substantially longer computing time required for the 10-noded tetrahedral models, we chose to conduct our analyses on the basis of models composed of four-noded tetrahedral elements.

Finite Element Analysis.

Because the goal of the study was to compare horn performance according to differences in shape, we controlled for variation in size and assigned identical material properties (36). For modeling simplicity and in the absence of more precise reference data, the models were assigned homogeneous and isotropic material properties on the basis of Young’s modulus values for the clypeus cuticle of horned dung beetles (E = 15.98 GPa) (37) and an average Poisson’s ratio (ν = 0.30) (38). The models were constrained from rigid body motion by fixing three nodes around the occiput, where the head attaches to the pronotum.

We simulated the three most important loading conditions that beetle horns experience during fights: vertical bending, lateral bending, and twisting (Movie S2). We scaled our models using the methods described by Dumont and colleagues (36) to remove the confounding effect of model size and compare the relative performance of the models solely on the basis of differences in shape. Specifically, to compare performance in terms of model stress ($\sigma =F/A$, where F is force and A is cross-sectional surface area) in the vertical and lateral bending models, we maintained the same force-to-surface area ratios (36). The three models were therefore scaled to the same surface area (723 mm², or the surface area of the Trypoxylus model), and the same total force (4 N) was applied to the horn tip, based on field estimates of the forces exerted by Trypoxylus males during fights (39). Similarly, to compare stress in our twisting models, we maintained the same torque-to-volume ratios. The models were therefore scaled to the same volume (116 mm³, or the volume of the Trypoxylus model), and the same total torque (32.8 Nmm) was applied to the widest points of the horn tip, based on the torque resulting from a 4-N force applied at the lateral-most tine in our Trypoxylus model (moment arm, 8.2 mm). Maximum stress of a cylinder under torsion ($\tau =16T/\pi d^3$, where T is torque and d is the diameter of the cylinder) is proportional to torque and inversely proportional to volume (40). Scaling our models in these ways generates null hypotheses of no differences in stress distributions and stress magnitudes, such that any differences among our models could be attributed entirely to differences in shape (see ref. 36 for details on scaling guidelines for finite element models).

Results from the finite element models indicate that the highest stresses generated in a horn during fights occur in the middle of the shaft, which matches the actual location of horn fractures for beetles in the field (39). Our finite element models therefore accurately predict the responses of horns to the forces incurred during fights.

Comparing Model Performance.

The structural performance of horns in response to the various loading conditions was evaluated on the basis of two criteria: strength and stiffness. First, we evaluated the strength of the horns by comparing model stress (in megapascals). Von Mises stress is a good predictor of failure resulting from ductile fracture (36), so for a given load, structures with lower Von Mises stress are less likely to fail, and therefore are interpreted as being a stronger structure. We evaluated model strength qualitatively, by visually comparing the Von Mises stress contour plots, and quantitatively, by comparing the maximum Von Mises stress values along the length of the horn (distal to the clypeus).

Second, we evaluated the performance of horns in terms of stiffness by comparing total strain energy (in millijoules). Assuming the function of a horn is to transmit forces to dislodge an opponent (23), horns that are stiffer (less compliant) for a given volume of material are more optimal than those that are less stiff (more compliant) (36). The work expended by an applied load in elastically deforming a structure is stored as elastic strain energy, so for a given load, the smaller the model’s strain energy, the less work that is lost to deformation, and thus the more effective the model is at transmitting fighting forces (36). Strain energy in bending ($U=F^{2}L/2EA$, where F is force, L is the beam length, E is the Young’s modulus, and A is the cross-sectional surface area) is proportional to force squared and inversely proportional to the cube root of volume (40). We therefore controlled for the effect of horn size in our vertical and lateral bending models by scaling the measured strain energies to conserve the same force squared-to-cube root of volume ratio (36). Similarly, because strain energy in twisting ($U=T^{2}L/2GI=T^{2}L/G\pi r^4$, where T is torque, L is the beam length, G is the shear modulus, I is the polar moment, and r is the radius of the cylinder) is proportional to torque squared and inversely proportional to volume (40), we removed the confounding effect of horn size in our twisting models by scaling the measured strain energies to conserve the same torque squared-to-volume ratio. Again, scaling our models in these ways generates null hypotheses of no differences in total strain energy, so any differences in performance are the result of differences in shape (36).

The actual values for stresses and strains should be interpreted with caution because of our simplifying assumptions of homogeneous and isotropic material properties. However, by applying identical material properties and scaling the models appropriately, we can interpret the relative performance of different horns with confidence (36).