Scaling description of the yielding transition in soft amorphous solids at zero temperature

Significance

Yield stress solids flow if a sufficiently large shear stress is applied. Although such materials are ubiquitous and relevant for industry, there is no accepted microscopic description of how they yield. Here we propose a scaling description of the yielding transition that relates the flow curve, the statistics of the avalanches of plasticity observed at threshold, and the density of local zones that are about to yield. Our description shares some similarity with the depinning transition that occurs when an elastic manifold is driven through a random potential, but also presents some striking differences. Numerical simulations on a simple elasto-plastic model find good agreement with our predictions.

Abstract

Yield stress materials flow if a sufficiently large shear stress is applied. Although such materials are ubiquitous and relevant for industry, there is no accepted microscopic description of how they yield, even in the simplest situations in which temperature is negligible and in which flow inhomogeneities such as shear bands or fractures are absent. Here we propose a scaling description of the yielding transition in amorphous solids made of soft particles at zero temperature. Our description makes a connection between the Herschel–Bulkley exponent characterizing the singularity of the flow curve near the yield stress Σ_c, the extension and duration of the avalanches of plasticity observed at threshold, and the density P(x) of soft spots, or shear transformation zones, as a function of the stress increment x beyond which they yield. We argue that the critical exponents of the yielding transition may be expressed in terms of three independent exponents, θ, d_f, and z, characterizing, respectively, the density of soft spots, the fractal dimension of the avalanches, and their duration. Our description shares some similarity with the depinning transition that occurs when an elastic manifold is driven through a random potential, but also presents some striking differences. We test our arguments in an elasto-plastic model, an automaton model similar to those used in depinning, but with a different interaction kernel, and find satisfying agreement with our predictions in both two and three dimensions.

Many solids will flow and behave as fluids if a sufficiently large shear stress is applied. In crystals, plasticity is governed by the motion of dislocations (1, 2). In amorphous solids, there is no order, and conserved defects cannot be defined. However, as noticed by Argon (3), plasticity consists of elementary events localized in space, called shear transformations, in which a few particles rearrange. This observation supports that there are special locations in the sample, called shear transformation zones (STZs) (4), in which the system lies close to an elastic instability. Several theoretical approaches of plasticity, such as STZ theory (4) or soft glassy rheology (5), assume that such zones relax independently or are coupled to each other via an effective temperature. However, at zero temperature and small applied strain rate $\dot{\mathrm{\gamma }}$, computer experiments (6–11) and very recent experiments (12, 13) indicate that local rearrangements are not independent: plasticity occurs via avalanches in which many shear transformations are involved, forming elongated structures in which plasticity localizes. If conditions are such that flow is homogeneous (as may occur, for example, in foams or emulsions), one finds that the flow curves are singular at small strain rate and follow a Herschel–Bulkley law $\Sigma -{\Sigma }_c\sim {\dot{\mathrm{\gamma }}}^{1/\mathrm{\beta }}$ (14, 15). These features are reproduced qualitatively by elasto-plastic models (16–20) in which space is discretized. In these models, a site that yields plastically affects the stress in its surroundings via some interaction kernel $\mathcal{G}$(r), argued to decay as a power law of distance and to display a fourfold symmetry (21), as supported by observations (22–24). This perturbation may trigger novel plastic events and lead to avalanches. However, even within this picture, the relationship between the avalanche dynamics and the singularity of the flow curves remains debated (7, 25).

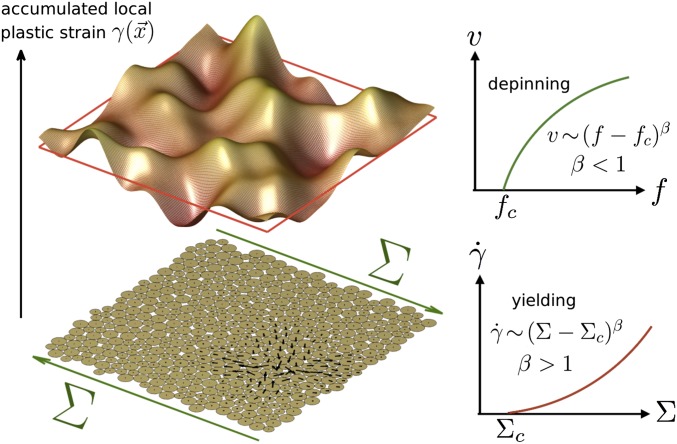
It is tempting to seek progress by building a comparison between the yielding transition and the much better understood depinning transition that occurs when an elastic interface of dimension d is driven in a d + 1 random environment (2, 26). The role that transverse displacements play in depinning corresponds to the local accumulated plastic strain $\mathrm{\gamma }\left(\overrightarrow{x}\right)$, and the total plastic strain γ can be identified with the center of mass of the interface, as illustrated in Fig. 1. Both phenomena display very similar properties: near the depinning threshold force F_c, the velocity v vanishes nonanalytically v ∼ (F − F_c)^β and the interplay between disorder and elasticity at threshold leads to broadly distributed avalanches corresponding to jerky motions of the interface. Much more is known about the depinning transition: it is a dynamical critical point characterized by two independent exponents related to avalanche extension and duration (26, 27). These exponents have been computed perturbatively with the functional renormalization group (28–30) and evaluated numerically with high precision (31, 32). The comparison between these two phenomena has led to the proposition that the yielding transition is in the universality class of mean-field depinning (33, 34). However, experiments find a reological exponent β > 1 against the β ≤ 1 predicted for elastic depinning, and numerical simulations display intriguing finite size effects that differ from depinning (9, 10, 35–37).

Fig. 1.

(Left) Analogy between the yielding transition of a d-dimensional amorphous solid and the depinning transition of an elastic interface of d dimensions in a space of d + 1 dimensions, illustrated here for d = 2. The height of the interface is the accumulated local plastic strain generated by local plastic rearrangements; one example of the latter appears in the bottom. (Right) the strain rate–stress (velocity–force) curves for the yielding (depinning) transition with β > 1 (β < 1) in yielding (depinning) transition.

Formally, elasto-plastic models are very similar to automaton models known to capture the depinning transition well (17); the key difference lies in the interaction kernel $\mathcal{G}$, long-ranged and of variable sign for elasto-plastic models while essentially a Laplacian for depinning with short-range elasticity. We recently showed (20) that in the presence of long-ranged interaction with variable sign, the distribution of shear transformations at a distance x from instability, P(x), is singular with P(x) ∼ x^θ, unlike in depinning for which θ = 0. As we shall recall, this singularity naturally explains the finite size effects observed in simulations. In this article, we argue that once this key difference with depinning is taken into account, the analogy between these two phenomena is fruitful and leads to a complete scaling description of the yielding transition. In particular, we find that the Herschel–Bulkley exponent is related to avalanche extension and duration via Eq. 9 and that the avalanche statistics may be expressed in terms of three independent exponents: θ, d_f, and z, characterizing, respectively, the density of shear transformations, the fractal dimension of the avalanches, and their duration.

Definition of Exponents

Several studies (see Table 2) characterized the yielding transition with several exponents, which we now recall.

Table 2.

Values of exponents as reported in the literature

	Value
Exponent	2d	3d	Lattice model	Molecular dynamics	Experiments
β	1.52	1.38	1.78 (43)	2 (45), 2.33 (8), 3(3d) (8)	2.22(3d) (46), 2.78 (47), 2.22(3d) (48)
ν/β	0.72	0.53	0.5 (19), 0.6 (43), 1 (20)	0.5 (7), 0.43 (8), 0.33(3d) (8)
τ	1.36	1.43	1.34 (49),1.25 (16)	1.3 (36), 1.3(3d) (36)	1.37–1.49(3d) (50), 1.5(3d) (60)
df	1.1	1.5	1.5 (20), 1.5 (43), 1 (16)	0.9 (36), 1.1(3d) (36), 1 (51), 1.5(3d) (51), 1.6(3d) (52)
(2 − τ)df	0.7	0.8	0.75 (16)	1 (10), 0.6 (36), 0.8(3d) (36)
z/df	0.52	0.43	0.68 (49)		0.5 (60)
θ	0.57	0.35		0.54 (36), 0.43(3d) (36), 0.5 (35), 0.5(3d) (35)

The exponents characterizing the relationships between length and strain rate $\mathrm{\xi }\sim {\dot{\mathrm{\gamma }}}^{-\mathrm{\nu }/\mathrm{\beta }}$, average avalanche size and system length $\langle S\rangle \sim L^{\left(2-\mathrm{\tau }\right)d_f}$, and avalanche durations with sizes $T\sim S^{z/d_f}$ are reported often and are shown here. Three-dimensional observations are labeled (3d); otherwise, the values correspond to 2D systems.

Flow Curves.

Rheological properties are singular near the yielding transition. Herschel and Bulkley (38) noticed that for many yield stress materials, $\Sigma ={\Sigma }_c+A{\dot{\mathrm{\gamma }}}^n$, where $\dot{\mathrm{\gamma }}$ is the macroscopic strain rate and Σ is the external shear stress. By analogy with depinning, we instead introduce the exponent β = 1/n, such that

$$\dot{\mathrm{\gamma }}\sim {\left(\Sigma -{\Sigma }_c\right)}^{\mathrm{\beta }}.$$ [1]

In contrast to depinning, one finds β > 1 in the yielding transition, as we explain below. Our analysis below focuses on the regime (Σ − Σ_c)/Σ_c ≪ 1; effects not discussed here are expected to affect the flow curves at larger stresses (39, 40).

Length Scales.

Near the yielding transition, the dynamics become more and more cooperative and are correlated on a length scale ξ:

$$\mathrm{\xi }\sim {\left|\Sigma -{\Sigma }_c\right|}^{-\mathrm{\nu }}.$$ [2]

Avalanche Statistics.

At threshold Σ = Σ_c, the dynamics occur by avalanches whose size we define as S ≡ ΔγL^d, where Δγ is the plastic strain increment due to the avalanche and L^d is the volume of the system. The normalized avalanche distribution ρ(S) follows a power law:

$$\mathrm{\rho }\left(S\right)\sim S^{-\mathrm{\tau }}.$$ [3]

In a finite system of size L, this distribution is cut off at some value S_c, where the linear extension of the avalanche is of order L, enabling definition of the fractal dimension d_f:

$$S_c\sim L^{d_f}.$$ [4]

A key exponent relates length and time scales; z characterizes the duration T of an avalanche whose linear extension is l:

$$T\sim l^z.$$ [5]

Density of Shear Transformations.

If an amorphous solid is cut into small blocks containing several particles, one can define how much stress x_i needs to be applied to the block i before an instability occurs. The probability distribution P(x) is a measure of how many putative shear transformations are present in the sample (20). Near the depinning transition, a similar quantity can be defined, and in that case it is well known that P(x) ∼ x⁰ (26). We have argued (20) that it must be so when the interaction kernel $\mathcal{G}$ is monotonic, i.e., its sign is constant in space. For an elastic interface, this is the case, as a region that yields will always destabilize other regions. This implies that locally, the distance to instability x_i always decreases with time until x_i < 0, when the block i rearranges. Thus, nothing in the dynamics allows the block i to forecast an approaching instability, and no depletion or accumulation is expected to occur near x_i = 0. By contrast, for the yielding transition, the sign of $\mathcal{G}$ varies in space. Thus locally, x_i jumps both forward and backward, performing some kind of random walk. Because x = 0 acts as an absorbing boundary condition (as the site is stabilized by a finite amount once it yields), one expects that depletion may occur near x = 0 (20, 37, 41). In ref. 20, we argued that P(x) indeed must vanish at x = 0 if the interaction is sufficiently long range (particularly if |$\mathcal{G}$| ∼ 1/r^d, as is the case for the yielding transition); otherwise, the system would be unstable: a small perturbation at the origin would cause extensive rearrangements in the system. Thus, the yielding transition is affected by an additional exponent θ that does not enter the phenomenology of the depinning problem:

$$P\left(x\right)\sim x^{\mathrm{\theta }},$$ [6]

with θ > 0. Using elasto-plastic models, we previously measured θ ∼ 0.4 for d = 3 and θ ∼ 0.6 for d = 2 (20), as we confirm here with improved statistics.

The definitions of the relevant exponents are summarized in Table 1 and their values, as reported in the literature, in Table 2.

Table 1.

The critical exponents and their expressions

Exponent	Expression	Relations	2d measured/prediction	3d measured/prediction
θ	P(x) ∼ xθ		0.57	0.35
z	T ∼ lz		0.57	0.65
df	$S_c\sim L^{d_f}$		1.10	1.50
β	$\dot{\mathrm{\gamma }}\sim {\left(\Sigma -{\Sigma }_c\right)}^{\mathrm{\beta }}$	β = 1 + z/(d − df)	1.52/1.62	1.38/1.41
τ	ρ(S) ∼ S−τ	$\mathrm{\tau }=2-\frac{\mathrm{\theta }}{\mathrm{\theta }+1}\frac{d}{d_f}$	1.36/1.34	1.45/1.48
ν	ξ ∼ (|Σ − Σc|)−ν	ν = 1/(d − df)	1.16/1.11	0.72/0.67

The third column contains the three scaling relations we derive in the text. We compare values measured in our elasto-plastic model, both in 2d and 3d, with the predictions from the scaling relations.

Scaling Relations

We now propose several scaling relations, which essentially mirror arguments made in the context of the depinning transition (SI Text), with the additional feature that P(x) is singular.

Stationarity.

Consider the application of a quasistatic strain in a system of linear size L, as represented in Fig. 2. The stress Σ fluctuates as the result of avalanches: an avalanche of size S leads to a stress drop proportional to the plastic strain Δγ ∼ S/L^d, of average 〈S〉/L^d. Using Eqs. 3 and 4 and assuming 2 > τ >1, one gets $\langle S\rangle \sim L^{d_f\left(2-\mathrm{\tau }\right)}$, so the average drop of stress is of order $L^{d_f\left(2-\mathrm{\tau }\right)-d}$.

Fig. 2.

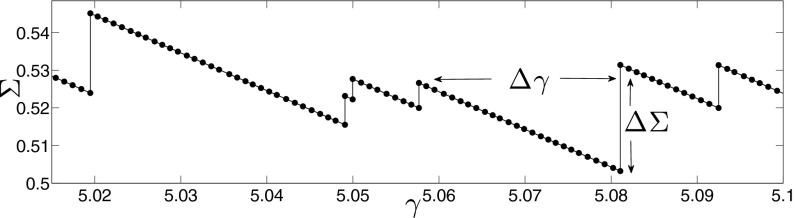
Example of a stress Σ vs. plastic strain γ signal from extremal dynamics simulations of our elasto-plastic model, which corresponds to quasistatic strain simulations in computer experiments. Avalanches relax the shear stress by some amount S/L^d. ΔΣ is the stress increment needed to trigger a new avalanche. In the stationary state, these two quantities must be equal on the average.

Between plastic events, the system loads elastic energy, and stress rises by some typical amount ΔΣ. ΔΣ is limited by the next plastic event and thus is inversely proportional to the rate at which avalanches are triggered. Although one might think that if the system were twice as large a plastic event would occur twice as soon (implying ΔΣ ∼ 1/L^d), this is not the case, and ΔΣ depends on system size with a nontrivial exponent (9, 10, 35, 36). As argued in refs. 35 and 37, one expects ΔΣ to be of order x_min, the weakest site in the system. If the x_i are independent, this implies that $\mathrm{\Delta }\Sigma \sim L^{-\frac{d}{\mathrm{\theta }+1}}$. In ref. 35, it was argued based on local considerations that θ = 1/2. Instead, our recent work (20) implies that θ is governed by the elastic interactions between plastic events and remains a nontrivial exponent that depends on interaction range and spatial dimension.

Supposing that in a stationary state, the average drop and jump of stress must be equal leads to $L^{d_f\left(2-\mathrm{\tau }\right)-d}\sim \mathrm{\Delta }\Sigma$ (9, 10, 35, 36); using our estimate of the latter, we get $L^{d_f\left(2-\mathrm{\tau }\right)-d}\sim L^{-\frac{d}{\mathrm{\theta }+1}}$, leading to our first scaling relation:

$$\mathrm{\tau }=2-\frac{\mathrm{\theta }}{\mathrm{\theta }+1}\frac{d}{d_f}.$$ [7]

As discussed in SI Text, a similar but not identical relation also holds for the depinning transition (26, 42).

Dynamics.

A powerful idea in the context of the depinning transition is that avalanches below threshold and flow above threshold are intimately related (26). Above threshold, the motion of the interface may be thought as consisting of several individual avalanches of spatial extension ξ, acting in parallel. We propose the same image for the yielding transition. If so, the strain rate $\dot{\mathrm{\gamma }}$ in the sample is simply equal to the characteristic strain rate of an avalanche of size ξ, leading to

$$\dot{\mathrm{\gamma }}=\frac{S}{T{\mathrm{\xi }}^d}\sim {\left(\Sigma -{\Sigma }_c\right)}^{\mathrm{\nu }\left(d-d_f+z\right)},$$ [8]

implying our second scaling relation, which to our knowledge was not proposed in this context:

$$\mathrm{\beta }=\mathrm{\nu }\left(d-d_f+z\right).$$ [9]

Statistical Tilt Symmetry.

If flow above Σ_c consists of independent avalanches of size ξ, then the avalanche-induced fluctuations of stress on that length scale, δΣ, must be of order

$$\mathrm{\delta }\Sigma \sim S_c/{\mathrm{\xi }}^d\sim {\left(\Sigma -{\Sigma }_c\right)}^{\mathrm{\nu }\left(d-d_f\right)}.$$ [10]

One expects that the fluctuations of stress on the scale ξ must be of order of the distance to threshold Σ − Σ_c. Eq. 10 then leads to

$$\mathrm{\nu }=\frac{1}{d-d_f}.$$ [11]

It was suggested in ref. 36 that Eq. 11 may apply at the yielding transition. A similar relation holds for depinning of an interface if the elasticity is assumed to be linear, a nontrivial assumption underlying Eq. 10. In that case, it can be derived using the so-called statistical tilt symmetry. In SI Text, we discuss evidence that linearity applies at the yielding transition, enabling us to use this symmetry to derive Eq. 11.

Overall, the scaling relations Eqs. 7, 9, and 11) allow to express the six exponents we have introduced in terms of three, which we choose to be θ, d_f, z. The corresponding relations are indicated in Table 1.

Elasto-Plastic Model

The phenomenological description proposed above may apply to real materials with inertial or overdamped dynamics, as well as to elasto-plastic models, although the yielding transition in these situations may not lie in the same universality class (36, 43). In what follows, we test our predictions in elasto-plastic models, implemented as in ref. 20, whose details are recalled here.

We consider square (d = 2) and cubic (d = 3) lattices of unit lattice size with periodic boundary conditions, where each lattice point i may be viewed as the coarse-grained description of a group of particles. It is characterized by a scalar stress σ_i, a local yield stress ${\mathrm{\sigma }}_i^{th}$, and a strain ${\mathrm{\gamma }}_i={\mathrm{\gamma }}_i^{el}+{\mathrm{\gamma }}_i^{pl}$. The total stress carried by the system is $\Sigma ={\displaystyle {\sum }_i{\mathrm{\sigma }}_i/L^d}$. The elastic strain satisfies ${\mathrm{\gamma }}_i^{el}\propto {\mathrm{\sigma }}_i$. The plastic strain is constant in time, except when site i becomes plastic, which occurs at a rate 1/τ_c if the site is unstable, defined here as $x_i\equiv {\mathrm{\sigma }}_i^{th}-{\mathrm{\sigma }}_i<0$. For simplicity, we consider that ${\mathrm{\sigma }}_i^{th}$ does not vary in space, and we use it to define our unit stress σ^th = 1. τ_c is the only time scale in the problem, and it defines our unit of time.

When plasticity occurs, the plastic strain increases locally and the stress is reduced by the same amount ${\mathrm{\delta }\mathrm{\gamma }}_i^{pl}=-{\mathrm{\delta }\mathrm{\sigma }}_i=\mathrm{\delta }{x}_i$. We assume that ${\mathrm{\delta }\mathrm{\gamma }}_i^{pl}={\mathrm{\sigma }}_i+\mathrm{\epsilon }$, where ε is some random number, taken to be distributed uniformly between −0.1 and 0.1. ε = 0 would correspond to imposing zero local stress after a plastic event (a choice we avoid as it sometimes leads to periodic dynamics). When a site relaxes, it affects the stress level on other sites immediately, such that

$$\mathrm{\delta }{x}_j=-\mathcal{G}\left({\overrightarrow{r}}_{ij}\right)\mathrm{\delta }{x}_i,$$ [12]

with $\mathcal{G}\left({\overrightarrow{r}}_{ij}\right)\propto \cos \left(4\mathrm{\varphi }\right)/r^2$ in an infinite 2D system under simple shear, and where ϕ is the angle between the shear direction and ${\overrightarrow{r}}_{ij}$ (21). In a finite system, $\mathcal{G}$ depends on the boundary conditions (21). At fixed stress, by definition $\mathcal{G}$(0) = −1 and stress conservation implies that the sum of $\mathcal{G}$ on any line or column of the lattice is zero. At fixed global strain, however, one plastic event reduces the stress by 1/L^d. When desired, we model this effect by modifying the interaction kernel as follows: $\mathcal{G}\left({\overrightarrow{r}}_{ij}\right)\to \mathcal{G}\left({\overrightarrow{r}}_{ij}\right)-1/L^d$.

In our model, the average plastic strain is defined as $\mathrm{\gamma }=\frac{1}{L^d}{\displaystyle {\sum }_i{\mathrm{\gamma }}_i^{pl}}$ and the strain rate simply follows $\dot{\mathrm{\gamma }}={\displaystyle {\sum }_i\langle {\delta \dot{\mathrm{\gamma }}}_i^{pl}\rangle /L^d}={\displaystyle \sum {\mathrm{\sigma }}_i\mathrm{\Theta }\left({\mathrm{\sigma }}_i-1\right)/\left({\mathrm{\tau }}_c{L}^d\right)}$, where Θ(x) is the Heaviside function. Above Σ_c, the system will reach a steady state with a finite $\dot{\mathrm{\gamma }}$. Below or in the vicinity of Σ_c, however, the system may stop spontaneously. When this happens, to generate a new avalanche, we trigger the dynamics by giving very small random kicks to the system (chosen to conserve stress on every line and column) until one site becomes unstable.

This elasto-plastic model essentially is identical to the automaton models introduced in ref. 44 in the context of the depinning transition, in which the role of the plastic strain ${\mathrm{\gamma }}_i^{pl}$ is played by the transverse displacement of the elastic interface u_i. The only qualitative difference is the form of $\mathcal{G}$.

Numerical Estimation of Critical Exponents

Flow Curves and Length Scales.

We first implement the extremal dynamics protocol: the average stress decreases by 1/L^d after each plastic event during avalanches, and increases again to generate a new active site at the beginning of a new avalanche. The corresponding stress–plastic strain curves shown in Fig. 2 allow us to estimate the critical stress Σ_c and the correlation length exponent ν from the fluctuations δΣ of Σ at different sizes:

$$\begin{array}{c}\langle {\Sigma }_c\left(L\right)\rangle ={\Sigma }_c+k_1{L}^{-\frac{1}{\mathrm{\nu }}}+\dots \\ \mathrm{\delta }\Sigma \left(L\right)=k_2{L}^{-\frac{1}{\mathrm{\nu }}}+\dots ,\end{array}$$ [13]

where 〈Σ_c(L)〉 is the mean stress and δΣ(L) the SD at a given size L, and k₁, k₂ are nonuniversal constants. From our data (SI Text), we obtain Σ_c = 0.5221 ± 0.0001, ν = 1.16 ± 0.04 for d = 2 and Σ_c = 0.5058 ± 0.0002, ν = 0.72 ± 0.04 for d = 3. These quantities also may be extracted reliably from finite strain rate measurements, as shown in SI Text.

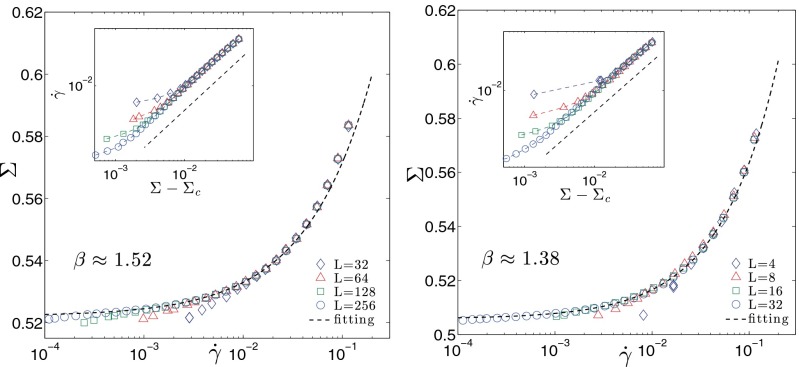
We then compute the flow curve at a fixed strain rate. The stress is adjusted to keep the fraction of unstable sites fixed. The determination of the exponent β is very sensitive to the value of Σ_c. Using the values obtained from the previous analysis, we find β = 1.52 ± 0.05 for d = 2 and β = 1.38 ± 0.03 for d = 3, as shown in Fig. 3.

Fig. 3.

(Insets) Flow curves $\dot{\mathrm{\gamma }}(\Sigma )$ in the vicinity of Σ_c for different system size L as indicated in the legend in d = 2 (Left) and d = 3 (Right). (Main Curves) The same flow curves in log-linear scale, fitted by the Herschel–Bulkley law, $\Sigma ={\Sigma }_c+A{\dot{\mathrm{\gamma }}}^{1/\mathrm{\beta }}$, which gives us β ∼ 1.52 in 2d, β ∼ 1.38 in 3d.

Avalanche Statistics.

Avalanche statistics may be investigated using extremal dynamics and Fig. 4. As documented in SI Text, this method leads for our largest system size to τ ∼ 1.2 for d = 2 and τ ∼ 1.3 for d = 3. This measure appears to have large finite size effects, however. We find that such effects are diminished if we work instead at constant stress Σ and consider ρ(S, Σ) as $\Sigma \to {\Sigma }_c^{-}$. In SI Text, we find using this method that τ = 1.36 ± 0.03 for d = 2 and τ = 1.45 ± 0.05 for d = 3.

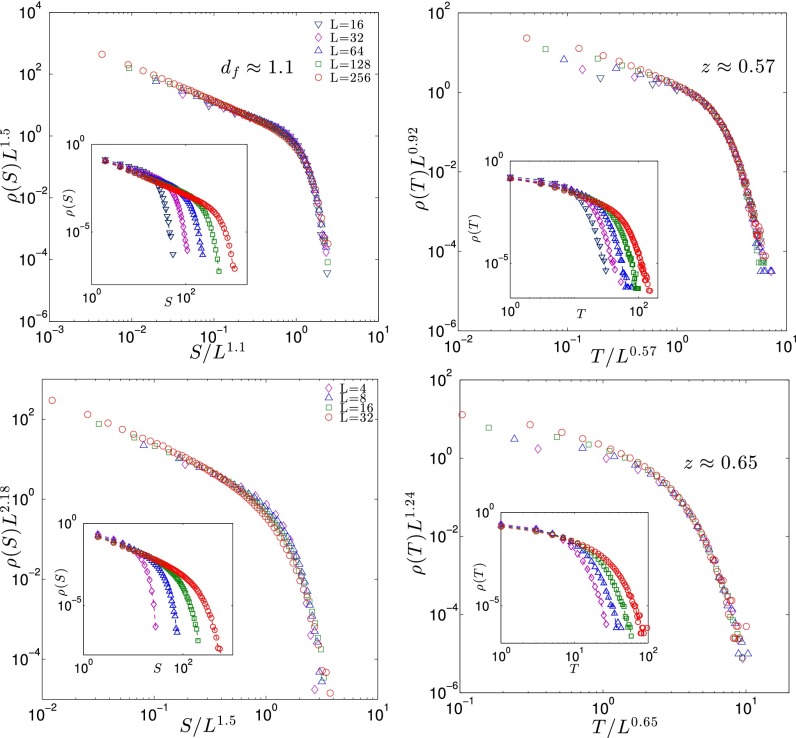
Fig. 4.

(Left, Insets) Avalanche size distribution ρ(S, L) for extremal dynamics as the system size L is varied in d = 2 (Upper) and d = 3 (Lower). (Main Plots) Rescaling avalanche size enables the collapse of these distributions, allowing a fractal dimension d_f to be extracted. (Right, Insets) Distribution ρ(T) of the duration of the avalanches for the system sizes as indicated in the legend in d = 2 (Upper) and d = 3 (Lower). (Main Plots) The cutoff present in these distributions can be collapsed by rescaling time, leading to an estimate of the dynamical exponent z.

Next, we evaluate the fractal dimension d_f and the dynamical exponent z using extremal dynamics. Here, the avalanche cutoff S_c corresponds to an avalanche of linear extension ∼L so that for large systems, one expects $\mathrm{\rho }\left(S,L\right)\sim S^{-\mathrm{\tau }}h\left(S/L^{d_f}\right)\sim L^{-d_f\tau }H\left(S/L^{d_f}\right)$, where h is some function and H(x) = x^−τh(x). This collapse is checked in Fig. 4 and leads to d_f = 1.10 ± 0.04 for d = 2 and d_f = 1.50 ± 0.05 for d = 3 (for the collapse, we used the values of τ measured with the constant stress protocol). Error bars are estimated by considering the range of exponents for which the collapse is satisfactory. To measure z, we record the duration T of each avalanche and compute the duration distribution ρ(T) for different system sizes. These distributions are cut off at some T_c, corresponding to the duration of avalanches of spatial extension L, so that T_c ∼ L^z. As shown in the right panels of Fig. 4, we indeed find a good collapse $\mathrm{\rho }\left(T,L\right)\sim T^{-{\tau }^{\prime }}{h}_2\left(T/L^z\right)\sim L^{-{\tau }^{\prime }z}{H}_2\left(T/L^z\right)$ with z = 0.57 ± 0.03, τ′ ∼ 1.6 for d = 2 and z = 0.65 ± 0.05, τ′ ∼ 1.9 for d = 3.

Density of Shear Transformations.

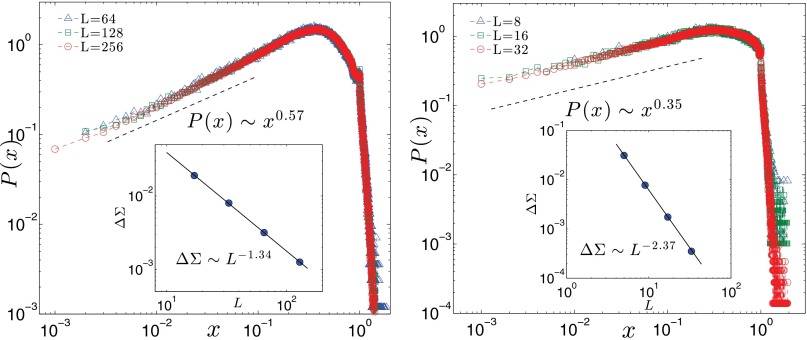
In elasto-plastic models, it is straightforward to access the local distance to thresholds x_i and to compute its distribution P(x) (20). Here we recall these results with improved statistics. We fix the stress at Σ_c and let the system evolve for a long enough time such that γ ≫ 1. The dynamics occasionally stop; at that point, we measure P(x) and average over many realizations. As shown in Fig. 5, we find θ = 0.57 ± 0.01 for d = 2, θ = 0.35 ± 0.01 for d = 3, where the error bar is from the error estimation of linear fit. Although in experiments P(x) is hard to access, the system size dependence of the average increment of stress where no plasticity occurs should be accessible, and follows $\mathrm{\Delta }\Sigma \sim L^{-d/\left(1+\mathrm{\theta }\right)}$. In Fig. 5 Insets, ΔΣ is computed via extremal dynamics, leading to slightly smaller exponents θ ≃ 0.50 for d = 2 and θ ≃ 0.28 for d = 3, a difference presumably resulting from corrections to scaling.

Fig. 5.

Shear transformation distribution P(x), where x is the local distance to an instability for d = 2 (Left) and d = 3 (Right). (Insets) Amplitude of stress increments ΔΣ before an instability occurs as a function of L, found to follow $\mathrm{\Delta }\Sigma \sim L^{-d/\left(1+\mathrm{\theta }\right)}$.

Theory vs. Numerics.

Our scaling relations now can be tested, and this comparison is shown in Table 1. We find very good agreements for all three scaling relations: Eqs. 7, 9, and 11.

Comparison with Molecular Dynamics and Experiments

Although elasto-plastic models are well-suited to test theories, they make many simplifications, and thus may not fall in the universality class of real materials. One encouraging item is our estimate of θ, which is very similar to the value extracted from finite size effects in molecular dynamics (MD) simulations using overdamped dynamics, as reported in Table 2. This is consistent with our finding (20) that θ (and τ) is independent of the choice of dynamical rules in our model, which however, may dramatically affect the dynamics. Concerning the latter, our choice that the interaction is instantaneous in time, although still long range, likely will affect the exponents z and β. We expect that if a more realistic time-dependent interaction kernel $\mathcal{G}\left(\overrightarrow{r},t\right)$ is considered (a costly choice numerically), the exponent z will satisfy z ≥ 1. According to Eq. 9, this will lead to larger values of β, in agreement with experiments.

The scaling relations for τ and ν in Table 1 appear to be supported by MD simulations. In ref. 36 for overdamped dynamics, d_f = 0.9 and θ ∼ 0.54 for d = 2, whereas d_f = 1.1 and θ ∼ 0.43 for d = 3, leading to τ ∼ 1.2 in both 2d and 3d, which compares well with their measured value τ = 1.3 ± 0.1. In d = 2, all numerics (36, 51) report d_f ∼ 1, leading to ν ∼ 1, as observed in ref. 7. In d = 3, there is some disagreement on the value of d_f: refs. 51 and 52 report d_f ∼ 1.5 as we do in our elasto-plastic model, in disagreement with ref. 36, for which d_f < d/2, implying that ν < 2/d. It would be useful to resolve this discrepancy, because in the depinning problem, when ν < 2/d, another length scale enters the scaling description, which affects particularly finite size effects (44, 53). In this situation, however, we expect our scaling description to be unchanged if ν is meant to characterize the correlations of the dynamics for Σ > Σ_c.

Conclusion

We have proposed a scaling description of stationary flow in soft amorphous solids, and it is interesting to reflect whether this approach can be applied to other systems. Plasticity in crystals shares many similarities with that of amorphous solids, and the far-field effect of a moving dislocation essentially is identical to the effect of a shear transformation (2). Thus, we expect that the stability argument of ref. 20 regarding the density of regions about to yield also applies in crystals, leading to a nontrivial exponent θ in that case too. Our scaling relations thus may hold in crystals, although the formation of structures such as domain walls might strongly affect the yielding transition.

Avalanches of plasticity are seen in granular materials in which particles are hard (12, 13). However, we believe that at least for overdamped systems, this behavior is only transient and that the elasto-plastic description does not apply to such materials under continuous shear. Some of us have argued that in this case, a picture based on geometry applies (54, 55), which also leads to a diverging length scale but of a different nature (56).

The scaling relations proposed here do not fix the values of the exponents, particularly that of θ. To make progress, it is tempting to seek a mean-field description of this problem that would apply beyond some critical dimension. Current mean-field models in which the interaction is random and does not decay with distance lead to θ = 1 (20, 41). However, the anisotropy is lost in this view, and the fact that θ diminishes as d increases when anisotropy is considered suggests that a mean-field model that includes anisotropy is needed. Such a model would be valuable in building a hydrodynamic description of flow that would apply, for example, to slow flow near walls (57, 58), a problem for which current descriptions do not include the role of anisotropy (25, 59).