Epitaxial growth of large-gap quantum spin Hall insulator on semiconductor surface

Significance

Quantum phase of matter is of great scientific and technological interest. The quantum spin Hall (QSH) insulator is a newly discovered two-dimensional material that exhibits topological edge state residing inside bulk energy gap, so that its edge is metallic with quantized conductance and its bulk is insulating. For its potential applications in spintronics and quantum computing, a large energy gap is desirable, e.g., for room-temperature application. So far, large-gap QSH insulators have been predicted only in freestanding films. Here we demonstrate the formation of a large-gap QSH state on a semiconductor substrate through epitaxial growth of heavy metal atoms on halogenated Si surface. Our findings not only reveal a new formation mechanism of large-gap QSH insulator, but may also pave the way for its experimental realization.

Abstract

Formation of topological quantum phase on a conventional semiconductor surface is of both scientific and technological interest. Here, we demonstrate epitaxial growth of 2D topological insulator, i.e., quantum spin Hall state, on Si(111) surface with a large energy gap, based on first-principles calculations. We show that the Si(111) surface functionalized with one-third monolayer of halogen atoms [Si(111)-$\sqrt{3}$×$\sqrt{3}$-X (X = Cl, Br, I)] exhibiting a trigonal superstructure provides an ideal template for epitaxial growth of heavy metals, such as Bi, which self-assemble into a hexagonal lattice with high kinetic and thermodynamic stability. Most remarkably, the Bi overlayer is atomically bonded to but electronically decoupled from the underlying Si substrate, exhibiting isolated quantum spin Hall state with an energy gap as large as ∼0.8 eV. This surprising phenomenon originates from an intriguing substrate-orbital-filtering effect, which critically selects the orbital composition around the Fermi level, leading to different topological phases. In particular, the substrate-orbital-filtering effect converts the otherwise topologically trivial freestanding Bi lattice into a nontrivial phase; and the reverse is true for Au lattice. The underlying physical mechanism is generally applicable, opening a new and exciting avenue for exploration of large-gap topological surface/interface states.

Topological insulators (TIs) (1–3) are distinguished from conventional insulators by robust metallic surface or edge states residing inside an insulating bulk gap. As these topological states are protected by time-reversal symmetry, they have negligible elastic scattering and Anderson localization (4, 5), rendering significant implications in electronic/spintronic and quantum computing devices. In this regard, 2D TI [i.e., the quantum spin Hall (QSH) insulator] has an advantage over its 3D counterpart as the edge states of the QSH insulator are more robust against nonmagnetic scattering, because the only available backscattering channel is forbidden. Many QSH insulators have been discovered (6–20), and most of them have a small energy gap. Recently, there has been an intensive search for 2D TIs with a large energy gap (17–20), which is of both scientific and practical interest, such as for room temperature applications. So far, however, most studied systems rely on freestanding films, and the existence of some 2D freestanding films could be in doubt because of their poor thermal or chemical stability; and even if they do exist, growth and synthesis of freestanding film is usually much harder than growth of thin film on substrate. Furthermore, the functional film often needs to be placed on a substrate in a device setting, but the electronic and topological properties of freestanding films will likely be affected by the substrate (21–23). Therefore, it is highly desirable to search for large-gap QSH states existing on a substrate while maintaining a large gap.

Here, we predict an interesting phenomenon of formation of QSH state on a conventional semiconductor surface with an energy gap as large as ∼0.8 eV, when heavy metal elements, such as Bi with large spin-orbit coupling (SOC), are grown on a one-third monolayer (ML) halogen-covered Si(111) surface. In specific, Si(111) surface functionalized with one-third ML of Cl, Br, or I exhibits a Si(111)-$\sqrt{3}$ ×$\sqrt{3}$-X (X = Cl, Br, I) reconstruction of trigonal symmetry due to strong steric repulsion between the halogen atoms, as observed in experiments (24–28); and F tends to form clusters. The reconstructed Si(111)-$\sqrt{3}$×$\sqrt{3}$-X surface provides an ideal template for epitaxial growth of Bi, which self-assembles into a hexagonal superstructure with high thermodynamic stability. Most remarkably, we found that this hexagonal Bi overlayer is atomically bonded to but electronically decoupled from the underlying Si substrate, exhibiting large-gap QSH states completely isolated from Si valence and conduction bands. It originates from an intriguing substrate orbital filtering effect in which the Si(111) substrate effectively selects suitable orbital composition around the Fermi level, to convert the otherwise topologically trivial freestanding Bi lattice into a nontrivial substrate-supported QSH insulator.

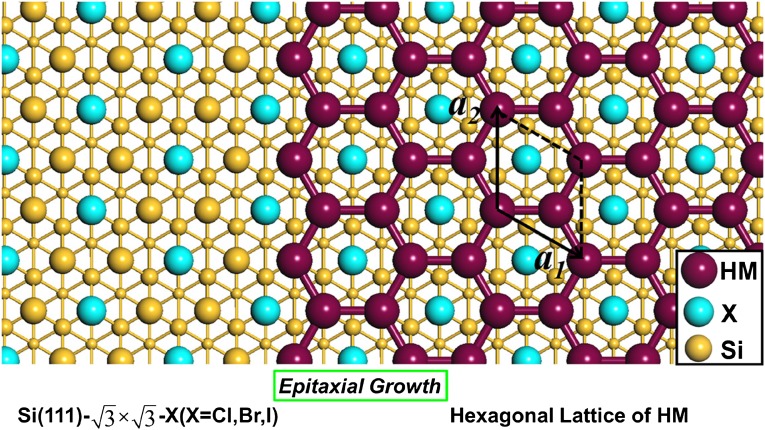
We have performed density functional theory (DFT) based first-principles calculations (see details in Supporting Information) of geometry, band structure, and band topology of 2D hexagonal lattices of Bi on Si(111)-$\sqrt{3}\times \sqrt{3}$-X (Cl, Br, I) surface. To better illustrate the substrate orbital filtering effect, we also performed similar calculations for hexagonal lattice of Au for comparison. It is worth noting that the Si(111)-$\sqrt{3\hspace{0.17em}}$×$\sqrt{3}$-X surface has the exposed Si atoms with one dangling bond arranged in hexagonal symmetry (Fig. 1), which serve as the preferred adsorption sites for Bi (Au) atoms, and hence driving the Bi atoms naturally to form a hexagonal lattice. Importantly, the resulting hexagonal Bi lattice is stabilized against segregation to form clusters by the halogen atoms in between the Bi atoms, overcoming a potential problem encountered by direct deposition of metal atoms on clean surface, e.g., deposition of heavy atoms on a magnetic insulator substrate to form Chern insulator (29).

Fig. 1.

Schematic illustration of the epitaxial growth of large-gap QSH states on Si substrate. We propose to fabricate the hexagonal lattices of heavy metal(HM) by direct deposition of heavy metal atoms onto Si(111)-$\sqrt{3}$×$\sqrt{3}$-X (X = Cl, Br, I) template. The surface unit cell vector (a₁, a₂) is also indicated.

There exists a very strong binding between the deposited Bi and the exposed Si in surface. The calculated adsorption length (d) and adsorption energy (E_ad) of Bi on the Si(111)-$\sqrt{3}$ ×$\sqrt{3}$-Cl surface are found to be 2.46 Å and 2.99 eV, respectively, typical of a covalent bond. Here, E_ad = E_{Bi @Cl-Si(111)} − (E_Bi + E_Cl-Si(111)), where E_{Bi@Cl−Si(111)}, E_Bi and E_Cl-Si(111) denote the energy of Bi adsorbed Si(111) surface [Bi@Cl-Si(111)], Bi atom, and surface without Bi, respectively. It is also found that forming Bi clusters on the surface is energetically unfavorable; e.g., forming Bi dimer is about 2.5 eV per unit cell higher in energy than the ground state. Moreover, a significant energy barrier exists for Bi to diffuse out of the adsorbed site. For instance, an energy barrier of 4.9 eV (5.4 eV) must be overcome for Bi to jump from Si to neighboring Bi (Cl) sites. These results indicate high thermodynamic as well as kinetic stability of the hexagonal Bi overlayer structure.

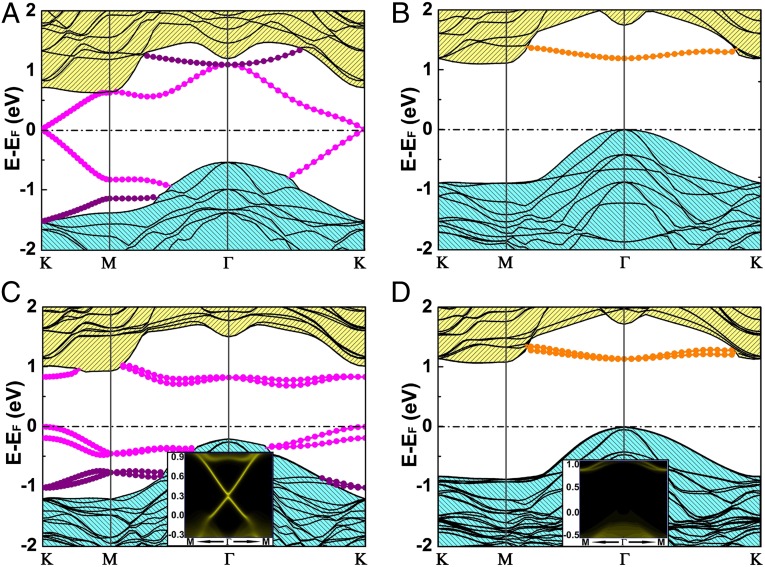
To examine band topology of Bi@Cl-Si(111) surface, we first purposely exclude SOC from calculation. The band structure of Bi@Cl-Si(111) is shown in Fig. 2A, along with that of Au@Cl-Si(111) in Fig. 2B. In Fig. 2A, there are two Dirac bands residing inside the bulk gap of Si with a Dirac point at K point, which locates exactly at the Fermi level. Analysis of band composition further showed that the two Dirac bands mainly consist of p_x orbital of Bi. Additionally, there is one weakly dispersive band, consisting of Bi p_y orbital and that sits below the bulk conduction band edge of Si, touches the upper Dirac band at Γ point. Another weakly dispersive band, which is a mixture of Bi p_y orbital and the valence bands of Si, touches the lower Dirac band at Γ point. We notice that if these two weakly dispersive bands were flat, this type of four-band structure would be (p_x, p_y) analog of graphene (30). In contrast, the band structure of Au@Cl-Si(111) is very different (Fig. 2B). There is no Dirac band or Dirac point; it is a typical semiconductor surface with a large band gap of ∼1.0 eV. Its surface states, consisting of mainly 6s orbital of Au, are above the bulk conduction band edge of Si.

Fig. 2.

Band structures of Bi and Au on Si(111)-$\sqrt{3}$×$\sqrt{3}$-Cl surface for (A) Bi and (B) Au without SOC, respectively; (C and D) with SOC. Bands compositions near Fermi level are indicated. C, Inset, shows the Dirac edge states within the SOC-induced band gap in Bi@Cl-Si(111), and D, Inset, shows no edge states within the band gap of Au@Cl-Si(111). The brightness is proportional to the magnitude of the states.

Next, the band structures with SOC are shown in Fig. 2 C and D. Comparing Fig. 2C with Fig. 2A, one sees that for Bi@Cl-Si(111), two Dirac bands are split apart and a large energy gap of 0.78 eV is opened at K point. Due to band dispersion, the global gap is slightly smaller, ∼0.75 eV between the minimum of upper Dirac band somewhere between Γ and K point and the maximum of the lower Dirac band at Γ. Considerable energy gaps are also opened by SOC between the weakly dispersive p_y bands and the Dirac p_x bands. We note that spin degeneracy of these bands is lifted (most noticeable at K point) due to the Rashba effect (31) induced by broken inversion symmetry of surface. Again in sharp contrast to the case of Bi, the SOC causes little change in band structure of Au@Cl-Si(111) (compare Fig. 2D with Fig. 2B), except for some Rashba-type spin splitting. Because standard DFT is known to underestimate semiconductor band gap, we further checked the results with higher level DFT method using screened hybrid functional of Heyd, Scuseria, and Ernzerhof (32) and the same electronic behaviors were obtained (Fig. S1). We also calculated band structures of Bi@Br-Si(111) and Bi@I-Si(111) surfaces (Fig. S2), which show the same physical behavior as Bi@Cl-Si(111) except a smaller gap.

To reveal surface topological properties, we calculated Z₂ topology number. As the spatial inversion symmetry is broken, we used a general approach for calculating Z₂ by considering the Berry gauge potential and Berry curvature associated with the Bloch wave functions, which does not require any specific point-group symmetry (33, 34). Indeed, we found that Z₂ = 1 for Bi@Cl-Si(111), Bi@Br-Si(111), and Bi@I-Si(111) surfaces, confirming their existence of QSH state. In contrast, Z₂ = 0 for Au@Cl-Si(111). Furthermore, we calculated the topological edge states by constructing edge Green’s function of a semi-infinite Bi@Cl-Si(111) surface. The local density of states (DOS) of Bi edge is shown in Fig. 2C, Inset, which clearly shows gapless edge states connecting the upper and lower bulk band edge to form a 1D Dirac cone at the center of Brillouin zone (Γ point). In contrast, no such edge state exists in Au@Cl-Si(111) surface (Fig. 2D, Inset).

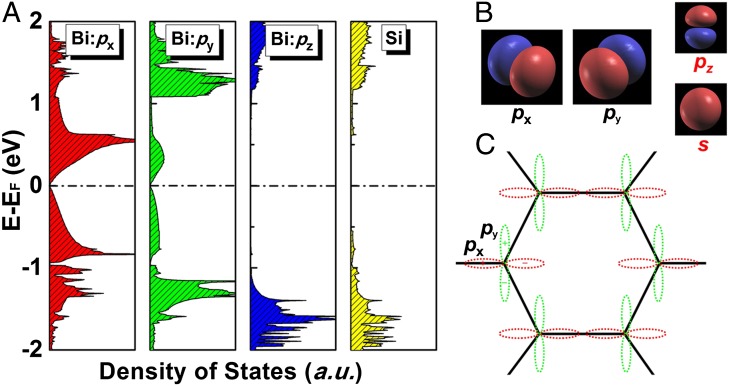
To understand the physical origin of QSH state in Bi@Cl-Si(111) but not in Au@Cl-Si(111), we next do an orbital analysis around the Fermi level. Fig. 3A shows the partial DOS of Bi@Cl-Si(111). It is seen that the p_z orbital of Bi hybridizes strongly with the dangling bond of the exposed surface Si atom overlapping in the same energy range. We calculated the maximally localized Wannier functions (WFs) of Bi by fitting the DFT band structures of a hypothetical freestanding hexagonal lattice with the WANNIER90 code (35). The resulting WFs are plotted in Fig. 3B, which shows the exact chemical characteristics of one s and three p orbitals of Bi. With the s orbital of Bi lying in deep energy, interaction with Si effectively removes the p_z bands away from the Fermi level, leaving only the p_x and p_y orbitals (Fig. 3C) to form two Dirac bands and two flat bands, which can be described by a four-band model of topological phase in a hexagonal lattice (12, 30). This indicates that the Cl-Si(111) substrate acts like an orbital filter, to selectively remove the p_z orbitals from the Bi lattice, reducing it from a trivial six-band lattice to a nontrivial four-band lattice, as we explain below.

Fig. 3.

Physical origin of QSH states on Si substrate. (A) The partial DOS projected onto p_x, p_y, and p_z orbitals of Bi, and the total DOS of neighboring Si atoms for Bi@Cl-Si(111). (B) The calculated Wannier functions characterized by s, p_x, p_y, and p_z orbitals of freestanding hexagonal lattice of Bi, with only p_x and p_y located near Fermi level. (C) Illustration of hexagonal lattice made of p_x and p_y orbitals on each site.

The concept of 2D TI was originally proposed by Kane and Mele (6) using the graphene model, in which an energy gap is opened at Dirac point in proportion to the strength of SOC. Unfortunately, the SOC of graphene is negligibly small, and much effort has later been devoted to remedy this problem (9, 19). There are two apparent conditions in the Kane–Mele model to create a 2D TI. One is the lattice symmetry, such as the hexagonal symmetry that produces Dirac band; the other is the SOC. Given these two conditions alone, one might think to create a large-gap 2D TI by constructing a planar hexagonal lattice of heavy metal atoms with large SOC. However, this turned out not to be generally true because there is a third condition of orbital selection associated with the Kane–Mele model.

We have performed first-principles calculations of band structure and band topology of freestanding 2D planar hexagonal lattices of Bi and Au, to examine whether they are theoretically 2D TIs having a large energy gap (Supporting Information). It is found that the two lattices have drastically different electronic and topological properties. The planar Bi lattice is a trivial insulator with Z₂ = 0, and the Au lattice is nontrivial with Z₂ = 1. Their topological difference is originated from the different orbital composition around the Fermi level. For Bi, the valence bands consist of three (p_x, p_y, and p_z) orbitals. The topology associated with the two bands from p_z orbital can be described by the single-orbital two-band Kane–Mele model; and the topology associated with other four bands from p_x and p_y orbitals can be described by the four-band model (12, 30). Note that separately either the two-band or four-band model gives rise to nontrivial band topology (Z₂ = 1); however, counting all six bands together, the total band topology is trivial (Z₂ = 0), as two odd topological numbers add to an even number. For Au, in contrast, the valence bands mainly consist of single s orbital, and SOC opens a gap of ∼70 meV, transforming the lattice into a 2D TI phase. Thus, the planar Au lattice can also be understood by the Kane–Mele model, except that it involves a single s orbital rather than the p_z orbital in graphene.

To transform the topologically trivial planar hexagonal lattice of Bi into a nontrivial phase, one efficient way is to select one p_z or two p_x and p_y orbitals, to realize the two-band or four-band model. In our Bi@Si(111)-$\sqrt{3}$ ×$\sqrt{3}$-X (Cl, Br, I) system, the exposed Si atom in the Cl-Si(111) surface interacts strongly with Bi and removes the p_z orbital of Bi, while p_x and p_y orbitals remain active near Fermi energy, as shown in Fig. 3A. In contrast, the Au atom has single s-orbital valence electron, and when it is bonded with the exposed surface Si atom, it simply saturates the Si dangling bond just like the Cl does. Consequently, the band structure of Au@Cl-Si(111) is essentially the same as that of the semiconducting pristine Cl-Si(111) surface. Specifically, we can describe the Bi@Cl-Si(111) using a simplified (p_x, p_y) four-band model Hamiltonian in a hexagonal lattice (12, 30), which produces either a flat-band Chern insulator or a 2D TI, depending on the location of the Fermi level. Due to large SOC of Bi (∼1.25 eV), QSH state with an energy gap as large as ∼0.8 eV is found, which is possibly the largest gap so far predicted.

We believe that, experimentally, it is highly feasible to realize the large-gap QSH states as we propose here, based on the existing related experiments. First, the required template of halogenated Si surface has already been widely studied in early surface science research (24–26), especially the one-third ML halogen-covered Si(111) surface exhibits the exact trigonal-symmetry reconstruction (25, 27, 28). Second, the epitaxial growth of metal overlayer on the one-third ML halogen-Si(111) template should be highly possible. For instance, hexagonal lattices of indium overlayer has been successfully grown on the Si(111)$\sqrt{3}$ ×$\sqrt{3}$-Au surface (36), although the surface bands of In hybridize strongly with those of underlying Si substrate (37), making this system topologically trivial. Nevertheless, the growth process can be borrowed for our purposes in realizing QSH states. Furthermore, it should be possible to grow stripes of Bi hexagonal lattice on the halogenated Si(111) surface, so that the helical edge state is naturally created for measurement at the domain boundary of the fully chlorinated Si(111) surface (a trivial insulator or conventional semiconductor) and the Bi@Cl-Si(111) stripe (a QSH insulator) (20). We envision that realization of topological edge states on Si surface, which may be used as dissipationless interconnects for electronic circuits (38), to significantly advance the current Si-based technology.

Methods

Our electronic structure calculations based on DFT were performed by using a plane wave basis set, the projector-augmented wave method, and the Perdew–Burke–Ernzerhof generalized gradient approximation for exchange-correlation potentials, as implemented in the Vienna ab initio package code (39). Calculations were performed with an energy cutoff of 500 eV on a 15 × 15 × 1 Γ-centered k-point mesh. Si(111) surfaces were modeled by using a slab geometry of ten atomic layers, with bottom surface terminated by H in a monohydride form. During structural optimization, both the tenth layer of Si atoms and the H atoms were fixed and all other atoms were fully relaxed until the atomic forces are smaller than 0.01 eV/Å. Details are presented in Supporting Information.