A self-consistent approach for determining pairwise interactions that underlie channel activation

Net free-energy measurements can be combined with mutant cycle analysis to determine interaction energies between specific amino acid pairs during channel activation.

Abstract

Signaling proteins such as ion channels largely exist in two functional forms, corresponding to the active and resting states, connected by multiple intermediates. Multiparametric kinetic models based on sophisticated electrophysiological experiments have been devised to identify molecular interactions of these conformational transitions. However, this approach is arduous and is not suitable for large-scale perturbation analysis of interaction pathways. Recently, we described a model-free method to obtain the net free energy of activation in voltage- and ligand-activated ion channels. Here we extend this approach to estimate pairwise interaction energies of side chains that contribute to gating transitions. Our approach, which we call generalized interaction-energy analysis (GIA), combines median voltage estimates obtained from charge-voltage curves with mutant cycle analysis to ascertain the strengths of pairwise interactions. We show that, for a system with an arbitrary gating scheme, the nonadditive contributions of amino acid pairs to the net free energy of activation can be computed in a self-consistent manner. Numerical analyses of sequential and allosteric models of channel activation also show that this approach can measure energetic nonadditivities even when perturbations affect multiple transitions. To demonstrate the experimental application of this method, we reevaluated the interaction energies of six previously described long-range interactors in the Shaker potassium channel. Our approach offers the ability to generate detailed interaction energy maps in voltage- and ligand-activated ion channels and can be extended to any force-driven system as long as associated “displacement” can be measured.

INTRODUCTION

Allosteric control of enzymatic activity is a well-known phenomenon in biological systems (Goodey and Benkovic, 2008). It often involves a ligand or metabolite that has no stereochemical resemblance to either products or substrates but exerts control on protein function by binding to a distal regulatory site. However, allosteric regulation is not just limited to substances that exert chemical potential. Activity of proteins such as ion channels can be controlled by voltage, mechanical stretch, or even heat (Hille, 2001). Understanding the molecular mechanisms underlying energy transduction in proteins requires identification of specific pathways involved in transmission of information from sensory modules to catalytic centers. Structural methods like nuclear magnetic resonance and x-ray crystallography provide high-resolution snapshots of conformational changes that underpin molecular communication, but ultimately direct measurement of energetic coupling is also necessary.

Interaction energies between specific residues involved in protein folding can be determined by way of mutant cycle analyses (Fig. 1 A; Ackers and Smith, 1985; Horovitz and Fersht, 1990; Horovitz et al., 1994; Di Cera, 1998). In this approach, perturbation energies are evaluated when a specific site (say X) is perturbed in the native protein and in the background of a secondary perturbation (say Y). If the two perturbation energies are equal, then it implies that the two sites are energetically independent, whereas unequal perturbation energies imply that the two sites interact. This methodology was first used to study protein–protein interactions in tRNA synthetase (Carter et al., 1984) and has now seen widespread application in the study of protein folding and conformational changes (Serrano et al., 1990; Schreiber and Fersht, 1995; Ranganathan et al., 1996). Of central importance is this question: How is the perturbation energy in each step evaluated?

Figure 1.

FMC versus GIA in voltage-gated ion channels. (A) Principle of the mutant cycle analysis, wherein two sites (X,Y) are mutated individually or jointly. By measuring the free energies of perturbation along each path, the interaction energy between the two sites can be assessed as ΔΔG_nonadd = ΔG_p4 − ΔG_p1 = ΔG_p2 − ΔG_p3. (B) The relative open probability versus voltage curve showing the half-maximal voltage of activation, V_1/2. The red dashed line is the tangent to the sigmoid curve at V_1/2, and the slope of this tangent is linearly related to the Boltzmann slope (z_app). In FMC, the free energy of perturbation along each path of the thermodynamic cycle in A is computed as Δ(z_appV_1/2)F. (C) The Q-V curve with the median voltage for activation, V_M, is depicted by the red vertical line. By definition, the two dashed areas on either side of the median voltage axis are equal. In GIA, the free energy of perturbation along each path of the thermodynamic cycle in A is computed as Δ(Q_maxV_M)F.

In the case of a binding reaction such as those involving protein–protein or protein–ligand interaction, free-energy changes associated with perturbations can be evaluated by directly monitoring binding. In many cases, however, functional activity is used as a surrogate measure of free energy of conformational transition. For instance, free energy of activation of voltage-gated and ligand-activated ion channels is evaluated based on their functional responses as evidenced in conductance-voltage (G-V) or conductance-ligand (typically referred to as dose response) relationships. If the channel has a single conducting state, these relationships reflect the channel open probabilities (P_O) at different voltages or ligand concentrations and are fitted to a logistic function. For voltage-activated processes, the free energy of activation of the channel is estimated as ΔG_app = zFV_1/2 (V_1/2 is the voltage that elicits half-maximal response, and z reflects the number of charges transferred during channel activation; Fig. 1 B). These free-energy measures can be combined with double mutant cycle analyses to estimate pairwise interaction energies between various sites in a voltage (Yifrach and MacKinnon, 2002; Sadovsky and Yifrach, 2007; DeCaen et al., 2008, 2009, 2011; Zandany et al., 2008; Yifrach et al., 2009; Wall-Lacelle et al., 2011; Cheng et al., 2013; Chamberlin et al., 2014)- or ligand-activated ion channels (Kash et al., 2003; Gleitsman et al., 2009; Shanata et al., 2012). This approach will be hereby referred to as the functional mutant cycle (FMC).

In most known voltage-gated ion channels, however, the process of channel activation comprises multiple intermediate closed states, before the channels finally open (Bezanilla et al., 1994; Zagotta et al., 1994a; Schoppa and Sigworth, 1998). The occupancies of the ensemble of nonconducting states are not adequately captured by the G-V curves, and their energetic contributions remain indeterminate. More significantly, the uncertainty associated with interaction energies quantified using simplified or empirical free-energy measures prevents a direct comparison with molecular simulations based on high-resolution structures. In some instances, multistate kinetic models are fitted to experimental behavior of proteins and the model parameters are directly used for mutant cycle analyses (Lee and Sine, 2005; Gupta and Auerbach, 2011). Although such an approach is likely to be better than simply measuring G-V curves, its use is limited to systems whose gating behavior can be adequately described by a well-constrained gating scheme. We should note that dose–response curves and G-V curves in allosteric systems under limiting conditions can lend themselves to linkage analysis to probe interaction energies (Chowdhury and Chanda, 2010; Sigg, 2013). However, this approach is also extremely time consuming and cannot be easily extended to obligatorily coupled systems (Chowdhury and Chanda, 2012b).

Recently, we described an alternate methodology to estimate the voltage- and ligand-dependent change in free energy during channel activation (Chowdhury and Chanda, 2012a, 2013), which was an extension of linkage analysis developed by Wyman and Gill (1990). We showed that this net free-energy change (ΔG_net) for a voltage-dependent channel can be calculated by measuring median voltage of activation from gating charge voltage curves (Fig. 1 C). An advantage of this approach is that it does not require us to build multistate kinetic models to calculate free energy of activation (Miller, 2012). Here, we test the proposition that these free-energy measurements can be combined with mutant cycle analyses to determine interaction energies between sites in a model-independent fashion. Previous studies on the Shaker K_V channel identified several putative interactors in the pore domain that were proposed to impact the last concerted pore opening transition (Yifrach and MacKinnon, 2002; Sadovsky and Yifrach, 2007). We find that the majority of these interaction pairs do not contribute significantly to the overall free energy of activation of the channel. Only a single residue pair, A391-T469, exhibits significant energetic nonadditivity, which in all likelihood reflects a long-range interaction between them mediated by networks of intervening residues. Extensive numerical simulations, using different multistate gating models, clearly show that generalized interaction-energy analysis (GIA) yields a self-consistent estimate of energetic nonadditivities. We expect that this approach will allow us to pursue large-scale analysis of interaction networks that underlie gating transitions in voltage- and ligand-gated ion channels.

MATERIALS AND METHODS

Mutagenesis and expression in Xenopus laevis oocytes

All clones used in this study were derived from a cDNA of the inactivation-removed Shaker K_V channel (Δ6–46) cloned into the pBSTA vector. Mutations were introduced by PCR using mismatch mutagenic primers (QuikChange; Agilent Technologies). All mutations were confirmed by sequencing the whole cDNA. For gating current measurements, mutations were introduced into the background of the W434F mutation and rendered the channel nonconducting without compromising other aspects of gating (Perozo et al., 1993). Mutant cDNAs were linearized using a NotI enzyme (New England Biolabs, Inc.) and transcribed into cRNAs using mMESSAGE mMACHINE T7 kit (Life Technologies).

Xenopus oocytes were removed surgically and treated with 1 mg/ml collagenase for 1–1.5 h to remove the follicular layer. Before injection, oocytes were incubated in ND-96 solution supplemented with 100 µg/ml gentamicin at 18°C, typically for 12–24 h. 50 nl cRNA at a concentration of 50–200 ng/µl was injected into oocytes. After injection, the oocytes were kept at 18°C in a solution containing 100 mM NaCl, 2 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, 5 mM HEPES, 0.1 mM DTT, and 0.2 mM EDTA, supplemented with 100 µg/ml gentamicin and 100 mg/ml bovine serum albumin. Ionic current measurements were performed 12–24 h after injection, whereas gating currents were measured 2–7 d after injection.

Electrophysiology

Ionic currents were measured on a cut-open oocyte voltage clamp (COVC) set-up (CA-1B; Dagan Corporation) as described previously (Gagnon and Bezanilla, 2010). The external solution used was 105 mM NMG-MES (N-methyl-d-glucamine methanesulfonate), 10 mM K-MES, 2 mM Ca-MES, and 10 mM HEPES, pH 7.4. The internal solution was 115 mM K-MES, 2 mM EGTA, and 10 mM HEPES, pH 7.4. Gating currents were measured either on a COVC or two-electrode voltage (TEV) clamp set-up. Some of the mutants investigated in this study exhibited low expression and their gating currents were measured on a TEV clamp set-up. The external solution used for gating current measurements in both set-ups was 115 mM NMG-MES, 2 mM Ca-MES, and 10 mM HEPES, pH 7.4. The internal solution used for gating current measurements on the COVC set-up was 115 mM NMG-MES, 2 mM EGTA, and 10 mM HEPES, pH 7.4. The recording pipette resistance for all electrophysiological measurements was 0.2–0.5 MΩ. Analogue signals were sampled at 20–250 kHz with a Digidata 1440 or 1320 interface (Molecular Devices) and low-pass filtered at 10 kHz.

Ionic currents were obtained by applying 100-ms-long depolarizing pulses from −120 to 80 mV in 2.5- or 5-mV increments. The holding potential was −120 mV. Capacitive transients and linear leak currents were subtracted online using the P/−4 method, during which the holding potential was −120 mV. After baseline subtraction, peak tail current amplitudes, elicited by repolarization pulses to −120 mV, were used to generate the relative open probability versus voltage (I/I_max) curves. Gating currents were obtained by applying a 50-ms-long depolarizing pulse to voltages from −120 to 20 mV (in 5-mV intervals). For measurements using COVC, the holding potential used was −120 mV, whereas on the TEV, the holding potential was −90 mV as it was not possible to hold the oocytes at −120 mV. Depolarization pulses were preceded and followed by 50-ms pre- and postpulses to −120 mV. Q-V curves for the W434F mutant measured in either of the two setups were superimposable. The capacitive transient and linear leak currents were subtracted online using the P/−4 or P/−8 method, with a subsweep holding potential of −120 or −90 mV (on COVC or TEV, respectively). After baseline readjustments, the on-gating current records were integrated over the duration of the depolarization pulse to obtain the gating charge displaced, which was used to compute the fractional gating charge displacement versus V curve (Q/Q_max vs. V or Q-V).

Data analysis

The I/I_max curve for each mutant was obtained by averaging the curves obtained from three to six oocytes. The curve was fitted to the Boltzmann equation:

$$\frac{I}{I_{\max }}=\frac{1}{\exp \left\{z_{app}F\left(V_{1/2}-V\right)/RT\right\}},$$

where z_app is the Boltzmann slope and V_1/2 is the voltage that elicits half-maximal response. The Boltzmann measure of free-energy change, ΔG_app, for each mutant was calculated as ΔG_app = z_appFV_1/2. The uncertainty associated with ΔG_app estimation (δΔG_app) was calculated as

$$\delta \Delta G_{app}=F\sqrt{{\left(\delta z_{app}{V}_{1/2}\right)}^2+{\left(z_{app}\delta V_{1/2}\right)}^2},$$

where δz_app and δV_1/2 are the standard error associated with estimation of z_app and V_1/2, respectively.

The nonadditivity in an FMC, ΔΔG_FMC, was calculated as

$$\Delta \Delta G_{FMC}={\left\{z_{app}F{V}_{1/2}\right\}}_{WT}+{\left\{z_{app}F{V}_{1/2}\right\}}_{S12}-{\left\{z_{app}F{V}_{1/2}\right\}}_{S1}-{\left\{z_{app}F{V}_{1/2}\right\}}_{S2},$$

where the subscripts indicate the WT channel, double mutant (S12), or the two single mutants (S1 or S2). The uncertainty associated with ΔΔG_FMC (δΔΔG_FMC) was calculated as

$$\delta \Delta \Delta G_{FMC}=\sqrt{{\left(\delta \Delta G_{app\Vert W}\right)}^2+{\left(\delta \Delta G_{app\Vert S12}\right)}^2+{\left(\delta \Delta G_{app\Vert S1}\right)}^2+{\left(\delta \Delta G_{app\Vert S2}\right)}^2},$$

where the terms in the brackets indicate the uncertainty associated with the ΔG_app estimates of the WT and double and two single mutants.

The fractional gating charge displacement curves for all of the mutants were obtained by averaging measurements performed on three to six oocytes. The median voltage of activation, V_M, for each Q-V curve was extracted by calculating the area between the Q-V curve and the ordinate axis, using the trapezoid method. For a Q-V curve with n points, the V_M is calculated as

$$V_M={\displaystyle {\sum }_{i=1}^{n-1}\frac{\left(Q_{i+1}-Q_i\right)\left(V_{i+1}+V_i\right)}{2}},$$

where Q_i and V_i are the i^th point on the Q_fV curve. The net free energy of activation of the channel is calculated as ΔG_C = Q_maxFV_M, where Q_max is the maximum number of charges transferred during voltage-dependent activation of the channel. For all of our calculations, we used a Q_max of 13.2 (Schoppa et al., 1992; Aggarwal and MacKinnon, 1996; Seoh et al., 1996). Although, Q_max for each of the mutations was not measured individually, it is unlikely that any of the mutants studied in this paper alter Q_max as they are not the primary gating charge–determining residues of the channel (Aggarwal and MacKinnon, 1996; Seoh et al., 1996). The uncertainty in ΔG_C was calculated as Q_maxFδV_M, where δV_M is the standard error of the V_M estimation.

The nonadditivity in a mutant cycle analysis was calculated using the median measure of free-energy change; this nonadditivity, ΔΔG_GIA, was calculated as

$$\Delta \Delta G_{GIA}=Q_{\max }F\left(V_{M\left|\right|W}+V_{M\left|\right|S12}-V_{M\left|\right|S1}-V_{M\left|\right|S2}\right).$$

The standard error associated with ΔΔG_GIA (δΔΔG_GIA) was calculated as

$$\begin{array}{l}\delta \Delta \Delta G_{GIA}=\\ Q_{\max }F\sqrt{{\left\{\delta {\left(V_M\right)}_{WT}\right\}}^2+{\left\{\delta {\left(V_M\right)}_{S1}\right\}}^2+{\left\{\delta {\left(V_M\right)}_{S2}\right\}}^2+{\left\{\delta {\left(V_M\right)}_{S12}\right\}}^2},\end{array}$$

where δ(V_M)_WT, δ(V_M)_S1, δ(V_M)_S2, and δ(V_M)_S12 are the uncertainties (standard error of the mean) associated with V_M measurement of the WT channel and the single and double mutant channels, respectively.

Simulations

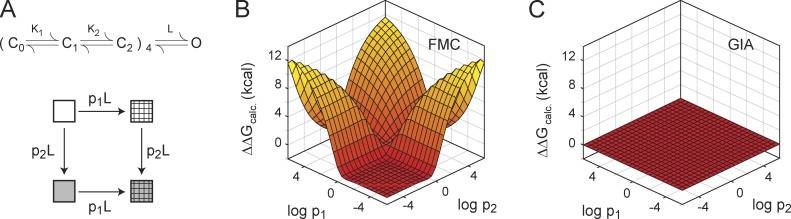
All simulations were performed with MATLAB version R2012b. The nonadditive energies for randomly generated mutant cycles were performed as follows. First we assume that all of the three mutants and the WT channel constituting the mutant cycle undergo voltage-dependent activation following the same scheme. This assumption implies that there is at least one discrete state Markov model (gating scheme) that can adequately describe the gating properties of all the mutants and the WT channel, constituting the mutant cycle. Various constructs of the cycle differ in the values of model parameters, although the number of closed and open states and their connectivities remain the same. This assumption is invoked only to simplify the algebraic representation of ΔG_net and ΔΔG_true (in terms of the different equilibrium parameters of the gating scheme) when we compare energetic nonadditivities using GIA and FMC. Each gating scheme is described by n equilibrium parameters whose magnitude at 0 mV are K₁, K₂,…, K_n and all of which have a standard exponential voltage dependence determined by parameters z₁, z₂,…, z_n, respectively. For the i^th equilibrium constant, the range of values (i.e., the parameter space) is determined to be $K_i^{\min }$ to $K_i^{\max },$ and similarly the voltage-dependent parameters also have a defined range of values $z_i^{\min }$ to $z_i^{\max }.$ In each mutant cycle, the model parameters for the WT were fixed, but those of the mutants were selected randomly within the given parameter space. For each mutant in the cycle, “2n” random numbers between 0 and 1 (a uniform random number generating function was used) were generated, each of which specified the extent of perturbation on the equilibrium constants or the voltage dependence parameters. The equilibrium constants of the mutant was assigned as $K_{i,mut}=K_i^{\min }{\left(K_i^{\max }/K_i^{\min }\right)}^R,$ where R is the random number, whereas the voltage-dependent parameters were assigned as $z_{i,mut}=z_i^{\min }+R\left(z_i^{\max }-z_i^{\min }\right)$ (the random numbers used for perturbation of K_i and z_i were independently generated). This process was repeated for all three mutants of the cycle and represents a situation where single and double mutants have multiple effects on channel energetics. The P_O-V and Q-V curves of the mutants were generated from which ΔG_app and ΔG_net was extracted. These parameters were then used to compute ΔΔG_FMC and ΔΔG_GIA for the cycle. This process was repeated for >600 cycles in two instances: first where the channel and its mutants follow the ZHA activation scheme (see Fig. 5 A) and second where they follow MWC activation scheme (see Fig. 6 C). This strategy allowed us to test the accuracy of ΔΔG_GIA over a large parameter space.

Figure 5.

Numerical analysis of interaction energies computed via FMC and GIA using the ZHA model. (A) The ZHA model of activation of the Shaker K_V channel. A mutant cycle is envisioned in which the WT channel and the mutants gate via the ZHA scheme. The two single mutants (hashed box and gray box) differ from the WT reference channel (open box) only in the value of the last concerted transition (by factors of p₁ and p₂). The effects of the two single mutants are additive such that for the double mutant (gray hashed box) the equilibrium constant of the last transition is p₁p₂L, whereas the other equilibrium constants are same as the WT channel. (B and C) Several such cycles were generated using different values of p₁ and p₂, and for each cycle, ΔΔG_FMC (B) and ΔΔG_GIA (C) were calculated from simulated P_O-V and Q-V curves, respectively, and plotted against p₁ and p₂.

Figure 6.

Comparison of nonadditivities evaluated with GIA and FMC from randomly sampled mutant cycles. (A–E) Several mutant cycles were generated via random sampling strategy. For each cycle, ΔΔG_FMC (A and D) and ΔΔG_GIA (B and E) were calculated and compared against ΔΔG_true. In A and B, each of the four constructs constituting the cycle follow a ZHA activation scheme, whereas in D and E, each of the four constructs constituting the cycle follow an MWC activation scheme (C), where J represents the intrinsic voltage-dependent activation constant of each voltage sensor, L is the intrinsic activation constant of the pore, and D is the allosteric interaction factor.

The parameter range sampled for the simulations performed using the ZHA scheme was $K_1^0:$ [0.005–5,000], $K_2^0:$ [0.1–100,000], L₀: [0.01–10000], z₁: [0.5–3.5], z₂: [0.5–3.5], and z_L: [0.25–2.5]. The parameters for the WT channel were fixed at $K_1^0:$ 5, $K_2^0:$ 100, L₀: 10, z₁: 2, z₂: 1.5, and z_L: 0.5 (which are close to the parameters for the Shaker K_V channel reported previously [Zagotta et al., 1994a; Ledwell and Aldrich, 1999]). The parameter space sampled for the simulations performed using the MWC scheme was J₀: [0.00001–10], L₀: [10⁻⁹–10⁻³], D: [1–100], z_J: [0.1–4], and z_L: [0.1–2] (D was maintained voltage independent in all cases). The parameters for the WT channel were fixed at J₀: 0.03, L₀: 10⁻⁶, D: 25, z_J: 0.6, and z_L: 0.3 (which are close to the parameters for the BK channel model reported previously [Horrigan and Aldrich, 2002]).

Online supplemental material

Figs. S1 and S2 show a family of gating and ionic current traces for Shaker potassium channel mutants that were investigated in this study. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201411184/DC1.

RESULTS

Principle of the GIA

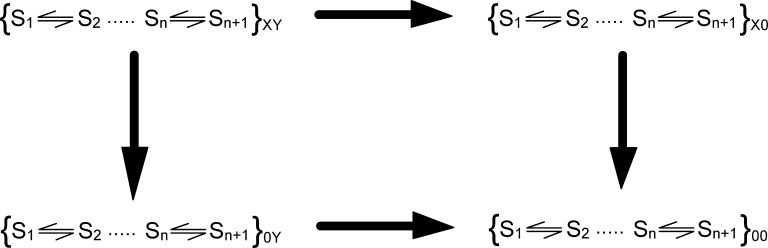
Let us consider a protein that exists in a passive form, S₁, which upon action of an external stimulus (such as ligand, voltage, etc.) undergoes a series of conformational changes to reach its final active form, S_n+1, via n sequential transitions (involving n − 1 intermediate states, S_i, i = 2, 3,…, n − 1). The free energy of each conformational state is G_i. On such a system we implement the mutant cycle analysis (Figs. 1 A and 2) to deduce the interaction energy between two residues, X and Y.

Figure 2.

Mutant cycle analysis for a multistate protein. The WT protein with unperturbed sites (XY) activates via multiple intermediate states, which enables the protein to switch between the initial conformation, S₁, and the final conformation S_n+1, which is driven by an external physical or chemical driving force (stimulus). The two single mutants (X0) or (0Y) and the double mutant (00) follow a similar activation scheme. The mutations can affect one or multiple transitions of the scheme, which might not be known a priori. In this case, the free energy of perturbation is calculated from the measurements of conjugate displacement associated with the transition from S₁ to S_n+1.

The residue X is perturbed in the native protein and in the background of the secondary perturbation, Y. As a consequence of these perturbations, the free energies of multiple intermediates may change. The interaction energy between the two residues in the state S_i (i = 1, 2,…, n), $G_{\mathrm{int}}^{\left(i\right)},$ can be described by the equation

$$G_{\mathrm{int}}^{\left(i\right)}=\left(G_i^{\left(X,Y\right)}-G_i^{\left(0,Y\right)}\right)-\left(G_i^{\left(X,0\right)}-G_i^{\left(0,0\right)}\right)\dots ,$$ (1)

where the superscripts on the free-energy terms on the right side of the equation indicate the unperturbed and singly and doubly perturbed systems, as shown in Fig. 2. Equations, analogous to Eq. 1, may be written for each of the conformational states of the protein.

To understand how these interactions drive gating transitions, we would like to measure the changes in these interaction energies when the channel undergoes a conformational change. From an experimental standpoint, we can measure the free-energy change associated with a conformational change, say between states S_i and S_i+1, by measuring the equilibrium constant, K_i, for the transition. This allows us to evaluate the difference in the interaction energies between the two states in two different conformations as

$$\begin{array}{l}{G}_{\mathrm{int}}^{\left(i+1\right)}-G_{\mathrm{int}}^{\left(i\right)}=\left\{\left(G_{i+1}^{\left(X,Y\right)}-G_{i+1}^{\left(0,Y\right)}\right)-\left(G_{i+1}^{\left(X,0\right)}-G_{i+1}^{\left(0,0\right)}\right)\right\}\\ -\left\{\left(G_i^{\left(X,Y\right)}-G_i^{\left(0,Y\right)}\right)-\left(G_i^{\left(X,0\right)}-G_i^{\left(0,0\right)}\right)\right\},\end{array}$$

which may be rewritten as

$$\begin{array}{l}\Delta \Delta G_i=\left(\Delta G_{i\to i+1}^{\left(X,Y\right)}-\Delta G_{i\to i+1}^{\left(0,Y\right)}\right)-\left(\Delta G_{i\to i+1}^{\left(X,0\right)}-\Delta G_{i\to i+1}^{\left(0,0\right)}\right)\\ =-RT\ln \left(\frac{K_i^{\left(X,Y\right)}{K}_i^{\left(0,0\right)}}{K_i^{\left(0,Y\right)}{K}_i^{\left(X,0\right)}}\right)=-RT\ln {\Omega }_i\dots .\end{array}$$ (2)

In Eq. 2, ΔΔG_i reflects $G_{\mathrm{int}}^{\left(i+1\right)}-G_{\mathrm{int}}^{\left(i\right)}$ and ΔG_i→i+1 is the free-energy difference between the states S_i and S_i+1, which can be written as −RTlnK_i. Ω_i reflects the nonadditivity of the equilibrium constants in the mutant cycle.

Next, suppose the nonadditive perturbation energy associated with each of the n conformational transitions (ΔΔG_i, i = 1, 2,…, n) are evaluated and we sum all of the ΔΔG_i measures to obtain the net nonadditivity of the two perturbations, ΔΔG_net:

$$\begin{array}{l}\Delta \Delta G_{net}={\displaystyle \sum _{i=1}^n\Delta \Delta G_i}=\left(\Delta G_{1\to n+1}^{\left(X,Y\right)}-\Delta G_{1\to n+1}^{\left(0,Y\right)}\right)\\ -\left(\Delta G_{1\to n+1}^{\left(X,0\right)}-\Delta G_{1\to n+1}^{\left(0,0\right)}\right)=-RT{\displaystyle \sum _{i=1}^n\ln {\Omega }_i}\dots ,\end{array}$$ (3)

where ΔG_i→i+1 is the free-energy difference between the states S₁ and S_n+1. This net energetic nonadditivity reflects the difference in the interaction energies between X and Y in the initial passive conformation and final active conformation. A protein might transit between its two limiting states following multiple pathways. Because most biological macromolecules obey the principle of microscopic reversibility, the net free-energy changes across all such pathways are necessarily identical. This implies that ΔΔG_net is path independent, and thus Eq. 3 holds for systems undergoing multistate transitions in modes that are sequential or parallel or combinations thereof.

How can we extract ΔΔG_net from experimental measurements? Recently, we described an approach to extract the ΔG_net for conformational change in proteins, driven by an external stimulus, in a model-independent manner (Chowdhury and Chanda, 2012a, 2013). The approach involves measuring the “conjugate displacement” associated with the stimulus, followed by an integral transformation of the conjugate displacement versus “stimulus intensity,” which directly yields the total work done during conformational change in the protein (Chowdhury and Chanda, 2012a, 2013; Sigg, 2013). This method was described in detail for voltage-gated ion channels, for which the conjugate displacement curve is the gating charge displacement versus voltage (Q-V) curve. From the measured Q-V curves we extract the median voltage of activation, V_M, and evaluate ΔG_net as Q_maxFV_M, where Q_max is the maximum amount of gating charges transferred during channel activation (or in other words the charge per channel). By incorporating such a free-energy measure in Eq. 3, we can obtain a measure of ΔΔG_net (Eq. 3). Because this approach of combining the mutant cycles with measurements of conjugate displacement curves is referred to as GIA, the ΔΔG_net in Eq. 3 will be renamed ΔΔG_GIA.

Experimental comparison of FMC analysis and GIA

FMC analysis and GIA use orthogonal experimental measurements to estimate the interaction energies between two sites. How do the interaction energies computed by these two methods compare against each other? In the prototypical Shaker K_V channel, previous FMC analysis has identified several strongly interacting residues (Yifrach and MacKinnon, 2002; Sadovsky and Yifrach, 2007). Some of the interaction partners are >10 Å away in the protein structure, which has led to the view that voltage-dependent channel opening involves dynamic rearrangements of long-range interaction networks. To estimate these interaction energies accurately, we reevaluated them using the GIA approach.

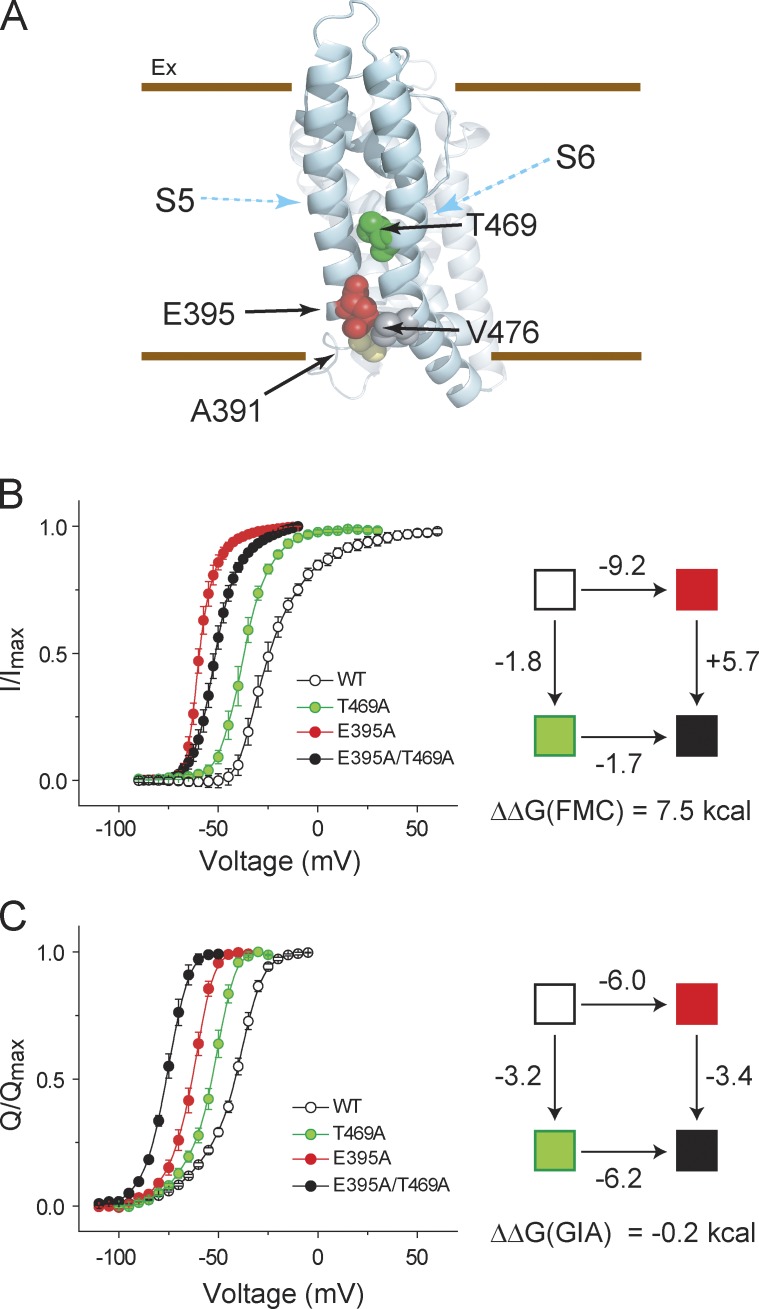
We focused on four residues (A391, E395, T469, and V476) located in the pore domain of the channel, a region likely to undergo significant conformational changes during channel gating (Fig. 3 A; Yifrach and MacKinnon, 2002; Sadovsky and Yifrach, 2007). First, we applied FMC to measure the interaction energy between sites E395 and T469. Two single and one double mutant were generated by mutating the sites to Ala, and their relative P_O-V curves were measured (along with that of the WT channel) by tail current analysis (Fig. 3 B and Fig. S1). Both single mutations result in large shifts in the P_O-V curves, and consistent with a previous study (Yifrach and MacKinnon, 2002), FMC analysis shows a large nonadditivity (ΔΔG_FMC ∼7.5 kcal) of the two perturbations (Table 1). Next, for each of the constructs, Q-V curves (Fig. 3 C and Fig. S1) were measured, which allowed us to calculate perturbation energies caused by mutations by using median analysis (Table 2; Chowdhury and Chanda, 2012a). Strikingly, GIA showed that the perturbations at these sites are energetically independent (ΔΔG_GIA ≈ 0; Table 3).

Figure 3.

Experimental comparison of interaction energies evaluated using FMC and GIA. (A) The structure of the pore domain of a single subunit of the K_V1.2/2.1 paddle chimera showing the four residues (black arrows) that were examined. The S5 and S6 segments are marked for clarity (cyan arrows). (B, left) I/I_max curves for the WT channel and three mutants (E395A, T469A, and E395A-T469A). (right) FMC analysis for the E395 and T469 pair (ET), with each box colored as in the G-V curves on the left. The perturbation energy along each path was assessed from the I/I_max curves. (C, left) Normalized gating charge displacement versus voltage curves (Q-V) in WT channel and three mutants (E395A, T469A, and E395A-T469A). (right) GIA for the ET pair with each box colored as in the Q-V curves on the left. The perturbation energy along each path was assessed from the V_M of the Q-V curves (assuming Q_max = 13.2 for all the mutations). Error bars represent SEM.

Table 1.

Nonadditivity of the perturbations at E395 and T469 evaluated using FMC

Mutant	V1/2 (±SEM)	z (±SEM)	n	ΔGapp (±SEM)
	mV			kcal
WT	−21.8 (±1.4)	2.5 (±0.07)	4	−1.3 (±0.09)
E395A	−59.3 (±0.6)	7.7 (±0.17)	4	−10.5 (±0.25)
T469A	−36.5 (±1.3)	3.7 (±0.32)	4	−3.1 (±0.29)
E395A-T469A	−50.8 (±1.0)	4.1 (±0.28)	3	−4.8 (±0.34)

The V_1/2 values of the G-V curves of the inactivation removed Shaker K_V (inactivation removed) channel, and the mutants are similar to those reported previously (Yifrach and MacKinnon, 2002). However, our fitted Boltzmann slopes (z) observed in this study are consistently lower than those reported previously. This can be attributed to the differences in the solutions used for functional measurements of the tail currents (110 mM NMG-MES/10 mM K-MES vs. 58 mM NaCl/40 mM RbCl). As a result of this difference in slopes, the ΔΔG_FMC calculated in this study (+7.5 ± 0.52 kcal/mol) is lower than that reported previously.

Table 2.

Median voltage of activation, V_M, and the net free energy of activation of mutants of the Shaker K_V channel

Mutant	VM (±SEM)	n	ΔGnet (±SEM)
	mV		kcal
WT	−44.7 (±1.0)	5	−13.6 (±0.3)
A391V	−46.0 (±0.9)	5	−14.0 (±0.3)
E395A	−64.6 (±0.9)	5	−19.6 (±0.3)
T469A	−55.4 (±0.8)	3	−16.8 (±0.2)
V476A	−61.0 (±0.9)	8	−18.5 (±0.2)
A391V-E395A	−66.4 (±0.9)	10	−20.1 (±0.3)
A391V-T469A	−46.4 (±0.8)	6	−14.1 (±0.2)
A391V-V476A	−66.7 (±0.8)	12	−20.2 (±0.2)
E395A-T469A	−75.7 (±0.8)	4	−23.0 (±0.2)
E395A-V476A	−78.8 (±1.4)	4	−23.9 (±0.4)
T469A-V476A	−68.0 (±1.0)	5	−20.6 (±0.3)

Gating currents for the mutants were measured either on a COVC or a TEV clamp set-up (bold). The V_M of the normalized Q-V curve for all of the mutants (averaged from measurements performed in n oocytes) are reported along with the SEM (δV_M). ΔG_net was evaluated as Q_maxFV_M and its standard error as Q_maxFδV_M.

Table 3.

Comparison of nonadditive perturbation energies, evaluated using GIA and FMC, for different pairwise mutations

Site pairs	ΔΔGGIA (±SE)	ΔΔGFMC
	kcal	kcal
A391-E395	−0.15 (±0.56)	9.12
A391-T469	3.12 (±0.53)	5.49
A391-V476	−1.33 (±0.55)	6.04
E395-T469	−0.12 (±0.53)	10.15 (7.5 ± 0.52)
E395-V476	0.64 (±0.65)	12.68
T469-V476	1.12 (±0.56)	7.48

ΔΔG_GIA for each residue pair and its standard error were calculated as described in Materials and methods. ΔΔG_FMC was calculated using the Boltzmann slope and V_1.2 of the G-V curves for the different mutants, reported in Yifrach and MacKinnon (2002). For the E395-T469 pair, our calculations of ΔΔG_FMC using the parameters reported in Table 1 are shown in parentheses.

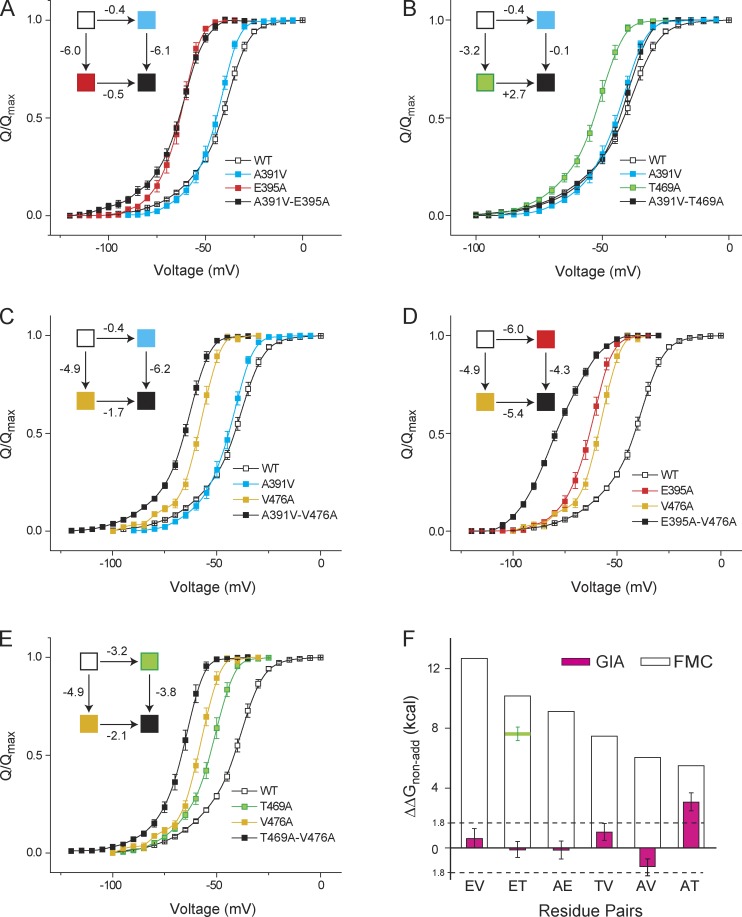
Next, we extended this comparison to other residue pairs that have been previously proposed to be involved in interactions (Fig. 4, Fig. S2, and Tables 2 and 3). Q-V curves of single mutants (A391V, E395A, T469A, and V476A) and all pairwise combination (double) mutants were measured to calculate ΔΔG_GIA. Studies in proteins show that interaction energies between noncharged residues range between 0.5 and 1.0 kcal/mol (Horovitz, 1996). We set the cut-off for interaction in a single subunit at 0.45 kcal/mol, and therefore, for a tetrameric channel it will be 1.8 kcal/mol. This is also above our experimental error associated with ΔΔG_GIA estimates, which was ∼0.6 kcal (≈RT). In all of the six possible pairs, we found that that ΔΔG_GIA and ΔΔG_FMC (reported previously) do not agree with each other. More importantly, except for the AT pair (i.e., A391-T469), all of the pairwise nonadditivities evaluated by GIA were below the significance level, suggesting that they are energetically independent.

Figure 4.

Interaction energies evaluated using GIA differ from those evaluated using FMC. (A–E) GIA was used to measure the interaction energies between A391-E395 (AE; A), A391-T469 (AT; B), A391-V476 (AV; C), E395-V476 (EV; D), and T469-V476 (TV; E). In each case the normalized Q-V curves of the single and double mutants were measured, from which the V_M was extracted and used to calculate the free energy of perturbation. The thermodynamic cycle for each pair is shown in the inset, in which each box corresponds to the WT or single or double mutants, colored as noted in the legends for each panel. (F) ΔΔG_GIA for each pair was calculated using the Q-V curves and compared with ΔΔG_FMC calculated using the Boltzmann fit parameters. For the ET pair, the horizontal green bar depicts ΔΔG_FMC evaluated under our experimental conditions. Error bars represent SEM.

Numerical simulations of GIA and FMC

This discrepancy in interaction energies evaluated using FMC and GIA prompted us to examine the robustness of the two approaches in measuring energetic nonadditivities. We performed numerical simulations using the 16-state ZHA model (Fig. 5; Hoshi et al., 1994; Zagotta et al., 1994a,b; Ledwell and Aldrich, 1999), which describes the voltage-dependent activation of the Shaker K_V channel. In this model, voltage sensor activation is described as a two-step sequential process occurring independently in different subunits, and once all voltage sensors are activated, a final concerted transition opens the channel pore. We constructed a hypothetical mutant cycle in which two mutations were envisioned to affect only the equilibrium constant of the last concerted transition and the double mutant to affect the same transition, additively (Fig. 5 A). Thus, by design, the cycle ensures that the two perturbations are energetically independent, and hence nonadditivity measurements should yield a null result. While holding the other equilibrium parameters constant, the magnitude of perturbation of each mutant was varied over 12 orders of magnitude, and in each case we calculated the ΔΔG using FMC (by simulating the P_O-V curves) and GIA (by simulating the Q-V curves). As shown in Fig. 5 (B and C), the FMC simulations show strong nonadditive energies, whereas the GIA simulations show that the nonadditivity is zero in all cases. This simulation suggests that even under limiting conditions when perturbations affect a single transition of the gating scheme, FMC analysis may report nonreal interaction energies.

Next, we considered a more general scenario where single mutations affect multiple transitions randomly and the double mutants may affect these transitions either additively or nonadditively. A hypothetical mutant cycle was created wherein the WT reference channel and the three mutants constituting the cycle were envisioned to be gated via the ZHA model. For each of the three mutants comprising a thermodynamic cycle, the values of the equilibrium parameters were randomly chosen from within a parameter space (see Materials and methods). The P_O-V and Q-V curves in each case were simulated and the ΔΔG_FMC and ΔΔG_GIA for the cycle were computed. This process was repeated for a large number (>600) of mutant cycles, and ΔΔG_FMC and ΔΔG_GIA for each cycle were then compared against the true nonadditive energy ΔΔG_true (Fig. 6, A and B), derived directly from the model equilibrium constants. ΔΔG_true was calculated as

$$\begin{array}{l}\Delta \Delta G_{true}=-4RT\ln \left(\frac{K_1^{WT}{K}_1^{S12}}{K_1^{S1}{K}_1^{S2}}\right)\\ -4RT\ln \left(\frac{K_2^{WT}{K}_2^{S12}}{K_2^{S1}{K}_2^{S2}}\right)-RT\ln \left(\frac{L^{WT}{L}^{S12}}{L^{S1}{L}^{S2}}\right),\end{array}$$

where the superscripts WT, S12, S1, and S2 indicate the equilibrium constants for the WT channel and the double and the two single mutant channels, respectively. The comparison reveals that ΔΔG_GIA and ΔΔG_true are identical for all cases (Fig. 6 B), whereas ΔΔG_FMC is not correlated with ΔΔG_true (Fig. 6 A).

Similar simulations were performed for an MWC-type allosteric scheme (Fig. 6 C). According to this scheme, voltage sensor activation and pore opening represent preexisting equilibria wherein the pore is intrinsically biased toward the closed state and voltage sensor activation causes a shift in this bias toward the open state through allosteric interactions. Such an activation scheme has been shown to accurately describe the voltage-dependent gating of the BK channel (Horrigan and Aldrich, 1999, 2002). For >600 mutant cycles generated by a random sampling strategy, we obtained ΔΔG_FMC and ΔΔG_GIA, whereas ΔΔG_true was calculated as

$$\begin{array}{l}\Delta \Delta G_{true}=-4RT\ln \left(\frac{J^{WT}{J}^{S12}}{J^{S1}{J}^{S2}}\right)\\ -4RT\ln \left(\frac{D^{WT}{D}^{S12}}{D^{S1}{D}^{S2}}\right)-RT\ln \left(\frac{L^{WT}{L}^{S12}}{L^{S1}{L}^{S2}}\right),\end{array}$$

where J and L represent the intrinsic equilibrium constant of activation, at 0 mV, for the voltage sensor and the pore and D represents the allosteric interaction factor. We find that ΔΔG_FMC and ΔΔG_true are highly divergent (Fig. 6 D), whereas ΔΔG_GIA and ΔΔG_true are equal in all tested cases (Fig. 6 E). The discrepancy between ΔΔG_GIA and ΔΔG_true is thus not just limited to the systems activating via the ZHA model but also extends to other multistate voltage-dependent systems (see Appendix for additional examples). These findings establish that GIA but not FMC can report energetic nonadditivities (residue-specific interaction energies) in a self-consistent manner irrespective of whether the perturbations affect single or multiple transitions.

DISCUSSION

In this study, we describe an experimental methodology to quantitatively determine the contribution of interaction energies between two sites of a protein to the overall free-energy change associated with a stimulus-driven conformational change of the protein. Our method is based on determining the energetic consequence of a perturbation in the presence of a secondary perturbation, by measuring the conjugate displacement of the process for each of the perturbed systems. This is fundamentally different from the canonical mutant cycle analyses, wherein functional activity of a protein is measured and used to empirically quantify the free energies. We show that the free energies of perturbations calculated via a median transformation of the conjugate displacement curve allow us to directly calculate the interaction energies between specific sites of a multistate protein, in a self-consistent manner, even in instances when the perturbations affect multiple transitions of the protein.

We implemented GIA on the voltage-gated Shaker K_V channel, for which the conjugate displacements associated with the voltage-dependent transformation can be conveniently obtained by measuring the gating charge displacement versus voltage (Q-V) curves. We used GIA to calculate the interaction energies between several pairs of residues on the pore domain of the channel, which undergoes large conformational changes during channel gating (Yellen, 1998). Many of the perturbed pair of sites are several angstroms away in the structure, and previous FMC studies have suggested that they constitute a long-range energetically coupled network of residues that are crucial for channel gating (Yifrach and MacKinnon, 2002; Sadovsky and Yifrach, 2007). However, using GIA, we find that all except for one (A391-T469) were energetically independent of each other. We should note that some of these differences in interaction energy measurements could arise because of the use of different backgrounds. We use W434F nonconducting mutant in our study, whereas conducting Shaker potassium channel was used as a background for FMC studies (to be discussed later). Numerical simulations of allosteric (MWC type) and the quasi-sequential nonallosteric (ZHA type) models show that GIA can provide estimates of nonadditivities over a large parameter space even when mutations affect different transitions during a multistep activation process.

In this study, the GIA approach is implemented by introducing alanine substitutions at each of the test sites, which removes all atoms in the native side-chains except the Cβ atom. Thus, the deduced energetic nonadditivity reflects the excess contribution of native residue pairs to the overall channel energetics, relative to the double alanine pair at the respective sites. Although a glycine substitution might be deemed better than alanine, the backbone flexibility introduced by glycine substitutions could introduce structural distortions to the protein and thus is not preferable in most instances (Faiman and Horovitz, 1996; Di Cera, 1998). Additionally, native alanine residues are frequently mutated to valine, which should not be directly compared with alanine-based mutant cycles (Yifrach and MacKinnon, 2002).

Interpreting GIA and FMC in terms of energy landscape

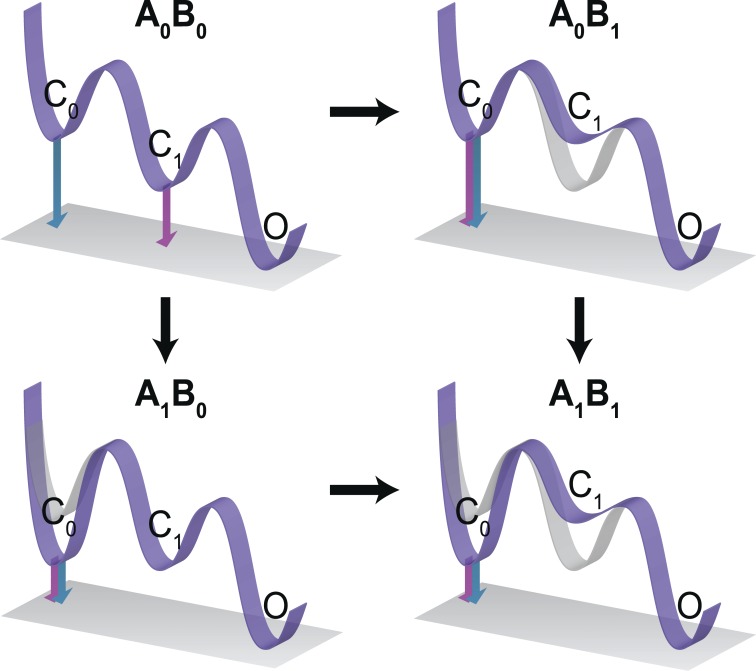
The false positives that are observed in the FMC approach can be rationalized by considering a simple three-state model of a channel with two closed states (C₀ and C₁) and one open state (O; Fig. 7). A G-V curve samples the occupancy of only the O state. As a consequence, the G-V–based free-energy estimate is dominated by the energy difference between the open state and most stable closed state. Mutations that alter the stability of the intermediate closed state or states could change the reference closed state. In the example shown, G-V–based energetics are informed by the energy difference between C₁ and O for the WT but C₀ and O for the other three mutants. Because of these differences in reference states, G-V–based perturbation energies are not comparable across mutations, which may contribute to inaccurate interaction energy estimates (Fig. 7). This problem is exacerbated as the number of intermediate closed states increase. In contrast, GIA always measures the energy difference between first and last states. This ensures that in the given example the Q-V–based energies always reflect the energy difference between the states C₀ and O. In other words, the GIA approach allows us to reduce the complexity of the multistate gating process to a simple comparison between binary states.

Figure 7.

Schematic depiction of FMC and GIA using energy profile diagrams. Each energy profile in the thermodynamic mutant cycle represents a three-state sequential gating process involving two closed states (C₀ and C₁) and an open state (O). One of the mutants destabilizes the state C₁ (A₀B₁), and the second mutant stabilizes state C₀ (A₁B₀), but the effect is additive on the double mutant (A₁B₁; i.e., C₁ is destabilized and C₀ is stabilized). The pink arrows show the free-energy difference computed by the G-V curves (as is done in FMC), whereas the blue arrows show the free-energy difference computed by the Q-V curves (as is done in GIA). Note that in GIA, the measured ΔG is that between C₀ and O in all four cases, whereas in FMC, the measured ΔG is between C₁ and O in A₀B₀ but between C₀ and O in the other three.

We note that energetic additivity in GIA will arise in three instances: (1) the sites truly do not interact, (2) the sites interact only in the intermediate states, or (3) the interaction between the two sites does not change between the initial resting and final activated states. Thus, additivity is not a proof for absence of interaction, but when nonadditivity is observed, one can be certain that the residue pairs synergistically contribute to the gating process.

When channel activation is truly a two-state process, the nonadditive energies of FMC will be self-consistent (Horovitz and Fersht, 1990). Another scenario where FMC might be self-consistent is when the Q-V and relative P_O-V curves of the channel and the mutants are widely separated along the voltage axis. In such instances, the P_O-V curve can be approximated to describe a single-step transition between the last closed and open states, which is reminiscent of specific mutants of the Shaker K_V channel (Ledwell and Aldrich, 1999; Soler-Llavina et al., 2006). ΔΔG_FMC obtained from Boltzmann fits to the P_O-V curves would reflect the nonadditivity in the last step of channel gating; however, the nonadditive energies in the earlier steps or the overall gating process will not be accessible. In contrast, as shown earlier (Eq. 3), ΔΔG_GIA reflects the summation of energetic nonadditivities in all of the steps from the initial resting state of the channel to the final open state of the channel. Irrespective of whether the nonadditivity arises because of changes in interresidue interactions in the initial, intermediate, or final steps, ΔΔG_GIA will reflect this nonadditivity as long as energetic nonadditivity in one transition is not compensated by that in another transition. Identifying the specific transitions that contribute to nonzero ΔΔG_GIA will require additional kinetic analysis.

Considerations for gating charge measurements

In the Shaker K_V channels, gating charge displacement curves have been measured in many different ways. In this study, we used the nonconducting W434F mutant to measure the Q-V curves. This mutant eliminates ion conduction by accelerating C-type inactivation, resulting in a putatively collapsed outer pore (Yang et al., 1997; Cordero-Morales et al., 2011). Gating charge of different channel mutants can also be obtained in the background of a second nonconducting mutant of the Shaker K_V channels: V478W, which stabilizes a hydrophobic seal responsible for pore closure and thereby occludes ion flux (Kitaguchi et al., 2004). A third strategy to measure gating currents is to use a high-affinity peptide toxin, such as Agitoxin, which blocks ion conduction (Aggarwal and MacKinnon, 1996). The final alternative is to measure gating currents under conditions when all permeant ions are washed off. Although the Q-V curves obtained from each of the four strategies are generally considered to be equivalent, there may be subtle differences between them, especially for mutant channels. Therefore, our interaction energies measured here should be considered as those obtained in the background of W434F mutant. A thorough and careful study will be needed to assess and compare these different strategies to extract the true perturbation energies for the WT channel.

Another consideration is whether V_M or V_1/2 of the Q-V curves can be used interchangeably for free-energy calculations. Although the Q-V curves of Shaker K_V channel and its mutants exhibit a slight asymmetry, in most instances, the Q-V curves can be adequately fitted to the symmetric Boltzmann equation and the median voltage of charge transfer (V_M) will be often similar to V_1/2, the voltage at which half of the gating charges have moved. In such situations, Boltzmann fit–derived V_1/2 values can be used instead of V_M values to compute the energetic nonadditivities despite the fact that the underlying gating is seldom restricted to two states. However, when the Q-V curves are split, V_1/2 values depend on the choice of model used for fitting and thus might not be unique (Chowdhury and Chanda, 2012a). In contrast, V_M is not obtained through model-specific equations and is characteristic for each Q-V curve.

Implementation of GIA requires prior knowledge of Q_max, the maximum gating charge transferred during full-scale activation, of the channel, and its mutants. Measurement of Q_max for a channel is a nontrivial problem and cannot be estimated simply from the slope of the Q-V curve (Bezanilla and Villalba-Galea, 2013). However, for the system under investigation, the gating charge–determining residues reside in the voltage sensor and are highly specific (Ahern and Horn, 2004). The specific sites that have been investigated in this study are uncharged, lie outside the electric field, and when perturbed are unlikely to significantly alter the Q_max of the channel. However, in implementing GIA to test for interactions between residues in the voltage sensor, it might be important to calibrate Q_max of the mutant channels to establish that the Q_max is not altered significantly by the perturbations.

Considerations for gating involving voltage-independent transitions

For many ion channels the maximum open probability ($P_O^{\mathit{max}}$) at depolarized potentials does not reach unity because the transition between the last closed and open states is voltage independent. In such situations, a correction factor ($-RT\ln P_O^{\mathit{max}}$) needs to be added to Q_maxFV_M to obtain an accurate measure of the free energy of channel activation (Chowdhury and Chanda, 2012a). Incorporating this correction factor, the energetic nonadditivity in GIA is

$$\Delta \Delta G_{GIA}=\Delta \Delta \left(Q_{\max }F{V}_M\right)-RT\ln \left(\frac{P_O^{\max ,S12}.P_O^{\max ,W}}{P_O^{\max ,S1}.P_O^{\max ,S2}}\right)\dots$$ (4)

In Eq. 4, the second term on the right side of the equation incorporates the maximum open probabilities of the WT and single (S1 and S2) and double (S12) mutants, as indicated in the superscript. The magnitude of this correction factor becomes significant (>1.8 kcal) only when $\left(P_O^{\max ,S12}.P_O^{\max ,W}\right)/\left(P_O^{\max ,S1}.P_O^{\max ,S2}\right)$ becomes larger than ∼25, which would imply that $P_O^{\mathit{max}}$ of at least one of the mutants is 25-fold lower than that of the WT channel. Although such an effect is possible, for many Shaker K_V channel mutants (in the voltage sensor and the pore), $P_O^{\mathit{max}}$ has been measured and found to be similar to that of the WT channel (Seoh et al., 1996; Ding and Horn, 2002). This implies that although $P_O^{\mathit{max}}$ measurements will improve the accuracy of the free-energy estimate, its contribution is likely to be small enough so as to not interfere with the identification of strongly interacting residue pairs. A similar consideration would apply to channels that exhibit constitutive opening even under hyperpolarizing conditions. As noted previously (Chowdhury and Chanda, 2012a, 2013), under situations when the $P_O^{\min }$ of the channel is significantly large, a correction factor amounting to $RT\ln \left(1-P_O^{\min }\right)$ needs to be incorporated in the overall free-energy equation to accurately quantify the free-energy difference between the initial and final state (along the charge coordinate) of the channel. However, such a correction factor will be significant (at level of the thermal energy) only when $P_O^{\min }$ > 0.7, which, although possible, is likely to be a rare occurrence.

We should emphasize that GIA provides the net free energy of interresidue interaction associated with gating transitions that are driven by externally applied force. The corrections described above are to take into account the free-energy contributions of transitions that are not driven by external force but are still functionally relevant. This means that GIA without any corrections provides us a model-free method for obtaining interaction energy change going from the initial force-dependent state to the final force-dependent state.

Concluding remarks

Finally, as a note of caution, we should add that the interaction energies measured by GIA are true interaction energies only if the free energy of the system can be simply expressed as a sum of components stemming from specific interactions (Mark and van Gunsteren, 1994). This underlying assumption may not hold true especially when higher-order mutant cycles are constructed, and therefore these interaction energies should be regarded as empirical interaction energies. But this assumption underpins all thermodynamic cycle analyses, and unlike FMC measurements, GIA measurements of interaction energies are self-consistent with multistate gating schemes.

Application of FMC analyses to multistate systems such as ion channels have long relied on empirical free-energy metrics that have been argued to be correlated (occasionally linearly) with the true free-energy change in the system. Such empiricism, although occasionally necessary, is associated with significant uncertainty and, as demonstrated through the simulations performed in this study, can potentially obscure essential molecular and thermodynamic features of the system. The firm thermodynamic foundation of GIA greatly reduces such ambiguities and therefore offers an indubitable strategy to identify residue-level interactions that account for the thermodynamic changes associated with structural dynamics of a protein as it is driven by an external force. Although the application of GIA based on normalized conjugated displacement curves needs to be carefully implemented, as has been described in detail in the previous sections, it offers a clear advancement over the traditional FMC analyses by circumventing the necessity of a two-state process approximation.

Although our discussion in this manuscript is focused mainly on the application of GIA for voltage-dependent systems, this principle can be extended to other stimulus-driven systems. For a ligand-driven transformation, the direct ligand-binding curve is the conjugate displacement curve, and by measuring the median ligand activity, we will be able to estimate the total free-energy change associated with the ligand-driven transformation in a model-independent fashion (Chowdhury and Chanda, 2013). A particular simplicity of such systems is that the maximum number of ligands that can bind the protein molecule (i.e., the protein–ligand stoichiometry) is highly unlikely to change with perturbations (unlike Q_max for voltage-dependent system). Thus, by combining mutant cycle analysis with ligand-binding measurements, the contributions of site-specific interaction energies to ligand dependent activation of proteins can also be assessed.

APPENDIX

An analytical comparison of nonadditive energies computed by FMC and GIA in example multistate systems

(Scheme A1)

(Scheme A2)

(Scheme A3)

Consider a voltage-dependent ion channel comprising two subunits. For simplicity we assume that the subunits are identical, such that they transfer an equal amount of gating charge during voltage-dependent activation. For such a system we envision three different gating schemes as shown above. In Scheme A1, the two subunits activate sequentially, following a particular order (say subunit 1 activates before subunit 2). The channel is open only when both subunits are activated. The equilibrium constants of the two steps have the same voltage dependence, q, but differ in their voltage-independent components. In Scheme A2, the two subunits activate independently, but activation of one subunit allosterically modulates the activation of the other, by a factor K₂/K₁, and the channels are open only when both subunits are activated. As in Scheme A1, both K₂ and K₁ have the same voltage dependence, q, but differ in their voltage-independent components. Scheme A3 is similar to Scheme A2, but with the central difference that channels are open when any one of the two (or both) subunits are activated (or in other words, the channel is closed only when both subunits are deactivated). For all three schemes, K₁ and K₂ are written as $K_i^0\exp \left(qFV\text{/}RT\right),$ where i = 1 or 2 and $K_i^0$ represents the voltage-independent component of the equilibrium constant. Furthermore, for all three schemes, the net free-energy change during voltage-dependent activation (i.e., the chemical component of the free-energy difference between the first and last states of the channel, as indicated by the red arrow) is the same: $\Delta G_{net}=-RT\hspace{0.17em}\ln \left\{K_1^0\hspace{0.17em}{K}_2^0\right\},$ and so is the total charge transferred during voltage-dependent activation: Q_max = 2q.

What is the P_O-V–based Boltzmann metric for the free-energy change in each of the three cases? We use the principle that the Boltzmann slope (obtained through fitting a Boltzmann equation to the P_O-V curve) can be approximated to the slope of the Hill-transformed P_O-V curve at V_1/2 (Yifrach, 2004), i.e.,

$$z_{app}=\frac{RT}{F}\frac{\partial }{\partial V}\ln {\left(\frac{P_O}{1-P_O}\right)|}_{V_{1/2}}.$$

Using the above equation, the Boltzmann measure of the free-energy change (i.e., ΔG_app = z_appFV_1/2) for the three schemes can be derived to be

$$\Delta G_{app-1}=-RT\left(1+\frac{2K_2^0}{2K_2^0+K_1^0+\sqrt{K_1^{0^2}+4K_1^0{K}_2^0}}\right).\ln \left(\frac{2K_1^0{K}_2^0}{K_1^0+\sqrt{K_1^{0^2}+4K_1^0{K}_2^0}}\right),$$

$$\Delta G_{app-2}=-2RT\left(\frac{K_2^0+K_1^0+\sqrt{K_1^{0^2}+K_1^0{K}_2^0}}{K_2^0+2K_1^0+2\sqrt{K_1^{0^2}+K_1^0{K}_2^0}}\right).\ln \left(\frac{K_1^0{K}_2^0}{K_1^0+\sqrt{K_1^{0^2}+K_1^0{K}_2^0}}\right),$$

$$\Delta G_{app-3}=-2RT\left(\frac{K_2^0+K_1^0+\sqrt{K_1^{0^2}+K_1^0{K}_2^0}}{K_2^0+2K_1^0+2\sqrt{K_1^{0^2}+K_1^0{K}_2^0}}\right).\ln \left(\frac{K_1^0{K}_2^0}{K_1^0+\sqrt{K_1^{0^2}+K_1^0{K}_2^0}}\right),$$

where ΔG_app-1, ΔG_app-2, ΔG_app-3 are the P_O-V–based Boltzmann measures of free-energy change for Schemes A1, A2, and A3, respectively. This derivation illustrates two major points. First, although in all three schemes the total free-energy change associated with full-scale activation of the channel is the same, the Boltzmann measure of free-energy change is different in the three cases. Thus, depending on the nature of the gating scheme, the free-energy change deduced from the P_O-V curves will be different. Second, and more importantly, for each of the three schemes, ΔG_app is not related to $K_1^0$ and $K_2^0$ by simple logarithmic relations (i.e., unlike ΔG_net). This nonlinear dependence may result in false positives when ΔG_app is used to compute interaction energies as is done in FMC applications.