Skip to main content
PMC home page
CPT: Pharmacometrics & Systems Pharmacology logoLink to CPT: Pharmacometrics & Systems Pharmacology
. 2014 Sep 3;3(9):e133. doi: 10.1038/psp.2014.30

A Mechanistic, Multiscale Mathematical Model of Immunogenicity for Therapeutic Proteins: Part 1—Theoretical Model

X Chen 1, T P Hickling 2, P Vicini 3,*
PMCID: PMC4211265  PMID: 25184733

Abstract

A mechanistic, multiscale mathematical model of immunogenicity for therapeutic proteins was formulated by recapitulating key biological mechanisms, including antigen presentation, activation, proliferation, and differentiation of immune cells, secretion of antidrug antibodies (ADA), as well as in vivo disposition of ADA and therapeutic proteins. This system-level model contains three scales: a subcellular level representing antigen presentation processes by dendritic cells; a cellular level accounting for cell kinetics during humoral immune response; and a whole-body level accounting for therapeutic protein in vivo disposition. The model simulations for in vivo responses against antigenic protein challenge are consistent with many known immunological observations. By simulating immune responses under various initial parameter conditions, the model suggests hypotheses for future experimental investigation and contributes to the mechanistic understanding of immunogenicity. With future experimental validation, this model may potentially provide a platform to generate and test hypotheses about immunogenicity risk assessment and ultimately aid in immunogenicity prediction.

With the rapid expansion of therapeutic proteins into an important class of medicines, the issue of unwanted immunogenicity has stimulated much research effort and regulatory attention. The consequences of immunogenicity, in particular the induction of antidrug antibodies (ADA), have the potential to become a serious issue during drug development, due to their impact on drug pharmacokinetics (PK), efficacy, and/or safety.1 Immunogenicity involves complex biological mechanisms, which could span multiple system scales, from subcellular processing and cellular interaction, to organ and whole-body functions. Although various techniques have been developed to assess the immunogenicity risk of therapeutic proteins,2,3,4,5,6,7 success in predicting immunogenicity is still not prevalent, due to the involvement of complicated mechanisms and large numbers of impacting factors.

Mathematical modeling may serve as a complementary approach to help understand immunogenicity, since it can quantitatively recapitulate, and especially integrate, complicated mechanisms. Mathematical models for the immune system mainly involve two categories of modeling techniques, differential equations (DEs) and agent-based models. DEs have a long history in modeling the immune system. For example, Bell8 developed a mathematical model for B-cell clonal selection and antibody production as early as 1970. Recently, the adaptive immune response to influenza A virus infection was modeled.9 Conversely, agent-based models are a more recent approach and model each entity (e.g., an immune cell) as an “agent,” which adapts its behaviors over time (e.g., movement and differentiation) based on rules that have stochastic components. Some recent examples include ImmunoGrid, an integrated large-scale agent-based model environment to simulate the human immune system,10,11 C-ImmSim, an agent-based simulator that combines computational immunology with bioinformatics,12,13 and the Basic Immune Simulator.14,15 One limitation for agent-based models is that they tend to require larger number of parameters than their DE counterparts, so it is often difficult for sufficient experimental data to be acquired to inform the model.16 Given the comparatively long experience with DE models, we developed our model using DEs, to minimize the number of required parameters. An added benefit of a DE model is that it can be easily integrated with downstream applications more traditional in drug discovery and development, such as PK/PD modeling.

The objective of this work was to establish a multiscale, mechanistic model that can capture the key underlying mechanisms for immunogenicity against antigenic therapeutic proteins. To focus on the essential model components, while having the potential for modular expansion, this model considers the antigen-presenting cells, CD4+ T helper cells, and B cells as the major immune cells. Since dendritic cells (DCs) are the most efficient antigen-presenting cells,17 they were chosen to represent all antigen-presenting cells in the model. DC activation could be driven by maturation/danger signals that are either signs of pathogen presence, e.g., endotoxin18 or by tissue damage upon drug administration. Due to the complexity of this process and the unavailability of many parameters, DC activation was simplified and modeled as being directly driven by endotoxin, particularly, lipopolysaccharide, which is widely used in immunology studies to activate DCs19 and is known to be present in many therapeutic protein dose forms.20 Once the DCs become activated, they uptake and process the therapeutic protein, in this context the antigen (Ag), and present the T-epitope from the Ag for subsequent T-cell activation. These processes are collectively called “antigen presentation,” a critical step for efficient activation of the adaptive immune system, which ultimately evokes ADA production and immune memory. Efficient antigen presentation eventually leads to the activation, proliferation, and differentiation of T and B cells, as well as the secretion of ADA that modify the in vivo disposition of Ag. Although B-cell activation can be T cell dependent or independent,21 the current model focuses on the first, because it leads to more robust antibody response with affinity maturation and isotype switching and is associated with more impactful clinical observations, such as high and persistent antibody titer.21

Our model was developed for mouse and human using species-specific parameters. When applied to simulate primary and secondary immune responses, the model was able to reasonably reproduce many immunological phenomena, such as enhanced secondary immune response and antibody affinity maturation. It was also applied to generate hypotheses regarding potential important factors for immunogenicity development, including T-epitope affinity, Ag dose, and naïve T- and B-cell number, and suggested directions for future investigation. We believe that its current structure and features make this system model suitable to mechanistically study the immunogenicity of therapeutic proteins.

Results

Mathematical model

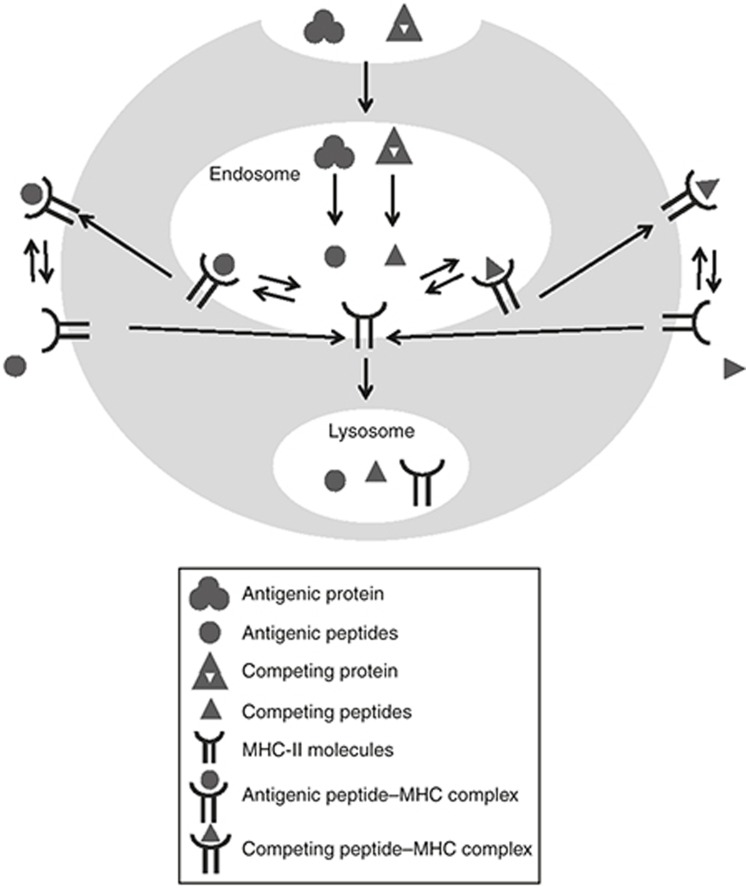
The multiscale model structure can be represented by the subcellular, cellular, and whole-body levels (Figures 1,Figures 2,Figure 3): The subcellular model, capturing antigen presentation processes in mature DCs (Figure 1), is built upon the work by Agrawal and Linderman.22 It is assumed that, when the mature DCs are first generated, no antigen presentation has happened, and all free major histocompatibility complex (MHC) molecules are located in the endosome.23 Antigenic proteins are then endocytosed into the endosomes of DCs and are digested into T-epitope peptides, which subsequently bind to MHC-II to appear on DC surfaces as T-epitope–MHC complexes for T-cell activation. The processing and presentation of endogenous competing proteins by DCs are also modeled, to reflect the fact that endogenous peptides can compete with T-epitopes for antigen presentation. To reproduce the physiology of MHC-II, our model includes six classical human MHC-II (2 HLA-DR, 2 HLA-DP, and 2 HLA-DQ) and two classical mouse MHC-II (H-2A(I-A) and H-2E(I-E) subclasses). The idea to model antigen presentation in detail is motivated by the availability of parameters for these processes, including, for example, in silico T-epitope prediction and experimental measurements of their MHC-binding affinities.24 These Ag-specific parameters can be fed to the model to simulate Ag-specific immune response. In addition, by capturing the genotype of MHC-II in the model, it is possible to simulate host/subject-specific immune responses based on the MHC-II alleles each subject carries.

Figure 1.

Figure 1

Open in a new tab

Model structure for the subcellular level, including processes for antigen presentation in mature dendritic cells. The symbols in the figure legends are described below, with corresponding equation number in Supplementary Materials shown between parentheses. Inline graphic: Antigenic protein, including antigenic protein in plasma (Ag, Eq. 27 in Supplementary Material) and antigenic protein in the endosome: (AgE, Eq. 4 in Supplementary Material); Inline graphic: antigenic peptide in endosome (pjE, Eq. 5 in Supplementary Material); Inline graphic: competing protein in the endosome (cpE, Eq. 9 in Supplementary Material); Inline graphic: competing peptide in the endosome (cptE, Eq. 10 in Supplementary Material); Inline graphic: MHC-II molecules, including those in the endosome (MEk, Eq. 6 in Supplementary Material) and those on dendritic cell membrane (Mk, Eq. 13 in Supplementary Material); Inline graphic: antigenic peptide-MHC complex, including those in the endosome (pjMEk, Eq. 7 in Supplementary Material) and those on cell membrane (pjMk, Eq. 8 in Supplementary Material); Inline graphic: competing peptide-MHC complex, including those in the endosome (cptMEk, Eq. 11 in Supplementary Material) and those on cell membrane (cptMk, Eq. 12 in Supplementary Material).

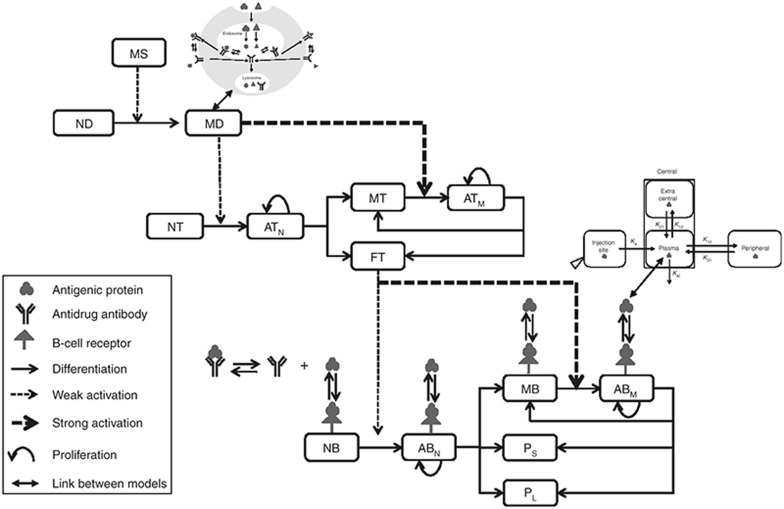
Figure 2.

Figure 2

Open in a new tab

Model structure for the cellular level, including cells, antigen, antidrug antibody, and B-cell receptor. The links between the three levels of the multiscale model are also illustrated to help interpretation. The acronyms are explained below, along with the corresponding equation number in the Supplementary Material shown between parentheses. MS: maturation signal (Eq. 1 in Supplementary Material); ID: immature dendritic (Eq. 2 in Supplementary Material); MD: mature dendritic (Eq. 3 in Supplementary Material); NT: naïve T (Eq. 14 in Supplementary Material); ATN: activated T from naïve T (Eq. 15 in Supplementary Material); ATM: activated T from memory T (Eq. 16 in Supplementary Material); MT: memory T (Eq. 17 in Supplementary Material); FT: functional T (Eq. 18 in Supplementary Material); NB: naïve B (Eq. 19 in Supplementary Material); ABN: activated B from naïve B (Eq. 20 in Supplementary Material); ABM: activated B from memory B (Eq. 21 in Supplementary Material); MB: memory B (Eq. 22 in Supplementary Material); PS: short-lived plasma (Eq. 23 in Supplementary Material); PL: long-lived plasma cell (Eq. 24 in Supplementary Material).

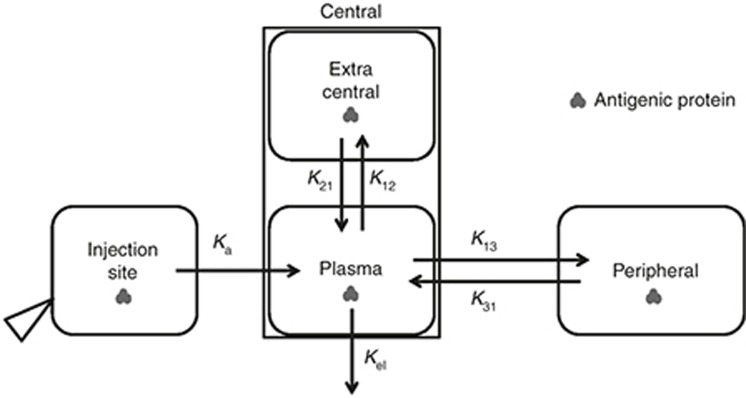
Figure 3.

Figure 3

Open in a new tab

Model structure for the whole-body level, accounting for the in vivo disposition of antigenic protein. Details are described in the Results section and also by Eqs. 26–29 in the Supplementary Materials.

The cellular level accounts for immune cells kinetics. At the cellular level (Figure 2), DCs serve as a connection between the innate and the adaptive immune system, by presenting T-epitopes for the activation of corresponding naïve helper T cells. Once the Ag-specific naïve T cells are activated by the DCs, they proliferate and differentiate into functional T cells to facilitate downstream B-cell activation or give rise to memory T cells that can be immediately activated via interacting with antigen-presenting DCs. Subsequently, antigen-specific naïve B cells, which recognize Ag through B-cell receptor, were fully activated upon stimulations from functional T cells and Ag-bound B-cell receptor. Activated B cells proliferate and differentiate into short-lived and long-lived plasma cells, as well as memory B cells. The plasma cells secrete ADA that modifies antigenic protein elimination, while the memory B cells behave similarly as naïve B cells and immediately react to an antigen challenge.

The whole-body level accounts for therapeutic protein in vivo disposition (Figure 3). The PK profile of therapeutic proteins is usually modeled by empirical compartmental models, which lump rapidly equilibrated tissues for drug distribution into a single compartment. In the current model, plasma is modeled as the space for the immune cells to reside and for the antigenic proteins to interact with the immune system, by assuming that lymphocyte move fast between lymph organs and the blood. To accurately describe the PK of the antigen, while modeling interaction between the Ag and the immune system, a modified compartmental model was constructed. An extended two-compartment model is illustrated as an example. A peripheral compartment includes slowly perfused tissues, as is usually done. The central compartment generally includes plasma and other rapidly perfused tissues and therefore can be regarded as the sum of plasma volume (Vp) and any extra volume in the central compartment (Vec). It is assumed that plasma and the extracentral compartment equilibrate very fast. By fitting the PK profile of the antigenic protein using this modified compartment model, the rate constants (k13, k31, and kel) and Vec can be estimated (once plasma volume and plasma to extracentral rate constants are assumed). Then, the modified compartmental model can be integrated into the rest of the mechanistic model to specifically model the Ag in vivo disposition.

The model details are provided in the Supplementary Materials, with the following organization:

  1. DC activation and differentiation;

  2. Antigen presentation by DCs;

  3. T-helper cell activation and differentiation;

  4. B-cell activation and differentiation;

  5. ADA in vivo disposition;

  6. Antigenic protein in vivo disposition.

The definitions of all model variables and parameters are provided in Supplementary Tables S1 and S2. By using the same model structure, but species-specific parameters, the model can be used to simulate immune responses in mouse and human. Parameters were collected from the literature as much as possible. More parameters are available for mouse compared with human: when there is no reference for human-specific parameters, the current model assumes that they are the same as the mouse parameters. The software Matlab (The MathWorks, Natick, MA) was used for model implementation and for the simulations described below.

Simulation of immune responses in human against a hypothetical antigen

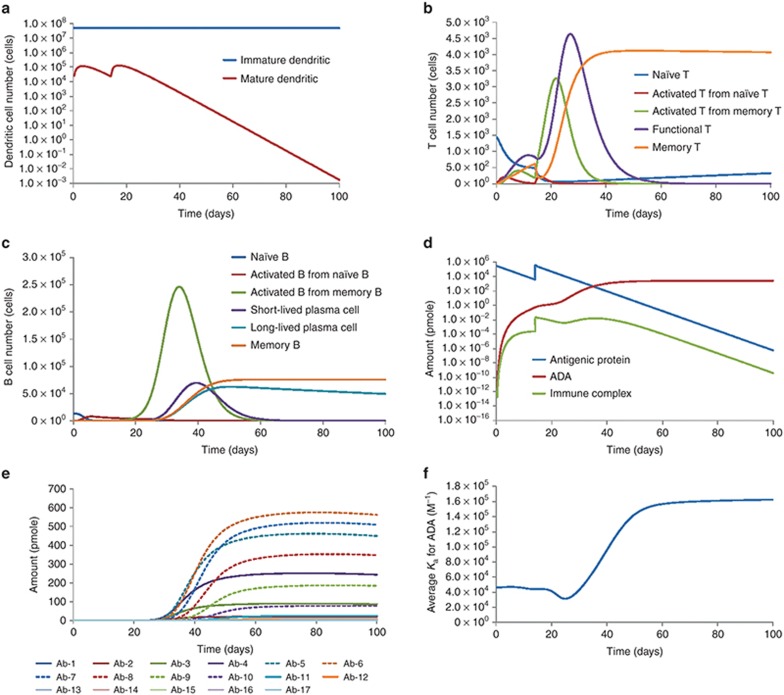
By inputting antigen-specific parameters for a hypothetical antigenic therapeutic protein, the basic model could simulate the human kinetic profiles for DCs, T cells, B cells, ADA, and average ADA affinity upon the injection of antigenic protein (Figure 4). In addition, the antigen presentation processes, including the internalization, processing, and presentation of antigenic protein and competing protein, are also captured by the model (Supplementary Figure S1). For this particular antigenic protein, the model predicts the generation of strong immune responses, reflected by the rapid activation and proliferation of immune cells, and the production of high level of ADA. The model also predicts greatly enhanced immune response upon secondary immunization, consistent with the immune memory phenomenon. The average antigen-binding affinity of ADA was also calculated to increase over time, which agrees with the antibody affinity maturation phenomenon observed after immunization.

Figure 4.

Figure 4

Open in a new tab

Simulation results of immune responses in human against a theoretical antigenic protein. The results include kinetic profiles for (a) dendritic cells; (b) helper T cells; (c) B cells; (d) antigenic protein, ADA, and immune complex; (e) polyclonal ADA (total 17 clones, whose antigen-binding affinity increases by twofold between clones, from clone 1 to clone 17); (f) average antigen-binding affinity of ADA. ADA, antidrug antibody.

Simulation of immune responses in human under various immune system conditions

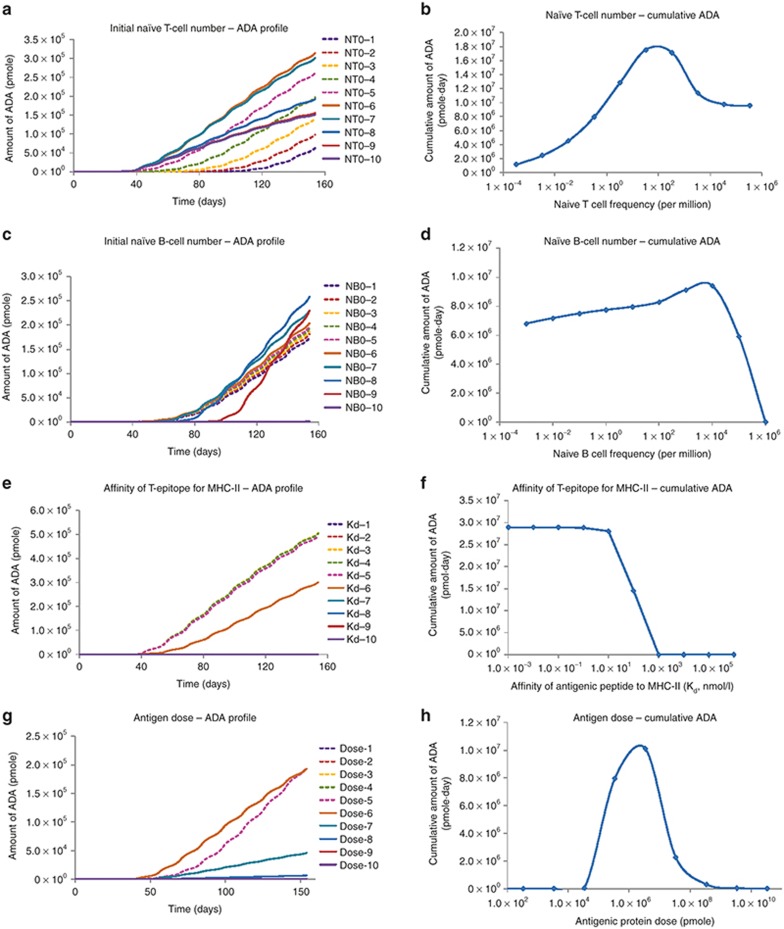
Several potential impacting factors for immunogenicity development, including naïve T-cell number, naïve B-cell number, binding affinity of T-epitopes to MHC-II, antigen dose, were tested for their impact on ADA generation by changing the parameter values over physiologically plausible range. The ADA kinetic profiles and the cumulative amount of ADA under various parameter conditions were summarized in Figure 5. The naïve T-cell number has a significant impact on the magnitude and the timing of ADA generation. The cumulative ADA response as a function of naïve T-cell number exhibited a bell shape (Figure 5b). In addition, a greater naïve T-cell number generally leads to a faster rise of the ADA (Figure 5a), with the earliest rising time around 40 days. In contrast, naïve B-cell number has less impact on ADA generation (Figure 5d). Within the normal parameter range (from 10–7 % to 101 % of total B cells), the cumulative ADA amounts varied only within twofold. Only when excessive number of naïve B cells are present (10–100% of total B cells), the amount of ADA drops dramatically. The binding affinities for T-epitopes (dissociation constant, Kd) demonstrate a strong impact on ADA magnitude, with the most sensitive range of 1 nmol/l to 1 µmol/l (Figure 5f). Ag dose also exhibited a bell-shaped relationship with the amount of ADA generated (Figure 5g,h).

Figure 5.

Figure 5

Open in a new tab

Model simulated ADA responses under physiologically plausible range of parameter values. (a,c,e,g) Model simulated kinetic profiles for ADA.(b,d,f,h) Cumulative amount of ADA during the simulation time against parameters of interest. The parameters of interest are: panels a and b, initial naïve T-cell number; panels c and d, initial naïve B-cell number; panels e and f, affinity of T-epitope for MHC-II; panels g and h, antigen dose. The numbers 1 to 10 on the left panels stand for 10 different parameter conditions, from low to high amounts. More details can be found in the Methods section. ADA, antidrug antibody.

Sensitivity analysis

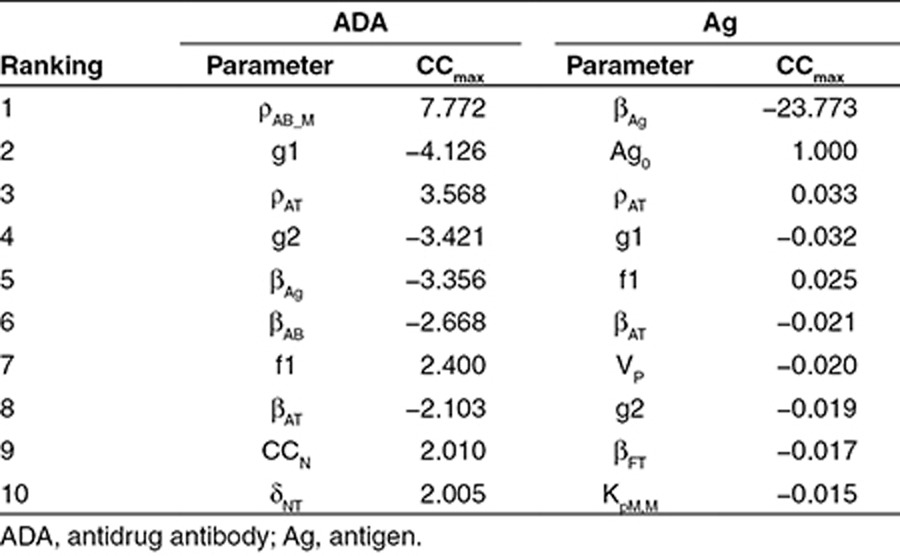
A sensitivity analysis for the Ag amount and the total ADA amount was performed against model parameters. The top 10 sensitive parameters are listed in Table 1. Six parameters are shared between Ag and ADA, including rate constants for the proliferation and death of activated T cells (ρAT, βAT), differentiation fraction of T cells (f1) and B cells (g1, g2), and elimination rate of the Ag (βAg). The other four parameters that have high sensitivity on ADA response are involved in T-cell activation (δNT), B-cell proliferation and death (ρAB_N, βAB), and T-cell–B-cell interaction (CCN). The other four sensitive parameters for Ag response include Ag PK parameters (Ag0, VP), number of T-epitope–MHC on DCs for half-maximum T-cell activation (KpM,M), and death rate for functional T cell (βFT).

Table 1. Sensitivity analysis: top 10 sensitive parameters.

graphic file with name psp201430t1.jpg

Open in a new tab

Discussion

By integrating key biological mechanisms for immunogenicity development, a mathematical model was developed for simulating humoral immune responses against antigenic therapeutic proteins. The model can reasonably reproduce many immunological phenomena, such as the enhanced secondary immune response, antibody affinity maturation, and antigen presentation. Figure 4 illustrates the simulation results for immune responses in human against two doses of a therapeutic protein. Notably, upon the secondary immune challenge, the magnitude of the immune response (number of immune cells, amount of ADA) is much higher than the primary response, consistent with the notion of immune memory. The model behavior for enhanced secondary immune response was achieved by the following model features: (i) incorporating memory T and memory B cells, which can get activated, proliferated, and differentiated into functional cells upon antigen stimulation; (ii) assigning lower activation threshold for memory cells compared to naïve cells25,26; (iii) assigning higher proliferation rate for activated memory B cells compared to activated naïve B cells.27 Another interesting result is the time profile of the average ADA affinity (Figure 4f), which gradually increases over time. This model behavior is achieved by treating the B-cell lineages, and the corresponding ADA, as polyclonal populations with different antigen-binding affinities. The model assumes that the activation, proliferation, and differentiation of B cells are dependent on the B-cell receptor occupancy, which is affected by their antigen-binding affinity. Therefore, when the amount of antigen is limited, B cells that have higher receptor-binding affinity to the antigen will be preferentially activated, producing ADA with higher average affinities over time.

After confirming that the model behaviors are reasonable, we also investigated the impact of several parameters of interest on the ADA responses, by changing the parameter values over a wide, physiologically plausible range (Figure 5).

Four parameters, including the number of naïve T cells, number of naïve B cells, MHC-binding affinity of T-epitope, and Ag dose, were studied in the simulation. Although not routinely assessed for immunogenicity risk, the naïve T- and B-cell numbers were probably important; this would be expected, since more naïve cells likely better prepare the immune system against antigen challenge. Interestingly, the model suggests that a bigger impact on ADA response may come from the number of naïve T cells, rather than naïve B cells (Figure 5b,d). The results indicate that a sufficient number of naïve T cells needs to be present to efficiently initiate an immune response, while the initial naïve B-cell number is not as critical. Even a small number of naïve B cells can be activated and proliferate to a sufficient size for mounting ADA response, as long as enough stimulation (T cells and Ag) is present. Studies have suggested that the size of naïve T-cell repertoire can vary dramatically depending on the antigenic T-epitope.28,29,30 Our result emphasizes the potential importance of measuring naïve T-cell number when assessing the immunogenicity risk of therapeutic proteins. The model simulations also indicate that excessive amounts of naïve T and B cells may cause the expected immune response to decline, rather than to increase (Figure 5b,d). This model behavior is caused by competition for resources, such as competing for DC help among T cells or competing for T-cell help and for antigen stimulation among B cells. Under the current simulation settings, frequencies to achieve the peak response are around 102 per million for naïve T and around 104 per million for naïve B cells.

MHC-binding affinity of T-epitope also demonstrated strong impact on the ADA response (Figure 5e,f). The simulation shows that higher MHC-binding affinity generally leads to greater ADA response, because of the higher number of peptide-MHC presented on DCs. Under the current settings, the sensitive affinity range for T-epitope is between 1 nmol/l and 1 µmol/l (dissociation constant, Kd), suggesting that T-epitopes with Kd weaker than 1 µmol/l are unlikely to induce strong immune response, while epitopes with very strong binding (Kd stronger than 1 nmol/l) probably have reached a plateau for inducing response. Interestingly, under the current simulation, the suggestion of 1 µmol/l as a weak binding affinity agrees with other publications' cutoff for binders vs. no-binders for class II T-epitope prediction and shows biological relevance.31,32

Lastly, the dose of the antigenic protein is a recognized impacting factor for immunogenicity development.33 In our simulation, a bell-shaped antigen dose–ADA response curve was obtained (Figure 5g,h), suggesting that the model can reasonably capture the immune tolerance phenomenon. As demonstrated above, the model can potentially be applied to formulate or test hypotheses related to immunogenicity development, by modifying the model components or changing the parameter values.

In order to identify sensitive model parameters for ADA and Ag kinetics, sensitivity analysis was performed for the model with human parameters (Table 1). Overall, ADA kinetics is much more sensitive to model parameters than Ag kinetics (except that, as expected, Ag kinetics is very sensitive to antigen elimination rate, βAg). This is reasonable when we consider that the model is constructed for simulating ADA response, so its parameter values have more direct impact on ADA kinetics, while the impact on Ag kinetics is mostly secondary, through the formation of immune complexes. The sensitivity analysis indicates that the activation, proliferation, and differentiation of helper T cells and B cells are critical processes in the development of immunogenicity, and these parameter values have a big impact on the model outcome. It would be helpful to further confirm these parameter values by doing controlled in vitro or in vivo experiments in the future.

The current model represents a starting point and has potential for future development. For example, while plasma is assumed as the space for the immune response, ideally the site of action should also include lymphoid organs such as lymph nodes, spleen, and bone marrow, where various immune reactions such as antigen presentation, clonal selection, and long-lived plasma cell survival take place. DC activation is modeled rather empirically in the current settings. Upon the availability of more information to expand this module, the LPS activation signal could be replaced or complemented by other danger signals, e.g., tissue damage on injection. Some human-specific parameter values are directly taken from mouse values, and they may be properly scaled from mouse to human or be determined by performing appropriate experiments.

Several features of this model should be highlighted. First, the model recapitulates and integrates essential biological components and mechanisms for the development of immunogenicity and provides a wide spectrum of predictions for the kinetics of the immune system. Second, the model simulations agree with many known immunological phenomena, such as immune memory, antibody affinity maturation, and immune tolerance. Last but not least, the model was developed by incorporating both antigen- and host-specific characteristics, since immunogenicity ultimately depends on both the antigenic properties of the protein and the immunological environment of the host. Antigen-specific characteristics, such as T- and B-epitope content and affinity, and host-specific characteristics, such as MHC-II genotype and naïve T- and B-cell numbers, are designed as potential inputs for simulation. Since many antigen or host characteristics can be obtained from experimental approaches, the model can potentially be applied to quantitatively integrate results from immunogenicity assessment studies and provide simulations/predictions about the putative immune responses in human.

In summary, a novel multiscale, mechanistic model was constructed for the development of immunogenicity against antigenic/therapeutic proteins, by mathematically describing key underlying mechanisms and collecting physiologically plausible parameters from scientific publications. As a result, the current model simulations reasonably agree with many accepted immunological phenomena. Here, we used the model to formulate and test some hypotheses on influential factors for immunogenicity. We believe that the model can be explored to potentially serve as a supplemental tool to aid immunogenicity risk assessment, by quantitatively integrating protein- or patient-specific information from in vitro and in vivo experiments or from clinical studies.

Methods

Simulation of immune responses in human against a hypothetical antigen

The in vivo immune responses in human against a hypothetical antigenic protein were simulated. The protein, with molecular weight of 150 kD, and a half-life of 2 days, was injected i.v. at 50 mg/kg on day 0 and day 14. It is assumed that one promiscuous T-epitope is present on this protein, which binds to three of the six MHC-II molecules for one human subject, with a strong binding affinity of 150 nmol/l. Assumptions are also made for antigen-specific naïve T and B cells, with naïve T-cell frequency at 0.33 per million and B-cell frequency at 10 per million. Other parameters are kept the same as the generic human parameter set. The simulation was run for 100 days from day 0, and the kinetics for cell populations, antigen presentation, antigenic protein, ADA, and immune complex were recorded.

Simulation of immune responses in human under various immune system conditions

To explore the model behavior while changing the values of several factors of interest, the corresponding parameters were varied within a large range. The factors tested included naïve T-cell number (NT0), naïve B-cell number (NB0), antigenic protein dose (Ag0), and T-epitope–binding affinity against MHC-II (Kd). The naïve T-cell frequency ranges from 3.3 10–4 to 3.3 105 per million, and the naïve B-cell frequency ranges from 10–3 to 106 per million. The antigenic protein doses are from 3.3 × 101 to 3.3 × 1010 pmol, while the MHC-II–binding affinities (Kd = koff/kon) of T-epitope are from 10–3 to 106 nmol/l. The other model parameters were adapted from the model for human response against a hypothetical protein. The ADA profiles and cumulative ADA over 154 days (area under the curve for ADA-time profile) were simulated.

Sensitivity analysis

We performed a sensitivity analysis to evaluate the impact of individual parameter values on the interested state variables. The sensitivity calculation was performed for two key state variables (amount of therapeutic protein and amount of ADA) against the system parameters. The parameter set used for sensitivity analysis is the human set.

Control coefficients are used as indicators for sensitivity. The control coefficients of variable x to parameter p (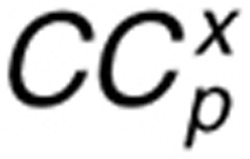Inline graphic) were calculated using the following equation34,35:

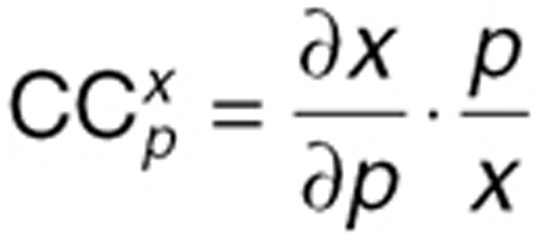graphic file with name psp201430e2.jpg

The finite difference method was used to approximate the derivative in the above equation, where h is the step size:

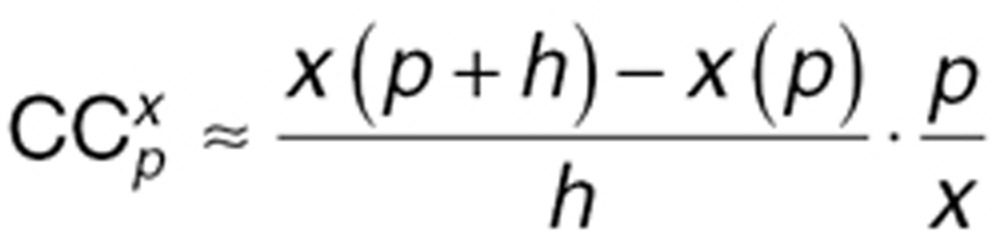graphic file with name psp201430e3.jpg

The step size h was chosen as h = 1%·p, because 1% increase in the value of p has been shown to yield numerically stable results.34 We reported CCmax, the 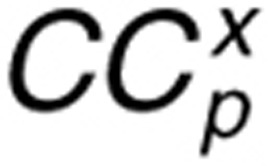Inline graphicvalue with the maximum absolute value over the time course of the system. A positive CCmax suggests that the parameter increase results in a increase in x value, while a negative CCmax means that the parameter increase causes a decrease in x value.

Author contributions

X.C., T.P.H., and P.V. wrote the manuscript. X.C., T.P.H., and P.V. designed the research. X.C., T.P.H., and P.V. performed the research.

Conflict of Interest

X.C., T.P.H., and P.V. are employed by Pfizer. X.C., T.P.H., and P.V. hold stock in Pfizer. Associate Editor P.V. was not involved in the review or decision process for this paper.

Study Highlights

graphic file with name psp201430i1.jpg

Acknowledgments

We would like to thank Bonita Rup for her valuable suggestions on the manuscript, and thank Mary Spilker and Michael Zager for their help during the model building processes. Portions of this work were presented at the 2013 AAPS National Biotechnology Conference, 20–22 May 2013, San Diego, CA (Poster Abstract NBC-13-0644).

Supplementary Material

Supplementary Figure S1
Click here for additional data file. (319.5KB, doc)
Supplementary Tables S1
Click here for additional data file. (84.4KB, pdf)
Supplementary Tables S2
Click here for additional data file. (166.4KB, pdf)
Supplementary Materials
Click here for additional data file. (2MB, doc)

References

  1. Chirmule N., Jawa V., Meibohm B. Immunogenicity to therapeutic proteins: impact on PK/PD and efficacy. AAPS J. 2012;14:296–302. doi: 10.1208/s12248-012-9340-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Justesen S., Harndahl M., Lamberth K., Nielsen L.L., Buus S. Functional recombinant MHC class II molecules and high-throughput peptide-binding assays. Immunome Res. 2009;5:2. doi: 10.1186/1745-7580-5-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Burshtyn D.N., Barber B.H. Dynamics of peptide binding to purified antibody-bound H-2Db and H-2Db beta 2m complexes. J. Immunol. 1993;151:3082–3093. [PubMed] [Google Scholar]
  4. Kruisbeek A.M., Shevach E., Thornton A.M. Proliferative assays for T cell function. Curr. Protoc. Immunol. 2004;Chapter 3:Unit 3.12. doi: 10.1002/0471142735.im0312s60. [DOI] [PubMed] [Google Scholar]
  5. Wullner D., et al. Considerations for optimization and validation of an in vitro PBMC derived T cell assay for immunogenicity prediction of biotherapeutics. Clin. Immunol. 2010;137:5–14. doi: 10.1016/j.clim.2010.06.018. [DOI] [PubMed] [Google Scholar]
  6. Tonomura N., Habiro K., Shimizu A., Sykes M., Yang Y.G. Antigen-specific human T-cell responses and T cell-dependent production of human antibodies in a humanized mouse model. Blood. 2008;111:4293–4296. doi: 10.1182/blood-2007-11-121319. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Steinitz K.N., et al. CD4+ T-cell epitopes associated with antibody responses after intravenously and subcutaneously applied human FVIII in humanized hemophilic E17 HLA-DRB1*1501 mice. Blood. 2012;119:4073–4082. doi: 10.1182/blood-2011-08-374645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bell G.I. Mathematical model of clonal selection and antibody production. J. Theor. Biol. 1970;29:191–232. doi: 10.1016/0022-5193(70)90019-6. [DOI] [PubMed] [Google Scholar]
  9. Lee H.Y., et al. Simulation and prediction of the adaptive immune response to influenza A virus infection. J. Virol. 2009;83:7151–7165. doi: 10.1128/JVI.00098-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Halling-Brown M., et al. ImmunoGrid: towards agent-based simulations of the human immune system at a natural scale. Philos. Trans. A. Math. Phys. Eng. Sci. 2010;368:2799–2815. doi: 10.1098/rsta.2010.0067. [DOI] [PubMed] [Google Scholar]
  11. Pappalardo F., et al. ImmunoGrid, an integrative environment for large-scale simulation of the immune system for vaccine discovery, design and optimization. Brief. Bioinform. 2009;10:330–340. doi: 10.1093/bib/bbp014. [DOI] [PubMed] [Google Scholar]
  12. Woelke A.L., von Eichborn J., Murgueitio M.S., Worth C.L., Castiglione F., Preissner R. Development of immune-specific interaction potentials and their application in the multi-agent-system VaccImm. PLoS One. 2011;6:e23257. doi: 10.1371/journal.pone.0023257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Rapin N., Lund O., Bernaschi M., Castiglione F. Computational immunology meets bioinformatics: the use of prediction tools for molecular binding in the simulation of the immune system. PLoS One. 2010;5:e9862. doi: 10.1371/journal.pone.0009862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Folcik V.A., An G.C., Orosz C.G. The Basic Immune Simulator: an agent-based model to study the interactions between innate and adaptive immunity. Theor. Biol. Med. Model. 2007;4:39. doi: 10.1186/1742-4682-4-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Folcik V.A., et al. Using an agent-based model to analyze the dynamic communication network of the immune response. Theor. Biol. Med. Model. 2011;8:1. doi: 10.1186/1742-4682-8-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Bauer A.L., Beauchemin C.A., Perelson A.S. Agent-based modeling of host-pathogen systems: the successes and challenges. Inf. Sci. (Ny) 2009;179:1379–1389. doi: 10.1016/j.ins.2008.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Janeway C., Travers P., Walport M., Shlomchik M.J.Immunobiology: The Immune system in Health and Disease6th edn. 321.Garland Science Publishing; New York, NY; 2005 [Google Scholar]
  18. Joffre O., Nolte M.A., Spörri R., Reis e Sousa C. Inflammatory signals in dendritic cell activation and the induction of adaptive immunity. Immunol. Rev. 2009;227:234–247. doi: 10.1111/j.1600-065X.2008.00718.x. [DOI] [PubMed] [Google Scholar]
  19. Foti M., et al. Upon dendritic cell (DC) activation chemokines and chemokine receptor expression are rapidly regulated for recruitment and maintenance of DC at the inflammatory site. Int. Immunol. 1999;11:979–986. doi: 10.1093/intimm/11.6.979. [DOI] [PubMed] [Google Scholar]
  20. Verthelyi D., Wang V. Trace levels of innate immune response modulating impurities (IIRMIs) synergize to break tolerance to therapeutic proteins. PLoS One. 2010;5:e15252. doi: 10.1371/journal.pone.0015252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. De Groot A.S., Scott D.W. Immunogenicity of protein therapeutics. Trends Immunol. 2007;28:482–490. doi: 10.1016/j.it.2007.07.011. [DOI] [PubMed] [Google Scholar]
  22. Agrawal N.G., Linderman J.J. Mathematical modeling of helper T lymphocyte/antigen-presenting cell interactions: analysis of methods for modifying antigen processing and presentation. J. Theor. Biol. 1996;182:487–504. doi: 10.1006/jtbi.1996.0190. [DOI] [PubMed] [Google Scholar]
  23. Ma J.K., Platt M.Y., Eastham-Anderson J., Shin J.S., Mellman I. MHC class II distribution in dendritic cells and B cells is determined by ubiquitin chain length. Proc. Natl. Acad. Sci. USA. 2012;109:8820–8827. doi: 10.1073/pnas.1202977109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Zhang Q., Wang P., Kim Y., Haste-Andersen P., Beaver J., Bourne P.E., et al. Immune epitope database analysis resource (IEDB-AR) Nucleic Acids Res. 2008;36:W513–W518. doi: 10.1093/nar/gkn254. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Yefenof E., Sanders V.M., Uhr J.W., Vitetta E.S. In vitro activation of murine antigen-specific memory B cells by a T-dependent antigen. J. Immunol. 1986;137:85–90. [PubMed] [Google Scholar]
  26. Kimachi K., Croft M., Grey H.M. The minimal number of antigen-major histocompatibility complex class II complexes required for activation of naive and primed T cells. Eur. J. Immunol. 1997;27:3310–3317. doi: 10.1002/eji.1830271230. [DOI] [PubMed] [Google Scholar]
  27. Tangye S.G., Avery D.T., Deenick E.K., Hodgkin P.D. Intrinsic differences in the proliferation of naive and memory human B cells as a mechanism for enhanced secondary immune responses. J. Immunol. 2003;170:686–694. doi: 10.4049/jimmunol.170.2.686. [DOI] [PubMed] [Google Scholar]
  28. Bacher P., et al. Antigen-reactive T cell enrichment for direct, high-resolution analysis of the human naive and memory Th cell repertoire. J. Immunol. 2013;190:3967–3976. doi: 10.4049/jimmunol.1202221. [DOI] [PubMed] [Google Scholar]
  29. Geiger R., Duhen T., Lanzavecchia A., Sallusto F. Human naive and memory CD4+ T cell repertoires specific for naturally processed antigens analyzed using libraries of amplified T cells. J. Exp. Med. 2009;206:1525–1534. doi: 10.1084/jem.20090504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Delluc S., Ravot G., Maillere B. Quantitative analysis of the CD4 T-cell repertoire specific to therapeutic antibodies in healthy donors. FASEB J. 2011;25:2040–2048. doi: 10.1096/fj.10-173872. [DOI] [PubMed] [Google Scholar]
  31. Wang P., et al. Peptide binding predictions for HLA DR, DP and DQ molecules. BMC Bioinformatics. 2010;11:568. doi: 10.1186/1471-2105-11-568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Southwood S., et al. Several common HLA-DR types share largely overlapping peptide binding repertoires. J. Immunol. 1998;160:3363–3373. [PubMed] [Google Scholar]
  33. Pier G., Lyczak J.B. Immunology, Infection, and Immunity. 2004. pp. 196–197.
  34. Zager M.G., Barton H.A. A multiscale, mechanism-driven, dynamic model for the effects of 5α-reductase inhibition on prostate maintenance. PLoS One. 2012;7:e44359. doi: 10.1371/journal.pone.0044359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lee E., Salic A., Krüger R., Heinrich R., Kirschner M.W. The roles of APC and Axin derived from experimental and theoretical analysis of the Wnt pathway. PLoS Biol. 2003;1:E10. doi: 10.1371/journal.pbio.0000010. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure S1
Click here for additional data file. (319.5KB, doc)
Supplementary Tables S1
Click here for additional data file. (84.4KB, pdf)
Supplementary Tables S2
Click here for additional data file. (166.4KB, pdf)
Supplementary Materials
Click here for additional data file. (2MB, doc)

Articles from CPT: Pharmacometrics & Systems Pharmacology are provided here courtesy of Wiley

RESOURCES