Abstract
Circular migrations are the periodic movement of individuals between multiple locations, observed in parts of sub-Saharan Africa. Relationships between circular migrations and HIV are complex, entailing interactions between migration frequency, partnership structure, and exposure to acute HIV infection. Mathematical modeling is a useful tool for understanding these interactions.
Two modeling classes have dominated the HIV epidemiology and policy literature for the last decade: one a form of compartmental models, the other network models. We construct models from each class, using ordinary differential equations and exponential random graph models, respectively.
Our analysis suggests that projected HIV prevalence is highly sensitive to the choice of modeling framework. Assuming initial equal HIV prevalence across locations, compartmental models show no association between migration frequency and HIV prevalence or incidence, while network models show that migrations at frequencies shorter than the acute HIV period predict greater HIV incidence and prevalence compared to longer migration periods. These differences are statistically significant when network models are extended to incorporate a requirement for migrant mens multiple partnerships to occur in different locations. In settings with circular migrations, commonly-used forms of compartmental models appear to miss key components of HIV epidemiology stemming from interactions of relational and viral dynamics.
Key words and phrases: Circular migrations, HIV transmission modeling, compartmental models, network models, Exponential Random Graph Models (ERGMs)
1. Introduction
1.1. Background and Motivation
Circular migrations – the periodic movement of individuals between two (or more) places [58], often between home and labor sites – is a relatively common practice in some countries in sub-Saharan Africa (for example South Africa [42, 46]). The relationship between circular migrations and HIV has been the focus of much recent epidemiological work in multiple countries (e.g. South Africa [43–45], Kenya [5], Zimbabwe [12,54], and Tanzania [11]). These relationships are complex [15, 46, 50]), with circular migration providing multiple mechanisms that have the potential to amplify HIV transmission in a population. While the epidemiological implications of coupling between two disconnected areas due to movement has been studied before [34], the partnerships of circularly migrant individuals have certain novel features (described in detail below), and the precise mechanisms that potentially amplify the impact of circular migrations on sexually transmitted infection are not fully understood. Modeling provides a useful approach to improve our understanding of these relationships, and test specific hypotheses (e.g. the association between migration frequency and HIV prevalence and incidence).
A recent review demonstrated that of the HIV transmission models developed for public health planning, about 87% were deterministic compartmental models [32], which are formulated using ordinary differential equations. Compartmental models have a rich history in helping researchers answer many questions about HIV transmission [48, 49], and continue to be the “work-horse” of model development [10]. Adaptations of these models are continuously being developed to answer contemporary questions in the epidemiology of HIV [2,4,7,18,19,21–24,35,55,59,60,65,69]. In compartmental models for HIV, compartments typically represent counts of individuals, with the relationships implicit within the calculation of the “force-of-infection” terms for the transition from susceptibles to infected. Further theoretical elaborations for modeling contact structure within the compartmental framework, based on the use of compartments representing pairs or triads of individuals, were developed earlier on in the HIV epidemic [16, 17, 28], although have played little subsequent role in the applied HIV modeling literature (with one recent exception [57];) we return to these in the discussion.
As per Johnson and White’s review [32], the other models used to inform policy decisions concerning HIV are stochastic. Network-based models are a particular formulation of stochastic models, and represent an alternative approach toward understanding HIV transmission. One value they add is to relax the “mass-action” assumptions of compartmental models [38] through explicit representation of actors, their attributes and infection transmission within partnerships. Network models have been adapted to study questions pertaining to HIV transmission more recently than compartmental models [14,20,25,27,53,61,66]. Although computationally intensive, the network modeling approach is able to capture a wider range of characteristics of the individuals and their partnerships in the model. As a consequence, modelers are periodically faced with the question of whether network models (with their additional computational complexity) are worth the extra time and effort.
This subset of model types (deterministic compartmental models and stochastic network models) collectively represent the commonly used toolkit for modeling the epidemiology of HIV and for determining HIV-related policy in settings like South Africa where circular migration is common. We thus explore the same set of model types in our investigations of circular migrations, and their impact on HIV transmission. Our two goals, then, are to understand the relationships between migration frequency and HIV transmission; and to identify apparent differences in these relationships according to the class of models used, among those commonly used in this setting.
The models we consider here help relax assumptions progressively. One value of this study is to make such assumptions explicit to future modelers, who can then assess which assumptions have large effects with respect to transmission outcomes [36]. Another benefit is to epidemiologists who might use conclusions from these analyses to design future studies to refine our understanding of circular migration [36]. Our overall goal is then best summarized as a “robustness assessment” [38] – where we demonstrate how robust conclusions in this transmission system are to underlying assumptions.
1.2. Sexual Behavior in a Circular Migration System
Movement between two locations influences the sexual behavior of circular migrants; for one, circular migrants may have the opportunity to maintain ongoing sexual partnerships at their home other partnerships in their workplace [46]. The sexual activity of migrant men at any given time is thus contingent upon their location; only partnership(s) with partners in the same location are “active” at any given time point (i.e. have a nonzero probability of a coital act at the time), while the partnership(s) in the other location are “inactive” at that time.
One epidemiological question that modeling has played a large role in addressing is the importance that concurrent, as opposed to sequential, relationships play in sustaining the generalized HIV epidemics of sub-Saharan Africa [9, 25, 39, 47, 51]. Within this literature, concurrency is defined as any case in which an individual has sex with one person temporally between two acts of sex with a second person [67]. Cases in which a circular migrant has one ongoing partner in the workplace and another in the village thus meet the definition of concurrency used in the field. However, existing models of concurrency all presume that the concurrent relations are all active simultaneously; i.e. that each one has a non-zero probability of a coital act each day. Circular migration of this type is thus distinct from either serial monogamy or from more commonly explored forms of concurrency.
Data published by Lurie et al. estimate that about 62% of men in the rural district of KwaZulu-Natal spend nights away from home [45]. While, in practice, both men and women may migrate [6, 8], more epidemiological work examining circular migrations has focused on men [42–46], and for this reason we restrict our attention to movement by men. In addition, Lurie et al. studied migrations between a rural district and two mining towns, one near the home district, and the other farther away. They observed that men who migrate close by tend to return home at least once a month, whereas those who migrate farther away generally return 3–4 times a year [46]. This theme of short and long migration intervals is central to this paper, and we will explore why these intervals are particularly important in the context of HIV transmission.
Lurie et al. also reported that about 30% of both migrant and non-migrant men report at least two current partners [44]. Additionally, the female partner was HIV-positive in about a third of serodiscordant couples in the study [45]. For some, the infection may have occurred before the initiation of this partnership, but for the remaining fraction, infection would have been acquired through a concurrent partnership. Statistical analyses also revealed migrant couples to be 2.5 times more likely than non-migrant couples to be HIV serodiscordant [45]. One modeling study has been published based on these data, employing a compartmental model [13]. This study modeled a mixture of short- and long-distance migrant men, assuming different starting prevalences between the home and the work sites (consistent with data from the Hlabisa Migration Project), and migration-associated partner change rates [13]. This study suggests that migration, if not in conjunction with riskier behavior, has almost no effect on the HIV prevalence among females, and motivated our interest in a more fundamental theoretical question: to isolate the impact of movement between disconnected areas, all other demographic, behavioral and epidemic assumptions for both locations being equal.
1.3. Acute HIV Infection
Acute HIV infection potentially plays a critical role in the impact of circular migrations on HIV transmission. Based on data presented by Wawer et al. [70], Hollingsworth et al. have estimated that the infectivity of an individual after sero-conversion is highest for a period of about 2.9 months after infection [30]. Other data sources [41] and other re-analyses of the Wawer data [1,56] differ in their numerical details but confirm higher infectiousness during acute infection. This period of acute infection is followed by a long period of stable chronic infectivity and a final, late-stage rise before death [30,70].
Circular migration systems entail unique interactions between acute infection and concurrency structures. Long-term concurrency can amplify HIV spread relative to long-term serial monogamy in multiple ways; one of these is by increasing the probability that an individual has sex with two partners in quick succession, allowing them to be infected by the first, and then transmit to the second while still in the acute stage. However, as described above, circular migration in which a man (or woman) has an ongoing partnership in two locations represents a unique form of concurrency; although circular migrants may have two partnerships that overlap in time, the risk of an individual exposing a partner to HIV during the acute stage is likely to be less than in other forms of concurrency. This reduction in risk is because a migrant, after being infected by a partner in one location, would not be expected to have sex with his other partner until he switches location. If the migration interval is sufficiently long, he would likely have passed through the stage of acute infection by that point. The magnitude of this effect, and the overall size of the epidemic, would thus be expected to be a function of intervals at which these circular migrations occur; overall size of the epidemic would be smaller at sufficiently long migration intervals.
1.4. Problem Statement
In this paper, we explicitly examine how different examples of compartmental and network models compare in their predictions of the impact of circular migrations on HIV prevalence trajectories over time, and the incidence of infection. We are particularly interested in the effect of the frequency of circular migration on the above outcomes – as demonstrated by each of our models.
2. Methods
2.1. Features Common to Compartmental and Network Models
We begin by describing the features common to all of our models, and then proceed to describe the particular features of compartmental models in Section 2.2 and network models in Section 2.3. We summarize the salient features of all our models in Table 1.
Table 1.
Salient Features of All Primary Models. Quotes (″) in a cell imply an identical entry to the cell above.
| Partnership Formation | Partnership Dissolution | Partnership Overlap | Migration | Location of Partners For Migrant Men with Multiple Simultaneous Partners | |
|---|---|---|---|---|---|
| Compartmental: Contact as Act | Relatively high to reflect that each sex act is a new partnership (represented by t in the infection model) | New partner is assumed for each act (acts are treated as separate contacts) | None | Memoryless process with mean time between migrations of 3 or 30 weeks | N/A |
| Compartmental: Contact as Partnership | Relatively low to reflect that each sex act occurs in a limited number of long-term partnerships (represented by t in the infection model) | Memoryless process with mean duration of 100 weeks | Average duration of 100 weeks is assumed for each partnership (multiple acts occur within each contact) | ″ | Unrestricted; locations of multiple partners are mutually independent |
| Network: Basic | Explicitly represented by the pairing of two individuals in the network; relatively low to reflect that each sex act occurs in a limited number of long-term partnerships | ″ | Explicitly represented within network model; all actors allowed to have concurrent partners, but those in more highly active groups (i.e. migrant men) are more likely to have them | ″ | Unrestricted; locations of multiple partners are mutually independent |
| Network: Restricted | ″ | ″ | ″ | ″ | Restricted; migrant men with two partners always have one in village and one in workplace |
2.1.1. Conceptualizing the Models
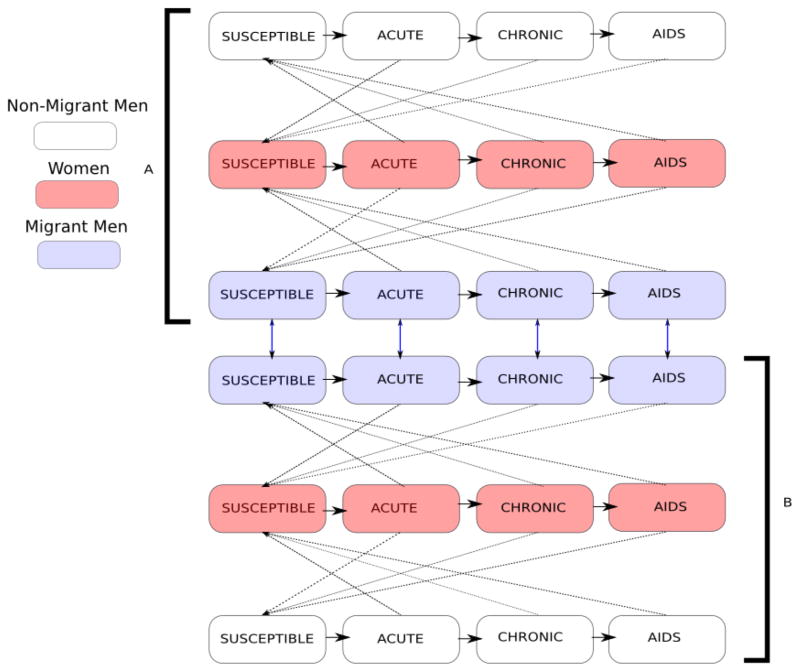
We follow a population which is equally divided by sex and between the two locations: a rural “village” and an urban “workplace.” We set up these symmetric conditions to isolate the effects of circular migrations in our models. We classify the individuals by infection status, migration status, sex, and current location. We assume that some, but not all, men, migrate, while female migration is not considered. This modeling assumption is consistent with some published epidemiological papers on circular migrations [44,45] which present data on migrations by men only. The population thus consists of six classes identified by migration status, sex, and current location (migrant men, non-migrant men and women, each in the urban and rural locations). Individuals in each class are stratified by stage of HIV infection as susceptible, acutely infected, chronically infected or infected with late-stage HIV (AIDS) for a total of 24 state variables (see Figure 1).
Figure 1.
Transfer diagram for migration system. The solid horizontal arrows show flows between infection states. The dotted diagonal show infection transfer between infected and susceptible individuals belonging to opposite sexes in the same location. The double-headed vertical arrows represent movement of migrant men between the two locations. Location A and Location B represent rural village and urban workplace, respectively.
2.1.2. State Transitions
Four types of transitions are considered: recruitment (due to sexual maturity), mortality (natural and AIDS-related), migrations (at periodic intervals for migrant men only), and disease progression (from susceptible, to acute, to chronic, to late-stage). Infections occur as a result of sexual contact between members of the susceptible and infected classes, of opposite sexes, in the same location. We describe the biological assumptions that drive transmission in detail below.
2.1.3. Behavioral Processes: Migration and Partnership Structure
We model migrations as a memoryless process. Migrations occur at average intervals of 3 weeks or 30 weeks between consecutive migrations. These migration frequencies are chosen to be illustrative of migrations by men in KwaZulu-Natal, South Africa, with some men migrating to a nearby location, and others to a location far away (as described in Section 1.2).
Migrant men are assumed to acquire twice as many partners over time as non-migrant men, since they may have partnerships in both locations. This is balanced by the fact that at any particular time migrant men have sex only with partners in their current location (“active” partners), which includes half of their partnerships on average. As a result, migrant men and non-migrant men have the same average number of sex acts per time unit. The specific methods to achieve this equivalence are different for compartmental and network models, and described in the respective sections below.
We further assume that partnerships average about 100 weeks (about 2 years) in duration, consistent with a separate network modeling study of heterosexuals in Sub-Saharan Africa [25].
2.1.4. Biological Processes: Infection Transmission and Disease Progression
We use a transmission probability of 0.0007 (per act) during chronic infection [70]. We model acute and late stage transmission probabilities as 26 and 7 times the chronic-stage probability [30]. We consider the mean duration of acute infection as 12 weeks [30]. The mean lengths of chronic and late stage are taken to be 500 weeks (approximately 9.6 years) and 40 weeks respectively [30]. Mean survival time for infected individuals is thus 552 weeks.
2.1.5. Demographic Structures: Recruitment and Mortality
We set the rate of natural mortality to model an average sexual lifespan of 45 years. Mortality due to late-stage HIV and the mean lifespan of infected individuals are described above. The recruitment rate is selected to balance natural mortality in a disease-free population.
2.1.6. Initial Conditions
We model a population of 5000 individuals (2500 men and 2500 women) at the start. For compartmental models, overall population size does not affect the results; we set it equal to that for network models for consistency. We introduce HIV in the population with one hundred women in each location infected at the start of the simulation, chosen to avoid stochastic die-off in the network models. The initially infected population is distributed among infection classes in proportion to the duration of each stage of infection.
2.1.7. Simulations and Outcomes of Interest
Given the initial conditions, we simulate HIV transmission in our population under the two compartmental and two network models through 5000 weeks using two compartmental and two network models. This simulated period is sufficiently long for the epidemic trajectories to stabilize under both modeling approaches. We explore two separate average migrations intervals (3 weeks and 30 weeks) with each model. We compare prevalence trajectories and the total number of new infections for each migration frequency across all models. We simulate 10 repetitions of each stochastic model to obtain metrics on the range of outcomes in this model; compartmental models are solved deterministically only once.
2.1.8. Computing and Software
All simulations are performed in the R programming language; we use the odesolve package for compartmental models [64] and the statnet suite of packages for network modeling [29].
2.2. Compartmental Models
2.2.1. Details Unique to Compartmental Models
As is common in the compartmental modeling literature [33,37,49], our transition rates from susceptible to infected compartments (called “force of infection”) depend on:
the average number of contacts,
the HIV status of the partner in each contact,
the probability of acquiring infection from an infected partner per contact.
However, “contact” is typically defined in one of two ways: as an individual sex act [3, 23, 24, 49, 62] or as the initiation of a partnership [4, 18, 19, 22, 35, 60, 65, 69]. The “contact-as-act” approach defines a contact as a sexual episode and assumes that a new partner is randomly chosen at every time step. This method estimates cumulative risk based on the number of sex acts per unit time assuming that the partner’s HIV status in each act is independent of the status at the previous time step. Thus, the contact-as-act approach has low transmission probability per contact but a high contact rate due to constant partner changes.
In contrast, in the “contact-as-partnership” approach, a contact is defined as the initiation of a new partnership, and the probability of transmission within that contact is aggregated over all of the coital acts that occur during the duration of a partnership. Contact-as-partnership models estimate cumulative risk per unit time based on the number of active partners, assuming that their HIV status is unchanged over the entire partnership. The per-act transmission probabilities are converted to the contact level using a standard binomial model, which estimates the probability to avoid multiple exposures to HIV (see Table 5 in Appendix A). As a result, in the contact-as-partnership approach, contact rates (often called “partner change rates”) are relatively low but the probability of transmission given contact is relatively high, since it reflects the probability of transmission over the course of the entire relationship.
Table 5.
Biological and behavioral parameters in the contact-as-partnership model. Biological parameters pA, pC pL are per-act transmission probabilities, subscript i represents one of the three infection-states, and βi shows the computation of per-partnership transmission probabilities for the three infection states. Behavioral parameters tMM., tNM., show number of sexual partners per unit time for migrant and non-migrant men respectively. Behavioral parameters tNF.,M, tNF.,NM show the number migrant and non-migrant partners per unit time of women respectively. The subscript. represents rural (R) or Urban (U) regions, and is identical in either case. The parameter d is the average duration of partnerships, taken as 100 weeks. The parameter n is the average number of coital acts within an active partnership per week.
| Biological Parameters | pC | 0.0007 |
| pA | 0.0007 × 26 | |
| pL | 0.0007 × 7 | |
| βi (for non-migrants) | 1− (1−pi)d×n | |
| βi (for migrants) | 1− (1−pi)d×n/2 | |
|
| ||
| Behavioral Parameters | n | 3 |
| d | 100 | |
| tMM. | 0.016 | |
| tNM. | 0.008 | |
| tNF.,M |
|
|
| tNF.,NM |
|
|
It is worth noting that the two interpretations of contact do not change the structure of differential equations which govern the model but affect only the model parameters representing the HIV transmission rates. Complete details of the model structure, parameter values, and differential equations are presented in Appendix A.
We follow the algorithm in [68] to compute the reproduction number R0 for each compartmental model (details in Appendix B).
2.2.2. Conservation of Sexual Acts
The parameter values in the contact-as-partnership case (Table 5) are chosen to reflect some basic known characteristics of migrants and non-migrants described above [46]. That is, the average number of new partners per unit time for migrant men is greater than that for non-migrant men [42, 46], though the average number of coital acts for migrant and non-migrant men is the same. These assumptions represent a strong form of “coital dilution,” the tendency for those with multiple partners to have fewer coital acts with each one than does someone with only one partner [63]; in our case a migrant man with partners in two locations has only half as many coital acts with each as a non-migrant man has with his one partner.
Since we are only modeling heterosexual transmission, we enforce balance of sexual contacts between sexes, i.e., the total number of contacts of males must equal the total number of contacts of their female partners in either location. Therefore, we set:
| (1) |
| (2) |
where tNF.,M is the contact rate between women and migrant men, tNF.,NM is the contact rate between women and non-migrant men while NNM., NMM., and NNF. is the number of non-migrant men, migrant men, and women, respectively at every time step. The dot. represents location, and the equations are identical for urban and rural locations.
In addition, we ensure equivalence between the two interpretations of contact by matching the sexual activity of individuals per unit time (more details in Appendix A.4).
2.3. Stochastic Network Models
2.3.1. Network Modeling Framework and Terminology
We now create alternate models of this system that explicitly track individuals (actors) in the population (including individual attributes) and the unique partnerships among actor pairs. These models are based on graphs, and we adopt graph-theoretic concepts and terminology. Consequently, “nodes” represent individuals, “node attributes” represent their characteristics (e.g. sex, location, migration status), and “edges” represent sexual partnerships between these individuals. An edge can exist at a given moment regardless of whether it currently entails coital acts (i.e. whether or not the pair are in the same location at that time or not); disease transmission is modeled explicitly within these partnerships, as described below. We call the undirected graph of nodes and edges at a single time point a “cross-sectional network,” or simply a “network” for brevity. The cumulative set of nodes and edges across time are called a “cumulative network” or “dynamic network.”
We use the framework of separable-temporal exponential random graph models (STERGMs) of Krivitsky et al. [40] to model the evolution of partnership structure in the population. This approach, a generalization of exponential random graph models (ERGMs; [31]), entails two statistical models, one governing partnership formation, and one governing partnership dissolution. Each is specified as an equation that indicates the factors that influence each tie in the network forming or breaking, and the magnitude of those effects [40]. One strength of the STERGM approach is that the predictors can involve the status of other relationships. For instance, a propensity towards monogamy means that any tie involving an actor currently in another relationship will be less likely to form. This dependence among the “dyads” (i.e. partnerships) in the population means that even though the underlying statistical model may be easy to express, it requires computational algorithms (such as MCMC) for both estimation of the model and simulation of dynamic networks from the model.
2.3.2. Network Modeling Formulation
The general form for an ERGM formation model equation is:
| (3) |
where yij,t is the random variable for the partnership status of persons i and j at time t; yij,t = 1 represents the existence of a partnership at time t, and yij,t = 0 represents its absence. The vector { } represents the set of n different network statistics that describe partnership formation, often prespecified by the researcher (e.g. the number of ties between migrant men and rural women; the number of ties between a migrant man and two or more women in the same location). The vector , represents “change statistics,” i.e. the amount by which these statistics change when the relationship yij toggles from “off” (yij = 0) to “on” (yij = 1). The corresponding vector { } represents the coefficients of these statistics, as in a standard linear model. The prime (′) symbol represents vector transposition. The left-hand side of the equation can be stated in words as the log-odds of actors i and j entering a partnership at time t+1, given that they were not in a partnership at time t.
The general form of the dissolution model equation is:
| (4) |
where the and vectors are analogous to those for formation, and may or may not contain the same terms. Here the left-hand side of the equation formally expresses the log-odds of relationship persistence, i.e. that the partnership between i and j exists at time t+1 given that it existed at time t. Despite this, we refer to this as the “dissolution” model to be consistent with other descriptions in the literature (since the dissolution probability is simply 1 minus the persistence probability) [26,27,53].
The methods for estimating the two θ vectors that maximize the likelihood of the observed network statistics for this type of data are derived in [40]. Those θs then define a probability distribution for all dynamic networks that will typically place most of its mass on networks that are similar to the proposed network statistics; we can thus simulate new dynamic networks from the model that stochastically retain the cross-sectional structures and partnership durations we posited, for any arbitrary network model.
We parameterized the network components of our models based on descriptions of behavioral data as presented in Section 2.1.3 [42,46]. As also explained in Section 2.1.3, we chose a mean partnership duration of 100 weeks [25]. Once again, we model prevalence trajectories at 3-week and 30-week average migration frequencies, and simulate 10 repetitions for each frequency in the two types of network models to account for the stochasticity of these models. We present theoretical 95% confidence intervals about the mean.
2.3.3. Basic Network Models
Network Estimation and Simulation: First, we develop network models that are comparable to the compartmental models of Section 2.2. The only z statistic in the dissolution model is the number of edges (partnerships); in ERGMs, the change statistic (δ) associated with this term equals 1 for all i, j actor pairs. Given this, the coefficient on it acts like an intercept, controlling overall partnership persistence and thus expected partnership duration. This simple model implies that all extant relationships have the same dissolution probability, as in the compartmental models. Any differences in the prevalence of different types of partnerships is thus controlled by the formation model.
For this basic model, the z+ formation statistic vector consists of six terms of the form m(ki, kj), where ki and kj represent the classes of the two actors in the partnership, and m represents the count of relationships of this type in the population. Here, the set of actor classes comprises five types: migrant men, non-migrant urban men, non-migrant rural men, urban women, and rural women. There are numerous structural zeros here, including any combinations in which ki and kj represent groups that are the same sex, or represent men in one location and women in the other. For each of these, m(ki, kj) is zero, and the corresponding θ is −∞. All other combinations are possible; we set m(ki, kj) for these to equal the expected number of edges of this type which make the cross-sectional partnership structure comparable to the contact-as-partnership compartmental model. We then use the statnet software to estimate the corresponding θ values. These θ estimates are then used to simulate the partnership formation and dissolution components of our disease simulation model [29].
Details of the Biological, Behavioral and Demographic Processes: Our basic assumptions and parameters regarding initial conditions, migration intervals and patterns, infectivity by stage, recruitment, and mortality are largely identical in the basic network models as for the compartmental models. Implementation occurs differently given the nature of the frameworks; here, most events are stochastic at the individual level, with a probability assigned to each potentially affected individual (or partnership in the case of transmission) and a separate stochastic draw for each case to determine event outcome. The one exception is that disease progression occurs as a step function in the network models, and as a memoryless process in the compartmental models. Since all partnerships between men and women are explicitly modeled, and transmission events occur within serodiscordant partnerships, we do not need a separate mechanism to guarantee conservation of sexual contacts.
2.3.4. Restricted Network Models
Network Estimation and Simulation: A key feature of the circular migration system is that a migrant man who has two ongoing partnerships should be much more likely to have each of those ongoing partnerships in separate locations. Our network model allows us to introduce this pattern in straightforward ways (see the discussion). We refer to this as the “restricted model” because the partnership structure of migrant men with multiple partners is restricted to exclude multiple partners in the same location. We restrict the partnership structure by adding additional terms to the z+ vector in (3). Formally, these statistics, which we call su and sr, represent the number of migrant men at a given time point with two or more partners in the urban and rural areas, respectively. Both of these terms are constrained to be 0, such that their corresponding θ values are estimated at −∞. The technical name for these terms in social network analysis is an attribute-specific 2-star [52]. The other coefficients are re-estimated so that they produce the correct number of edges during simulations in the light of these new constraints. The substantive consequences of this constraint are that no migrant man has more than two partners in total at any moment in time, and for migrant men with multiple partners one partner is in the urban and the other is in the rural location.
Note the inherent challenge of modeling dependency in the partnership structure of migrant men here; the location of the second partnership of a migrant man now depends on the first. Aside from this change in the partnership structure of migrant men, all other aspects of this model – the underlying biology, demographic and behavior – are identical to those described for the basic network models above.
We do not present R0 computations in the network models, because that is an open area of research beyond the scope of this paper.
3. Results
3.1. Comparing Results Across all Models
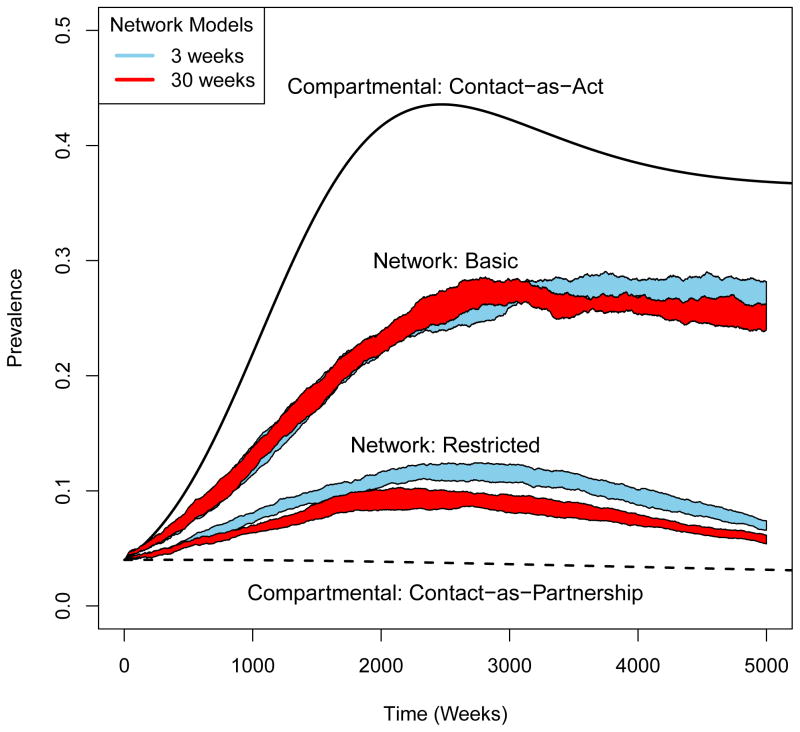
We present a graphical comparison of migrations at 3- and 30-week intervals in each model in Figure 2. We observe that in the contact-as-act compartmental models, a large epidemic is quickly produced (equilibrium prevalence: 36.7%). In the contact-as-partnership version, a small epidemic is produced (equilibrium prevalence: 1.6%). The two migration frequencies produce identical prevalence trajectories within each of these models. Higher prevalence in the contact-as-act models is consistent with our computations of the reproduction number R0 : 1.58 in the contact-as-act case and 1.19 in the contact-as-partnership case.
Figure 2.
Comparison of prevalence trajectories at 3 and 30-week migration frequencies in all the models we study.
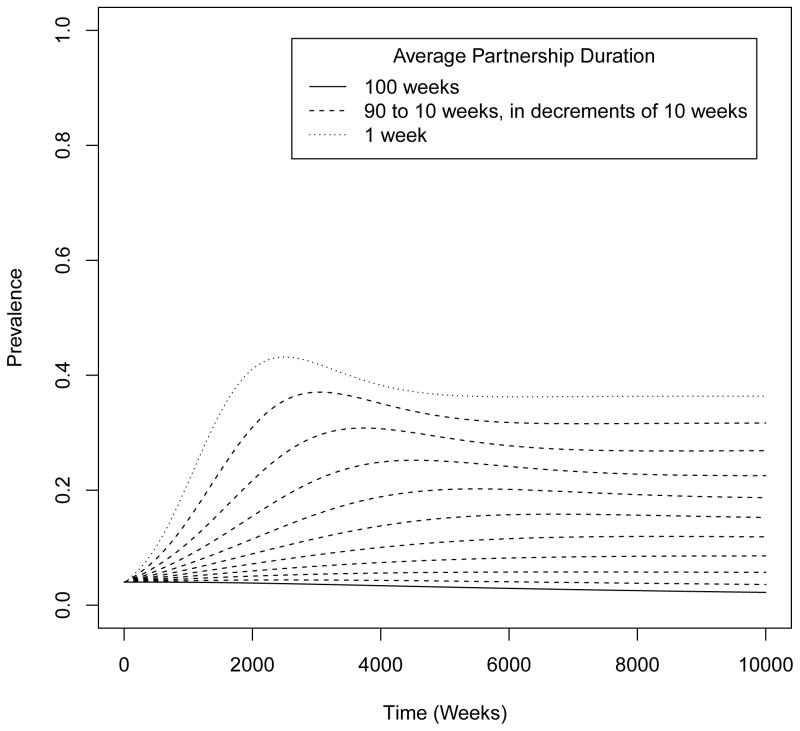
We explore the large difference in the two versions of compartmental models in Figure 3. The plot of the prevalence trajectories for various intermediate partnership durations shows the increase in the projected prevalence when partnership duration decreases, and consider the contact-as-act models as a limiting case for the shortest average partnership duration in the contact-as-partnership models.
Figure 3.
Prevalence trajectories at intermediate partnership durations between the two extremes: contact-as-act (which has a mean partnership duration of 1 week) and contact-as-partnership (which has a mean partnership duration of 100 weeks).
The basic network models produce a prevalence between the contact-as-act and contact-as-partnership cases. Ten experimental repetitions showed a mean prevalence of 26.9% (95% CI: 25.7%, 28.2%) after 5000 weeks when migrations occurred at 3-week intervals (on average) and at 25.2% (95% CI: 24.0%, 26.3%) when the average migration frequency is 30 weeks. Restricted network models, produce an equilibrium prevalence lower than the basic network models; mean prevalences of 6.9% (95% CI: 6.6%, 7.4%) at 3-weekly migrations, and 5.8% (95% CI: 5.4%, 6.1%) at 30-weekly migrations.
3.2. Impact of Migration Within Each Model
Contact-as-act and contact-as-partnership models project the same number of new infections (and identical prevalence trajectories) through 5000 weeks – 13,126 in the former and 736 in the latter – for different migration frequencies. Thus, under the compartmental formulation, endemic prevalence and number of new infections are independent of the migration frequency.
In the basic network models, we see 6,793 and 6,680 new infections, and prevalence trajectories that mostly overlap at the two average migration frequencies. In the restricted network models, migrations at an average interval of 3 weeks produce 3,186 new infections, while migrations at an average of 30 weeks produce 2,639 new infections. Two sample t-tests show a statistically significant difference in the number of new infections in the restricted network models (p = 0.0001), but not in the basic network models (p = 0.16). We also observe that the prevalence trajectory at the shorter migration interval is distinctly higher than the trajectory at the longer interval.
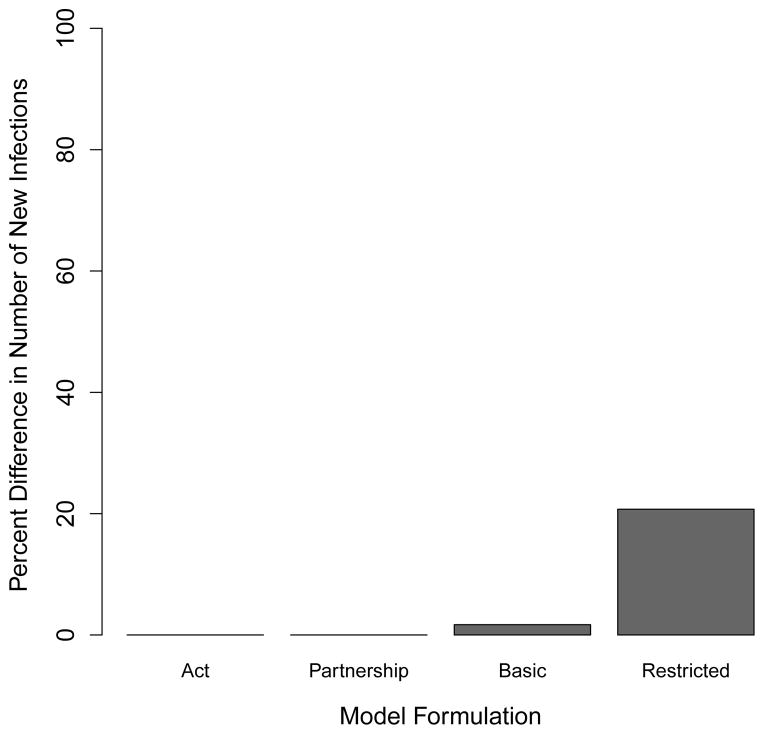
We use the above numbers to calculate and plot the proportional difference in the mean number of infections produced at the two migration frequencies, relative to the number of infections every 30 weeks across all models in Figure 4. Our basic network models show a slight increase (1.7%) in the number of new infections produced in migrations every 3 weeks relative to the number of infections produced with migrations every 30 weeks. The restricted network models show a much larger increase (20.7%) for the same measure.
Figure 4.
Comparison of number of new infections through 5000 weeks across all primary models. The barplot shows the per cent increase in the number of new infections with 3-week migrations relative to 30-week migrations. The “act” and “partnership” bars represent the number of new infections the compartmental contact-as-act and contact-as-partnership cases respectively. The “basic” and “restricted” bars represent the number of new infections in the basic and restricted network models respectively.
4. Discussion
4.1. Interpreting our Outcomes
4.1.1. Prevalence Trajectory Across Different Models
We have simulated HIV epidemics using different modeling approaches to see how they project the epidemiological impact of circular migration of male workers. We set up identical conditions in the two locations at the beginning to isolate the effects of circular migrations. Each successive model then helps us relax some underlying simplifying feature from the previous model. We started with the contact-as-act compartmental models that assume mixing is homogeneous and instantaneous [37], and each sex act occurs with a different individual, whose infection status is randomly assigned based on the current distribution of infections in the population. Contact-as-partnership models allow us to relax this assumption about behavior and transmission, and explicitly consider transmission within partnerships. Our basic network models allow us to explicitly consider individuals, their partnerships, and emergent serodiscordance during the course of partnerships. The restricted network models further allow us to consider dependence in the partnerships of migrant men, and require multiple partnerships for this group to occur in different locations.
The differences in the simulated trajectories of epidemics in the various models emerge for multiple reasons. As is well understood, the fundamental assumption of the contact-as-act models is clearly unrealistic since a significant number of sexual partnerships would be expected to last for a long time and therefore a limited fraction of individuals will be exposed to HIV. In that sense, the contact-as-act approach overestimates the epidemic size.
The frequently used alternative definition of contact as partnership eliminates this problem, by recognizing that when an individual is in a discordant relationship, transmission within that relationship can only happen once, and all subsequent coital acts are “lost opportunities” for the virus. However, this contact-as-partnership version of the compartmental model introduces an additional limitation: the determination of which couples are discordant occurs only at the outset of the relationship; there is no mechanism to allow relationships that begin as concordant negative to subsequently involve a transmission after one member becomes infected from another concurrent relationship. This is despite the fact that such overlapping relationships implicitly occur in our model quite frequently; for instance, the average partner acquisition rate for a migrant man is 0.016 new partners per week, and relationships average 100 weeks in duration; migrant men are in an average of 1.6 relationships at a time. Evaluating serostatuses at the start of the relationships only, and thus not allowing for sero-discordance to develop during the course of partnerships, is the likely reason for the low estimation of epidemic size in the contact-as-partnership version of compartmental models.
Network models evaluate relative serostatuses of two partners at every time step and thus allow for sero-discordance to occur during the course of a partnership. Indeed, the network models produce prevalence trajectories in between the trajectories produced by the contact-as-act and the contact-as-partnership compartmental models. Additionally, we note that the basic network models show a higher prevalence than the restricted models. This difference presumably occurs since multiple partners of migrant men are required to be in separate locations in the restricted models; therefore sexual contact (and consequent infection transmission) between the migrant man and his partner in the other location has to wait until the time to migration has passed.
4.1.2. Impact of Migration Frequency on Outcomes
We also observe that both compartmental models suggest no impact of migration on the HIV transmission regardless of its frequency. This is because individuals who move from one location to another at a given time are equally matched by the same number and distribution by HIV status moving in the opposite direction. In contrast, when the HIV epidemic is simulated with the basic network models, which were intentionally designed to mimic many of the mechanisms embedded in the compartmental models, we see that migrations at 3-week average interval, produce a slightly larger epidemic than migrations at a 30-week average interval. When the partnership structure of migrant men is restricted – a reasonable assumption for men who spend extended periods of time in two locations – the difference in epidemic size is large, and statistically significant.
This model alone shows a large effect of the frequency of migration on onward transmission of HIV. The direction of this effect – migrations at intervals shorter than the length of acute infection produce a bigger epidemic than migrations at intervals longer than the length of acute infection – is in line with our hypothesis.
4.2. Limitations and Future Work
In practice, frequency of circular migration is likely much more variable between individuals, and dependent on other individual circumstances. Better data on the behavior of migrants, and models that utilize these data may help us learn more about the relationship between migration frequency and HIV transmission. Models that incorporate migrations by women [6,8], multiple locations, and more complex migration patterns will be needed to further understand the implications of circular migrations on HIV transmission. The restricted network model, and its ability to handle dependence in partnerships of migrant men, may provide one starting point to model such dynamics well.
One artifact of the restricted model we developed here was that a migrant man could have a maximum of two partnerships at any given time. This artifact was not present in the basic network models, and future work using models developed here may want to address this limitation in the restricted models.
The compartmental models that we explored showed no effect of migration frequency on HIV prevalence. Of course, as mentioned in the Introduction, these are not the only approaches for conceiving of partnerships within compartmental models; they are merely the ones commonly used in the field of applied HIV epidemiology and policy analysis in this region. Those alternative approaches includes models based on rich theoretical work [16, 28], but which, to our knowledge, have only been used in one HIV modeling application [57] in the last decade. These “pair formation models” represent single individuals in one set of compartments and pairs in ongoing partnerships in another set. The latter are distinguished by the pairs’ serostatuses (neither, one, or both HIV-positive), and, since individuals in them are allowed to have outside contacts, it is possible for pairs to move from one serostatus compartment to another after relational formation. Unfortunately for our interests here, that approach is limited to having the additional contacts be one-off acts.
For the case of circular migration, a proper representation of the system requires the possibility of at least two ongoing partnerships, and, as we saw when comparing the basic and restricted network cases, the ability to capture the propensity that these partners are likely to be in different locations and thus be active at different times. One other early paper did propose a model for tracking actor triplets (an individual and her/his two concurrent partners) in a compartmental framework [17]. Although this method gets closer to our scenario, it does not allow for either of the concurrent partners to also have other partners; each triplet is isolated in the social network. Thus, the larger chains that are made possible by a high prevalence of concurrent partnerships and that can foster disease transmission are still not represented. These longer chains become intractable within a compartmental framework as their length increases, while network models are able to represent them naturally. Our work here suggests that the methodological challenges inherent in currently used approaches to HIV modeling, if not properly recognized, could lead to models that misconstrue the effects that migration frequency has on HIV epidemics in settings with circular migration.
Our goal here was to compare the most commonly used adaptations of compartmental models to study their predictions. Other methods might include using stochastic compartmental models [38] where transitions are described using continuous time Markov chains. Analyzing models that relax other structural assumptions is an interesting research area – and one we leave for future work.
4.3. Conclusions
We see that representative models from the model classes that are commonly used in HIV epidemiology, despite being made as similar as possible given the constraints of those classes, produce very different epidemics overall in this context. This is due in part to the inability for either the contact-as-act or the more popular contact-as-partnership formulation to represent the complex interactions between partnership structure and the viral dynamics of acute infection. Network models can be considerably more complex to develop than compartmental ODE models, and network modelers are often asked whether the effort is “worth it.” The answer depends on the purpose for which the model is needed, as is true for all models, with the goal to develop models that are “as simple as possible, but no simpler” [38]. This work suggests that to understand the epidemiological effects of circular migrations – and thus evaluate the impacts of interventions proposed in settings where circular migrations play a major role – the answer is yes.
Acknowledgments
Partial support for this research came from a Eunice Kennedy Shriver National Institute of Child Health and Human Development research infrastructure grant, R24 HD042828, to the Center for Studies in Demography & Ecology at the University of Washington.
Appendix A. Formulation of Compartmental Models: Assumptions, Equations and Parameter Sets
Here we describe details of the model structure, parameter values, and differential equations that are first described in Section 2.2. We denote the four stages of infection (susceptible, acute, chronic and late) by S, A, C and L respectively, and describe a state by the notation SXYZ, AXYZ, CXYZ or LXYZ where X denotes the migration status of the individual (migrant M or non-migrant N); Y denotes the sex (male M or female F); and Z denotes the location (urban workplace U or rural village R). Thus, for example, SMMU represents a susceptible migrant male in the urban area. Since females do not migrate in the model, the first subscript N for females is redundant, but we include it for symmetry.
Tables 2 and 3 show the demographic parameters and initial values of the state variables that remain constant for either interpretation. The system of equations (described below in Section A.1) is simulated over 5000 time steps with the parameter values in Table 3. Each time step represents 1 week. Tables 5 and 4 provide values for the biological and behavioral parameters that are different for the contact-as-partnership and contact-as-act models respectively. These values are selected so the number of coital acts is the same across the two models, and in the mean per-act transmission probability.
Table 2.
Demographic and biological parameters: These parameters are identical in the contact-as-act and the contact-as-partnership cases.
| Parameter | Notation | Value | |
|---|---|---|---|
| Demographic Parameters | Natural Mortality Rate | μ | 1/(45 × 52) |
| AIDS-related Mortality Rate | μd | 1/40 | |
| Fertility Rate | ν | 1250/(45 × 52) | |
|
| |||
| Biological Parameters | Acute-Stage Duration | 1/γ | 12 weeks |
| Chronic-Stage Duration | 1/η | 500 weeks | |
| Late-Stage Duration | 1/μd | 40 weeks | |
Table 3.
Initial values for state variables. These initial values are the same in both contact-as-act and contact-as-partnership approaches. Total population size is 5000, including 2500 men and 2500 women. These men and women are divided equally between the two locations. In each location, half the men are migrant, and half the men are non-migrant.
| State Variable | Value |
|---|---|
|
| |
| Susceptible Migrant Males | 1250 |
| Acutely Infected Migrant Males | 0 |
| Chronically Infected Migrant Males | 0 |
| Late-Stage Infected Migrant Males | 0 |
| Susceptible Females | 2450 |
| Acutely Infected Females | 12/552 × 100 |
| Chronically Infected Females | 500/552 × 100 |
| Late-Stage Infected Females | 40/552 × 100 |
| Susceptible Non-Migrant Males | 1250 |
| Acutely Infected Non-Migrant Males | 0 |
| Chronically Infected Non-Migrant Males | 0 |
| Late-Stage Infected Non-Migrant Males | 0 |
Table 4.
Biological and behavioral parameters in the contact-as-act model. Biological parameters βA, βC βL are per-act transmission probabilities, subscript i represents one of the three infection-states, and βi shows the computation of per-partnership transmission probabilities for the particular infection-state. Behavioral parameters t... are set to 2.4 to have a mean number of 2.4 sexual acts per week in the population. The subscript. represents rural (R) or urban (U) regions.
| Biological Parameters | βC | 0.0007 |
| βA | 0.0007 × 26 | |
| βL | 0.0007 × 7 | |
|
| ||
| Behavioral Parameters | tMM. | 2.4 |
| tNM. | 2.4 | |
| tNF.,M | 2.4 | |
| tNF.,NM | 2.4 | |
A.1. Compartmental Models
We begin by considering susceptible migrating urban males. We describe the rate of change in this population (with one week taken as one time unit) as
| (5) |
where δ is the rate of migration between the urban and rural area. The parameter ν is the number per unit time that enter the entire population. The parameter βx,y denotes the probability that disease is transmitted in an act (in the contact-as-act case), and the probability that disease is transmitted during the course of a partnership (in the contact-as-act case); the first subscript x represents acute (A), chronic (C) or late (L) stage, and the second subscript represents the migrant status of the male partner: migrant (M) or non-migrant (NM). We present detailed calculations below. Since urban migrant men account for one-eighth of the total population, the number of new arrivals per unit time in this group is ν/8. The parameter μ denotes the rate of natural mortality. The parameter tXYZ is the contact rate; we use t instead of the more common c to avoid confusion with the chronic stage of infection (for which we use C).
The change in population of acutely infected migrating urban males is
| (6) |
where γ1 is the rate at which an acutely infected individual becomes chronically infected.
The change in the population of chronically infected migrating urban males is
| (7) |
where γ2 is the rate of chronic to late-stage transition. The change in population of late-stage migrating urban males is
| (8) |
where μd is the rate of mortality due to the disease.
Now we consider the females in the urban area. An urban female can become infected either by an infected male in one of the three infectious states, who is either a migrant or a non-migrant. Therefore we have
| (9) |
| (10) |
| (11) |
and
| (12) |
to describe the various interactions of females in the urban area.
The interactions of the non-migrant males are similar to those of the migrant males defined in equations (5) to (8), without the migration term. Thus,
| (13) |
| (14) |
| (15) |
| (16) |
describe the changes in population for the four infection states of urban non-migrant males.
The basic structure of equations (5) to (16) is the same for the rural area with the location sub-script U replaced by R (for rural). Thus, we have a system of 24 interacting equations.
A.2. Computational Details of the Infection Model
In the interpretation of contact as partnership, we take a hypothetical value of 100 weeks as the average duration of partnerships. The per-act transmission probabilities are converted to the partnership-level and are given in Table 5. To convert these probabilities, the constants βA,M and βA,N represent the probabilities that infection is transmitted during the course of a partnership when the partnerships involve acutely infected migrant and non-migrant men, respectively. If pi is the probability of transmission per coital act during the stage i of infection, then
| (17) |
and
| (18) |
where d is the average duration of the partnerships and n is the number of coital acts per time unit for an active partnership. The division by 2 in the exponent for migrant men reflects the fact that each of their relationships is active only half of the time. Thus, while migrant men have twice as many partners per unit time as non-migrant men, the amount of sex men in both groups have is the same. That is, the total number of sexual acts that migrant and non-migrant men have are now equal, since overall coital frequency for a man does not depend on his number of partners.
In the contact-as-act approach, β simply represents the per-act transmission probabilities as shown in Table 4.
A.3. Modeling Fertility and Mortality
We consider two types of mortality: natural mortality (μ) and mortality due to the disease (μd). Thus 1/μ is the average sexual lifespan of an uninfected individual. We assume that an uninfected individual will remain sexually active from the age of 15 years to the age of 60 years; thus setting μ = 1/(45 × 52) sets the sexual lifespan of an individual to (45 × 52) weeks, or 45 years. The average lifespan of an infected individual is 552 weeks, comprising acute, chronic and late stages that last on average for 12, 500 and 40 weeks respectively [30].
To solve for the number of arrivals in the population per unit time, we set equation (5) equal to 0 in the disease free state. Then
implying
| (19) |
Therefore, there are 625/(45 × 52) individuals that enter the sub-population of susceptible migrant men in the urban location per week. The other sub-populations of men have the same number of arrivals per week, and each of the two sub-populations of women have 1250/(45 × 52) individuals that arrive per unit time.
A.4. Equivalence of the Two Interpretations of Contact
To understand this equivalence, consider the initial conditions; we start with 3000 partnerships, of which 2000 are accounted for by migrant men, and 1000 are accounted for by non-migrant men. Since there are 1250 total non-migrant men in the population, and all of their partnerships are active, the average number of active partnerships per person per unit time (“active mean degree”) of non-migrant men is 1000/1250=0.8. The active mean degree of migrant men is the same, because exactly half of their total partnerships are active at any given time, and their population size is also 1250 (yielding 1000/1250 =0.8 active mean degree). The balance of partnerships between genders and the 1:1 sex ratio at the outset imply that women have the same active mean degree at this time point as well.
We assume 3 sexual acts per week per active partnership, which implies an average of 0.8 × 3 = 2.4 (consistent with estimates presented in [70]) sexual acts per person per week, for each group (migrant men, non-migrant men, and women). We set coital frequency at 2.4 sexual acts per person per week in the contact-as-act model, and thus, the two definitions of contact are comparable in terms of coital acts per person per unit time at the start. As the simulation moves forward in time, and the sex ratio changes, equations 1 and 2 guarantee that sexual acts between the two sexes are conserved, and the two interpretations of contact remain comparable.
Appendix B. R0 Computations for Compartmental Models
We follow the algorithm outlined in [68] to compute the reproduction number R0. Our system consists of three infectious states for migrant-men (AMM., CMM., LMM.), women (ANF., CNF., LNF.), and non-migrant men (ANM., CNM., LNM.), giving a total of nine infected states in each location. Each of these groups (migrant-men, women and non-migrant men) have a population of susceptibles that form the uninfected state in each group. In this study we consider two locations, but since the two locations are structurally identical, we base our calculations on one location and nine infected states. We ignore the migration parameter δ because we only consider one location. As our analysis has shown, the migration parameter has no effect on infection transmission in either interpretation of “contact” in the framework of compartmental models.
We define a column-vector
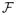 as the rate of production of new infections in each of the nine infectious states outlined above. Since the chronic and late-stages consist only of flows from the acute stage, no new infections are produced in the states. Therefore, vector
as the rate of production of new infections in each of the nine infectious states outlined above. Since the chronic and late-stages consist only of flows from the acute stage, no new infections are produced in the states. Therefore, vector
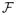 consists of non-zero entries in the first, fourth and seventh positions, and zeros everywhere else.
consists of non-zero entries in the first, fourth and seventh positions, and zeros everywhere else.
We then
Define a new 9×9 matrix F as where x is each of the nine infectious states.
Define a vector
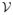 that consists of everything except the new infections in the nine infectious states.
that consists of everything except the new infections in the nine infectious states.Define matrix where x is as defined above.
Compute the dominant eigenvalues for FV−1 at the disease-free equilibria to obtain R0.
Our compulations yield R0 values of 1.58 and 1.19 when contact is defined as act and partnership respectively. In Figure 2, the former interpretation of contact yielded an equilibrium prevalence of 1.6% and the latter interpretation yielded an equilibrium prevalence of 36.7%. Given these prevalences, the estimate for R0 appears high, especially in the contact-as-partnership case. But these estimates are approximations, and the important result for us is the relative differences in the magnitude of the R0 estimates in the two interpretations of contact, and the consistency of the higher estimate with the higher prevalence (as seen in the contact-as-act case).
Contributor Information
Aditya Khanna, Email: khanna7@uw.edu, International Clinical Research Center, Department of Global Health, University of Washington, 325 Ninth Ave Seattle WA 98104.
Dobromir Dimitrov, Email: ddimitro@scharp.org, Fred Hutchinson Cancer Research Center, PO Box 19024, 1100 Fairview Ave. N. Seattle WA 98109.
Steven Goodreau, Email: goodreau@uw.edu, Department of Anthropology, University of Washington, Campus Box 353100, Seattle WA 98105.
References
- 1.Abu-Raddad LJ, Longini IM. No HIV stage is dominant in driving the HIV epidemic in sub-Saharan Africa. AIDS. 2008 May;22(9):1055–1061. doi: 10.1097/QAD.0b013e3282f8af84. [DOI] [PubMed] [Google Scholar]
- 2.Alistar SS, Owens DK, Brandeau ML. Effectiveness and cost effectiveness of expanding harm reduction and antiretroviral therapy in a mixed HIV epidemic: a modeling analysis for Ukraine. PLoS Med. 2011 Mar;8(3):e1000423. doi: 10.1371/journal.pmed.1000423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bailey NT. The use of operational modeling of HIV/AIDS in a systems approach to public health decision making. Math Biosci. 1991 Dec;107(2):413–430. doi: 10.1016/0025-5564(91)90017-d. [DOI] [PubMed] [Google Scholar]
- 4.Boily MC, Dimitrov D, Abdool Karim SS, Masse B. The future role of rectal and vaginal microbicides to prevent HIV infection in heterosexual populations: implications for product development and prevention. Sex Transm Infect. 2011 Dec;87(7):646–653. doi: 10.1136/sextrans-2011-050184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brockerhoff Martin, Biddlecom Ann E. Migration, behavior and the risk of HIV in Kenya. International Migration Review. 1999;33(4):833–856. [Google Scholar]
- 6.Byass P, Alberts M, Burger S. Motherhood, migration and mortality in Dikgale: modelling life events among women in a rural South African community. Public Health. 2011 May;125(5):318–323. doi: 10.1016/j.puhe.2011.02.012. [DOI] [PubMed] [Google Scholar]
- 7.Cambiano V, Phillips AN. Modelling the impact of treatment with individual antiretrovirals. Curr Opin HIV AIDS. 2011 Mar;6(2):124–130. doi: 10.1097/COH.0b013e328343ad66. [DOI] [PubMed] [Google Scholar]
- 8.Camlin CS, Hosegood V, Newell ML, McGrath N, Barnighausen T, Snow RC. Gender, migration and HIV in rural KwaZulu-Natal, South Africa. Plos One. 2010 Jul;5(7):e11539. doi: 10.1371/journal.pone.0011539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Carnegie NB, Morris M. Size matters: concurrency and the epidemic potential of HIV in small networks. PLoS ONE. 2012;7(8):e43048. doi: 10.1371/journal.pone.0043048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cassels Susan, Clark Samuel J, Morris Martina. Mathematical models for HIV transmission dynamics. JAIDS- Journal of Acquired Immune Deficiency Syndrome. 2008 Mar;47(Supplement 1) doi: 10.1097/QAI.0b013e3181605da3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Coast E. Local understandings of, and responses to, HIV: Rural-urban migrants in Tanzania. Social Science & Medicine. 2006 Aug;63(4):1000–1010. doi: 10.1016/j.socscimed.2006.03.009. [DOI] [PubMed] [Google Scholar]
- 12.Coffee MP, Garnett GP, Mlilo M, Voeten HACM, Chandiwana S, Gregson S. Patterns of movement and risk of HIV infection in rural Zimbabwe. Journal of Infectious Diseases. 2005 Feb;191:S159–S167. doi: 10.1086/425270. [DOI] [PubMed] [Google Scholar]
- 13.Coffee Megan, Lurie Mark N, Garnett Geoff P. Modelling the impact of migration on the HIV epidemic in South Africa. AIDS. 2007;21:343–350. doi: 10.1097/QAD.0b013e328011dac9. [DOI] [PubMed] [Google Scholar]
- 14.Cuadros DF, Crowley PH, Augustine B, Stewart SL, Garcia-Ramos G. Effect of variable transmission rate on the dynamics of HIV in sub-Saharan Africa. BMC Infect Dis. 2011;11:216. doi: 10.1186/1471-2334-11-216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deane KD, Parkhurst JO, Johnston D. Linking migration, mobility and HIV. Tropical Medicine & International Health. 2010 Dec;15(12):1458–1463. doi: 10.1111/j.1365-3156.2010.02647.x. [DOI] [PubMed] [Google Scholar]
- 16.Dietz K, Hadeler KP. Epidemiological models for sexually transmitted diseases. J Math Biol. 1988;26(1):1–25. doi: 10.1007/BF00280169. [DOI] [PubMed] [Google Scholar]
- 17.Dietz K, Tudor W. Triangles in heterosexual HIV transmission. AIDS Epidemiology: Methodological Issues. 1992:143–155. [Google Scholar]
- 18.Dimitrov DT, Boily MC, Baggaley RF, Masse B. Modeling the gender-specific impact of vaginal microbicides on HIV transmission. J Theor Biol. 2011 Nov;288:9–20. doi: 10.1016/j.jtbi.2011.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Eaton JW, Johnson LF, Salomon JA, Barnighausen T, Bendavid E, Bershteyn A, Bloom DE, Cambiano V, Fraser C, Hontelez JA, Humair S, Klein DJ, Long EF, Phillips AN, Pretorius C, Stover J, Wenger EA, Williams BG, Hallett TB. HIV Treatment as Prevention: Systematic Comparison of Mathematical Models of the Potential Impact of Antiretroviral Therapy on HIV Incidence in South Africa. PLoS Medicine. 2012 Jul;9(7):e1001245. doi: 10.1371/journal.pmed.1001245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Enns EA, Brandeau ML, Igeme TK, Bendavid E. Assessing effectiveness and cost-effectiveness of concurrency reduction for HIV prevention. Int J STD AIDS. 2011 Oct;22(10):558–567. doi: 10.1258/ijsa.2011.010322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Garnett GP, White PJ, Ward H. Fewer partners or more condoms? Modelling the effectiveness of STI prevention interventions. Sex Transm Infect. 2008 Oct;84(Suppl 2):4–11. doi: 10.1136/sti.2008.029850. [DOI] [PubMed] [Google Scholar]
- 22.Gomez GB, Borquez A, Caceres CF, Segura ER, Grant RM, Garnett GP, Hallett TB. The Potential Impact of Pre-Exposure Prophylaxis for HIV Prevention among Men Who Have Sex with Men and Transwomen in Lima, Peru: A Mathematical Modelling Study. PLoS Med. 2012 Oct;9(10):e1001323. doi: 10.1371/journal.pmed.1001323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Goodreau SM, Goicochea LP, Sanchez J. Sexual role and transmission of HIV Type 1 among men who have sex with men, in Peru. J Infect Dis. 2005 Feb;191(Suppl 1):S147–158. doi: 10.1086/425268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Goodreau SM, Golden MR. Biological and demographic causes of high HIV and sexually transmitted disease prevalence in men who have sex with men. Sex Transm Infect. 2007 Oct;83(6):458–462. doi: 10.1136/sti.2007.025627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Goodreau SM, Cassels S, Kasprzyk D, Montao DE, Greek A, Morris M. Concurrent partnerships, acute infection and HIV epidemic dynamics among young adults in Zimbabwe. AIDS and Behavior. 2012;16(2):312–322. doi: 10.1007/s10461-010-9858-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goodreau Steven M. A decade of modelling research yields considerable evidence for the importance of concurrency: A response to Sawers and Stillwaggon. Journal of the International Aids Society. 2011 Mar;14:12. doi: 10.1186/1758-2652-14-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Goodreau Steven M, Carnegie Nicole B, Vittinghoff Eric, Lama Javier R, Sanchez Jorge, Grinsztejn Beatriz, Koblin Beryl A, Mayer Kenneth H, Buchbinder Susan P. What drives the us and peruvian hiv epidemics in men who have sex with men (MSM)? PLoS ONE. 201211;7(11):e50522. doi: 10.1371/journal.pone.0050522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hadeler KP, Waldstatter R, Worz-Busekros A. Models for pair formation in bisexual populations. J Math Biol. 1988;26(6):635–649. doi: 10.1007/BF00276145. [DOI] [PubMed] [Google Scholar]
- 29.Handcock Mark S, Hunter David R, Butts Carter T, Goodreau Steven M, Morris Martina. statnet: Software tools for the statistical modeling of network data. Seattle, WA: 2003. Version 2.0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hollingsworth TD, Anderson RM, Fraser C. HIV-1 transmission, by stage of infection. Journal Of Infectious Diseases. 2008 Sep;198(5):687–693. doi: 10.1086/590501. [DOI] [PubMed] [Google Scholar]
- 31.Hunter David R, Goodreau Steven M, Handcock Mark S. Goodness of fit of social network models. Journal of the American Statistical Association. 2008 Mar;103(481):248–258. [Google Scholar]
- 32.Johnson LF, White PJ. A review of mathematical models of HIV/AIDS interventions and their implications for policy. Sex Transm Infect. 2011 Dec;87(7):629–634. doi: 10.1136/sti.2010.045500. [DOI] [PubMed] [Google Scholar]
- 33.Keeling Matthew James, Rohani Pejman. Modeling infectious diseases in humans and animals. Princeton University Press; Princeton: 2008. [Google Scholar]
- 34.Keeling MJ, Rohani P. Estimating spatial coupling in epidemiological systems: a mechanistic approach. ECOLOGY LETTERS. 2002 Jan;5(1):20–29. [Google Scholar]
- 35.Kim JH, Koopman JS. HIV transmissions by stage in dynamic sexual partnerships. J Theor Biol. 2012 Apr;298:147–153. doi: 10.1016/j.jtbi.2011.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Koopman J. Modeling infection transmission. Annu Rev Public Health. 2004;25:303–326. doi: 10.1146/annurev.publhealth.25.102802.124353. [DOI] [PubMed] [Google Scholar]
- 37.Koopman JS. Modeling infection transmission- the pursuit of complexities that matter. Epidemiology. 2002 Nov;13(6):622–624. doi: 10.1097/00001648-200211000-00004. [DOI] [PubMed] [Google Scholar]
- 38.Koopman JS. Infection transmission science and models. Jpn J Infect Dis. 2005 Dec;58(6):3–8. [PubMed] [Google Scholar]
- 39.Kretzschmar M, Carael M. Is concurrency driving HIV transmission in sub-Saharan African sexual networks? The significance of sexual partnership typology. AIDS Behav. 2012 Oct;16(7):1746–1752. doi: 10.1007/s10461-012-0254-6. [DOI] [PubMed] [Google Scholar]
- 40.Krivitsky Pavel N, Handcock Mark S, Morris Martina. Adjusting for network size and composition effects in exponential-family random graph models. Statistical Methodology. 2011;8(4):319339. doi: 10.1016/j.stamet.2011.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Leynaert AM, Downs B, Downs I, de Vincenzi AM, de Vincenzi I. Heterosexual transmission of human immunodeficiency virus: variability of infectivity throughout the course of infection. european study group on heterosexual transmission of HIV. American Journal of Epidemiology. 1998;148(1):88–96. doi: 10.1093/oxfordjournals.aje.a009564. [DOI] [PubMed] [Google Scholar]
- 42.Lurie M. igration and AIDS in Southern Africa: a review. South African Journal of Science. 2000 Jun;96:343–347. [Google Scholar]
- 43.Lurie Mark, Harrison Abigail, Wilkinson David, Karim Salim Abdool. Circular migration and sexual networking in KwaZulu/Natal: implications for the spread of HIV and other sexually transmitted diseases. Health Transition Review Supplement 3. 1997;7:17–27. [Google Scholar]
- 44.Lurie Mark, Williams Brian G, Zuma Khangleani, Mkaya-Mwamburi David, Garnett Geoff P, Swat Michael D, Gittelsohn Joel, Karim Salim Abdool. The impact of migration on HIV-1 transmission in South Africa. Sexualy Transmitted Diseases. 2003 Feb;30(2):149–156. doi: 10.1097/00007435-200302000-00011. [DOI] [PubMed] [Google Scholar]
- 45.Lurie Mark, Williams Brian G, Zuma Khangleani, Mkaya-Mwamburi David, Garnett Geoff P, Swat Michael D, Gittelsohn Joel, Karim Salim Abdool. Who infects whom? HIV-1 concordance and discordance among migrant and non-migrant couples in South Africa. AIDS. 2003;17:2245–2252. doi: 10.1097/00002030-200310170-00013. [DOI] [PubMed] [Google Scholar]
- 46.Lurie Mark N. The epidemiology of migration and HIV/AIDS in South Africa. Journal of Ethnic and Migration Studies. 2006 May;32(4):649–666. [Google Scholar]
- 47.Mah TL, Halperin DT. Concurrent sexual partnerships and the HIV epidemics in Africa: evidence to move forward. AIDS Behav. 2010 Feb;14(1):11–16. doi: 10.1007/s10461-008-9433-x. [DOI] [PubMed] [Google Scholar]
- 48.May RM, Anderson RM. Transmission dynamics of HIV-infection. Nature. 1987 Mar;326(6109):137–142. doi: 10.1038/326137a0. [DOI] [PubMed] [Google Scholar]
- 49.May RM, Anderson RM. The transmission dynamics of human immunodeficiency virus (HIV) Philosophical Transactions Of The Royal Society Of London Series B-Biological Sciences. 1988 Oct;321(1207):565–607. doi: 10.1098/rstb.1988.0108. [DOI] [PubMed] [Google Scholar]
- 50.Meyers Laurel Ancel. Contact network epidemiology: Bond percolation applied to infectious disease prediction and control. Bulletin (New Series) of the American Mathematical Society. 2007 Jan;44(1):63–86. [Google Scholar]
- 51.Morris M, Vu L, Leslie-Cook A, Akom E, Stephen A, Sherard D. Comparing Estimates of Multiple and Concurrent Partnerships Across Population Based Surveys: Implications for Combination HIV Prevention. AIDS Behav. 2013 Sep; doi: 10.1007/s10461-013-0618-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Morris Martina, Handcock Mark S, Hunter David R. Specification of exponential-family random graph models: Terms and computational aspects. Journal of Statistical Software. 200712;24(4):1–24. doi: 10.18637/jss.v024.i04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Morris Martina, Kurth Ann E, Hamilton Deven T, Moody James, Wakefield Steve. Concurrent partnerships and HIV prevalence disparities by race: Linking science and public health practice. American Journal of Public Health. 2009 Jun;99(6):1023–1031. doi: 10.2105/AJPH.2008.147835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mundandi C, Vissers D, Voeten H, Habbema D, Gregson S. No difference in HIV incidence and sexual behaviour between out-migrants and residents in rural Manicaland, Zimbabwe. Tropical Medicine & International Health. 2006 May;11(5):705–711. doi: 10.1111/j.1365-3156.2006.01614.x. [DOI] [PubMed] [Google Scholar]
- 55.Nagelkerke NJ, Hontelez JA, de Vlas SJ. The potential impact of an HIV vaccine with limited protection on HIV incidence in Thailand: a modeling study. Vaccine. 2011 Aug;29(36):6079–6085. doi: 10.1016/j.vaccine.2011.06.048. [DOI] [PubMed] [Google Scholar]
- 56.Pinkerton SD. Probability of HIV transmission during acute infection in Rakai, Uganda. AIDS And Behavior. 2008 Sep;12(5):677–684. doi: 10.1007/s10461-007-9329-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Powers KA, Ghani AC, Miller WC, Hoffman IF, Pettifor AE, Kamanga G, Martinson FE, Cohen MS. The role of acute and early HIV infection in the spread of HIV and implications for transmission prevention strategies in Lilongwe, Malawi: a modelling study. Lancet. 2011 Jul;378(9787):256–268. doi: 10.1016/S0140-6736(11)60842-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Quinn Thomas C. Population migration and the spread of types 1 and 2 human immunodeficiency viruses. Proceedings of the National Academy of Sciences. 1994 Mar;91:2407–2414. doi: 10.1073/pnas.91.7.2407. Colloquium Paper. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Reidy WJ, Goodreau SM. The role of commercial sex venues in the HIV epidemic among men who have sex with men. Epidemiology. 2010 May;21(3):349–359. doi: 10.1097/EDE.0b013e3181d62147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Reniers G, Armbruster B. HIV status awareness, partnership dissolution and HIV transmission in generalized epidemics. PLoS ONE. 2012;7(12):e50669. doi: 10.1371/journal.pone.0050669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Rocha LE, Liljeros F, Holme P. Simulated epidemics in an empirical spatiotemporal network of 50,185 sexual contacts. PLoS Comput Biol. 2011 Mar;7(3):e1001109. doi: 10.1371/journal.pcbi.1001109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Romieu I, Sandberg S, Mohar A, Awerbuch T. Modeling the AIDS epidemic in Mexico City. Hum Biol. 1991 Oct;63(5):683–695. [PubMed] [Google Scholar]
- 63.Sawers L, Isaac AG, Stillwaggon E. HIV and concurrent sexual partnerships: modelling the role of coital dilution. J Int AIDS Soc. 2011;14:44. doi: 10.1186/1758-2652-14-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Woodrow Setzer R. odesolve: Solvers for ordinary differential equations. 2012 Version 0.9-9. [Google Scholar]
- 65.Sorensen SW, Sansom SL, Brooks JT, Marks G, Begier EM, Buchacz K, Dinenno EA, Mermin JH, Kilmarx PH. A mathematical model of comprehensive test-and-treat services and HIV incidence among men who have sex with men in the United States. PLoS ONE. 2012;7(2):e29098. doi: 10.1371/journal.pone.0029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tobin KE, German D, Spikes P, Patterson J, Latkin C. A comparison of the social and sexual networks of crack-using and non-crack using African American men who have sex with men. J Urban Health. 2011 Dec;88(6):1052–1062. doi: 10.1007/s11524-011-9611-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.UNAIDS Reference Group on Measurement and Modeling. HIV: consensus indicators are needed for concurrency. Lancet. 2010 Feb;375(9715):621–622. doi: 10.1016/S0140-6736(09)62040-7. [DOI] [PubMed] [Google Scholar]
- 68.van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences. 2002 Nov;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 69.Wagner BG, Blower S. Universal Access to HIV Treatment versus Universal ‘Test and Treat’: Transmission, Drug Resistance & Treatment Costs. PLoS ONE. 2012;7(9):e41212. doi: 10.1371/journal.pone.0041212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wawer MJ, Gray RH, Sewankambo NK, Serwadda D, Li XB, Laeyendecker O, Kiwanuka N, Kigozi G, Kiddugavu M, Lutalo T, Nalugoda F, Wabwire-Mangen F, Meehan MP, Quinn TC. Rates of HIV-1 transmission per coital act, by stage of HIV-1 infection, in Rakai, Uganda. Journal Of Infectious Diseases. 2005 May;191(9):1403–1409. doi: 10.1086/429411. [DOI] [PubMed] [Google Scholar]