Turnover and accumulation of genetic diversity across large time-scale cycles of isolation and connection of populations

Abstract

Major climatic and geological events but also population history (secondary contacts) have generated cycles of population isolation and connection of long and short periods. Recent empirical and theoretical studies suggest that fast evolutionary processes might be triggered by such events, as commonly illustrated in ecology by the adaptive radiation of cichlid fishes (isolation and reconnection of lakes and watersheds) and in epidemiology by the fast adaptation of the influenza virus (isolation and reconnection in hosts). We test whether cyclic population isolation and connection provide the raw material (standing genetic variation) for species evolution and diversification. Our analytical results demonstrate that population isolation and connection can provide, to populations, a high excess of genetic diversity compared with what is expected at equilibrium. This excess is either cyclic (high allele turnover) or cumulates with time depending on the duration of the isolation and the connection periods and the mutation rate. We show that diversification rates of animal clades are associated with specific periods of climatic cycles in the Quaternary. We finally discuss the importance of our results for macroevolutionary patterns and for the inference of population history from genomic data.

1. Introduction

Successive environmental changes have often modified species habitat in the past, repeatedly isolating and connecting populations, successively suppressing and allowing migration between them. During the climatic cycles of the Quaternary period, many species experienced repeated long periods of isolation into refugia followed by population reconnection [1]. At least five wet–dry periods occurred within the African continent in which water-level fluctuations have successively isolated and connected ecosystems [2]. Such dynamics are often associated with rapid species and population diversification, for example, allopatric differentiations of African buffalo populations [3], giraffe [4] and their associated predators (e.g. lions [5]). Similarly, repeated hybridizations within and between watersheds are expected to have played an important role for Cichlid adaptive radiation [6,7]. In Europe and North America, past climatic cycles led to isolation and connection events in many land animals such as mammals [1], birds [8], insects [9], and also in marine, coastal and freshwater species [10,11]. It is thus now widely recognized that climatic and geological events impact population genetics and speciation patterns at different temporal and spatial scales [12].

Isolation and connection events are common features of virus history. Their dependency on the host isolate viral populations in between transmission events. Events of reconnection of populations occur through superinfections (co-infections) [13,14]. Such isolation and connection events have been widely observed and constitute a major cause of pandemics and failures in virus control. For example, a mix of swine, avian and human influenza was responsible for the 2009 swine flu outbreak [15].

Previous studies showed that population genetic diversity is slightly impacted by migration fluctuation and that its influence can be approximated with an effective migration rate [16,17]. By contrast, high transient values of genetic diversity can be observed following a single [18] or multiple [19] connection events. Those results raised several questions. In particular, would these high transient values of genetic diversity cumulate, be maintained or decrease under cycles of isolation and connection? Answers to this question are not only of theoretical interest, but also have strong implications for the understanding of the mechanisms of adaptation and diversification. Adaptation from standing genetic variation might be more common than from de novo mutations as alleles from stranding genetic variation are present at higher frequency, can switch selective value and are compatible with the background genome [20–23]. Transient excesses of genetic diversity could then provide the raw material for adaptation from standing genetic variation. Similarly, it could increase diversification by promoting speciation [24] and decreasing extinction rate (preventing inbreeding depression [25], but see outbreeding depression [26]). This view is supported by theoretical and empirical works on speciation and adaptive radiation, which suggest that a high level of pre-existing neutral genetic diversity in founder populations is determinant to have a high rate of speciation [21,27–30]. Finally, simulation studies have shown that cycles of isolation and connection of populations can trigger species diversification [31].

While a single [18] or multiple [19] events of populations connection can generate a large excess of neutral genetic diversity within populations, the conditions of existence and maintenance of such genetic diversity excesses remain to be determined. To investigate these questions, we analytically describe the dynamics of genetic diversity under successive periods of isolation and connection of populations (migration cyclically takes a value of 0 and m) of different durations. Assuming that all alleles are selectively neutral, we disentangle the relative importance of the length of the isolation and connection periods in regard to the mutation rate, the migration rate, the number of populations and the initial population genetic diversity. We characterize equilibrium trajectories and transient values of genetic diversity towards equilibrium. We determine four domains in which genetic diversity has a determined behaviour in regards to genetic diversity accumulation and turnover. Then, using clades from the main animal orders, we assess the relationship between diversification rate and length of the isolation and connection periods during the climatic cycles of the Quaternary. Finally, we discuss the implication of our results for species adaptation to novel environments, macroevolution and the inference of population history.

2. Dynamics of genetic diversity under cycles of connection and isolation

To study the dynamics of genetic diversity, we consider n populations of size N (diploid individuals) that are cyclically connected and isolated. Connection and isolation events are of regular periods of length P generations each. Under this model, we determine the recursion equations describing the dynamics of genetic diversities within and across isolation and connection periods and the long-term equilibrium trajectory of genetic diversity. We assume a finite island model with migration that varies between 0 (isolation) and (n − 1)/n (panmixia [32,33]), non-overlapping generations (Wright–Fisher model [34,35]) and consider that mutations (rate μ) follow the infinite allele model [36].

(a). The dynamics of genetic diversities within connection and isolation periods

The dynamics of genes in populations under the finite island model can be described by transitions in gene identities between generations [33]. Using the relationship between gene identity, F, and genetic diversity, H, H = 1 − F, the genetic diversity H(t) at generation t can be decomposed into the within-population genetic diversity, h_s(t), and the between-population genetic diversity, h_b(t) [33]:

2.1

where h_s(t) and h_b(t) correspond to the probability that two genes, randomly sampled from the same and from different populations, respectively, are different [37].

The dynamics of genetic diversity (equation (2.1)) can be described solving the equations of [33] (electronic supplementary material, S1). The change in genetic diversities after P generations during a connection period and during an isolation period, H_c(P) and H_i(P), respectively, become

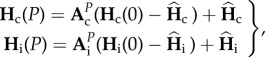2.2

where H_c(0) and H_i(0) are the initial genetic diversities during the connection and the isolation periods 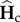and and are their expected value at equilibrium [36,38]. Matrices A_c and A_i are transition matrices which determine the probability of identity of two genes in the same or in different populations, given their previous identity in the same or in different populations, they follow [33]

2.3a

with parameters

2.3b

2.3c

2.3d

2.4

In equation (2.3a), a (resp. b) corresponds to the probability that two genes sampled in the same population (resp. different populations) were in the same population in the previous generation, and c corresponds to the probability that two genes sampled in the same population are copies of the same gene (from [39]); (1 − μ)² corresponds to the probability that neither of the two genes mutated. Thus, (1 − μ)²a(1 − c) (resp. (1 − μ)²b(1 − c)) is the probability that two genes that were identical and in the same population (resp. different populations) at a given generation are still identical and in the same population at the next generation; (1 − μ)²(1 − a) (resp. (1 − μ)²(1 − b)) is the probability that two genes that were identical and in the same population (resp. different populations) at a given generation are still identical and in different populations at the next generation.

(b). The dynamics of genetic diversities across cycles of connection and isolation

From equation (2.2), we derive the recurrence equations describing the dynamics of genetic diversity across multiple cycles k of connection and isolation. We obtain the genetic diversities, 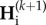, at the end of any cycle k + 1 (end of isolation period), given genetic diversities, 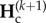, at the end of the connection period of the same cycle k + 1. Similarly, 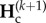depends on 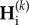, the genetic diversities at the end of the previous cycle k, thus we have

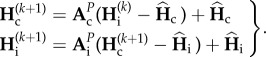2.5

These equations provide a full description of the transient dynamics of genetic diversities across any number of cycles k of duration P. Equation (2.5) can be solved analytically. To do so, we first substitute the expression of in the equation of (equation (2.5)), which leads to an inhomogeneous linear recurrence equation:

2.6a

where

2.6b

and C is a constant vector which depends on the values of 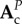, 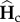and .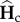

As matrix I − Γ_c is invertible, equation (2.6) has an equilibrium value, 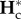, and its solution is

2.7

Consequently, the dynamics of genetic diversities at the end of each cycle k are determined by matrix Γ_c. Similarly, the matrix 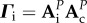determines the dynamics of 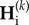. As Γ_i and Γ_c have the same eigenvalues, the behaviour of genetic diversity studied here is independent of the order of the sequence of connection and isolation events.

(c). Equilibrium trajectory of genetic diversities under cycles of connection and isolation

The equilibrium trajectory of genetic diversities is reached when two consecutive isolation events, with a connection event in between, have the same genetic diversity values, i.e. when

2.8

Denoting 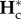and 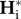the equilibrium values of 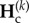and 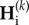, respectively, equations (2.5) and (2.8) lead to

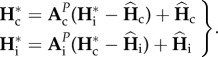2.9

By solving equation (2.9), we have

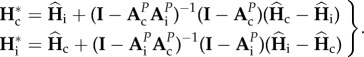2.10

From equation (2.10), it can be seen that the equilibrium trajectory depends only on the parameters of the model (M, θ, n, N and P), and are independent from the initial value of genetic diversities.

(d). The duration of the transient dynamics and the behaviour of genetic diversities

Here, we determine the duration of the transient dynamics (relaxation time or time to equilibrium values) for the within- and between-population genetic diversities during connection and isolation periods—respectively P_C, P_T, P_I and P_S—and we show how they influence the behaviour of genetic diversities across and within cycles. We define the relaxation time τ as the time required to converge to equilibrium value, such that λ^τ = δ and thus τ = ln(δ)/ln(λ) with δ a small value (0 < δ < 1) and λ the corresponding eigenvalue in the transition matrix. The relaxation times for h_s and h_b within a connection (P_C and P_T) and an isolation event (P_I and P_S) are thus determined by the two eigenvalues of matrix A_c and the two eigenvalues of matrix A_i (from highest to lowest). From equations (2.3a) and (2.4), and assuming small migration and mutation rates (i.e. 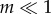and 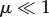) and large population sizes (i.e. 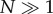), and as ln(1 − X) = −X + o(X), we have

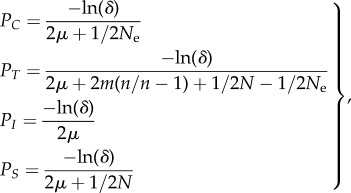2.11

where 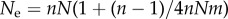corresponds to the effective population size under the finite island model [40].

The expressions of P_C, P_I and P_S in equation (2.11) have also an interpretation in the coalescence framework (the ‘coalescent with killings’ [41]) as the denominator in expressions corresponds to the log probability that lineages did not mutate or coalesce within a generation.

Given the relaxation times and the period length P, we can determine whether genetic diversities remain in transient states. Five situations can be described.

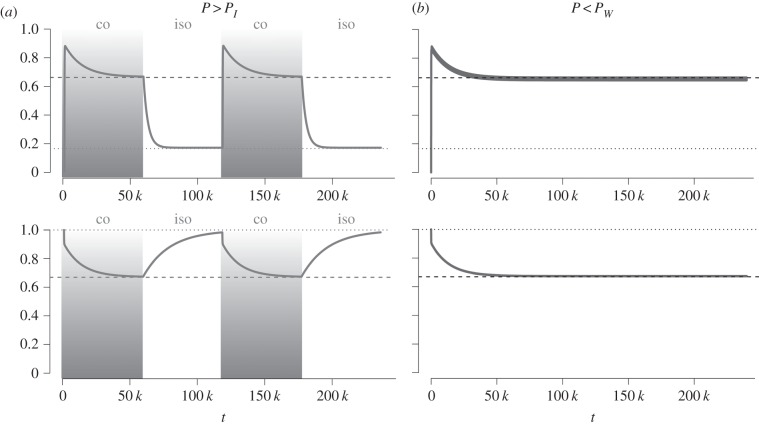
First, both within- and between-population genetic diversities reach successively their equilibrium values during isolation and connection periods within a timeframe shorter than P (i.e. the highest relaxation time from equation (2.11), P_I, is smaller than P; figure 1a). Therefore, after each event, 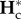and 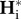tend to their respective equilibrium, 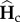and .

Figure 1.

Trajectories of within- (h_s) and between-population (h_b) genetic diversities under cycles of isolation and connection: (a) in the long-period domain P > P_I and (b) in the short-period domain P < P_W. The dashed and dotted lines represent the expected equilibrium value when populations are connected and isolated, respectively. In (a), both h_s and h_b reach their expected equilibrium value at the end of each connection and isolation period. In (b), both h_s and h_b tend to their equilibrium value of connection (dashed line) with very small fluctuations. Parameters are M = 40, n = 10, N = 2 000, μ = 2.5 × 10⁻⁵. (a) P = 60 000, (b) P = 150.

Second, genetic diversities reach their equilibrium value during the connection periods, but not during isolation periods, i.e. P_I and P_C (from equation (2.11)) are larger and smaller than P, respectively. 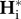does not reach the isolation equilibrium value within P, whereas 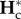tends to its equilibrium value within P. Genetic diversities at the beginning of the connection period have transient values corresponding to the one observed at the end of the isolation period.

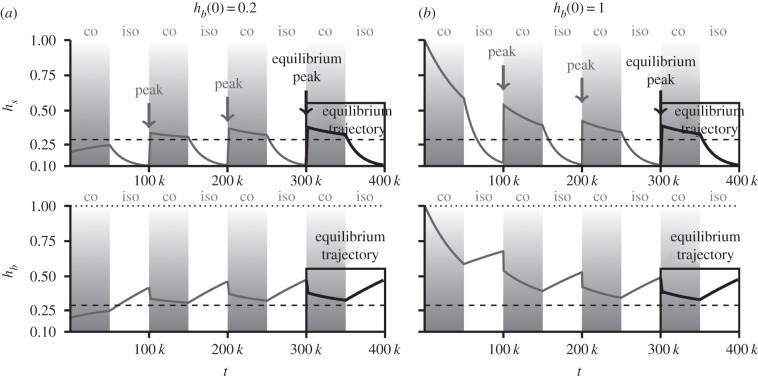
Third, genetic diversities do not reach their equilibrium value, neither during isolation nor during connection periods. This implies that all relaxation times during connection and isolation are larger than P. The trajectory of the successive peaks of h_s (i.e. the successive maximum values of h_s in each cycle) monotonously tends to an equilibrium value (arrows in figure 2, and electronic supplementary material S2 for panmixia). However, the trajectory of genetic diversities to their equilibrium values presents strong fluctuations (figure 2), caused by the succession of peaks of genetic diversity generated by connection events. Their direction, increasing or decreasing, depends on the initial value of between-population genetic diversity, h_b(0). When h_b(0) is below its equilibrium value, successive connection events generate peaks of genetic diversity of increasing values (figure 2a). When h_b(0) is above its equilibrium value, successive connection events generate peaks of genetic diversity with decreasing values (figure 2b).

Figure 2.

Trajectories of within- (h_s) and between-population (h_b) genetic diversities under cycles of isolation and connection in the domain P_W < P < P_I when initial genetic diversity h_b(0) is (a) low and (b) high. In (a), when h_b(0) is low, the successive peaks of within-population genetic diversity (grey arrows) increase in size, while in (b) they decrease in size. In both (a) and (b), the equilibrium trajectories of genetic diversity (framed by a rectangle) are the same. Parameters are M = 400, θ = 0.1 n = 4, N = 10 000, P = 50 000 generations.

Fourth, periods of isolation P are so short that they do not impact values of genetic diversity (negligible genetic differentiation during isolation). In this situation, the value of genetic diversities at the end of the isolation period is close to the one at the end of the connection period of the same cycle, k, and we have 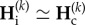. From equation (2.5), this implies that the smallest eigenvalue, λ, of matrix A_i at the power P is close to 1, 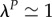. Consequently, we can define the maximum number of generations, P_W, for which genetic diversities are not impacted by isolation periods. P_W can be obtained from 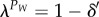, where δ′ is a small number. Thus, we have

2.12

The dynamics of genetic diversities when the period is smaller than P_W are illustrated in figure 1a: the first event of connection generates a large peak of genetic diversity, owing to the quick distribution among populations of mutations accumulated during isolation. Following this major change in genetic diversity, the successive isolation and connection events generate only very small fluctuations of genetic diversity values in their trajectories to their equilibrium. The time to reach their equilibrium value is the same as under constant migration (without cycles; electronic supplementary material, S2).

Fifth, genetic diversity values are very high owing to a very high mutation rate and are weakly impacted by connection and isolation events. The limit of the domain can be derived with a threshold value of the scaled mutation rate, θ_sat (the scaled mutation rate is 4Nμ) for which genetic diversities remain high and approximately constant. This situation occurs when 4Nμ/(1 + 4Nμ) > 1 − α, where α is a small number, and implies that 4Nμ > θ_sat = (1 − α)/α. Note that the saturation of genetic diversity values is a consequence of having an infinite allele model.

In summary, we have found five situations where cycles of isolation and connection have a different impact on the trajectories of genetic diversity. Interestingly, the limit between these situations depends mainly on the mutation rate μ, the population size N and the number of generations (duration) of the connection and isolation periods P (see equation (2.11)).

Those results are robust to stochasticity. Indeed, considering that the length of the isolation and connection periods P is a random variable leads to qualitatively similar results, as long as the variance of P is smaller than a determined threshold (electronic supplementary material, S3).

(e). The dynamics of the excess of genetic diversity within populations

We now describe the dynamics of the excess of within-population genetic diversities under cycles of connection and isolation, relative to their expected equilibrium values (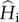 and 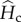), as a function of the period length P and model parameters. We focus on two measures that are representative of two important processes: genetic diversity turnover and accumulation. Genetic diversity turnover is measured as the amplitude of the variations of the excess of within-population genetic diversity within an isolation and connection cycle (i.e. the difference between maximum and minimum value of h_s). This quantity provides information on whether the excess of h_s is fluctuating or stationary. Genetic diversity accumulation is measured as the mean excess of within-population genetic diversity during the cycles. This quantity provides information on the overall excess of h_s produced by the cycles of isolation and connection. These values are computed numerically from equations (2.2) and (2.5) and represented in figure 3.

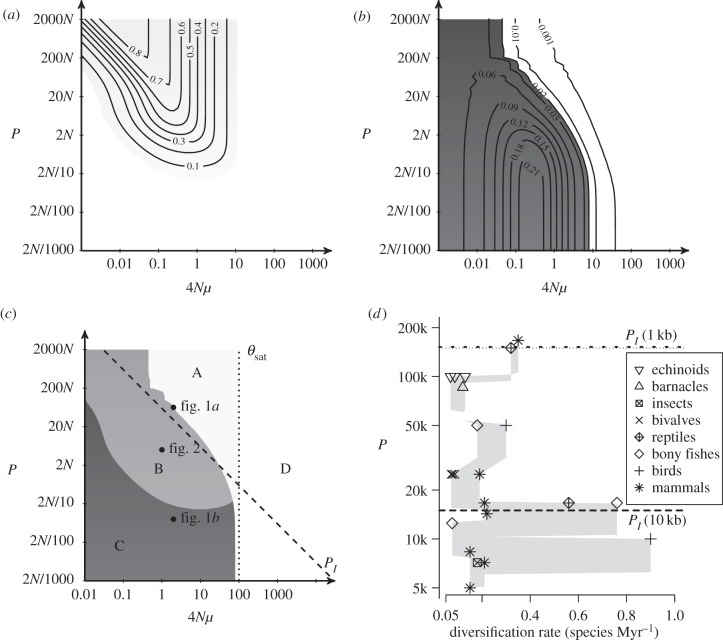
Figure 3.

(a) Turnover and (b) accumulation of within-population genetic diversity h_s during cycles of isolation and connection, as a function of the period P and the scaled mutation rate 4Nμ, (c) domains of turnover and accumulation of h_s, (d) relationship between P and the net diversification rate of clades from the major animal orders. Turnover of h_s is measured as the amplitude of the variations of h_s within a cycle. Accumulation of h_s is measured as the mean excess of h_s per generation compared to its expected equilibrium value. In (c), Domain A presents large turnover of h_s. Domain B presents both turnover and accumulation of h_s. Domain C presents small turnover and large accumulation of h_s. In domain D, h_s saturates and all h_s values are larger than 0.9 during the cycles. Parameters in (a–c) are n = 10 populations, m = 0.01 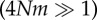, 2N = 1000 for each population, 200 000 generations. (d) P and net diversification rate for species representative of the main animal orders: mammals (Muridae, Ursidae, Bovidae, Cervidae, Hystricidae, Cercopithecidae, Cebidae, Cricetidae [42]), birds (passerines, [43], Darwin's finches, [44]), reptiles (collubrid snakes, [42], annoline lizards, [45]), bony fishes (Ictalurus, Cyprinidae, [42], cichlids, [46]), insects (Tipulidae, Formicinae [42]), bivalves (Petricolidae, Mesodematidae, Semelidae [42]), barnacles [42] and echinoids (Mellitidae, Clypeasteridae, Laganidae [42]). P corresponds to the period of climatic cycles in generations (100 000 years cycles divided by the generation time of each species). The shaded area represents the range of diversification rates, computed in sliding windows of 0.2 log₁₀(years) (see alternative window sizes in the electronic supplementary material, figure S1). The dashed and dotted lines represent the values of P_I for a gene of 1 and 10 kb (haplotype blocks in Eukaryotes range from 10 kb to hundreds of kb [47]), respectively, and a mutation rate of 10⁻⁸ bp⁻¹ (mutation rates in animals range from 10⁻⁹ bp⁻¹ to 5.10⁻⁸ bp⁻¹ [48]).

The highest turnover of genetic diversity is observed when the period lengths are large (P > 2N; figure 3a) and when the mutation rate is moderate (4Nμ < θ_sat = 9). The lowest turnover of genetic diversity is observed when the mutation rate is high (4Nμ > θ_sat = 9) or when 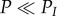. When 4Nμ > θ_sat, genetic diversity is saturated by mutations: isolation and connection events do not impact the value of genetic diversity in populations as the genetic diversity is at its maximum value (close to 1).

The highest amount of cumulated genetic diversity is observed when isolation and connection periods are smaller than 2N. In this case, relaxation times are larger than the periods. Consequently, genetic diversities remain in a transient state and can cumulate over time. The lowest cumulated genetic diversity is observed when the mutation rate is high and genetic diversity is saturated by mutations (4Nμ > θ_sat), or when P > P_I.

From the estimation of the value of genetic turnover and accumulation, we can define four domains in which genetic diversities have a specific behaviour in regard to turnover and accumulation (figure 3c). In domain A, genetic diversity turnover is observed and no accumulation of genetic diversity occurs. Domain A is defined by P > P_I and 4Nμ < θ_sat. In domain B, both accumulation and turnover of genetic diversity are observed. Domain B is defined by approximately P_I/60 < P < P_I, and 4Nμ < θ_sat. In domain C, genetic diversity cumulates across cycles, and there is almost no variation of genetic diversities within cycles. Domain C is defined by 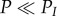and 4Nμ < θ_sat. Finally, in domain D, genetic diversity is saturated, 4Nμ > θ_sat, thus any demographic change will not impact its value.

3. Species diversification and climatic cycles

An important result of our model is that populations which undergo long-period cycles (domain A) experience a turnover of genetic diversity, whereas populations which undergo short-period cycles (domain C) cumulate genetic diversity. To assess whether these two behaviours could have an impact on species diversification patterns, we investigate the relationship between the known climatic cycles and empirical net diversification rates of animal clades in the Quaternary period (see corresponding reference in the legend of figure 3d); the clades chosen are representative of the main animal orders and include—but are not restricted to—radiations. Recent Quaternary climatic cycles have a periodicity of approximately 100 000 years [49,50]. From this periodicity, we can estimate for each animal the corresponding period P (in generations). Then, we computed the range of diversification rates as a function of the period P (figure 3d).

The range of diversification rates (shaded area figure 3d) decreases with period P (two-sided Spearman correlation test, coefficient −0.76139, p-value < 2.2 × 10⁻¹⁶). The highest diversification rates (the most notorious examples of adaptive radiations: cichlid fishes, Darwin's finches and colubrid snakes) are observed between P = 10 000 and P = 15 000 generations and are associated with the domains B and C where genetic diversity is accumulated across cycles.

These results are expected to be robust to shorter-period cycles (e.g. 20 000 or 41 000 years, as in the early Quaternary [50]) as we use a logarithmic scale for the period, which is weakly affected by a fivefold change. In addition, longer isolation periods than connection periods (as expected in glacial oscillations) will not change the general behaviour of our model. Indeed, the amount of cumulated genetic diversity is mainly determined by the duration of the isolation period and P_I (figure 3c) that is defined by model parameters during isolation.

4. Discussion

Although there is increasing evidence of the importance of large-scale environmental changes for the generation and maintenance of genetic diversity, they received few and only recently attention [19,31]. Our study identifies domains where genetic diversities have specific behaviours. In domain A (P > P_I and 4Nμ < θ_sat; figure 3c), genetic diversities undergo large variations, allowing for a high turnover of genetic diversity. The lower limit P_I of this domain can be large; for example, we show that for animals, it is of the order of 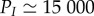generations for typical mutation rates and a sequence of 10 kb (figure 3d). In this domain, high rates of molecular evolution are expected for animals with a short generation time (as observed for small mammals [51], birds [52] and invertebrates [53]). In domains B and C (P < P_I and 4Nμ < θ_sat; figure 3) genetic diversity cumulates across successive cycles of isolation and connection. Species experiencing such cycles of isolation and connection are predicted to have large amounts of genetic diversity, increasing their adaptive potential [20,21]. Interestingly, species with the highest diversification rates of the Quaternary belong to this domain, for example, the cichlid fishes in Africa [46] and Darwin's finches [44]. We show that successive isolation and connection periods in domain B (figure 2) can also lead to a decrease in genetic diversity when the initial level of genetic diversity is high. The existence of two alternative outcomes could explain why populations which underwent similar isolation and connection events in their history can display different genetic signatures such as found for the meadow grasshopper (0.7–0.9% pairwise sequence difference) and for the hedgehog populations (6–12% pairwise sequence difference) in Europe [1]. In addition, it could partially explain why some clades which experienced short-period cycles of connection and isolation do not display large diversification rates (mammals [42,54]).

Isolation events might be associated with a reduction of the size of populations [1,55,56]. While strong bottlenecks can cause population extinction, a reduced population size will not affect the relaxation time P_I (equation (2.11)). Thus, the limit between the domains (figure 3c) where genetic diversity cumulates or turnover across cycles remains unchanged. However, reduced population size will decrease the relaxation time P_W, limiting the size of the domain (C; figure 3c) where genetic diversities remain approximately constant within cycles. Population dynamics within cycle (population growth, generation overlap) are also expected to impact our predictions. Slow recovery from population size changes will decrease P_W and strong generation overlap will reduce the transient excess of genetic diversity.

Our results suggest that climatic cycles may drive high genetic diversity accumulation or turnover in populations, leading, respectively, to increased or reduced diversification rates. Although the relationship between genetic diversity and species diversification is supported by some empirical [24,28] and theoretical evidence [57], this hypothesis is still in debate. More generally, there is a lack of comprehensive understanding of the relationship between micro- and macroevolution patterns. Most investigations focused on adaptation and ignored the impact of neutral demographic changes [58,59]. These relationships deserve more investigations, which might answer critical questions in phylogeography, such as the origin of species' pumps [60].

Hughes & Eastwood [61] suggested that extrinsic causes such as geological events, rather than key innovations, could trigger species diversification. Our results propose that such extrinsic causes lead to different dynamics of the genetic diversity depending on species' generation time. We expect that other life-history traits such as dispersal, generation overlap, habitat specialization or mating system might also influence the level of genetic diversity and the rate of molecular evolution [62]. Further investigations in that direction are needed to provide a better understanding of the interaction between extrinsic causes, life-history traits and patterns of diversification.

Our result have implications for the inference of population demographic history from genome polymorphism [63]. We predict that genomic regions having different diversity levels might have different diversity dynamics (e.g. increase and decrease) when experiencing the same cycles of connection and isolation. This effect might be important given the high heterogeneity of polymorphism along genomes [64], or when considering molecular markers with different mutation rates (e.g. allozymes, single nucleotide polymorphisms and microsatellites). In addition, genomic regions might experience different levels of gene flow [65] which could have a direct impact on the dynamics of genetic diversity. These features should be accounted for and could be used to develop robust inference methods. A large range of demographic scenarios, including multiple migration changes, have been implemented in inference methods [63,66], but very few methods account for such heterogeneity [67].

Our results suggest that reconnection events (secondary contacts) after large periods of isolation can provide to populations a large excess of genetic diversity. Thus, they reveal a mechanism that maintains high genetic diversity as unexpectedly observed in some domesticated organisms despite strong selection (e.g. gene flow between domesticated and wild populations, in rice [68] and cats [69]) and also observed—although undesirable—in pathogens [70]. This mechanism—events of isolation and reconnection over a large number of generations—is predominant in pathogens and occurs at different levels and scales. Indeed, pathogens can jump from one species to another after a very long period of isolation and adapt rapidly (e.g. avian flu [15,71] and human immunodeficiency virus [14]). Pathogen admixture can occur between related populations from different isolated geographical regions [13,72]. Pathogens are isolated within hosts in between transmission events and can reconnect through superinfection [73]. Finally, isolation and reconnection events within hosts between genetic compartments (e.g. cerebrospinal fluid, gut mucosa, urine, plasma) are increasingly recognized [74,75]. How pathogen diversity is related to their past demography, their structure or the environment they encountered remain to be explored in more detail. This might be a timely issue, because organisms (invasive species, local adapted population, viruses and other pathogens) have increased opportunities to encounter previously isolated related populations owing to climate change and increased ease of travel worldwide.

Data accessibility

This study involves no original data.

Funding statement

This project was supported by the Swiss National Science Foundation (grants no. PZ00P3_139421/1 and 31003A-130065), by an Interdisciplinary grant from the Faculty of Biology and Medicine (FBM) of the University of Lausanne and by the Department of Ecology and Evolution of the University of Lausanne.