Efficient Algorithms for Multivariate Linear Mixed Models in Genome-wide Association Studies

Abstract

Multivariate linear mixed models (mvLMMs) are powerful tools for testing SNP associations with multiple correlated phenotypes while controlling for population stratification in genome-wide association studies. We present computationally-efficient algorithms for fitting mvLMMs and computing likelihood ratio tests that improve on existing approximate methods in i) computation speed, ii) power/p value calibration, iii) ability to deal with more than two phenotypes. We illustrate these features on real and simulated data.

Multivariate linear mixed models (mvLMMs)¹ have been widely applied in genetics, including estimating cross-tissue heritability of gene expression², assessing pleiotropy and genetic correlation between complex phenotypes ^3-6, detecting quantitative trait loci⁷, understanding evolutionary patterns⁸ and assisting animal breeding programs⁹. Recently, mvLMMs have become increasingly important in genome-wide association studies (GWASs), both because of their effectiveness in accounting for sample relatedness^3,7,10 and population stratification^3,11-17 and because of a growing appreciation of the power gains from multivariate association analyses^3,18-22. Indeed, ²² emphasizes that multivariate analyses can increase power not only to detect pleiotropic genetic variants, but also genetic variants that affect only one of multiple correlated phenotypes.

However, fitting mvLMMs is computationally non-trivial, involving a multi-dimensional optimization for a potentially non-convex function. Current algorithms for fitting a single mvLMM (implemented in software GCTA^4,23, WOMBAT²⁴, ASREML²⁵) employ two types of optimization algorithm: an initial Expectation-Maximization-like (EM) algorithm, followed by a Newton-Raphson-like (NR) algorithm. This combines the benefits of the stability of EM (every iteration increases the likelihood) with the faster convergence of NR (²⁶; Supplementary Note). Their computational complexity for n individuals and d phenotypes is O(t₁n³d³+t₂n³d⁷) where t₁, t₂ are the maximum number of iterations of EM and NR respectively (Supplementary Note). Using these methods to perform the likelihood ratio test (LRT) in GWAS would require repeated application to the s SNPs, with resulting computational complexity O(s(t₁n³d³+ t₂n³d⁷)), which is impractical for GWAS with large s and moderate n. Consequently no existing method can perform the LRT for mvLMMs in GWAS settings. The only available method along these lines (MTMM³) can perform only an approximate LRT, and only for two phenotypes.

Here, we present a computationally-efficient algorithm, and a software implementation in GEMMA^16,17 (Genome-wide Efficient Mixed Model Association; Supplementary Software; http://stephenslab.uchicago.edu/software.html), for fitting mvLMMs with one covariance component (in addition to the residual error term), and for performing the LRT for association in GWASs. The algorithm builds on linear algebra techniques previously used for univariate LMMs^12,13,17, and, combined with several additional tricks, extends them to multivariate LMMs. Our algorithms very substantially reduce the computational burden of computing LRTs for GWAS, by avoiding repeating the expensive O(n³) operations for every SNP. Specifically, after an initial single O(n³) operation (eigen-decomposition of the relatedness matrix), our algorithms have per-SNP complexity that is O(n²), reducing the overall computational complexity to O(n³+n²d+s(n²+t₁nd²+t₂nd⁶)). In effect, our algorithms (detailed in Supplementary Note) provide the multivariate analogue of the univariate algorithms EMMA²⁷, and FaSTLMM/GEMMA/CM^12,13,17. Our algorithms provide the first computationally practical approach to computing LRTs for mvLMMs in reasonably large GWAS (e.g. 50,000 individuals) and modest numbers of phenotypes (e.g. 2-10).

To illustrate the benefits of our new algorithms we used two data sets: a mouse GWAS from the Hybrid Mouse Diversity Panel (HMDP) with four blood lipid phenotypes and a human GWAS from the Northern Finland Birth Cohort 1966 (NFBC1966) with four blood metabolic traits (Online Methods). The HMDP data are a small GWAS with strong relatedness among many individuals; the NFBC1966 data are a larger GWAS with weak relatedness among most individuals.

Even for fitting a single mvLMM, our algorithms and implementation are substantially faster than existing implementations of existing algorithms in software GCTA and WOMBAT (Table 1). For example, for the NFBC1966 data, with d=4, GEMMA takes about 7 minutes compared with 8 hours for WOMBAT. The gains for larger d would be even greater.

Table 1.

Comparison of computing time of different methods for parameter estimation in a single mvLMM, and for performing likelihood ratio tests in GWASs. Results are shown for both HMDP and NFBC1966 data sets. All computation was performed on a single core of an Intel Xeon L5420 2.50GHz CPU. n is the number of individuals, s is the number of SNPs, d is the number of traits, c is the number of covariates (c=1 here), t₁ is the number of iterations used in the EM type algorithm and t₂ is the number of iterations used in the NR type algorithm. Notice that the computing time for GEMMA is essentially the same for all d, because in GEMMA the computing time is dominated by the initial O(n³) eigen-decomposition step; the following optimization iterations are negligible. The sn² step in GEMMA could be replaced with an snr step if the relatedness matrix is of rank r.

Method	Time Complexity	Computation Time
		HMDP (n=656, s=108,562)			NFBC1966 (n=5255, s=319,111)
		d=2	d=3	d=4	d=2	d=3	d=4
Fitting a single mvLMM
GEMMA	O(n3+n2d+n2c+t1nc2d2+t2nc2d6)	< 1 s	< 1 s	< 1 s	6.7 min	6.7 min	6.7 min
WOMBAT	O(t1n3(d + c)3+t2n3d7)	12.5 s	39.2 s	71.0 s	31.0 min	127.6 min	477.3 min
GCTA	O(t1n3(d + c)3+t2n3d7)	11.2 s	--	--	38.2 min	--	--
Genome-wide applications
GEMMA	O(n3+n2d+n2c+s(n2+t1nc2d2+t2nc2d6))	6.2 min	13.7 min	28.5 min	4.4 h	4.8 h	5.8 h
MTMM	O(t1n3(d + c)3+t2n3d7+sn2d2)	16.4 min	--	--	58.0 h	--	--

However, the more practically important gains of our new algorithms come in GWAS applications. Here, no existing algorithm is practical for computing the LRT for even d=2. Extrapolating from Table 1 suggests that existing algorithms, if implemented in software, might take over 14 days for HMDP and over 18 years for NFBC1966. As far as we are aware, the only current practical competitor for our method is a method implemented in software MTMM³, which uses an approximate LRT (aLRT)^11,15 to reduce per-SNP computation time to O(n²). Specifically, the aLRT avoids the expensive repeated optimization of the variance components under the alternative H₁ for each SNP, by re-using part of the pre-estimated variance components under the null H₀ (fit using software ASREML). However, the aLRT is guaranteed to underestimate the LRT (Supplementary Note), and in the univariate setting this has been shown to produce mis-calibrated p values and/or loss of power^13,17.

To illustrate this in the multivariate setting we performed null and alternative simulations using the HMDP data (Online Methods). Consistent with the univariate findings, MTMM p values are systematically larger than expected under the null, with the most significant p values being almost an order of magnitude less significant than they should be (Fig. 1a). In contrast, p values from the GEMMA LRT are well-calibrated (Fig. 1a). Thus, although in principle the mvLMM likelihood surface could be non-convex, with multiple local optima, and this could cause our p values to be mis-calibrated, in practice this appears not to happen. However, we found that obtaining well-calibrated p values requires both the EM and NR algorithms: use of EM only can lead to poor convergence of the LRT, resulting in underestimation of p values similar to MTMM (Supplementary Fig. 1). The systematic inflation of MTMM’s p values under the null presumably accounts for MTMM’s loss of power relative to GEMMA in simulations under the alternative (Fig. 1c).

Figure 1.

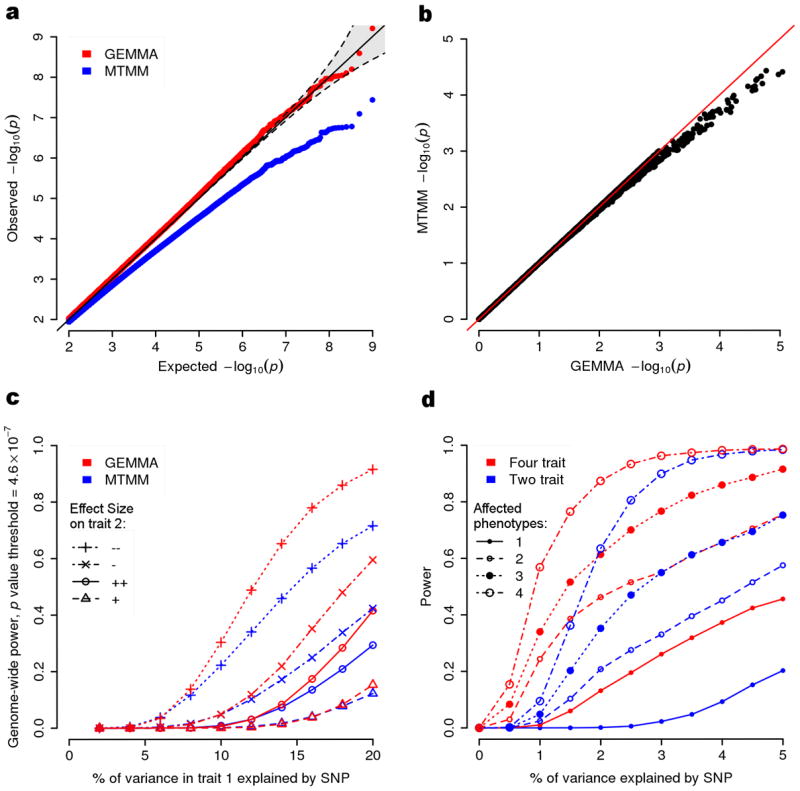
Illustration of the statistical benefits of our new algorithms implemented in GEMMA. (a) A QQ-plot showing the improved calibration of GEMMA p values compared with those from MTMM for simulated null data. Gray shaded area indicates 0.025 and 0.975 point-wise quantiles of the ordered p values under the null distribution. (b) GEMMA p values are consistently more significant than MTMM p values for the HMDP data. (c) Gain in power for GEMMA compared with MTMM in four different simulation scenarios based on the HMDP data. x-axis in shows the proportion of phenotypic variance in the first phenotype explained (PVE) by the SNP, while the point symbol and line type indicate the SNP effect direction (compared with its effect on the first phenotype) and size (quantified by PVE) on the second phenotype (+: opposite direction, 0.8PVE; ×: opposite direction, 0.2PVE; o: same direction, 0.8PVE; Δ: same direction, 0.2PVE). (d) Simulation results illustrating the potential gain in power from four-phenotype vs two-phenotype analyses.

We also compared GEMMA and MTMM on the real phenotypes for both datasets. Since MTMM is implemented only for d=2, we analyzed all pairs of traits. For these data, GEMMA ran 2-12 times faster than MTMM (Table 1). In particular, in the NFBC1966 data, GEMMA takes about four hours for a two-phenotype analysis that takes MTMM almost two and a half days. Consistent with the simulations, and with theory, the MTMM p values for HMDP are consistently less significant (up to 6 fold less significant) than p values from GEMMA (Fig. 1b), and in many cases are substantially less significant than would be expected even under the null (Supplementary Fig. 2-3). For NFBC1966 the two methods produce similar p values (Supplementary Fig. 4-5), consistent with univariate assessments that show the aLRT to work well when, as in NFBC1966, the sample size is large, individuals are not closely related and the marker effect size is small.

Our methods and software also make possible, for the first time, GWAS analysis using mvLMMs with more than two phenotypes. Here, we briefly illustrate via simulations and real data analysis the power and benefits of various multivariate analyses.

Figure 1b and Supplementary Figure 6 show simulation results, based on both HDMP and NFBC1966 data, comparing power of the multivariate LRT of all four phenotypes vs conducting all six two-phenotype analyses and applying a Bonferroni correction for the six tests performed. In these simulations the four-phenotype analysis is consistently more powerful (or as powerful) as the two-phenotype analyses, even when only one or two of the four phenotypes are truly associated with genotype (Fig. 1b and Supplementary Fig. 6). While it may seem counter-intuitive that a four-phenotype analysis is more powerful than a two-phenotype analysis even when exactly two phenotypes are associated with genotype, this is actually expected, for reasons discussed in²²: including unassociated phenotypes in the multivariate analysis can increase power if these unassociated phenotypes are correlated with the associated phenotypes.

We also applied four-phenotype, two-phenotype, and univariate analyses to the NFBC1966 data. In total, 45 SNPs from 14 genetic regions pass a significance level of 0.05 after Bonferroni correction (both for the number of SNPs and, in univariate and two-phenotype analyses, for the number of tests) in either the four-phenotype, two-phenotype, or univariate analyses. As expected, some SNPs show stronger signals in the four-phenotype analysis, whereas others show stronger signals in a two-phenotype or univariate analysis. Comparing the four-phenotype analysis with the univariate analysis (Supplementary Table 1 and Supplementary Fig. 7), 16 SNPs were significant in the four-phenotype analysis and not the univariate analysis; whereas 3 SNPs were significant only in the univariate analysis. Comparing the four-phenotype analysis with the two-phenotype analysis (Supplementary Table 2 and Supplementary Fig. 7), 1 SNP was significant in the four-phenotype analysis and not the two-phenotype analysis, whereas no SNP was significant only in the two-phenotype analysis.

These results support the idea that multivariate tests can be more powerful than multiple univariate or pairwise tests. However, it is also clear that in a GWAS setting no single test will be the most powerful to detect the many different types of genetic effects that could occur. Indeed, it is possible to manufacture simulations so that any given test is most powerful²². Thus different multivariate and univariate tests should be viewed as complementary to one another, rather than competing.

Our algorithms are not without limitations. Perhaps the most fundamental is that, like its univariate counter-parts, our algorithms only apply to mvLMMs with one variance component (in addition to the residual error term). However, with additional assumptions our algorithms may be extended to more variance components²⁸. Our methods also require complete phenotypes – this can be dealt with by imputing missing phenotypes before association tests (Supplementary Note and Supplementary Fig. 8). Finally, although our implementation of the EM algorithm scales only quadratically with the number of phenotypes, d, and so could be applied to reasonably large d, in practice there could remain both computational and statistical barriers to applying these methods to even quite modest values of d (e.g. d≈10). Computationally, the number of iterations required to converge for larger d will inevitably increase, and ultimately this could be the main barrier to application for large d. Statistically, the number of parameters in the mvLMM is also quadratic in the number of phenotypes (d(d+1) parameters in the two variance components). Therefore, with moderate sample size, it may be desirable to assume structure for the variance components, or incorporate additional prior information (e.g. ²⁹ and references therein).

The most computationally expensive part of our method, as in the univariate case, is an initial eigen-decomposition. This not only requires a large amount of physical memory, but also becomes computationally intractable in practice for large n (e.g. >50,000). Low rank approximations to the relatedness matrix^12,17,30 can alleviate both computation and memory requirements, and could allow mvLMMs to be applied to very large GWASs.

Online Methods

Software

GEMMA software is available as Supplementary Software and at http://stephenslab.uchicago.edu/software.html.

Genotype and Phenotype Data

We analyzed two data sets: the Hybrid Mouse Diversity Panel (HMDP)³¹ and the Northern Finland Birth Cohort 1966 (NFBC1966) Study³².

The HMDP data includes 100 inbred strains with four phenotypes (high-density lipoprotein, HDL; total cholesterol, TC; triglycerides, TG; unesterified cholesterol, UC) and four million high quality fully imputed SNPs (SNPs are downloaded from http://mouse.cs.ucla.edu/mousehapmap/full.html). We excluded mice with missing phenotypes for any of these four phenotypes. We excluded non-polymorphic SNPs, and SNPs with a minor allele frequency less than 5%. For SNPs that have identical genotypes, we tried to retain only one of them (by using “--indep-pairwise 100 5 0.999999” option in PLINK³³). This left us with 98 strains, 656 individuals and 108,562 SNPs. We quantile transformed each phenotype to a standard normal distribution to guard against model mis-specification. We used the product of centered genotype matrix as an estimate of relatedness^16,17,34,35. Note that the sample size used here is smaller than the original study³¹, and the phenotypes are quantile-transformed instead of log transformed for robustness.

The NFBC1966 data contains 5402 individuals with multiple metabolic traits measured and 364,590 SNPs typed. We selected four phenotypes (high-density lipoprotein, HDL; low-density lipoprotein, LDL; triglycerides, TG; C-reactive protein, CRP) among them, following previous studies³. We selected individuals and SNPs following previous studies^11,32 with the software PLINK³³. Specifically, we excluded individuals with missing phenotypes for any of these four phenotypes or having discrepancies between reported sex and sex determined from the X chromosome. We excluded SNPs with a minor allele frequency less than 1%, having missing values in more than 1% of the individuals, or with a Hardy-Weinberg equilibrium p value below 0.0001. This left us with 5,255 individuals and 319,111 SNPs. For each phenotype, we quantile transformed the phenotypic values to a standard normal distribution, regressed out sex, oral contraceptives and pregnancy status effects³², and quantile transformed the residuals to a standard normal distribution again. We replaced the missing genotypes for a given SNP with its mean genotype value. We used the product of centered and scaled genotype matrix as an estimate of relatedness^11,17,34,35.

In both data sets, we quantile transformed each single phenotype to a standard normal distribution to guard against model misspecification. Although this strategy does not guarantee that the transformed phenotypes follow a multivariate normal distribution jointly, it often works well in practice when the number of phenotypes is small (see, e.g. ²²). For both data sets, we used a standard mvLMM with an intercept term (without any other covariates), and test each SNP in turn. Because the software MTMM relies on the commercial software ASREML to estimate the variance components in the null model, we modified the MTMM source code so that it can read in the estimated variance components from GEMMA.

Simulations

To check if GEMMA and MTMM produce calibrated p values, we randomly selected 100,000 real genotypes in the HMDP data. We simulated 10,000 phenotypes under the null, based on the real relatedness matrix and the estimated genetic and environmental covariance matrices (for HDL and TG). We calculated p values for each SNP-phenotype pair in turn (one billion pairs). We did not perform comparisons based on the NFBC1966 data, partly because GEMMA and MTMM produce identical p values there, and partly because the sample size in NFBC1966 makes it computationally impractical to perform billions of association tests to check for the type I error at the genome-wide significance level.

To compare power between GEMMA and MTMM, we used real genotypes from the HMDP and NFBC1966 data, and we simulated phenotypes by adding genotype effects back to the original phenotypes^15,17. Specifically, we first identified SNPs unassociated with the four phenotypes based on one-phenotype, two-phenotype and four-phenotype analyses (LRT p value > 0.1 in any of the 11 tests). We ordered the SNPs (76,780 in HMDP and 208,145 in NFBC1966) satisfying these criteria by their genomic location, and selected from them 10,000 evenly spaced SNPs to act as causal SNPs. For each causal SNP, we specified its effect size for the first trait (HDL) to explain a particular percentage of the phenotypic variance (proportion of variance explained, or PVE). Afterwards, we specified its effect for the second trait (TG) so that the proportion of variance in the second trait explained by the SNP equals to either 20% or 80% of the PVE in the first trait. We considered effect sizes for the two traits to be either in the same direction or in the opposite directions, and we added the simulated effects back to the original phenotypes to form the new simulated phenotypes. For each pre-specified PVE (ranged from 2% to 20% in HMDP and 0.04% to 0.4% in NFBC1966), we simulated 10,000 sets of phenotypes, one for each causal SNP, and calculated the p value for each SNP-phenotype pair. We calculated statistical power as the proportion of p values exceeding the genome-wide significance level at the conventional 0.05 level after Bonferroni correction (p=4.6×10⁻⁷ for HDMP and p=1.6×10⁻⁷ for NFBC1966). Notice that we simulated phenotypes based on HDL and TG in both data sets, and the two phenotypes are positively correlated in HMDP but negatively correlated in NFBC1966.

Our algorithms rely on fully observed phenotypes. To make the method more widely applicable, we developed a phenotype imputation scheme to impute missing phenotypes where necessary (Supplementary Note). To show the power gain of our imputation scheme versus simply dropping individuals with partially missing phenotypes, we performed a simulation study. Specifically, we used the same set of simulated phenotypes described above, but randomly made 2.5%, 5% or 10% of the individuals to have one phenotype missing. We calculated p values for each SNP-phenotype pair from the two approaches using GEMMA, and calculated statistical power at the conventional 0.05 level after Bonferroni correction.

Finally, we performed a power comparison between the four-phenotype analysis and the two-phenotype analysis using GEMMA, using simulations based on the two data sets. Specifically, we used the same set of 10,000 SNPs described above to act as causal SNPs, and we simulated phenotypes by adding genotype effects to the observed phenotypes, as above. For each causal SNP, we made it to affect either one, two, three or four phenotypes. When the causal SNP affected two or four phenotypes, its effects on randomly selected half of the traits were in the opposite direction as its effects on the other half. When the causal SNP affected three phenotypes, its effects on randomly selected two traits were in the opposite direction as its effect on the third trait. The SNP effect size for each affected phenotype was simulated independently to account for a pre-specified PVE of that phenotype (ranged from 0.5% to 5% in HMDP and 0.04% to 0.4% in NFBC1966), which was further scaled with a random factor draw from a uniform distribution U(0.8, 1). The simulated effects were added back to the original phenotypes to form the new simulated phenotypes. For the four-phenotype analysis, we calculated the p value for each SNP-phenotype pair and we calculated statistical power at the conventional 0.05 level after Bonferroni correction (p=4.6×10⁻⁷ for HDMP and p=1.6×10⁻⁷ for NFBC1966). For the two-phenotype analysis, we obtained the minimal p value from the six pair-wise analyses for each SNP, and calculated statistical power as the proportion of these p values exceeding either the same significance level (p=4.6×10⁻⁷ for HDMP and p=1.6×10⁻⁷ for NFBC1966), or a significance level that was further adjusted to account for the six tests performed (p=7.6×10⁻⁸ for HDMP and p= 2.6×10⁻⁸ for NFBC1966).