Abstract
The electric field created by a condensed phase environment is a powerful and convenient descriptor for intermolecular interactions. Not only does it provide a unifying language to compare many different types of interactions, but it also possesses clear connections to experimental observables, such as vibrational Stark effects. We calculate here the electric fields experienced by a vibrational chromophore (the carbonyl group of acetophenone) in an array of solvents of diverse polarities using molecular dynamics simulations with the AMOEBA polarizable force field. The mean and variance of the calculated electric fields correlate well with solvent-induced frequency shifts and band broadening, suggesting Stark effects as the underlying mechanism of these key solution phase spectral effects. Compared to fixed-charge and continuum models, AMOEBA was the only model examined that could describe non-polar, polar, and hydrogen bonding environments in a consistent fashion. Nevertheless, we found that fixed-charge force fields and continuum models were able to replicate some results of the polarizable simulations accurately, allowing us to clearly identify which properties and situations require explicit polarization and/or atomistic representations to be modeled properly, and for which properties and situations simpler models are sufficient. We also discuss the ramifications of these results for modeling electrostatics in complex environments, such as proteins.
Keywords: vibrational Stark effect, polarizable force fields, electrostatics, intermolecular interactions, MD benchmark
1. Introduction
A molecule in solution experiences a complex range of electrostatic interactions from the solvent molecules in its environment – these interactions play a central role in defining the dynamics and ensemble properties of the liquid solution phase. One way of describing these interactions in a collective fashion is to consider the total electric field they exert on a molecule of interest, or a particular part of that molecule. A key advantage of this electric field picture is that it provides a unifying language for comparing the relative importance of diverse specific interactions such as hydrogen bonds and π-stacking, as well as nonspecific interactions such as dipole-dipole and dipole-induced dipole.
Electric fields can be calculated using models at many different levels of theory,1-7 and possess a clear connection to experimental observables,8-10 especially those involving molecular vibrations.11-17 The frequency shifts of certain vibrations have been shown to report on the local electrostatic field experienced by the vibration.11,14,17,18 Moreover, the sensitivity of a given vibration’s frequency to electric fields can be experimentally calibrated using vibrational Stark spectroscopy,19 wherein an external electric field of order 100 MV/cm is applied onto a vitrified sample containing the vibrational probe of interest, and the resultant effect on the infrared spectrum is recorded.
Over the previous decade, it has been found that several local high-frequency vibrations such as the C=O and C≡N stretch respond to electric fields in a linear fashion,18-20 obeying the equation:
| (1) |
where ν̄obs is the observed frequency of a vibrational probe in a particular environment, is the (absolute) electric field the environment exerts onto the vibrational probe, ν̄0 is the frequency of the probe in a reference state calibrated to zero electric field, and is the vibrational probe’s difference dipole (also called the Stark tuning rate), which is determined by Stark spectroscopy and has values between 0.03–0.1 D/f for different vibrations, translating to field sensitivities of 0.5–1.7 cm−1/(MV/cm)/f.19-21 Where models have been used to assign electric fields to different environments, vibrational frequencies have appeared to maintain linear sensitivity to fields on the order of 101 MV/cm.11,12 is a vector quantity, though for highly localized modes such as the C=O and C≡N stretch, the vibration is assumed to behave as a one-dimensional oscillator, implying that the difference dipole is parallel to the diatomic fragment’s bond axis.19 For a number of vibrational probes we have investigated, the Stark tuning rate has been shown to be largely invariant of the environment’s electric field, leading us to consider it an intrinsic property of the oscillator.20,22,23 f is the local field correction factor, and its meaning and value is described in the discussion.
This effect has been extended to model frequency shifts observed upon introducing vibrational probes into various condensed phase environments – such as solvents,5,23,24 ionic liquids,25,26 membranes,27,28 and proteins6,13,14,20-23,29 – where electric fields arise from local intermolecular interactions. In particular, the suggestion that solvent-induced (optical) frequency shifts are actually Stark effects was first voiced by Platt in 1961,30 and later elaborated by Liptay.31 According to this suggestion, a model for calculating solvent fields (i.e., the electric field the solvent collectively exerts onto a solute) may be able to predict solvent-induced vibrational frequency shifts according to Eq. 1.
Recent work23 using molecular dynamics (MD) simulations with a fixed-charge force field has borne out this prediction. In particular, the use of an atomistic representation of the solvent called attention to the electrostatic effects of specific interactions such as hydrogen bonds, showing that their influence on vibrational frequencies is also amenable to an electrostatic interpretation. The C=O frequency shifts of the model solute acetophenone were found to be well explained by solvent electric field in all solvents examined. However, electronic polarizability is expected to contribute significantly to all intermolecular interactions in solution, suggesting that force fields with explicit treatments of polarization would provide a more accurate and physical description of the condensed phase and the electric fields associated with it.
Solvent fields are important because they attach a quantitative measure to solvation forces, which have long served as useful models for understanding the interactions underlying biomolecular structure and dynamics.2,32-34 However, since solvents are composed of many fewer unique constituents than biomolecules, they can benchmark models of condensed phase effects without the stringent sampling issues or force field complexity characteristic of biological systems. Additionally, solvent fields and solvent-induced frequency shifts can be combined to build field-frequency calibration curves to assist the measurement of electrostatic fields in biomolecular systems, which can establish quantitative connections between molecular structure and biological function.23,35
In the following, we describe simulations of acetophenone dissolved in several solvents and calculate the electric fields the solvents exert on the carbonyl group of acetophenone using the AMOEBA force field. AMOEBA is an atomistic model that incorporates polarizability explicitly by conferring upon each atomic site a point dipole that is induced according to the self-consistent electric field arising from all other sites.36 This additional sophistication in the model influences the calculated solvent fields in a number of important ways. These electric fields are compared to those obtained with the previously published MD simulations using fixed-charge force fields,23 and two continuum models: the Onsager reaction field,1 and the Poisson-Boltzmann equation.3,4 Results from the fixed-charge force fields and the continuum models share a number of characteristics in common with the AMOEBA solvent fields, but they each differ in characteristic ways. By noting the similarities and differences between solvent fields for acetophenone determined using continuum, fixed-charge, and polarizable models, we can validate which aspects of condensed phase electrostatic interactions are reproduced by the simpler models, while also calling attention to what properties require explicit polarization or an atomic representation to be consistent with experimental frequency shifts.
2. Methods
2.1. Simulation Overview
Acetophenone (structure shown in Figure 1A) was placed at the center of a cubic box filled with solvent molecules. In total, seven solvents were considered: acetonitrile, dibutylether, dimethyl sulfoxide, n-hexane, tetrahydrofuran, valeronitrile, and water. The aforementioned solvents were chosen based on the separation of acetophenone’s C=O vibrational frequency when dissolved in them, implying that they span a large range in electric field, and because they do not contain carbonyl groups, enabling accurate measurements of acetophenone’s C=O peak. All simulations were carried out using the Tinker 6.2 molecular modeling package.37 During production dynamics, the electric field experienced by the C=O vibration of acetophenone from the solvent environment was calculated in each snapshot by finding the electric fields at the C-atom and O-atom, projecting them along the C=O unit vector, and then taking the average. This operation is equivalent to the dot product on the right-hand side of Eq. 1 because for carbonyls, the difference dipole is assumed to be parallel with the C=O bond axis.19,38 The electric field defined in this way is denoted |Fvib|. The electric field drop along the C=O bond (also referred to as the field drop) is defined as the difference between the projected fields at the C-atom and O-atom, and is denoted |ΔFvib|. The simple procedure devised to calculate electric fields is described in methods section 2.4.
Figure 1.
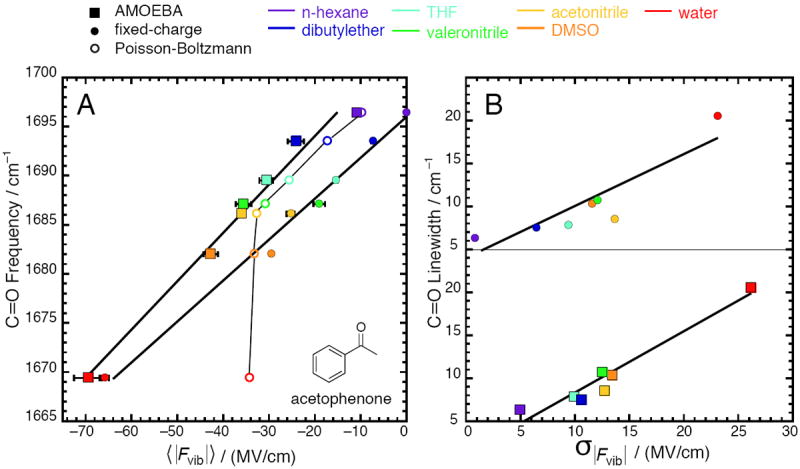
Correlation between calculated electric fields and properties of the C=O vibration on acetophenone for seven solvents (data given in Tables 1 and 2). Squares represent electric fields from simulations with the AMOEBA force field; closed circles represent electric fields from simulations with a fixed-charge force field23; open circles represent electric fields from solving the Poisson-Boltzmann equation. (A) Peak vibrational frequency correlates strongly with average electric field; (B) Full-width at halfmaximum (linewidth) correlates moderately with electric field standard deviation. In (A), the regression line is ν̄C=O = 0.484 〈|Fvib|〉 +1703.6 with R2 = 0.98 for AMOEBA, and ν̄C=O = 0.412 〈|Fvib|〉 + 1695.9 with R2 = 0.99 for fixed-charge. Estimates of the standard error for the slope and intercept are 0.0029 and 1.2 for AMOEBA, and 0.0020 and 0.6 for fixed-charge. For Poisson-Boltzmann, R2 = 0.6, and the trace is a guide to the eye, not a regression. In (B), the regression line is LWC=O = 0.714σ|Fvib| + 1.14 with R2 = 0.94 for AMOEBA, and LWC=O = 0.626σ|Fvib| + 3.46 with R2 = 0.8 for fixed-charge.
2.2. Parameterization
We used the AMOEBA water model,39 and parameters for acetonitrile and dimethyl sulfoxide were taken from recently published work.40 Acetophenone, n-hexane, dibutyl ether, tetrahydrofuran, and valeronitrile were parameterized according to the following protocol.
The multipole parameters for n-hexane, valeronitrile, and dibutyl ether were taken from the closest relatives in the AMOEBA force field for organic molecules. n-Hexane was constructed with the alkane methyl (C and H) and alkane methylene (C and H) atom types. The same four alkane atom types were also used in valeronitrile and dibutyl ether, though atom types in acetonitrile (for valeronitrile) and dimethyl ether (for dibutyl ether) were used as well. For the latter two molecules, small changes (< 0.1e) were made to the partial charges at the interfacing atoms to enforce charge neutrality. Acetophenone and tetrahydrofuran were assigned multipole parameters de novo using the POLEDIT utility in Tinker 6.2 and following the prescription in the supplementary information of Ren et al.40 Briefly, the procedure involves fitting the ab initio electrostatic potential surface evaluated at the MP2/aug-cc-pVTZ level to a distributed set of multipoles fixed at the nuclear positions.41 Polarizability and van der Waals parameters were used unchanged from the recommendations in Ren et al.40
As for the valence parameters for n-hexane, valeronitrile, and dibutyl ether, the majority was taken from the analogous atom types in AMOEBA without modification – similar to the multipole parameters. Torsional parameters that were present in AMOEBA were used without modification; if absent, the corresponding generalized AMBER force field (GAFF) parameter was used.42 The valence parameters for acetophenone and tetrahydrofuran were determined using the VALENCE utility in Tinker 6.2. This procedure estimates equilibrium values and force constants by drawing appropriate values from a library, which are then refined by fitting the MM-derived normal mode frequencies against QM frequencies evaluated at the B3LYP/6-311++G(2d,2p) level43,44 with anharmonic corrections.45,46 As VALENCE does not automate estimation of torsional parameters, these were taken from the GAFF force field.42 These parameterizations were able to reproduce room-temperature liquid densities to within 1– 2% following 100 ps of equilibration. All of the parameters for the solvent molecules are given in the supplementary information.
2.3. Solvation Simulation Methods
Acetopheone was placed at the center of a cubic box (with edge lengths equal to 45 Å) filled with solvent molecules. Between 8–10 × 103 atoms were needed to fill up the volume. These solvent boxes were energy minimized first in GROMACS47 using 1000 steps of steepest descent with the GAFF force field,42 and then further minimized in Tinker down to an rms energy gradient per atom of 1.0 kcal/mol/Å with the AMOEBA force field described above. The minimized coordinates were equilibrated for 100 ps in the NPT ensemble with reference temperature and pressure set to 298 K and 1.0 atm respectively. During equilibration, dynamics were evolved according to the velocity Verlet method using a time-step of 1.0 fs. The temperature was regulated with the Andersen thermostat (with a coupling time of 0.1 ps and reference temperature of 298 K), and the pressure with the Berendsen barostat (with a coupling time of 2.0 ps and reference pressure of 1.0 atm) in order to facilitate rapid convergence. The particle mesh Ewald method48 was used to implement long-range electrostatics, and the real space cut-off distance for Ewald summation as well as for van der Waals interactions was set to 10.0 Å. The convergence threshold applied during computation of self-consistent induced dipoles was 10−3 D.
Production runs were started from the final positions and velocities of the equilibration runs, and continued for an additional 100 – 2000 ps during which snapshots were recorded every 10 fs. Two separate production trajectories were carried out for each solvent: a “short” run (ca. 150 ps) which employed stringent simulation settings, and a “long” run (ca. 1500 ps) which sacrificed some precision for speed. The trajectories’ results were compared to ascertain the relative trade-offs between sampling and computational precision. During the short (but more precise) simulations, most of the settings from the equilibration runs were maintained except that the self-consistent induced dipole threshold was set down to 10−5 D. Additionally, the Beeman integrator was used,49 the temperature was regulated with the Bussi thermostat,50 and the pressure was regulated with the Monte Carlo barostat, both with 1.0 ps coupling times. During the long simulations, the RESPA multiple-timescale integrator was used with a time-step of 2.0 fs,51 and the induced dipole threshold was brought up to 10-3 D. The fluctuation-suppressing Berendsen barostat was used in order to maintain compatibility with the RESPA integrator as implemented in Tinker.
2.4. Solvent Field Calculations
We developed the following procedure for extracting electric fields from the instantaneous coordinates of the solvent box. At every step where a snapshot of the atomic coordinates was written, the induced dipole moments were additionally printed to a separate output file. Because atomic polarizabilities are defined as scalars (isotropic) in AMOEBA, the induced dipole at any atomic site is collinear and proportional with the total electric field there, including the contributions from both permanent as well as other induced moments. The electric field is obtained then simply by dividing the induced dipole (in Debye) of the atom of interest (either at C or O) by that atom’s polarizability parameter (in Å3) and multiplying by 299.79 to convert from D Å-3 to MV/cm (the conversion factor is the rescaled speed of light in cgs units).
Electric fields determined in this way will naturally contain Coulombic interactions as well as all polarization effects because all of these components contribute to the induced dipoles when evaluating the potential energy. An essential consideration about these total electric fields is that they contain the “self-field” arising from the permanent multipoles on the same molecule as the probe, as well as the self-polarization between distal moieties on the same molecule. These intramolecular contributions lie outside the definition of the electric field that we employ as the electric field due to the environment, and our goal is to use the electric field as a descriptor for intermolecular interactions. In our definition, the electric field on any atom in a molecule is necessarily zero when the molecule is isolated in the gas phase. In this way, the electric field due to the environment uses the isolated molecule in the gas phase as the reference state.
To remove the contribution of the self-field from the total field, we took every snapshot during solvent dynamics and stripped away all the solvent molecules, leaving acetophenone in its instantaneous configuration at that moment in the trajectory. The induced dipoles on the atoms of interest for the solute-only system were evaluated (without running dynamics) and converted into electric fields. This field was subtracted from the corresponding field from the trajectory, to admit the electric field due to the environment; i.e., the solvent field. Mathematically, these steps correspond to:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
In Eqs. 2-4, i indexes over the C-atom and O-atom of the carbonyl probe, αi is the atomic polarizability of the ith atom, and is the induced dipole of the ith atom. In Eq. 2, the total electric field on atom i, , is calculated by including all atoms in the solvent-box (as they are during the simulation), whereas in Eq. 3, the self-field, , is found by isolating the solute. The difference in Eq. 4 filters off the self-field contribution, leaving the desired electric field due to the environment. Finally, the electric field experienced by the vibration is found by projecting along the C=O bond vector and averaging (Eq. 5), and the electric field drop by projecting and subtracting (Eq. 6) as mentioned previously. Implementation of this method is described in detail in supplemental methods.
2.5. Poisson-Boltzmann Calculations
The Poisson-Boltzmann (PB) equation is a prescription for calculating the electrostatic potential for an arbitrary charge density and dielectric map:
| (7) |
where , , , and are the position-dependent dielectric, electrostatic potential, charge density, and ionic strength respectively. Eq. 7 provides a general way of calculating the electrostatic properties of a system comprised of one region that is represented atomistically (via atomic coordinates and charges, ), and another region that that is represented implicitly (via a position-dependent dielectric function, ).52 PB models are important to examine alongside fully atomistic approaches because they are used to model solvents inexpensively as continua, and it forms the theoretical framework for implicit solvation models, which greatly reduce the number of explicit atoms needed in a simulation.53,54 We represented acetophenone as an optimized configuration of atoms bearing GAFF force field point charges, and the solvent as a polarizable continuum. As the PB approach intrinsically averages over solvent degrees of freedom, and the solvent field is largely independent of the solute configuration, we carried out single-point calculations. The solute molecule was enclosed by a surface defined by the atomic radii parameters optimized by Swanson et al. for smoothed surfaces,54 inside of which an internal (solute) dielectric of 2 was designated, and outside of which was designated a medium whose dielectric was set equal to the experimental static dielectric constant55 of each of the seven solvents examined. The full PB equation was solved numerically on a cubic grid with a mesh spacing of 0.25 Å using the APBS software package4 with point charges smoothed via cubic B-splines, while the dielectric bounding surface was smoothed with a 7th order polynomial. The latter two options are necessary for accurate calculations of electrostatic forces.54,56 The calculated electrostatic forces experienced by the C and O atoms (in kJ mol−1 Å−1) were divided by their respective charges (in elementary charges) and multiplied by 1.03627 to give the local electric field on each atom in units of MV/cm. This electric field is dominated by a self-field from the solute’s charges, which we remove by performing a reference calculation in which the solvent dielectric is set to 1 and the internal dielectric is maintained. The reference calculation isolates the self-field, and the difference between the total field and the self-field, analogous to Eq. 4, gives the electric field due to the solvation environment. The electric field experienced by the vibration and the electric field drop were calculated according to Eqs. 5-6, as specified above.
3. Results
3.1. Average Electric Fields in Solution
Ensemble averages and standard deviations of each solvent’s electric field as calculated with the AMOEBA simulations are reported in Table 1. Here and in the following, the values reported reflect those from the short simulations; data from the long simulations are recorded in Table S2. The average electric field in the non-polar solvent, n-hexane, was −10.9 MV/cm. The negative sign associated with the electric field implies an overall energetically favorable interaction between the C=O moiety and its environment. Throughout the trajectories, there were a few snapshots in which the instantaneous field exerted on C=O was positive, though these were rare (less than 1% of snapshots for all solvents), and they contribute little to the ensemble average.
Table 1.
Electric fields in seven solvents calculated by MD with the AMOEBA force field
| Solvent | Simulation Time / ps a | |Fvib| / (MV/cm) b | |ΔFvib| / (MV/cm) c | ||
|---|---|---|---|---|---|
| mean | std. dev. | mean | std. dev. | ||
| n-Hexane | 181.4 | -10.91± 0.37 | 4.91 | -6.98 ± 0.21 | 5.20 |
| Dibutyl ether d | 106.2 | -24.16 ± 1.74 | 10.49 | -16.60 ± 1.25 | 10.98 |
| Tetrahydrofuran | 151.0 | -30.63 ± 1.47 | 9.95 | -18.53 ± 2.13 | 10.56 |
| Valeronitrile | 181.6 | -35.73 ± 1.54 | 12.49 | -23.16 ± 1.76 | 12.72 |
| Acetonitrile | 240.1 | -36.11 ± 0.82 | 12.69 | -25.10 ± 0.45 | 12.49 |
| Dimethyl sulfoxide | 171.8 | -42.85 ± 1.38 | 13.39 | -26.49 ± 0.70 | 12.60 |
| Water | 110.7 | -69.50 ± 3.04 | 26.12 | -51.88 ± 3.89 | 25.00 |
Data reflect results from the stringent (short) simulations of acetophenone in a box filled with various solvents. Electric fields were sampled every 10 fs.
The electric field experienced by the C=O bond, as defined by Eq. 5.
The electric field drop over the C=O bond, as defined by Eq. 6.
Dibutyl ether exhibits uniquely slow dynamics, implying that these data do not reflect a converged ensemble (see Figure S1 and analysis).
Solvents of increasing polarity were found to exert increasingly large electric fields, with dimethyl sulfoxide (DMSO) exerting −42.8 MV/cm onto C=O. Water, which is capable of forming hydrogen bonds (H-bonds) to C=O, was associated with the largest solvent field (−69.5 MV/cm) by a considerable margin. The large electric field attendant upon formation of an H-bond can be explained by considering the fact that O–H bonds have large bond dipole moments, and due to the small size of the hydrogen atom, they can approach the C=O bond very closely. The electric field due to a dipole decays as the inverse cube of the distance, so small changes in distance are significant.
The vibrational frequency of the C=O bond is known to be a sensitive reporter of its local environment and its solvatochromic trends have been extensively explored by using empirical solvent polarity scales.57-60 According to Figure 1A (boxes), the solvent-induced frequency shifts are also well explained by the average electric field each solvent exerts onto the vibration, a preferable explanatory variable due to its more fundamental nature. The relationship produces a regression line with form ν̄C=O = 0.484 〈|Fvib|〉 + 1703.6. In this regression, the slope represents the sensitivity of the vibrational frequency to field, corresponds to the magnitude of from Eq. 1, and can be compared to the empirical Stark tuning rate; the intercept represents a reference frequency associated with zero electric field, corresponds to ν̄0 from Eq. 1, and can be compared to the empirical vibrational frequency of acetophenone in the gas phase, vide infra.
The average electric fields determined with the long trajectories are generally 10–20 % smaller than those for the short. The difference is statistically significant, as the correlation-adjusted errors in the average electric fields are between 3–5 % for most of the solvents, suggesting that longer trajectories can better sample energetically unfavorable configurations that bring down the ensemble-averaged field magnitudes. Nevertheless, the difference is small, suggesting that the electric fields have mostly converged by 100 ps of sampling. Finally, the slope and intercept of the field-frequency model constructed with the fields from the long trajectories (0.507 cm-1/(MV/cm) and 1702.6 cm-1 respectively) are within the estimates of the error of the regression line parameters in Figure 1A (±0.03 cm-1/(MV/cm) and ±1.1 cm−1 respectively). We chose to focus on the short trajectories in the main text because they admitted a regression line with a slightly higher R2 (0.98 compared to 0.96).
The average electric fields are similar to some extent to what we previously calculated using analogous methods and a fixed-charge force field (Figure 1A, closed circles).23 Where we refer to a fixed-charge force field, parameters for organic molecules came from the generalized AMBER force field (GAFF) as given by Caleman et al.,42 water was described by the TIP3P model,61 and the potential function’s form was that used in AMBER. In particular, the fixed-charge model was equally capable of describing the change in average electric field associated with solvent polarity, as reflected in the similarity of the increase in electric field passing from n-hexane to DMSO (32.0 MV/cm for AMOEBA and 29.5 for fixed-charge), and the similarity of the two models’ slopes in Figure 1A (0.412 and 0.484 cm−1/(MV/cm)). The most obvious difference is that the fixed-charge model assigns the non-polar solvent n-hexane an electric field almost equal to zero, whereas AMOEBA assigns it a significant favorable field. This deviation becomes less pronounced in more polar solvents, such that the AMOEBA water model and the TIP3P model assign water an identical average electric field within error. This effect can clearly be seen by observing that the two regression lines in Figure 1A approach each other, and converge near water’s electric field.
On the other hand, the PB equation (Table 2 and open circles in Figure 1A) predicts an electric field in n-hexane that is virtually identical to the ensemble-averaged field calculated with AMOEBA simulations. For the solvents of relatively low polarity (up to acetonitrile), the PB equation agrees impressively with AMOEBA to within 1–5 MV/cm. The increase in solvent field from n-hexane to DMSO is 23.5 MV/cm, in qualitative agreement with the all-atom models, although the agreement is stronger if one considers the span between n-hexane and acetonitrile (see Figure 1A). However, the PB equation predicts almost no increase in electric field for the two most polar solvents (DMSO and water) over acetonitrile, failing to explain the large bathochromic shifts associated with these solvents. The sudden non-linear behavior of the curve for the PB model past acetonitrile (Figure 1A) can be attributed to the well-known fact that continuum solvent models omit the effect of specific interactions such as H-bonds. However, the present data afford two additional insights. First, that despite the fact DMSO has no clear H-bond donating capacity, it appears to form some kind of specific interaction as based on the larger PB–AMOEBA discrepancy (10 MV/cm); and second, that for water, the error incurred by omitting the effect of H-bonding is quite severe.
Table 2.
Electric fields in seven solvents calculated by solving the PB equation
3.2. Heterogeneity of Electric Fields in Solution
Whereas AMOEBA and fixed-charge models appear to be largely in agreement regarding the average properties of the electric field in solution, especially for polar solvents, they contrast strikingly with regard to the field heterogeneity.
The standard deviation of the electric field distribution reflects the field’s temporal heterogeneity over the trajectory, and is one contributor (though often the dominant one) to the infrared band’s linewidth because inhomogeneous broadening results from an oscillator sampling different environments (electric fields). Figure 1B shows the relationship between linewidth and the solvent field distribution’s standard deviation; the data for AMOEBA and the fixed-charge models are vertically displaced for clarity. AMOEBA predicts, on the whole, a more widely spread distribution. The fixed-charge–AMOEBA discrepancy is largest for n-hexane and becomes less significant for more polar solvents. More significantly, the fixed-charge model generated field spreads that correlate rather poorly with linewidth (R2 of 0.80), whereas the correlation coefficient using the AMOEBA model (0.94) is quite good. This finding suggests that AMOEBA captures the heterogeneity characteristic of each solvent more accurately.
Spatial heterogeneity is represented by differences in the electric field at two separate points, rather than at two different times. A measure of spatial heterogeneity that is pertinent to the C=O vibration is the electric field drop along the bond-length, as defined by Eq. 6, and shown in Tables 1 and 2. AMOEBA predicts significant field drops in all seven of the solvents studied, and the magnitude of the field drop systematically increases with solvent polarity (Figure 2). These results are strikingly different than those obtained with a fixed-charge model,23 which predict an essentially homogeneous electric field along the C=O bond in solvents except for water. The large electric field drop created by water can be explained by considering that the sizable fields in this environment are due to H-bonds, which are highly local interactions that are principally mediated through the H-bond accepting O-atom. Essentially, the “extra” electric field water exerts over DMSO is mostly due to the one or two water molecules in close contact with the O-atom on the solute. On the other hand, the fixed-charge model predicts that all the other (aprotic) solvents produce small field drops along the C=O bond.
Figure 2.
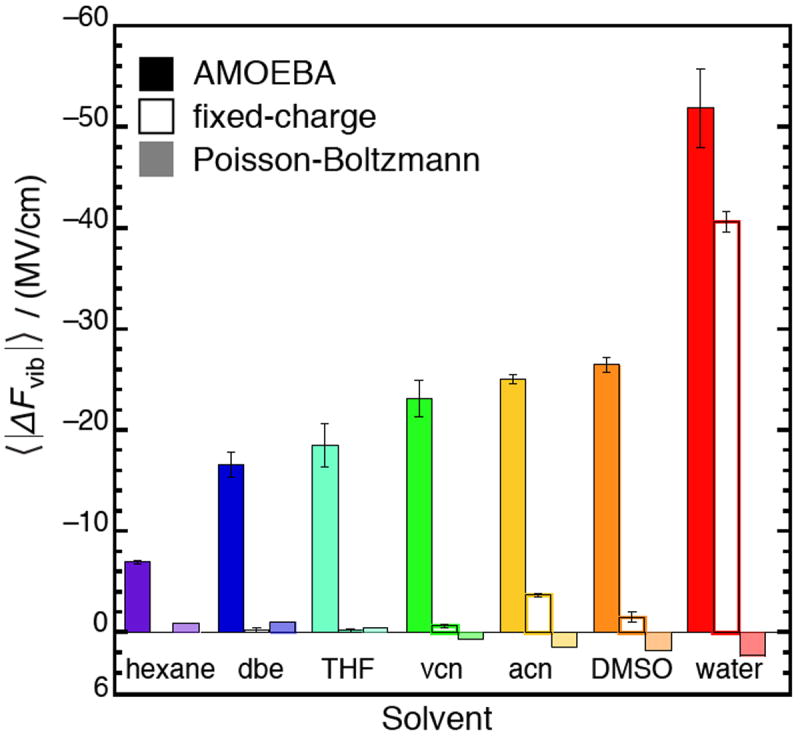
The average electric field drop across the C=O bond for seven solvents (see Eq. 6 for definition), calculated from simulations with the AMOEBA and fixed-charge force fields and from solving the Poisson-Boltzmann equation. Fixed-charge models predict very homogeneous fields, with drops close to zero, except in water. AMOEBA predicts field drops increase monotonically with solvent polarity, and a very large field drop in water. The Poisson-Boltzmann equation predicts relatively homogeneous fields, and sometimes inverts the sign of the field drop.
The continuum PB-based approach predicts very small electric field drops for all solvents (Figure 2), and in a few cases (including water) predicts the electric field to be larger on the C-atom than on the O-atom. This sign inversion is qualitatively inconsistent with physical intuition. It is apparent that the PB equation does not describe the spatial heterogeneity of the solvent’s interactions well because the solvent degrees of freedom are effectively all integrated out.
From comparing these three approaches, one might suggest that the electric field heterogeneity is a qualitative measure of the specificity of a given solvent’s interactions. Continuum models, which omit specific interactions, naturally predict electric field drops to be close to zero. In a fixed-charge all-atom model, the concept of an H-bond emerges, marked by the appearance of a highly heterogeneous field along the C=O bond. H-bonds are represented in a binary way though, as the non-H-bonding solvents all have small field drops. The AMOEBA model presents a more nuanced picture in which H-bonds are still the source of the largest field drops, but the binary character of H-bonding is replaced with a spectrum in which solvents of intermediate polarity produce field drops of intermediate magnitude.
3.3. Dynamics of Electric Fields in Solution
Field-field autocorrelation functions were calculated from the long polarizable trajectories. Correlation functions calculated from the short polarizable trajectories were noisy (intense sampling is required to obtain converged correlation functions), while correlation functions calculated from trajectories using fixed-charge models generally displayed oscillatory features that resulted in poor fits to exponential decay functions. For all the long polarizable simulations, the correlation decays could be fit well to a double exponential decay (R2’s between 0.98–0.99), but could not be fit well to a single exponential decay (R2’s between 0.87–0.95). The parameters of these fits are compiled in Table 3, and Figure 3 displays field-field autocorrelation functions for three solvents (dibutyl ether, DMSO, and water) at early lag times. The time constants from this analysis correspond roughly to how long it takes the solvent to randomize its structure, using the electric field as a proxy for the collective solvation coordinate.62 According to the linear Stark equation (Eq. 1), the instantaneous vibrational frequency is proportional to the electric field that the vibration experiences, implying that the field-field correlation function effectively encodes the frequency-frequency correlation function, which can be interrogated experimentally by 2-D IR.15,63
Table 3.
Fitting parameters of the electric field autocorrelation functions for the C=O vibration in seven solvents a
| Solvent | Simulation Time / ps b | R2 | Fast process | Slow process | Offset | |||
|---|---|---|---|---|---|---|---|---|
| Δ1 / ps−2 | τ1 / ps | Δ2 / ps−2 | τ2 / ps | Δ0 / ps−2 | ||||
| n-Hexane | 1008 | 0.98 | 0.640 | 0.108 | 0.242 | 0.861 | 0.051 | |
| Dibutyl ether | 1402 | 0.99 | 0.430 | 0.162 | 0.310 | 4.57 | 0.237 | |
| Tetrahydrofuran | 1242 | 0.99 | 0.553 | 0.151 | 0.452 | 2.30 | 0.006 | |
| Valeronitrile | 986.3 | 0.99 | 0.611 | 0.141 | 0.431 | 2.84 | -0.031 | |
| Acetonitrile | 1895 | 0.99 | 0.898 | 0.112 | 0.167 | 1.11 | 0.020 | |
| Dimethyl sulfoxide | 1361 | 0.99 | 0.696 | 0.104 | 0.317 | 1.99 | 0.022 | |
| Water | 699.8 | 0.98 | 0.432 | 0.080 | 0.465 | 0.928 | 0.041 | |
Autocorrelation functions were calculated for the field experienced by the vibration (|Fvib|), and then fit to the function: CFF (t) = Δ0 + Δ1 exp(−t/τ1)+ Δ2 exp(−t/τ2).
Data reflect results from the long (less stringent) simulations of acetophenone in a box filled with various solvents. Electric fields were sampled every 10 fs. Fits were carried out on the first 10 ps of the correlation function, after which the correlation function mostly oscillated around zero.
Figure 3.
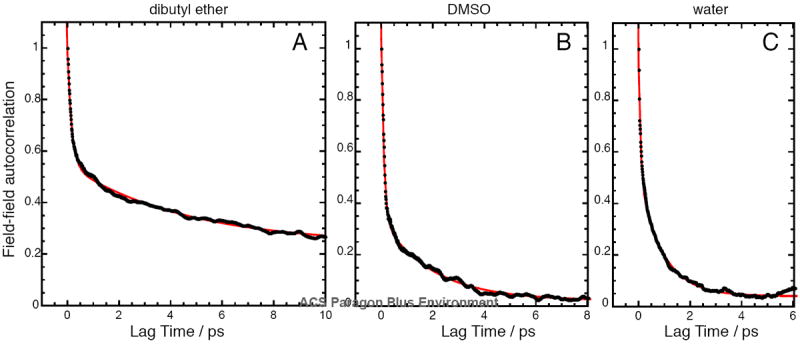
Normalized electric field autocorrelation functions of the C=O vibration on acetophenone in three different solvents: (A) dibutyl ether; (B) dimethyl sulfoxide; (C) water. Black dots represent the autocorrelation data points, and the red trace represents a fit to a double exponential decay. In all cases, the data could not be fit well to a single exponential decay. Fit parameters for all solvents are given in Table 3. The solvents examined share a characteristic time constant for fast dephasing (~100 fs), but have different time constants for the slow dynamics. Dibutyl ether is the only solvent with a significant offset, consistent with the 100 ps trajectory not reflecting the true ensemble average (see footnote d in Table 1).
Six of the seven solvents examined in this study shared common dynamical characteristics. The solvents universally possess a fast process with a time constant of about 100 fs that accounts for about half of the total dephasing. In the nitrile-based solvents (acetonitrile and valeronitrile), the weight of this fast component is greater. After 100 fs, each solvent exhibits a second slower process with time constants that are more idiosyncratic to each solvent, with n-hexane and water being on the faster side (ca. 900 fs), and tetrahydrofuran and valeronitrile on the slower end (ca. 2.5 ps). Qualitatively, the more polar solvents exhibit a faster second decorrelation timescale (a trend that has been observed empirically64), although n-hexane stands out as a clear exception. Finally, all but one of the solvents (dibutyl ether) possess offsets very close to zero, implying that most of the dynamics can fully relax within 10 ps. The fast dynamics is consistent with the good agreement between results from the short and long trajectories, mentioned earlier.
One solvent – dibutyl ether – displayed very different behavior from all the others. It shares the same fast timescale process with the other solvents, but afterwards, its fields dephase slowly, with a second time constant of 4.6 ps. Moreover, the presence of a large offset of 0.237 implies that there is a significant contribution from slow dynamics on the tens of picoseconds timescale. Indeed, simple visualization of the field trajectory for dibutyl ether (Figure S1) confirms the presence of electric fields altering between distinct average values over long periods. The presence of slow dynamics complicates reliable determination of ensemble-averaged properties, which may explain in part why the data point for dibutyl ether fell somewhat off the regression line in Figure 1A.
4. Discussion
4.1. Comparison between AMOEBA and Fixed-charge Models
The most obvious differences between the solvent fields calculated using a polarizable model versus a fixed-charge model is the presence of moderately large electric fields in the non-polar solvent n-hexane. The origin of this field is relatively simple to rationalize: it reflects the polarization that the C=O fragment’s permanent dipole induces in the surrounding medium’s electron density, which then exercises a field back onto the C=O group. Clearly, explicit polarization is required to capture this effect. The “extra” ~10 MV/cm attributed to C=O’s polarization of its environment results in larger discrepancies compared to the fixed-charge model for the non-polar solvents. To what extent is this ~10 MV/cm physically meaningful or an artifact associated with the reference state? To address this question, we note that the intercept of Figure 1A (1703.6 cm−1) compares favorably with the C=O frequency of acetophenone as a vapor (1703 cm−1 57,65). The similarity of these numbers is impressive, and suggests that the AMOEBA model consistently describes (and can connect) the gas phase and condensed phase.
As polarity of the solvent increases and a larger portion of the solvent field arises instead from permanent dipoles of the solvent (rather than induced), the percent discrepancy between the AMOEBA and fixed-charge force fields becomes smaller, and in the most polar solvent, the models agree to within 5%. This observation highlights quite clearly that explicit polarizability is most needed at an interface between a polar and a non-polar molecule (e.g., acetophenone and n-hexane).66 As an aside, proteins are often characterized by a delicate interplay between non-polar and polar moieties, which would suggest that electrostatic interactions in proteins might also demand an explicitly polarizable model to be properly described.
For homogeneous systems, i.e., systems in which all the molecules are either polar or non-polar, the fixed-charge model reproduces AMOEBA’s electric fields, implying that it is capable of reproducing electronic polarization effects on average. By “absorbing” the polarization effect into the charges, fixed-charge force fields include polarization in a mean field sense.67 In non-homogeneous systems, the role of polarization is context-dependent and cannot be programmed into the charge parameters effectively; in these situations, we believe the fixed-charge model gives qualitatively incorrect results, based on its inconsistency with the sizable empirical frequency shift between acetophenone in the gas-phase and in n-hexane.
4.2. Comparison between AMOEBA and PB Models
The PB equation predicts a non-zero field in n-hexane, producing a value that is almost identical to AMOEBA’s. The magnitude of a particular solvent’s electric field in a continuum model is determined by the solvent’s dielectric constant; since the dielectric constant naturally reflects electronic as well as orientational degrees of freedom, continuum models are particularly well suited for describing the induced interactions between a polar molecule in a nonpolar environment. The overall scale of the solvent fields depend on how close the polarizable medium can get to the solute atoms (the radius parameters54) and how strongly the solute atoms can polarize the surrounding medium (the charge parameters42). From noting AMOEBA’s and PB’s strong agreement for five of the seven solvents examined, this work demonstrates that the PB equation (when equipped with optimized charge and radius parameters) reproduces the scale and the trends in solvent fields of a much more expensive polarizable/atomistic model, at least for simple systems.
On the other hand, because the PB model (and continuum models in general) cannot describe the effects of specific interactions like H-bonds, it predicts the electric field in water to be about half what the TIP3P and AMOEBA water models estimate. While a different set of dielectric settings (Tables S3–S4) or solute charges (Tables S5–S6) can produce an electric field for water that agrees somewhat better with the atomistic models, we point out that for any choice of the charge, radius, or dielectric parameters, the PB equation will predict similar electric fields for DMSO and water, which is qualitatively incorrect, based on the large empirical frequency shift between acetophenone in DMSO and in water. Therefore, PB’s underestimation of electric fields in water cannot be fixed in a physically consistent way. These findings intimate at potential limitations to implicit solvation schemes for MD simulations on proteins, in which modified forms of the PB equation are employed to model the aqueous environment.52 The average electric field and the electric field drop may prove to be useful physical properties to parameterize against to produce implicit solvent models that better account for water’s distinctively strong and heterogeneous electrostatic interactions.
From inspecting all three models in Figure 1A, it is apparent that the continuum and fixed-charge models exhibit complementary weaknesses. Whereas the fixed-charge model can aptly describe specific interactions (and attendant large fields), it gives pathological results in non-polar solvents (small fields); the continuum model excels at describing non-polar solvents, but gets worse at describing more polar solvents, producing qualitatively unphysical results once H-bonds are involved. This point is expressed visually in Figure 1A, where the AMOEBA and PB traces track closely onto one another around n-hexane, but diverge going out to larger fields.
4.3. Comparison to the Onsager model
For a solute modeled as a point dipole (of magnitude μ0) in a spherical cavity, the PB model can be mapped onto a simple analytic expression.1 With these simplifications, the average solvent field is given by the Onsager reaction field:68
| (8) |
In Eq. 8, n is the solute’s refractive index and a is the cavity radius, which is typically estimated from the molecule’s density and formula weight. Following this prescription, electric fields were calculated using the Onsager model and are compared against the fields calculated with AMOEBA and PB in Figure 4. As they are both continuum models, the Onsager and PB models exhibit qualitatively the same behavior – describing the solvents of lower polarity well, but systematically underestimating the fields in the most polar solvents. The overall scale of the solvent fields in the Onsager model is smaller than the PB model’s. Because the cavity radius is an ad hoc parameter, especially for non-spherical molecules such as acetophenone, it is reasonable that the Onsager model’s predictions for the overall scale will be only approximate. The PB equation estimates the scale of solvent fields in better agreement with AMOEBA (note that the PB trace is closer to AMOEBA’s than the Onsager trace) presumably because the cavity’s structure is accounted for explicitly. If water is excluded, the regression lines associated with the continuum models become more meaningful: the slope for the PB model’s regression line (0.526 ± 0.08 cm−1/(MV/cm)) is within error of AMOEBA’s, while the Onsager model produces a slope of 0.657 cm−1/(MV/cm). Nevertheless, the ratio |FDMSO|/|Fhexane| is independent of the cavity radius so it serves as a better basis for evaluating the Onsager model – Onsager predicts this ratio to be 3.3, which is almost the same as PB (3.4) and in qualitative agreement with AMOEBA (3.9).
Figure 4.
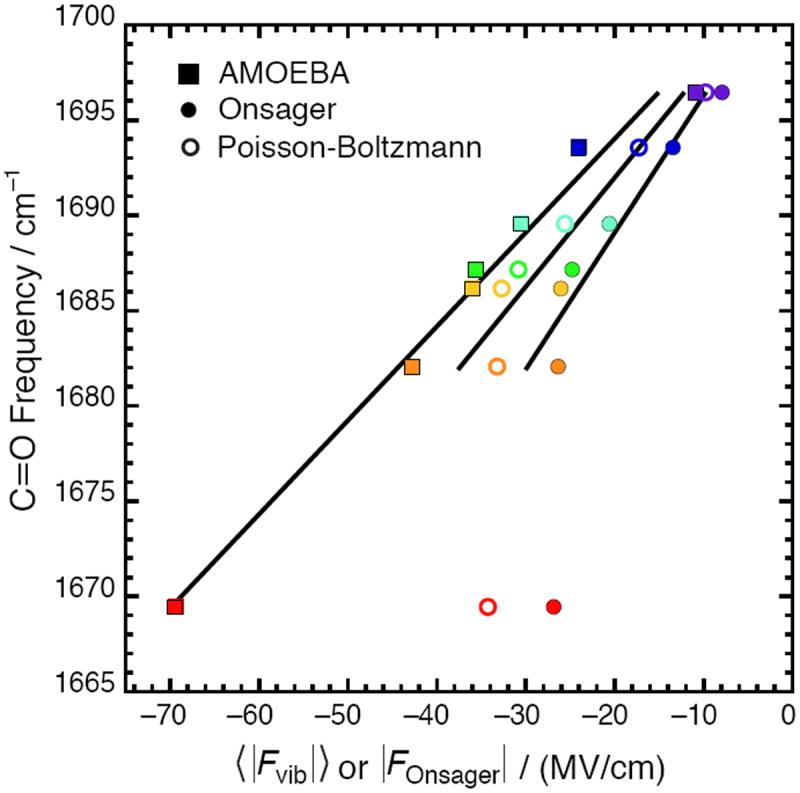
Comparison between the average electric field predicted by AMOEBA, the Poisson-Boltzman equation, and the Onsager model for seven solvents (see Fig. 1 for color code). AMOEBA fields are reproduced from Figure 1 with error bars removed for clarity. The Onsager fields are calculated from Eq. 8 using μ0 = 2.95 D, n2 = 2.35, and a3 = 46.3 Å3. Excluding water, the regression line is ν̄C=O = 0.657|FOnsager| +1702.2 with R2 = 0.91 for Onsager and ν̄C=O = 0.526 〈|Fvib|〉 + 1702.2 with R2 = 0.92 for PB.
4.4. Comments on the Electric Field Calculation
The difference calculated in Eq. 4 results in what we call the electric field due to the environment. This electric field includes the field due to all the permanent multipoles on the solvent atoms, as well as the field due to all the induced dipoles on the solvent atoms – induced both by the presence of the solute and the solvent molecules. Explicitly, it does not include the field due to the solute’s own permanent multipoles, nor the field due to the induced dipoles on the solute atoms induced by the solute atoms (the molecule’s intrinsic polarization). However, the electric field does include the contributions from the induced dipoles on solute atoms due to the presence of the solvent molecules. We call this subtle contribution the difference self-field, as it refers to the change in the molecule’s self-field imparted by the solvent. The same reference state obtained with AMOEBA by removing the solvent molecules is established in the PB model by setting the solvent dielectric to 1. However, by maintaining the solute (internal) dielectric at 2 in the reference state, the difference self-field is properly evaluated as intrinsic polarization is discarded along with the fields from the solute’s permanent charges. We found that reference calculations employing a homogeneous dielectric (i.e., solute and solvent dielectrics set equal), led to poorer agreement with AMOEBA’s electric field predictions (see Tables S3–S4).
The separation between a molecule and its environment becomes subtle in a polarizable model, although it is achievable if one carefully defines the reference state. We believe that the electric fields reported in this paper are coming close to reflecting the absolute magnitudes of the electric fields in liquid solutions (within the scope of the adopted definition). Indeed, the electric fields we calculated for water (−69.5 MV/cm) and tetrahydrofuran (−30.6 MV/cm) agree excellently with those calculated using QM/MM methods (−69.8 MV/cm, −28.5 MV/cm respectively),7 with the caveat that the QM/MM work focused on a different solute (acetonitrile); solvent fields also depend on the solute’s identity because the solvent field fundamentally reflects a reorganization process of the solvent reacting to the solute.1 The close correspondence between the gas-phase C=O frequency for acetophenone and the intercept of AMOEBA’s and PB’s field-frequency curves also supports this claim.
Using the method described above to calculate fields from AMOEBA simulations, the desired electric fields, , are of the same order of magnitude as (and generally within a factor of 2). In other words, the calculated solvent fields are not tiny portions on top of the self-fields, averting a dilemma in which we would have to take the difference between two large numbers with close values. This feature is not trivial because molecules’ self-fields arising from their own nuclei and electrons are actually very large (of order ~103–104 MV/cm); the reasons why this behavior is not found in the present calculations is that AMOEBA excludes Coulombic interactions between multipoles and damps self-consistent polarization between close atoms in the same molecule, whose interactions are instead described by valence terms.36,67 In PB calculations, electrostatic forces at the atomic sites can be subject to numerical instability because of the presence of point charges. Using the appropriate smoothing algorithms,56 the calculated fields were only 10–30 times smaller than the self-fields, resulting in accurate results that agreed well with the other methods. We found that different dielectric boundary smoothing methods or grid spacings resulted in trivial changes (Tables S7–S8). In principle, the same Eqs. 2-6 and reference state definition could be applied to calculating fields in a quantum mechanical model, but care would be needed to obtain a reliable difference between two large numbers with close values.
Another critical aspect of the electric field calculation was the choice to define the electric field experienced by the vibration in the simple manner expressed by Eq. 5. There is no unique way to define how a vibration senses its electrostatic environment, and many prescriptions (so-called frequency maps) have been developed17,70-72 – most are substantially more complex than Eq. 5. Our defense of Eq. 5 is based on its ability to produce values that correlate strongly with solvent-induced frequency shifts, its intuitive appeal, conceptual parsimony, and transferability across many different levels of theory. On that note, and by themselves had slightly worse explanatory power than 〈|Fvib|〉 to describe variation in C=O frequencies (based on t-values and R2’s), and running a bivariate regression with those variables as independent explanatory variables gave an identical R2 as the regression using just 〈|Fvib〉| as the explanatory variable. Therefore, we believe 〈|Fvib|〉 is a simple and sufficient descriptor of the environment’s electrostatic state, at least so far as the C=O frequency of acetophenone is concerned, and likely for the C=O frequency of other carbonyl-containing molecules as well.
4.5. Comments on Electric Field Scale
The calculations presented shed light on what is the overall scale of electric field that a polar solute experiences in liquid solutions. The three models employed (Poisson-Boltzmann, fixed-charge force field, AMOEBA force field) qualitatively agree it is on the order of 10–100 MV/cm, and that the change in field between a polar and non-polar solvent, |FDMSO| − |Fhexane|, is about −30 MV/cm. On the other hand, acetophenone’s frequency shift between these two solvents is 14.4 cm−1 and when combined with the measured Stark tuning rate of acetophenone, , of 1.05 cm−1/(MV/cm),23 one would predict the quantity |FDMSO| − |Fhexane| to be −14 MV/cm. The scale of solvent electric fields predicted by models is therefore about twice as large as that suggested from the experimental solvent-induced frequency shifts and Stark tuning rate. This discrepancy has been observed in a few recent contributions23,73; however, it has apparently gone largely unnoticed in prior literature, likely because correlations between model and observation were too weak for the models to make quantitative claims about the electric fields’ absolute scale, and because of the practice of introducing post hoc dielectric rescaling factors.6,11,14,22,35,74 The present work presents two new models of solvent fields (AMOEBA and PB) in addition to the fixed-charge simulations previously reported,23 which in combination with the solventinduced frequency shifts corroborate an estimate of ca. 0.5 cm−1/(MV/cm)) for the effective tuning rate of the C=O vibration of acetophenone in liquid solution. Since this value is two-fold smaller than the measured difference dipole of acetophenone from Stark spectroscopy,23 we here consider potential systematic reasons for why the effective Stark tuning rate in liquid solution could be different from what is measured in solid solution in vibrational Stark spectroscopy.
One key consideration is the local field effect, which modulates electric fields applied through an external voltage, but does not affect the environment field (also known as the internal field in earlier literature) created by solvent molecules. When an external field is applied to a sample (as in a Stark experiment), the local field on a C=O probe due to the external charges will differ from the accurately known external (Maxwell) field by a factor called the local field correction factor (f).18,75 The local field will generally be larger because of extra contributions arising from polarization of the medium surrounding the C=O probe induced by the external field. The extent to which the local field is greater than the external field is not precisely known, and so experimental Stark tuning rates are reported as – a product between the microscopic Stark tuning rate, , and the local field correction factor.
f has traditionally been estimated to be between 1.1–1.4 for frozen organic glasses18,68 (the environment in which Stark spectroscopy is typically carried out) based on classic formulations from continuum dielectric theory. We found however that standard treatments omit important aspects of the local field effect, and that a more likely range for f is between 1.4–1.8 (see the supplementary discussion for derivation), implying that the microscopic Stark tuning rate for acetophenone, , is estimated to be between 0.58–0.75 cm−1/(MV/cm), a range also in agreement with ab initio DFT calculations (see Figure S3). It deserves mention that models for the local field effect based on continuum dielectric theory make assumptions that are not appropriate for microscopic properties,18 and polarizable force fields may provide a means to make progress on describing the local field effect microscopically.75
A second consideration is the fact that the difference dipole of a vibration comprises both an intrinsic portion arising from anharmonicity,14,19 , (present when the vibrational chromophore is in the gas phase) and an induced portion, , arising from the interaction between the environment’s electric field and the vibration’s difference polarizability.76 The induced portion of the difference dipole in a given environment will be reflected differently in the Stark and solvatochromism experiments. The induced difference dipole caused by an environment will be observed in full measure when a small external field supplements the field furnished by the environment, as in Stark spectroscopy. On the other hand, a frequency shift caused by a solvent field does not reflect the whole induced difference dipole present in the enviroment field, but rather, only half of it, since was itself due to the environment field that induced it. This is expressed mathematically as an alteration of Eq. 1 to
| (9) |
On the other hand, in Stark spectroscopy, the difference dipole detected includes without the attenuating factor of one-half. This difference could make the tuning rate in a Stark experiment somewhat higher if the environment field in the Stark experiment is large enough to make the induced difference dipole significant (see Figure S3).76 While the difference polarizability is generally found to be small for vibrational transitions,14,19-23 the electric fields in solid solutions can be very large because of increased solvent organization.77 High level ab initio frequency calculations on polar diatomic molecules have shown that at larger electric fields, the quadratic contribution to frequency shifts (and by extension, the induced contribution to the difference dipole) is non-negligible.78
Our current hypothesis is that a combination of the local field effect and the induced difference dipole explain the ca. 2-fold disagreement between the effective tuning rate from solvent-induced frequency shifts and the difference dipole measured in Stark spectroscopy. Needless to say, these hypotheses must be independently tested, as other unexplored sources of discrepancy are also possible. In particular, one previous study that focused on the O–H vibration of phenol in complex with various H-bond acceptors found that no local field correction was necessary to bring to accord the slope of the field-frequency curve and the Stark tuning rate.79 A careful retrospective is necessary (and underway) to comprehend electric field calculations and vibrational Stark effects into a unified paradigm.
A critical consequence that follows from this discussion is that the electric fields in the condensed phase are larger than what would be estimated from vibrational frequency measurements coupled with the observed Stark tuning rate. In particular, the electric field acetophenone’s C=O moiety experiences in water would be quite large (ca. 70 MV/cm). The presence of water on the same linear regression line (Figure 1A) implies that the C=O vibration maintains linear sensitivity to electric field out to fields as high as 70 MV/cm.12 For perspective, an electric field of this magnitude would impose an energetic penalty of ~6.7 kcal mol−1 on a point dipole of 1 D to reverse its orientation. To connect this number to experiment, in the classic aqueous ferrous-ferric self-exchange reaction, the outer-sphere reorganization energy involves the effective reversal of a dipole consisting of ±0.5 e displaced over the diameter of an iron atom.62,80 Modeling iron’s van der Waals radius at 2 Å, the magnitude of the dipole to be reversed is ~9.6 D, implying a reorganization energy of 64 kcal mol−1. The experimental reorganization energy based on Marcus theory is 67 kcal mol−1.80 This short calculation illustrates that the large electric fields reported in Table 1 have some physical basis, though more systematic tests are still needed.
5. Concluding Remarks
The notion that solvent-induced spectral shifts are related to the Stark effect is an old one.30,31 With the help of polarizable force fields, we have extended that reductionist concept and posit that solvent effects, hydrogen bonding, and condensed phase effects can all be quantitatively interpreted as electric field (Stark) effects. The task falls mostly to using a model of sufficient sophistication to calculate the average electric field in the environment of interest. To reiterate, only polarizable models (e.g., AMOEBA and PB) can account for the condensed phase shift (gas-phase to n-hexane), an atomistic model (e.g., AMOEBA and fixed-charge) is necessary to account for H-bonding shifts (DMSO to water), and all three categories of models can account for shifts associated with solvent polarity (n-hexane to DMSO). Therefore, AMOEBA was the only model examined that could properly describe non-polar environments and highly polar H-bonding environments consistently. Polarizable force fields such as AMOEBA are uniquely suited for this task, because two major components that are needed to describe the electric field in the condensed phase accurately are polarization and sampling. Polarization is missing in fixed-charge models, and sampling is unwieldy in ab initio treatments. We found that fixed-charge force fields can recapitulate certain aspects of the polarizable model, but they are less adept at describing interactions between polar and non-polar entities,66 which would seem to be critical when simulating proteins. Drawing analogies to solvation phenomena has been useful in the past for developing models and interpreting data on protein structure and dynamics. We believe that vibrational frequency shifts lend themselves well to an interpretation that is transferable between solvents and proteins, and that they will continue to lead to physical insights on the organized environments of proteins and how functional properties emerge from them.
Supplementary Material
Acknowledgments
S.D.F. thanks the NSF pre-doctoral fellowship and the Stanford Bio-X interdisciplinary graduate fellowship for support. This work was supported in part by grants from the NIH (to S.G.B., GM27739; to P.R., GM106137; to V.S.P., U54 GM072970). Simulations were carried out largely on Stanford’s Certainty cluster, which is financially supported by the NSF (Award 0960306) under the American Recovery and Reinvestment Act of 2009. We would also like to thank Prof. Nathan Baker for reading and reviewing a draft of this paper.
Footnotes
Supporting Information. Electric field trajectories and histograms, full electric field data tables, PB controls with alternative settings, modifications to TINKER source code and Python scripts needed for calculating electric fields with AMOEBA, and AMOEBA parameters for all molecules simulated. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Onsager L. Electric Moments of Molecules in Liquids. J Am Chem Soc. 1936;58:1486–1493. [Google Scholar]
- 2.Marini A, Muñoz-Losa A, Biancardi A, Mennucci B. What is Solvatochromism? J Phys Chem B. 2010;114:17128–17135. doi: 10.1021/jp1097487. [DOI] [PubMed] [Google Scholar]
- 3.Honig B, Nicholls A. Classical Electrostatics in Biology and Chemistry. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 4.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of Nanosystems: Application to Microtubules and the Ribosome. Proc Natl Acad Sci USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lee H, Lee G, Jeon J, Cho M. Vibrational Spectroscopic Determination of Local Solvent Electric Field, Solute–Solvent Electrostatic Interaction Energy, and Their Fluctuation Amplitudes. J Phys Chem A. 2012;116:347–357. doi: 10.1021/jp209709e. [DOI] [PubMed] [Google Scholar]
- 6.Suydam IT, Snow CD, Pande VS, Boxer SG. Electric Fields at the Active Site of an Enzyme: Direct Comparison of Experiment with Theory. Science. 2006;313:200–204. doi: 10.1126/science.1127159. [DOI] [PubMed] [Google Scholar]
- 7.Ringer AL, MacKerell AD., Jr Calculation of the Vibrational Stark Effect Using a First-Principles Quantum Mechanical/Molecular Mechanical Approach. J Phys Chem Lett. 2011;2:553–556. doi: 10.1021/jz101657s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Prakash MK, Marcus RA. An Interpretation of Fluctuations in Enzyme Catalysis Rate, Spectral Diffusion, and Radiative Component of Lifetimes in Terms of Electric Field Fluctuations. Proc Natl Acad Sci USA. 2007;104:15982–15987. doi: 10.1073/pnas.0707859104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Batchelor J. Theory of Linear Electric Field Shifts in Carbon-13 Nuclear Magnetic Resonance. J Am Chem Soc. 1975;97:3410–3415. [Google Scholar]
- 10.Lockhart D, Kim P. Internal Stark Effect Measurement of the Electric Field at the Amino Terminus of an Alpha Helix. Science. 1992;257:947–951. doi: 10.1126/science.1502559. [DOI] [PubMed] [Google Scholar]
- 11.Laberge M, Vanderkooi J, Sharp K. Effect of a Protein Electric Field on the CO Stretch Frequency. Finite Difference Poisson–Boltzmann Calculations on Carbonmonoxycytochromes c. J Phys Chem. 1996;100:10793–10801. [Google Scholar]
- 12.Dalosto SD, Vanderkooi JM, Sharp KA. Vibrational Stark Effects on Carbonyl, Nitrile, and Nitrosyl Compounds Including Heme Ligands, CO, CN, and NO, Studied with Density Functional Theory. J Phys Chem B. 2004;108:6450–6457. doi: 10.1021/jp0310697. [DOI] [PubMed] [Google Scholar]
- 13.Waegele MM, Culik RM, Gai F. Site-Specific Spectroscopic Reporters of the Local Electric Field, Hydration, Structure, and Dynamics of Biomolecules. J Phys Chem Lett. 2011;2:2598–2609. doi: 10.1021/jz201161b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Park ES, Boxer SG. Origins of the Sensitivity of Molecular Vibrations to Electric Fields: Carbonyl and Nitrosyl Stretches in Model Compounds and Proteins. J Phys Chem B. 2002;106:5800–5806. [Google Scholar]
- 15.Eaves JD, Tokmakoff A, Geissler PL. Electric Field Fluctuations Drive Vibrational Dephasing in Water. J Phys Chem A. 2005;109:9424–9436. doi: 10.1021/jp051364m. [DOI] [PubMed] [Google Scholar]
- 16.Lee H, Choi J-H, Cho M. Vibrational Solvatochromism and Electrochromism of Cyanide, Thiocyanate, and Azide Anions in Water. Phys Chem Chem Phys. 2010;12:12658–12669. doi: 10.1039/c0cp00214c. [DOI] [PubMed] [Google Scholar]
- 17.Choi J-H, Cho M. Vibrational Solvatochromism and Electrochromism of Infrared Probe Molecules Containing C≡O, C≡N, C=O, or C–F Vibrational Chromophore. J Chem Phys. 2011;134:154513. doi: 10.1063/1.3580776. [DOI] [PubMed] [Google Scholar]
- 18.Bublitz GU, Boxer SG. Stark Spectroscopy: Applications in Chemistry, Biology, and Materials Science. Annu Rev Phys Chem. 1997;48:213–242. doi: 10.1146/annurev.physchem.48.1.213. [DOI] [PubMed] [Google Scholar]
- 19.Andrews SS, Boxer SG. Vibrational Stark Effects of Nitriles I. Methods and Experimental Results. J Phys Chem A. 2000;104:11853–11863. [Google Scholar]
- 20.Park ES, Andrews SS, Hu RB, Boxer SG. Vibrational Stark Spectroscopy in Proteins: A Probe and Calibration for Electrostatic Fields. J Phys Chem B. 1999;103:9813–9817. [Google Scholar]
- 21.Suydam IT, Boxer SG. Vibrational Stark Effects Calibrate the Sensitivity of Vibrational Probes for Electric Fields in Proteins. Biochemistry. 2003;42:12050–12055. doi: 10.1021/bi0352926. [DOI] [PubMed] [Google Scholar]
- 22.Fafarman AT, Boxer SG. Nitrile Bonds as Infrared Probes of Electrostatics in Ribonuclease S. J Phys Chem B. 2010;114:13536–13544. doi: 10.1021/jp106406p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fried SD, Bagchi S, Boxer SG. Measuring Electrostatic Fields in Both Hydrogen Bonding and non-Hydrogen Bonding Environments using Carbonyl Vibrational Probes. J Am Chem Soc. 2013;135:11181–1192. doi: 10.1021/ja403917z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Aschaffenburg D, Moog R. Probing Hydrogen Bonding Environments: Solvatochromic Effects on the CN Vibration of Benzonitrile. J Phys Chem B. 2009;113:12736–12743. doi: 10.1021/jp905802a. [DOI] [PubMed] [Google Scholar]
- 25.Zhang S, Shi R, Ma X, Lu L, He Y, Zhang X, Wang Y, Deng Y. Intrinsic Electric Fields in Ionic Liquids Determined by Vibrational Stark Effect Spectroscopy and Molecular Dynamics Simulation. Chem Eur J. 2012;18:11904–11908. doi: 10.1002/chem.201201257. [DOI] [PubMed] [Google Scholar]
- 26.Zhang S, Zhang Y, Ma X, Lu L, He Y, Deng Y. Benzonitrile as a Probe of Local Environment in Ionic Liquids. J Phys Chem B. 2013;117:2764–2772. doi: 10.1021/jp312251q. [DOI] [PubMed] [Google Scholar]
- 27.Alfieri KN, Vienneau AR, Londergan CH. Using Infrared Spectroscopy of Cyanylated Cysteine to Map the Membrane Binding Structure and Orientation of the Hybrid Antimicrobial Peptide CM15. Biochemistry. 2011;50:11097–11108. doi: 10.1021/bi200903p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hu W, Webb LJ. Direct Measurement of the Membrane Dipole Field in Bicelles Using Vibrational Stark Effect Spectroscopy. J Phy Chem Lett. 2011;2:1925–1930. [Google Scholar]
- 29.Manor J, Feldblum ES, Zanni MT, Arkin IT. Environment Polarity in Proteins Mapped Noninvasively by FTIR Spectroscopy. J Phys Chem Lett. 2012;3:939–944. doi: 10.1021/jz300150v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Platt JR. Electrochromism, a Possible Change of Color Producible in Dyes by an Electric Field. J Chem Phys. 1961;34:862. [Google Scholar]
- 31.Liptay W. Electrochromism and Solvatochromism. Angew Chem Int Ed. 1969;8:177–188. [Google Scholar]
- 32.Tanford C. The Hydrophobic Effect and the Organization of Living Matter. Science. 1978;200:1012–1018. doi: 10.1126/science.653353. [DOI] [PubMed] [Google Scholar]
- 33.Chimenti MS, Castañeda CA, Majumdar A, García-Moreno B. Structural Origins of High Apparent Dielectric Constants Experienced by Ionizable Groups in the Hydrophobic Core of a Protein. J Mol Biol. 2011;405:361–377. doi: 10.1016/j.jmb.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Abbyad P, Shi X, Childs W, McAnaney TB, Cohen BE, Boxer SG. Measurement of Solvation Responses at Multiple Sites in a Globular Protein. J Phys Chem B. 2007;111:8269–8276. doi: 10.1021/jp0709104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bagchi S, Fried SD, Boxer SG. A Solvatochromic Model Calibrates Nitriles’ Vibrational Frequencies to Electrostatic Fields. J Am Chem Soc. 2012;134:10373–10376. doi: 10.1021/ja303895k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio RA, Jr, Head-Gordon M, Clark GNI, Johnson ME, Head-Gordon T. Current Status of the AMOEBA Polarizable Force Field. J Phys Chem B. 2010;114:2549–2564. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ponder JW. Tinker: Software Tools for Molecular Design, 6.2. Washington University School of Medicine; Saint Louis, MO: 2012. [Google Scholar]
- 38.Andrews SS, Boxer SG. Vibrational Stark Effects of Nitriles II. Physical Origins of Stark Effects from Experiment and Perturbation Models. J Phys Chem A. 2002;106:469–477. [Google Scholar]
- 39.Ren P, Ponder JW. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J Phys Chem B. 2003;107:5933–5947. [Google Scholar]
- 40.Ren P, Wu C, Ponder JW. Polarizable Atomic Multipole-Based Molecular Mechanics for Organic Molecules. J Chem Theory Comput. 2011;7:3143–3161. doi: 10.1021/ct200304d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stone AJ. Distributed Multipole Analysis: Stability for Large Basis Sets. J Chem Theory Comput. 2005;1:1128–1132. doi: 10.1021/ct050190+. [DOI] [PubMed] [Google Scholar]
- 42.Caleman C, van Maaren PJ, Hong M, Hub JS, Costa LT, van der Spoel D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J Chem Theory Comput. 2012;8:61–74. doi: 10.1021/ct200731v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. Ab initio Calculation of Vibrational Absorption and Circular Dichroism Spectra using Density Functional Force Fields. J Phys Chem. 1994;98:11623–11627. [Google Scholar]
- 44.Krishnan R, Binkley JS, Seeger R, Pople J. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J Chem Phys. 1980;72:650. [Google Scholar]
- 45.Barone V. Anharmonic Vibrational Properties by a Fully Automated Second-order Perturbative Approach. J Chem Phys. 2005;122:014108. doi: 10.1063/1.1824881. [DOI] [PubMed] [Google Scholar]
- 46.Adamo C, Cossi M, Rega N, Barone V. Theoretical Biochemistry: Processes and Properties of Biological Systems, Theoretical and Computational Chemistry. Vol. 9. Elsevier; New York: 1990. [Google Scholar]
- 47.Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J Chem Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 48.Darden T, York D, Pedersen L. Particle Mesh Ewald: An N·log(N) method for Ewald Sums in Large Systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 49.Beeman D. Some Multistep Methods for Use in Molecular Dynamics Calculations. J Comp Phys. 1976;20:130–139. [Google Scholar]
- 50.Bussi G, Donadio D, Parrinello M. Canonical Sampling Through Velocity Rescaling. J Chem Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 51.Tuckerman M, Berne BJ, Martyna GJ. Reversible Multiple Time Scale Molecular Dynamics. J Chem Phys. 1992;97:1990. [Google Scholar]
- 52.Fogolari F, Brigo A, Molinari H. The Poisson-Boltzmann equation for Biomolecular Electrostatics: A Tool for Structural Biology. J Mol Recognit. 2002;15:377. doi: 10.1002/jmr.577. [DOI] [PubMed] [Google Scholar]
- 53.Gilson M, Honig B. Calculation of Electrostatic Potentials in an Enzyme Active Site. Nature. 1987;330:84–86. doi: 10.1038/330084a0. [DOI] [PubMed] [Google Scholar]
- 54.Swanson JMJ, Adcock SA, McCammon JA. Optimized Radii for Poisson–Boltzmann Calculations with the AMBER Force Field. J Chem Theory Comput. 2005;1:484–493. doi: 10.1021/ct049834o. [DOI] [PubMed] [Google Scholar]
- 55.Wohlfarth C. Static Dielectric Constants of Pure Liquids and Binary Liquid Mixtures in Landolt-Börnstein database. In: Madelung O, editor. Macroscopic and Technical Properties of Matter. Vol. 6. Springer-Verlag; Berlin: 1991. [Google Scholar]
- 56.Im W, Beglov D, Roux B. Continuum Solvation Model: Computation of Electrostatic forces from Numerical Solutions to the Poisson-Boltzmann equation. Comp Phys Comm. 1998;111:59–75. [Google Scholar]
- 57.Bellamy LJ, Williams RL. Infra-red Spectra and Solvent Effects. Part 2. Carbonyl Absorptions. Trans Faraday Soc. 1959;55:14–18. [Google Scholar]
- 58.Taylor PJ. The i.r. Spectroscopy of Some Highly Conjugated Systems—I. Rationale of the Investigation. Spectrochim Acta A. 1976;32:1471–1476. [Google Scholar]
- 59.Nam SI, Min ES, Jung YM, Lee MS. Fermi Resonance and Solvent Dependence of the C=O Frequency Shifts of Raman Spectra: Cyclohexanone and 2-Cyclohexen-1-one. Bull Korean Chem Soc. 2001;22:989–993. [Google Scholar]
- 60.Huber CJ, Anglin TC, Jones BH, Muthu N, Cramer CJ, Massari AM. Vibrational Solvatochromism in Vaska’s Complex Adducts. J Phys Chem A. 2012;116:9279–9286. doi: 10.1021/jp3070536. [DOI] [PubMed] [Google Scholar]
- 61.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J Chem Phys. 1983;79:926. [Google Scholar]
- 62.Marcus R. On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I. J Chem Phys. 1956;24:966–978. [Google Scholar]
- 63.Khalil M, Demirdöven N, Tokmakoff A. Coherent 2D IR Spectroscopy: Molecular Structure and Dynamics in Solution. J Phys Chem A. 2003;107:5258–5279. [Google Scholar]
- 64.Brookes JF, Slenkamp KM, Lynch MS, Khalil M. Effect of Solvent Polarity on the Vibrational Dephasing Dynamics of the Nitrosyl Stretch in an FeII Complex Revealed by 2D IR Spectroscopy. J Phys Chem A. 2013;117:6234–6243. doi: 10.1021/jp4005345. [DOI] [PubMed] [Google Scholar]
- 65.NIST Mass Spec Data Center, Stein, S. E., “Infrared Spectra” in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Eds. Linstrom, P. J.; Mallard W. G. (http://webbook.nist.gov, retrieved August 13, 2013). Note that this reference reports acetophenone’s gas-phase C=O frequency as 1703 cm−1, whereas ref. 57 reports it as 1709 cm−1
- 66.Jorgensen WL, Tirado-Rives J. Potential Energy Functions for Atomic-Level Simulations of Water and Organic and Biomolecular Systems. Proc Natl Acad Sci USA. 2005;102:6665–6670. doi: 10.1073/pnas.0408037102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ren P, Chun J, Thomas DG, Schnieders MJ, Marucho M, Zhang J, Baker NA. Biomolecular Electrostatics and Solvation: A Computational Perspective. Quart Rev Biophys. 2012;45:427–491. doi: 10.1017/S003358351200011X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Bottcher CJF. Theory of Electric Polarization. Elsevier; Amsterdam: 1973. [Google Scholar]
- 69.Thole BT. Molecular Polarizabilities Calculated with a Modified Dipole Interaction. Chem Phys. 1981;59:341–350. [Google Scholar]
- 70.Bouř P, Keiderling TA. Empirical Modeling of the Peptide Amide I band IR Intensity in Water Solution. J Chem Phys. 2003;119:11253–11262. [Google Scholar]
- 71.Ham S, Kim J-H, Lee H, Cho M. Correlation between Electronic and Molecular Structure Distortions and Vibrational Properties. II. Amide I modes of NMA–nD2O Complexes. J Chem Phys. 2003;118:3491–3498. [Google Scholar]
- 72.Morales CM, Thompson WH. Molecular-level Mechanisms of Vibrational Frequency Shifts in a Polar Liquid. J Phys Chem B. 2011;115:7597–7605. doi: 10.1021/jp201591c. [DOI] [PubMed] [Google Scholar]
- 73.Jha SK, Ji M, Gaffney KJ, Boxer SG. Direct Measurement of the Protein Response to an Electrostatic Perturbation that Mimics the Catalytic Cycle in Ketosteroid Isomerase. Proc Natl Acad Sci USA. 2011;108:16612–16617. doi: 10.1073/pnas.1113874108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Fafarman AT, Sigala PA, Schwans JP, Fenn TD, Herschlag D, Boxer SG. Quantitative, Directional Measurement of Electric Field Heterogeneity in the Active Site of Ketosteroid Isomerase. Proc Natl Acad Sci USA. 2012;109:E299–308. doi: 10.1073/pnas.1111566109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Kohler BE, Woehl JC. Measuring Internal Electric Fields with Atomic Resolution. J Chem Phys. 1995;102:7773–7781. [Google Scholar]
- 76.Vauthey E, Holliday K, Wei C, Renn A, Wild UP. Stark Effect and Spectral Hole-burning: Solvation of Organic Dyes in Polymers. Chem Phys. 1993;171:253–263. [Google Scholar]
- 77.Bublitz GU, Boxer SG. Effective Polarity of Frozen Solvent Glasses in the Vicinity of Dipolar Solutes. J Am Chem Soc. 1998;120:3988–3992. [Google Scholar]
- 78.Sowlati-Hasjin S, Matta CF. The Chemical Bond in External Electric Fields: Energies, Geometries, and Vibrational Stark Shifts of Diatomic Molecules. J Chem Phys. 2013;139:144101. doi: 10.1063/1.4820487. [DOI] [PubMed] [Google Scholar]
- 79.Saggu M, Levinson NM, Boxer SG. Direct Measurements of Electric Fields in Weak OH⋯π Hydrogen Bonds. J Am Chem Soc. 2011;133:17414–17419. doi: 10.1021/ja2069592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Zwolinski BJ, Marcus RJ, Eyring H. Inorganic Oxidation-Reduction Reactions in Solution Electron Transfers. Chem Rev. 1955;55:157–180. The 67 kcal mol−1 figure comes from the empirical free energy barrier (16.7 kcal mol−1) and the equation λo = 4ΔG‡ for self-exchange reactions. The Marcus equation for the outer sphere reorganization energy predicts λo to be 45 kcal mol−1. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


