Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2014 Oct 21;107(8):1794–1801. doi: 10.1016/j.bpj.2014.09.003

Nanomechanical Mapping of Hydrated Rat Tail Tendon Collagen I Fibrils

Samuel J Baldwin 1, Andrew S Quigley 1, Charlotte Clegg 1, Laurent Kreplak 1,∗
PMCID: PMC4213719  PMID: 25418160

Abstract

Collagen fibrils play an important role in the human body, providing tensile strength to connective tissues. These fibrils are characterized by a banding pattern with a D-period of 67 nm. The proposed origin of the D-period is the internal staggering of tropocollagen molecules within the fibril, leading to gap and overlap regions and a corresponding periodic density fluctuation. Using an atomic force microscope high-resolution modulus maps of collagen fibril segments, up to 80 μm in length, were acquired at indentation speeds around 105 nm/s. The maps revealed a periodic modulation corresponding to the D-period as well as previously undocumented micrometer scale fluctuations. Further analysis revealed a 4/5, gap/overlap, ratio in the measured modulus providing further support for the quarter-staggered model of collagen fibril axial structure. The modulus values obtained at indentation speeds around 105 nm/s are significantly larger than those previously reported. Probing the effect of indentation speed over four decades reveals two distinct logarithmic regimes of the measured modulus and point to the existence of a characteristic molecular relaxation time around 0.1 ms. Furthermore, collagen fibrils exposed to temperatures between 50 and 62°C and cooled back to room temperature show a sharp decrease in modulus and a sharp increase in fibril diameter. This is also associated with a disappearance of the D-period and the appearance of twisted subfibrils with a pitch in the micrometer range. Based on all these data and a similar behavior observed for cross-linked polymer networks below the glass transition temperature, we propose that collagen I fibrils may be in a glassy state while hydrated.

Introduction

Collagen is the primary protein component that provides structural integrity to mammalian tissues. Of the 28 varieties of collagen, types I, II, III, V, XI, XXIV, and XXVII form fibrils that provide mechanical strength to tissues such as bone, tendon, ligament, and skin (1–3). There is a vast body of literature describing the architecture and macroscopic mechanical properties of these tissues and how they are influenced by age, anatomical location, damage, exercise, and disease (4–11). In contrast, the relationship between structure and mechanical properties at the single collagen fibril level is much less understood despite some recent advances (3).

Collagen fibrils are linear aggregates of 300 nm long tropocollagen molecules that have a diameter of 1.5 nm and a distinctive triple-helical structure (3,12). Tens to hundreds of thousands of tropocollagen molecules are covalently bound to each other by cross-links and packed radially in a semicrystalline fashion to form 50 to 500 nm wide fibrils spanning microns to millimeters in length (13). There are two intermediate stages of organization between individual molecules and the fibril, the microfibril, and the subfibril. The microfibril consists of five strands of laterally organized collagen molecules with a diameter of 4–8nm (14), the subfibril has a diameter of around 25 nm but is not as well described in the literature as the microfibril (15). Both the individual molecules and the intermediate structures run almost parallel to the fibril axis, the molecules are staggered with respect to each other giving rise to 67 nm wide bands also named D-periods. The current molecular model of the D-period involves two regions, one where all the molecules overlap and one where 20% of the molecules are missing due to an axial gap. The relative length of these regions is 0.46 and 0.54 of the 67 nm D-period, respectively. This model was proposed on the basis of electron microscopy images of negatively stained collagen fibrils and further refined with small angle x-ray scattering data of rat tail tendon (16,17).

Mechanical measurements of single collagen fibrils are typically performed under tension using microelectromechanical devices or nanotensile testers, in bending where a microcantilever is used to apply loads on suspended fibrils, and via atomic force microscopy (AFM)-based nanoindentation (18–23). These studies acknowledge that collagen fibrils are heterogeneous yet only provide a single value for their mechanical properties. Previous nanoindentation measurements on dried collagen I fibrils demonstrated a factor of two in elastic modulus between the overlap and the gap region of the D-period (24). Another strong indication that mechanical properties are not homogeneous along a collagen fibril is the occurrence of discrete plastic deformations observed along fibrils inside overloaded bovine tail tendons (25). Both results are strong incentives to develop a method capable of mapping mechanical properties of an entire fibril at high spatial resolution while in a hydrated state.

The technique of choice that combines mechanical measurements and high spatial resolution is an AFM mode named force-distance (FD) curve-based imaging (26). In this mode an FD curve is measured at each pixel of the image allowing to generate maps of various mechanical properties such as the elastic modulus, the deformation of the sample under a given load, the adhesion force between tip and sample, and the amount of mechanical energy dissipated. In this study, we take advantage of the high-throughput capabilities of the technique to generate modulus maps of single collagen fibrils in water at a spatial resolution around 10 nm and at indentation speeds around 105 nm/s. We demonstrate that collagen fibrils stiffen by a factor of seven when varying the indentation speed from 102 to 106 nm/s. This effect allows us to observe the D-period in the elastic modulus channel. We report a 20% decrease in modulus from the overlap to the gap region of the D-period as well as long-range fluctuations in modulus along the length of the fibrils that have not been reported so far. Furthermore, collagen fibrils exposed to temperatures between 50 and 62°C and cooled back to room temperature show a sharp decrease in modulus and a swelling of the fibril. This is also associated with a disappearance of the D-period and the appearance of twisted subfibrils in the modulus channel of the image that persists upon dehydration of the collagen fibril.

Materials and Methods

Sample preparation

Rat tails were dissected to extract tendon fascicles for use as a sample source. First, the dermal layers were removed from the tail exposing the skeletal frame and tendons of the tail. To prevent tensile loading during tendon extraction, a scalpel blade was inserted between the skeletal structure and the tendon and was used to sever connecting material. Tendons were then lifted from the skeletal structure and stored in 20 ml phosphate buffered saline (PBS) with 500 μl of antibacterial cocktail (Sigma-Aldrich, St. Louis, MO). Collagen fibrils were dissected from tail fascicles of 2-year-old rats in PBS. To minimize fibril damage, a thin glass rod was used as the main dissection tool. Fascicles were held at one end with tweezers while the glass rod was inserted into the fascicle and moved along its longitudinal axis to allow gentle separation of the hierarchical subcomponents. Great care was taken to keep the fascicles hydrated at all times during this process. The PBS solution containing the dissected fibrils were transferred to glass bottom petri dishes with a pipet and left for 30 min allowing the fibrils to physically adhered to the glass substrate. The dishes were then rinsed three times with deionized water to remove unattached material and residual salts. The samples were either used immediately or kept at 4°C until AFM measurement.

AFM

All the experiments were performed with a Bioscope Catalyst atomic force microscope (Bruker, USA) mounted on an IX71 inverted microscope (Olympus, Tokyo, Japan) with a differential interference contrast module and a 100×, 1.3NA, oil immersion objective. This setup allowed the optical visualization of single collagen fibrils in water before AFM imaging. Samples were imaged in peak force quantitative nanomechanical mapping mode using ScanAsyst liquid+ (Bruker, Santa Barbara, CA) cantilevers with a nominal spring constant of 0.7 N/m, a nominal tip radius of 2 nm, and an equivalent cone half-angle of 18°. Before each experiment the cantilever spring constant was calibrated with the thermal noise method (27). Images were acquired at a cantilever oscillation frequency of 1 kHz, a scanning frequency of 0.5 Hz, and at an indentation speed between 400 and 1200 μm/s. The longitudinal axis of the collagen fibrils measured in this work was perpendicular to the fast scan axis unless otherwise mentioned. All indentation speed and heating images were taken at an imaging speed of 5 μm/s, whereas the 20, 40, and 80 μm maps were acquired at 2, 5, and 10 μm/s, respectively. The peak force was kept between 1 and 10 nN depending on the scan size. The total number of pixels per image was kept constant at 65,536.

We also used the heating stage of the Bioscope Catalyst to expose single collagen fibrils to different temperatures. Due to condensation issues it was not possible to continuously image the fibrils while increasing the temperature. For each AFM measurement the fibril was first kept at the target temperature for 15 or 30 min and then cooled down to room temperature (∼25°C) and imaged at that temperature. During each heating and cooling cycle, the sample was covered to limit evaporation. The heating and cooling rates were around 10 and 2°C per minute, respectively. The total amount of water was fixed to 3 ml to ensure a constant temperature profile between samples. Mechanical maps were acquired by peak force quantitative nanomechanical mapping once the sample had cooled to 25°C. Each fibril was either exposed to 62°C for 30 min or treated to subsequent temperatures of 50, 55, 58, 60, and 62°C, in that order, each time for 15 min. After the final heating and cooling cycle, the samples were dehydrated and imaged once more to reveal topological structures not visible in the hydrated state.

Data analysis

Force curves were selected from an area ±10% of the fibrils diameter from the apex of the collagen fibril by a simple filtering methodology (Figs. S1–S4 and supplement S5 in the Supporting Material). Based on the shape of our tips and the typical indentation depth that was in the order of 30 nm, we used the Sneddon model including adhesion to fit each force curve and extract the modulus in the radial direction (28,29). The Poisson ratio of a collagen fibril was assumed to be 0.5 as accepted in the literature for an incompressible material (30). The point of tip-fibril contact was determined by least square fitting of the force curve (31). The influence of the underlying glass substrate was minimized by only fitting the force curves to an indentation depth of 10% of the zero force height of the fibril, according to Bueckle’s rule (32,33). The zero force height of the fibril was estimated by adding the height and deformation channels, extracting the values along the apex of the fibril and averaging; this value was typically around 200 nm. The deformation of the fibril at any given point was estimated using the distance between the approach and the retract curve at a given force value. We used 15% of the peak force value to estimate the deformation and saw no significant difference when varying the peak force percentage to values as low as 5% of the peak force. Below this threshold the measurement of the deformation was unreliable.

In some cases we imaged fibrils over their entire length. Mechanical maps of each section of a given fibril were stitched manually. Modulus profiles were extracted along the entire fibrils and Fourier transformed to reveal periodic fluctuations. We used adjacent averaging to remove long wavelength fluctuations from the data to determine the amplitude of the short wavelength fluctuations observed.

Results

Influence of indentation speed

Typically, AFM-based indentation measurements on collagen fibrils are performed at indentation speeds in the μm/s range (30). To investigate the viscoelastic response of collagen fibrils in water, we measure the dependency of the modulus with indentation speed over four decades from 100 nm/s to 1.2 mm/s (Fig. 1). To average out spatial variations and fibril-to-fibril variations we use three different fibrils and a 5 μm long segment for each fibril. The order in which we measure the FD curves for the different indentation speeds is different for each fibril to avoid bias due to indentation history. The modulus is weakly dependent on the logarithm of the indentation speed below roughly 70 μm/s and then increases 5- to 10-fold in one decade (Fig. 1). The same behavior is observed for each fibril individually but the range of modulus is large in the high-speed regime. When acquiring modulus maps we are in the regime where the collagen fibril appears to stiffen significantly compared to previously published modulus data that are typically obtained at an indentation speed of 1 μm/s (30). Interestingly, the indentation speed dependence observed in this study is very similar to the one observed for a model cross-linked polymer network below the glass to rubber transition (34). In the glass state the mobility of the chains within the network is constrained in comparison to the rubber state, yielding an apparent stiffening of the network for indentation speeds well above the mobility of the chains. This means that in our case we are acquiring modulus maps in a regime where some characteristic relaxation mechanism of the molecules within a fibril is suppressed giving rise to an elastic contrast that should depend mainly on the molecular density.

Figure 1.

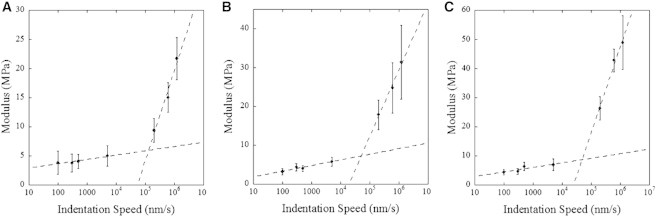
Figure 1

Open in a new tab

Dependence of the modulus with indentation speed. The modulus of three different collagen fibril segments 5 μm in length as a function of indentation speed. Logarithmic least square fits through the data are shown as dashed lines, highlighting the presence of two distinct regimes. Error bars are the standard deviation of each measurement.

Modulus variations along a single fibril

A first demonstration of the capabilities of our approach is the observation of the D-period in the modulus maps of single collagen fibrils in water. At a scan size of 2 × 2 μm the D-period is visible in the height, the modulus, and the deformation channels (Fig. 2). The variation between gap and overlap regions in each channel is small, 2–3 nm for the height and deformation, and several MPa for the modulus. However, the three channels are correlated with the overlap region being higher, stiffer, and less deformable than the gap region as expected (Fig. 2, B–D). Over a two microns range the modulus maps are quite uniform except for the D-period, but it is not true at length scales of tens of microns.

Figure 2.

Figure 2

Open in a new tab

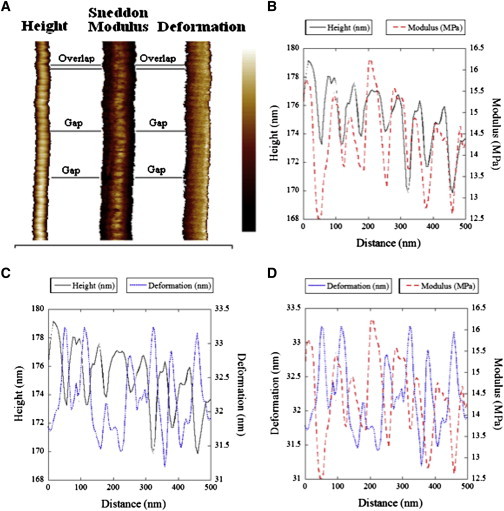
Observation of the D-period along a hydrated fibril. (A) Height, modulus, and deformation channel of a single collagen fibril. The differences in apparent diameter of the fibril are due to the choice of scale bar range used for each channel to visualize the D-period. Scale Bar: Height 140–190 nm; Modulus 0–30 MPa; Deformation 20–40 nm. The length of the fibril is 2 μm. (B–D) Comparison of the height, modulus, and deformation channels are shown for 500 nm segments showing the alignment of the modulus and height of the fibril and the 90° phase shift between the modulus and deformation of the fibril. The D-period is visible in all three channels. The overlap region appears higher, stiffer, and less deformable than the gap region. To see this figure in color, go online.

Imaging fibril segments of 80, 40, and 20 μm at 45, 20, and 8 nm pixel resolution, respectively, reveals long-range variations in modulus that are on the micron scale (Fig. 3, A–C). Two interesting features are fibril ends and sharp bends that exhibit lower moduli than their surroundings. The modulus behavior of these defects appear as at least a fourfold decrease in modulus at the defect site with a linear gradient toward the average modulus of the fibril spanning ∼5 μm (Fig. 3, arrows, and Fig. S6). From the Fourier transforms of the radius modulus profiles extracted from the 40 and 20 μm maps, we can accurately measure the D-period at 66.4 ± 0.2 nm and 67.6 ± 0.2 nm, respectively (Fig. 4, A and B).

Figure 3.

Figure 3

Open in a new tab

Modulus maps of collagen fibrils. (A) 80 μm long segment of fibril at 45 nm pixel resolution. (B) 40 μm long fibril at 20 nm pixel resolution, the modulus decays from the center to the ends. (C) 20 μm long segment of fibril at 8 nm pixel resolution, a sharp bend appears softer than its surrounding. Color Scale Bar: 0–30 MPa (A and C); 0–50 MPa (B). Length scale bar: (A) 20 μm, (B) 10 μm, (C) 5 μm. To see this figure in color, go online.

Figure 4.

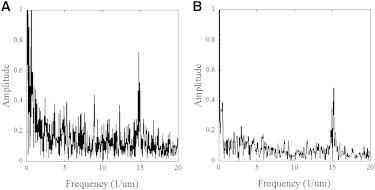
Figure 4

Open in a new tab

Periodicity along single fibrils. Fourier transforms of the modulus profiles extracted from the apex of two fibrils in Fig. 3A 40 μm long fibril at 20 nm pixel resolution. (B) 20 μm long segment of fibril at 8 nm pixel resolution. The peak corresponding to the D-period is clearly visible in both cases.

To estimate the average contrast in modulus between the gap and overlap regions of the D-period, we use both maps, (Fig. 3, B and C), excluding the 5 μm segments surrounding the sharp bend and fibril ends, respectively (Table 1). Calculating the moduli of the gap and overlap regions from the average moduli of the fibril and the root mean-square of the D-period reveals a gap/overlap ratio of 0.80 ± 0.04 and 0.82 ± 0.04 for the 20 and 40 μm maps, respectively. This is in excellent agreement with the molecular density ratio between the two regions as proposed by Hodge and Schmitt (16). This in turn indicates that the modulus scales locally with the molecular density as mentioned previously.

Table 1.

Summary of D-band Modulus variation and period with standard deviation (modulus data) and pixilation (D-period) as error

Fibril length (μm) Average modulus (MPa) Gap modulus (MPa) Overlap modulus (MPa) Gap/overlap D-period (nm)
20 16 ± 3 14.5 ± 0.6 18.1 ± 0.6 0.80 ± 0.04 67.6±.2
40 33 ± 6 30 ± 1 37 ± 1 0.82 ± 0.04 66.4±.2
80 16 ± 4 NA NA NA NA
Open in a new tab

Structural and mechanical alterations due to exposure to high temperatures

As a next step, we measure the modulus of 5 μm long segments of two collagen fibrils exposed to temperatures ranging from 25°C to 62°C in water (Fig. 5). We use a softer cantilever than stated previously with a spring constant of 0.25 N/m and an indentation velocity of 1.2 mm/s. At 25°C the two fibrils show a modulus and zero force height of 12.7 ± 0.3 MPa and 250 nm (Fig. 5, A and B), and 9.8 ± 0.2 MPa and 350 nm (Fig. 5, D and E), respectively. These modulus values are below the 20–40 MPa range mentioned previously for the same indentation speed. This is due to the use of a different cantilever (MSNL, Bruker) with a lower spring constant of 0.25 N/m compared to previous measurements (Fig. 1). The lower spring constant cantilever had a maximum measurable modulus of ∼15 MPa. This was selected to provide higher contrast at the lower elastic moduli observed after fibrils were exposed to a temperature >50°C. The behavior of the fibril between 25 and 50°C was checked with a ScanAsyst cantilever and showed the same behavior as the MSNL cantilever. To compare results from both fibrils, we normalize all radial modulus values to the ones obtained before any temperature exposure. After exposure to temperatures above 50°C, fibrils exhibited a sharp decrease in elastic modulus when measured at room temperature (Fig. 5). This decrease in elastic modulus progressed with exposure to temperatures as high as 62°C. At which point the radial elastic modulus was found to be around 1 MPa, or 10% of its original value. This decrease in elastic modulus was found to persist up to 36 h after temperature exposure, suggesting a permanent alteration to the elastic modulus of the fibril.

Figure 5.

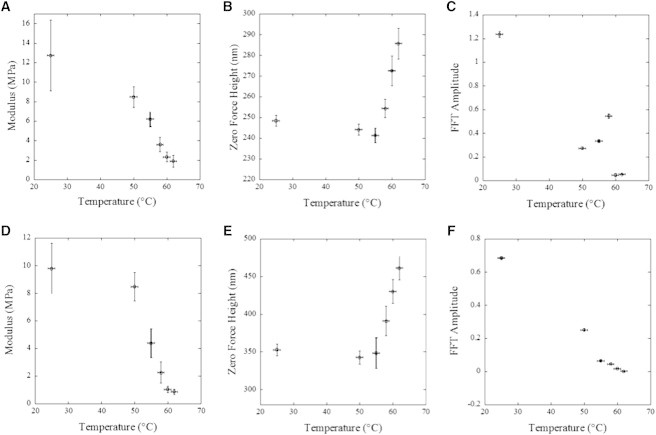
Figure 5

Open in a new tab

Dependence of fibril structure with temperature exposure. The modulus (A and D), zero force height (B and E), and FFT amplitude of the modulus profile at the D-period wavelength (C and F) for two 5 μm segments acquired from two collagen fibrils as a function of applied temperature. The indentation speed was 1.2 mm/s. Vertical error bars are the standard deviation of each measurement.

The softening of the fibrils for temperatures above 50°C is accompanied by two structural changes. The zero force height of the fibrils increases by 15% and 30%, respectively (Fig. 5, B and E), and the D-period disappears completely from the modulus maps (Fig. 5, C and F). To quantify this disappearance we compute the fast Fourier transform (FFT) of the modulus profile extracted from the apex of each fibril after each temperature exposure. The amplitude of the D-period peak in the FFT is a measure of its visibility in the modulus maps. This quantity is presented in Fig. 5 and shows that the D-period has completely disappeared after exposure to 60°C.

The disappearance of the D-period is associated with the appearance of subfibrilar structures that are only barely visible in the peak force error channel (data not shown) when the fibril is perpendicular to the fast scan axis as in Fig. 6 A. However, they appear clearly on the elastic modulus maps when the fibril is tilted 45° from the fast scan axis (see Fig. 6 C) or when the fibril is dried (see Fig. 6 E). The subfibrilar structures were determined to be subfibrils as their diameter (∼20–40 nm), was far larger than that of microfibrils, 4–8 nm (15). Our best modulus map image showing subfibrils with a pitch in the micron range was obtained after directly exposing a fibril to 62°C for 30 min and then cooling it back to 25°C (Fig. 6 C). These structures were not observed on the fibril at 25°C before heating (Fig. 6 B) or after dehydration (Fig. 6 D). All the fibrils exposed to a temperature of 62°C, stepwise (Fig. 6 A) or directly (Fig. 6 C) show both a D-period and subfibrils with a minimum diameter of 20 nm when dehydrated (Fig. 6 E). No alteration to the D-period was observed between dehydrated control fibrils, 67.6 ± 2.7 nm (n = 2) (Fig. S7 C), and fibrils dehydrated after being exposed to 62°C, 66.1 ± 1.5 nm (n = 2) (Fig. S7 D). However, the height difference between the overlap and gap regions decreases from 5.6 ± 0.3 nm (n = 2) to 2.8 ± 0.3 nm (n = 2) after exposure to 62°C. This is coupled with a decrease in the relative length of the gap region from 44 ± 2% (n = 2) of the D-period to 34 ± 2% (n = 2) of the D-period. These two values are different from the relative length of the gap region, 54% of the D-period, measured by x-ray scattering for hydrated fibrils at room temperature (17). The discrepancy between the x-ray value and the AFM value of control fibrils can be attributed to a combination of drying and AFM imaging artifacts due to the tip shape (35).

Figure 6.

Figure 6

Open in a new tab

Structural changes in fibrils exposed to high temperatures. Modulus and Log modulus channels of two collagen fibrils after repeated temperature exposure from 25–62°C as seen in Figs. 5 and 6A, and a fibril before (B) and after (C) 30 min exposure to 62°C. Peak force error channel images of a typical dehydrated collagen fibril (D) and of a fibril exposed to 62°C for 30 min before dehydration (E). To see this figure in color, go online.

Discussion

Collagen I fibrils may behave as a polymer network in a glassy state when indented

In solution, the triple helix motif characteristic of tropocollagen molecules becomes unstable around body temperature (36). Within a fibril the same structural motif shows an increased thermal stability due to the proximity of neighboring chains. The decrease in mobility of the molecules in the crowded fibril environment compared to a dilute solution is associated with a decrease in conformational entropy at a given temperature. This is the so-called polymer in a box model of collagen fibril denaturation. In other words, below the denaturation temperature, typically 65°C, the molecules within a collagen fibril are less mobile than above that threshold (37). This is comparable to polymer networks where the relaxation time characteristic of chain motion increases significantly below the glass transition temperature. As mentioned previously the dependency between elastic modulus and indentation speed of polymer networks below the glass transition temperature is very similar to the one observed for collagen I fibrils at room temperature (Fig. 1) (34). Based on this comparison, we found that collagen I fibrils display a characteristic relaxation time of 0.1 ms, estimated using a typical deformation of 20 nm and a critical indentation speed around 70 μm/s (Fig. 1). When the experimental time is smaller than the relaxation time the collagen fibril stiffens by nearly sevenfold within the accessible range of indentation speeds (Fig. 1). In that regime the collagen molecules have no time to rearrange locally and should deform cooperatively. The resulting deformation should be similar to the one observed after permanently indenting dried collagen fibrils (23). Using a 20 nm radius tip, Wenger and co-workers (23) achieved an imprint depth of 30 nm that extended along the fibril axis over two D-periods. If this picture holds for the high indentation speed regime observed in this study, this means that all the collagen molecules in contact with the tip apex during indentation are bent homogeneously. It follows that the measured modulus should be proportional to the molecular density. With this in mind the amplitude of the modulus contrast observed within a D-period (Fig. 2) is directly related to fluctuations in molecular density. Furthermore, our observation that the modulus of the gap region is 80% of the modulus of the overlap region supports the quarter-staggered model of collagen fibril axial structure proposed by Hodge and Schmitt (16).

The effects of temperature exposure on collagen I fibrils’ structure and mechanical properties

The glassy state model discussed in the previous section predicts that collagen fibrils should soften as the temperature is raised toward 65°C. This is confirmed by our temperature exposure experiments with an onset of softening around 50°C and an overall 10-fold decrease in modulus (Fig. 5). Based on similar results obtained for a model cross-linked polymer network, we expect at most a fivefold decrease in modulus when crossing the glass to rubber transition (34). The extra twofold decrease can be attributed to fibril swelling due to water uptake (Fig. 5). Assuming that the length of the fibril remains constant due to the absorption to the glass substrate, and that the measured modulus at high indentation speed scales with molecular density as mentioned previously, the 30% increase in fibril height (Fig. 5) should yield a 1.7-fold decrease in modulus due to the shift in molecular density associated with the increase of the fibrils cross-sectional area.

Water uptake by the fibril also has important structural effects beyond radial swelling. The D-period disappears almost completely from the modulus maps in the hydrated state above 50°C (Fig. 5) but it is visible in the dehydrated state albeit with a reduced height contrasts between gap and overlap regions. A simple explanation for these results is a homogenization of the molecular density along the fibril axis due to water uptake. Details of the homogenization mechanism are difficult to infer from our data. However, it is likely that most of the water uptake is concentrated in the overlap region because it has a higher molecular density than the gap region at room temperature. Nevertheless, the situation is complicated by the appearance of twisted subfibrils after temperature exposure (Fig. 6, C and E), indicating that water may accumulate between these subfibrils rather than being uniformly distributed in the fibril cross section. These twisted structures are similar to those seen in in vitro fibrils with no temperature exposure (Fig. S7).

Finally, our temperature exposure experiments on single fibril are in excellent agreement with second harmonic generation (SHG) measurements of rat tail tendons (38) and pig corneal stroma (39). In both cases the SHG signal intensity decreases with temperature exposure in a similar way than the modulus in our study (Fig. 5). It has been shown previously that the large SHG signal observed on collagen fibrils is due to the tight packing and alignment of weakly efficient harmonophores (40). A radial swelling associated with an increase of angular spread of the molecules with respect to the fibril axis as seen in our study would yield a sharp decrease in SHG signal intensity. Matteini et al. (39) came to the same overall conclusions based on theoretical considerations.

Effect of mechanical deformations

There is mounting evidence that tensile loading can generate plastic deformations called kinks along collagen fibrils (25). These kinks are short segments of the fibrils, around 200 nm in length, that are characterized by a decreased enthalpy of denaturation and an increased sensitivity to trypsin digestion compared to pristine collagen fibrils (41,42). In this study, there is no indication that removing the fibrils from their tissue leads to the formation of kinks but we observe two other types of mechanical damage, ruptured ends and sharply bent segments (Fig. 3). In both cases the modulus decreases by three- to fourfold compared to pristine regions of the same fibrils. The surrounding area exhibits a decrease in modulus while still exhibiting the D-period with the same 20% contrast between gap and overlap regions. The only point where the D-period is not observed is right at the point where the mechanical deformation took place (Fig. S6). Interestingly, the sharply bent segments display a much higher zero force height than the pristine segments of the fibril, whereas the ruptured end of the fibril has a zero force height consistent with its pristine region. This suggests that the two types of damage are distinct, although having the same effect on the modulus of the fibril. Because the quarter-staggered organization of the fibrils does not seem affected, we propose that the observed decrease in modulus is due to a loss of mature cross-links between tropocollagen molecules (ruptured end) and/or the uptake of water in the fibril bend, similar to what is observed with temperature exposure. This loss of the glassy state could be associated with the uptake of water in the fibril bend, similar to fibrils exposed to temperatures higher than 58°C. Alternatively, the possibility of the loss of mature cross-links is strongly supported by modulus data obtained on fibrils assembled in vitro from acid solubilized tropocollagen molecules extracted from rat tail tendon. These fibrils have a modulus five times smaller than the one of ex vivo fibrils, which is consistent with an absence of mature cross-links (43), and still show the dependency on indentation speed characteristic of a glassy state (Fig. S8).

Conclusion

In this study, we demonstrate that nanomechanical mapping of entire collagen fibrils at indentation speeds around 105 nm/s can detect subtle changes in molecular dynamics and fibril architecture due to an external stimulus such as temperature. This is opening the road for the study of mechanical damage at the single fibril and the study of gene mutations that are suggested to impact collagen fibril structure and mechanical properties.

Acknowledgments

L.K. acknowledges support from the Discovery grant program of the National Science and Engineering Research Council (NSERC) and from the Canadian Foundation for Innovation (CFI). S.B. is the recipient of a PhD scholarship from the NSERC funded CREATE program ASPIRE at Dalhousie University. A.Q. and C.C. received undergraduate summer research scholarships from NSERC to participate in this project.

Supporting Material

Document S1. MATLAB Sorting executable S5 and seven figures
mmc1.pdf (4.2MB, pdf)
Document S2. Article plus Supporting Material
mmc2.pdf (5.2MB, pdf)

References

  • 1.Exposito J.Y., Valcourt U., Lethias C. The fibrillar collagen family. Int. J. Mol. Sci. 2010;11:407–426. doi: 10.3390/ijms11020407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Kannus P. Structure of the tendon connective tissue. Scand. J. Med. Sci. Sports. 2000;10:312–320. doi: 10.1034/j.1600-0838.2000.010006312.x. [DOI] [PubMed] [Google Scholar]
  • 3.Gautieri A., Vesentini S., Buehler M.J. Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up. Nano Lett. 2011;11:757–766. doi: 10.1021/nl103943u. [DOI] [PubMed] [Google Scholar]
  • 4.Diamant J., Keller A., Arridge R.G. Collagen; ultrastructure and its relation to mechanical properties as a function of ageing. Proc. R. Soc. Lond. B Biol. Sci. 1972;180:293–315. doi: 10.1098/rspb.1972.0019. [DOI] [PubMed] [Google Scholar]
  • 5.Woo S.L., Debski R.E., Fenwick J.A. Injury and repair of ligaments and tendons. Annu. Rev. Biomed. Eng. 2000;2:83–118. doi: 10.1146/annurev.bioeng.2.1.83. [DOI] [PubMed] [Google Scholar]
  • 6.Camacho N.P., Hou L., Boskey A.L. The material basis for reduced mechanical properties in oim mice bones. J. Bone Miner. Res. 1999;14:264–272. doi: 10.1359/jbmr.1999.14.2.264. [DOI] [PubMed] [Google Scholar]
  • 7.Abramowitch S.D., Yagi M., Woo S.L. The healing medial collateral ligament following a combined anterior cruciate and medial collateral ligament injury—a biomechanical study in a goat model. J. Orthop. Res. 2003;21:1124–1130. doi: 10.1016/S0736-0266(03)00080-9. [DOI] [PubMed] [Google Scholar]
  • 8.Lavagnino M., Arnoczky S.P., Tian T. Collagen fibril diameter distribution does not reflect changes in the mechanical properties of in vitro stress-deprived tendons. J. Biomech. 2005;38:69–75. doi: 10.1016/j.jbiomech.2004.03.035. [DOI] [PubMed] [Google Scholar]
  • 9.Magnusson S.P., Hansen P., Kjaer M. Tendon properties in relation to muscular activity and physical training. Scand. J. Med. Sci. Sports. 2003;13:211–223. doi: 10.1034/j.1600-0838.2003.00308.x. [DOI] [PubMed] [Google Scholar]
  • 10.Misof K., Landis W.J., Fratzl P. Collagen from the osteogenesis imperfecta mouse model (oim) shows reduced resistance against tensile stress. J. Clin. Invest. 1997;100:40–45. doi: 10.1172/JCI119519. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Screen H.R., Toorani S., Shelton J.C. Microstructural stress relaxation mechanics in functionally different tendons. Med. Eng. Phys. 2013;35:96–102. doi: 10.1016/j.medengphy.2012.04.004. [DOI] [PubMed] [Google Scholar]
  • 12.Ramachandran G.N., Kartha G. Structure of collagen. Nature. 1955;176:593–595. doi: 10.1038/176593a0. [DOI] [PubMed] [Google Scholar]
  • 13.Kadler K.E., Holmes D.F., Chapman J.A. Collagen fibril formation. Biochem. J. 1996;316:1–11. doi: 10.1042/bj3160001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Raspanti M., Reguzzoni M., Martini D. Evidence of a discrete axial structure in unimodal collagen fibrils. Biomacromolecules. 2011;12:4344–4347. doi: 10.1021/bm201314e. [DOI] [PubMed] [Google Scholar]
  • 15.Zhao T., Weinhold P.S., Dahners L.E. Some observations on the subfibrillar structure of collagen fibrils as noted during treatment with NKISK and cathepsin G with mechanical agitation. J. Electron Microsc. (Tokyo) 2011;60:177–182. doi: 10.1093/jmicro/dfr005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Hodge A.J., Schmitt F.O. The charge profile of the tropocollagen macromolecule and the packing arrangement in native-type collagen fibrils. Proc. Natl. Acad. Sci. USA. 1960;46:186–197. doi: 10.1073/pnas.46.2.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Orgel J.P., Miller A., Wess T.J. The in situ supermolecular structure of type I collagen. Structure. 2001;9:1061–1069. doi: 10.1016/s0969-2126(01)00669-4. [DOI] [PubMed] [Google Scholar]
  • 18.Eppell S.J., Smith B.N., Ballarini R. Nano measurements with micro-devices: mechanical properties of hydrated collagen fibrils. J. R. Soc. Interface. 2006;3:117–121. doi: 10.1098/rsif.2005.0100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Svensson R.B., Mulder H., Magnusson S.P. Fracture mechanics of collagen fibrils: influence of natural cross-links. Biophys. J. 2013;104:2476–2484. doi: 10.1016/j.bpj.2013.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.van der Rijt J.A., van der Werf K.O., Feijen J. Micromechanical testing of individual collagen fibrils. Macromol. Biosci. 2006;6:697–702. doi: 10.1002/mabi.200600063. [DOI] [PubMed] [Google Scholar]
  • 21.Graham J.S., Vomund A.N., Grandbois M. Structural changes in human type I collagen fibrils investigated by force spectroscopy. Exp. Cell Res. 2004;299:335–342. doi: 10.1016/j.yexcr.2004.05.022. [DOI] [PubMed] [Google Scholar]
  • 22.Yang L., van der Werf K.O., Feijen J. Mechanical properties of native and cross-linked type I collagen fibrils. Biophys. J. 2008;94:2204–2211. doi: 10.1529/biophysj.107.111013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Wenger M.P., Bozec L., Mesquida P. Mechanical properties of collagen fibrils. Biophys. J. 2007;93:1255–1263. doi: 10.1529/biophysj.106.103192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Minary-Jolandan M., Yu M.F. Nanomechanical heterogeneity in the gap and overlap regions of type I collagen fibrils with implications for bone heterogeneity. Biomacromolecules. 2009;10:2565–2570. doi: 10.1021/bm900519v. [DOI] [PubMed] [Google Scholar]
  • 25.Veres S.P., Lee J.M. Designed to fail: a novel mode of collagen fibril disruption and its relevance to tissue toughness. Biophys. J. 2012;102:2876–2884. doi: 10.1016/j.bpj.2012.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dufrêne Y.F., Martínez-Martín D., Müller D.J. Multiparametric imaging of biological systems by force-distance curve-based AFM. Nat. Methods. 2013;10:847–854. doi: 10.1038/nmeth.2602. [DOI] [PubMed] [Google Scholar]
  • 27.Sader J.E., Larson I., White L.R. Method for the calibration of atomic-force microscope cantilevers. Rev. Sci. Instrum. 1995;66:3789–3798. [Google Scholar]
  • 28.Maugis D., Barquins M. Fracture mechanics and adherence of viscoelastic bodies. J. Phys. D Appl. Phys. 1978;11:1989–2024. [Google Scholar]
  • 29.Sneddon I. The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965;3:47–57. [Google Scholar]
  • 30.Grant C.A., Brockwell D.J., Thomson N.H. Tuning the elastic modulus of hydrated collagen fibrils. Biophys. J. 2009;97:2985–2992. doi: 10.1016/j.bpj.2009.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Stolz M., Raiteri R., Aebi U. Dynamic elastic modulus of porcine articular cartilage determined at two different levels of tissue organization by indentation-type atomic force microscopy. Biophys. J. 2004;86:3269–3283. doi: 10.1016/S0006-3495(04)74375-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Persch G., Born C., Utesch B. Nano-hardness investigations of thin-films by an atomic-force microscope. Microelectron. Eng. 1994;24:113–121. [Google Scholar]
  • 33.Bueckle H. American Society for Metals; Materials Park, OH: 1973. The Science of Hardness Testing and its Research Applications. [Google Scholar]
  • 34.Tranchida D., Kiflie Z., Piccarolo S. Nanoscale mechanical characterization of polymers by atomic force microscopy (AFM) nanoindentations: viscoelastic characterization of a model material. Meas. Sci. Technol. 2009;20:095702–095710. [Google Scholar]
  • 35.Ricci D., Braga P.C. Recognizing and avoiding artifacts in AFM imaging. Methods Mol. Biol. 2004;242:25–37. doi: 10.1385/1-59259-647-9:25. [DOI] [PubMed] [Google Scholar]
  • 36.Leikina E., Mertts M.V., Leikin S. Type I collagen is thermally unstable at body temperature. Proc. Natl. Acad. Sci. USA. 2002;99:1314–1318. doi: 10.1073/pnas.032307099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Miles C.A., Ghelashvili M. Polymer-in-a-box mechanism for the thermal stabilization of collagen molecules in fibers. Biophys. J. 1999;76:3243–3252. doi: 10.1016/S0006-3495(99)77476-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Lin S.J., Hsiao C.Y., Dong C.Y. Monitoring the thermally induced structural transitions of collagen by use of second-harmonic generation microscopy. Opt. Lett. 2005;30:622–624. doi: 10.1364/ol.30.000622. [DOI] [PubMed] [Google Scholar]
  • 39.Matteini P., Cicchi R., Pini R. Thermal transitions of fibrillar collagen unveiled by second-harmonic generation microscopy of corneal stroma. Biophys. J. 2012;103:1179–1187. doi: 10.1016/j.bpj.2012.07.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Deniset-Besseau A., Duboisset J., Schanne-Klein M.C. Measurement of the second-order hyperpolarizability of the collagen triple helix and determination of its physical origin. J. Phys. Chem. B. 2009;113:13437–13445. doi: 10.1021/jp9046837. [DOI] [PubMed] [Google Scholar]
  • 41.Veres S.P., Harrison J.M., Lee J.M. Repeated subrupture overload causes progression of nanoscaled discrete plasticity damage in tendon collagen fibrils. J. Orthop. Res. 2013;31:731–737. doi: 10.1002/jor.22292. [DOI] [PubMed] [Google Scholar]
  • 42.Veres S.P., Harrison J.M., Lee J.M. Mechanically overloading collagen fibrils uncoils collagen molecules, placing them in a stable, denatured state. Matrix Biol. 2014;33:54–59. doi: 10.1016/j.matbio.2013.07.003. [DOI] [PubMed] [Google Scholar]
  • 43.Eyre D.R., Wu J.J. Collagen cross-links. Top. Curr. Chem. 2005;247:207–229. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. MATLAB Sorting executable S5 and seven figures
mmc1.pdf (4.2MB, pdf)
Document S2. Article plus Supporting Material
mmc2.pdf (5.2MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES