Thermodynamics of Antimicrobial Lipopeptide Binding to Membranes: Origins of Affinity and Selectivity

Abstract

The development of novel antibiotic drugs is one of the most pressing biomedical problems due to the increasing number of antibiotic-resistant pathogens. Antimicrobial peptides and lipopeptides are a promising category of candidates, but the molecular origins of their antimembrane activity is unclear. Here we explore a series of recently developed antimicrobial lipopeptides, using coarse-grained molecular-dynamics simulations and free energy methods to uncover the thermodynamics governing their binding to membranes. Specifically, we quantify C16-KGGK’s binding affinity to the two types of membrane by umbrella sampling. We also examined the origin of C16-KGGK’s selectivity for bacterial versus mammalian membranes by systematically varying the peptide sequence and salt concentration. Our data showed that the C16 hydrophobic tail is the main contributor to its affinity to lipid membrane, whereas the peptide portion is mainly responsible for its selectivity. Furthermore, the electrostatic interaction between the cationic peptide and anionic bacterial membrane plays a significant role in the selectivity.

Introduction

The progressively increasing number of antibiotic-resistant bacterial strains confronts the 21st century with a severe medical problem. This necessitates the development of new antibiotics that are less likely to incur evolved resistance. Among the candidates are antimicrobial peptides (AMPs), which are natural components of the innate immune system of various multicellular organisms (1). Many AMPs were found to have minimal inhibitory concentrations against bacteria in the micromolar range (2). As a result, there has been growing interest in the past two decades to develop new antibiotic drug based on AMPs (3).

It has been shown that AMPs selectively target and permeabilize the bacterial membranes based on the membranes’ lipid composition. Inasmuch as membrane composition is a large-scale quantity that is relatively conserved during evolution, AMPs are less likely to incur evolved resistance (4). Systematic studies suggest that the majority of AMPs are cationic, and assume amphipathic structures when bound to membranes (5). The cationic side chains presumably help peptides target bacterial membranes, which tend to be enriched in anionic lipids relative to animals, whereas the amphipathic structure stabilizes binding in the membrane-water interface.

Several models have been proposed to explain the molecular mechanism of AMPs, including the barrel-stave model (6), which posits a well-structured pore with peptides oriented in a transbilayer conformation, and the carpet model (7), which suggests that peptides remain bound interfacially, and coat the outer surface of the cell, destabilizing it.

However, AMPs are not ideal drugs: they are far larger than typical druglike molecules, tend to be expensive to synthesize, and are prone to peptidase degradation when used internally (8,9). This suggests that the best case for a drug based on a natural linear AMP is a topical antibiotic. If we are going to raise this ceiling, a different approach will likely be required. To develop antimicrobial drugs that utilize AMPs’ activity and yet bypass these issues, Avrahami and Shai (10,11) came up with the idea of acylating small cationic peptides to make them sufficiently hydrophobic to bind the membrane without significantly increasing their size. They showed that a series of membrane-inactive short peptides can be made antimicrobial-active by conjugating fatty acids to them (10,11). More recently, Makovitzki et al. (12) examined a set of tetrapeptides with two lysines, a single D-amino acid (to confer immunity to peptidases), and a palmitoyl chain attached to the N-terminus. This work showed that several of them were potent antimicrobials that did not cause significant hemolysis, but which damaged model vesicles in a manner suggesting that their effectiveness was due to their membrane activity. More recent work on similar peptides showed that they are similarly effective at clearing infections in vivo (13). The most potent of these peptides, C16-KGGK (where C16- denotes the palmitoyl chain attached to the N-terminus and the letter in bold denotes the D-enantiomer), has a minimal inhibitory concentration in the micromolar range against several species of bacteria and fungi.

The same structural simplicity of these antimicrobial lipopeptides (AMLPs) that makes these molecules easy to synthesize is also an advantage in exploring their mechanism, because they have fewer “moving parts” than conventional AMPs, such as magainins or melittin. For all these reasons, we believe AMLPs are much more promising drug candidates than natural AMPs and an attractive target for basic research, particularly via molecular dynamics simulations. Most of the experimental studies on these compounds to date are based on macroscopic properties measured in bulk experiments such as dye-leakage or cell death, so relatively little is known on a molecular level. MD simulations can help us visualize how the molecules interact with each other. These insights generate hypotheses that can be tested experimentally and can suggest new experimental work.

Over the past two decades, molecular dynamics simulations have made significant contributions to membrane biophysics (14–16) and the studies of AMPs (17). However, the all-atom molecular dynamics simulations are computationally expensive, which usually make the timescales relevant to biological processes inaccessible. One way to get around this issue is to use a coarse-grained (CG) model, where each particle in the simulation represents a number of actual atoms. This approach greatly reduces the computational cost of the calculation, by both reducing the number of degrees of freedom in the system and allowing a much larger timestep. Thus, one can greatly extend the reach of molecular simulation methods, although in the process some physical fidelity is sacrificed. One of the most popular CG force fields for simulating membranes and membrane proteins is the MARTINI force field (18), where four heavy atoms are merged into one particle. It has been shown that the MARTINI force field runs at least two orders of magnitude faster than a comparable atomic model (19,20), and in many cases produces qualitative and even quantitative agreement with experiments (18,21–25).

Previously, our lab has examined these lipopeptides and their interaction with membranes using a combination of all-atom and coarse-grained molecular-dynamics simulations. The all-atom work explored the structural effects of lipopeptides after binding (26), whereas the coarse-grained simulations focused primarily on the binding process (27). The latter work showed that micelles of C16-KGGK will spontaneously bind to the surface of a bacteria-like membrane bilayer (a 2:1 mixture of POPE and POPG lipids), but not to a mammal-like (pure POPC) membrane. And, upon binding, the lipopeptides effectively demix the membrane, preferentially drawing in the anionic POPG lipids. This suggests that the selectivity of C16-KGGK for bacterial membrane is driven by electrostatics.

In this study, we quantitate this intuition by directly computing the free energy change upon binding individual lipopeptides to membranes with different compositions. By varying the nature of the peptide portion, the membrane composition, and external salt concentration, we are able to tease out the thermodynamic origins of the lipopeptides’ affinity for membranes, as well as their preferential binding to anionic membranes. We also use this data to understand the structural changes undergone by both the lipopeptide and the membrane during the binding process.

Methods

System construction

All systems were modeled using the coarse-grained force-field software, MARTINI, ver. 2.1 (last modified on January 26, 2011) (18,21,28). The C16 molecule is constructed from the MARTINI model of a palmitoyl chain. The KGGK and GGGG were constructed directly from the MARTINI peptide model, whereas C16-KGGK and C16-GGGG were created by merging the MARTINI palmitoyl with the respective peptide. The MARTINI model cannot resolve backbone chirality, so L- and D-amino acids were treated identically. However, we do not expect this to be a serious limitation; these peptides are too short to form a secondary structure, and experiments have shown that varying the backbone chirality does not affect their properties significantly (29).

Two types of membrane bilayer were used. One is a Gram-negative bacteria-like bilayer with a 2:1 mixture of POPE (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine) and POPG (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoglycerol). The other one is a mammal-like bilayer, represented by pure POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine). The membrane bilayers were built using the methods in previous work (27). Total numbers of lipids in all cases are 480: 320 POPE + 160 POPG for the bacteria-like membrane and 480 POPC for the mammal-like membrane, distributed symmetrically between the two leaflets. For each system, the small molecule (a C16-KGGK, C16-GGGG, KGGK, GGGG, or C16) was placed ∼50 Å from the center-of-mass (COM) of the bilayer. Next, we added 14,757 waters, and sodium and chloride ions such that the system was electrically neutral with a free salt concentration of either 100 mM or 1 M.

Umbrella sampling

The potentials of mean force (PMFs) of binding of one small molecule (C16-KGGK, C16-GGGG, KGGK, GGGG, or C16) to a membrane bilayer was calculated using umbrella sampling and the weighted histogram analysis method (WHAM) (30,31). The reaction coordinate (RC) was the distance between the center-of-mass (COM) of the membrane bilayer and that of the small molecule, projected along the membrane normal (the z axis).

We chose to explicitly sample only a subset of the full reaction coordinate, starting with the small molecule free in solution and finishing when the peptide starts to enter the membrane interior. The representation of the rest of the reaction coordinate is discussed below in Free Energy Calculation. The specific ranges sampled are shown in Table 1.

Table 1.

The range of reaction coordinate where the umbrella sampling was performed in different systems

Systema	Distance to the membrane center ([minimum, maximum] in Å)
C16-KGGK	[15, 42]
C16-GGGG	[7, 42]
C16	[0, 42]
KGGK	[15, 42]
GGGG	[15, 42]

^aFor both POPE/POPG and POPC membranes.

For each system, the RC was divided into 30–35 windows, where each window has a different location for the minimum of the restraint. The force constants for the harmonic restraints were generally chosen to be 1000 kJ/(mol nm⁻²). However, we noticed that the PMFs in this work always plateau at large RC values, where no obvious free energy barrier exists, and we decided to use much smaller force constants (∼100 kJ/(mol nm⁻²)); as a result, the simulations in this region each sampled a broader range of values, allowing us to use fewer trajectories. When we ran WHAM (31), we used 300 bins, and a tolerance of 0.0001. The statistical uncertainty at each bin was estimated using bootstrapping, with 100 bootstrap trials for each PMF; we estimated the correlation time involved in solving the WHAM equation (30) for each time series using block averaging.

Simulation protocol

All simulations were performed using the software GROMACS, vers. 4.5.4 and 4.5.5 (32,33). As in the previous study (27), we used a 10-fs time step, and updated the neighbor list every five steps. Simulations were performed in isothermal-isobaric (NPT) ensemble with Nosé-Hoover temperature coupling (34,35) and the Parrinello-Rahman barostat (36), set to 300 K and 1 bar, respectively. Electrostatics were accounted for using the shift function with a Coulomb cutoff of 12 Å. Shift was used for van der Waals as well, with a switch distance of 9 Å and a cutoff of 12 Å.

Free energy calculation

To compute the free energy of binding from the PMF, we need to divide the system into bound and unbound states, after which the free energy change upon binding can be calculated as ΔG = −k_BT ln P_bound/P_unbound, where P_state is the probability of a particular state. Additional terms related to the standard concentrations of the system—physically, the entropy loss for the small molecule to find the membrane surface—are neglected, inasmuch as they are the same for all systems studied.

In general, the obvious choice to separate two states is the top of the barrier between them. However, for the cases considered here, there generally is no barrier between the states, so as an alternative we looked at the conformation of the small molecule. For C16-KGGK or C16-GGGG, we looked at the state of the acyl chain, and defined the bound state as the z-position, where it exists primarily in the inserted state, solvated by the lipid hydrocarbon region as opposed to water; there is generally a transition region of a few Ångstroms where both states are populated. For the unacylated peptides, we chose the barrier such that the peptide is at the same location as it was for the analogous lipopeptide. Similarly, for C16 we chose to separate bound and unbound such that the acyl chain is located at the same height as in the C16-KGGK case. Boundary between the Bound and Unbound State in the Supporting Material contains more details, including the determination of the boundary between the two states. Although alternative definitions are possible (e.g., break the two states where the PMF reaches the plateau value), the result is just to shift all free energies by roughly the same amount; the conclusions drawn will be the same.

As mentioned above, in the systems with peptides and lipopeptides, we chose not to explicitly sample the full range of the reaction coordinate. Although we could have dragged the lipopeptide all the way to the center of the membrane, doing so would require us to pull the charged peptide portion into the center of the membrane, either desolvating the charged lysine side chains and polar backbone or creating a significant water fault. Although we could do this, previous work has shown that this kind of simulation converges very slowly, and that in general an enormous computational effort is required to avoid hysteresis (37). Moreover, the treatment of water faults is a known weakness of the MARTINI water model (37). In this case, we are not interested in the barrier to exchange between leaflets, but rather only in the binding free energies. Because the states in which the peptide is buried in hydrocarbon are obviously unfavorable relative to the states in which the acyl chain is in the hydrophobic region but the peptide portion interacts with the headgroups and water, they will make relatively little contribution to the overall free energy of binding. As such, we chose instead to sample only as far as was needed to see the PMFs begin curving upward, and from there we extrapolated back to z = 0. In particular, we used the polynomial form

$$f\left(z\right)=\{\begin{array}{ll}F\left(z\right)\hfill & \text{if}z<z_1\hfill \\ F\left(z\right)+S\left(z\right)\hfill & \text{if}{z}_1\le z<z_c\hfill \\ e\hfill & \text{if}{z}_c\le z,\hfill \end{array}$$ (1)

with z being the RC,

$$F\left(z\right)=\sum _{i=0}^N{c}_i{z}^i\text{and}$$

$$S\left(z\right)=A{\left(z-z_1\right)}^3+B{\left(z-z_1\right)}^2,$$

where A and B are given by the boundary condition

$$\{\begin{array}{c}S\left(z_c\right)+F\left(z_c\right)=e\\ S^{\prime }\left(z_c\right)+F^{\prime }\left(z_c\right)=0.\end{array}$$ (2)

The highest degree of the polynomials, N, was chosen so that the fitted curve in the range of extrapolation increases as the RC decreases. A range of values for z₁ and z_c were iterated and at each step of iteration the parameters (c_i and e) were optimized by a Nelder-Mead Simplex optimizer (38). No such fitting or extrapolation was applied to the PMFs for C16 binding, inasmuch as the umbrella sampling windows covered the full range of RC values from 0 to 42 Å.

We did systematic testing to estimate the error in the estimated binding free energy introduced by this procedure, and found that it is quite small, <0.3 kcal/mol in all the systems in this study. This can be easily verified by making a still harsher (and less accurate) approximation and assuming that the free energy in the unsampled region is infinite, such that it has zero probability, and thus does not contribute to the binding free energy. For the example of C16-KGGK, this approximation shifts the binding free energy relative to the polynomial fit by 0.1 kcal/mol or less for both membranes.

Results

Potentials of mean force

Fig. 1 shows the PMFs computed for all of the small molecules treated. All of the lipopeptide PMFs (Fig. 1, A–D) have the same basic shape, although the height of the plateau with respect to the bound state varies somewhat; in all cases, the free energy drops monotonically as the lipopeptide approaches and binds to the membrane, meaning that binding is always favorable and barrierless. By contrast, the PMFs for the unacylated peptides are quite different: GGGGs increase monotonically upon association with membranes, whereas KGGKs have a very shallow surface-bound well.

Figure 1.

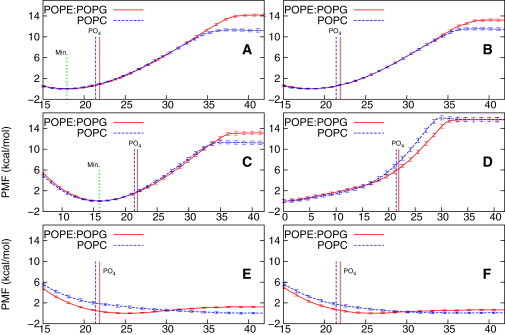
PMFs in kcal/mol (Y axis) as a function of the COM distance in Ångstroms (X axis) between the membrane (POPE/POPG in solid and POPC in dashed line) and (A) C16-KGGK with 0.1 M NaCl, (B) C16-KGGK with 1 M NaCl, (C) C16-GGGG, (D) C16, (E) KGGK, or (F) GGGG. (Vertical dotted line) Minima of the PMFs in panels A and C. The COM distance between the phosphate group (PO₄) and the membrane center of each type of membrane bilayer (labeled by vertical lines of the same line types as those used in plotting the corresponding PMFs). To see this figure in color, go online.

Free energy of binding

We computed the binding free energies from the PMFs as discussed in Free Energy Calculation. Fig. 2 shows the ΔG of each ligand with POPC and POPE/POPG membranes; the corresponding values are listed in Table S1 in the Supporting Material. We see that ΔG(C16) is the most favorable value; if we factor the binding free energy on a per-methylene basis, we get a transfer free energy of –0.9 kcal/mol, consistent with the value of $-1.0$ kcal/mol measured for the transfer of hydrocarbons from water to hexadecane (39).

Figure 2.

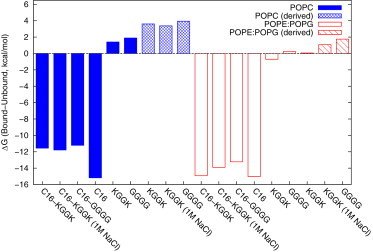
Free energy of binding different small molecules, to POPE/POPG (open) or POPC (solid) membrane in kcal/mol. The label “derived” indicates that the peptides’ binding free energy was computed using ΔG (peptide) = ΔG (lipopeptide) − ΔG (C16), as opposed to the others, which were computed directly from the PMFs. To see this figure in color, go online.

From this data set, we can see that the binding of all the ligands containing C16 to membranes is favorable. Furthermore, the binding of C16 is more favorable than that of either lipopeptide to either bilayer, whereas the unacylated peptides have positive (or near-zero) ΔGs, suggesting that

• 1.The acyl chain is the primary driver of lipopeptides’ affinity for bilayers, and
• 2.The peptide contribution is unfavorable.

This can be made more explicit by defining ΔG_der (peptide) = ΔG(lipopeptide) − ΔG(C16), which we also plot in Fig. 2. Interestingly, these derived values are consistently more unfavorable than those computed directly. The difference between the derived and directly calculated values may be due to the rotational entropy lost when C16 is inserted in the membrane but tethered to the peptide.

Selectivity for POPE/POPG membrane

Considering Fig. 2, it is clear that the affinity of C16 for the two membranes differs only negligibly, whereas the lipopeptides have several k_BT higher affinities for the anionic PE/PG membrane. To quantify the membrane selectivity, we subtracted the binding free energy of each lipopeptide and C16 to POPC membrane from that to POPE/POPG membrane and plotted the difference (ΔΔG, POPE/POPG − POPC) in Fig. 3. (The corresponding ΔΔGs are listed in Table S2.) The ΔΔGs for both lipopeptides are negative, which means the binding of both lipopeptides favors the anionic POPE/POPG membrane over the zwitterionic POPC membrane. This supports the hypothesis that lipopeptide selectivity for bacterial membranes is driven at least in part by differences in thermodynamic affinity.

Figure 3.

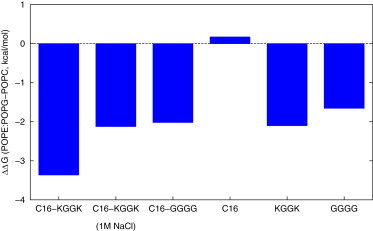
Difference in ΔG of binding different small molecules, between the POPE/POPG membrane and POPC membrane (negative values indicate that binding POPE/POPG is more favorable). To see this figure in color, go online.

Discussion

Membrane binding enhanced by lipidation

One standard complaint about conventional AMPs is that they are too large to be convenient drug molecules. However, the intrinsic polarity of the peptide backbone (40) means that peptides can only accumulate enough hydrophobicity to bind membranes by having a significant number of hydrophobic side chains; combined with the requirement to have positive charge to confer selectivity for anionic membranes, this puts a strong lower limit on the sequence length for a putative AMP. This is why the smallest natural AMPs are, at 12 amino acids, far larger than typical druglike molecules. This minimum size creates a number of problems with their use as internal drugs: they are more expensive to synthesize and purify, harder to store, and more likely to evoke an immune response than smaller peptides. Longer peptides are also more challenging from a basic science perspective; the conformational plasticity of peptides makes mutation experiments hard to interpret and greatly slows the statistical convergence of computer simulations (41,42).

One way around this is to tag the peptide with another hydrophobic moiety—in this case, a fatty acid—to provide the needed lipophilicity without requiring a long peptide. In this work, we performed rigorous free energy calculations on an example of this type, C16-KGGK, to uncover the thermodynamics driving both its affinity for membranes and its selectivity for bacterial versus mammalian membranes.

The results indicate that the dominant part of the membrane affinity is, as expected, driven by the binding of the fatty acid portion of the lipopeptide to the membrane interior. Interestingly, this quantity is only minimally sensitive to the nature of the lipid headgroups, even though the POPE/POPG membranes we used in this work have smaller area/lipid and somewhat more ordered acyl chains than POPC. As a result, we conclude that the acyl chain makes no significant contribution to selectivity, at least in our model system; real bacterial membranes may differ from their mammalian counterparts not just in headgroup composition, but also in acyl-chain composition and concentration of sterols. In addition, real bacteria will also have other complicating factors, including an outer membrane or a lipopolysaccharide layer for Gram-positive and Gram-negative bacteria, respectively.

By contrast, the peptide portion of the lipopeptide makes a net unfavorable contribution to binding affinity in most cases, as predicted by the Wimley-White interfacial hydrophobicity scale (40); the only exception is KGGK binding to the anionic POPE/POPG membrane, where the binding free energy is small but favorable. The unfavorability of peptide binding is unsurprising, because of the significant penalty to desolvate the backbone; only the cationic peptide binding to the anionic bilayer has enough favorable interactions to compensate. If this is the case, then reducing the electrostatic interactions between the peptide side chains and the membrane should decrease both the affinity and selectivity. Although this could be tested artificially in a simulation by reducing the charges on the lysine side chains or increasing the dielectric, we chose an approach more amenable to experiment and increased the salt concentration. As expected, increasing the salt concentration from 0.1 to 1 M reduces the affinity of C16-KGGK to the charged POPE/POPG membranes by roughly 1.0 kcal/mol, but leaves the POPC affinity essentially unchanged. This prediction could be tested experimentally, for instance using isothermal titration calorimetry (43).

Free energy of binding is not additive

Amino acid hydrophobicity scales have a long history in the study of membrane proteins folding and insertion (40,44–50). These scales are mostly designed to operate on single amino-acid residues and usually applied to explain the thermodynamics of small peptides or large proteins. One key assumption underlying these models is that transfer free energies are additive; in other words, the models predict that the change in membrane affinity upon performing a single-point mutation is dependent only on the identity of the two amino acids, and not on any contextual information. This implies that there is no cooperativity between different residues in generating the overall conformational ensemble. This assumption often works well in the context of large folded proteins, because point mutations usually do not grossly change the fold of the protein even when they alter its thermodynamic stability. However, it has been demonstrated both computationally (51) and experimentally (48,50) that cooperativity could play important roles.

Indeed, our results indicate that there is significant cooperativity between the peptide and the C16, when we consider the free energy of binding the whole lipopeptide to membrane, i.e., ΔG(lipopeptide) ≠ ΔG(peptide) + ΔG(C16). For example, the presence of the peptide effectively tethers one end of the C16 chain to the membrane-water interface, reducing entropy of the acyl chain in the membrane-bound state relative to C16 without the peptide. On the other hand, the attachment of the two components to each other changes their equilibrium penetration depth in the membrane. This is highlighted when we projected the PMFs on the peptide-membrane COM distance. (See Projecting the Potentials of Mean Force on the Peptide-Membrane Degree of Freedom in the Supporting Material for details about how the projection was done.) As compared to the PMFs with peptides alone in Fig. 1, E and F, which have no or very shallow minima at relative large distances from the membrane, the PMFs in Fig. S4 in the Supporting Material on the same degree of freedom with the acyl chain attached have much deeper minima at ∼21–22 Å.

In fact, the latter greatly resemble the PMFs on the lipopeptide-membrane distance except the whole curves are shifted to the right by a constant. As a result, the two components of the lipopeptide are tightly coupled to each other and the affinity of whole lipopeptide is not simply the sum of the affinities of the pieces, violating the assumptions underlying the use of a hydrophobicity scale. Similar problems will arise if a change in sequence significantly alters the conformational ensemble of the peptide (for instance by changing the secondary structure or orientation of the peptide backbone in the membrane). These short peptides do not have a real native state to begin with, meaning that there are broad ranges of conformations within a narrow free energy range; small changes in the peptide sequence could easily shift this conformational ensemble, leading to unpredictable changes in affinity. As a result, short peptides of the kind studied here are in many ways a “worst case” for prediction by hydrophobicity scales.

Selectivity for bacterial membranes

In contrast to the C16, the peptides (and their cognate lipopeptides) have significantly different affinities for POPC and POPE/POPG membranes. This difference is visualized in Fig. 3, which shows the ΔΔGs comparing the binding free energies to different membranes (negative values indicate that POPE/POPG binding is more favorable). The ΔΔG of C16-GGGG, which is ∼ –2.0 kcal/mol, represents the baseline for the other AMLPs’ selectivity inasmuch as it has a basic backbone scaffold present in peptide sequences of all the other AMLPs (12); in the MARTINI force field there is essentially no difference between alanine and glycine. As the potential for favorable electrostatic interactions increases (going from C16-GGGG to C16-KGGK at high salt, to C16-KGGK with 0.1 M NaCl), the ΔΔGs become progressively more favorable—suggesting that electrostatics play a primary role in driving selectivity for bacterial membranes, despite the relatively small contribution to overall affinity.

If we attribute the difference between GGGG and KGGK solely to the charges on the lysines, we come up with an electrostatic contribution of –1.3 kcal/mol to ΔΔG, which is ∼40.0% of the total. This is also consistent with the fact that the neutral mammalian-like membrane is less sensitive to the variation of charges on the peptides than the anionic bacterial-like membrane (see Fig. 2 and discussion in Membrane Binding Enhanced by Lipidation). There is an interesting analogy in the theory of protein folding, where the residues that convey specificity (the ones that drive the protein to one fold instead of another) may not be the ones that contribute most to the folded state’s stability as measured using mutagenesis (52).

Mechanism of membrane entry

One interesting question is by what mechanism the lipopeptides enter the membrane. Previous simulation work showed that the presence of a short acyl chain alters the binding mechanism (53). On one hand, the C16 portion has by far the highest affinity; on the other, electrostatic interactions have a far longer range. Our simulations suggest that both mechanisms are in play. When the lipopeptide is restrained at distances where it can just barely touch the membrane, it samples two distinct populations of states: one where the lysines interact with the lipid phosphates, and another where the first bead of the acyl chain is buried in the hydrophobic core. This is manifested by the distribution of the distance between the last bead of the C16 tail and the COM of the membrane, as shown in Fig. 4.

Figure 4.

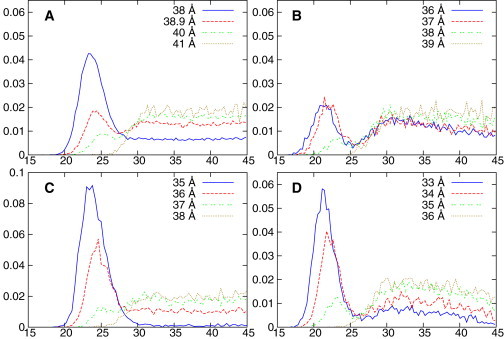
The normalized probability distribution (Y axis) as a function of the distance in Å (X axis) between the terminal hydrocarbon bead of either C16-KGGK (A and B) or C16-GGGG (C and D) and the center of either POPE/POPG (A and C) or POPC (B and D) membrane bilayer in different umbrella sampling windows, whose centers are labeled using different line types as shown in the figure legends. To see this figure in color, go online.

These distributions are typically bimodal with a narrow peak at small distance, indicating the strong hydrophobic interactions between C16 and the membrane, and a very broad peak at large distances, which corresponds to the large rotational entropy of the C16 tail when it is not absorbed in the membrane. This suggests that aside from the canonical pathway where the C16 leads all the way as the lipopeptide is inserted into the membrane, the peptide portion can touch the membrane surface first, which is then followed by a 180° turn to position the C16 tail into the membrane. The initial conformation of this alternative pathway can be partially stabilized by the favorable electrostatic interaction between the cationic peptides and the anionic lipids in the case of POPE/POPG membrane or merely by the expense of the rotational entropy lost.

Meanwhile, we observed slight changes in the radius of gyration (R_GYR) of the C16 tail as the lipopeptide got closer to the membrane. As shown in Fig. 5, such changes are indicated by, at most, a +0.2 Å shift in the most probable R_GYR values. Most interestingly, such changes were reversed as the C16 got more deeply inserted into the membranes, where its R_GYR distribution resembled mostly what it was in the unbound state. This is more pronounced in the case of C16-GGGG than that of C16-KGGK, and suggests that there is potentially a delay between the binding of the C16 tail and the peptide headgroup where the former part was snatched first by the membrane whereas the latter remain unbound. However, the overall changes in the C16 tail in the process of the lipopeptide’s binding is minuscule. In fact, we visually validated from the simulations that the C16 tail remained mostly in an extended conformation (similar to the membrane-bound state) even when the lipopeptide was far away from the membrane.

Figure 5.

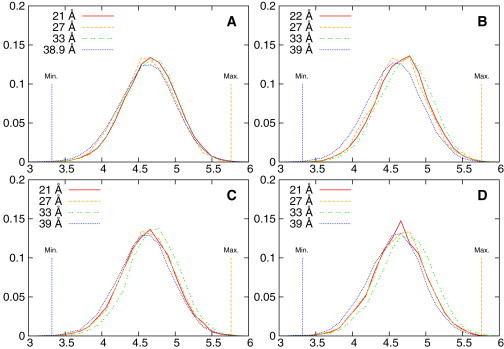
The normalized probability distribution (Y axis) as a function of the radius of gyration (R_GYR) in Å (X axis) of the C16 tail of C16-KGGK (A and B) or C16-GGGG (C and D) in the presence of either POPE/POPG (A and C) or POPC (B and D) membrane bilayer in different umbrella sampling windows, whose centers are labeled using different line types, as shown in the figure key. (Vertical lines) Maximal and minimal R_GYR values. The maximum and the minimum were calculated by assuming the C16 chain in a completely stretched (straight line) and a completely folded (square) configuration, respectively. To see this figure in color, go online.

At the same time, the lipids around the lipopeptides became more and more organized as the lipopeptides approached the membranes. Lateral radial distribution functions (LRDFs), shown in Fig. 6, indicate that both C16-KGGK and C16-GGGG strongly attract POPG lipids while excluding POPE lipids; they appear to have minimal effects on the packing of POPC membranes. Such lateral enrichment of POPG lipids is even stronger in the case of C16-KGGK than that of C16-GGGG. These are consistent with both lipopeptides’ selectivity for POPE/POPG versus POPC, as discussed in Selectivity for Bacterial Membranes. The lateral organization of lipids around the lipopeptide returned to bulk level at 20 Å, which suggests that the lipid organization of the rest of the bilayer remained unchanged.

Figure 6.

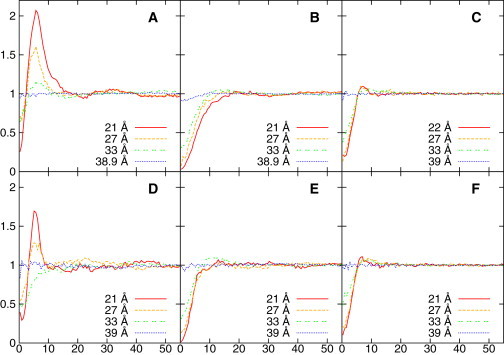
The lateral distribution of POPG (A and D), POPE (B and E), and POPC (C and F) around C16-KGGK (A–C) or C16-GGGG (D–F) in different umbrella sampling windows, whose centers are labeled using different line types as shown in the figure legends. Y axis is normalized density. X axis is the lateral distance in Å. To see this figure in color, go online.

All these data together help us build a vivid picture of the lipopeptide binding to membrane: It randomly rotates arriving at the membrane surface and positions its hydrophobic tail toward the membrane center. As it inserts into the membrane, it preferentially clusters specific lipid components around itself to stabilize its binding to the membrane. In all the cases we consider in this study, different lipopeptides tend to reach relatively the same penetration depth into the membrane as indicated by in the free energy minima in Fig. 1; the 2–3 Å difference between C16-KGGK and C16-GGGG is accounted for by the difference in their intrinsic length. This means that the furthest hydrophobic bead from the membrane center in the C16 tail of the lipopeptides in each case is at approximately the same COM distance from the membrane center. We confirmed that such distances are indeed in the range of 15.6 and 15.8 Å in all cases, which means they are almost the same within the resolution of the coarse-grained model we use.

Electrostatic screening by high salt

Varying the concentration of free salt in solution is an approach commonly used to experimentally (but rarely computationally) modulate electrostatic interactions. Here, we re-ran the C16-KGGK PMF after raising the NaCl concentration from 0.1 M to 1 M, and saw its affinity to POPE/POPG drop roughly 1 kcal/mol (see Fig. 1 and see Table S1). Interestingly, the difference in the affinities of C16-KGGK to POPE/POPG and POPC in high salt is almost identical to that of C16-GGGG in low salt, suggesting that a significant portion of the selectivity can be screened out (presumably due to electrostatic interactions available to lysine but not glycine). It would be interesting to test this phenomenon experimentally, perhaps with isothermal titration calorimetry. One could imagine performing one of the standard vesicle leakage experiments at different salt concentrations to see whether high salt diminishes the difference between the AMLP concentration required to induce leakage in POPE/POPG versus POPC. Along the same lines, we attempted simulations using still higher salt concentrations, but found that MARTINI significantly underestimates the solubility of NaCl; in simulations with 2 M salt, we found a significant number of ions in the membrane interior (between the leaflets), suggesting that the model’s limited electrostatics representation cannot handle salt conditions so far from the physiological regime where it was parameterized.

Comparison to equilibrium all-atom simulations

The purpose of using CG models is to reduce the computational cost of running a given calculation, but the increased efficiency is only valuable if the results are reasonable; there is always a faster way to get an incorrect answer. As a quality control, we compared the coarse-grained simulations of C16-KGGK in the umbrella sampling windows corresponding to the PMF minimum to a set of all-atom (AA) simulations performed previously. We refer the reader to Comparison to Equilibrium All-Atom Simulations in the Supporting Material for details about the AA simulations as well as the methods used in calculating the quantities we are comparing here.

Equilibrium positioning of lipopeptides in the membrane

One simple but crucial test is to ask whether the lipopeptides sample the same bound state in CG and AA calculations. To test this, we compared their locations in the membrane. We find in the AA simulations that, on average, the lipopeptide’s centroid is 16.8 and 15.2 Å from the membrane center for the POPE/POPG and POPC membranes, respectively—slightly less than the 17.9 Å minimum seen in the CG PMFs as shown in Fig. 1. The differences are likely due to the presence of a far higher concentration of lipopeptides in the AA simulations (10 mol % in the AA versus 0.2 mol % in the CG case).

Lateral radial distribution functions of lipids

As we discussed in Selectivity for Bacterial Membranes, and in Mechanism of Membrane Entry, C16-KGGK has higher affinity for POPG than POPE or POPC due to favorable electrostatic interactions. Here we examined whether such interactions are also seen in the AA simulations. Fig. S2 shows that the AA and CG calculations produce very similar LRDFs for POPC around the lipopeptide. However, the CG model appears to overestimate the lateral affinity for POPG relative to the all-atom model; part of this is again likely due to the presence of additional lipopeptides in the AA calculations, and the rest due to the known overestimated favorability of lysine-phosphate interactions (27) and the general limitations of the MARTINI electrostatic model.

Fraction of contacts to different lipids

As a way to look at C16-KGGK’s local environment during the binding process, we calculate the fraction of contacts that C16-KGGK made with lipids and water. As shown in Fig. S3, we got consistent results between the AA and CG simulations; the fluctuations are much smaller for the AA plots (panels B and D) because 1), these plots represent the average over four independent trajectories, and 2), the results are averaged over the 20 lipopeptides found in each AA simulation. Most notably, the lipid contacts in the AA cases were still drifting by the end of the simulations (which is more obvious if individual data sets are plotted instead of their average), indicating that the lateral diffusion of lipids is a very slow process that is challenging to capture using a AA model but much more approachable in the CG model.

Overall, despite the different simulation setups we used for CG-versus-AA simulations, e.g., the number of lipids and lipopeptides, we found the CG properties we compared agreed at least qualitatively and sometimes quantitatively with the AA ones. The largest difference is the CG simulations’ apparent overestimate of the preference for POPG over POPE; we think this issue is an artifact in the MARTINI CG model with unpolarizable water, which has been reported before (27,37,54). Although this might affect the absolute values of $\Delta \text{G}$ and $\Delta \Delta \text{G}$, it is evident that the basic phenomenon is present in the AA simulations as well, indicating that the preference is not entirely artifactual.

Validation against the MARTINI polarizable water model

As we discussed in Comparison to Equilibrium All-Atom Simulations, our CG simulations reproduce the AA structural properties of the systems reasonably well except that the CG model exaggerates the peptide-POPG interaction (see Fig. S2). Despite the different setups between the CG and AA simulations (see Comparison to Equilibrium All-Atom Simulations), the MARTINI unpolarizable water model has been known to give incorrect PMFs for the inserting of charged amino acids such as lysine and arginine to membrane (54,55). The errors arise mostly from the underestimated barriers of absorbing charged side chains by the membrane hydrophobic core. Although the absorption of the amino acid side chains in the membrane interior is not the focus in this study and we purposely avoided simulating these highly unfavorable states (see Free Energy Calculation), we still want to estimate the errors due to the misrepresented interactions in our PMF calculations.

In principle, one could use an all-atom model to recalculate the PMFs, but this is computationally very challenging. Instead, we applied an improved MARTINI model with polarizable water (56) to one of our systems, C16-KGGK with POPE/POPG, where the electrostatic interactions are most prominent and important to the lipopeptide’s selectivity. This improved CG model has been shown to have better physical fidelity in representing the interactions between charged polar molecules and membrane (56). We refer the readers to Potential of Mean Forces Calculation Using the Polarizable MARTINI Water Model in the Supporting Material for the details of PMF calculation. As shown in Fig. 7, the PMF from the polarizable water (PW) model is very similar to the unpolarizable water (UNPW) one except that the slope is slightly steeper in the PW than the UNPW, indicating slightly larger mean forces were experienced by the lipopeptide when it binds to membrane. Most interestingly, the minima and the plateaus of the PMFs in both cases are almost identical and the overall binding free energies are very close, which are –14.5 kcal/mol and –14.9 kcal/mol for the respective PW and UNPW. This indicates that the UNPW model we used is a very good approximation of the PW model for this study.

Figure 7.

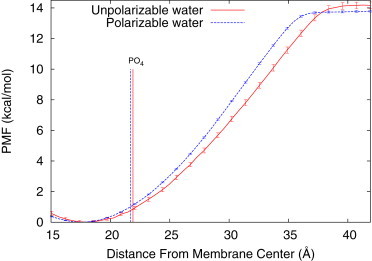
PMFs in kcal/mol as a function of the COM distance between C16-KGGK and the POPE/POPG membrane using either the MARTINI unpolarizable water model or the MARTINI polarizable water model. The COM distances between the phosphate group (PO₄) and the membrane center of each model are labeled by vertical lines of the same line types as those used in plotting the corresponding PMFs. To see this figure in color, go online.

Future directions

This article presents well-converged PMFs for individual lipopeptides and peptides binding to lipid bilayers designed to model bacterial and mammalian membranes. The results demonstrate that the acyl chain accounts for the dominant portion of the lipopeptides’ affinity for membranes; whereas the peptide portions generally make an unfavorable contribution, they give the lipopeptides selectivity for bacterial over mammalian membranes.

That said, there are two areas where these calculations could be improved going forward:

• 1.The MARTINI coarse-grained model, while generally effective and broadly applied, is not a flawless representation of lipid-protein interactions, particularly highly charged objects (27,37,54). It would be good to refine these calculations using one of the better coarse-grained water models, e.g., MARTINI polarizable water (56) or the BMW water model (55), or even perform analogous calculations using an all-atom model. We did apply the MARTINI polarizable water model to the C16-KGGK with POPE/POPG membrane system and got almost identical binding free energy (see Validation against the MARTINI Polarizable Water Model for details). Using an all-atom model on the same systems would be extremely costly computationally; in this work, each PMF required at least 30 μs of sampling, despite the fact that kinetics are enhanced in MARTINI relative to all-atom simulations.
• 2.These calculations can be viewed as determining the binding thermodynamics in the extreme dilution limit for the lipopeptides. Previous experiments (57) and simulations (26,27) have shown that lipopeptides of this type form nanoscale structures such as micelles or fibrils at even moderate concentrations; these aggregated states are thought to contribute to the lipopeptides’ improved bioavailability and resistance to degradation relative to conventional AMPs. As such, the binding affinity from the aggregated state (e.g., a micelle) would be arguably more relevant biologically. Such calculations are likely to be extremely challenging technically, because unlike an individual lipopeptide, the micelle as a whole will have slow relaxations orthogonal to the obvious reaction coordinate.

Conclusion

The study quantitatively characterizes the binding thermodynamics for C16-KGGK, a potent AMLP, to models of bacterial and mammalian membranes. The simple coarse-grained model allows us to perform rigorous free energy calculation that would be too expensive with all-atom models. Our results are consistent with the experimental evidence where the lipidation of otherwise inert cationic peptides enhances their interaction with membrane (12). Most interestingly, C16-KGGK is selective for the bacterial-like membrane over the mammalian-like membrane and electrostatics contribute ∼40.0% to the overall ΔΔG of binding, suggesting that electrostatics play a significant role in AMLPs’ selectivity. Moreover, we found that increasing the NaCl concentration decreased C16-KGGK’s binding affinity to the bacterial-like membrane while not affecting that to the mammalian-like membrane, and thus reduced its selectivity.

Our umbrella sampling simulations also captured important features of the conformational ensembles of lipopeptides’ binding to membranes. They revealed that the lipopeptide can bind to membranes via different paths, led by either hydrophobic interactions with the acyl chains or electrostatic ones between lysine side chains and the lipid phosphates. We also found that the lipopeptides’ binding to the bacterial-like membrane was partially stabilized by recruiting POPG lipids around itself, consistent with previous data published by our group (27).