Sparsity Inducing Prior Distributions for Correlation Matrices of Longitudinal Data

Abstract

For longitudinal data, the modeling of a correlation matrix R can be a difficult statistical task due to both the positive definite and the unit diagonal constraints. Because the number of parameters increases quadratically in the dimension, it is often useful to consider a sparse parameterization. We introduce a pair of prior distributions on the set of correlation matrices for longitudinal data through the partial autocorrelations (PACs), each of which vary independently over [−1,1]. The first prior shrinks each of the PACs toward zero with increasingly aggressive shrinkage in lag. The second prior (a selection prior) is a mixture of a zero point mass and a continuous component for each PAC, allowing for a sparse representation. The structure implied under our priors is readily interpretable for time-ordered responses because each zero PAC implies a conditional independence relationship in the distribution of the data. Selection priors on the PACs provide a computationally attractive alternative to selection on the elements of R or R⁻¹ for ordered data. These priors allow for data-dependent shrinkage/selection under an intuitive parameterization in an unconstrained setting. The proposed priors are compared to standard methods through a simulation study and a multivariate probit data example. Supplemental materials for this article (appendix, data, and R code) are available online.

1. Introduction

Determining the structure of an unknown J × J covariance matrix Σ is a long standing statistical challenge, including in settings with longitudinal data. A key difficulty in dealing with the covariance matrix is the positive definiteness constraint. This is because the set of values for a particular element σ_ij that yield a positive definite Σ depends on the choice of the remaining elements of Σ. Additionally, because the number of parameters in Σ is quadratic in the dimension J, methods to find a parsimonious (lower-dimensional) structure can be beneficial.

One of the earliest attempts in this direction is the idea of covariance selection (Dempster, 1972). By setting some of the off-diagonal elements of the concentration matrix Ω = Σ⁻¹ to zero, a more parsimonious choice for the covariance matrix of the random vector Y is achieved. A zero in the (i, j)-th position of Ω implies zero correlation (and further, independence under multivariate normality) between Y_i and Y_j, conditional on the remaining components of Y. This property, along with its relation to graphical model theory (e.g., Lauritzen, 1996), has led to the use of covariance selection as a standard part of analysis in multivariate problems (Wong et al., 2003; Yuan and Lin, 2007; Rothman et al., 2008). However, one should be cautious when using such selection methods as not all produce positive definite estimators. For instance, thresholding the sample covariance (concentration) matrix will not generally be positive definite, and adjustments are needed (Bickel and Levina, 2008).

Model specification for Σ may depend on a correlation structure through the so-called separation strategy (Barnard et al., 2000). The separation strategy involves reparameterizing Σ by Σ = SRS, with S a diagonal matrix containing the marginal standard deviations of Y and R the correlation matrix. Let 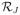denote the set of valid correlation matrices, that is, the collection of J × J positive definite matrices with unit diagonal. Separation can also be performed on the concentration matrix, Ω = TCT so that T is diagonal and C ∈ 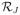. The diagonal elements of T give the partial standard deviations, while the elements c_ij of C are the (full) partial correlations. The covariance selection problem is equivalent to choosing elements of the partial correlation matrix C to be null. Several authors have constructed priors to estimate Σ by allowing C to be a sparse matrix (Wong et al., 2003; Carter et al., 2011).

In many cases the full partial correlation matrix may not be convenient to use. In cases where the covariance matrix is fixed to be a correlation matrix such as the multivariate probit case, the elements of the concentration matrix T and C are constrained to maintain a unit diagonal for Σ (Pitt et al., 2006). Additionally, interpretation of parameters in the partial correlation matrix can be challenging, particularly for longitudinal settings as the partial correlations are defined conditional on future values. For example, c₁₂ gives the correlation between Y₁ and Y₂ conditional on the future measurements Y₃, …, Y_J. An additional issue with Bayesian methods that promote sparsity in C is calculating the volume of the space of correlation matrices with a fixed zero pattern; see Section 4.2 for details.

In addition to the role R plays in the separation strategy, in some data models the covariance matrix is constrained to be a correlation matrix for identifiability. This is the case for the multivariate probit model (Chib and Greenberg, 1998), Gaussian copula regression (Pitt et al., 2006), certain latent variables models (e.g. Daniels and Normand, 2006), among others. Thus, it is necessary to develop methods specific for estimating and/or modeling a correlation matrix.

We consider this problem of correlation matrix estimation in a Bayesian context where we are concerned with choices of an appropriate prior distribution p(R) on 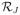. Commonly used priors include a uniform prior over 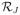(Barnard et al., 2000) and Jeffrey’s prior p(R) ∝ |R|^−(J+1)/2. In these cases the sampling steps for R can sometimes benefit from parameter expansion techniques (Liu, 2001; Zhang et al., 2006; Liu and Daniels, 2006). Liechty et al. (2004) develop a correlation matrix prior by specifying each element ρ_ij of R as an independent normal subject to R ∈ 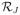. Pitt et al. (2006) extend the covariance selection prior (Wong et al., 2003) to the correlation matrix case by fixing the elements of T to be constrained by C so that T is the diagonal matrix such that R = (TCT)⁻¹ has unit diagonal.

The difficulty of jointly dealing with the positive definite and unit diagonal constraints of a correlation matrix has led some researchers to consider priors for R based on the partial autocorrelations (PACs) in settings where the data are ordered. PACs suggest a practical alternative by avoiding the complication of the positive definite constraint, while providing easily interpretable parameters (Joe, 2006). Kurowicka and Cooke (2003, 2006) frame the PAC idea in terms of a vine graphical model. Daniels and Pourahmadi (2009) construct a flexible prior on R through independent shifted beta priors on the PACs. Wang and Daniels (2013a) construct underlying regressions for the PACs, as well as a triangular prior which shifts the prior weight to a more intuitive choice in the case of longitudinal data. Instead of setting partial correlations from C to zero to incorporate sparsity, our goal is to encourage parsimony through the PACs. As the PACs are unconstrained, selection does not lead to the computational issues associated with finding the normalizing constant for a sparse C. We introduce and compare priors for both selection and shrinkage of the PACs that extends previous work on sensible default choices (Daniels and Pourahmadi, 2009).

The layout of this article is as follows. In the next section we will review the relevant details of the partial autocorrelation parameterization. Section 3 proposes a prior for R induced by shrinkage priors on the PACs. Section 4 introduces the selection prior for the PACs. Simulation results showing the performance of the priors appear in Section 5. In Section 6 the proposed PAC priors are applied to a data set from a smoking cessation clinical trial. Section 7 concludes the article with a brief discussion.

2. Partial autocorrelations

For a general random vector Y = (Y₁,…, Y_J)′ the partial autocorrelation between Y_i and Y_j (i < j) is the correlation between the two given the intervening variables (Y_i+1, …, Y_j−1). We denote this PAC by π_ij, and let Π be the upper-triangular matrix with elements π_ij. Because the PACs are formed by conditioning on the intermediate components, there is a clear dependence on the ordering of the components of Y. In many applications such as longitudinal data modeling, there is a natural time ordering to the components. With an established ordering of the elements of Y, we refer to the lag between Y_i and Y_j as the time-distance j − i between the two.

We now describe the relationship between R and Π. For the lag-1 components (j − i = 1) π_ij = ρ_ij since there are no components between Y_i and Y_j. The higher lag components are calculated from the formula (Anderson, 1984, Section 2.5),

$${\pi }_{ij}=r_1^{-1/2}{r}_2^{-1/2}\left[{\rho }_{ij}-{\mathbf{r}}_1^{\prime }(i,j){\mathbf{R}}_3{(i,j)}^{-1}{\mathbf{r}}_2(i,j)\right],$$ (1)

where ${\mathbf{r}}_1^{\prime }(i,j)=({\rho }_{i,i+1},\dots ,{\rho }_{i,j-1}),{\mathbf{r}}_2^{\prime }(i,j)=({\rho }_{j,i+1},\dots ,{\rho }_{j,j-1})$, and R₃(i, j) is the sub-correlation matrix of R corresponding to the variables (Y_i+1,…, Y_j−1). The scalars r_l (l = 1, 2) are $r_l=1-{\mathbf{r}}_l^{\prime }(i,j){\mathbf{R}}_3{(i,j)}^{-1}{\mathbf{r}}_l(i,j)$. Equivalent to (1), we may define the partial autocorrelation in terms of the distribution of the (mean zero) variable Y. Let Ỹ = (Y_i+1,…, Y_j−1)′ be the vector (possibly empty or scalar) of the intermediate responses, and ${\mathbf{b}}_i^{\prime }\stackrel{\sim }{\mathbf{Y}}$ and ${\mathbf{b}}_j^{\prime }\stackrel{\sim }{\mathbf{Y}}$ be the linear least squares predictors of Y_i and Y_j given Ỹ, respectively. Then, ${\pi }_{ij}=\text{corr}\{Y_i-{\mathbf{b}}_i^{\prime }\stackrel{\sim }{\mathbf{Y}},Y_j-{\mathbf{b}}_j^{\prime }\stackrel{\sim }{\mathbf{Y}}\}$, and it is reasonable to consider π_ij to define the correlation between Y_i and Y_j after correcting for Ỹ.

Examination of formula (1) shows that the operation from R to Π is invertible. By inverting the previous operations recursively over increasing lag j − i, one obtains the correlation matrix from the PACs by ρ_i,i+1 = π_i,i+1 and

$${\rho }_{ij}={\mathbf{r}}_1^{\prime }(i,j){\mathbf{R}}_3{(i,j)}^{-1}{\mathbf{r}}_2(i,j)+r_1^{1/2}{r}_2^{1/2}{\pi }_{ij}$$

for j − i > 1. As the relationship between R and Π is one-to-one, the Jacobian for the transformation from R to Π can be computed easily. The determinant of the Jacobian is given by

$$\mid J(\mathbf{\Pi })\mid =\prod _{i<j}{(1-{\pi }_{ij}^2)}^{-[J-1-(j-i)]/2}$$ (2)

(Joe, 2006, Theorem 4). Notationally, we let R(Π) denote correlation matrix corresponding to the PACs Π. Similarly, Π(R) represents the set of PACs corresponding to correlation matrix R. When it is clear from context, we continue to use only the matrix R or Π and not the functional notation.

The key advantage in using PACs is that parameters are unconstrained (Joe, 2006). For the correlation matrix R, the subset of values in (−1, 1) that ρ_ij can take satisfying the positive definite constraint is determined by the configuration of the other elements of R. For a geometric interpretation of this phenomenon, see Rousseeuw and Molenberghs (1994). For the PACs, each π_ij can take any value in (−1, 1), regardless of the choice of the remaining π’s. This is especially important in the selection context, as setting certain elements of R (or the partial correlation matrix C) to zero can greatly restrict the sets of values that yield a positive definite matrix for other elements in R (C).

Define SBeta(α, β) to be the beta distribution shifted to the support (−1, 1), i.e., the density proportional to (1 + y)^α−1(1 − y)^β−1 for y ∈ (−1, 1). Daniels and Pourahmadi (2009) use the PACs to form a prior on R by letting each π_ij come from this shifted beta distribution where the two shape parameters depend on the lag j − i, with the special case where each π_ij ~ SBeta(1, 1). We call this the flat-PAC (or flat-Π) prior since it specifies a uniform distribution for each of the PACs. Wang and Daniels (2013a) advise using a triangular prior with SBeta(2,1) which (weakly) encourages positive values for the PACs.

The result in (2) shows that we can write the flat prior of Barnard et al. (2000) in terms of a prior on the PACs. We call the prior p_fR(R) ∝ I(R ∈ 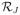) the flat-R prior since it is uniform over the space 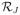. Hence, the flat-R is equal to p_fR(Π) ∝ |J(Π)|⁻¹, which has a contribution from π_ij of ${(1-{\pi }_{ij}^2)}^{[J-1-(j-i)]/2}$. Note that p_fR(Π) is the product of independent SBeta(α_ij, β_ij) distributions for each π_ij, where α_ij = β_ij = 1+[J −1−(j −i)]/2. This provides an unconstrained representation of the flat-R prior.

In longitudinal/ordered data contexts, we expect the PACs to be negligible for elements that have large lags. We exploit this concept via two types of priors. First, we introduce priors that shrink PACs toward zero with the aggressiveness of the shrinkage depending on the lag. Next, we propose, in the spirit of Wong et al. (2003), a selection prior that will stochastically choose PACs to be set to zero.

3. Partial autocorrelation shrinkage priors

3.1. Specification of the shrinkage prior

Using the PAC framework, we form priors that will shrink the PAC π_ij toward zero. It has long been known that shrinkage estimators can produce greatly improved estimation (James and Stein, 1961). As previously noted, π_ij = 0 implies that Y_i and Y_j are uncorrelated given the intervening variables (Y_i+1, …, Y_j−1). In the case where Y has a multivariate normal distribution, this implies independence between Y_i and Y_j, given (Y_i+1, …, Y_j−1). We anticipate that variables farther apart in time (and conditional on more intermediate variables) are more likely to be uncorrelated, so we will more aggressively shrink π_ij for larger values of the lag j − i.

We let each π_ij ~ SBeta(α_ij, β_ij) independently. As we wish to shrink toward zero, we want E{π_ij} = 0, so we fix α_ij = β_ij. It is easily shown that

$$\text{Var}\{{\pi }_{ij}\}=\frac{4{\alpha }_{ij}{\beta }_{ij}}{{({\alpha }_{ij}+{\beta }_{ij})}^2({\alpha }_{ij}+{\beta }_{ij}+1)},$$

which we denote by ξ_ij. We recover the SBeta shape parameters by ${\alpha }_{ij}={\beta }_{ij}=({\xi }_{ij}^{-1}-1)/2$. Hence, the distribution of π_ij is determined by its variance ξ_ij. Rather than specifying these J(J − 1)/2 different variances, we parameterize them through

$$\text{Var}\{{\pi }_{ij}\}={\xi }_{ij}={\epsilon }_0{\mid j-i\mid }^{-\gamma },$$ (3)

where ε₀ ∈ (0, 1) and γ > 0. Clearly, ξ_ij is decreasing in lag so that higher lag terms will generally be closer to zero. We let the positive γ parameter determine the rate that ξ_ij decreases in lag.

To fully specify the Bayesian set-up, we must introduce prior distributions on the two parameters, ε₀ and γ. To specify these hyperpriors, we use a uniform (or possibly a more general beta) for ε₀ and a gamma distribution for γ. We require γ > 0, so ξ_ij = ε₀|j − i|^−γ remains an decreasing function of lag. In the simulations and data analysis of Sections 5 and 6, we use γ ~ Gamma(5,5), so that γ has a prior mean of 1 and prior variance of 1/5. We use a moderately informative prior to keep γ from dominating the role of ε₀ in ξ_ij = ε₀|j − i|^−γ. A large value of γ will force all ξ_ij of lag greater than one to be approximately zero, regardless of the value of ε₀.

3.2. Sampling under the shrinkage prior

The utility of our prior depends on our ability to incorporate it into a Markov chain Monte Carlo (MCMC) scheme. For simplicity we assume that the data consists of Y₁, …, Y_N, where each Y_i is a J-dimensional normal vector with mean zero and covariance R, which is a correlation matrix so as to mimic the computations for the multivariate probit case. Let 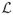(Π|Y) denote the likelihood function for the data, parameterized by the PACs, Π.

The MCMC chain we propose involves sequentially updating each of the J(J − 1)=2 PACs, followed by updating the hyperparameters determining the variance of the SBeta distributions. To sample a particular π_ij, we must draw the new value from the distribution proportional to 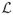(π_ij, Π_(−ij)|Y) p_ij(π_ij), where p_ij(π_ij) is the SBeta(α_ij, β_ij) density and Π_(−ij) represents the set of PACs except π_ij. Due to the subtle role of π_ij in the likelihood piece, there is no simple conjugate sampling step. In order to sample from 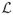(π_ij, Π_(−ij)|Y) p_ij(π_ij), we introduce an auxiliary variable U_ij (Damien et al., 1999; Neal, 2003), and note that we can rewrite the conditional distribution as

$$\mathcal{L}({\pi }_{ij},{\mathbf{\Pi }}_{(-ij)}\mid \mathbf{Y})p_{ij}({\pi }_{ij})={\int }_0^{\infty }I\{u_{ij}<\mathcal{L}({\pi }_{ij},{\mathbf{\Pi }}_{(-ij)}\mid \mathbf{Y})p_{ij}({\pi }_{ij})\}\mathrm{d}{u}_{ij},$$ (4)

suggesting a method to sample π_ij in two steps. First, sample U_ij uniformly over the interval [0, 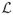(π_ij, Π_(−ij)|Y)p_ij(π_ij)], using the current value of π_ij. We then draw the new π_ij uniformly from the slice set 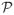= {π : u_ij < 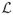(π, Π_(−ij)|Y)p_ij(π)}. Because this set lies within the compact set [−1, 1], 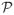could be calculated numerically to within a prespecified level of accuracy, but this is not generally necessary due to the “stepping out” algorithm of Neal (2003).

The variance parameters, ε₀ and γ, are not conjugate so sampling new values in the MCMC chain requires a non-standard step. We also update them using the auxiliary variable technique.

4. Partial autocorrelation selection priors

4.1. Specification of the selection prior

Having developed a prior that shrinks the partial autocorrelations toward zero, we now consider prior distributions that give positive probability to the event that the PAC π_ij is equal to zero. Again, this zero implies that Y_i and Y_j are uncorrelated given the intervening variables (Y_i+1, …, Y_j−1) with independence under multivariate normality. The selection priors are formed by independently specifying the prior for each π_ij as the mixture distribution,

$${\pi }_{ij}~{\epsilon }_{ij}\text{SBeta}({\alpha }_{ij},{\beta }_{ij})+(1-{\epsilon }_{ij}){\delta }_0,$$ (5)

where δ₀ represents a degenerate distribution with point mass at zero. In the shrinkage prior we parameterize the shifted beta parameters α_ij, β_ij to depend on lag, but here we generally let α = α_ij and β = β_ij and incorporate structure through the modeling choices on ε_ij. While there is flexibility to make any choice of these shifted beta parameters α, β, we recommend as default choices either a uniform distribution on [−1, 1] through α = β = 1 (Daniels and Pourahmadi, 2009) or the triangular prior of Wang and Daniels (2013a) by α = 2, β = 1; alternatively, independent hyperpriors for α, β could be specified.

The value of ε_ij gives the probability that π_ij will be non-zero, i.e. will be drawn from the continuous component in the mixture distribution. Hence, we have the probability that Y_i and Y_j are uncorrelated, given the interceding variables, is 1 − ε_ij. As the values of the ε’s decrease, the selection prior places more weight on the point-mass δ₀ component of the distribution (5), yielding more sparse choices for Π. As with our parameterizations of the variance ξ_ij in Section 3.1, we make a structural choice of the form of ε_ij so that this probability depends on the lag-value. We let

$${\epsilon }_{ij}={\epsilon }_0{\mid j-i\mid }^{-\gamma },$$ (6)

similar to our choice of ξ_ij in the shrinkage prior.

This choice (6) specifies the continuous component probability to be an polynomial function of the lag. Because ε_ij is decreasing as the lag j − i increases, P(π_ij = 0) increases. Conceptually, this means that we anticipate that variables farther apart in time (and conditional on more intermediate variables) are more likely to be uncorrelated. As with the shrinkage prior, we choose hyperpriors of ε₀ ~ Unif(0, 1) and γ ~ Gamma(5,5).

4.2. Normalizing constant for priors on R

One of the key improvements of our selection prior over other sparse priors for R is the simplicity of the normalizing constant, as mentioned in the introduction. Previous covariance priors with a sparse C (Wong et al., 2003; Pitt et al., 2006; Carter et al., 2011) place a flat prior on the non-zero components c_ij for a given pattern of zeros. However, the needed normalizing constant requires finding the volume of the subspace of 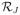corresponding to the pattern of zeros in C. This turns out to be a quite difficult task and provides much of the challenge in the work of the three previously cited papers.

We are able to avoid this issue by specifying our selection prior in terms of the unrestricted PAC parameterization. As the value of any of the π_ij’s does not effect the support of the remaining PACs, the volume of [−1, 1]^J(J−1)/2 corresponding to any configuration of Π with J₀ (≤ J(J − 1)/2) non-zero elements is 2^J₀, the volume of a J₀-dimensional hypercube. Because this constant does not depend on which elements are non-zero, we need not explicitly deal with it in the MCMC algorithm to be introduced in the next subsection. Further, we are able the exploit structure in the order of the PACs in selection (i.e. higher lag terms are more likely to be null), whereas in Pitt et al. (2006), the probability that c_ij is zero is chosen to minimize the effort required to find the normalizing constant.

An additional benefit of performing selection on the partial autocorrelation as opposed to the partial correlations C is that the zero patterns hold under marginalizations of the beginning and/or ending time points. For instance, if we marginalize out the Jth time point, the corresponding matrix of PACs is the original Π after removing the last row and column. However, any zero elements in C will not be preserved because corr(Y₁, Y₂|Y₃, …, Y_J) = 0 does not generally imply that corr(Y₁, Y₂|Y₃, …, Y_J−1) = 0.

4.3. Sampling under the selection prior

Sampling with the selection prior proceeds similarly to the shrinkage prior scheme with the main difference being the introduction of the point mass in (5). As before we sequentially update each of the PACs, by drawing the new value from the distribution proportional to 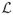(π_ij, Π_(−ij)|Y) p_ij(π_ij), where p_ij(π_ij) gives the density corresponding the prior distribution in (5) (with respect to the appropriate mixture dominating measure). We cannot use the slice sampling step according to (4) but must write the distribution as

$$\mathcal{L}({\pi }_{ij},{\mathbf{\Pi }}_{(-ij)}\mid \mathbf{Y})p_{ij}({\pi }_{ij})={\int }_0^{\infty }I\{u_{ij}<\mathcal{L}({\pi }_{ij},{\mathbf{\Pi }}_{(-ij)}\mid \mathbf{Y})\}{p}_{ij}({\pi }_{ij})\mathrm{d}{u}_{ij}.$$ (7)

For the selection prior, we sample U_ij uniformly over the interval from zero to 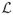(π_ij, Π_(−ij)|Y), using the current value of π_ij, and then draw π_ij from p_ij(·), restricted to the slice set 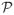= {π: u_ij < 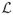(π, Π_(−ij)|Y)}.

To sample from p_ij(·) restricted to 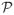, let F(x) = P(π_ij ≤ x) denote the (cumulative) distribution function for the prior (5) of π_ij. Note that F (x) is available in closed form when the SBeta distribution is uniform or triangular. We then draw a random variable Z uniformly over the set F( 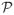) ⊂ [0, 1], and the updated value of π_ij is F⁻¹(Z) = inf{π : F(π) ≥ Z}. This is simply a version of the probability integral transform. It is relatively straight-forward to verify that sampling according to (7) instead of (4) using the “stepping out” algorithm of Neal (2003) leaves the stationary distribution invariant.

The similarity between the sampling steps for the shrinkage and selection priors is notable. Consider the situation when the parameter of concern is the vector of regression coefficients for a linear regression model. With a shrinkage prior these regression coefficients may be drawn simultaneously. But when using a selection prior, each coefficient must be sampled one at a time, and each step requires finding the posterior probability it should be set to zero. For linear models the computational effort required for selection is often much greater than under shrinkage.

In the PAC context, this is not the case. We cannot update the PACs in blocks under the shrinkage prior, so there is no computational benefit relative to selection. Because we sample from the probability integral transform restricted to 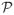, there is also no need to compute the posterior probability that the parameter is selected. Hence, the computational effort for the shrinkage and selection is roughly equivalent. Finally, with the exception of the minor step of updating the hyperparameters, the non-sparse flat-Π and triangular priors also require a similar level of computational time as the selection and shrinkage priors.

To sample the parameters ε₀ and γ defining the mixing proportions ε_ij, we introduce the set of dummy variable ζ_ij = I(π_ij ≠ 0), which have the property that P(ζ_ij = 1) = ε_ij. The sampling distributions of ε₀ and γ depend on Π only through the set of indicator variables ζ_ij. As with the variance parameters of the shrinkage priors, we incorporate a pair of slice sampling steps to update the hyperparameters.

5. Simulations

To better understand the behavior of our proposed priors, we conducted a simulation study to assess the (frequentist) risk of their posterior estimators. We consider four choices A–D for the true covariance matrix in the case of six-dimensional (J = 6) data. R^A will have an autoregressive (AR) structure with ${\rho }_{ij}^A={0.7}^{\mid j-i\mid }$. The corresponding Π^A has values of 0.7 for the lag-1 terms and zero for the others, a sparse parameterization. For the second correlation matrix R^B we choose the identity matrix so that all of PACs are zero in this case. The Π^C has a structure that decays to zero. For the lag-1 terms ${\pi }_{i,i+1}^C=0.7$, and for the remaining terms, ${\pi }_{ij}^C={0.4}^{j-i-1}$, j − i > 1. Neither Π^C nor R^C have zero elements, but ${\pi }_{ij}^C$ decrease quickly in lag j − i. Finally, we consider a correlation matrix that comes from a sparse Π^D,

$${\mathbf{\Pi }}^D=\left[\begin{array}{cccccc}1& .9& .3& 0& 0& 0\\ 0.90& 1& .8& .4& .1& 0\\ 0.80& 0.80& 1& .6& .2& 0\\ 0.62& 0.67& 0.60& 1& .8& .3\\ 0.58& 0.63& 0.58& 0.80& 1& .7\\ 0.46& 0.50& 0.45& 0.69& 0.70& 1\end{array}\right],$$

where the upper-triangular elements correspond to Π^D and the lower-triangular elements depict the marginal correlations from R^D. Note that while Π^D is somewhat sparse, R^D has only non-zero elements.

For each of these four choices of the true dependence structure and for sample sizes of N = 20, 50, and 200, we simulate 100 datasets. For each dataset a posterior sample for Π (and hence, R) is obtained by running an MCMC chain for 5000 iterations, after a burn-in of 1000. We use every tenth iteration for inference, giving a sample of 500 values for each dataset. We consider the performance of both the selection and shrinkage priors on Π. For the selection prior, we perform analyses with SBeta(1, 1) (i.e., Unif(−1; 1)) and SBeta(2, 1) (triangular prior) for the continuous component of the mixture distributions (5). In both the selection and shrinkage priors, the hyperpriors are ε₀ ~ Unif(0, 1) and γ ~ Gamma(5,5). The estimators from the shrinkage and selection priors are compared with the estimators resulting from the flat-R, flat-PAC, and triangular priors. Finally, we consider a naive shrinkage prior where γ is fixed at zero in (3). Here, all PACs are equally shrunk with variance ξ_ij = ε₀ independently of the lag.

We consider two loss functions in comparing the performance of the seven prior choices: L₁(R̂, R) = tr(R̂ R⁻¹) − log |R̂ R⁻¹| − p and L₂(Π̂, Π) = Σ_i<j(π̂_ij − π_ij)². The first loss function is the standard covariance log-likelihood loss (Yang and Berger, 1994), whose Bayes estimator is E{R⁻¹}⁻¹. Because this quantity generally does not have a unit diagonal, we use R̂₁= S E{R⁻¹}⁻¹ S, where S = [diag(E{R⁻¹})]^1/2 is the diagonal matrix that guarantees R̂₁ is a correlation matrix. The Bayes estimator for L₂ is R̂₂ = R (E{Π}), the correlation matrix corresponding to the posterior mean of Π.

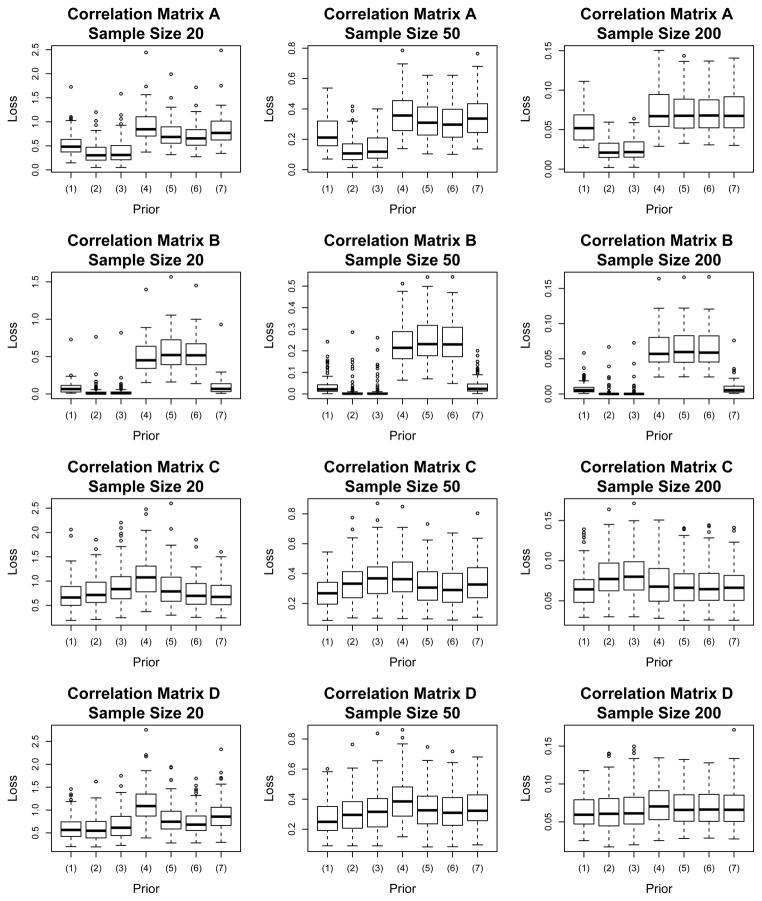
We estimate the frequentist risk for R^k, k ∈ {A, B, C, D}, by averaging the loss over the 100 datasets. Table 1 contains the estimated risk by loss function, prior choice, sample size, and true correlation matrix. When evaluating the risk for loss function l, we are using the estimator R̂_l for l = 1, 2. Figure 1 contains the box plots of the observed losses for L₁ with R̂₁. Plots using loss function 2 look similar and have been excluded for brevity. The Monte Carlo standard errors for the risk estimates are contained in the online supplementary materials.

Table 1.

Risk estimates for simulation study with dimension J = 6. Correlation matrices: A autoregressive structure; B independence; C non-zero decaying; D sparse. Loss functions: L₁(R̂, R) = tr(R̂ R⁻¹) − log |R̂ R⁻¹| − p; L₂(Π̂, Π) = Σ_i<j(π̂_ij − π_ij)².

R	N	Loss Fcn	Risk Estimates by Prior
			Shrinkage	Selection (2,1)	Selection (1,1)	flat-R	flat-Π	Triangular	Naive Shrink
A	20	1	0.54	0.36	0.40	0.91	0.75	0.70	0.84
A	50	1	0.24	0.13	0.15	0.37	0.32	0.32	0.35
A	200	1	0.055	0.025	0.025	0.074	0.072	0.071	0.073
B	20	1	0.087	0.031	0.029	0.49	0.56	0.54	0.100
B	50	1	0.038	0.015	0.014	0.231	0.250	0.249	0.039
B	200	1	0.008	0.002	0.002	0.064	0.065	0.065	0.009
C	20	1	0.73	0.79	0.93	1.10	0.87	0.76	0.73
C	50	1	0.28	0.34	0.37	0.38	0.33	0.31	0.35
C	200	1	0.066	0.082	0.084	0.073	0.070	0.070	0.069
D	20	1	0.62	0.61	0.68	1.13	0.83	0.75	0.90
D	50	1	0.28	0.30	0.32	0.40	0.34	0.33	0.35
D	200	1	0.063	0.064	0.066	0.073	0.071	0.070	0.071
A	20	2	0.26	0.13	0.14	0.52	0.46	0.44	0.48
A	50	2	0.13	0.039	0.045	0.23	0.21	0.20	0.22
A	200	2	0.035	0.0057	0.0059	0.052	0.051	0.051	0.051
B	20	2	0.070	0.019	0.017	0.41	0.47	0.45	0.077
B	50	2	0.034	0.012	0.011	0.210	0.227	0.227	0.035
B	200	2	0.008	0.002	0.002	0.063	0.064	0.063	0.008
C	20	2	0.39	0.44	0.51	0.65	0.52	0.44	0.42
C	50	2	0.15	0.20	0.22	0.22	0.19	0.18	0.20
C	200	2	0.040	0.055	0.057	0.044	0.044	0.043	0.043
D	20	2	0.30	0.29	0.32	0.56	0.47	0.42	0.47
D	50	2	0.15	0.17	0.18	0.22	0.20	0.19	0.20
D	200	2	0.037	0.037	0.039	0.044	0.043	0.043	0.044

Figure 1.

Box plots of the observed loss using L₁ (R̂_1, R) for the J = 6 cases. The prior distributions compared are (1) shrinkage, (2) selection (2,1), (3) selection (1,1), (4) flat-R, (5) flat-Π, (6) triangular, and (7) naive shrinkage.

It is immediately clear that the shrinkage and selection priors dominate the two flat priors for correlation matrices A and B. These are the matrices that have the most sparsity. From the box plots we see the losses for the middle 50% of datasets for the selection priors fall completely below the middle 50% for the four competitors. For R^A we see risk reductions between 29 and 60% for the sparse estimators over the estimators from the flat priors with N = 20; for N = 200 the improvements range from 24 to 66%. In the independence case, the estimators from the shrinkage and selection priors outperform the flat estimators by margins between 82 and 97%. While our focus is mainly on the comparison of the sparse priors to the others, we note that generally the triangular and flat-Π choices are best among the four competitors, with the naive shrinkage prior performing quite well for R^B.

For Π^C all of the seven prior choices perform comparably. From Figure 1 we see that the middle 50% of the losses fall in the same range for each of the sample sizes. For all sample sizes the shrinkage prior is (slightly) favored, and for N = 20 the estimated risk for flat-R is visibly worse than the others. Recall that ${\pi }_{ij}^C$ is decreasing in lag but is not equal to zero. In fact, the smallest element ${\pi }_{16}^C={(0.4)}^4=0.0256$ which may not be close enough to zero to be effectively zeroed out, explaining why the selection priors are less effective for Π^C than in the other scenarios.

When we consider estimating the sparse correlation matrix Π^D, the shrinkage and selection priors outperform the four other priors. From Table 1 we see that for loss function 1 and the N = 20 sample size the estimated risk decreases by 45 (25), 46 (27) and 40 (18) percent for the estimates from the shrinkage, selection (2,1), and selection (1,1) priors over the flat-R (flat-Π) priors. This is quite a substantial drop for the small sample size. For the other sample sizes we still observed a clear decrease over the flat priors. For N = 50 there is a drop of 30 (19), 24 (11), and 19 (5) percent for the sparse priors over the flat priors, and with N = 200 a decrease of 13 (10), 12 (9), and 10 (6) percent.

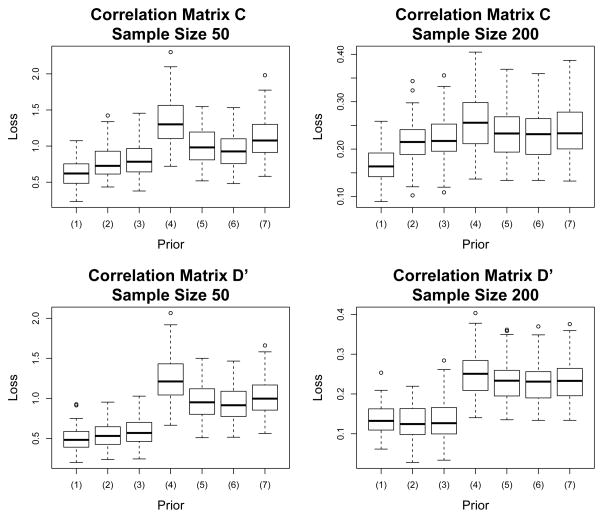
To investigate how our priors behave as J increases, we repeat the analysis using the non-sparse decaying R^C and a sparse R^D′ with the dimension of the matrix increased to J = 10. Again, ${\pi }_{i,i+1}^C=0.7$ for the lag-1 terms and ${\pi }_{ij}^C={0.4}^{j-i-1}$ for all j − i > 1, and we expand the previous R^D to the 10 × 10 R^D′ shown in Table 2. As before the above diagonal elements are from Π^D′ and the below diagonal elements from the corresponding R^D′. Π^D′ is very sparse, while R^D′ has no zero elements. We consider sample sizes of 50 and 200. Risk estimates and box plots for this simulation are displayed in Table 3 and Figure 2.

Table 2.

10 × 10 PAC matrix Π^D′ shown above the diagonal and its respective correlation matrix R^D′ shown below the diagonal.

$${\mathbf{\Pi }}^{D^{\prime }}=\left[\begin{array}{cccccccccc}1& .9& .3& 0& 0& 0& 0& 0& 0& 0\\ 0.90& 1& .8& .4& .1& 0& 0& 0& 0& 0\\ 0.80& 0.80& 1& .6& .2& 0& 0& 0& 0& 0\\ 0.62& 0.67& 0.60& 1& .8& .3& 0& 0& 0& 0\\ 0.58& 0.63& 0.58& 0.80& 1& .7& 0& 0& 0& 0\\ 0.46& 0.50& 0.45& 0.69& 0.70& 1& .8& .4& .1& 0\\ 0.37& 0.40& 0.36& 0.55& 0.56& 0.80& 1& .6& .2& 0\\ 0.31& 0.34& 0.30& 0.46& 0.47& 0.67& 0.60& 1& .8& .3\\ 0.29& 0.32& 0.29& 0.43& 0.44& 0.63& 0.58& 0.80& 1& .7\\ 0.23& 0.25& 0.23& 0.34& 0.35& 0.50& 0.45& 0.69& 0.70& 1\end{array}\right]$$

Table 3.

Risk estimates for simulation study with dimension J = 10. Correlation matrices: C nonzero decaying; D′ sparse. Loss functions: L₁(R̂, R) = tr(R̂ R⁻¹) − log |R̂ R^−1| − p; L₂(Π̂, Π) = Σ_i<j(π̂_ij − π_ij)².

R	N	Loss Fcn	Risk Estimates by Prior
			Shrinkage	Selection (2,1)	Selection (1,1)	flat-R	flat-Π	Triangular	Naive Shrink
C	50	1	0.63	0.77	0.83	1.33	1.00	0.94	1.12
C	200	1	0.165	0.215	0.221	0.254	0.232	0.229	0.238
D′	50	1	0.49	0.54	0.59	1.26	0.97	0.93	1.03
D′	200	1	0.134	0.130	0.133	0.250	0.230	0.227	0.235
C	50	2	0.38	0.48	0.51	0.88	0.72	0.67	0.75
C	200	2	0.110	0.155	0.159	0.184	0.174	0.171	0.174
D′	50	2	0.27	0.31	0.34	0.77	0.69	0.66	0.69
D′	200	2	0.085	0.080	0.082	0.184	0.178	0.175	0.178

Figure 2.

Box plots of the observed loss using L₁(R̂₁,R) for J = 10. The prior distributions compared are (1) shrinkage, (2) selection (2,1), (3) selection (1,1), (4) flat-R, (5) flat-Π, (6) triangular, and (7) naive shrinkage.

From both Table 3 and Figure 2 it is clear that estimation of the correlation matrix is greatly improved under the sparse priors. In the simulations of both dimensions we find that the estimators from the triangular selection prior tend to be slightly better than the selection prior with SBeta(1,1). With the sparse correlation matrix R^D′ the risk under the sparse priors are about half of the risk of the flat prior under both sample sizes. Recall that Π^C is not sparse but has elements which decay exponentially. Because many of the large lag components are very small, the selection priors provide stability by explicitly zeroing many of these out. For the larger sample size, the flat priors do comparatively better although still worse than the sparse priors.

We have demonstrated that the sparse priors yield improved estimation of the correlation matrix in a variety of data situations. In order to investigate the performance in the standard situation where the true dependence structure is unknown, we apply the sparsity and shrinkage priors to a data set obtained from a smoking cessation clinical trail.

6. Data analysis

The first Commit to Quit (CTQ I) study (Marcus et al., 1999) was a clinical trial designed to encourage women to stop smoking. As weight gain is often a viewed as a factor decreasing the effectiveness of smoking cessation programs, a treatment involving an exercise regimen is utilized to try to increase the quit rate. The control group received an educational intervention of equal time. The study ran for twelve weeks, and patients were encouraged to quit smoking at week 5. As the study required a significant time commitment (three exercise/educational sessions a week), there is substantial missingness due to study dropout. As in previous analyses of this data (Daniels and Hogan, 2008), we assume this missingness is ignorable.

For patient i = 1,…, N (N = 281), we denote the vector of quit statuses by Q_i = (Q_i1,…, Q_iJ)′. We only consider the responses after patients are asked to quit, weeks 5 through 12 (J = 8). Here Q_it = 1 indicates a success (not smoking) for patient i at time t (1 ≤ t ≤ J, corresponding to week t + 4), Q_it = −1 for a failure (smoking during the week), and Q_it = 0 if the observation is missing. Following the usual conventions of the multivariate probit regression model (Chib and Greenberg, 1998), we let Y_i be the J-dimensional vector of latent variables corresponding to Q_i. Thus, Q_it = 1 implies that Y_it ≥ 0, and Q_it = −1 gives Y_it < 0. When Q_it = 0, the sign of Y_it represents the (unobserved) quit status for the week.

We assume the latent variables follow a multivariate normal distribution Y_i ~ N_J (μ_i, R) for i = 1,…, N, where μ_i = X_iβ, X_i is a J × q matrix of covariates and β a q-vector of regression coefficients. As the scale of Y is unidentified, the covariance matrix of Y is constrained to be a correlation matrix R. We consider two choices of X_i: ‘time-varying’ which specifies a different μ_it for each time within each treatment group (q = 2J) and ‘time-constant’ which gives the same value of μ_it across all times within treatment group (q = 2).

With the time-constant and time-varying choices of the mean structure, we consider the following priors for R: shrinkage, selection, flat-R, flat-Π, triangular, naive shrinkage, and an autoregressive (AR) prior. The AR prior assumes an AR(1) structure for R, that is, ρ_ij = ρ^|j−i| and π_i,i+1 = ρ and π_ij = 0 if |j − i| > 1. We assume a Unif(−1, 1) distribution for ρ. As in the risk simulation, we consider the selection prior with both SBeta(1, 1) and with SBeta(2, 1) for the continuous component. The remaining prior distributions to be specified are ε₀ ~ Unif(0, 1), γ ~ Gamma(5, 5), and the prior on the regression coefficients β is flat.

To analyze the data we run an MCMC chain for 12,000 iterations after a burn-in of 3000. There are three sets of parameters to sample in the MCMC chain: the regression coefficients, the correlation matrix, and the latent variables. The conditional for β given Y and R is multivariate normal. Sampling the correlation matrix evolves as discussed in Sections 3.2 and 4.3 using the residuals Y_i − μ_i. The latent variables Y_i, which are constrained by Q_i, are sampled according to the strategy of Liu et al. (2009, Proposition 1). With the shrinkage prior the autocorrelation of all PACs was less than 0.1 within 20 iterations. With the higher lag terms of the selection prior, the autocorrelation does not decrease as quickly due to discrete component of the distribution (π_ij may be equal to zero for many iterations), but the lag 1 and 2 terms also have autocorrelations less than 0.1 in 20 iterations. Based on these autocorrelation values, we retain every tenth iteration of each chain to use for inference. Trace plots and other graphical diagnostics further confirm good mixing of the chain.

To compare the specification based on our prior choices, we make use of the deviance information criterion (DIC; Spiegelhalter et al., 2002). The DIC statistic can be viewed similarly to the Bayesian or Akaike information criterion, but the DIC does not require the user to “count” the number of model parameters. This is key for Bayesian models that utilize shrinkage and/or sparsity priors as it is not clear whether or how one should count a parameter that has been set to or shrunk toward zero. To that end, let

$$\text{Dev}=-2\text{loglik}(\widehat{\mathit{\beta }},\widehat{\mathbf{R}}\mid \mathbf{Q})=\sum _i-2\text{loglik}(\widehat{\mathit{\beta }},\widehat{\mathbf{R}}\mid {\mathbf{Q}}_i)$$ (8)

be the deviance or twice the negative log-likelihood with the parameters β̂ and R̂. Here β̂ is the posterior mean, and for the correlation estimate R̂, we use the first of the estimators we considered in Section 5, R̂ = S E{R⁻¹}⁻¹ S with S = [diag(E{R⁻¹})]^1/2. The complexity of the model is measured by the term p_D, sometimes called the effective number of parameters. This p_D is calculated as

$$p_D=\mathrm{E}\{-2\text{loglik}(\mathit{\beta },\mathbf{R}\mid \mathbf{Q})\}-\text{Dev},$$ (9)

where the expectation is over the posterior distribution of the parameters (β, R). The DIC model comparison statistics is DIC = Dev + 2p_D, the sum of terms measuring model fit and complexity. Smaller values of DIC are preferred.

As Wang and Daniels (2011) point out, the DIC should be calculated using the observed data, which in this case is the quit status responses Q_i not the latent variables Y_i. Hence the log-likelihood for Q_i at parameters (β, R) is equal to

$$\text{loglik}(\mathit{\beta },\mathbf{R}\mid {\mathbf{Q}}_i)=log\left({\int }_{{(-\infty ,\infty )}^J}I\{Q_{it}{y}_t\ge 0\forall t\}\phi (\mathbf{y}\mid {\mathbf{X}}_i\mathit{\beta },\mathbf{R})\mathrm{d}\mathbf{y}\right),$$ (10)

where φ(·|μ, Σ) is the J-dimensional multivariate normal density with mean μ and covariance matrix Σ. The integral in (10) is not tractable but can be estimated using importance sampling (Robert and Casella, 2004, Section 3.3). See the appendix in the online supplementary materials for details about estimating the DIC. The model fit (Dev), complexity (p_D), and comparison (DIC) statistics are in Table 4; DIC statistics were estimated with a standard error of approximately 0.5.

Table 4.

Model comparison statistics for the CTQ data.

Mean Structure	Correlation Prior	Dev	pD	DIC
Time-constant	Shrinkage	1031	14	1060
Time-constant	Selection (2,1)	1042	12	1066
Time-constant	Selection (1,1)	1044	12	1068
Time-constant	Triangular	1029	20	1068
Time-constant	flat-Π	1029	20	1069
Time-constant	Naive shrinkage	1033	20	1074
Time-constant	AR	1071	3	1078
Time-constant	flat-R	1043	21	1086
Time-varying	Shrinkage	1022	25	1071
Time-varying	Triangular	1017	30	1077
Time-varying	Selection (2,1)	1033	22	1077
Time-varying	Selection (1,1)	1036	22	1080
Time-varying	flat-Π	1019	30	1080
Time-varying	Naive shrinkage	1023	31	1085
Time-varying	AR	1068	13	1093
Time-varying	flat-R	1034	31	1097

We see that the models that use a mean structure that depends only on treatment and not time t tend to have lower DIC values. The time-varying models are penalized in the p_D term for having to estimate the additional 14 regression coefficients. Of the correlation priors the flat-R and AR priors perform much worse than the shrinkage, selection, triangular, and flat-PAC priors with the same mean structure. Additionally, the selection prior that uses the triangular form for SBeta (α = 2, β = 1) tend to have a smaller DIC than the SBeta(1,1) priors. From Table 4 we determine the prior choice that best balances model fit with parsimony is clearly the model with time-constant mean structure and the shrinkage prior on the correlation matrix prior.

Using this best fitting model, the posterior mean of β is (−0.504, −0.295) implying that the marginal probability (95% credible interval) of not smoking during a given study week is Φ(−0.504) = 0.307 (0.24, 0.37) for the control group and Φ(−0.295) = 0.384 (0.32, 0.45) for the exercise group, where Φ(·) is the distribution function of the standard normal distribution. The test of the hypothesis that the control treatment is as effective as the exercise treatment (i.e., H₀ : β₁ ≥ β₂) has a posterior probability of 0.06, providing some evidence to the claim that exercise improves cessation results.

We now examine in more detail the effect the shrinkage prior has on modeling the correlation matrix. The posterior means (95% credible interval) of the shrinkage parameters are ε̂₀ = 0.406 (0.25, 0.60) and γ̂ = 2.44 (1.6, 3.4). With a value of γ greater than 1, the variance of π_ij is decaying to zero fairly rapidly. The posterior mean of Π is

$$\widehat{\mathbf{\Pi }}=\left[\begin{array}{cccccccc}1.00& 0.70& 0.12& 0.02& 0.05& 0.00& 0.00& \hfill -0.01\\ 0.71& 1.00& 0.83& 0.16& 0.09& 0.02& 0.01& \hfill 0.00\\ 0.64& 0.84& 1.00& 0.81& 0.12& 0.10& 0.06& \hfill 0.02\\ 0.56& 0.74& 0.82& 1.00& 0.78& 0.24& 0.09& \hfill 0.03\\ 0.51& 0.64& 0.69& 0.79& 1.00& 0.81& 0.37& \hfill 0.04\\ 0.48& 0.61& 0.66& 0.74& 0.83& 1.00& 0.88& \hfill 0.21\\ 0.48& 0.61& 0.67& 0.74& 0.83& 0.89& 1.00& \hfill 0.78\\ 0.40& 0.52& 0.57& 0.63& 0.70& 0.77& 0.80& \hfill 1.00\end{array}\right],$$

with the lower diagonal values giving the elements of R̂. We see that the PACs are far from zero in only the first two lags and the remaining π’s are close to zero. This is because these partial autocorrelations have been shrunk almost to zero in most iterations.

7. Discussion

In this paper we have introduced two new priors for correlation matrices, a shrinkage prior and a selection prior. These priors choose a sparse parameterization of the correlation matrix through the set of PACs. In the selection context, by stochastically selecting the elements of Π to zero out, our model finds interpretable independence relationships for normal data and avoids the need for complex model selection of the dependence structure. A key improvement of the selection prior over existing methods for sparse correlation matrices is that our approach avoids the complex normalizing constants seen in previous work. Additionally, in settings with time-ordered data, the partial autocorrelations are more interpretable than the full partial correlations, as they do not involve conditioning on future values.

While the examples we have considered here involve situations where the covariance matrix was constrained (as in the data example) or known (as in the simulations) to be a correlation matrix, the extension to arbitrary Σ is simple. Returning to the separation strategy Σ = SRS (Barnard et al., 2000), a prior for Σ can be formed by placing independent priors on S and R, i.e. p(Σ) = p(R)p(S). Using one of the proposed priors for p(R), sensible choices of p(S) include an independent inverse gamma for each of the ${\sigma }_{jj}^2$ or a flat prior on {S = diag(σ₁₁, …, σ_JJ) : σ_jj > 0}. This leads to a prior on Σ with sparse PACs.

The simulations and data we have considered here deal with Y of low or moderate dimension. We provide a few comments regarding scaling of our approach for data with larger J. As we believe that PACs of larger lag play a progressively smaller role in describing the (temporal) dependence, it may be reasonable to specify a maximum allowable lag for non-zero PACs. That is, we choose some k such that π_ij = 0 for all j − i > k and sample π_ij (j − i ≤ k) from either our shrinkage or selection prior. Banding the Π matrix is related to the idea of banding the covariance matrix (Bickel and Levina, 2008), concentration matrix (Rothman et al., 2008), or the Cholesky decomposition of Σ⁻¹ (Rothman et al., 2010). Banding Π has also been studied by Wang and Daniels (2013b). In addition to reducing the number of parameters that must be sampled, other matrix computations will be faster by using properties of banded matrices.

Related to this, modifications to the shrinkage prior may be needed for larger dimension J. Recall that the variance of π_ij is ξ_ij = ε₀|j − i|^−γ. For large lags, this can be very close to zero leading to numerical instability; recall the parameters of the SBeta distribution are inversely related to ξ_ij through ${\alpha }_{ij}={\beta }_{ij}=\left({\xi }_{ij}^{-1}-1\right)/2$. Replacing (3) with ξ_ij = ε₀ min{|j − i|, k}^−γ or ξ_ij = ε₀ + ε₁|j −i|^−γ to bound the variances away from zero or banding Π after the first k lags provide two possibilities to avoid such numerical issues.

Further, we have parametrized the variance component and the selection probability in similar ways in our two sparse priors. The quantity is of the form ε₀|j − i|^−γ for both ξ_ij in (3) and ε_ij in (6), but other parameterizations are possible. We have considered some simulations (not included) allowing the variance/selection probability to be unique for lag, i.e. ε_ij = ε_|j−i|. A prior needs to be specified for each of these J − 1 ε’s, ideally decreasing in lag. Alternatively, one could use ε₀/|j − i|, which can be viewed as a special case where the prior on γ is degenerate at 1. In our experience results were not very sensitive to the choice of the parameterization, and posterior estimates of Π and R were similar.

In addition, we have focused our discussion on the correlation estimation problem in the context of analysis with multivariate normal data. We note that these priors are additionally applicable in the context of estimating a constrained scale matrix for the multivariate Student t-distribution. Consider the random variable Y ~ t_J (μ, R, ν). That is, Y follows a J-dimensional t-distribution with location (mean) vector μ, scale matrix R (constrained to be a correlation matrix), and ν degrees of freedom (either fixed or random). Using the gamma-mixture-of-normals technique (Albert and Chib, 1993), we rewrite the distribution of Y to be Y|τ ~ N_J (μ, τ⁻¹R) and τ ~ Gamma(ν/2, ν/2). Sampling for R as part of an MCMC chain follows as in Sections 3.2 and 4.3 using ${\mathbf{Y}}^{\ast }=\sqrt{\tau }(\mathbf{Y}-\mathit{\mu })$ as the data. However, one should note that a zero PAC π_ij implies that Y_i and Y_j are uncorrelated given Y_i+1, …, Y_j−1, but this is not equivalent to conditional independence as in the normal case.