Helicity conservation by flow across scales in reconnecting vortex links and knots

Significance

Ideal fluids have a conserved quantity—helicity—which measures the degree to which a fluid flow is knotted and tangled. In real fluids (even superfluids), vortex reconnection events disentangle linked and knotted vortices, jeopardizing helicity conservation. By generating vortex trefoil knots and linked rings in water and simulated superfluids, we observe that helicity is remarkably conserved despite reconnections: vortex knots untie and links disconnect, but in the process they create helix-like coils with the same total helicity. This result establishes helicity as a fundamental building block, like energy or momentum, for understanding the behavior of complex knotted structures in physical fields, including plasmas, superfluids, and turbulent flows.

Abstract

The conjecture that helicity (or knottedness) is a fundamental conserved quantity has a rich history in fluid mechanics, but the nature of this conservation in the presence of dissipation has proven difficult to resolve. Making use of recent advances, we create vortex knots and links in viscous fluids and simulated superfluids and track their geometry through topology-changing reconnections. We find that the reassociation of vortex lines through a reconnection enables the transfer of helicity from links and knots to helical coils. This process is remarkably efficient, owing to the antiparallel orientation spontaneously adopted by the reconnecting vortices. Using a new method for quantifying the spatial helicity spectrum, we find that the reconnection process can be viewed as transferring helicity between scales, rather than dissipating it. We also infer the presence of geometric deformations that convert helical coils into even smaller scale twist, where it may ultimately be dissipated. Our results suggest that helicity conservation plays an important role in fluids and related fields, even in the presence of dissipation.

In addition to energy, momentum, and angular momentum, ideal (Euler) fluids have an additional conserved quantity—helicity (Eq. 1)—which measures the linking and knotting of the vortex lines composing a flow (1). For an ideal fluid, the conservation of helicity is a direct consequence of the Helmholtz laws of vortex motion, which both forbid vortex lines from ever crossing and preserve the flux of vorticity, making it impossible for linked or knotted vortices to ever untie (1, 2). Because conservation laws are of fundamental importance in understanding flows, the question of whether this topological conservation law extends to real, dissipative systems is of clear and considerable interest. The general importance of this question is further underscored by the recent and growing impact knots and links are having across a range of fields, including plasmas (3, 4), liquid crystals (5, 6), optical (7), electromagnetic (8), and biological structures (9–11), cosmic strings (12, 13), and beyond (14). Determining whether and how helicity is conserved in the presence of dissipation is therefore paramount in understanding the fundamental dynamics of real fluids and the connections between tangled fields across systems.

The robustness of helicity conservation in real fluids is unclear because dissipation allows the topology of field lines to change. For example, in viscous flows vorticity will diffuse, allowing nearby vortex tubes to “reconnect” (Fig. 1 A–C), creating or destroying the topological linking of vortices. This behavior is not unique to classical fluids: analogous reconnection events have also been experimentally observed in superfluids (15) and coronal loops of plasma on the surface of the sun (16). In general, these observed reconnection events exhibit divergent, nonlinear dynamics that makes it difficult to resolve helicity dynamics theoretically (4, 17, 18). On the other hand, experimental tests of helicity conservation have been hindered by the lack of techniques to create vortices with topological structure. Thanks to a recent advance (19), this is finally possible.

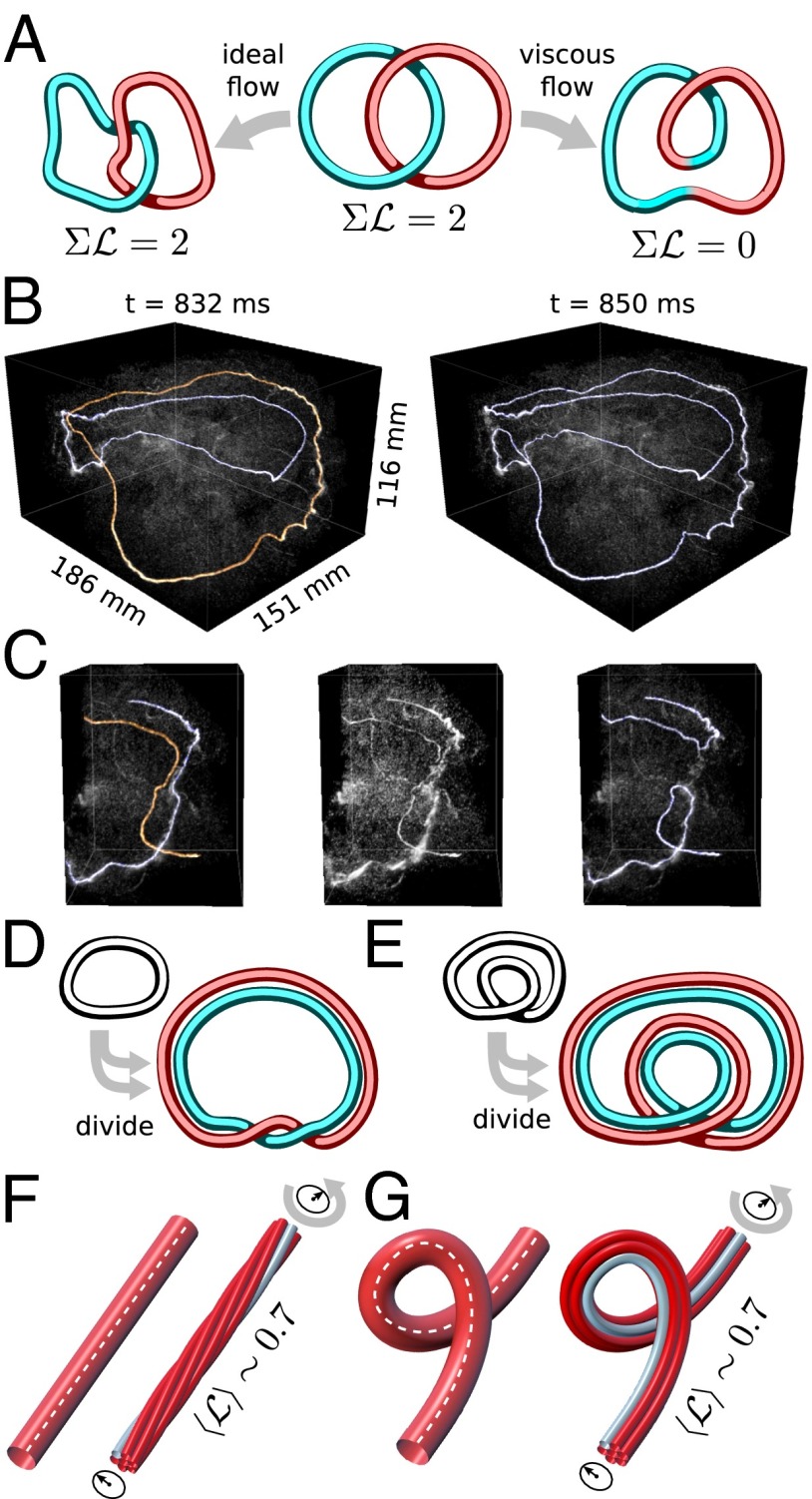
Fig. 1.

(A) A sketch of the evolution of vortex tube topology in ideal (Euler) and viscous (Navier–Stokes) flow. Dissipative flows allow for reconnections of vortex tubes, and so tube topology is not conserved. (B) Two frames of a 3D reconstruction of a vortex reconnection in experiment, which turns an initially linked pair of rings into a single twisted ring. (C) A close-up view of the reconnection in B. (D) If a tube is subdivided into multiple tubes, linking between the two may be created by introducing a twist into the pair. (E) Similarly, if a coiled tube is subdivided, linking can result even without adding twist. This can be seen either by calculating the linking number for the pair, or imagining trying to separate the two. (F) In a continuum fluid, the vortex tube may be regarded as a bundle of vortex filaments, which may be twisted. In this case, a twist of $\mathrm{\Delta }\theta \sim 0.7\times 2\pi$ results in a total helicity of $\mathrm{\mathscr{H}}\sim 0.7{\mathrm{\Gamma }}^2$. (G) If the vortex tube is coiled, linking will also be introduced, as in E. Conceptually, this coiling can be regarded as producing a net rotation of the vortex bundle even when it is everywhere locally untwisted.

By performing experiments on linked and knotted vortices in water, as well as numerical simulations of Bose–Einstein condensates [a compressible superfluid (20)] and Biot–Savart vortex evolution, we investigate the conservation of helicity, in so far as it can be inferred from the center-lines of reconnecting vortex tubes. We describe a new method for quantifying the storage of helicity on different spatial scales of a thin-core vortex: a “helistogram.” Using this analysis technique, we find a rich structure in the flow of helicity, in which geometric deformations and vortex reconnections transport helicity between scales. Remarkably, we find that helicity can be conserved even when vortex topology changes dramatically, and identify a system-independent geometric mechanism for efficiently converting helicity from links and knots into helical coils.

Topology and Helicity

Topology in a fluid is stored in the linking of vortex lines. The simplest example of linked vortex lines is a joined pair of rings (Fig. 1A); however, the same topology can be obtained with very different geometries, for example, by twisting or coiling a pair of rings (Fig. 1 D and E).

Vortex loops in fluids (e.g., Fig. 1 B and C) consist of a core region of concentrated vorticity, ω, that rotates around the vortex center-line, surrounded by irrotational fluid motion. In the language of vortex lines, vortices should therefore be regarded as “bundles” of vortex “filaments” (e.g., Fig. 1 F and G), more akin to stranded rope than an infinitesimal line. In this case, topology can be stored either by linking and knotting of bundles, or by linking of nearby filaments within a single bundle.

The hydrodynamic helicity quantifies the degree of vortex linking present in a flow; in terms of the flow field, $\mathit{u}\left(\mathit{r}\right)$ (where r is the spatial coordinate), it is given by the following:

$$\mathrm{\mathscr{H}}={\displaystyle \int \mathit{u}\cdot \mathit{\omega }\hspace{0.17em}{d}^{3}r},$$ [1]

where the vorticity is $\mathit{\omega }=\mathbf{\nabla }\times \mathit{u}$. This quantity is exactly conserved for ideal fluids (1, 21). The connection between helicity and the linking between vortex tubes was first noted by Moffatt (1), who showed that for a flow consisting of thin, closed vortex lines ${\mathcal{C}}_n$, the helicity is equivalently given by the following:

$$\mathrm{\mathscr{H}}={\displaystyle \sum _{i,j}{\mathrm{\Gamma }}_i{\mathrm{\Gamma }}_{\mathrm{j\hspace{0.17em}}}\frac{1}{4\pi }{\displaystyle \underset{{\mathcal{C}}_i}{\oint }{\displaystyle \underset{{\mathcal{C}}_j}{\oint }\frac{{\mathit{x}}_i-{\mathit{x}}_j}{{\left|{\mathit{x}}_i-{\mathit{x}}_j\right|}^3}\cdot \left(d{\mathbf{\ell }}_i\times d{\mathbf{\ell }}_j\right)}}},$$ [2]

where ${\mathrm{\Gamma }}_i$ and ${\mathit{x}}_i$ correspond to the circulation (vorticity flux) and path of vortex tube ${\mathcal{C}}_i$. The resulting double path integral was recognized as the Gauss linking integral, which measures the linking between the paths ${\mathcal{C}}_i$ and ${\mathcal{C}}_j$ or in the case $i=j$ the writhe (coiling and knotting) of a single path.

For finite thickness vortex tubes, one may subdivide the bundle into N infinitesimal filaments each with strength $\mathrm{\Gamma }/N$, and compute Eq. 2 in the limit $N\to \infty$ (22, 23). The result is conveniently expressed as the sum of three terms, each geometrically distinct contributions to the same measure of topology:

$$\mathrm{\mathscr{H}}={\displaystyle \sum _{i\ne j}{\mathrm{\Gamma }}_i{\mathrm{\Gamma }}_j\hspace{0.17em}{\mathrm{ℒ}}_{ij}}+{\displaystyle \sum _i{\mathrm{\Gamma }}_i^2\hspace{0.17em}\left(W{r}_i+T{w}_i\right)},$$ [3]

where ${\mathrm{ℒ}}_{ij}$ is the linking number between bundles i and j, $W{r}_i$ is the writhe of the bundle center-line, and $T{w}_i$ is the total twist of each bundle. Both the linking number and writhe are given by the Gauss linking integral for the bundle center-line. The writhe of a curve quantifies its total helix-like coiling and knotting. The twist is given by $Tw=\frac{1}{2\pi }{\displaystyle \oint \left(\widehat{\mathit{n}}\times {\partial }_s\widehat{\mathit{n}}\right)\cdot d\mathbf{\ell }}$, where $\widehat{\mathit{n}}$ is a normal vector on each path that describes the bundle orientation.

The first sum of Eq. 3, for $i\ne j$, measures the linking between bundles, whereas the second sum, over i, measures the linking between filaments within each bundle. The topological contribution of twist can be visualized by subdividing a ring (with flux Γ) into a pair of filaments (with flux $\mathrm{\Gamma }/2$), that twist around each other as shown in Fig. 1D. Similarly, the topological contribution of writhe can be seen in Fig. 1E; in each case, the resulting helicity is $\mathrm{\mathscr{H}}=1{\mathrm{\Gamma }}^2$. Each of these examples produces a helicity equal to an integer multiple of ${\mathrm{\Gamma }}^2$; however, for a bundle, the helicity is a flux-weighted average linking, which need not be an integer multiple of ${\mathrm{\Gamma }}^2$ (e.g., if a filament does not close in a single trip around the bundle) (23). The bundle sections shown in Fig. 1 F and G each have a helicity of $\mathrm{\mathscr{H}}\sim 0.7{\mathrm{\Gamma }}^2$, resulting from twist or coil, respectively. The topological equivalence of these two geometrically distinct bundles can be seen by taking the coiled bundle and pulling on the ends; straightening out the coil results in a compensating twist, which conserves the helicity.

Although the linking number between bundles and the writhe of each bundle can be calculated from the center-line alone, measuring the twist requires additional information about the fine structure of the vortex core, which is challenging to resolve experimentally. For the remainder of the paper, we consider only the “center-line helicity,” given by the following:

$${\mathrm{\mathscr{H}}}_c/{\mathrm{\Gamma }}^2={\displaystyle \sum _{i\ne j}{\mathrm{ℒ}}_{ij}}+{\displaystyle \sum _{i}W{r}_i}.$$ [4]

This geometric quantity is equivalent to the total helicity if we assume that all vortex tubes have the same circulation, ${\mathrm{\Gamma }}_i\to \mathrm{\Gamma }$, and are locally untwisted, $T{w}_i=0$ (see SI Text, Definition of the Center-Line Helicity and Fig. S1 for a discussion of the definition of center-line helicity). We note that twist is naturally dissipated by viscosity, and for a twisted straight line vortex filament, this occurs at a rate $\frac{{\partial }_{t}Tw}{Tw}=-\frac{8\pi \nu }{A_{\mathrm{eff}}}$, where v is the kinematic viscosity and $A_{\text{eff}}$ is the bundle cross sectional area (SI Text, Helicity Dissipation for a Twisted Core). For typical experimental parameters, this can be estimated to be faster than the overall dynamics of the center-line motion.

Methods

To explore the behavior of thin-core vortices in experiment, we create shaped vortex loops in water, akin to the familiar smoke ring, but imaged with buoyant microbubbles instead of smoke. Our vortex loops are generated by impulsively accelerating specially shaped, 3D printed hydrofoils (see Fig. S2 for corresponding meshes and hydrofoil profile). Upon acceleration, a “starting vortex” whose shape traces the trailing edge of the hydrofoil is shed and subsequently evolves under its own influence; using this technique, it is possible to generate arbitrary geometry and topology, including links and knots (19). To study the effects of topology, we focus on the behavior of the most elemental linked and knotted vortices: Hopf links and trefoil knots, both of which can be created with high fidelity. Our vortices have a typical width of 150 mm and circulation of $\mathrm{\Gamma }=20,000$ mm²/s, and we use water as the experimental fluid. The Reynolds number is of order $Re\sim 2\times {10}^4$.

These vortices are tracked using ∼100-μm microbubbles, generated by hydrolysis, which are trapped in the core of the rapidly spinning vortices (e.g., Fig. 1 B and C). These bubbles are in turn imaged with high-speed laser scanning tomography of a $230\times 230\times 230$-mm volume at a resolution of ${384}^3$ and a rate of 170 ${\mathrm{s}}^{-1}$. Using these data, we trace the vortex cores by first identifying line-like features in the volumetric data and then connecting them to create closed 3D paths (24–26), approximated as polygons with ∼3,000 points. Some disruption of the imaging and tracking results from vortex reconnections, but careful adjustment of the experimental parameters allows vortices to be tracked immediately before and after reconnections. From these paths, physical quantities such as energy, momentum, and helicity can be directly calculated as path integrals, and the geometric nature of this description allows direct comparison with other fluid systems, including simulations of superfluids and idealized thin core vortex models, both of which will be described later. We rescale all of the vortex lengths in terms of the initial length, $L_0$, and rescale the time in terms of the inital r.m.s. vortex radius, $\overline{r}=\sqrt{\langle {\left|\mathit{x}\right|}^2\rangle -{\left|\langle \mathit{x}\rangle \right|}^2}$, and circulation, Γ: $t^{\prime }=t\times \mathrm{\Gamma }/{\overline{r}}^2$ (both $\overline{r}$ and $L_0$ are calculated from the designed vortex geometry, determined by the hydrofoil shape). Technical details for all systems are described in SI Text, Experimental Vortex Generation and follow established methods (19, 27–29). Note that, for our experimental vortices, we can estimate the rate of twist dissipation as ${\partial }_{t}Tw/Tw\sim 5{\hspace{0.17em}\text{s}}^{-1}$, whereas the overall vortex motion has a timescale of order 1 s (SI Text, Helicity Dissipation for a Twisted Core).

Experimental Results

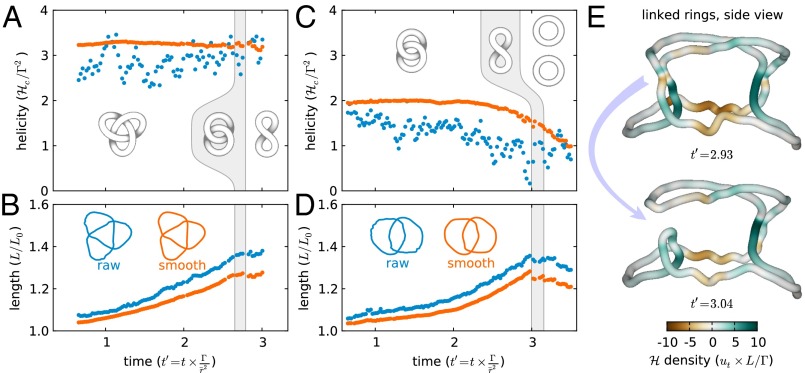
As was found in previous studies (18, 19, 27), our initially linked and knotted vortices disentangle themselves through local reconnections into topological trivial vortex rings. This change in tube topology might be expected to result in a corresponding change of the helicity, because it is a global measure of the vortex topology. For example, a reconnection event that changes a pair of linked rings into a single coiled ring (e.g., Fig. 1A) should result in a sudden, discontinuous jump of the helicity by $\left|\mathrm{\Delta }{\mathrm{\mathscr{H}}}_c\right|\sim 1\hspace{0.17em}{\mathrm{\Gamma }}^2$. Recently, more detailed analytical results have also indicated that helicity may be dissipated in a reconnection event (17). Remarkably, our experimental measurements of the total center-line helicity, ${\mathrm{\mathscr{H}}}_c$, show that it is nearly unaffected by reconnections (Fig. 2 A and C). As numerical computation of writhe is sensitive to small-scale noise in the extracted path, applying a small amount of local smoothing to the raw path data dramatically improves the measurement. We do this by convolving the raw vortex center-line traces, ${\mathit{x}}_i\left(s\right)$ (where s is the path-length coordinate), with a windowed sinc function with a spatial cutoff of $\lambda =50$ mm, which is about 5% of the total vortex length of both the links and knots. Remarkably, we find that a vortex initially shaped into a trefoil vortex knot (Fig. 2 A and B) is observed to have nearly constant center-line helicity, ${\mathrm{\mathscr{H}}}_c/{\mathrm{\Gamma }}^2=3.25\pm 0.04$, even though it is undergoing dramatic changes in geometry and topology. Similarly, the initially linked pair of rings (Fig. 2 C and D) also shows no jump in the helicity through reconnection events, even though on longer timescales the center-line helicity is seen to change from ${\mathrm{\mathscr{H}}}_c\sim 2{\mathrm{\Gamma }}^2$ to $\sim 1{\mathrm{\Gamma }}^2$, apparently via geometric deformations. Taken together, we conclude that any jump in helicity is less than $\mathrm{\Delta }{\mathrm{\mathscr{H}}}_c\lesssim 0.05{\mathrm{\Gamma }}^2$ per reconnection for our vortices.

Fig. 2.

(A and B) The computed center-line helicity (${\mathrm{\mathscr{H}}}_c$) and length for of an experimental trefoil knot vortex through the first two reconnection events (out of three total). The teal data indicate the raw experimental traces, whereas the orange data have been smoothed with a windowed sinc function whose spatial cutoff is $\lambda =50$ mm (the total vortex length is ∼1 m). The gray Inset diagrams indicate the topologies at different stages of the vortex evolution. (C and D) The center-line helicity and length for a linked pair of vortex rings in experiment, through two reconnections. (E) Two traces of a pair of initially linked vortices in experiment, just before and after a reconnection event. The traces are colored according to the computed local helicity density, $h=\mathrm{\Gamma }{u}_t$, calculated using the Biot–Savart law.

The apparent absence of a helicity jump indicates that the vortices are spontaneously arranging themselves into a geometry that allows center-line helicity to be conserved through reconnections. This proceeds via a simple geometric mechanism: at the moment of topology-changing reconnection, the reassociation of vortex lines creates writhing coils in regions that were previously free of writhe, thus converting center-line helicity from linking to writhe (or vice versa) each time a reconnection takes place. The remarkable efficiency of the helicity transfer results from the precise way in which the curves approach each other. The vortex sections where the reconnection is taking place are almost perfectly antiparallel just before the reconnection event (Fig. 1C). This means that the reassociation of vortex tubes that occurs during the reconnection will not change the crossing number in any projection of the vortex tube center-line. Because the writhe can be computed as the average crossing number over all orientations, this implies the total linking and writhing, ${\displaystyle \sum Lk}+{\displaystyle \sum Wr}$, should be conserved, and hence the center-line helicity as well. (See SI Text, Theory of Helicity Conservation Through a Reconnection, and Fig. S3 for a description of this mechanism purely in terms of planar link diagrams.) Alternatively, one can consider the helicity density in the reconnecting region, obtained by computing the tangential flow, $h=\mathrm{\Gamma }{u}_t$ (Fig. 2E). If the annihilated sections are close and antiparallel, the sum of this helicity density should approach zero, conserving helicity (1). Interestingly, this antiparallel configuration is expected to form naturally if the vortex tubes are stretching themselves while conserving energy, which seems to happen spontaneously for vortices whose tube topology is nontrivial (19).

Conversion of Linking and Knotting to Coiling on Different Scales.

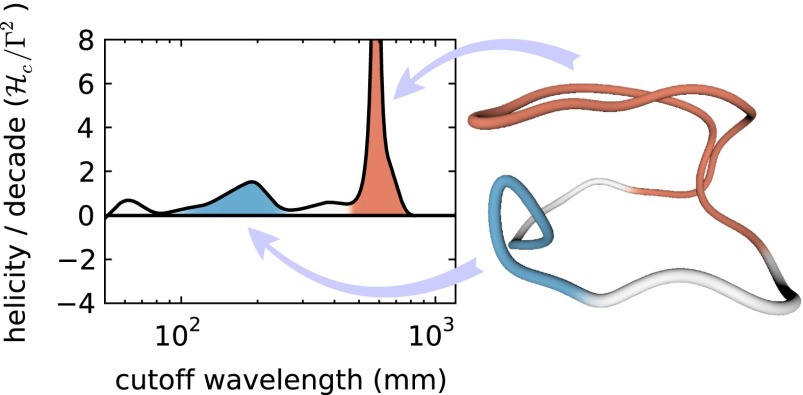
The simple geometric mechanism we find for the conservation of center-line helicity through reconnections implies a transfer of helicity across scales that should be quantifiable. Although volumetric Fourier components have been used as measures of helicity content on different scales for flows with distributed vorticity (30), for thin core vortices the distance along the vortex provides a natural length scale. To quantify the storage of helicity as a function of scale along the vortex filament, we compute the helicity as a function of smoothing, ${\mathrm{\mathscr{H}}}_c\left(\lambda \right)$, where λ is a hard spatial cutoff scale introduced by convolving the vortex path with a sinc kernel of variable width (this is the same procedure used to smooth the raw data, described above, but with varying cutoff). When this smoothing is applied, helix-like distortions of the path with period less than λ will be removed, and so the contribution of those helical coils to the overall helicity is also removed. The derivative of this function, ${\partial {\mathrm{\mathscr{H}}}_c|}_{\lambda }$, then quantifies the helicity content stored at spatial scale λ (Fig. 3 and Movies S1 and S2).

Fig. 3.

The coiling component of a helistogram for an experimental pair of linked rings just after the first reconnection ($t^{\prime }=3.25$), with a colored image of the experimental data trace used to compute the helistogram. The peaks in the helistogram correspond to coils at two different length scales, which are color coded. In each case, the length of the segment colored is equal to the cutoff wavelength for that peak. Each coil contains approximately one unit of helicity.

Ultimately, there is a component of the helicity that is not removed by even long-scale smoothing; for the relatively simple topologies studied here, the resulting writhe is nearly integer. This integer component arises because as it is smoothed, the path becomes nearly planar and the integer contribution corresponds to the crossing number in this effective planar projection. We refer to this as an effective integer knotting number, akin to linking, and the component removed by smoothing as “coiling,” which is produced by helical distortions.

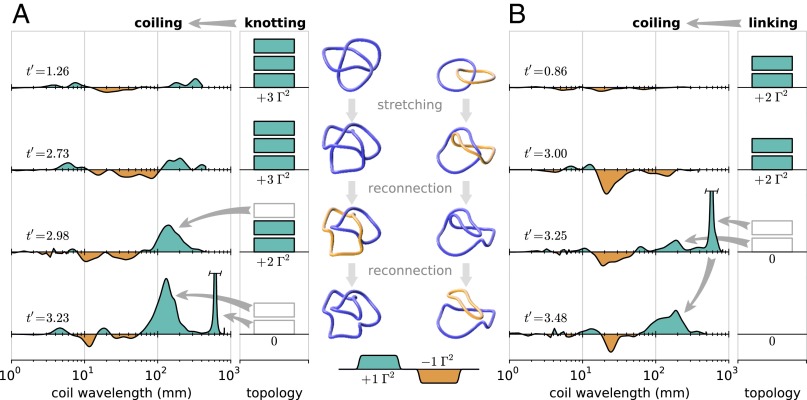
Fig. 4 shows the helistogram for our trefoil knots and linked rings before, during, and after the reconnection process (see also Movie S3). In both cases, we observe that the initial deformation accompanying the stretching produces small helical deformations across a range of scales; in the case of the trefoil knot, these are nearly perfectly balanced, whereas the linked rings create a strong helix at a scale of 20–30 mm with a helicity opposed to the overall linking. During the reconnections, we see an immediate transfer from knotting or linking to coiling. In the case of the linked rings, the first reconnection creates an unlinked geometry immediately (Fig. 4B; $t^{\prime }=3.25$), but in doing so creates a large-scale folded coil with a spatial scale of ∼600 mm, which then quickly reconnects to form coils at 100–200 mm (Fig. 3). The trefoil knot (Fig. 4A and Movie S4) has similar dynamics; although it is still topologically nontrivial after the first reconnection (Fig. 4A; $t^{\prime }=2.98$), it becomes a pair of linked rings that unlinks in a similar manner to the initially linked rings.

Fig. 4.

(A and B) Helistograms for A, a trefoil knot B, linked rings in a viscous fluid experiment (the dataset is the same as shown in Fig. 2 A–D; the total vortex length is $\sim 1$ m for both). The left portion of each series of plots shows the helicity contribution due to coiling on different spatial scales, obtained by computing ${\partial }_n{\mathrm{\mathscr{H}}}_c(\lambda ={10}^n)$, where λ is the cutoff wavelength for a windowed sinc smoothing. The right portion of each plot shows the irreducible contribution to the helicity originating from the global vortex topology. Both the coiling and topological contributions are scaled so that the total helicity is proportional to the filled area of the plots. The center column shows images of the numerically traced vortices smoothed to $\lambda =100$ mm.

In both cases, we find that helicity stored on long spatial scales, whether they be knots or links, appears to be intrinsically unstable, cascading through reconnections to smaller spatial scales. Moreover, this process coincides with the overall stretching that occurs when the topology is nontrivial; after the reconnections take place, the length of the vortices appears to stabilize.

Related mechanisms for helicity conservation through reconnections have been suggested in simple models of dissipative plasmas, for example by converting linking to internal twist (22, 31, 32).

Helicity Conservation in Simulated Superfluids.

The mechanism we observe for helicity conservation through reconnections is entirely geometric, suggesting it may be present in other fluid-like systems as well. To test this possibility, we simulate the evolution of vortex knots in a superfluid with the Gross–Pitaevskii equation (GPE) (20). Although superfluids are inviscid, they are not ideal Euler fluids; thus, vortex reconnections are possible and vortex topology is not conserved. Unlike a classical fluid, which has finite vortex cores, superfluid vortices are confined to a line-like phase defect (33, 34); here, we track the center-line helicity (Eq. 4) computed for the phase defect path.

Recently, methods have been demonstrated for creating vortex knots in superfluid simulations (27). We have extended this technique to create initial states with phase defects of arbitrary geometry using velocity integration for flow fields generated by the Biot–Savart law (see SI Text, Gross-Pitaevskii Equation for details), allowing us to generate vortices with the same initial shape as our experiments. We simulate the subsequent vortex evolution using standard split-step methods, and extract the vortex shape by tracing the phase defects in the resulting wave function. We model vortices with initial radii of $\overline{r}=6$–$48\xi$, where ξ is the healing length that sets the size of a density-depleted region that surrounds the vortex line. (Our simulations use a uniform grid size of $0.5\xi$ and range in resolution from ${64}^3$ to ${512}^3$.)

As has been previously observed, we find that vortex knots are intrinsically unstable in superfluids, undergoing a topological and geometrical evolution qualitatively similar to our experimental data (Fig. 5; see Fig. S4 and Movie S5 for a corresponding helistogram). In particular, we find that the reconnections are heralded by an overall stretching of the vortex, which abruptly stops after the reconnections take place. Unlike the experimental data, we also observe a discrete jump in the center-line helicity across the reconnection, ranging from $\mathrm{\Delta }{\mathrm{\mathscr{H}}}_c\sim 0.1-1{\mathrm{\Gamma }}^2$ per reconnection, which is a strong function of the initial vortex size (note that, in the simulations, all three reconnections happen simultaneously). If we compute the helicity jump just across the reconnection event, defined as the time during which the colliding vortices are less than 2ξ apart (i.e., when the density depleted regions have already merged), we find a clear $\mathrm{\Delta }{\mathrm{\mathscr{H}}}_c\sim {\overline{r}}^{-1.0}$ trend. We observe slightly different results when considering the overall drop in helicity across the entire simulation, from $t^{\prime }= 0-4$, consistent with $\mathrm{\Delta }{\mathrm{\mathscr{H}}}_c\sim {\overline{r}}^{-0.7}$ trend, which may be a combination of prereconnection deformation effects and the reconnection jump. In particular, the prereconnection helicity data seems to converge for $\overline{r}\gtrsim 18\xi$, suggesting the finite-core size is not important in this regime before the reconnection.

Fig. 5.

(A) Renderings of density isosurfaces ($\rho =0.5{\rho }_0$) for a trefoil vortex knot ($\overline{r}=12\xi$), simulated with the GPE. The initially knotted configuration changes to a pair of unlinked rings whose writhe conserves most of the original helicity. (B) Renderings of different sized trefoil knots, where the tube radius is given by the healing length, ξ, which acts as an effective core size for the superfluid vortex. (C and D) The computed center-line helicity (${\mathrm{\mathscr{H}}}_c$) and length for of a range of GPE-simulated trefoil knots. The data are only shown when the distance between vortex lines is $r_{min}>2\xi$. (E) The helicity jump per reconnection event as a function of size ratio for GPE-simulated trefoil knots. The open squares are the total drop between $t^{\prime }=0$ and $t^{\prime }=4$, whereas the circles indicate the drop during the reconnection event, defined as the missing region in C where the vortex tubes overlap. Larger knots, relative to ξ, are found to conserve helicity better by either measure.

We attribute the loss of center-line helicity to the fact that the finite size of the depleted density core in the GPE simulations leads the reconnections to begin before the vortices are perfectly antiparallel, resulting in less efficient conservation. It is unclear whether the same effect is present in the experiments, due to the difficulties associated with accurately tracking significantly smaller vortices; however, we note that the expected core-to-vortex size ratio for our experiments is close to that of the largest GPE simulations and we do not observe such a jump. Previous studies of the simulated dynamics of reconnections in superfluids and classical fluids suggest that there may be differences in the details of the reconnection behavior (35–37). Nonetheless, we observe that the same conversion of linking and knotting to coiling is present in our superfluid model, indicating that the geometric mechanism for helicity transport across scales that we find in experiment is generic.

Writhe to Twist Conversion.

Although helicity change is usually understood as being associated with topological changes, we also observe a gradual change in center-line helicity even when reconnections are not taking place, for example in the experimental linked rings (Fig. 2C) or the GPE simulations before a reconnection (Fig. 5C). Because the center-line topology is not changing, this helicity change must be attributable to a geometric effect: coiling must have been dissipated or converted to internal twist, which we do not resolve (or is not present, in the case of the GPE).

A dramatic example of this effect can be seen in “leap-frogging” vortices, where a pair of same-sized vortices placed front to back repeatedly passes through one another. Although this configuration has no center-line helicity if both vortices are perfect rings, a helical winding can be added to one of the rings to give the structure nonzero writhe and hence nonzero center-line helicity. We model the time evolution of this structure as a thin-core vortex using a simple inviscid Biot–Savart model (see SI Text, Biot-Savart Evolution of Thin Core Vortices for details), and find that the helicity varies widely as the vortices repeatedly pass through one another (Fig. 6 E and F and Movie S6).

Fig. 6.

(A) Illustrations of mechanisms for storing helicity on different spatial scales; in each case, the helicity of the depicted region is the same, ${\mathrm{\mathscr{H}}}_c=2{\mathrm{\Gamma }}^2$. Although linking is global in nature, both coiling and twisting are local—they produce linking between different subsections of the vortex tube, or in this case different edges of the illustrated ribbon. (B and C) Diagrams of reconnection events in locally antiparallel or parallel orientations. The antiparallel reconnection does not change helicity because it does not introduce a new “crossing” of the projected tubes, unlike the parallel reconnection. This antiparallel configuration tends to form spontaneously for topologically nontrivial vortices, even in the absence of viscosity, in which case helicity is efficiently converted from global linking to local coiling. (D) Coiling can be converted to twisting by stretching helical regions of the vortex; this mechanism conserves total helicity because it does not change the topology, but results in an apparent change of helicity when twist cannot be resolved. (E and F) The helicity (E) and length (F) as a function of time for a simulated geometrical evolution of a circular vortex ring (yellow) leap-frogging a vortex ring with a helix superimposed (blue).

This variation of the helicity is caused by the fact that the vortices are stretching and compressing each other as a function of time: whenever one vortex passes through another, it must be shrunk to fit inside, resulting in a change of the helix pitch. A simple model of this change can be constructed by first noting that the writhe of a straight helical section is as follows: $W{r}_{\text{helix}}=N\left(1-\cos \theta \right)$, where N is the number of turns and θ is the pitch angle. In the limit of a small pitch angle: $W{r}_{\text{helix}}\approx \frac{2{\pi }^2{a}^2}{L^2}{N}^3$, where a and L are the radius and length of the cylinder around which the helix is wound (Fig. 6D and SI Text, Definition of Center-Line Helicity). If the flow is a uniform, volume-conserving strain, the number of turns is conserved and $a\propto L^{-1/2}$, resulting in ${\mathrm{\mathscr{H}}}_c/{\mathrm{\Gamma }}^2=Wr\propto L^{-3}$. This simplistic model qualitatively captures the center-line helicity of the leap-frogging helix of Fig. 6E, indicating that the center-line helicity changes primarily because the helical ring is being stretched and compressed. In general, we expect geometric deformations of the vortex—including stretching—should result in continuous changes of the center-line helicity.

Does this imply helicity is not conserved even when the topology is constant? As discussed in the introduction, helicity can also be stored in twist of the vortex bundle, which is neglected in the center-line helicity. As a method for keeping track of the vortex bundle orientation, consider it is a ribbon. If we imagine wrapping this ribbon around a cylinder N times, we expect the linking between the edges of the ribbon to remain constant even if the cylinder changes shape (Fig. 6D). In this case, the total helicity is constant: $\mathrm{\mathscr{H}}/{\mathrm{\Gamma }}^2=N=W{r}_{\text{helix}}+Tw$ [this is a restatement of the Călugăreanu–White–Fuller theorem (7, 38)]. As the writhe contribution varies dramatically as the vortex is stretched, we conclude that twist must be created in the vortex core to compensate.

We expect similar conversion of writhe to twist is happening for stretching knots and links, although the nonuniform stretching present there produces a rich structure across scales, as seen in our helistograms (Fig. 4). For experimental vortices, the compensating twist should be present, but we are not able to directly resolve it; doing so is a challenging goal for future investigations. As previously noted, however, this twist should be dissipated relatively rapidly by viscosity if the core is small compared with the overall vortex dimensions. In the case of GPE-simulated vortices, the helicity smoothly varies before the reconnections—when rapid stretching is present—and because there is no method for storing twist it is simply lost. However, after the reconnections, the length and helicity stabilize, despite the fact that the vortices have large oscillating coils. (The smallest vortices show a slow decay of helicity after reconnection because short wavelength coils, $\lambda \sim \xi$, are radiated away as sound waves in the GPE.)

Geometric and Topological Mechanisms for Helicity Conservation.

Our results show that helicity can be conserved in real fluids even when vortex topology is not, and that helicity may not be conserved even when tube topology is invariant. Vortex reconnections do not simply dissipate helicity, but rather mediate a flow from knotting and linking to coiling, typically from large scales to smaller scales (Fig. 6). The efficient conversion of helicity through a reconnection is due to the antiparallel vortex configuration (Fig. 6B) that forms naturally in our reconnecting vortices. Deformation of vortices may also convert coiling into twist on even smaller scales, where it may ultimately be dissipated. Interestingly, stretching plays a critical role in both topological and nontopological mechanisms for helicity transport, and is also observed to happen spontaneously for initial linked or knotted vortices. The mechanisms for helicity transport, from linking to coiling to twisting, all have a natural interpretation in terms of the field-line geometry, and as such these mechanisms may play an important role in any tangled physical field. Taken as a whole, our results suggest that helicity may yet be a fundamental conserved quantity, guiding the behavior of dissipative complex flows, from braided plasmas to turbulent fluids.

Note Added in Proof.

In the concluding stages of this work we became aware of a parallel effort by Laing et al. (39), who independently identified the mechanism for conservation of link and writhe through reconnections and constructed a rigorous proof of the conservation of writhe of curves under the assumption of antiparallel reconnecting segments.