Double-stranded RNA under force and torque: Similarities to and striking differences from double-stranded DNA

Significance

RNA, like DNA, can form double helices held together by the pairing of complementary bases, and such helices are ubiquitous in functional RNAs. Here we apply external forces and torques to individual double-stranded RNA molecules to determine the mechanical properties and conformational transitions of these fundamental biological building blocks. For small forces and torques, RNA helices behave like elastic rods, and we have determined their bending, stretching, and twisting stiffness. Surprisingly, we find that RNA shortens when it is overwound, whereas DNA lengthens. Finally, we twist RNA until it buckles and forms a loop, and find the timescale of this transition to be much slower for RNA compared with DNA, suggesting unexpected differences in their flexibilities on short length scales.

Abstract

RNA plays myriad roles in the transmission and regulation of genetic information that are fundamentally constrained by its mechanical properties, including the elasticity and conformational transitions of the double-stranded (dsRNA) form. Although double-stranded DNA (dsDNA) mechanics have been dissected with exquisite precision, much less is known about dsRNA. Here we present a comprehensive characterization of dsRNA under external forces and torques using magnetic tweezers. We find that dsRNA has a force–torque phase diagram similar to that of dsDNA, including plectoneme formation, melting of the double helix induced by torque, a highly overwound state termed “P-RNA,” and a highly underwound, left-handed state denoted “L-RNA.” Beyond these similarities, our experiments reveal two unexpected behaviors of dsRNA: Unlike dsDNA, dsRNA shortens upon overwinding, and its characteristic transition rate at the plectonemic buckling transition is two orders of magnitude slower than for dsDNA. Our results challenge current models of nucleic acid mechanics, provide a baseline for modeling RNAs in biological contexts, and pave the way for new classes of magnetic tweezers experiments to dissect the role of twist and torque for RNA–protein interactions at the single-molecule level.

RNAs are central to many biological processes. In addition to well-characterized roles as messenger, transfer, ribosomal, viral, and spliceosomal RNA, RNA molecules have more recently discovered functions including enzymatic activity, gene silencing, and sensing of metabolites. In many of these contexts, structures rich in double-stranded RNA (dsRNA) helices encounter mechanical strains; examples include the packaging of dsRNA viral genomes into capsids, deformations of the ribosome during translation (1, 2), and more generally conformational changes of functional RNAs while folding or due to interactions with proteins (3, 4). In addition, RNA is emerging as a material for engineered nanostructures both in vitro (5) and in vivo (6). A quantitative understanding of these processes requires accurate knowledge of the elastic properties and conformational transitions of RNA under forces and torques.

For double-stranded DNA (dsDNA), the mechanical properties and structural transitions under forces and torques have been mapped out rigorously (7–10). Its elastic responses to bending, stretching, and twisting deformations of the standard B-form helix (Fig. 1 A and B), characterized by the bending persistence length A, the stretch stiffness S, the torsional persistence length C, and the twist–stretch coupling D, have been accurately determined using single-molecule manipulation techniques (SI Appendix, Table S1 and Materials and Methods). In addition, single-molecule techniques have provided a comprehensive view of the force–torque phase diagram of dsDNA (7, 9, 11). Knowledge of the elastic constants and conformational transitions of dsDNA has had a tremendous impact and set the stage for implementing, modeling, and interpreting numerous experiments involving DNA (7, 8, 10), its interactions with proteins (12, 13) and other binding partners, its behavior in confined environments, and its assembly into engineered nanostructures (14).

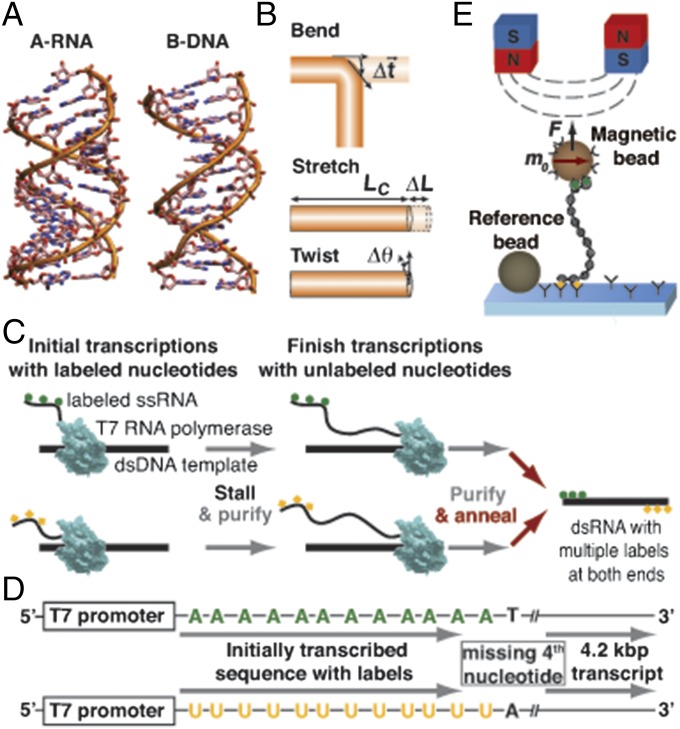
Fig. 1.

Construction of a torsionally constrained double-stranded RNA for magnetic tweezers measurements. (A) Comparison of A-form dsRNA [Protein Data Bank (PDB) ID code 1RNA (57)] and B-form dsDNA [PDB ID code 2BNA (58)]. (B) Cartoon of the elastic deformations of dsRNA: bending, stretching, and twisting. (C) Schematic of the protocol to generate double-stranded RNA molecules with multiple attachment points at both ends. Initial transcription reactions incorporate multiple biotinylated adenosine (green circles) or digoxigenated uracil (yellow squares) bases and stall at a fourth nucleotide. After purification, transcription reactions are restarted and complete the 4.2-kbp transcripts. In the final step, the purified RNA strands are annealed to yield dsRNA with chemical modifications at each end. (D) Schematic of the two DNA templates used to generate dsRNA with multiple labels at both ends. (E) Cartoon of a magnetic tweezers experiment on dsRNA (not to scale). A streptavidin-coated magnetic bead is tethered to an anti-digoxigenin–coated surface by a dsRNA molecule with multiple attachment points at both ends. A surface-attached reference bead is tracked simultaneously for drift correction. Permanent magnets above the flow cell are used to exert a stretching force F and to control the rotation of the magnetic bead via its preferred axis m₀. N, north pole; S, south pole.

In contrast, much less is known about dsRNA, despite its overall structural similarity. Like DNA, RNA can form right-handed double helices. In contrast to DNA, RNA forms an A-form helix with a radius of ∼1.2 nm and a length increase per base pair of ∼2.8 Å, ∼20% wider and shorter than B-form dsDNA (Fig. 1A). Although recent single-molecule stretching experiments using torsionally unconstrained dsRNA have revealed its bending persistence length (15, 16), stretch modulus (16), and an overstretching transition (16, 17), its response to torsional strains and structural transitions under forces and torques is unknown. This dearth of information on dsRNA is partially due to the relative difficulty, compared with dsDNA, of assembling RNA constructs suitable for single-molecule force and torque measurements. Here we use single-molecule magnetic tweezers (MTs) measurements on fully torsionally constrained dsRNA molecules to provide a comprehensive view of dsRNA mechanics that includes its complete elastic response, its force–torque phase diagram, and its dynamics of loop formation.

Results

Torsionally Constrained dsRNA Constructs for Magnetic Tweezers.

We constructed fully double-stranded RNA constructs with multiple attachment points at both ends suitable for MTs torque measurements by annealing two complementary single strands that carry multiple biotin or digoxigenin labels at their respective 5′ ends (Fig. 1 C and D and Materials and Methods). The functionalized single-stranded constructs were generated by carrying out initial in vitro transcription reactions that incorporated labeled nucleotides and stalled at a missing fourth nucleotide (Fig. 1 C and D). After purification, transcription reactions were restarted and completed in the presence of all four unlabeled nucleotides. The final annealed 4.2-kbp dsRNA constructs can be tethered between an anti-digoxigenin–coated flow cell surface and streptavidin-coated magnetic beads for manipulation in the MTs (Fig. 1E).

Force–Extension Response of dsRNA.

Using the ability of MTs to exert precisely calibrated stretching forces (18, 19) (Materials and Methods and SI Appendix, Fig. S1), we first probed the force–extension response of dsRNA. The stretching behavior of torsionally relaxed dsRNA at low forces (F < 5 pN) is well-described by the (inextensible) worm-like chain (WLC) model (20, 21) (SI Appendix, Fig. S2A). From fits of the WLC model, we determined the contour length L_C = 1.15 ± 0.02 µm and the bending persistence length A_RNA = 57 ± 2 nm in the presence of 100 mM monovalent salt (SI Appendix, Fig. S2A), in good agreement with the expected length (1.16 µm, assuming 0.28 nm per bp) (22, 23) and previous single-molecule stretching experiments (15, 16). A_RNA decreases with increasing ionic strength (16) (SI Appendix, Fig. S1), in a manner well-described by models that partition it into an electrostatic and a salt-independent component (SI Appendix, Fig. S1K). Taking into account the salt dependence, A_RNA is consistently ∼20% larger than A_DNA at the same ionic strength (SI Appendix, Fig. S1).

Stretching dsRNA at forces >10 pN, we observed elastic stretching that can be fit by the extensible WLC model (21, 24) up to ∼40 pN (SI Appendix, Fig. S2B) and an overstretching transition for torsionally unconstrained molecules (SI Appendix, Fig. S2C), in agreement with previous single-molecule studies (16, 17). From fits of the extensible WLC model, we found S_RNA = 350 ± 100 pN, about threefold lower than S_DNA (SI Appendix, Fig. S1G and Table S1). Our value for the S_RNA is in reasonable agreement with, although slightly lower than, the value of S_RNA ∼500 pN determined in single-molecule optical tweezers measurements (25), possibly due to subtle differences between magnetic and optical tweezers experiments. For torsionally unconstrained molecules, the overstretching transition is marked by a rapid increase in extension to 1.8 ± 0.1 times the crystallographic length over a narrow force range at F = 54 ± 5 pN (SI Appendix, Fig. S2C). In contrast, using our torsionally constrained dsRNA, we observed enthalpic stretching beyond the contour length but no sharp overstretching transition up to F = 75 pN (SI Appendix, Fig. S2D). The increased resistance to overstretching for torsionally constrained dsRNA compared with torsionally unconstrained dsRNA is qualitatively similar to the behavior of dsDNA (26–28) (SI Appendix, Fig. S1 H and I). The dependence of the overstretching transition for dsRNA on torsional constraint and on salt (SI Appendix, Fig. S2 C and D) suggests that it might involve melting as well as a transition to a previously unidentified conformation that we name “S-RNA,” in analogy to S-DNA (SI Appendix, Fig. S1).

Twist Response of dsRNA.

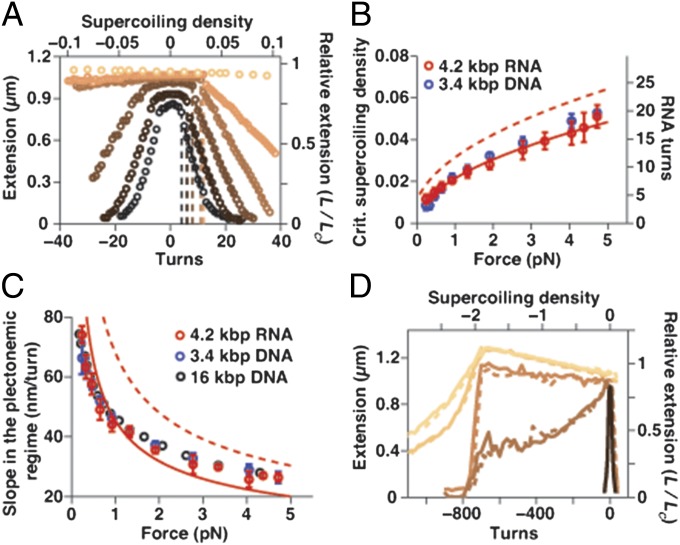
We used the ability of MTs to control the rotation of the magnetic beads (18) to map out the response of dsRNA upon over- and underwinding at constant stretching forces. Starting with a torsionally relaxed molecule (corresponding to zero turns in Fig. 2), the tether extension remains initially approximately constant upon overwinding (corresponding to increasing linking number) until the molecule reaches a buckling point (Fig. 2A, dashed lines and SI Appendix, Fig. S3). Further overwinding beyond the buckling point leads to a rapid linear decrease of the tether extension with an increasing number of turns, due to the formation of plectonemes. The critical supercoiling density σ_buck for buckling increases with stretching force and agrees within experimental error with the values found for DNA and with a mechanical model originally developed for supercoiled DNA (9) (Fig. 2B and SI Appendix, Materials and Methods). The decrease in extension per added turn in the plectonemic regime provides a measure for the size of the plectonemes and decreases with increasing stretching force (Fig. 2C). The extension vs. turns slopes for dsRNA are within experimental error of those for dsDNA, and are in approximate agreement with the mechanical model for supercoiling (Fig. 2C). Underwinding the dsRNA tether at stretching forces F < 1 pN gives rise to a buckling response similar to what is observed upon overwinding and the formation of negatively supercoiled plectonemes. In contrast, for F > 1 pN, the over- and underwinding response is asymmetric and the tether extension remains approximately constant upon underwinding (Fig. 2A), likely due to melting of the double helix, as has been observed for DNA (29) (SI Appendix, Fig. S3 K and L).

Fig. 2.

Response of dsRNA to changes in linking number at various stretching forces. (A) Rotation–extension curves for dsRNA at different stretching forces (0.25, 0.5, 1, 2, 4, and 5.5 pN, from dark to light). The top axis shows the supercoiling density, σ = ΔLk/Lk₀ (SI Appendix, Materials and Methods). Dashed lines denote the buckling points at positive turns, and solid lines denote linear fits to the extension in the plectonemic region. (B) Critical supercoiling density for buckling as a function of applied force for dsRNA and dsDNA. A simple mechanical model for supercoiling (8) predicts the right trend (dashed line), whereas a refined model (9) provides a good fit to the dsRNA data with the torsional stiffness of the plectonemic state (P) set to 23 ± 3 nm (solid line). (C) Slope of the rotation–extension curves in the plectonemic regime at σ > 0 for dsRNA and dsDNA. The 16-kbp dsDNA data are from ref 59. The simple mechanical mode again predicts the right trend (dashed line), whereas the refined model provides an approximate fit to the dsRNA data with P = 20 ± 3 nm (solid line). Data points in B and C are means and SEM of at least five independent measurements. (D) Rotation–extension curves for dsRNA out to large negative σ at F = 0.5, 2, 3, 6, and 7.5 pN (dark to light). Solid lines indicate unwinding; dashed lines indicate subsequent rewinding. All data presented were obtained in the presence of 100 mM NaCl.

If unwinding at F > 1 pN is continued for several hundred turns, we eventually observe another structural transition marked by an abrupt change in the extension vs. turns response at a supercoiling density of σ ∼ –1.9 (Fig. 2D). We term this previously unidentified highly underwound and left-handed RNA conformation with a helicity of –12.6 bp per turn “L-RNA,” in analogy to what has been observed for highly underwound DNA (11) (SI Appendix, Fig. S3L). We note that the helicity and elongation that we observe for L-RNA under torsional constraint are similar to what has been proposed for the NMR solution structure of a short (6-bp) GC-rich dsRNA fragment in 6 M monovalent salt (30). However, further investigation is necessary to elucidate structural details of torsionally strained left-handed dsRNA.

Finally, for F > 5 pN, dsRNA ceases to undergo a buckling transition even upon overwinding (Fig. 2A, top curve). We propose that dsRNA undergoes a transition to a highly overwound conformation termed “P-RNA” under these conditions, in analogy to experimentally observed P-DNA (31) and in line with modeling predictions based on molecular dynamics simulations of dsRNA (32).

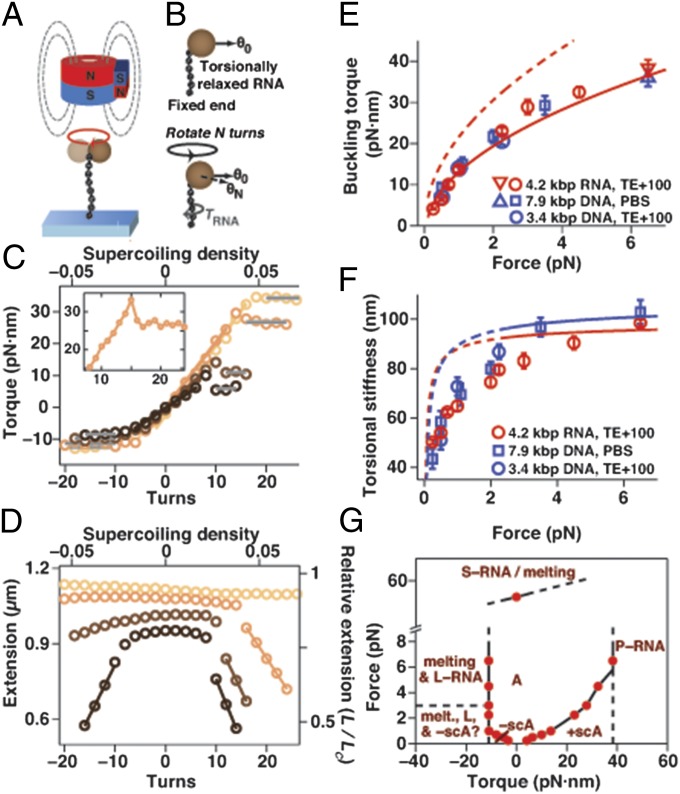
To further quantify the torsional response of dsRNA, we carried out magnetic torque tweezers (33–35) measurements that directly monitor the torque response of the nucleic acid tether upon over- and underwinding by tracking the rotation angle about the tether axis and using a modified magnet geometry compared to conventional magnetic tweezers (Fig. 3 A and B and SI Appendix, Fig. S4). Starting from a torsionally relaxed molecule (corresponding to zero turns), we initially observe a linear response of the torque to over- and underwinding (Fig. 3C). Upon overwinding beyond the linear response regime, the torque saturates when the molecule undergoes the buckling transition (for F < 5 pN; marked by a concomitant rapid decrease in the tether extension; Fig. 3D) or the A-to-P–form transition (for F > 5 pN; at a critical torque Γ_A-to-P = 38.3 ± 2 pN·nm). We determined the values of the postbuckling torque Γ_buck as a function of stretching force from the torque plateaus in the plectonemic regime (Fig. 3E). Similar to σ_buck, Γ_buck for dsRNA agrees within experimental error with the values determined for dsDNA and with a simple mechanical model (Fig. 3E). Immediately before the torque assumes the plateau value Γ_buck, we observe a torque “overshoot,” qualitatively similar to what has been recently reported for dsDNA (35, 36) (Fig. 3C, Inset). Upon underwinding, the torque saturates when the molecule buckles and forms negative plectonemes (for F < 1 pN; again marked by a rapid decrease in tether extension) or melts (for F > 1 pN; at a melting torque of −11 ± 1 pN·nm, independent of stretching force).

Fig. 3.

Torque response of dsRNA at various stretching forces. (A) Schematic of a magnetic torque tweezers (MTTs) measurement on dsRNA. The MTTs are a variant of MTs that enables the measurement of torque. (B) Principle of torque measurements in MTTs. After overwinding (or underwinding) the dsRNA tether by N turns, the dsRNA exerts a restoring torque on the bead that leads to a shift in the equilibrium angular position from θ₀ to θ_N. This shift can be directly converted to torque (SI Appendix, Fig. S4). (C) Rotation–torque curves for 4.2-kbp dsRNA at F = 0.5, 1, 3, and 6.5 pN (dark to light). Gray lines correspond to fits to the torque plateaus to determine buckling and melting torques. Colored lines are linear fits to determine the torsional stiffness. (Inset) Additional data for F = 3 pN. (D) Rotation–extension curves corresponding to the measurements in C. Solid lines indicate linear fits in the plectonemic regime. (E) Buckling torques as a function of applied stretching force for dsRNA and dsDNA, determined from the plateaus in the rotation–torque data at positive turns. The data points at 6.5 pN (triangles) correspond to the critical torques for P-RNA and P-DNA formation. The prediction of a simple mechanical model for supercoiling (8) captures the right trend (dashed line), whereas a refined model (9) provides a good fit to the dsRNA data with the torsional stiffness of the plectonemic state set to P = 21.6 ± 2 nm (solid line). (F) Effective twist persistence length C for dsRNA and dsDNA as a function of F determined from linear fits of the torque vs. applied turns data in the elastic twist regime. The lines are fits of the Moroz–Nelson model (37), with the high force data (F > 2.5 pN; solid lines) yielding limiting values of C_RNA = 100 ± 2 nm and C_DNA = 109 ± 4 nm. Data points for dsRNA in E and F are means and SEM of at least five independent measurements; data for 7.9-kbp DNA are from ref. 34. (G) Phase diagram for dsRNA as a function of applied force and torque. Red points connected by solid lines correspond to transitions directly measured in this work. Dashed lines correspond to putative transition regions that have not been directly observed. A, A-form dsRNA; −scA and +scA, negatively and positively supercoiled A-form dsRNA, respectively. L-RNA, P-RNA, and S-RNA denote the alternative dsRNA conformations discussed in the main text.

We determined the effective twist persistence length C_RNA from the slopes in the linear torque–response regime, where the torque after N turns is 2π·N·k_BT·C_RNA/L_C (where k_B is Boltzmann’s constant and T is the absolute temperature; Fig. 3C, solid colored lines). C_RNA increases with increasing force and is 99 ± 5 nm at F = 6.5 pN. Compared with dsDNA, C_RNA is similar to but slightly lower than C_DNA, and both quantities exhibit similar force dependence, in qualitative agreement with a model valid in the high force limit (37) (Fig. 3F and SI Appendix, Materials and Methods). Combining the results from stretching and torque measurements at different forces, we delineate the phase diagram for dsRNA as a function of applied force and torque (Fig. 3G).

Twist–Stretch Coupling.

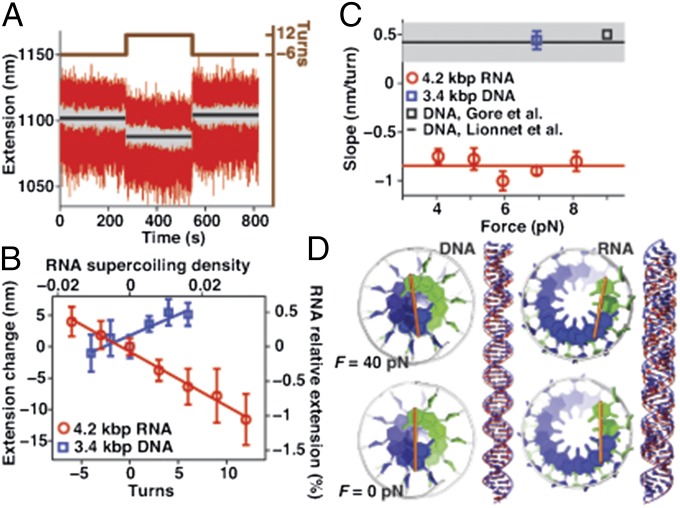
The linear elastic rod model has a fourth parameter, D, that describes the coupling between twist and stretch. We measured the twist–stretch coupling for dsRNA by monitoring changes in the extension upon over- and underwinding while holding the molecule at constant stretching forces that are large enough to suppress bending and writhe fluctuations (38, 39) (Fig. 4A). We found that for small deformations (in the range –0.02 < σ < 0.025, which excludes the melting, buckling, and A-to-P–form transitions) dsRNA shortens upon overwinding, with a slope of (d∆L/dN)_RNA = –0.85 ± 0.04 nm per turn, independent of stretching force in the range F = 4–8 pN (Fig. 4 B and C). This is in stark contrast to dsDNA, which we observed to lengthen upon overwinding by (d∆L/dN)_DNA = +0.44 ± 0.1 nm per turn (Fig. 4 B and C), in good agreement with previous measurements (38–41). Our measurements suggest that dsRNA has a positive twist–stretch coupling equal to D_RNA = –S_RNA·(d∆L/dN)_RNA/(2π·k_BT) = +11.5 ± 3.3 (assuming S_RNA = 350 pN; SI Appendix, Materials and Methods), in contrast to the negative twist–stretch coupling of dsDNA (38–41), D_DNA = –17 ± 5.

Fig. 4.

Double-stranded RNA has a positive twist–stretch coupling. (A) Time traces of the extension of a dsRNA tether held at F = 7 pN and underwound by −6 or overwound by 12 turns. Raw traces (120 Hz) are in red and filtered data (10 Hz) are in gray. The data demonstrate that dsRNA shortens when overwound. (B) Changes in tether extension upon over- and underwinding at F = 7 pN of a 4.2-kbp dsRNA and a 3.4-kbp dsDNA tether. Linear fits to the data (lines) indicate that the dsDNA lengthens by ∼0.5 nm per turn, whereas the dsRNA shortens by ∼0.8 nm per turn upon overwinding. Symbols denote the mean and standard deviation for four measurements on the same molecule. (C) Slopes upon overwinding of dsRNA and dsDNA tethers as a function of F (mean and SEM of at least four molecules in TE + 100 mM NaCl buffer). Data of Lionnet et al. (38) are shown as a black line with the uncertainty indicated in gray; data from Gore et al. (39) are shown as a black square. The red line is the average over all dsRNA data. (D) Models of oppositely twisting 50-bp segments of dsDNA (Left) and dsRNA (Right) under 0 and 40 pN stretching forces, derived from base pair-level models consistent with experimental measurements (SI Appendix, Table S6 and Materials and Methods). The orange bars represent the long axis of the terminal base pair.

Dynamics at the Buckling Transition.

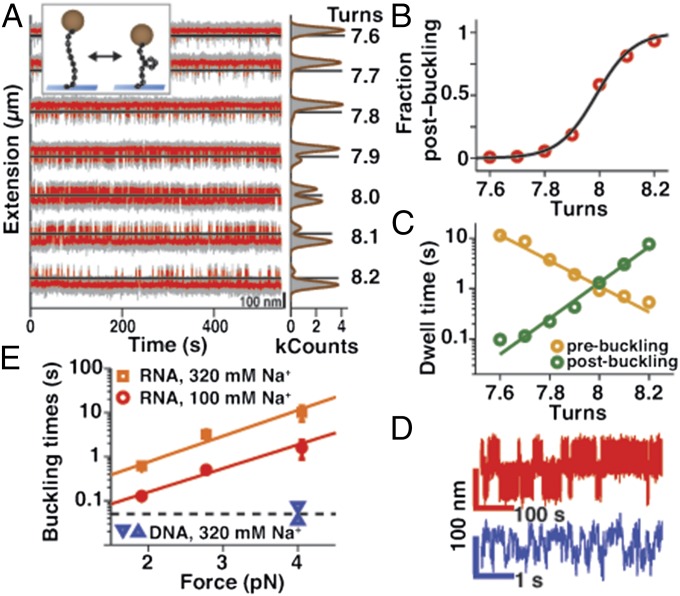
Next, we investigated the dynamics at the buckling transition. When a dsRNA was twisted close to the critical supercoiling density, we observed jumps in the extension traces, corresponding to transitions between the pre- and postbuckling states (Fig. 5A). Recording extension traces at a fixed number of applied turns, the population of the postbuckling state increases whereas the population of the prebuckling state decreases with an increasing number of applied turns (Fig. 5A). After selecting a threshold to separate the pre- and postbuckling states (SI Appendix, Fig. S5 A–D), the pre- and postbuckling populations and dwell time distributions can be quantified. The dependence of the postbuckling population on the number of applied turns is well-described by a two-state model (42) (Fig. 5B and SI Appendix, Materials and Methods) from which we determined the number of turns converted from twist to writhe during the buckling transition ΔN_b ∼4 turns (SI Appendix, Fig. S5L). The dwell times in the pre- and postbuckling state are exponentially distributed (SI Appendix, Fig. S5 E–G), and their mean residence times depend exponentially on the number of applied turns (Fig. 5C). We determined the overall characteristic buckling times τ_buck, that is, the dwell times at the point where the pre- and postbuckling states are equally populated, from fits of the exponential dependence of the mean residence times on the number of applied turns (Fig. 5C and SI Appendix, Materials and Methods). τ_buck increases with increasing salt concentration and stretching force (Fig. 5E). The force dependence of τ_buck is well-described by an exponential model (solid lines in Fig. 5E), τ_buck = τ_buck,0·exp(d·F/k_BT); from the fit we obtain the buckling time at zero force τ_buck,0 = 13 and 52 ms and the distance to the transition state along the reaction coordinate d = 5.1 and 5.5 nm for the 100 and 320 mM monovalent salt data, respectively.

Fig. 5.

Slow buckling transition for dsRNA. (A) Time traces of the extension of a 4.2-kbp dsRNA tether for varying numbers of applied turns (indicated on the far right) at the buckling transition for F = 2 pN in 320 mM NaCl. (Right) Extension histograms (in gray) fitted by double Gaussians (brown lines). Raw data were acquired at 120 Hz (gray) and data were filtered at 20 Hz (red). (Inset) Schematic of the buckling transition. (B) Fraction of the time spent in the postbuckling state vs. applied turns for the data in A and fit of a two-state model (black line; SI Appendix, Materials and Methods). (C) Mean residence times in the pre- and postbuckling state vs. applied turns for the data in A and fits of an exponential model (lines; SI Appendix, Materials and Methods). (D) Extension vs. time traces for dsRNA (red) and dsDNA (blue) both at F = 4 pN in TE buffer with 320 mM NaCl added. Note the different timescales for dsRNA and dsDNA. (E) Characteristic buckling times for 4.2-kbp dsRNA in TE buffer with 100 mM (red points) and 320 mM (orange points) NaCl added (mean and SEM of at least four independent molecules). Solid lines are fits of an exponential model. Measurements with 3.4-kbp dsDNA tethers in 320 mM NaCl at F = 4 pN yielded characteristic buckling times of ∼50 ms (horizontal dashed line); however, this value represents only an upper limit, because our time resolution for these fast transitions is biased by the acquisition frequency of the CCD camera (120 Hz). For comparison, we show data for 10.9- and 1.9-kbp DNA (upper and lower triangles, respectively) from ref. 42.

Interestingly, comparing τ_buck for dsRNA with dsDNA of similar length under otherwise identical conditions (Fig. 5 D and E), we found that the buckling dynamics of dsRNA are much slower than those of dsDNA, with the characteristic buckling times differing by at least two orders of magnitude. For example, we found τ_buck = 10.1 ± 3.7 s for dsRNA compared with ∼0.05 s for dsDNA at F = 4 pN and 320 mM salt (Fig. 5E).

Discussion

Our experiments are consistent with dsRNA behaving as a linear elastic rod for small deformations from the A-form helix, and allow us to empirically determine all four elastic constants of the model: A, S, C, and D (SI Appendix, Table S1). To go beyond the isotropic rod model, toward a microscopic interpretation of the results, we describe a “knowledge-based” base pair-level model that considers the six base-step parameters slide, shift, rise, twist, roll, and tilt (SI Appendix, Fig. S6 and Materials and Methods; a full description of modeling for a blind prediction challenge is given in ref. 43). Average values and elastic couplings of the base-step parameters for dsRNA and dsDNA from a database of nucleic acid crystal structures are used in a Monte Carlo protocol to simulate stretching and twisting experiments (SI Appendix, Materials and Methods). This base pair-level model correctly predicts the bending persistence length for dsRNA to be slightly larger than for dsDNA, S_RNA to be at least a factor of two smaller than S_DNA, and C to be of similar magnitude for dsRNA and dsDNA (SI Appendix, Table S2). The significant difference in stretch modulus S between dsRNA and dsDNA can be explained from the “spring-like” path of the RNA base pairs’ center axis, compared with dsDNA (SI Appendix, Fig. S6B). Beyond the agreement with experiment in terms of ratios of dsRNA and dsDNA properties, the absolute values of A, S, and C all fall within a factor of two of our experimental results for both molecules.

Whereas the values for A, S, and C are fairly similar for dsRNA and dsDNA, our experiments revealed an unexpected difference in the sign of the twist–stretch coupling D for dsRNA and dsDNA. The twist–stretch coupling has important biological implications, such as for how mutations affect binding sites, because a base pair deletion or insertion changes not only the length but also the twist of the target sequence, changes that need to be compensated by distortions of the nucleic acid upon protein binding (39). Nevertheless, accounting for the twist–stretch coupling D in a model of nucleic acid elasticity appears to be challenging. Previous elastic models originally developed for dsDNA (44, 45) predict a positive twist–stretch coupling for dsRNA, in agreement with our measurements for D_RNA although at odds with the results for dsDNA (SI Appendix, Materials and Methods). In contrast, elastic models that consider a stiff backbone wrapped around a softer core give negative D predictions for both dsRNA and dsDNA (39, 46). Likewise, the base pair-level Monte Carlo model yields a negative twist–stretch coupling for both dsDNA and dsRNA, disagreeing with the positive sign we observe for D_RNA (SI Appendix, Table S2), although we note that relatively modest changes to the base-step parameters can reproduce the experimentally observed value for D_RNA (Fig. 4D and SI Appendix, Materials and Methods). Interestingly, an all-atom, implicit-solvent model of dsDNA homopolymers found A-form dsDNA to unwind upon stretching whereas B-form dsDNA overwound when stretched close to its equilibrium conformation (47). Although these simulation results are in qualitative agreement with our findings for A-form dsRNA and B-form dsDNA, their simulation predicts un- and overwinding, respectively, by ∼3° per 0.1 nm, which corresponds to values of |D| ∼50, namely a factor of three to five larger in magnitude than the experimentally observed values for D_RNA and D_DNA. In summary, a complete microscopic understanding of the twist–stretch coupling for both dsRNA and dsDNA may require higher-resolution (all-atom, explicit-solvent) models and novel experimental methods.

A second surprising contrast between dsRNA and dsDNA is the much slower buckling dynamics for dsRNA. The two orders of magnitude difference in τ_buck is particularly astonishing, because the parameters that characterize the end points of the buckling transitions and the difference between them, such as σ_buck (Fig. 2B), Γ_buck (Fig. 3E), the extension jump (SI Appendix, Fig. S5I), and ΔN_b (SI Appendix, Fig. S5L), are all similar (within at most 20–30% relative difference) for dsRNA and dsDNA. Several models that describe the buckling transition in an elastic rod framework (characterized by A and C) find reasonable agreement between experimental results for dsDNA and the parameters that characterize the end points of the buckling transition (42, 48–50). In contrast, there is currently no fully quantitative model for the buckling dynamics. A recent effort to model the timescale of the buckling transition for dsDNA found submillisecond buckling times, much faster than what is experimentally observed, suggesting that the viscous drag of the micrometer-sized beads or particles used in the experiments might considerably slow down the observed buckling dynamics for dsDNA (48).

The observed difference in τ_buck suggests that the transition state and energy barrier for buckling are different for dsRNA and dsDNA. We speculate that because the transition state might involve sharp local bending of the helix (on a length scale of ∼5 nm, suggested by the fit to the force dependence; Fig. 5E), the observed difference might possibly be due to high flexibility of dsDNA on short length scales, which would lower the energetic cost of creating sharp transient bends. An anomalous flexibility of dsDNA on short length scales is hotly debated (51), and has been suggested by different experiments, including cyclization assays in bulk using ligase (52) or at the single-molecule level using FRET (53), small-angle X-ray scattering measurements on gold-labeled samples (54), and atomic force microscopy imaging of surface-immobilized DNA (55), even though the evidence remains controversial (51). If the observed difference in τ_buck between dsDNA and dsRNA is indeed due to an anomalous flexibility of dsDNA on short length scales, a clear prediction is that similar experiments for dsRNA should fail to observe a corresponding level of flexibility. In addition, this striking, unpredicted difference between dsDNA and dsRNA again exposes a critical gap in current modeling of nucleic acids.

In conclusion, we have probed the elastic responses and structural transitions of dsRNA under applied forces and torques. We find the bending and twist persistence lengths and the force–torque phase diagram of dsRNA to be similar to dsDNA and the stretch modulus of dsRNA to be threefold lower than that of dsDNA, in agreement with base pair-level model predictions. Surprisingly, however, we observed dsRNA to have a positive twist–stretch coupling, in agreement with naïve expectations but in contrast to dsDNA and to base pair-level modeling. In addition, we observe a striking difference of the buckling dynamics for dsRNA, for which the characteristic buckling transition time is two orders of magnitude slower than that of dsDNA. Our results provide a benchmark and challenge for quantitative models of nucleic acid mechanics and a comprehensive experimental foundation for modeling complex RNAs in vitro and in vivo. In addition, we envision our assay to enable a new class of quantitative single-molecule experiments to probe the proposed roles of twist and torque in RNA–protein interactions and processing (4, 56).

Materials and Methods

See SI Appendix, Materials and Methods for details. In brief, the double-stranded RNA constructs for magnetic tweezers experiments were generated by annealing two 4,218-kb complementary single-stranded RNA molecules that carry multiple biotin or digoxigenin labels at their respective 5′ ends (Fig. 1C). The product of the annealing reaction is a 4,218-bp (55.6% GC content) fully double-stranded RNA construct with multiple biotin labels at one end and multiple digoxigenin labels at the other end that enable attachment to streptavidin-coated magnetic beads and the anti-digoxigenin–coated surface, respectively (Fig. 1E). For control measurements on dsDNA, we used several different constructs. Unless otherwise noted, we used 3.4- or 20.6-kbp dsDNA molecules that were ligated at their respective ends to ∼0.6-kbp PCR-generated DNA “handles” that include multiple biotin or digoxigenin labels. To test whether in particular the surprising differences in twist–stretch coupling and buckling dynamics between dsRNA and dsDNA might be influenced by the fact that our dsRNA construct carried labels on only one strand at each end whereas the standard dsDNA constructs for MTs measurements carried labels on both strands on both ends, we generated an alternative DNA construct with labels on only one strand at each end (SI Appendix, Fig. S7A). The alternatively labeled dsDNA construct behaved identically, within experimental error, to the conventional dsDNA constructs (SI Appendix, Fig. S7 B and C), suggesting that the labeling procedure does not affect the observed mechanical properties.

Measurements were conducted using custom-built magnetic tweezers in Tris-EDTA (TE) buffer (Sigma; pH 8.0) containing 10 mM Tris⋅HCl and 1 mM EDTA supplemented with SUPERase·In RNase inhibitor (Ambion; 0.1 U/µL final concentration) and with varying amounts of NaCl added.