DNA supercoiling: A regulatory signal for the λ repressor

Significance

Low levels of λ repressor (CI) can autoenhance expression and lysogeny (quiescence) of bacteriophage λ infection. However, additional CI mediates an autorepressive DNA loop. Supercoiling catalyzes looping in unstretched plasmids, but whether supercoiling catalyzes looping under tension, and whether the cI promoter within the loop becomes superhelically isolated were investigated. CI efficiently partitioned plasmids into topological domains and formed barriers to the passage of supercoiling from one into another. Furthermore, in single DNA molecules twisted with magnetic tweezers, CI-mediated DNA loops confined as much as −15% to +11% supercoiling. Finally, under gentle tensions likely to occur in vivo, supercoiling was essential for looping. CI may exploit supercoil-driven looping events to regulate the lysogenic/lytic switch.

Abstract

Topoisomerases, polymerases, and the chirality introduced by the binding of histones or nucleoid-associated proteins affect DNA supercoiling in vivo. However, supercoiling is not just a by-product of DNA metabolism. Supercoiling is an indicator of cell health, it modifies the accessibility of chromatin, and coordinates the transcription of genes. This suggests that regulatory, protein-mediated loops in DNA may sense supercoiling of the genome in which they are embedded. The λ repressor (CI) maintains the quiescent (lysogenic) transcriptome of bacteriophage λ in infected Escherichia coli. CI-mediated looping prevents overexpression of the repressor protein to preserve sensitivity to conditions that trigger virulence (lysis). Experiments were performed to assess how well the CI-mediated DNA loop traps superhelicity and determine whether supercoiling enhances CI-mediated DNA looping. CI oligomers partitioned plasmids into topological domains and prevented the passage of supercoiling between them. Furthermore, in single DNA molecules stretched and twisted with magnetic tweezers, levels of superhelical density confined in CI-mediated DNA loops ranged from −15% or +11%. Finally, in DNA under tensions that may occur in vivo, supercoiling lowered the free energy of loop formation and was essential for DNA looping. Supercoiling-enhanced looping can influence the maintenance of lysogeny in the λ repressor system; it can encode sensitivity to the energy level of the cell and creates independent topological domains of distinct superhelical density.

The idea that metaphase chromatin in vivo is hierarchically coiled and looped is widely embraced by researchers even if structures of the intermediate levels between the string of nucleosomes and the condensed chromosome arm are still poorly understood. Even in interphase, chromatin loops are known to underlie the regulation of certain genes and are widely believed to functionally group related genes. In eukaryotes, chromatin conformation capture experiments reveal loops of hundreds of kilobases or even megabases throughout the genomes (1, 2). Recent experiments show not only that such structural domains coincide with transcriptional boundaries, but transcriptional activity effectively remodels domains and alters supercoiling of the DNA (3). Transcription also alters supercoiling in prokaryotes (4), in which there is evidence for some 400–500 dynamic domains ranging from 2 to 66 kbp in size (5). Key questions about chromatin domains are whether or not junctions created by soluble or membrane-bound proteins that secure these loops can block supercoil diffusion and maintain torsional differences between two adjacent loops of chromatin, and whether supercoiling favors the formation of loops.

There are systems in which supercoiling is associated with defining DNA domains. The Mu bacteriophage seems to recruit the gyrase enzyme of the Escherichia coli host to supercoil the 37-kbp bacteriophage genome and juxtapose the ends to catalyze transpositional replication (6). Barriers to the free diffusion of supercoils appear to exist in this large domain, although their composition is unknown (7). The γδ resolvase enzyme of bacteria has been exploited to create a superhelical density sensor in vivo (4). This enzyme is involved in insertion element transposition and its activity is a function of the superhelical density of the target. With this tool, Higgins and collaborators have been able to detect the effect of transcription on local levels of supercoiling in the bacterial chromosome. An intriguing variation of such experiments demonstrated that a lac repressor loop isolating one of the two recombination sites that must align severely inhibited recombination (8). There is clearly a biochemical relationship between supercoiling and looping by which loops may constrain catalytic superhelical density and superhelical density may catalyze looping, especially between distant DNA segments.

A plasmid is a simple system in which simultaneous binding of soluble protein with high affinity for two sets of recognition sites widely separated along the DNA contour creates two topological domains. Previously published experiments have shown that simultaneous lac repressor (LacI) binding to synthetic tandem sequences of lac repressor binding sites can divide a plasmid into separate topological domains in which the supercoiling level in one domain is independent from the other (9). In those experiments, supercoils constrained in a 2.9-kbp LacI-mediated loop diffused through the protein closure as slowly as 0.0062 supercoils per min. Obviously those loops were much larger than the 100- to 400-bp loops usually created in E. coli by LacI.

Because the LacI tetramer might have evolved not only to secure loops but also to overcome the resistance to bending DNA into small loops, new experiments were conducted with the bacteriophage λ repressor (CI), which secures a 2,317-bp loop in the phage DNA through specific binding to a pair of tripartite recognition sites (operators). The CI-mediated loop has no appreciable bending resistance, but the entropic penalty associated with forming such a long loop is significant, 10.2 kcal/mol (10, 11). Recent work demonstrated that an octamer plus an adjacent tetramer, and likely even larger, partially nonspecific oligomers, secure a loop between these sites to maintain the lysogenic state of the phage (11–13). Here, to probe the λ repressor oligomer as a torsional barrier, experiments were conducted using plasmids with operators separated by supercoiled and nicked segments of DNA 2,312:3,928 (supercoilied:nicked), 4,000:2,317, or 4,001:1,051 bp in length. The rates at which supercoils diffused from the supercoiled segments through CI-mediated junctions to dissipate in the nicked, torsionally unconstrained segments varied inversely with the size of the nicked segments.

Such experiments probed the stability of CI junctions against biochemically accessible levels of supercoiling. To access arbitrary, higher levels of torsion, linear DNA segments with these operators were mechanically twisted with magnetic tweezers by up to ±10%, and the superhelical density captured in spontaneous CI-mediated loops was measured. Superhelical density in DNA exists as an equilibrium between overtwisting (or undertwisting) double helices and writhing to form superhelices. At low tension (less than 1 pN), the molecule tends to writhe, forming loose coils or plectonemes, whereas increased tension shifts the equilibrium toward a twisted, extended form. This equilibrium is easily observed in extension vs. twist curves produced using magnetic tweezers (14). In the current study, when the DNA under low tension was highly twisted to form plectonemes, the CI protein frequently secured loops in the DNA tether, shortening the overall extension and trapping supercoils in the CI-mediated loop. Comparing extension vs. twist curves for unlooped and looped tethers suggests that unlooped DNA forms plectonemes with wider gyres than looped DNA. Thus, the loop may nucleate a more tightly wrapped plectoneme.

These experiments probed whether CI-mediated loop closures constituted torsional barriers, but supercoiling has also been shown to enhance the cooperativity of oligomerization to sharpen the transition from the unlooped to the looped state as a function of concentration (15). If looping were sensitive to discrete levels of supercoiling, it would imply that superhelical density can act as a general signal that directs transcriptional events, as has been shown for transcriptional repression by the gal repressor (16). Here, to quantitatively investigate CI-mediated looping as a function of superhelical density, looped/unlooped equilibria were measured in DNA tethers with different levels of mechanically introduced twist. A threshold level of negative supercoiling was essential for looping in DNA under slight tension. In addition, although increased tension diminished looping, additional negative supercoiling could compensate to maintain a constant level of looping.

Results

λ Repressor Secures DNA Loops and Is a Barrier to Supercoil Diffusion.

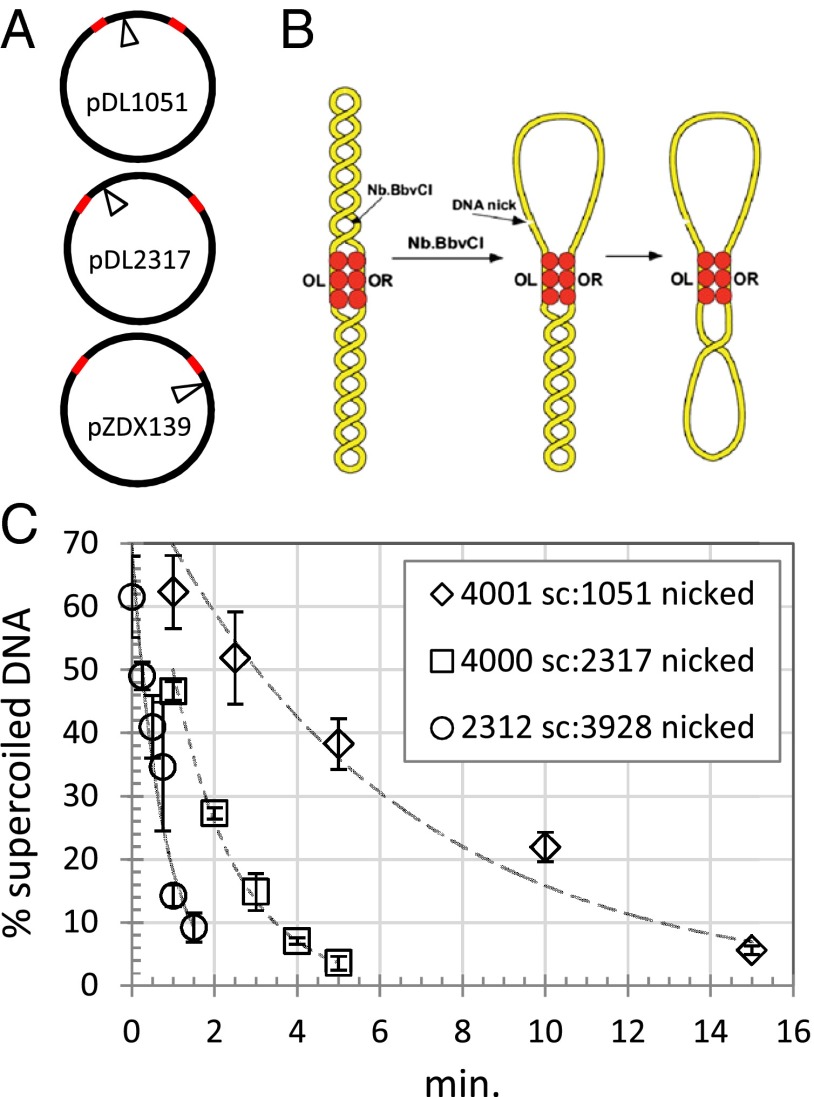
It was previously demonstrated using gel electrophoresis of topoisomers that soluble proteins like the lac and gal repressors and the λ O protein can trap supercoils in DNA loops and form barriers to prevent supercoil diffusion between topological domains (9). One experiment used DNA-binding proteins that recognize and simultaneously bind widely separated sequences to partition plasmids into topologically distinct segments before nicking one segment with a site-specific endonuclease for various time intervals before religation, and characterizing the resulting topoisomers. Nicking has been shown to relieve torsion on the timescale of milliseconds (17). This method was adopted to test whether and to what extent λ repressor traps supercoils in one of two domains created by looping plasmid DNA (Fig. 1A), and how quickly superhelical density traverses the λ repressor barrier into the nicked domain where it rapidly dissipates (Fig. 1B).

Fig. 1.

Supercoil diffusion through CI barriers. (A) The location of a nicking site for the enzyme Nb.BbvCI is shown relative to the OR and OL operators in plasmids pDL1051, pDL2317, and pZDX139. Red segments represent λ operators OL1–3 and OR1–3. (B) A topological barrier experiment with CI (red circles). Upon binding to OL and OR operators, the loop securing CI functions as a barrier that blocks supercoil diffusion. A DNA nick introduced by the endonuclease Nb.BbvCI quickly relaxes superhelicity within the upper loop. Superhelicity in the bottom loop slowly diffuses through the CI-mediated topological barrier where it then dissipates quickly. (C) Supercoiling slowly dissipated from supercoiled domains of plasmids partitioned by a CI-mediated loop. DNA-nicking assays were as described in Materials and Methods (Figs. S1 and S2). The percentage of remaining supercoiled DNA was plotted as a function of the incubation time. Fitting with an exponential decay yielded time constants of 0.74, 1.5, or 6.1 min for partitions of (supercoiled/nicked) 2,312:3,928, 4,000:2,317, or 4,001:1,051 bp, respectively.

In plasmids with initial supercoiling densities around −6.1%, the λ repressor efficiently trapped supercoils (Fig. S1) that decayed exponentially over time in an apparently stochastic, single-step process (Fig. 1C and Fig. S2). Superhelical density diffused through the loop-securing CI oligomer most rapidly from the supercoiled 2,312-bp segment in pZDX139 into the corresponding 3928-bp nicked segment and most slowly from the supercoiled 4,001-bp segment in pDL1051 into the corresponding 1,051-bp nicked segment. Notably, the exponential decay constants for the diffusion of supercoiling were inversely related to the size of the nicked domain (Fig. 1C). All of the loops created by λ repressor in these plasmids are long enough so that any strain due to bending DNA was negligible, and the supercoiling energies present in the initially supercoiled segments of pDL2317 and pDL1051 were similar. This result suggests that the entropy decrease associated with looping torsionally relaxed DNA governs the stability of the barrier. It is smallest for segments of ∼400 bp and increases for the formation of progressively longer loops. The higher entropic penalty associated with securing a 3,928-bp loop would make it less stable than either the 2,317- or the 1,051-bp loop.

CI Loops Can Constrain High Levels of Supercoiling.

To examine whether or not more torsional energy can be confined within a loop secured by λ repressor, the superhelical density was varied in the range of ±10% using the tweezer (14) to twist DNA tethers in the absence or presence of CI protein (Fig. S3). The superhelical density of the tethers is defined as σ = (Lk − Lk₀)/Lk₀ = n/Lk₀, in which Lk₀ is the calculated number of the right-handed helical turns in relaxed, B-form dsDNA (base pairs/10.4 base pairs per turn), and n is the number of twists mechanically applied to a tether with respect to the torsionally relaxed (most extended) conformation. In the absence of protein, when the torque in the tether surpassed a critical level, the molecule buckled and formed plectonemes that reduced the extension of the tether (Fig. 2, black curve). Under moderate tension, less than 0.5 pN, either undertwisting or overtwisting produces similar plectonemes of B-form DNA and symmetric extension vs. twist curves.

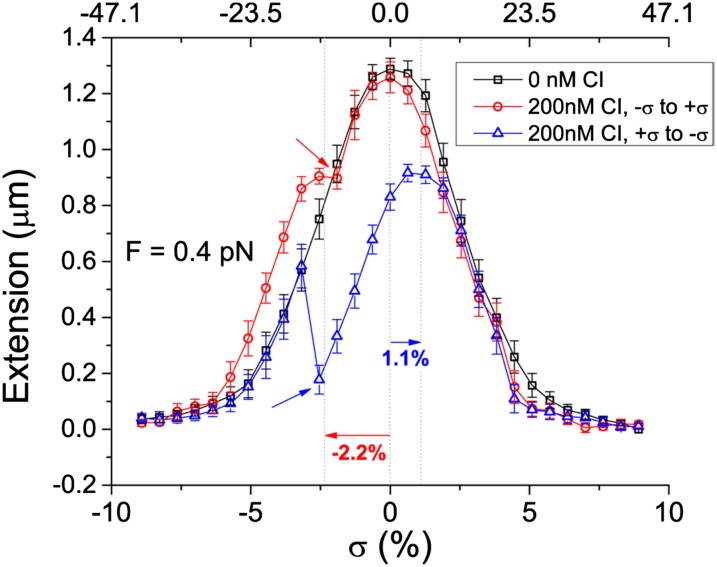
Fig. 2.

Representative extension vs. twist curves showing shifted and reduced maxima upon loop formation. Under 0.4 pN of tension in the absence of CI protein (black), a tether with a 1,051-bp loop formed plectonemes that reduced extension for both positive and negative twist. With 200 nM CI protein (red and blue), as the twist was relaxed from −10% (red) or 10% (blue) superhelical density levels (bottom axis), reduced maxima were observed with shifts (horizontal arrows) that indicated the change in superhelical density of the looped tether (top axis). The superhelical density, σ, of these loops was –0.115 (red) or 0.057 (blue). Upon rupture of the loops (inclined arrows), the tether extension suddenly returned to unlooped values. Series of points are connected by segments to facilitate understanding. Error bars represent the SDs of the length measurements.

Plectonemes also formed when DNA was twisted under moderate tension in the presence of CI, but when highly plectonemic molecules were mechanically relaxed from either positive or negatively twisted extremes, extension vs. twist curves were often shifted and/or exhibited maxima reduced by a length proportional to the separation between operator sites as a fraction of the entire tether length (Fig. 2 and Fig. S4, red and blue vs. black curves). The shift indicated the amount of superhelical density that had become constrained within a CI-mediated DNA loop and was therefore isolated from the remainder of the DNA tether. Both negative and positive shifts were observed, and the widely distributed levels of superhelical density constrained in the loop varied from −15% to 11% (Fig. S5), even though plectonemes were formed by twisting the DNA tether only ±10%. With a homogeneous distribution of superhelical density, the fraction of the total applied twists that become trapped in the loop should equal the ratio of the loop length and the total tether length. However, extensively twisted molecules will also have localized sections of writhe. All loops will trap a length-proportional share of twist, but those that also encompass writhe may exhibit even higher total superhelical density.

In the case of a tether with operator sites separated by 1,051 or 2,317 bp, many CI-mediated loops ruptured as the twist was relaxed (Fig. 2, red and blue), and the extension vs. twist curve data abruptly returned to values recorded for the unlooped tether in the control data (Fig. 2, black). However, CI-mediated loops were remarkably stable to torsional loads. In most cases, the loop either did not rupture until an oppositely coiled plectoneme outside the loop had begun to form and shrink the extension (Fig. 2, blue) or did not rupture at all (Fig. S4). In fact, most CI barriers endured several minutes of torque created between plectonemes of opposite handedness. This torque is in the range of 14–20 pN⋅nm, twice the buckling torque observed at the indicated tension (18). Only a few loops ruptured at a lower torque before a plectoneme began to form outside the loop (Fig. 2, red).

As for 1,051- and 2,317-bp loops, similar experiments were conducted using DNA with operator sites separated by 393 bp. Within mechanically produced plectonemes, 393-bp loops often formed, which shifted the extension vs. twist curves upon mechanically untwisting. However, this smaller loop formed more readily, and experiments at higher tension were possible. Unexpectedly, the amount of superhelicity trapped in CI-mediated loops increased with tension (Table 1). Tension alters the conformational equilibrium of a DNA tether under torsional strain to favor twist over writhe, and twist diffuses rapidly along DNA (19), so superhelical density should be more delocalized under tension. However, if tension reduces the number of plectonemes in the tether, the superhelical density might be restricted to one plectoneme. This would effectively localize the superhelical density, so that it can be captured more easily in a loop surrounding that plectoneme.

Table 1.

Loops 393 bp-long trapped more supercoils at higher tension

Tension, pN	Trapped supercoils	N
0.2	−3.2 ± 0.8	5
0.35–0.4	−3.8 ± 3.3	5
0.44–0.51	−5.3 ± 2.3	6
0.65–0.71	−6.7 ± 3.2	3

Fitting extension vs. twist curves, like those in Fig. 2, for DNA tethers with separations between operators of 393 bp produced estimates of the average, constrained superhelical density. N is the number of observations.

Loops Alter Effective DNA Elasticity.

In absence of CI protein, the dependence of DNA extension on the superhelical density, σ, can be described by the analytical approach described in ref. 20. Briefly, the method is based on the assumption that the free energy in a DNA fragment at a given tension depends on the degree of superhelicity. Three different regimes can be defined corresponding to the following: (i) purely stretched DNA for | σ | < | σ_s | for which $\mathrm{\Delta }G=-g+\left(1/2\right)c_s{\sigma }^2$, (ii) purely plectonemic DNA for | σ | > | σ_p | for which $\mathrm{\Delta }G=\left(1/2\right)p{\sigma }^2$, and (iii) a mixture of the two “pure” states for | σ_s | < | σ | < | σ_p | for which $\mathrm{\Delta }G=-g/\left(1-p/c_s\right)+\sqrt{2pg/\left(1-p/c_s\right)}\left|\sigma \right|$. In these free-energy expressions, g is the force-dependent free energy of stretched, nicked DNA and c_s is the force-dependent, twist stiffness of stretched DNA. The statistical mechanical expressions for these two quantities are published (20). They both depend on the persistence lengths of DNA bending, A, and twisting, C. The constant p is instead related to the twist stiffness for plectonemic DNA, P, through the expression: $p=K_{B}TP{\omega }_0$, where ${\omega }_0=2\pi /3.6$ nm⁻¹ is used to convert the superhelicity to an angle of rotation per contour length. The threshold values of supercoiling that separate the three regimes can be calculated as $\left|{\sigma }_s\right|=\left(1/c_s\right)\sqrt{2pg/\left(1-p/c_s\right)}\text{\hspace{0.17em}and\hspace{0.17em}}\left|{\sigma }_p\right|=(1/p)\sqrt{2pg/(1-p/c_s)}$. As the superhelicity changes, the force derivative of the free energy gives the relative DNA extension, $z/L=-\left(\partial \mathrm{\Delta }G\right)/\left(\partial F\right)$, where z is the DNA extension and L is the DNA contour length.

Using these expressions, the data for the extension vs. twist curves for pDL1051 DNA without CI protein, across the entire range of tension investigated, gave satisfactory fits with A = 50 nm, C = 95 nm (Table 2). These values correspond well with those determined in single-molecule measurements (21–23), theoretical modeling (20, 24, 25), and bulk measurements (26, 27). In presence of CI, the extension vs. twist curves corresponding to looped tethers were fitted using the same expressions replacing σ by the difference, σ − σ_L, with σ_L as the shift of the extension maxima; for the looped DNA tethers, σ_L directly revealed the superhelical density constrained within the loops (Table 2). The relative DNA extension was obtained, in this case, by multiplying the force derivative of the free energy by ΔL, which characterize the relative decrease in DNA extension due to loop formation. Similarly to measurements for nucleosome formation (28), magnetic tweezers permitted direct and quantitative measurement of the superhelicity associated with the transient CI-mediated loop in a DNA molecule.

Table 2.

Lower tension and CI-mediated looping soften DNA tether torsionally

Curve	∆L, fractional	<σL+>, %	<σL−>, %	A, nm	C, nm	P, nm
0.4 pN looped	−0.24 ± 0.04	5.6	−6.4	50	95	8.6 ± 2.3
0.4 pN unlooped						11.0 ± 1.0
0.2 pN looped	−0.27 ± 0.04	5.3	−4.3			6.9 ± 1.8
0.2 pN unlooped						8.3 ± 0.9

Estimates of the tether length change, ΔL, and the average, constrained, positive or negative superhelical densities were obtained from fits of extension vs. twist data shown in Fig. 2.

As shown in Table 2, the magnitudes of positive or negative constrained superhelicity, <σ_L +> and <σ_L −>, averaged 4–6%. The reduction in length upon loop formation was commensurate with the size of the loop, 1,051/4,947 = 0.21. P was lower at lower tension (0.2 pN) and in the presence of looped DNA. Plectonemes are torsionally softer at lower tension (20) but also became softer when the CI-mediated loop formed (Discussion). P was lower than previously reported values from single-molecule experiments (29), perhaps due to the higher concentration of salt in the present experiments.

Supercoiling Influences the Ability of λ CI Repressor to Secure DNA Loops.

Clearly, CI protein-secured loops constitute barriers to supercoil diffusion in plasmids and even artificially high levels of superhelicity in single DNA tethers. To further explore the interaction between supercoiling and loop topology, the spontaneity of looping in gently stretched tethers was characterized as a function of superhelical density for several different loop sizes.

Negative supercoiling lowered free energy of looping.

Loop formation and rupture was monitored in a 4,397-bp DNA tether (loop length, 393 bp) in the presence of wild-type CI at a concentration of 160 nM (Fig. S6). Dynamic, CI-mediated looping has been observed in tethered particle motion experiments in which there is no tension on the tether and no torsional control (11, 30, 31). Magnetic tweezers can be used to control torsion, but they also gently stretch the DNA (Fig. S3). Stretching torsionally relaxed DNA prevents looping, because it eliminates thermal fluctuations that bring together distant sites along the DNA tether. However, looping was observed in tethers that were mechanically untwisted by at least 0.5%. Although 393-bp loops formed spontaneously even at forces of 0.8 pN, longer loops only formed at lower tension. In control traces at 0.2 pN without CI, 1,051-bp loops did not form (Fig. 3, left panels, gray traces). In contrast, with 200 nM CI and negative superhelical density between −1.061% to −1.349%, spontaneous looping was observed (Fig. 3, left panel, black traces). Further increasing negative superhelical density might promote even more looping, but loops cannot be reliably distinguished from plectonemes that form at such low tensions. Distinguishable, longer loops only formed under tensions less than or equal to 0.4 pN, and loop formation in even longer loops of 1,231 or 1,662 bp, required even lower tension. In the associated histograms, as the superhelical density became progressively more negative, the probability of observing the ∼1-μm–long, unlooped DNA tether progressively decreased, whereas the probability of observing the shorter, looped form near 0.8-μm length increased (Fig. 3, right panel). Loop formation was significantly enhanced by further supercoiling.

Fig. 3.

Negative superhelical density favors DNA loop formation. Representative recordings of extension vs. time (Left) and respective extension histograms (Right) for single DNA tethers under 0.2 pN tension, show the formation and rupture of 1,051-bp loops at different supercoiling levels. In the absence of CI protein, the DNA extension was constant appearing as a single peak on the respective extension histogram. The peak corresponding to the unlooped tether shifted slightly toward shorter values as negative superhelical density increased. In the presence of 200 nM CI, the extension of the tether intermittently shifted between looped and unlooped configurations creating telegraphic signals that gave rise to bimodal histograms. An additional −0.3% of twist was enough to shift the DNA from nearly evenly splitting time in looped and unlooped states to remaining almost always looped.

Extension vs. time recordings showing loop formation/rupture were analyzed using the “change point” algorithm (Materials and Methods) to determine when the DNA extension changed significantly. Refinement with an expectation-maximization clustering algorithm allowing two states produced a best estimate of the actual transitions between states in the recordings. Based on this reconstruction, the dwell times in each of the two states were tabulated and fit as exponential distributions to determine the characteristic lifetimes of the looped (τ_L) and unlooped (τ_U) configurations (Figs. S6, lower panel, and S7). The characteristic values of τ_L and τ_U at different forces for different values of DNA mechanical untwisting ranged between 2 and ∼35 s as a function of superhelicity (Fig. S8). For 393-bp looping, as σ increased, the characteristic unlooped lifetime decreased and that of the looped lifetime increased. For larger 1,051-bp loops, the same trend was observed for unlooped lifetime, whereas the average looped lifetime fluctuated around 5 s. The looped and unlooped lifetimes for 1,231- and 1,662-bp loops did not exhibit any trend as a function of supercoiling.

Increased negative superhelical density offsets increased tension to favor looping.

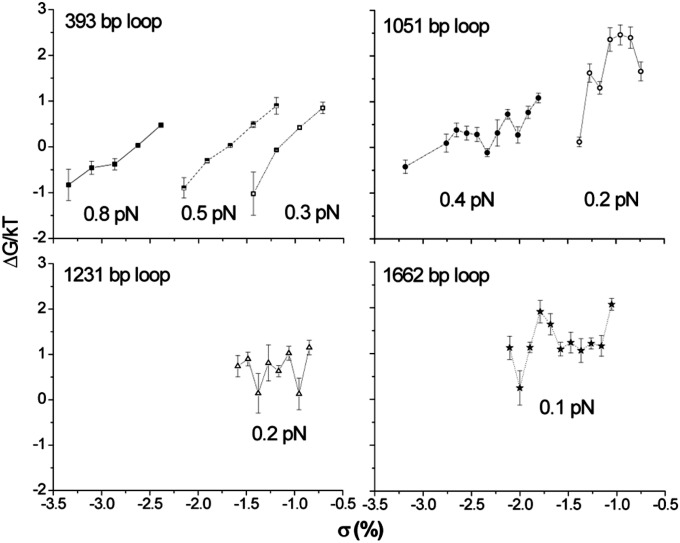
The free energy for loop formation under specific tension and supercoiling levels was calculated from the looped and unlooped lifetimes. Looping was observed only across a narrow range of superhelical density for a given tension, because with too little negative σ, no looping occurred, and with too much, the molecule formed plectonemes, making it impossible to detect looping events. However, within these limits, and especially for the 393- and 1,051-bp loops at higher tension, ∆G decreased with more negative superhelicity (Fig. 4). In fact, the level of excess superhelicity compensated for increased tension. For the 393- and 1,051-bp loops as the tension increased, the free energy of looping could be maintained low by mechanically untwisting the tether even further. Estimates of the free-energy change for CI-mediated DNA looping in vivo are −3.5 kcal/mol (13, 32). This is the result of the favorable free-energy change from assembly of an octamer plus a tetramer to secure the loop, −9.1 kcal/mol plus −2.4 kcal/mol, which compensates for the unfavorable entropy change associated with large loops. Less cooperative loop-securing proteins, like the bidentate lac repressor tetramer, fail to achieve less than 9–10 kcal/mol free energy change in vivo for the sizes of loops used in these experiments (33). The in vitro data with loops ranging from 393 to 1,662 indicates that a minimum amount of negative superhelicity lowers the ΔG by a factor of 4, and further mechanical untwisting makes looping spontaneous (negative ΔG). Favorable free-energy changes were determined for cooperative CI binding that secured loops in negatively supercoiled plasmids (15), and negative superhelical density may be critical for spontaneous DNA looping in vivo.

Fig. 4.

The calculated free energy (∆G) for the formation of loops under different tensions and superhelical density levels based on the lifetimes of looped and unlooped states. For identical loops under identical tension, more negative superhelical density decreased ∆G. This trend was clearer for smaller loops (393 and 1,051 bp) than for bigger ones (1,231 and 1,662 bp).

Discussion

The idea that loops and genome domains can sequester supercoiling may have important implications for regulatory processes within the loop/domain. The present data show that approximately wild-type–length CI-mediated loops, 2,312 bp, can sequester superhelicity for an average of 44 s. Other CI-mediated loops with shorter, corresponding nicked domains sequester superhelicity for even longer. Furthermore, quite high levels of superhelicity can be constrained in a CI-mediated DNA loop. Such CI-constituted “insulators” could topologically separate the rexA and rexB genes that reside within the DNA loop between the OR and OL operator sites. The efficiency of transcription is known to depend on the supercoiling of the template, and these genes are involved in phage exclusion and triggered cell death. In addition to creating steric features that regulate the cI promoter, the CI-mediated loop may maintain negative superhelical density, and therefore a basal level of transcription, at the rexA and rexB promoters to ensure the availability of RexA and RexB to counteract further infection of the lysogenic bacterium. This might also protect the lysogen from cell death in conditions of nutrient starvation by preserving supercoiling (transcription) at the rexB gene to maintain levels of RexB that antagonize mazEF-triggered cell death (34).

The fact that negative superhelicity favors the formation of CI-mediated loops in DNA under slight tension suggests that the λ phage uses supercoiling as a signal. Polymerases are known to be able to exert tens of piconewtons of tension (35), much more than was investigated in the experiments presented here, and transcription can produce large values of superhelicity (36). DNA supercoiling has been shown to be a general regulatory mechanism in several organisms (37–39) and superhelical domains seem to serve as locus control mechanisms for related human genes (3, 36). These genomic observations correlate well with recent single-molecule work with E. coli RNA polymerase demonstrating that transcriptional pausing increases and the transcription rate decreases as a function of torque in the DNA template (40). A very intriguing linkage between DNA supercoiling, nucleoid-associated proteins, and the ordering of genes exists in bacteria and is suggested to coordinate oxygen and nutrient availability with chromosome structure (41). This body of work solidly demonstrates that superhelical density is a fundamental parameter in gene regulation.

In the present experiments, mechanical untwisting certainly catalyzed DNA looping into topologically distinct domains, suggesting that negative superhelicity may toggle the lytic vs. lysogenic switch when the λ bacteriophage infects an E. coli bacterium. During quiescent infection of E. coli by bacteriophage λ, the λ repressor binds to operators separated by 2,317 bp, causing a loop that represses transcription of cI. This DNA loop, which circumscribes a few promoters, is stabilized by and can effectively constrain negative superhelical density for an average of 44 s. These features suggest that the phage genome may have evolved to facilitate quiescent propagation through lysogeny regulated by efficient, negative supercoiling enhanced looping during favorable growth conditions for the bacteria. It is well known that significant UV damage triggers recombinase A-catalyzed CI degradation that trips the switch toward lysis. However, if conditions only mildly deteriorate or limited UV damage occurs, diminished superhelical density could destabilize looping to attenuate CI autorepression and block the switch to lysis in cells that are likely to recover and remain viable hosts (42).

These experiments demonstrate that an archetypical regulatory loop in prokaryotic transcriptional regulation effectively divides a DNA molecule into loops of distinct superhelical densities and that loop formation is catalyzed by DNA mechanical untwisting. Such features are essential for transcriptional regulation through superhelical density, which could be the most dynamic of all epigenetic “marks.” In the future, correlations of transcription and DNA supercoiling within topological domains, such as that produced by bacterial repressors, would greatly enhance our understanding of the dynamics of transcriptional regulation.

Materials and Methods

Materials and suppliers as well as sequences of all plasmid DNA templates (Table S1 and Dataset S1) and primers (Table S2) are listed in SI Materials and Methods. Experiments to determine the extent of superhelicity trapped in CI-mediated loops and measurement the rates of diffusion through the CI barrier were performed using the plasmid nicking assay described in ref. 9. Methods to tether paramagnetic beads with single DNA molecules were similar to previously published protocols (43), and stretching and twisting DNA tethers were performed similarly to previously published reports (28, 44) as was the subsequent data analysis (45). Complete details are available in SI Materials and Methods.