Network-Based Identification of Biomarkers Coexpressed with Multiple Pathways

Abstract

Unraveling complex molecular interactions and networks and incorporating clinical information in modeling will present a paradigm shift in molecular medicine. Embedding biological relevance via modeling molecular networks and pathways has become increasingly important for biomarker identification in cancer susceptibility and metastasis studies. Here, we give a comprehensive overview of computational methods used for biomarker identification, and provide a performance comparison of several network models used in studies of cancer susceptibility, disease progression, and prognostication. Specifically, we evaluated implication networks, Boolean networks, Bayesian networks, and Pearson’s correlation networks in constructing gene coexpression networks for identifying lung cancer diagnostic and prognostic biomarkers. The results show that implication networks, implemented in Genet package, identified sets of biomarkers that generated an accurate prediction of lung cancer risk and metastases; meanwhile, implication networks revealed more biologically relevant molecular interactions than Boolean networks, Bayesian networks, and Pearson’s correlation networks when evaluated with MSigDB database.

Introduction

The accurate assessment of disease susceptibility, progression, and treatment response in individual patients is a critical prerequisite for personalized therapy. High-throughput genome-scale profiling technologies have the potential to allow such molecular diagnostics. To date, there have been few gene expression-based tests applied in clinics for disease intervention. This fact puts a premium on developing innovative methodologies to embed biological relevance into biomarker identification.

With the completion of the Human Genome Project, the emphasis of genome-wide studies has shifted from cataloging a “parts list” of signature genes and proteins to elucidating the networks of interactions that occur among them.^1,2 Molecular network analyses have been used to improve disease classification^3–6 and identify novel therapeutic targets.^7–11 Nevertheless, major challenges include the development of methods for efficiently constructing genome-scale interaction networks¹² and the identification, from among the enormous number of genes, of a particular set of markers with the highest capacity for molecular diagnostics, prognostics, and prediction of treatment response.^13,14

Here, we will give a comprehensive overview of computational methods used for biomarker identification, including rank-based feature selection methods and major network methodologies used in systems biology. Furthermore, we provide a performance comparison of several network models used in studies of cancer susceptibility, disease progression, and prognostication. Specifically, implication networks, as implemented in the Genet package, were used in conjunction with other rank-based feature selection algorithms to identify lung cancer diagnostic and prognostic biomarkers. The molecular interactions among the identified biomarkers were revealed with implication networks, Boolean networks, Bayesian networks, and Pearson’s correlation networks. Each was then evaluated with five collections of gene sets and biological pathways from the MSigDB¹.

Rank-Based Methods for Biomarker Identification

The emerging use of biomarkers may enable physicians to make treatment decisions based on the specific characteristics of individual patients and their tumors, instead of population statistics.¹⁵ In current genome-wide association studies, genes are ranked according to their association with the clinical out-come, and the top-ranked genes are included in the classifier. To identify the most powerful biomarkers in individualized prognostication, state-of-the-art feature selection methods^16–18 should be widely applied.

Attribute selection techniques can be categorized as those that rank individual attributes (filters) or those that rank subsets of attributes. Commonly used individual feature filtering methods include Cox models,¹⁹ ANOVA, Bhattacharyya distance, divergence-based methods,²⁰ gain ratio, information gain, relief,^21,22 linear discriminant analysis,²³ and random forests.^24–26 Algorithms that evaluate subsets of features include correlation-based feature selection, consistency-based subset evaluation, wrapper,^21,22 self-organizing maps (SOM),²⁷ independent component analysis,^28–30 partial least squares,³¹ principal component analysis (PCA),^32–34 kernel PCA,^35,36 sliced inverse regression,³⁷ and logistic regression.³⁸ Exhaustive search, branch-and-bound search, sequential search (forward or backward), floating search, “plus l-take away r” selection,³⁹ Tabu search,⁴⁰ ant colony optimization,^41,42 genetic algorithms,^43,44 simulated annealing,^45–47 and stochastic hill climbing⁴⁸ can be used as search strategies in feature selection. Only the first two search methods guarantee the optimal subset; the rest generate suboptimal results. However, the worst-case complexity of the first two search methods is exponential, and therefore, these two methods are not feasible for a large dataset. Some feature selection algorithms such as significant analysis of microarray (SAM)⁴⁹ and the multivariate permutation test (MPT) are designed specifically for gene filtering.⁵⁰ As the number of variables is much greater than the sample size in high-throughput applications, feature pre-selection using the t- or F-test⁵¹ and nonparametric Wilcoxon statistics^52,53 are used in processing raw high-throughput data.

Regularized Linear Models

Regularized linear models can also be used to identify biomarkers. Linear models are used to study the effects of multiple factors on the response variable or used to construct a prediction model. In microarray studies, linear models such as ANOVA or ordinary least square (OLS) linear regression models were used to analyze gene expression changes or to construct classification models.^54,55 In the general context, an OLS linear regression model predicts the response of variable y (formulated in Figure 1A), which estimates the set of coefficients β by minimizing the residual squared error.

Figure 1.

Coefficient estimation for regularized linear models. Equations to estimate the coefficient vectors in (A) OLS linear regression model, (B) lasso, (C) elastic net, and (D) network-constrained regularization models.

In genomic studies, where the curse of dimensionality phenomenon with the large p (number of predictors) small n (number of samples) is common, linear models are fitted along with certain penalty terms called regularized linear models. Two common regularized linear models used in genomic studies are lasso (least absolute shrinkage and selection operator)⁵⁶ and elastic net.⁵⁷ Lasso imposes an L1-norm penalty (Fig. 1B) to the model to enforce shrinkage and to avoid the over-fitting problem in the large p small n situation commonly present in genome studies. However, lasso performs poorly in data with high colinearity⁵⁸ and selects only one out of a group of genes sharing the same biological process. In order to enable the selection of genes belonging to the same biological process or pathway, elastic net was proposed.⁵⁷ This is basically an extension of lasso through combining the L2-norm along with the L1-norm penalty (Fig. 1C). The combination of both L1-norm and L2-norm penalties aims to allow both shrinkage and grouping of gene variables. However, the grouping feature of elastic net would lead to the selection of highly redundant genes and therefore the incapability of pinpointing a small subset of predictive genes.

With the abundant resources and increasing knowledge of biological regulatory networks, protein–protein interactions (PPI), signaling pathways, and known relationships among genes could be incorporated into the regression model. The network could be represented by a graph, and the graph’s corresponding Laplacian matrix could then be applied as a penalty in the regression models (Fig. 1D). By having the graph Laplacian matrix as the penalty term, the smoothness of the coefficients is applied over the topography of the graph instead of solely to the correlations among the genes. In other words, the a priori knowledge of the functional relations among genes is embedded into the model through the network (graph) and could reveal a set of genes that are more biologically relevant instead of a set of correlated genes (which could be redundant). The network-constraint regularized model has been proposed to identify biomarkers associated with patient survival time,⁵⁹ and a network-constraint logistic model was used to identify biomarkers for tumor subtype⁶⁰ with cancer genomic data. These network-regularized regression models outperform lasso and elastic net with simulation data in both studies.^59,60 In a cancer susceptibility study of glioblastoma and tumor subtype analysis with breast cancer profiles of The Cancer Genome Atlas (TCGA) consortium, these two network-constraint regularized regression models identified biomarkers confirmed in published literature.^59,60

General Methodologies for Modeling Molecular Networks

It has been noted that individual biomarkers showing strong association with disease outcome are not necessarily good classifiers.^61–63 Because genes and proteins do not function in isolation, but rather interact with one another to form modular machines,⁶⁴ understanding the interaction networks is critical to unraveling the molecular basis of disease. Molecular network analysis has led to promising applications in identifying new disease genes^65–70 and disease-related subnetworks,^71–80 mapping cause-and-effect genetic perturbations,^81–84 and classifying diseases.^3–6,85,86 The various computational models that have been developed for molecular network analysis can be roughly categorized into three classes¹²: logical models to demonstrate the state of entities (genes/proteins) at any time as a discrete level^87–90; continuous models to represent real-valued network processes^91–96 and activities^97–102; and single-molecule models^103–105 to simulate small regulatory networks and mechanisms.^106–110

Logical models

In the category of logical models, Boolean networks⁸⁷ were recently used to analyze the relationship between regulation functions and network stability in a yeast transcriptional network¹¹¹ and the dynamics of cell-cycle regulation.¹¹² The structure of Boolean networks can be learned from gene expression profiles.^113–115 Boolean networks can provide important biological insights into regulation functions and the existence and nature of steady states (ie, polarity gene expression)¹¹⁶ and network robustness. Nevertheless, as the number of global states is exponential in the number of entities and the analysis relies on an exhaustive enumeration of all possible trajectories, this method is computationally expensive and only practical for small networks.¹² Because of insufficient experimental data or incomplete understanding of a system, several candidate regulatory functions may be possible for an entity. To express uncertainty in regulatory logic, the probabilistic Boolean network (PBN) was developed¹¹⁷ and used to model a 15-gene subnetwork inferred from human glioma expression data.¹¹⁸ The synchronous dynamics of a Boolean network can be captured by a Petri net,¹¹⁹ which is a nondeterministic model widely used for detecting active pathways and state cycles¹²⁰ and for analyzing large metabolic pathways^121–124 and regulatory networks.¹²⁵ Another model, module networks, infers the regulation logic of gene modules as a decision tree, given gene expression data.¹²⁶ The Boolean implication networks presented by Sahoo et al.^127,128 used scatter plots of the expression between two genes to derive the implication relations in the whole genome. To date, Boolean implication networks have not been applied in biomarker discovery.

Markov networks are another family of logical models used to infer the inter-relationships among genes. Markov network, also known as Markov random field, is a statistical framework to analyze and visualize conditional relationships between sets of random variables. The structure of the conditional relationships could be exhaustively explored because of the Markov properties.¹²⁹ In the graphical form, vertices represent random variables and the edges between vertices denote the conditional dependencies between the variables. For example, variables A and B are connected if A is predictive of B, independent of all other variables. Markov networks are efficient in representing the distributions over a very high dimension of variables. Therefore, Markov networks could be used to infer the underlying structure of relationships among the genes in cancer patients. These methods are advantageous when only the genomic data are available and the clinical covariates are not available or not predictive of the disease. A commonly used Markov network in high-throughput genomic data is Graphical Gaussian Model (GGM). GGM has been applied to infer the relationships among sets of random variables with continuous values. In bioinformatics, GGM has been applied to study the patterns of relationships and associations between a large-scale of genes based on DNA microarray gene expression data.^130,131 Because of the large dimensionality of genomic data, the original GGM has a few challenges when applied to high-throughput data. The first challenge is that a large number of observations are required in order to obtain reliable estimates of the conditional dependencies between variables¹³²; whereas genomic data have tens of thousands of genes involved but only with a few hundred observations. The second challenge lies in the model selection. As the number of models grows super-exponentially with the number of genes, only a small subset of models can be tested.¹³² The third challenge is that a dense network with a large number of edges connecting numerous genes involved makes interpretability unfeasible.¹³³ It has been known that biological networks are not fully connected. Instead, a biological network is sparse and free scale. To overcome these challenges, variations and extensions of GGM were proposed. Among these include the modified GGM approach that first infers small subnetworks of three genes (tri-graph) and then combines the subnetworks into the proposed complete network.¹³¹ This modified GGM was applied to elucidate the regulatory network of two isoprenoid biosynthesis pathways in Arabidopsis thaliana.¹³¹ Another example is the application of a regularization procedure to estimate a sparse precision matrix in the setting of GGM.¹³⁴ A novel threshold gradient descent (TGD) regularization is applied for imposing penalization estimation of the GGM and thus accounts for the curse of dimensionality issue in high-throughput genomic data.

With the advancement of technology in recent years, sequencing technology is gradually replacing DNA microarray to measure genome-wide gene expression profiles as RNA- sequencing technologies yield less technological variation than microarrays.¹³⁵ Different from the typical log-ratio expression values from microarray data that follow approximately a Guassian distribution, RNA-seq data measurements are in read counts of how many times a transcript has been mapped to the specific genomic location. These read counts are non-negative integer values, which follow approximately a Poisson distribution.^135–137 Therefore, Poisson graphical models should then be used for analyzing next-generation sequencing data instead of Gaussian graphical models. Various methods proposed to model the underlying structure of multivariate count data of Poisson distribution suffer from deficiencies, including infeasibility of applying the contingency table-based approach when the number of variables is extremely high,¹²⁹ and limitations of modeling only the marginal distributions of independent variables¹³⁸ or modeling only negative dependencies.¹³⁹ Recently, an approach was proposed to overcome these deficiencies in modeling regulatory networks from sequencing count data.¹⁴⁰ Specifically, the proposed log-linear Poisson graphical model estimates the model parameters locally via neighborhood selection by fitting L1-norm penalized data to a log-linear model and provides high computational efficiency with the employment of a fast parallel algorithm. The proposed log-linear Poisson graphical model was applied on breast cancer microRNA data and revealed known regulator modules of breast cancer. It also discovered novel microRNA clusters and hubs that provide further insights into regulatory mechanisms of breast cancer.¹⁴⁰

Since the last decade, TCGA consortium has been profiling various genomic data from hundreds of patients of various cancer types to facilitate the understanding of molecular mechanisms underlying these deadly diseases. A few logical models have been proposed to utilize this abundant resource. One example is the Multi-Dendrix method, which is a linear programming algorithm to learn a set of driver pathway modules with both high mutual exclusivity and coverage of patients from somatic mutation data.¹⁴¹ Applications of Multi-Dendrix to glioblastoma and breast cancer from TCGA consortium identified mutation genes overlapping with known oncogenic pathways, including PI(3)K in glioblastoma and p53 and GATA3 in breast cancer. Another example is a method known as pathway recognition algorithm using data integration on a genomic model (PARADIGM).¹⁴² PARADIGM employs a probabilistic graphical model based on factor graphs to infer network modules perturbed in cancer patients through integration of various genomic data. The strength of PARADIGM over other methods is that it integrates various genomic data, ranging from gene expression, copy number data, methylation data, and even known interactions from known signaling pathways.

Bayesian belief networks

A recent formalism, Bayesian belief networks, is recognized as one of the most promising methodologies for prediction under uncertainty.^48,143 Bayesian networks express complex causal relations within the model and predict events based on partial or uncertain data computed by joint probability distributions and conditionals.^144–147 Bayesian networks have been utilized to aid clinical decision- making¹⁴⁸ and to model cellular networks,¹⁴⁹ including genome- wide gene interactions,¹⁵⁰ protein interactions,^151–153 and causal influences in cellular signaling networks.¹⁵⁴ In modeling signal pathway interactions, Bayesian networks not only automatically elucidated most of the traditionally reported signaling relationships but also predicted novel inter-pathway network causalities, which were verified experimentally.¹⁵⁴

A Bayesian belief network (BBN) is a directed acyclic graph that represents probabilistic relationships among uncertain variables. The graph is made of nodes and arcs where the nodes represent uncertain variables and the arcs the causal/relevance relationships between the variables. Each node is associated with a node probability table (NPT). The NPT captures the conditional probabilities of a node given the value of its parent nodes. For nodes without parents, the NPTs are simply the marginal probabilities or prior distributions. There are several ways to determine the probabilities for the NPTs. We can accommodate both subjective probabilities elicited from domain experts and probabilities based on objective data. Each uncertain variable represents an event or a proposition.

The acyclic structure of Bayesian networks clearly represents the primary cause in the directed graph, which is appealing in predictions. Nevertheless, the number of possible networks is exponential in the number of nodes under consideration, which makes it impossible to evaluate all possible networks. Thus, heuristic searches are used to construct Bayesian networks. Furthermore, it is not always possible to determine the causal relationships between nodes, ie, the direction of the edges, owing to a property known as Markov equivalence.^155,156 More importantly, the acyclic Bayesian network structure was unable to model feedback loops, which are essential in signaling pathways¹⁵⁴ and genetic networks.^157–159 To overcome this limitation, a more complex scheme, dynamic Bayesian networks, was explored for modeling temporal microarray data.^160,161 As an expansion of Bayesian networks, a probabilistic version of the MetaReg model,¹⁶² represented as a factor graph,^163,164 was developed¹⁶⁵ to facilitate changes in the network structure (refinement) and inclusion of additional entities (expansion).¹⁶⁶

Implication networks

As an alternative to Bayesian networks, an implication network model employs a partial order knowledge structure (POKS) for structural learning and uses the Bayesian theory for inference propagation.^167,168 When using Dempster–Shafer theory for belief updating, this implication network methodology is termed as a Dempster– Shafer belief network.^169,170 An implication network is a general methodology for reasoning under uncertainty, as are other alternative formalisms such as neural networks,^171,172 dependency networks,¹⁷³ Gaussian networks,¹⁷⁴ Mycin’s certainty factors,¹⁷⁵ Prospector’s inference nets,^176,177 and fuzzy sets.¹⁶⁷ POKSs are closed under union and intersection of implication relations, and have the formal properties of directed acyclic graphs. The constraints on the partial order can be entirely represented by AND/OR graphs.^167,178 When the constraints on the partial order are relaxed, the implication networks can represent cyclic relations among the nodes. In this condition, the implication network structure is a directed graph with nodes connected by implication (causal) rules, which can contain cycles such as feedback loops.

Recently, implication networks have been used to model concurrent coexpression with major disease signaling hallmarks for lung cancer prognostic biomarker identification.^179,180 In these studies, genome-wide coexpression networks specifically associated with different prognostic groups were constructed using implication networks. Candidate genes coexpressed with six or seven major lung cancer signaling hallmarks were identified from these disease-associated genome-wide coexpression networks. These candidate genes were further selected to form prognostic gene signatures using rank-based methods including Cox model, Relief and random forests.¹⁸⁰ The selected biomarker sets form biologically relevant networks when evaluated with curated databases of PPI, chromosome locations, signaling pathways, cis-regulatory motifs/transcription factor binding sites, cancer related gene sets, and gene ontology. This network-based approach identified extensive prognostic gene signatures that outperformed existing ones that were identified using traditional rank-based methods. These results demonstrate that rather than using traditional methods to merely evaluate statistical association with disease outcome, embedding biological relevance into network modeling of the human genome could identify clinically important disease biomarkers.

Approach and Implementation of Implication Networks: Genet

The implication networks can be inducted automatically and dynamically from a dataset by using prediction logic. The structure of the implication network does not represent causal relationship as in the Bayesian network. Instead, it represents implication relationship among the nodes, such as A = >B. Unlike the Bayesian networks that need the complete knowledge of the real-world in order to build the correct causal model once and for all, the implication networks can be constructed dynamically and efficiently based on available data. Therefore, the implication network construction is more flexible than that of the Bayesian networks. The inducted implication network is a directed graph. Each node represents an individual variable or hypothesis. Each arc in the graph signifies the existence of a direct implication (eg, influence) rule between two adjacent nodes. The value of one variable is dependent on the values of all variables that influence it. When evidence from distinct sources is observed for certain nodes, it is combined by the Dempster–Shafer scheme.¹⁸¹

Genet² is an implementation of the novel implication networks based on prediction logic to construct disease-mediated genome-wide coexpression networks, permitting cyclic relations. To model crosstalk with signaling pathways, Genet allows users to input major disease signaling hallmark proteins for identifying candidate genes that are concurrently coexpressed with these signaling pathways. To identify the final biomarker set, Genet could conveniently link to state-of-the-art feature selection methods, including univariate Cox model, random forests, and the Relief algorithm.

The overall process of identifying gene signatures using Genet is as follows: (1) constructing genome-wide coexpression networks using prediction logic (P < 0.05, z-tests) for each disease state or patient group. (2) By comparing the logic relations connecting each pair of genes between the disease-associated coexpression networks, differential network components were obtained, constituting the disease-specific coexpression networks. (3) Selecting candidate genes displaying a direct significant (P < 0.05, z-tests) coexpression relation with the specified signaling hallmark genes from the disease-specific coexpression networks. (4) Identifying a final biomarker set (gene signature) from the candidate genes by using Relief, random forests, or Cox model.

Since the implication network induction algorithm takes dichotomous variables, the gene expression profiles need to be discretized into binary values; whereas the final step of gene selection and disease classification is performed with the original microarray data. The collection of signaling hallmark genes should be selected according to disease relevance. For example, multiple signaling proteins from the KEGG human non-small cell lung cancer signaling pathways³ were selected as disease hallmarks to identify coexpressed prognostic gene biomarkers.¹⁸⁰

Genet is implemented with a combination of C and R, where the C-executable is run through the R interface. This implementation was used as we employed extensive dynamic memory relocation in C to keep track of the derived genome-scale coexpression relations, which makes the package highly efficient in computation time and memory use. The package runs on Windows OS (Windows Vista or higher) with a minimum of 4 GB of RAM. It requires only 40 minutes for an analysis with 20K genes in 256 patient samples. We have linked Genet with Cox model and random forests implemented in R. JavaScript was written to invoke Relief implemented in WEKA (22)¹.

Comparison of Network Models in Cancer Signature Identification

Genet was employed in a few genome-wide coexpression network studies to identify prognostic gene signatures for lung cancer.^179,180 The proposed methodology identified a total of 21 gene signatures¹⁸⁰ that outperformed previously reported ones identified using traditional feature selection methods on the same datasets.¹⁸² Genet was also applied to model smoking-mediated coexpression networks on a selected set of genes associated with lung cancer survival and smoking history. A seven-gene¹⁸³ and a six-gene smoking-associated signature¹⁸⁴ were identified for accurate diagnosis and prognosis of lung cancer in smokers.

Next, the biological relevance of the coexpression networks derived with Genet was compared with other network models. Based on five collections of gene sets and pathways from the MSigDB, a coexpression relation was considered a true positive (TP) if the pair of genes satisfy any of the following: (1) present on the same chromosome or cytogenetic band; (2) in the same curated or canonical pathway; (3) share cis-regulator motif, binding motif, or transcription factor binding site; (4) annotated by the same GO term; or (5) within the same computational gene sets mined from cancer-oriented microarray data. The coexpression relation was considered a false positive (FP) if the gene pair does not satisfy all five conditions listed above. If at least one gene in the pair is not annotated, a coexpression relation was labeled as nondiscriminatory (ND). Coexpression relations labeled as ND were excluded in the evaluation as they were not confirmed. Once all relations were labeled, precision (TP/[TP + FP]) and q-value (FP/[TP + FP]) of the disease-mediated coexpression networks were computed. Null distributions of precisions and q-values were generated in 1,000 random permutations of the class labels in the test cohort. From the null statistics, the statistical significance (P) of the precision is indicated by the chance of getting higher precision from the null distribution. The false discovery rate (FDR) of the disease-mediated coexpression networks is the average of the q-value from the null distribution.

Comparison with Boolean networks

On the lung cancer patient cohorts from the Director’s Challenge Study,¹⁸⁵ coexpression networks derived with Genet and Boolean implication networks were compared. Results showed that coexpression relations derived from Boolean implication networks did not include many of the major lung cancer hallmarks, which made it unfeasible to select marker genes coexpressed with multiple signaling pathways.

The large number of relations derived from the implication networks had been a source of concern for false discovery on the derived coexpression relations. This limitation could be overcome by tuning the minimum precision (∇min) parameter in the induction algorithm employed in Genet. In contrast, the Boolean implication network does not provide further information on tuning the parameters. This makes Genet more flexible than the Boolean implication networks. While comparing the networks derived from two methods, ∇min was tuned to be within 0.75 and 0.81 so that the coexpression networks derived from Genet are at a size comparable to those derived from the Boolean implication networks. Results showed that the precisions for the networks derived from both methods were greater than 95%. However, only precision of the implication networks with ∇min = 0.78 was statistically significant (P < 0.04). The precision of the implication networks with ∇min = 0.75 was borderline significant (P < 0.06) and that of the Boolean implication networks was not significant (P < 0.21) (Fig. 2A). On the other hand, the FDR of the derived networks was all less than 5% (Fig. 2B).

Figure 2.

Precision (A) and FDR (B) of the disease-specific coexpression networks derived with Boolean implication networks and Genet. Genome-wide coexpression networks were constructed for good prognosis and poor prognosis patient groups, respectively, in the training cohort from Shedden et al.¹⁸⁵ The disease-specific networks derived with both models were compared in terms of precision and FDR. An asterisk (*) above the bar indicates that the precision is significantly (P < 0.05) higher than the null precisions in 1,000 permutations.

Comparison with Bayesian networks

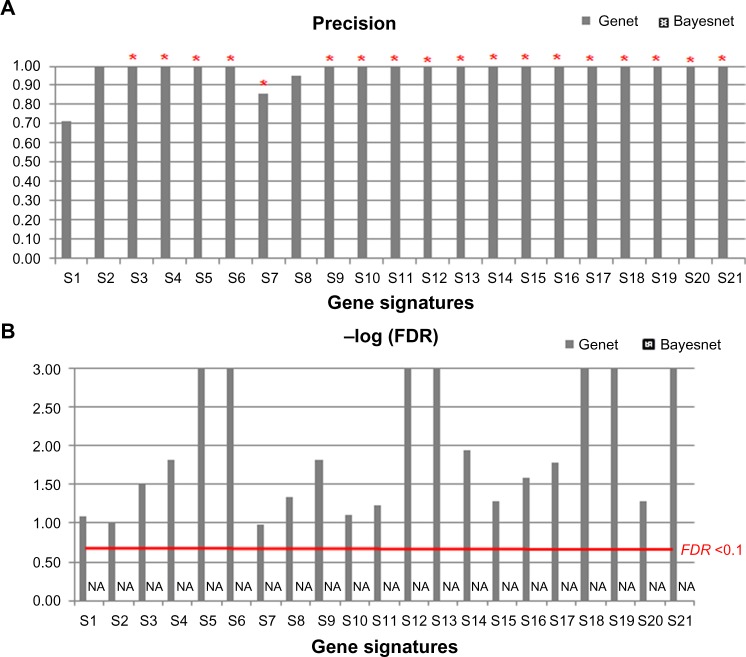
In comparison with the Bayesian networks (Bayesnet) modeled with TETRAD IV⁵ for the 21 signatures identified, the disease-specific coexpression networks derived using Genet and Bayesnet have comparably high precisions and low FDR (FDR < 0.1) on the training cohort from the Director’s Challenge Study. However, in the more robust approach that is based on the coexpression relations commonly present in the networks derived on the training cohort and the two test cohorts, for all 21 signatures, there was no relation commonly found in the disease-specific coexpression networks derived in all three cohorts using Bayesnet. On the other hand, the relations derived from the training cohort using Genet could be successfully reproduced in both test cohorts with significantly high precision (precision = 1 for 18 signatures; Fig. 3A) and low FDR (FDR < 0.1; Fig. 3B).

Figure 3.

Comparison of the disease-specific coexpression networks derived with Genet and Bayesian networks. Comparisons of the disease-specific coexpression relations validated in two test cohorts in terms of precision (A) and FDR (B) for the 21 identified prognostic lung cancer gene signatures. For the Bayesian networks, the precision is zero for all 21 gene signatures in (A) and the FDR is NA in (B) because no coexpression relation was validated by both test cohorts. The asterisk (*) above the bar indicates that the precision is significantly (P < 0.05) greater than null precisions in 1,000 permutations.

Comparison with Pearson’s correlation networks

In comparing the smoking-mediated coexpression networks of the signatures and hallmark genes with those derived from the Pearson’s correlation coexpression networks, the precisions and FDR are comparable.¹⁸⁴ However, as discussed in the Introduction, the relations represented in Pearson’s correlation coexpression network do not describe the directions of the associations. In contrast, coexpression networks derived with Genet describe both the directions of the regulation between pair of genes.

In the few studies with Genet, mean expression of each gene was used as the cutoff to discretize the gene expression into binary values, which would include all patient samples for the network induction. Instead of using the mean expression values, more stringent statistics, such as mean +/− standard deviation, could be used to partition gene expression into discrete values. However, it would lead to the removal of patient samples that do not meet the predefined threshold.

Conclusions

Unraveling complex molecular interactions and networks and incorporating clinical information in the modeling will present a paradigm shift in molecular medicine. Embedding biological relevance via modeling molecular networks and pathways has become increasingly important for biomarker identification in cancer susceptibility and metastasis studies. As guidance, a few commonly used methods in biomarker identification are summarized in Table 1. In summary, the rank-based methods and regularized models are used when a response variable, ie, clinical outcome, is available; whereas network models would not require any outcome or response variable to be fitted in the model. These methods could be used for different kinds of high-throughput data, including mRNA/miRNA expression from microarrays, mutation from Single Nucleotide Polymorphism (SNP) arrays, and read counts from next-generation sequencing data. Our studies show that a combination of network models and rank-based feature selection methods could identify gene signatures with accurate diagnostic and prognostic performance, and reveal biologically relevant molecular networks. In this review, multiple network-based models were evaluated in several case studies, with implication networks outperforming Bayesian belief networks, Boolean networks, and Pearson’s correlation coexpression networks.

Table 1.

Summary of commonly used methods for biomarker identification.

METHOD	INPUT HIGH-THROUGHPUT DATA*	RESPONSE VARIABLE
Rank-based methods
SAM49	Expression	Comparison of two conditions
Random forests24–26	Expression	Gaussian
Cox model19	Expression, Mutation	Survival time and Event
F-statistics51	Mutation	Comparison of two conditions
Regularized models
Lasso56	Expression, Mutation, Read counts	Gaussian
Elastic net57	Expression, Mutation, Read counts	Gaussian
Network-constraint regularized model59	Expression, Mutation, Read counts, Gene-interaction Network	Gaussian
Network-constraint logistic model60	Expression, Mutation, Read counts, Gene-interaction Network	Binary
Network based methods
Graphical Gaussian Models130,131	Expression	Not required
Poisson graphical models135–137	Read counts	Not required
Multi-Dentrix141	Mutation	Not required
PARADIGM142	Integration of Expression, Mutation, and Biological function and interaction data	Not required
Bayesian belief networks149	Expression	Not required
Implication networks179,180	Expression, Mutation	Not required

Notes:

^*Expression, mRNA/miRNA expression profiled with microarray. Mutation, mutation profiled with SNP array or next-generation sequencing. Read counts, mRNA/miRNA expression profiled with next-generation sequencing.