Surrogate measures and consistent surrogates

Summary

Surrogates which allow one to predict the effect of the treatment on the outcome of interest from the effect of the treatment on the surrogate are of importance when it is difficult or expensive to measure the primary outcome. Unfortunately, the use of such surrogates can give rise to paradoxical situations in which the effect of the treatment on the surrogate is positive, the surrogate and outcome are strongly positively correlated, but the effect of the treatment on the outcome is negative, a phenomenon sometimes referred to as the "surrogate paradox." New results are given for consistent surrogates that extend the existing literature on sufficient conditions that ensure the surrogate paradox is not manifest. Specifically, it is shown that for the surrogate paradox to beman.est it must be the case that either there is (i) a direct effect of treatment on the outcome not through the surrogate and in the opposite direction as that through the surrogate or (ii) confounding for the effect of the surrogate on the outcome, or (iii) a lack of transitivity so that treatment does not positively affect the surrogate for all the same individuals for which the surrogate positively affects the outcome. The conditions for consistent surrogates and the results of the paper are important because they allow investigators to predict the direction of the effect of the treatment on the outcome simply from the direction of the effect of the treatment on the surrogate. These results on consistent surrogates are then related to the four approaches to surrogate outcomes described by Joffe and Greene (2009, Biometrics 65, 530–538) to assess whether the standard criterion used by these approaches to assess whether a surrogate is "good" suffices to avoid the surrogate paradox.

1. Introduction

There has been considerable interest in the statistics literature on measures and statistical methods for assessing the adequacy of a surrogate outcome (Prentice, 1989; Freedman et al., 1992; Lin et al., 1997; Gail et al., 2000; Taylor et al., 2005; Burzykowski et al., 2005; Follmann, 2006; Chen et al., 2007; Gilbert and Hudgens, 2008; Joffe and Greene, 2009; Wolfson and Gilbert, 2010; Huang and Gilbert, 2011). The use of a surrogate outcome may be desirable in randomized trials if the cost or length of follow-up required to obtain data on the outcome of interest is thought prohibitive. A variety of statistical approaches and measures have been proposed. In a recent article, Joffe and Greene (2009) summarize a number of these statistical approaches from the perspective of causal inference and discuss relations between these approaches.

A smaller literature on surrogate outcomes has considered what is sometimes referred to as the "surrogate paradox." It may be the case that the treatment has a positive effect on the surrogate, that the surrogate and outcome are strongly positively associated and yet that the treatment itself has a negative effect on the outcome! We might refer to such cases as instances of the "surrogate paradox." This was illustrated dramatically is the case of trial evaluating the effect of drug treatment on ventricular arrhythmia, taken as a surrogate for mortality. Ventricular arrhythmia is strongly associated with mortality; several drugs were tested in randomized trial, were found to lower ventricular arrhythmia, and were approved by the Food and Drug Administration. However, in follow-up it became clear that the drugs increased rather than decreased mortality (Moore, 1995; Fleming and DeMets, 1996). One important task then with regard to surrogate outcomes - and the one which will be the focus of this paper - is determining when data concerning the effect of treatment on the surrogate can be used to make decisions about the direction of the effect of the treatment on an outcome. In two papers Chen et al. (2007) and Ju et al. (2010) discuss sufficient conditions which, if satisfied by a surrogate, will avoid the surrogate paradox. They refer to surrogates that avoid the surrogate paradox as "consistent surrogates."

There has been little effort to relate these sufficient conditions to the statistical measures and approaches that have been used to assess and measure surrogacy. This paper introduces new criteria for consistent surrogates and then revisits the survey of approaches described by Joffe and Greene (2009), evaluating each in light of the surrogate paradox. Sections 2 and 3 summarize the results of Chen et al. (2007) and Ju et al. (2010) on consistent surrogates and then extend their results further to allow for more general settings and to provide a characterization of conditions which are necessary for the surrogate paradox to occur (analogously, are sufficient to avoid it). The conditions and the results of the paper are important because they allow investigators to predict the direction of the effect of the treatment on the outcome simply from the direction of the effect of the treatment on the surrogate. Section 4 then considers the role and significance of the surrogate paradox for each of approaches described by Joffe and Greene (2009). Section 5 illustrates the surrogate paradox in the various approaches and Section 6 offers some concluding remarks.

2. Definitions for Surrogates and the Surrogate Paradox

Let A be a treatment of interest that we will assume randomized; let Y be the outcome of interest and let S be a proposed surrogate. Let Y_a and S_a be counterfactual outcomes (or potential outcomes) for Y and S for each individual that would have been obtained if treatment A had, possibly contrary to fact been set to a. Finally let Y_as be the counterfactual outcome for each individual that would have been obtained if A had been set to a and if S had been set to s. Contrasts of the form Y_as − Y_a′s are referred to as controlled direct effects (Pearl, 2001). Below we will also describe so-called "natural direct effects" (Robins and Greenland, 1992; Pearl, 2001) but unless otherwise indicated "direct effects" will refer to "controlled direct effects." We restrict our attention to settings in which A, S, Y are measured for all individuals. We thus do not consider cases in which for some individuals an event Y can occur before S is measured; see Gilbert and Hudgens (2008) and Wolfson and Gilbert (2010) for discussion of these settings.

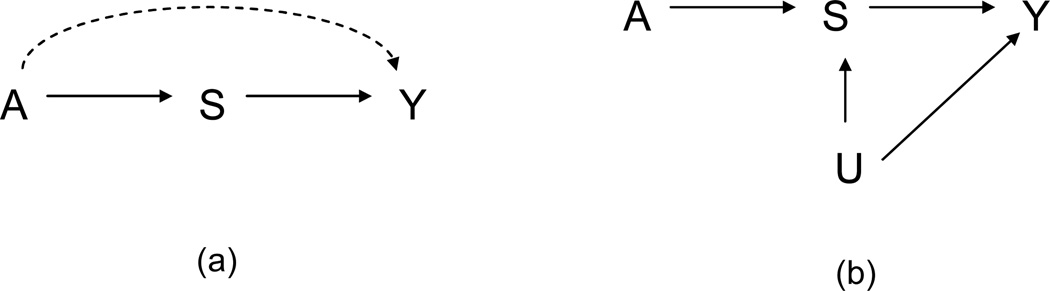
In what follows we will consider several definitions in the literature concerning surrogate outcomes and discuss how these various definitions are related to the surrogate paradox. In what is now considered a classic paper, Prentice (1989) suggested that a surrogate should be such that a test of the null of no effect of the treatment A on surrogate S should serve as a valid test of the null of no effect of the treatment A on outcome Y. Prentice proposed the following two main criteria for assessing this and a variable satisfying such criteria has subsequently been referred to as a "statistical surrogate" (Frangakis and Rubin, 2002).

Statistical Surrogate (Prentice Criteria)

S is said to be a surrogate for the effect of A on Y if (i) Y is independent of A conditional on S; (ii) S and Y are correlated.

The criteria are suggested by the diagram in Figure 1a. Suppose there is no controlled direct effect of A on Y , then if there is no effect of A on S it then follows that there will be no effect of A on Y. Moreover, in this diagram if there is no direct effect of A on Y then A will be independent of Y conditional on S. But the criteria does not give the desired result if there are unmeasured confounders of S and Y as in Figure 1b. There could be correlation between A and Y conditional on S due to U even if A has no direct effect on Y. The Prentice criterion might only be a reasonable requirement if we could control for the common causes of S and Y.

Fig. 1.

Examples illustrating surrogate outcomes.

Prompted perhaps in part by these concerns, Frangakis and Rubin (2002) used the potential outcomes framework to propose an alternative criterion to evaluate surrogates and referred to a surrogate that satisfied this criterion as a "principal surrogate."

Principal Surrogate (Frangakis and Rubin, 2002)

S is said to be a principal surrogate for the effect of A on Y if for all s, pr(Y₁|S₁ = S₀ = s) = pr(Y₀|S₁ = S₀ = s).

Essentially a principal surrogate requires that whenever the treatment does not change the surrogate (S₁ = S₀ = s) there is no difference in the distribution of potential outcomes with versus without treatment. If a surrogate satisfied this property then an effect of A on Y will be present only if an effect of A on S is present. If Y is binary the definition of a principal surrogate is equivalent to E(Y₁ − Y₀|S₁ = S₀ = s) = 0, a condition that may be referred to as no principal strata direct effects (VanderWeele, 2008). This could likewise be referred to as the property of "average causal necessity" (Gilbert and Hudgens, 2008). If Y is not binary, then principal surrogacy as defined above requires the stronger condition pr(Y₁|S₁ = S₀ = s) = pr(Y₀|S₁ = S₀ = s). Lauritzen (2004) proposed a slightly stronger definition related to surrogacy that he referred to as a "strong surrogate":

Strong Surrogate (Lauritzen, 2004)

S is a strong surrogate for the effect of A on Y if the causal diagram in Figure 1b is valid.

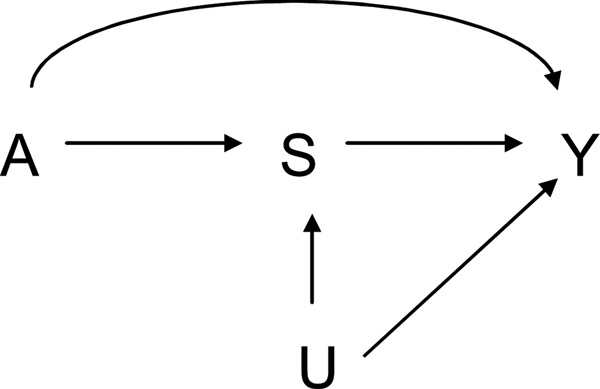
Conceived of another way, S is a strong surrogate for the effect of A on Y if A is an instrument for the effect of S on Y (Lauritzen, 2004). If S is not a strong surrogate then the causal diagram would be that in Figure 2, where if the treatment is randomized, U can be taken as the principal stratum (S₀, S₁) so that Figure 2 makes no assumption about counterfactual distributions beyond that implied by the randomization of A. The variable S will be a strong surrogate for the effect of A on Y if the "controlled direct effects" (Pearl, 2001) are such that Y_1s − Y_0s = 0 for all s. A strong surrogate is also a principal surrogate (Lauritzen, 2004; VanderWeele, 2008) but the reverse implication does not hold because principal surrogacy only requires no direct effects when S₁ = S₀ = s and only requires this in distribution, not for all individuals. Note also that a strong surrogate will be a statistical surrogate if there is no common cause of the surrogate and the outcome as in Figure 1a but a strong surrogate need not be a statistical surrogate if there is such a common cause as in Figure 1b.

Fig. 2.

Causal diagram allowing for an effect of A on Y not through the putative surrogate S.

Chen et al. (2007) introduced one further notion concerning surrogacy which they referred to as a consistent surrogate. Chen et al. (2007) restricted discussion of consistent surrogates to setting which involved a strong surrogate. Below we will generalize Chen et al.’s definition to one which allows for a direct effect of A on Y. Chen et al. (2007) defined a strong surrogate S to be a consistent surrogate for the effect of A on Y if, (a) for a positive average causal effect of S on Y , a non-positive (non-negative) average causal effect of A on S implies a non-positive (non-negative) average causal effect of A on Y , (b) for a negative average causal effect of S on Y , a non-positive (non-negative) average causal effect of A on S implies a non-negative (non-positive) average causal effect of A on Y and (c) a null average causal effect of A on S implies a null average causal effect of A on Y.

If a surrogate is not consistent in this sense then we may have effect reversal: treatment A may have a positive effect on S and S on Y but the effect of A on Y may be negative! Chen et al. (2007) refer to such effect reversal as instances of the "surrogate paradox." Chen et al. (2007) went on further to give an example showing that neither a principal surrogate nor even a strong surrogate necessarily satisfies the properties of a consistent surrogate. Both principal surrogates and strong surrogates are subject to the surrogate paradox. This is somewhat surprising as the notions of a principal surrogate and a strong surrogate are already quite stringent; it is also rather disturbing in that such effect reversal seems to completely undermine the value of a surrogate marker. In the next section we review and extend results concerning sufficient conditions that ensure the surrogate paradox is avoided. First, however, we generalize slightly the notion of a consistent surrogate described by Chen et al. (2007) so as to allow for settings in which the surrogate is not a strong surrogate (i.e. the treatment may have a direct effect on the outcome not through the surrogate) and for settings in which we may not be willing to talk about the "causal effect" of the surrogate on the outcome and may not be willing to envision interventions on the surrogate S.

Consistent Surrogate

S is said to be a a consistent surrogate for the effect of A on Y if (a) when S and Y are positively associated, a non-positive (non-negative) average causal effect of A on S implies a non-positive (non-negative) average causal effect of A on Y , (b) when S and Y are negatively associated a non-positive (non-negative) average causal effect of A on S implies a non-negative (non-positive) average causal effect of A on Y. A surrogate that is not a consistent surrogate is said to exhibit the surrogate paradox.

The focus of the remainder of this paper will be on articulating conditions under which the surrogate paradox as defined above is avoided i.e. when data on the effect of A on S in conjunction with knowledge that the surrogate and outcomes are strongly correlated can together be used to draw conclusions about the direction of the effect of the treatment A on the outcome Y.

3. Results on Consistent Surrogates to Avoid the Surrogate Paradox

Chen et al. (2007) gave the following sufficient conditions concerning avoiding the surrogate paradox.

Proposition 1 (Chen et al., 2007)

If S is a strong surrogate for the effect of A on Y (i.e. if Figure 1b is a valid causal diagram) then if (a) E(Y|s, u) is non-decreasing in s for all u and (b) pr(S> s|a, u) is non-decreasing in a for all s, u, then E(Y_a) = E(Y|a) is non-decreasing in a.

Viewed another way, if S is a strong surrogate (no direct effects of treatment on the outcome not through the surrogate) and if conditions (a) and (b) are satisfied then the effect of A on Y will be in the direction expected and the surrogate paradox avoided: E(Y_a) is non-decreasing in a so E(Y₁) − E(Y₀) ≥ 0. The result remains true if in both conditions (a) and (b), "non-decreasing" is replaced by "non-increasing"; if only one of conditions (a) or (b), "non-decreasing" is replaced by "non-increasing" then the conclusion of Proposition 1 changes to E(Y_a) = E(Y|a) is non-increasing in a. Similar remarks hold for the other propositions below. Note that to avoid the surrogate paradox (i.e. to ensure a consistent surrogate) a non-negative average causal of A on S is not sufficient; rather one needs the effect to be non-negative in the distributional sense that pr(S > s|a, u) is non-decreasing in a for all s, u; this is sometimes referred to as "distributional monotonicity"(VanderWeele et al., 2008; VanderWeele and Robins, 2009, 2010). Note that the assumption that S is a strong surrogate is not a testable assumption. Note also there may be different variables U for which Figure 1b could be a valid causal diagram. The conclusion of Proposition 1 will hold if there is any U such that Figure 1b is a causal diagram and such that conditions (a) and (b) hold. Similar points pertain also to Propositions 2–4 below.

Ju and Geng (2010) generalized the result of Chen et al. (2007) to give a stronger conclusion if condition (a) is also replaced by one of distributional monotonicity.

Proposition 2 (Ju and Geng, 2010)

If S is a strong surrogate for the effect of A on Y (i.e. if Figure 1b is a valid causal diagram) and if (a) pr(Y > y|s, u) is non-decreasing in s for all y, u and (b) pr(S > s|a, u) is non-decreasing in a for all s, u, then pr(Y_a > y) = pr(Y > y|a) is non-decreasing in a.

Here we get the slightly stronger conclusion that not simply does A increase Y on average but that the effect of A on Y is also distributionally monotonic. In fact, as discussed in the online supplement, both of these results of Chen et al. (2007) and Ju and Geng (2010) follow almost immediately from the theory of signed causal directed acyclic graphs (VanderWeele and Robins, 2009, 2010). Moreover, more general results are possible. The definitions and results above have essentially been concerned with the case in which the effect of A on Y is entirely through S. In most cases, this will likely be unrealistic. A good surrogate may account for a large portion of the effect of A on Y but it is unlikely that the surrogate accounts for all of this effect. Likely there will be an effect of A on Y not through S as in Figure 2. It is shown in the online supplement that the following two results hold; these generalize Chen et al. (2007) and Ju and Geng (2010) respectively by allowing for an effect of A on Y not through S.

Proposition 3

In the causal diagram in Figure 2, if (a) E(Y|a, s, u) is non-decreasing in a and s for all u and (b) pr(S > s|a, u) is non-decreasing in a for all s, u then E(Y_a) = E(Y|a) is non-decreasing in a.

Similar results hold under non-increasing rather than non-decreasing functional relationships. Proposition 3 has an important and intuitive interpretation. Suppose that in a randomized trial we find a positive average causal effect of A on S and we know that S and Y are strongly positively correlated. This is often the setting encountered with surrogate outcomes. In this setting, under what circumstances might the surrogate paradox arise? When might the effect of A on Y be negative rather than positive? Proposition 3 states that at least one of three things must occur if we are to get this effect reversal. First, there may be a negative direct effect of A on Y not through S (i.e. the first part of assumption (a) that E(Y|a, s, u) is non-decreasing in a may be violated). Second, it may be the case that although S and Y are positively correlated this may not indicate the actual causal relationship of S on Y ; the association may be due to confounding by U (i.e. the second part of assumption (a) that once we condition on U, E(Y|a, s, u) is non-decreasing in s may be violated). Third, even if neither of these first two phenomenon occur, it may be the case that even though A positively affects S on average and S positively affects Y, A may not positively affect S for all individuals; it may decrease S, and thus decrease Y for some individuals; we may have a lack of transitivity (i.e. assumption (b), the assumption concerning distributional monotonicity which guarantees that this is avoided, may be violated). In summary, if the surrogate paradox is to occur we either need (i) a direct effect of A on Y not through S in the opposite direction or (ii) confounding for the effect of S on Y, or (iii) a lack of transitivity so that A does not positively affect S for all the same individuals for which S positively affects Y. In thinking about whether the surrogate paradox might occur and whether one ought to draw conclusions concerning an outcome of interest from the analysis of the results concerning a surrogate, an investigator could think through each of these three possibilities. Proposition 3 states that at least one of them must occur if the surrogate paradox is to arise.

Proposition 4 below gives a somewhat stronger conclusion concerning distributional monotonicity of the effect of A on Y under somewhat stronger assumptions. Proposition 4 generalizes the results of Ju and Geng (2010) to allow for a direct effect of A on Y. If the outcome Y is binary Propositions 3 and 4 are equivalent.

Proposition 4

In the causal diagram in Figure 2, if (a) pr(Y > y|a, s, u) is non-decreasing in a and s for all y, u and (b) pr(S > s|a, u) is non-decreasing in a for all s, u then pr(Y_a > y) = pr(Y > y|a) is non-decreasing in a.

In the next section we will relate these results on consistent surrogates to various statistical and causal approaches to the analysis of surrogate outcomes.

4. Consistent Surrogates and Measures of Surrogacy

Joffe and Greene (2009) considered four different approaches that have been proposed to evaluate surrogates or to measure the extent of surrogacy and they derived relations between them under linear model assumptions. Here we will revisit each of these four approaches in light of the results above on consistent surrogates. These four approaches could broadly be described as (i) a "proportion-explained" approach, (ii) an "indirect effects" approach, (iii) a "meta-analytic" approach and (iv) a "principal stratification" approach. We will consider each in turn. Each of these approaches may tell us something about the role that the surrogate S plays in the relationship between treatment A and outcome Y. Here, however, we will assess whether these approaches help us evaluate whether a surrogate is consistent i.e. whether the surrogate paradox is avoided. We will consider the metrics that are used to evaluate surrogacy in each of these four approaches and consider whether these metrics correspond in any way to ensuring that one has a consistent surrogate.

Freedman et al. (1992) proposed using a “proportion explained" measure to assess surrogacy. Suppose one were to regress the outcome Y on the exposure A:

$$E(Y|A=a)={\mathrm{\Phi }}_0+{\mathrm{\Phi }}_{1}a$$

and then regress the outcome Y on the exposure A and the surrogate S:

$$E(Y|A=a,S=s)={\theta }_0+{\theta }_{1}a+{\theta }_{2}s$$

The proportion of the total effect explained by the surrogate is then taken as:

$$({\mathrm{\Phi }}_1-{\theta }_1)/{\mathrm{\Phi }}_1$$ (1)

which is equivalent to 1 − θ₁/Φ₁. Statistical inference for this measure is also described by Lin et al. (1997). The measure does, however, suffer from problems if either Φ₁ is small or if the model for E(Y|A = a, S = s) is not correctly specified (Molenberghs et al., 2002). A similar measure is sometimes used in the setting of "mediation analysis" to assess the proportion of the effect of A on Y mediated by S. In the setting of mediation analysis this measure is problematic because there may be confounding of the effect of S on Y by U; this can occur even if treatment A is randomized since the surrogate S is generally not randomized. Because of this confounding using the proportion in (1) as a measure of mediation can be highly problematic (Robins and Greenland, 1992; Pearl, 2001; VanderWeele, 2010). However, in the context of surrogacy (rather than mediation) if the goal is simply to assess how much of the effect of A on Y can be predicted by the effect of A on S these concerns about confounding may be less relevant. Even if U is a common cause of S and Y, if because of U, S give important information about Y then S may still be a good surrogate insofar as it may be possible to predict the sign of the effect of A on Y from the sign of the effect of A on S. Although the measure in (1) of the "proportion explained" may thus serve as a useful measure, it is not immune to the surrogate paradox. An example is given below in which the average causal effect of A on S is positive, the average causal effect of S on Y is positive, "proportion explained" is 100%, but the effect of A on Y is negative. This can occur because it may be the case that A does not positively affect S for the same individuals for which S positively affects Y. Nothing in the "proportion explained" measure guarantees the distributional monotonicity needed to avoid the surrogate paradox. Thus even if a surrogate is judged to be "good" from the standpoint of having a high proportion explained, this does not guarantee that the surrogate is consistent.

The second approach considered by Joffe and Greene (2009) may be referred to as the "indirect effects" approach. This was essentially the approach pursued by Taylor et al. (2005). This approach relies on the counterfactual framework and specifically counterfactual definitions of what are now often called natural indirect effects (Pearl, 2001). The alternative notion of controlled direct effect (Pearl, 2001), although useful for assessing whether there is an effect of the treatment on the outcome not through the surrogate, cannot be employed directly to assess mediation (Robins and Greenland, 1992). The average natural indirect effect is defined as E(Y_1S1 − Y_1S0) and measures the effect comparing setting the treatment to present with the surrogate set to what it would have been with versus without the treatment (Robins and Greenland, 1992; Pearl, 2001). For it to be non-zero the treatment must have an effect on the surrogate (i.e. S₁ and S₀ must differ) and then the surrogate must have an effect of the outcome (i.e. the change in the surrogate from S₀ to S₁ must have an effect on Y). This is thus sometimes referred to as a "mediated effect." A measure of surrogacy may then be taken as the "proportion mediated" i.e. the proportion of the natural indirect effect to the total effect:

$$\frac{E(Y_{1S_1}-Y_{1S_0})}{E(Y_1-Y_0)}.$$ (2)

The conditions for identification and estimation of the natural direct and indirect effect are described elsewhere (Pearl, 2001; Taylor et al., 2005; Joffe and Greene, 2009; VanderWeele and Vansteelandt, 2010; Imai et al., 2010) and are beyond the scope of this paper. Identification of the natural indirect effect does, however, require control for common causes of the intermediate S and the outcome Y (Pearl, 2001; Joffe and Greene, 2009; VanderWeele and Vansteelandt, 2010). The advantage of this approach to surrogate measures is that, provided the natural indirect effect has been correctly identified and estimated, it gives the actual effect of the treatment on the outcome through the surrogate. Likewise, the natural direct effect, E(Y_1S0 − Y_0S0), can be used to assess whether there is an effect of the treatment on the outcome not through the surrogate and one could evaluate whether this was in the opposite direction of the direct effect. The natural indirect and direct effects sum to the total effect: E(Y_1S1 − Y_1S0) + E(Y_1S0 − Y_0S0) = E(Y_1S1) − E(Y_0S0) = E(Y₁) − E(Y₀). Thus, if the natural direct and indirect effects were known this could be useful in diagnosing the surrogate paradox if these two effects were in opposite directions. The difficulties are, however, effectively transferred to the challenge of identifying and consistently estimating the natural indirect effect, E(Y_1S1 − Y_1S0). The identification conditions needed to identify this natural indirect effect are quite strong (Pearl, 2001; VanderWeele, 2010) which constitutes a disadvantage to this approach. Within the "indirect effects" approach, the criterion generally used to assess whether a surrogate is "good" (whether the proportion mediated is large) unfortunately, however, does not help guarantee that a surrogate is consistent. As will be seen in the illustration below, we can in fact have a high proportion mediated (even 100% mediated) in settings in which S exhibits the surrogate paradox. Although the natural direct and indirect effects themselves (if known) could be useful in diagnosing the surrogate paradox, the proportion mediated criterion itself does not ensure a surrogate is consistent.

The "indirect effects" approach, taken as a measure of surrogacy, also suffers from another problem. Consider the causal diagram in Figure 3 in which the surrogate S has no effect on the outcome Y. Now it may be the case that although S has no effect on Y, it may, because of a common cause U, serve as a very good proxy for Y. Knowing about the value of S may be strongly predictive of what will occur with Y potentially for both the treatment and the control arm of a trial. In this case, S could still be a very useful and informative surrogate. However, the natural indirect effect, E(Y_1S1 − Y_1S0), would be 0 because S has no effect on Y. The measure of surrogacy in (2) would be 0 even though S might be a highly informative surrogate. Whereas the "proportion explained" measure is essentially too liberal for mediation (but may be useful for surrogacy), the "indirect effect" measure is too conservative to assess surrogacy (even though it may be of use in assessing mediation). A good surrogate need not mediate the effect of treatment on the outcome if it is otherwise informative of the effect of treatment on the outcome. Conceived of another way, although confounding is important to consider in evaluating the surrogate paradox, when considering measures of surrogacy it is not always simply a problem to be gotten rid of, but can provide valuable relations between S and Y which may be helpful in predicting the effect of A on Y from the effect of A on S. The "indirect effects" approach by attempting to control for or eliminate confounding essentially misses this potentially important source of information concerning surrogacy. The "indirect effect" measure of surrogacy in (2) may be of use when most of the effect of A on Y is in fact mediated through S and when the confounding between S and Y is weak but in general it eliminates, rather than incorporates, information that may be of importance for assessing the value of a surrogate.

Fig. 3.

Example of a surrogate S with no effect on the outcome Y.

Much of the literature seems to treat the problems of surrogacy and direct/indirect effects as almost interchangeable problems, and certainly the concepts and methods that have been employed have overlapped considerably for surrogacy and mediation. The goals, however, are quite different. In mediation analysis, we are interested specifically in whether there is an effect of treatment on the outcome that operates through the intermediate. This setting may also be of interest when assessing the properties of a surrogate; but with surrogate outcomes there are settings, as illustrated in Figure 3 above, in which a variable may serve as a very valuable surrogate even if it does not mediate at all the effect of treatment on the outcome. Whereas mediation concerns the pathways by which effects arise, surrogacy concerns principally whether we are able to predict the direction of one effect (of treatment on the outcome) by using another (the treatment on the surrogate). Confounding plays a very different role in questions of mediation versus questions of surrogacy. Whereas it is a problem in assessing mediation, it may be an important source of information in surrogacy. The causal estimands best used to capture mediation and surrogacy also differ. The natural indirect effect (Robins and Greenland, 1992; Pearl, 2001) is arguably the most important counterfactual contrast when assessing mediation. However, as argued above, it may, at least in some settings, be of limited interest in assessing surrogacy. A good surrogate need not mediate the effect. While methods developed for mediation and for surrogacy will undoubtedly inform methodology in the other area, the goals and the questions of each setting should be firmly kept in view in deciding on what concepts, definitions and methods are most relevant.

The third approach considered by Joffe and Greene (2009) may be referred to as the "meta-analytic" approach. It may be applied to subgroups defined across studies (as in traditional meta-analysis) or by creating subgroups based on covariates. Burzykowski et al. (2005), for example, propose using either multiple studies or multiple groups defined by covariates within a study to assess surrogacy. Let Φ_j denote the effect of treatment A on the outcome Y in the jth study/group. Let ϕ_j denote the effect of treatment on the surrogate in the jth study/group. Note that estimation of Φ_j and ϕ_j relies only on the assumption of randomization. To assess surrogacy visually, we could plot estimates of Φ_j against estimates of ϕ_j. For a good surrogate, we would hope to find (i) a monotonic relationship between ϕ_j and Φ_j, (ii) when ϕ_j = 0 then Φ_j = 0 and (iii) in a (possibly non-parametric) regression of estimates of Φ_j on estimates of ϕ_j we should not find much variability around the regression line. If the relationship between Φ_j and ϕ_j is approximately linear we could run a linear regression of estimates of Φ_j on estimates of ϕ_j and use the R² in this regression

$$R^2=\mathit{\text{Corr}}({\mathrm{\Phi }}_j,{\varphi }_j)$$ (3)

as a measure of surrogacy. For this approach to work, however, there must of course be variation in Φ_j and ϕ_j and there must be multiple studies or subgroups in which to estimate effects. Let us now turn to the question of the relation of the meta-analytic approach to the surrogate paradox and the notion of a consistent surrogate. The meta-analytic approach does not give a criterion that ensures the absence of the surrogate paradox, but it can help diagnose and circumvent it. With the meta-analytic approach, if sample sizes are sufficiently large and estimates and modeling assumptions sufficiently precise, an investigator will be able to identify which studies or subgroups are subject to effect reversal (the surrogate paradox) and, for such subgroups, avoid the use of the surrogate. The meta-analytic approach does not give a criterion for avoiding the surrogate paradox but may be of use in detecting groups for which the surrogate is not consistent.

The fourth approach to surrogacy considered by Joffe and Greene (2009) is that of "principal stratification." This approach builds on the initial insights of Frangakis and Rubin (2002) and was developed more fully by Follmann (2006), Gilbert and Hudgens (2008), Wolfson and Gilbert (2010) and Huang and Gilbert (2011). Using notions of principal stratification (i.e. conditioning on the joint counterfactual (S₀, S₁)), Gilbert and Hudgens (2008) define as a measure of surrogacy what they call the "causal effect predictiveness surface" given by:

$$CEP(s_1,s_0)=E(Y_1-Y_0|S_1=s_1,S_0=s_o).$$ (4)

If we knew CEP(s₁, s₀) then we would know for each principal stratum (S₁ = s₁, S₀ = s₀) what the effect of treatment would be. For a binary outcome, the notion of principal surrogacy of Frangakis and Rubin (2002) is simply that CEP(s₁, s₀) = 0 for s₁ = s₀. For example, suppose the surrogate is binary. The effects CEP(0, 0) and CEP(1, 1) are sometimes referred to as "dissociative effects" and CEP(1, 0) (or CEP(0, 1)) as an "associative effect". Principal surrogacy requires that the dissociative effects are zero: CEP(0, 0) = CEP(1, 1) = 0 i.e. that when the treatment does not change the surrogate, the treatment will not change the outcome. Principal surrogacy is often taken as a criterion for a "good surrogate." The notion is theoretically appealing. Unfortunately, as already indicated above, a principal surrogate does not prevent the surrogate paradox (Chen et al., 2007). A principal surrogate need not be a consistent surrogate. This is also illustrated in the example below. If we knew the causal predictive surface CEP(s₁, s₀) for each principal stratum (S₁ = s₁, S₀ = s₀) then this could potentially be useful in diagnosing the surrogate paradox. For example, if we knew we had a principal surrogate (i.e. CEP(0, 0) = CEP(1, 1) = 0) and if we also had monotonicity of the effect of A on S so that the principal stratum (S₁ = 0, S₀ = 1) was empty, then the direction of the average treatment effect of A on Y would be of the same sign as CEP(1, 0). However, the criterion of "principal surrogacy" alone (which itself may be difficult to assess) does not ensure a consistent surrogate. Accordingly, Gilbert and Hudgens (2008) modify the definition of a principal surrogate from that of Frangakis and Rubin (2008) to also require what they call 1-sided average causal sufficiency that, for a binary outcome, S₁ > S₀ implies P(Y₁ = 1|S₁ = s₁, S₀ = s₀) > P(Y₀ = 1|S₁ = s₁, S₀ = s₀). If a surrogate S has the properties of causal necessity and 1-sided average causal sufficiency, it is straightforward to verify that S cannot exhibit the surrogate paradox. This modified criteria could then be used for diagnosing the surrogate paradox.

Unfortunately, like the "indirect effects" approach, the "principal stratification" approach also requires strong assumptions for identification of the causal predictiveness surface. Moreover, even when assumptions have been made to identify effect measures, one still does not know which individuals fall into which strata and thus the measures are difficult to use in making decisions prospectively about which individuals should or should not be treated. Notions of surrogacy based on principal stratification are theoretically appealing but difficult to identify in practice. Alternative designs and additional assumptions (Follmann, 2006; Huang and Gilbert, 2011) can help with identification of these effects; alternatively, Follmann (2006) and Huang and Gilbert (2011), have argued that an alternative estimand that conditions only on S₁ and ignores S₀ may be easier to identify from data and still of interest, though, as with others, the value of such alternative estimands in ensuring a consistent surrogate is unclear.

In summary, none of the approaches to surrogate outcomes is entirely immune to the surrogate paradox. For the "proportion explained", "indirect effects" and "principal stratification" approaches, none of the standard criterion guarantee a consistent surrogate. The "proportion explained" may be 100% and yet the surrogate paradox may still arise. Likewise the "proportion mediated" using the ratio of the natural indirect effect to the total effect may be 100% and again the surrogate paradox may arise. Finally, a surrogate may be a "principal surrogate" but not a consistent surrogate - the surrogate paradox may still be present. The "meta-analytic" approach does not provide a criterion to avoid the surrogate paradox but it can be useful in diagnosing it. Likewise in the "indirect effects" approach if the natural direct and indirect effects were known, these could be useful in diagnosing the surrogate paradox if it were due to the direct and indirect effects being in opposite directions; and in the principal stratification approach, if the causal predictiveness surface were known this could likewise be useful in diagnosing the surrogate paradox. Unfortunately, however, both the "indirect effects" approach and the "principal stratification" approach suffer from issues of lack of identification; strong assumptions are in general needed to identify these effects, though alternative study designs or sensitivity analysis techniques can sometimes be useful. In light of the aforementioned issues concerning the problems with the surrogate paradox and difficulties in identification, the "meta-analytic" approach may offer the most promise for assessing surrogate outcomes and for making policy and treatment decisions. The approach in principle relies only on randomization assumptions and does not consider effects that require stronger assumptions to identify; moreover, it allows for easier diagnosis of effect reversal manifested in the surrogate paradox. Nonetheless, it is not without its disadvantages as the sample size requirements for effective implementation may be prohibitively large (Gail et al., 2000). Wu et al. (2011) have also recently proposed some empirical criterion to assess consistent surrogate but sample size requirements may likewise make practical implementation difficult.

5. Illustration

To illustrate some of the difficulties with the various approaches considered, especially in the absence of subgroup data required by the meta-analytic approach, consider the following example. Suppose A is randomized, that pr(S₁ = 0, S₀ = 0) = pr(S₁ = 1, S₀ = 1) = pr(S₁ = 2, S₀ = 2) = 0.1, pr(S₁ = 1, S₀ = 0) = 0.5, and pr(S₁ = 1, S₀ = 2) = 0.2 and finally suppose Y = (0.1) * 1(S = 1) + 1(S = 2) + ε_Y, where ε_Y is a standard normal random variable. Here it can be calculated that E(S_a=1 − S_a=0) = 0.3, E(Y_s=2 − Y_s=1) = 1, E(Y_s=1 − Y_s=0) = 0.1 but E(Y_a=1 − Y_a=0) = −0.13 so that the surrogate paradox is present, with a positive effect of A on S, a positive effect of S on Y, no direct effect of A on Y not through S, but a negative overall effect of A on Y; S is not a good surrogate. If we apply the "proportion explained" approach we get a proportion explained estimate of 100%, suggesting that S is a perfect surrogate. If we apply the "indirect effects" approach, the natural indirect effect and total effect are both −0.13, suggesting 100% mediation and thus that S is a good surrogate, which it is not. The surrogate does, moreover, satisfy Prentice’s criteria. Finally, using principal strata, we would have CEP(0, 0) = CEP(1, 1) = CEP(2, 2) = 0, implying that S is a "principal surrogate" and, by this criterion, thus a good surrogate. In this example, the associative effect CEP(S₁ = 1, S₀ = 0) = 0.1, which is of the opposite sign of the overall effect of treatment on the outcome and of the other associative effect, CEP(S₁ = 1, S₀ = 2) = −0.9. If we were to use as a criterion for a "good surrogate" either (i) the proportion explained, or (ii) the ratio of the natural indirect effect to total effect, or (iii) principal surrogacy, then all three of these approaches would suggest that we have a good surrogate, when, in fact, with the surrogate coded as S ∈ (0, 1, 2), the sign of the effect of the treatment on the surrogate is the opposite of the sign of the effect of the treatment on the outcome, even though the surrogate has a positive effect on the surrogate and even though there is no direct effect of treatment on the outcome not through the surrogate. In this example, failure of transitivity causes the problem. In other examples, unmeasured confounding or the presence of a direct effect may give rise to the surrogate paradox. Note that in this particular example a recoding of S to (0, 1, 10) would resolve the surrogate paradox in that the effect of the treatment on the surrogate would be of the same sign as that of the treatment on the outcome.

6. Concluding Remarks

The surrogate paradox is an important problem. If the effect of the treatment on the surrogate is in the opposite direction of the effect of the treatment on the outcome of interest, policy and treatment decisions may be severely misguided. In the case of ventricular arrhythmia, this very problem resulted in an estimated 50,000 excess deaths (Moore, 1995). In this paper, we have reviewed definitions relevant to surrogate outcomes and have specifically considered how these definitions are related to the surrogate paradox, namely that, the effect of the treatment on the surrogate may be positive, the surrogate and outcome strongly positively associated, but the effect of the treatment on the outcome might still be negative. Such effect reversal can arise with what has been defined as "statistical surrogates" (Prentice, 1989), "principal surrogates" (Frangakis and Rubin, 2002) and "strong surrogates" (Lauritzen, 2004). We have reviewed and extended results on sufficient conditions that ensure a surrogate is "consistent" i.e. that it avoids the surrogate paradox. These results extend previous literature by showing that there are sufficient conditions that avoid the surrogate paradox even when there is a direct effect of the treatment on the outcome not through the surrogate. The results show that for the surrogate paradox to arise at least one of the following must be present: (i) a direct effect of the treatment on the outcome not through the surrogate, (ii) confounding of the surrogate-outcome relationship or (iii) a lack of transitivity so that the treatment does not change the surrogate for all the same persons for whom the surrogate changes the outcome. The conditions and the results of the paper are important because they provide simple conditions which allow investigators to predict the direction of the effect of the treatment on the outcome from the direction of the effect of the treatment on the surrogate. We have seen how these notions of consistent surrogates are related to four surrogate assessment approaches described by Joffe and Greene (2009): the "proportion explained" approach (Freedman et al., 1992), the "indirect effects" approach (Taylor et al., 2005), the "meta-analytic" approach (Burzykowski et al., 2005) and the "principal stratification" approach (Frangakis and Rubin, 2002). All potentially suffer from the surrogate paradox. In particular, without imposing further conditions, none of these approaches’ criteria to assess whether a surrogate is "good" (e.g. "100% proportion explained", "100% proportion mediated", "principal surrogacy") is sufficient to ensure that the surrogate paradox is avoided. However, a modification of the "principal surrogacy" criterion (Gilbert and Hudgens, 2008) does suffice. The "meta-analytic" approach may also prove useful in in making treatment decisions based on surrogates and circumvents some of the identification issues of other approaches, though sample size requirements (Gail et al., 2000) may make this impractical.

In this paper, we have focused on the task of determining when data concerning the effect of treatment on the surrogate can be used to make decisions about the direction of the effect of the treatment on an outcome i.e. of assessing whether a surrogate is consistent. We have considered the value of a number of different results and approaches to surrogate outcomes in accomplishing this task. Surrogates may however be useful in other tasks. For example, we might be interested in determining the extent to which we can predict the outcome once we observe the treatment and surrogate; or the extent to which we could use treatment, surrogate and outcome data in one population to predict the effect of treatment on outcomes in another population (or the effect of a different treatment in the same population) for which only data on treatment and surrogate are available. Future research could consider the value of the various approaches considered here (proportion explained, indirect effect, meta-analytic, principal stratification) or other approaches in accomplishing these other tasks and goals for which surrogates may be of use.