Mining Tertiary Structural Motifs for Assessment of Designability

Abstract

The observation of a limited secondary-structural alphabet in native proteins, with significant sequence preferences, has profoundly influenced the fields of protein design and structure prediction (Simons et al., 1997; Verschueren et al., 2011). In the era of structural genomics, as the size of the structural dataset continues to grow rapidly, it is becoming possible to extend this analysis to tertiary structural motifs and their sequences. For a hypothetical tertiary motif, the rate of its utilization in natural proteins may be used to assess its designability - the ease with which the motif can be realized with natural amino acids. This requires a structural similarity search methodology, which rather than looking for global topological agreement (more appropriate for functional categorization of proteins or domains), identifies detailed geometric matches. In this chapter we introduce such a method, called MaDCaT, and demonstrate its use by assessing the designability landscapes of two tertiary structural motifs. We also show that such analysis can establish structure/sequence links by providing the sequence constraints necessary to encode designable motifs. As a logical extension of their secondary-structure counterparts, statistics of tertiary structural preferences will likely prove extremely useful in de novo protein design and structure prediction.

1. Introduction

The universe of natural protein structures appears to be degenerate, with many frequentlyrepeating structural motifs (Vanhee et al., 2010; Verschueren et al., 2011). This is certainly apparent on the level of secondary structure as the majority of structured residues in folded proteins are found in either α-helices or β-strands (Joosten et al., 2011). However, the structural degeneracy goes beyond that. For example, clear preferences have been found for the ways in which secondary-structural elements come together in folded proteins. Helix-helix interactions in trans-membrane (TM) proteins (Walters and DeGrado, 2006) as well as overall topologies of TM proteins (Fuchs and Frishman, 2010) have been effectively classified and shown to have strong geometric biases. In soluble proteins, helixhelix crossings represent a classical example of a structural motif with strong geometric preferences (Kallblad and Dean, 2004; Moutevelis and Woolfson, 2009; Testa et al., 2009; Grigoryan and Degrado, 2011). Other well-established biases in super-secondary arrangements include packing of α-helices against β-sheets (Hu and Koehl, 2010), shearing and twisting of β-sheets (Ho and Curmi, 2002), β-turn and α-α linking geometries (Hutchinson and Thornton, 1994; Engel and DeGrado, 2005), and others (Platt et al., 2003). In fact, when Fernandez-Fuentes and co-workers structurally classified all motifs consisting of two secondary-structural elements (α-helices or β-strands) connected by a loop, they found the different classes to occur at very different frequencies in the Protein Data Bank (PDB) (Fernandez-Fuentes et al., 2010). The structural degeneracy of proteins is further evident at the level of domains (i.e. separable globular segments of structure), which are highly reused in nature (Marchler-Bauer et al., 2011), domain-domain and domain-peptide interaction interfaces (Vanhee et al., 2009; London et al., 2010; Vanhee et al., 2010; Stein et al., 2011), and even at the level of full-length protein structures, which are amenable to systematic hierarchical classification (Greene et al., 2007; Andreeva et al., 2008).

There can be several explanations for why some seemingly reasonable geometries appear to be very rare in proteins while others are very frequent. This may in part be due to incomplete coverage of the protein structural universe by the PDB, though at its present size the database is believed to have nearly saturated many structural features (Zhang and Skolnick, 2005; Baeten et al., 2008; Fernandez-Fuentes et al., 2010). Stochasticity in early evolution may have also contributed to higher prevalence of some types of structures over others. However, an important reason is likely that some structures are simply more difficult to realize using the twenty naturally-occurring amino acids. This concept has been referred to as the designability of a protein structure, loosely defined as the number of amino-acid sequences capable of folding into it (Govindarajan and Goldstein, 1996; Li et al., 1996; Helling et al., 2001; England et al., 2003; Wingreen et al., 2004; Grigoryan and Degrado, 2011). Designability is a complex property that combines many physical factors. Certainly, designable structures must be able to accommodate a variety of amino-acid combinations in an energetically-favored fashion. In fact, Koehl and Levitt have shown that the magnitude of the sequence space compatible with a natural protein backbone correlates well with natural sequence diversity (Koehl and Levitt, 2002). But designability is also related to less easily-measurable properties such as fold specificity – that is, whether for a given sequence the structure is optimal from within the continuum of possible folds. Designable structures should represent such an optimum for many sequences and several investigators have demonstrated this to be highly structure dependent (Govindarajan and Goldstein, 1996; Wingreen et al., 2004). Additional factors contributing to natural utilization of structural motifs may include folding/unfolding rates and robustness to small changes in environmental conditions.

As a result of combining many desirable but difficult-to-compute properties, designability is of significant utility in such fields as computational protein design or structure prediction. In design, one would like to a priori limit oneself to considering only highly designable structural templates. In structure prediction, designability would be a useful filter for discarding likely non-native structures. Natural structures are certainly expected to be at least somewhat designable. As a consequence, many methods in computational protein design have relied on using native backbone structures (Reina et al., 2002; Kortemme et al., 2004), building novel structures from combinations of native segments (Kuhlman et al., 2003; Azoitei et al., 2011), or incorporating measures of native-like structural arrangements into scoring functions (Simons et al., 1997). Related approaches have also shown significant promise in structure prediction (Rohl et al., 2004; Zhang et al., 2011).

The natural abundance of a structural motif and its designability are related. Thus, a potential approach for evaluating the designability of a motif is to measure the degree of its recurrence in natural structures. Larger structural motifs, which contain pairs of segments not in contact and free to evolve independently, may not be sampled well either in the PDB or indeed in nature. However, this concern is greatly diminished for compact structural motifs, whose possible geometries are more likely to be well represented in the known structural universe (Vanhee et al., 2009; Fernandez-Fuentes et al., 2010; Grigoryan and Degrado, 2011; Verschueren et al., 2011). Further, even without any assumptions on the saturation of the PDB, if we do observe a motif to be highly recurrent, it is very likely designable. That is, we do not expect many false positives. On the other hand, false negatives - designable motifs that are labeled undesignable owing to poor representation in the PDB, are possible due to limited database size (especially for large motifs). This type of an error is reasonably tolerable in the context of protein design, as long as designable structures can still be identified that meet all other design criteria. Finally, one may often need to compare the designabilities of different motifs of the same size (e.g. different specific geometries of a given topology). For this purpose, only relative recurrence rates are important, which are expected to be more robust to database size and bias effects.

To enable an abundance-based metric of designability, an efficient method of searching for protein structural similarity is required. Many computational approaches have been proposed under the general category of protein structural comparison (Choi et al., 2004; Hasegawa and Holm, 2009; Budowski-Tal et al., 2010; Holm and Rosenstrom, 2010). Since designability is likely highly sensitive to the precise local geometry, one needs a method for finding matches to the detailed arrangement of atoms in the query structure. Here we present such a method, which we term MaDCaT (Mapping of Distances for the Categorization of Topology), and provide example of its usage for describing the designability landscape of several structural motifs. A C++ implementation of MaDCaT, along with a web-based tool for structural similarity searching, can be found at: http://www.grigoryanlab.org/madcat/.

Quantification of designability provides a systematic filter for engineering novel protein structures. This is particularly useful in de novo design applications, where there is no guarantee that the hypothesized structure is easily achievable with natural amino acids. Further, it is known that many apparently feasible structural templates are in fact non-designable (Grigoryan and Degrado, 2011). Recently, MaDCaT was used to impose designability in engineering peptide assemblies around singlewalled carbon nanotubes (Grigoryan et al., 2011). Because the designed structure was entirely unprecedented in nature, there was not a clear basis for the choice of assembly geometry. Imposing high designability via MaDCaT provided such a basis, reducing the very large space of apparently reasonable geometries down to the single most appropriate structure. MaDCaT can be similarly used to provide a designability filter in other de novo design applications, provided that the desired structure is partitioned into motifs small enough to be likely well sampled in nature and the PDB, but large enough to capture important tertiary structural information. Designability may also provide a useful filter in structure prediction, where a localized density of non-designable motifs could serve as an indicator of a poorly predicted region.

2. MaDCaT

MaDCaT relies on a distance-map representation of protein structure. A distance map is a 2-dimensional matrix that stores distances between atoms of a protein (Choi et al., 2004). This representation is essentially lossless in that there is a one-to-one correspondence between 3-dimensional (3D) structures and distance maps, to within chirality (i.e. mirror-image structures produce the same distance matrices) (Dattorro, 2012). In its current implementation MaDCaT considers distances between only C_α atoms (see Fig. 1). Though some structural information is lost in this way, the overall backbone geometry is preserved (Gront et al., 2007). This also comes with the convenience of representing a structure in an amino-acid independent manner, which is useful for relating structure and sequence for designable motifs (see section 3). On the other hand, the search methodology does not assume that only C_α atoms are used, so it is easy to extend the approach to deal with additional backbone atoms, side-chain atoms or pseudo-atoms (e.g. side-chain centroids). Distance maps are a particularly convenient representation for structural similarity searches because 1) they contain enough information to identify detailed matches and 2) two distance maps can be compared in a computationally efficient manner (see below), without having to invoke optimal structural superpositions, as with other similarity metrics such as root mean squared deviation (RMSD).

Figure 1.

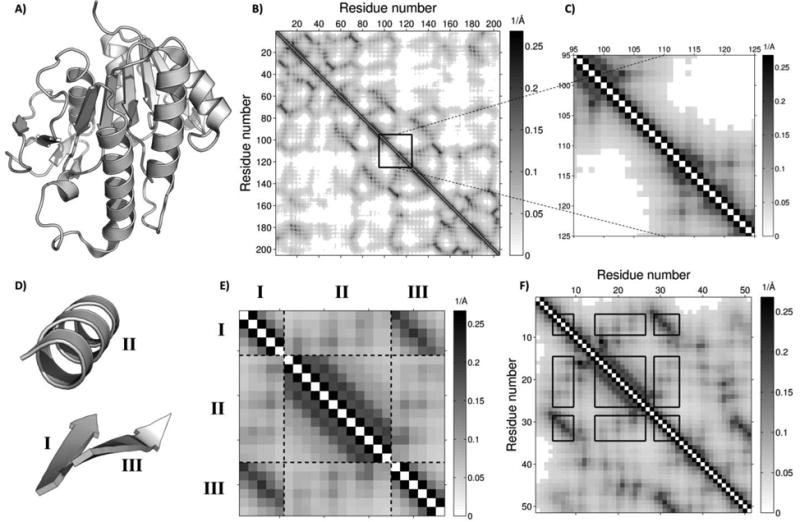
Distance-map representation of protein structure. A) PDB entry 1HE4 used to demonstrate distance map-based representation. B) The matrix of inverse distances corresponding to 1HE4 (values below 1/25 Å^-1 are set to zero and shown in white). When searching this structure for a match against a single-segment query, only diagonal alignments of the query map need to be considered, with an example alignment outlined in black. C) Magnified version of the diagonal alignment region. D) and E) are a multi-segment query structure and its corresponding distance map, respectively. Dotted lines in E) denote breaks between adjacent segments and roman numerals illustrate the correspondence between query segments in D) and sub-maps in E). F) A potentially matching alignment of the query map onto a database map (outlined in black) may have gaps between adjacent segments of the query. Further, the sequence order of segments is not guaranteed to be the same in the query and the match.

2.1. Similarity Score

Consider two protein structures (or structural segments), S₁ and S₂, each with n residues. Let r₁(i, j) and r₂(i, j) be the distances between the C_α atoms of i-th and j-th residues in S₁and S₂, respectively. A reasonable metric of similarity between the two structures, assuming a linear correspondence between residues, is the Euclidian norm:

$$d_{1,2}=\sqrt{\sum _{i<j}{[r_1(i,j)-r_2(i,j)]}^2}$$ (1)

A possible issue with this score is that most of its magnitude is likely to arise from far-away C_α atoms, because larger distances imply larger potential deviations in two related structures. On the other hand, for the purpose of assessing designability and linking sequence to structure, it is the closely contacting residue pairs that are likely most important. For this reason, in its current implementation MaDCaT uses inverse distances. Given S₁ and S₂, distance maps are stored as, respectively:

$$M_1(i,j)=\frac{1}{r_1(i,j)};M_2(i,j)=\frac{1}{r_2(i,j)}$$ (2)

with the corresponding score:

$$s_{1,2}=\parallel M_1-M_2\parallel \sqrt{\sum _{i<j}{[M_1(i,j)-M_2(i,j)]}^2}$$ (3)

a better indicator of local structural similarity. Though this score has worked well for our applications, the search method in MaDCaT is very general so any other functions of distance can be used. Hereafter, distance maps will refer to matrices of inverse distances, as in equation 2.

An added benefit of using maps of inverse distances is that they are particularly well suited for sparse representation. This is because the less “important” distances above a suitably chosen cutoff r_cut, corresponding to map entries below 1/r_cut, can be replaced with zeros in the map. Such sparse matrices not only reduce storage and memory requirements, but also result in significant speedups of the search procedure (see below). Finally, because they resemble interatomic interaction potentials, inverse distances (and their powers) are perhaps more natural basis functions for expressing structural similarity than distances themselves.

2.2. The Algorithm

As the input query, MaDCaT takes any structure composed of an arbitrary number of disjoint segments. The query is converted to its distance-map representation and used to search a database of proteins with pre-computed distance maps. Each segment within the query is considered as a whole and is only matched against segments of consecutive residues in database structures. The goal of the algorithm is to find alignments of segments in the query structure onto regions of database structures in a way that optimizes the score in equation 3. Because it is usually not know a priori what scores are good for a given query structure, MaDCaT finds the L best scoring alignments, where L is a user-specified value. In cases where an appropriate score cutoff does exist, it can be specified and will speed up the search. To introduce the algorithm, we shall first consider the case when the query is composed of a single segment and then generalize to multi-segment structures.

2.2.1. Single-segment structures

In this case, one only needs to consider alignments of the query distance map on the main diagonal of database maps (Fig. 1B). Although this is a straight-forward computation, its time cost of O(n² · N · m) (where n is the length of the query structure, N is that for an average database structure, and m is the number of database structures) can get high in practice, especially for large query structures. MaDCaT mitigates this by taking advantage of the sparsity of distance maps. Consider a particular alignment of the query map Q onto a database map M, the score for which is s(Q,M,k) = Σ_i<j[Q(i, j) – M(i + k, j + k)]², where i and j iterate over the elements of Q, and k is the offset defining the alignment (for simplicity, the square root in equation 3 will be omitted hereafter; this does not change the relative ordering of matches, and the root function can always be applied as a last stage in the calculation). Many elements M(i + k, j + k) may be zero, especially for large query maps (white cells in Figure 1C). The contribution to the total score of these elements is dependent only on Q, such that for a given Q a default score that assumes all corresponding elements in the database map to be zero can be computed once ahead of time, s_d = Σ_i<j Q(i, j)². Then, in order to find the score for a specific alignment, s(Q, M, k), s_d needs to be updated to reflect only the non-zero elements of M corresponding to Q in the alignment:

$$s(Q,M,k)=s_d+\sum _{\underset{M(i+k,j+k)\ne 0}{i<j}}({[Q(i,j)-M(i+k,j+k)]}^2-Q{(i,j)}^2)$$ (4)

Zero values in our distance maps, which store inverse distances, correspond to atom pairs farther apart than a given cutoff r_cut (by default, 25 Å is used in MaDCaT). Because the number of atom pairs within a certain distance cutoff grows at most linearly with the number of residues in the structure, this modification gives an asymptotic time of O(n · N · m), and results in significant speedups in practice.

It is also easy to imagine how simple heuristics can be used to significantly cut down on the number of alignments that need to be considered for a given query map/database map pair. These could be based on secondary-structure matching, or other local structural properties. Whereas heuristics are reasonably safe for query structures with good matches in the database, they can present significant artifacts in cases of rare on unusual queries. Since one of the envisioned uses of MaDCaT was the ability to start with an implausible hypothetical structure and progressively move towards a nearby more designable one, no heuristic pre-filters are currently available in MaDCaT, though the implementation does support them.

2.2.2. Multi-segment structures

In cases where the query structure consists of multiple disjoint segments, the query map can be thought of as composed of sub-maps (Fig. 1D-E). Each of these sub-maps represents either a contiguous segment of structure or an interface between two segments (diagonal and off-diagonal sub-maps in Fig. 1E, respectively). An alignment of the query structure onto a database structure involves the placement of each segment of the query onto an equally-sized contiguous region in the database structure. In distance-map terms, this means that diagonal maps of the query line up along the diagonal of the database map (without overlaps), and off-diagonal maps align at the resulting intersection points (see Fig. 1F). Because the alignment of individual segments is independent, the number of potential alignments grows exponentially with the number of segments. In fact, finding the optimal alignment is known to be NP-hard (Lathrop, 1994).

MaDCaT applies a branch-and-bound approach to solving this combinatorial problem, reminiscent of the approach first introduced by Holm and Sander (Holm and Sander, 1996). The algorithm represents the space of possible alignments as a search tree. At each level i of the tree, a choice has to be made as to the alignment of the i-th segment. This tree is traversed, top to bottom, making a specific choice for the alignment of the i-th segment, and moving onto the (i + l)-st. The key part of the algorithm, which enables it to give up on unproductive combinations of segment alignments early on, is the computation of a lower bound on the score of an incomplete alignment. Sub-map alignments are visited in the order of best to worst lower bound, such that as soon as the bound becomes larger than the L-th worst match found so far (where L is the desired number of top matches), the current branch can be safely terminated. When the top branch is terminated, the search tree is completely pruned. The lower bound is based on pre-scoring each individual sub-map of the query against the database map, in all relevant alignments (e.g. diagonal sub-maps are scored only in diagonal alignments). Based on these scores, lower bounds for incomplete alignments are estimated by relaxing some constraints on the remainder of the alignment (e.g. allowing sub-maps in the same column of the query map to align in different columns of the database map).

To aid in searching for larger structures or those with more than a few segments, MaDCaT has an optional greedy setting that enables it to give up on segment alignments purely based on the score of the diagonal sub-map. Using this filter eliminates the optimality guarantee that MaDCaT otherwise provides, and may lead to significantly different results for queries without well-matching structures in the database. The greedy filter requires that the similarity score in equation 3 accumulate from throughout the query matrix, rather than originating heavily from a particular sub-map. For a given userspecified greediness level g, the filter requires that the score originating from each sub-map s be no worse than g · m_s · (w_L/m), where w_L is the worst score among the top L solutions currently found, m is the total mass of the query matrix (the sum of all elements), and m_s is the mass originating from sub-map s. Although any value can be specified for g, values above 1.0 make most sense, with larger values corresponding to less greediness.

As described above, the search algorithm will consider alignments of query segments that map arbitrarily far apart in sequence of database structures. In fact, all sequence-order permutations of segments in the query structure are automatically considered by MaDCaT (e.g. the motif in Fig. 1D will match similar motifs in the database, even if the order of the three secondary-structure elements in the database structure is different). This is useful when one only cares to find matches to the segments themselves (e.g. segments represent discontinuous chains) or when all the ways of bridging the gaps between the segments are of interest. MaDCaT additionally enables one to limit the number of residues that map between two consecutive segments, by establishing lower and/or upper bounds. This can be useful when one aims to investigate motifs of a certain length for bridging two or more structural segments.

2.2.3. Interfacial searches

In some applications, the inter-segment interfacial geometry may be of more interest than the segments themselves. For example, this may be the case where one looks for starting structures to mimic one side of an existing protein-protein interface. For such cases, MaDCaT allows one to search for inter-segment portions of distance maps (e.g. the sub-map at the intersection of segments I and II in Fig. 1E). From the standpoint of computational efficiency, interfacial searches have the advantage of requiring fewer independent sub-maps, but also have the disadvantage that they can be aligned almost anywhere in database maps. Overall running times are thus comparable in practice.

2.2.4. Dali versus MaDCaT

The algorithm underlying MaDCaT bares resemblance to the structure search technique by Holm and Sander, now part of the Dali search suite (Holm and Sander, 1996; Holm and Rosenstrom, 2010). However, there are important differences between MaDCaT and Dali. With MaDCaT, the query represents an exact specification of the structure of interest (e.g. precisely defined contiguous segments and locations of allowed gaps) and the results are provably optimal matches from the given database. On the other hand, the aim of Dali is to discover close matches to sub-structures of the query. These sub-structures are not fixed a priori, and although they may cover the entire query in some cases, they are determined by a series of heuristic techniques that try to identify larger conserved regions but avoid visiting the entire search space (Holm and Sander, 1993; Holm and Sander, 1994; Holm and Sander, 1996). These differences arise primarily from different intended uses of the methods. Dali is very well suited for identifying overall structural similarities between proteins or larger protein fragments (in fact, it requires a minimum chain length of 30 residues to perform a search). For example, Dali has been used to identify topological “attractors” in protein structure space (Holm and Sander, 1996). On the other hand, with MaDCaT we aim to find close matches to precisely-defined tertiary structural motifs, aiming to quantify their designabilities. The provable optimality of MaDCaT matches is particularly critical for the latter goal.

2.2.5. Obtaining MaDCaT

MaDCaT is implemented as a C++ suite, freely available under the terms of the GNU General Public License (see http://www.grigoryanlab.org/madcat/). Inquiries about commercial licensing should be directed to the corresponding author. Support programs for MaDCaT (e.g. for building database and query maps and analysis of results) utilize the Molecular Software Library (MSL)(Kulp et al., 2012), freely available at http://msl-libraries.org. The web interface for MaDCaT is currently limited to searching over a sub-sample of the PDB, which does not find the best available matches to a motif, but in our experience can still be used to grossly estimate its designability.

3. Quantifying Designability

Several investigators have shown that the universe of sequences compatible with a native protein backbone (or close structural variations thereof) in an in silico protein design experiment correlates with evolutionary sequence profiles of the protein (Kuhlman and Baker, 2000; Koehl and Levitt, 2002; Smith and Kortemme, 2011). So, when a structure is designable, computational protein design can often identify some of the sequence space compatible with it, albeit much room for improvement remains (Boas and Harbury, 2007; Pantazes et al., 2011). However, presently it is not easy to recognize that a structure is not designable using computation protein design. This is a particular limitation for de novo protein design, where novel protein structures are proposed and are not guaranteed to be designable. Thus, a method for quantifying designability is sorely needed.

3.1. Motif usage in nature varies significantly

We expect different local geometries of protein structure to have different designabilities and thus to have been sampled at different rates in nature. To illustrate the sensitivity of this effect, we shall consider abundance as a function of small perturbations in local geometry for two structural motifs –the parallel dimeric α-helical coiled coil and an α-helix packed against a parallel two-strand β-sheet, αββ (see Fig. 2).

Figure 2.

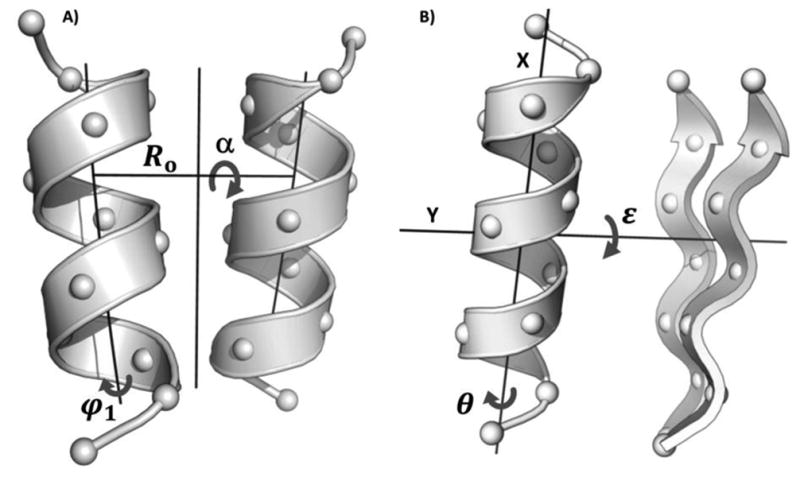
Some of the structural parameters defining a parallel α-helical coiled coil (in A) and an αββ motif (in B). A) For formal definitions of superhelical radius R_o, pitch angle α, and helical phase φ₁ see references (Crick, 1953; Grigoryan and Degrado, 2011). In this work, R_o was fixed at 4.88 Å. B) To model the ideal αββ motif, an initial structure was generated by fitting a naturally occurring αββ motif (taken from PDB entry 3EGD, residue ranges 505-511, 615-628, and 632-638) with ideal secondary structure elements (i.e. with exactly repeating backbone φ/ψ angles). Helical phase θ was defined as a rotation around the helical axis X. The crossing angle ε was encoded as a rotation around axis Y defined to be orthogonal to X and in the plane formed by X and the third principal axis of the β-sheet (the “out-of-plane” component). The two parameters were taken to be zero for the initially-fit ideal αββ motif.

The backbone of a coiled-coil structure is well described with simple parametric equations modeling the α-helix wrapping around a larger superhelix (Crick, 1953; Grigoryan and Degrado, 2011). For an ideal parallel structure, critical parameters are R₀ – the radius of the superhelix, α – the pitch angle of the superhelical curve with respect to the interface axis, and φ₁ - the helical phase defining helical sides facing each other (see Fig. 2A). Whereas it is easy to imagine how superhelical radius may affect the designability of a structure (e.g. packing preferences of interface-lining amino acids at least partially explain R₀ variations (Grigoryan and Degrado, 2011)), it is less clear that certain pitch angles and phases should necessarily be selectively preferred. To look at how α and φ₁ affect designability, we systematically varied these parameters in the context of a 12-residue fragment of an ideal parallel dimeric coiled-coil backbone, using MaDCaT to find all non-redundant structural matches in the PDB for each sampled structure. Both phase and pitch angle were varied around their previously found canonical values (Grigoryan and Degrado, 2011) in 30 increments (between –20° and +10° for α, and –24° and +6° for φ₁), resulting in 900 structures. A non-redundant subset of the PDB, generated by taking the first member of each sequence cluster produced by blastclust (Camacho et al., 2009) at 30% sequence identity, was used as the search database. Fig. 3A shows a contoured heatmap of the number of close structural hits as a function of structural parameters. The significant bias for specific geometries is obvious in this motif. Though both pitch angle and phase contribute to designability, changes in the latter are much more tolerable and many phases can be accommodated (see also Fig. 3B-C). The most designable region corresponds to the canonical range of values identified in an earlier analysis (Grigoryan and Degrado, 2011). Figs. 3A-B also show a less designable but still populated region of positive pitch angles corresponding to right-handed crossings.

Figure 3.

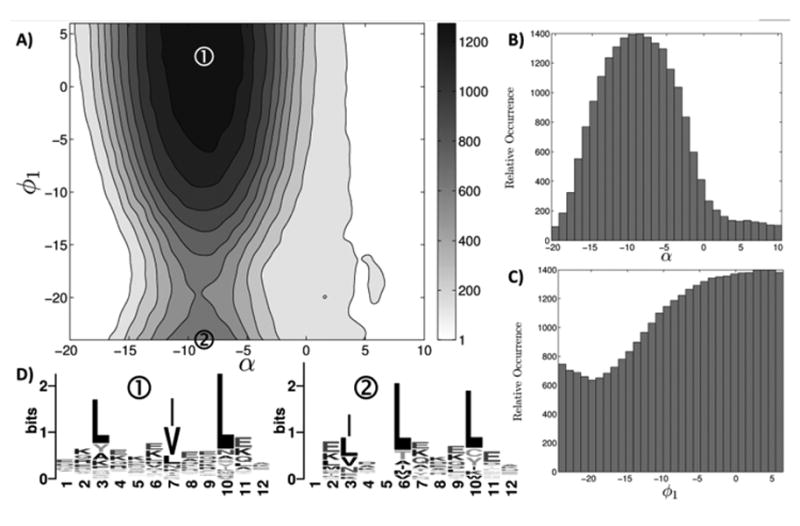
The designability landscape of the parallel dimeric coiled coil motif. A) The number of matches identified by MaDCaT within 1.0 Å RMSD of the query structure, as a function of its pitch angle α and helical phase ϕ₁. For each value of α B) plots the number of matches maximized over all values of ϕ₁ sampled. The equivalent for ϕ₁ is plotted in C). For two highly designable structures (marked with circled numbers in A), D) shows sequence logos originating from close matches. RMSD cutoffs of 0.7 Å and 0.4 Å were used for generating the left and the right sequence logos, respectively.

Fig. 4 illustrates the results of a similar analysis for the αββ motif. Here the varied parameters were the helix-sheet crossing angle ε and the helical phase θ (see Fig. 2B). Both parameters were varied between -30° and +30°, in 31 steps, for a total of 961 structures. The heatmap in Fig. 4A describes the designability landscape of this motif. Once again, we see that phase is a weaker determinant of designability than crossing angle (see also Figs. 4B-C).

Figure 4.

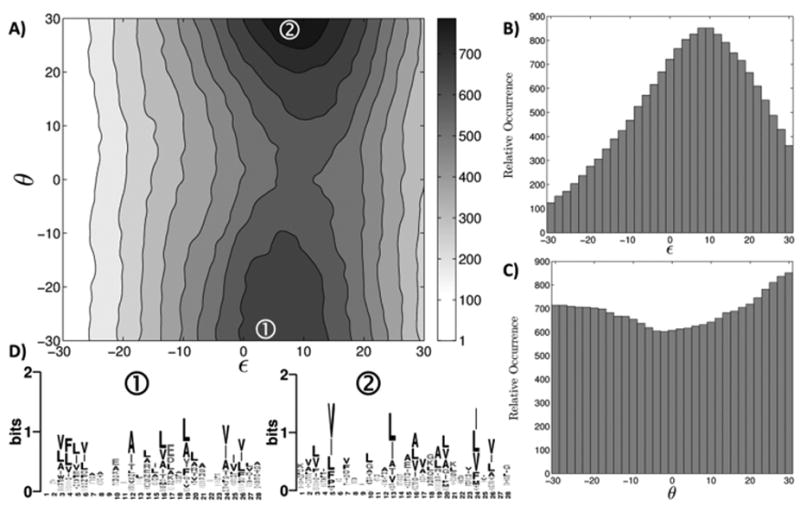
The designability landscape of the αββ motif. A) The number of matches identified by MaDCaT within 1.5 Å RMSD of the query structure, as a function of its crossing angle ε and helical phase θ. For each value of ε B) plots the number of matches maximized over all values of θ sampled. The equivalent for θ is plotted in C). For two highly designable structures (marked with circled numbers in A), D) shows sequence logos originating from close matches with RMSD to the query below 1.0 Å.

With both motifs, very drastic changes in designability can result upon seemingly small perturbations to structure. Fig. 5 shows structures with very different designabilities for the αββ motif. It is difficult to tell a priori which structure is more designable. On the other hand, MaDCaT enables rapid quantification of designability in a systematic manner for an arbitrary motif.

Figure 5.

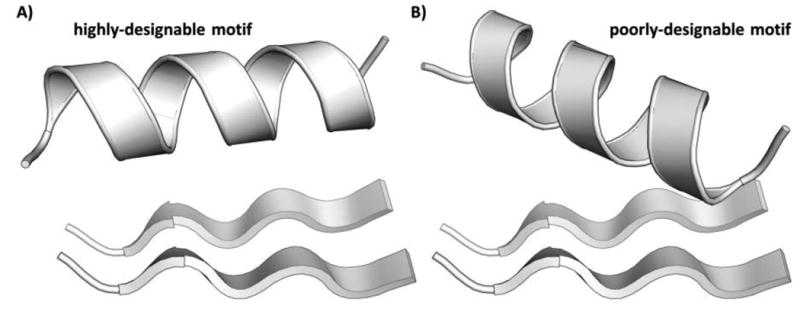
Examples of designable and non-designable instances of the αββ motif. The structure in A) has 44 unique examples, within 1.0 Å RMSD, in the non-redundant subset of the PDB used for searching, compared to 0 such examples for the structure in B).

3.2. Connection between structure and sequence

An important additional piece of information revealed by finding close matches to a structural motif are sequence constraints required to realize the given motif. Since the different matches come from different structure/sequence contexts, significantly conserved amino acids are likely important for stabilizing the motif itself or for encoding its structural specificity. On the other hand, positions with weak conservation can tolerate many different amino acids and are likely important for adjusting to the specific context. Such insight is highly useful in protein design as it significantly constraints the productive sequence space (Grigoryan et al., 2011). This information can also, in principle, be used for structure prediction to assure that all local structural motifs in the predicted model are consistent with their corresponding sequences.

Figure 3D shows the amino-acid distributions in the sequences of close matches corresponding to two different designable coiled-coil geometries (Crooks et al., 2004). Canonical coiled coils exhibit a seven-residue sequence repeat, designated with letters abcdefg, with a and d positions generally occupied with hydrophobic amino acids. The main difference between the two motifs is the helical phase and this is clearly reflected in the sequence logos as a register shift. Whereas the first motif starts with position b, such that residues 3 (d), 7 (a), and 10 (d) are hydrophobic, the second motif starts with an f, leading to residues 3 (a), 6 (d), and 10 (a) being hydrophobic. Though decades of study have led to a very good understanding of coiled-coil position-specific amino-acid preferences, the above analysis can be performed for any structural motif, rapidly revealing sequence preferences in a geometry-specific manner.

Figure 4D shows a similar analysis for two designable geometries of the αββ motif. Though the amino-acid preferences here are less pronounced than for the coiled coil, clear trends are still evident and the differences between the two geometries are apparent. Such sequence trends can be used to encode a specific geometry in design.

The sequence logos above capture only position-specific distributions, ignoring inter-position correlations. In principle, the latter can also be extracted from sequence alignments of matches, provided enough sequences are available, and these data can be equally useful in design or structure prediction. In fact, significant inter-positional correlations can flatten individual (marginalized) position distributions, leading to apparently lower information content by the standard sequence-logo analysis. Many methods for extracting meaningful mutual correlations between alignment positions have been proposed and can be employed here (for a recent example see (Morcos et al., 2011)).

4. Further developments

Though at present MaDCaT is efficient enough for many practical applications, further improvements in computational speed need to be pursued. Because structural searching is an example of an “embarrassingly parallel” problem, leveraging the massive parallelism offered by GPU technologies is one potential direction. Heuristics-based pre-filtering or pre-classification of database structures, already explored in the literature (Kolodny et al., 2005; Hasegawa and Holm, 2009; Budowski-Tal et al., 2010), may offer another fruitful avenue for efficiency gains, though it must be performed carefully not to bias search accuracy based on motif type. In the limit of very rapid (lookup-like) structural searching, designability analysis may be incorporated as a routine step in such applications as structural sampling for structure prediction, in alternating between sequence and structure selection for de novo protein design, or in automatic refinement of experimentally-determined structures.

5. Summary

Protein structural comparison, classification, and searching for structural similarity are problems that have received considerable attention in the last several decades (Hasegawa and Holm, 2009). It has been shown that such methodologies can be used for establishing evolutionary and functional relationships between proteins (Ouzounis et al., 2003). Here and in prior work (Grigoryan and Degrado, 2011; Grigoryan et al., 2011), we have demonstrated that structural similarity, when considered at a detailed local level, can also shed light on the designability of different structural motifs comprising proteins. It can provide a connection between structure and sequence, invaluable in de novo computational protein design, and potentially in structure prediction. MaDCaT is a tool particularly well suited for establishing such links, as its definition of similarity is focused on the precise local geometry, with particular emphasis on close contacts. By making MaDCaT freely available, we hope to stimulate its application in protein design and structure prediction, as well as its further development.