Modeling the dynamic interaction of Hebbian and homeostatic plasticity

Summary

Hebbian and homeostatic plasticity together refine neural circuitry, but their interactions are unclear. In most existing models, each form of plasticity directly modifies synaptic strength. Equilibrium is reached when the two are inducing equal and opposite changes. We show that such models cannot reproduce ocular dominance plasticity (ODP) because negative feedback from the slow homeostatic plasticity observed in ODP cannot stabilize the positive feedback of fast Hebbian plasticity. We propose a new model in which synaptic strength is the product of a synapse-specific Hebbian factor and a postsynaptic-cell-specific homeostatic factor, with each factor separately arriving at a stable inactive state. This model captures ODP dynamics and has plausible biophysical substrates. We experimentally confirm model predictions that plasticity is inactive at stable states and that synaptic strength overshoots during recovery from visual deprivation. These results highlight the importance of multiple regulatory pathways for interactions of plasticity mechanisms operating over separate timescales.

Introduction

Hebbian plasticity and homeostatic plasticity are the two major forms of activity-dependent plasticity that modify neuronal circuits (Turrigiano 2008). We use “Hebbian plasticity” to refer to plasticity that depends on the correlations between pre- and post-synaptic activity, such that excitatory synapses that effectively drive a postsynaptic cell grow stronger, while ineffective synapses are weakened. This is a positive feedback mechanism – strong synapses grow stronger – that in models typically leads to synaptic instability in the absence of additional biological constraints (Miller and MacKay 1994, Turrigiano 2008). Synaptic homeostasis is a negative feedback mechanism that typically involves nonspecific scaling of all excitatory or inhibitory synapses onto a cell to oppose changes in overall activity levels. This is thought to maintain activity levels within a dynamic range and more generally to stabilize neuronal circuit function despite the positive feedback of Hebbian plasticity (Turrigiano 2008). It is not known how these two forms of plasticity interact in biological systems (Shepherd and Huganir 2007, Turrigiano 2011, 2008).

Ocular dominance plasticity (ODP) in primary visual cortex (V1) has been a standard system in which to study experience-dependent plasticity (Espinosa and Stryker 2012). During the critical period for ODP, monocular deprivation (MD) - the closure of one eye - induces rapid weakening of responses to the closed eye and subsequent strengthening of responses to the open eye (Frenkel and Bear 2004, Hofer et al. 2006, Mrsic-Flogel et al. 2007). A recovery period with binocular vision following MD causes both eyes’ response levels to return to normal. Recently, three separable processes have been identified underlying this plasticity in mouse V1 (Kaneko et al. 2008a,b):

• Weakening of the closed eye’s responses is rapid, occuring over the first 3 days of MD, and appears to be mediated by Hebbian plasticity because of its dependent on calcium entry through N-methyl-D-aspartate (NMDA) receptors acting on calcium calmodulin kinase type II (Taha et al. 2002). This weakening shares other molecular features of Hebbian long-term depression (LTD) (Heynen et al. 2003, Yoon et al. 2009) but differs from LTD in its dependence on protein synthesis (Lee et al. 2003, Shepherd and Huganir 2007, Taha and Stryker 2002). It is not a ected by blockade of tumor necrosis factor-α (TNF-α) or the tyrosine receptor kinase B (TrkB) receptor (Kaneko et al. 2008a,b).

• Strengthening of the open eye is slower, commencing only after about 3 days, and appears to be mediated by homeostatic synaptic scaling: it is specifically prevented by blockade of TNF-α (but not of TrkB) (Kaneko et al. 2008a,b), which induces a global form of homeostatic synaptic scaling (Stellwagen and Malenka 2006). TNF-α induces a uniform scaling up of the strengths of excitatory synapses in response to a lowering of overall activity levels. This occurs without alteration in Hebbian plasticity as assessed by the percentage changes of synaptic strengths induced by LTP or LTD (Stellwagen and Malenka 2006).

• Recovery from MD under binocular vision is specifically prevented by blockade of TrkB (Kaneko et al. 2008a). TrkB has a variety of actions on synaptic plasticity. It is required for the growth of new synapses in neuronal cell culture (Meyer-Franke et al. 1998) and is involved in stabilization of Hebbian long-term potentiation (LTP) (Figurov et al. 1996, Kovalchuk et al. 2002, Lai et al. 2012, Sermasi et al. 2000, Tanaka et al. 2008).

The slow onset of homeostatic scaling, relative to the fast onset of Hebbian plasticity, poses a problem. Synaptic dynamics under Hebbian plasticity alone are typically unstable until synaptic strengths (“weights”) are driven to saturation near maximum or minimum allowed values (e.g., Miller and MacKay 1994). In models that combine Hebbian with homeostatic plasticity (or with mechanisms similar to homeostatic plasticity, such as multiplicative normalization of synaptic strengths or metaplasticity), homeostatic plasticity generally stabilizes a set of unsaturated weights that would be unstable under Hebbian plasticity alone (Bienenstock et al. 1982, Cooper et al. 2004, Miller and MacKay 1994, Oja 1982, Toyoizumi and Miller 2009, Toyoizumi et al. 2013, von der Malsburg 1973). However, such stabilization fails if homeostatic plasticity is too slow compared to unstable Hebbian plasticity (Cooper et al. 2004, Zenke et al. 2013). This is an example of the more general result that slow negative feedback cannot stabilize a fast, unstable positive feedback process. Thus, the slow onset suggests that homeostasis cannot stabilize Hebbian ODP.

To solve this problem, Hebbian plasticity must arrive on its own at a stable steady state, and this stability must not be disturbed by slow, ongoing homeostatic plasticity. We show that this solution can be instantiated, and the experimental results robustly reproduced, by a simple model in which the total synaptic strength is the product of two factors: a synapse-non-specific factor, applicable to the entire postsynaptic cell, controlled by homeostatic plasticity; and a synapse-specific factor, controlled by Hebbian plasticity. In addition to demonstrating the model’s ability to account for existing results, we experimentally test several key predictions of the model, including a lack of constitutive but opposed Hebbian and homeostatic plasticity at a stable state of the weights and a TNF-α-dependent overshoot of formerly closed-eye weights upon reopening of the closed eye after MD.

Results

MD effects on single-synapse plasticity models in the monocular cortex

In monocular cortex, which receives input only from the contralateral eye, similar dynamics of Hebbian and homeostatic plasticity are seen as in binocular cortex. During the first 3 days of MD, the strength of the closed eye’s input decreases by about 25-30% in an NMDA-dependent manner (Frenkel and Bear 2004, Heynen et al. 2003, Kaneko et al. 2008a). During the subsequent 3 days of MD, the closed-eye input strength homeostatically increases back to near baseline levels, an increase dependent on TNF-α (Kaneko et al. 2008b). Although this dynamical behavior under MD is simple, existing models cannot reproduce it, as we will show, because homeostatic plasticity that is slow enough to allow significant initial depression of the synaptic weight is too slow to stabilize plasticity.

We consider in this section a very simple, one-synapse model of monocular cortex: a single postynaptic cell with activity y receives a single input with synaptic strength w and activity x. We assume the output activity is given by y = wx, and take the input activity x to be constant in each condition, x = 1 for normal visual experience and x < 1 under MD (for simplicity we take activities and weights to be unitless numbers). By assuming a single input, we are in essence assuming that the synapses projecting to the monocular cortex are relatively homogeneous, so that w and x indicate the average synaptic strength from and average activity of the LGN inputs from the contralateral eye. Similarly, y indicates the average activity of monocular cortex. Later in the paper we consider a heterogeneous population of inputs in binocular cortex and show that the conclusions reached here are unchanged.

The BCM rule

A learning rule that is commonly used to describe ODP and that includes both Hebbian and homeostatic elements is the Bienenstock-Cooper-Munro (BCM) rule (Bienenstock et al. 1982, Cooper et al. 2004). In this model, an active input (x > 0) undergoes LTP if the postsynaptic activity y is greater than a threshold, θ, and undergoes LTD if y < θ; this is the Hebbian element. With the simple system considered here, this part of the BCM rule can be written

$${\tau }_w\frac{dw}{dt}=xy(y-\theta )$$ (1)

where T_w is a time constant that sets the Hebbian learning rate.

The homeostatic element of the BCM rule arises through the dynamic adjustment of θ over time to keep average postsynaptic activity near a set-point activity level, y₀. θ is a superlinear function of the average firing rate, typically $\theta =\overline{y^2}∕y_0$ where $\overline{y^2}$ is the average of y² over some averaging time. Taking this averaging time to be T_θ, the dynamics of θ can be written

$${\tau }_{\theta }\frac{d\theta }{dt}=-\theta +y\frac{y}{y_0}$$ (2)

When the model is switched to the MD condition, the weight initially decreases and subsequently increases. Consider starting at the fixed point for the normal (x = 1) condition, y = θ = w = y₀. Immediately after MD onset, input activity x and thus y = wx are reduced, so y < θ. This causes LTD under Eq. 1 and thus further reduction in y. However, since y < y₀, θ moves toward an equilibrium value $y\frac{y}{y_0}$ that is less than y. Once θ becomes less than y, the Hebbian rule causes LTP and y rises.

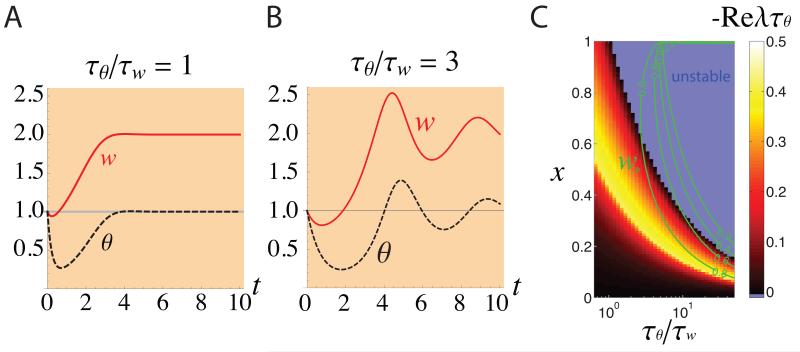
The speed of the decrease in θ, and thus of the switch from LTD to LTP, is determined by the time constant T_θ (Eq. 2). The speed of LTD is controlled by T_w (Eq. 1). In order to have significant initial LTD, T_θ must be sufficiently large, relative to T_w, so that significant LTD occurs before θ adapts. When T_θ/T_w is sufficiently small, θ adapts quickly, before the synaptic weight significantly changes, so that there is very little initial synaptic depression (Fig. 1A). However, as T_θ/T_w is increased, the fixed point under normal rearing becomes unstable even as the degree of synaptic depression under MD (initiated with this unstable normal-rearing fixed point as initial condition) remains small (Fig. 1C), and this MD leads to large oscillations of synaptic strengths (Fig. 1B). The oscillations arise because, when y reaches y₀, θ still reflects the earlier weight values, so weight change continues in the same direction until θ “catches up”. Instability occurs when the threshold change is so slow that the threshold never catches up (Cooper et al. 2004, Zenke et al. 2013) (when T_θ/T_w > 1/(x²y₀) for Eqs. 1-2).

Figure 1.

The dynamics of the synaptic strength under the BCM learning rule in the monocular cortex during MD initiated at time 0. The synaptic strength w (red line) and the activity dependent threshold θ (black dashed-line), were plotted vs. time for homeostatic plasticity that is the same speed as (A: T_θ = T_w) or slower than (B: T_θ = 3T_w) Hebbian plasticity. The initial condition (t = 0) was set to the fixed point under normal rearing (which is unstable for T_θ = 3T_w, see (C)). For faster homeostatic plasticity, there is little initial depression of synaptic strength (A). When the homeostasis is slowed, however, the normal-rearing fixed point becomes unstable (c.f. C), and the synaptic strength exhibits large oscillations under MD (B). We took the set point activity to be y₀ = 1, which sets the units of activity. We set input activity x = 1 in the normal condition, x = 1/2 under MD. We set T_w = 0.2 days; numbers on the x-axis represent days. (C) A systematic study of the BCM learning rule, as a function of input activity x and speed of homeostatic plasticity, T_θ/T_w. We characterized the dynamics of synaptic strength under MD by two variables: the depth of synaptic depression, measured as the strength w_* at the first trough of synaptic strength relative to the pre-MD (x = 1) strength of w = 1 (green contour lines); and the stability of the fixed point w = 1/x, as measured by the stability index −ReλT_θ (color plot; more positive values of the stability index indicate greater distances from instability; negative values mean the fixed point is unstable). Here, λ is the eigenvalue with greatest real part of the system linearized about the fixed point. For choices of x and T_θ/T_w that reproduce w_* ~ 0.7, as in experiments, the synaptic strength dynamics are unstable for a wide range of x including the normal rearing condition x = 1. The results shown in this figure are general and do not depend on any specific parameter choices (e.g., on choosing x = 1 to represent normal rearing), as explained in Supplemental Information, section S1.

In the BCM model, both $\frac{dw}{dt}$ and $\frac{d\theta }{dt}$ are zero at the fixed point. However, biological weights will constantly fluctuate under ongoing changes in activity. Such fluctuations induce destabilizing Hebbian plasticity, which can only be stabilized by fast homeostatic plasticity (i.e., fast changes in θ). In this sense, the BCM model requires that the two forms of plasticity are constitutively active but opposed in the vicinity of any fixed point.

Addition of stable Hebbian terms and a homeostatic term

To try to prevent loss of stability with slow homeostatic plasticity, we next consider an intrinsically stable Hebbian rule. In addition, we would like the model to be physiologically realistic in three respects in which the BCM rule is not. First, LTP and LTD should saturate, whereas in the BCM rule there is no limit to synaptic potentiation and LTD can reduce weights to zero. Second, in a model with multiple synapses, homeostatic plasticity should multiplicatively scale synaptic strengths, preserving the relative strengths of different synapses, as suggested by homeostatic scaling of the distribution of miniature excitatory postsynaptic potentials (mEPSPs) (Kaneko et al. 2008b, Stellwagen and Malenka 2006, Turrigiano 2011, Turrigiano et al. 1998). The sliding threshold of the BCM rule does not produce multiplicative changes in synaptic strengths. Third, homeostatic plasticity is induced by blockade of activity through bath application of tetrodotoxin (TTX) or under blockade of NMDA receptors, both in vitro (TTX: Turrigiano et al. 1998; NMDA block: Kaneko et al. 2008b; both: Stellwagen and Malenka 2006) and in vivo in V1 during the critical period (TTX, Maffei and Turrigiano 2008; NMDA, see Fig. 7A). Under the BCM rule there is no plasticity when the pre- or the post-synaptic firing rate is zero or when NMDA receptors are blocked.

We again consider our one-input model of the monocular cortex. We assume that synaptic strength is modified by the sum of an LTP term, an LTD term, and a multiplicative homeostatic term. LTP occurs when the product of pre- and postsynaptic activities, xy, is greater than a fixed threshold θ, while LTD occurs for xy < θ. To make the Hebbian plasticity intrinsically stable, the LTP and LTD terms saturate when the weight w reaches a maximal value w_max or minimal value w_min, respectively, consistent with experiments suggesting a limited range of strengths of individual synapses (O’Connor et al. 2005, Petersen et al. 1998). A nonzero minimal weight value is important because multiplicative homeostatic plasticity cannot potentiate synaptic strength if it reaches zero. The homeostatic term changes the weight to move the time-averaged postsynaptic activity ȳ toward the set-point value y₀. This term induces weight change proportional to w, which – once we consider multiple inputs – will make the homeostasis multiplicative, scaling all weights by a common factor rather than adding or subtracting a common amount from all weights. A parameter γ determines the strength (or equivalently, the learning speed) of homeostasis relative to Hebbian plasticity.

We let [x]₊ represent the operation of setting negative values to zero, that is, [x]₊ = x when x > 0 and [x]₊ = 0 otherwise. Then the equation for weight change is

$${\tau }_w\frac{dw}{dt}={[w_{\max }-w]}_{+}{[xy-\theta ]}_{+}-{[w-w_{\min }]}_{+}{[\theta -xy]}_{+}+\gamma w(1-\stackrel{‒}{y}∕y_0)$$ (3)

The first term in Eq. 3 is the LTP term, the second is the LTD term, and the third is the homeostatic term. This equation does not have the problems just noted for the BCM rule: in Eq. 3, LTP and LTD both saturate; homeostatic plasticity induces a multiplicative scaling of weights; and homeostatic plasticity will occur even in the absence of pre- or post-synaptic activity.

The delay in the signal driving homeostatic learning is determined by the time, T_ȳ, over which the postsynaptic activity is averaged to produce ȳ. Assuming an exponentially-weighted average with time constant T_ȳ, the equation for ȳ is

$${\tau }_{\stackrel{‒}{y}}\frac{d\stackrel{‒}{y}}{dt}=-\stackrel{‒}{y}+y$$ (4)

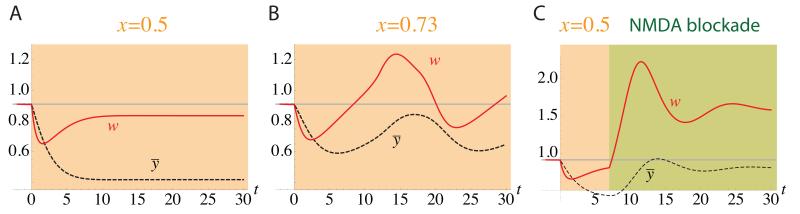
We choose parameters to reproduce the results of MD in the monocular cortex (Kaneko et al. 2008b) (see Supplemental Information, section S2). This model can reproduce fast LTD and slow homeostatic plasticity in the monocular cortex under MD. However, this outcome was fragile and sensitive to parameter values. Figure 2A shows the simulated result of the plasticity rule under strong MD (x = 0.5). The synaptic weight rapidly decreased and reached about 70% of the pre-MD value after 2 days of MD. Delayed homeostatic plasticity then started, due to the loss of postsynaptic activity, and scaled up the synaptic strength to about 90% of the pre-MD value. This result is consistent with the experimental observation. However, the result depended sensitively on the input strength under MD. Figure 2B shows a result of a simulation under weaker MD (x = 0.73). In this case, the synaptic strength settled into a stable oscillation (see phase plane analysis, Supplemental Information, section S3 and Fig. S1).

Figure 2.

Simulation results of plasticity in the monocular cortex during MD, using a learning rule with a stable Hebbian component and a homeostatic component (Eqs. 3–4). The synaptic strength, w, and the average postsynaptic activity, ȳ, are plotted for stronger MD (A; x = 0.5) and weaker MD (B; x = 0.73). For the model to reproduce the experimental result, as in A, parameters must be tuned so that the dynamics remain relatively near the stable fixed point under Hebbian plasticity alone. When the combined Hebbian/homeostatic dynamics move sufficiently far from that fixed point, the Hebbian dynamics are unstable and cannot be stabilized by slow homeostatic plasticity, yielding oscillations (B) or instability. The MD fixed point in (A), though non-oscillatory, involves constitutive but opposed LTD and homeostatic plasticity, so that blockade of Hebbian plasticity beginning at day 7 of MD yields a marked homeostatic increase in weight (C). Parameters: w_max = 1, w_min = 0.6, T_w = 0.3 day, T_ȳ = 3 days, y₀ = 0.8, θ = 0.6, γ = 0.23. X-axis: time in days.

This behavior is similar to that of the BCM rule explored previously. The problem is a general one that does not depend on arbitrary details of the implementation (e.g., use of a threshold nonlinearity [x]₊ as opposed to more smooth nonlinearities): for sufficiently slow homeostatic plasticity, there will be input values yielding oscillations or instability. The saturation limits ensure that the Hebbian terms in Eq. 3, by themselves, have a stable fixed point. However, the system’s fixed point – the steady state values of w and ȳ of the entire system, including the homeostatic term – may be at values of w distinct from this Hebbian-only fixed point. When the two fixed points are sufficiently far apart, small perturbations of w away from the fixed point will be amplified by fast Hebbian positive feedback and the slow homeostatic negative feedback through change in ȳ either cannot catch up (instability) or takes a long time to catch up (oscillations). In sum, system stability depends on choosing parameters for which the Hebbian and system fixed points are sufficiently near, but they are unlikely to remain near across multiple input values. We are once again faced with the fact that slow homeostatic plasticity cannot stabilize a fast unstable (positive-feedback) dynamics.

Even when the MD fixed point is near enough to the Hebbian fixed point to prevent oscillations (Fig. 2A), LTD and homeostatic upscaling are constitutively active but cancelling. (We show in Supplemental Information, section S2 that such constitutive plasticity always occurs at fixed points of Eqs. 3-4 for values of x outside of a finite range.) As a result, if Hebbian plasticity is blocked, a large homeostatic change in the synaptic weight will occur (Fig. 2C), a possibility we now test.

Experimental Test I: Lack of constitutive plasticity at steady states

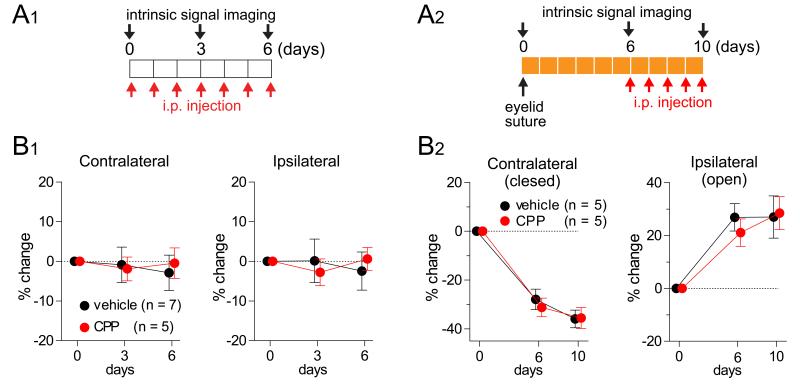
As we have just seen, plasticity models in which Hebbian and homeostatic plasticity compete to directly alter a single factor, w, make the general prediction that, for at least some rearing conditions, Hebbian and system fixed points should not coincide. This means that Hebbian and homeostatic plasticity are both constitutively active at the system steady state, inducing equal and opposite weight changes that cancel. While a rule might have both forms of plasticity separately zero at one steady state, it would require fine tuning of parameters for separate cancellations to occur at multiple steady states corresponding to different rearing conditions.

To test this prediction experimentally, we blocked Hebbian plasticity by a partial blockade of NMDA receptors using daily intraperitoneal injection of a low dose of the NMDA-blocker CPP. This regime was shown to block NMDA-receptor-dependent plasticity in mouse V1 (in the same strain of mice studied here) during the critical period and in adulthood: it blocks NMDA-receptor-dependent expression of the immediate early gene product Zif268 and blocks ODP in response to MD but does not block visual behavior or the responses of neurons in mouse V1 (Sato and Stryker 2008). As we will discuss later, it leaves homeostatic plasticity intact, while appearing to block Hebbian plasticity, when applied during days 3-7 of MD (Fig. 7A). We injected CPP during each of two different, approximately steady states during the critical period for ODP in mice: during normal rearing, and during the last 3 days of a 10-day MD (Fig. 3). At each steady state, the blockade caused no significant change in either eye’s response strength in V1, as assessed with intrinsic signal imaging, relative to control animals (daily vehicle injection), in contrast to the outcome seen in Fig. 2C. This indicates that Hebbian and homeostatic plasticity are each separately nearly zero at each of the two steady states.

Figure 3.

Lack of constitutive plasticity at steady states: Hebbian plasticity and homeostatic plasticity are each separately inactive under normal rearing (A₁, B₁) and after 6 days of monocular deprivation (A₂, B₂). (A) Experimental designs. An NMDA receptor antagonist (CPP) or vehicle solution was injected intraperitoneally for 6 days under normal rearing (A₁) or for the last 4 days of a 10-day MD period (A₂). (B) In each case, responses in binocular V1 to stimulation through each eye were unchanged by the NMDA receptor block, suggesting a lack of ongoing plasticity in these conditions. Baseline response levels were indistinguishable in CPP and control animals (Fig. S7). Data are represented as mean ± SEM.

Note that this experiment does not speak against the BCM model. In that model, all plasticity is stopped by NMDA blockade. However, we have noted other empirical problems with the BCM model.

Our proposed solution: A model with Hebbian and homeostatic factors that multiply to produce synaptic strength

We have seen that the observed combination of fast synaptic depression and slow homeostatic plasticity after MD cannot be robustly reproduced by traditional plasticity models, in which the Hebbian and homeostatic components directly compete to control the same factor. Furthermore, the constitutive, equal and opposite forms of plasticity predicted to exist at a steady state by models with separate, competing homeostatic and Hebbian terms are not found experimentally.

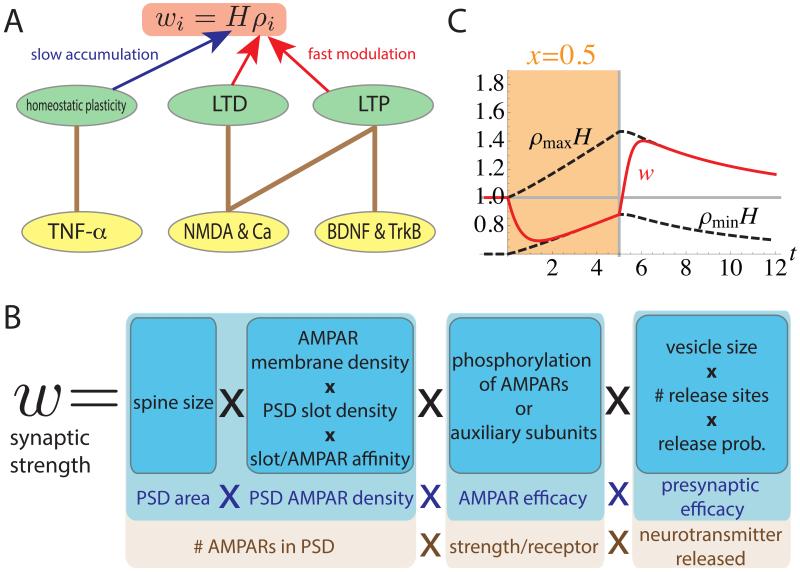
This motivates our proposed solution: a model in which a synapse-specific Hebbian factor, ρ, and a postsynaptic-cell-specific homeostatic factor, H, each with their own learning dynamics, are multiplied to give the synaptic strength: w = Hρ (Fig. 4A). LTP and LTD rapidly modify ρ in an NMDA-dependent manner, while homeostatic plasticity more slowly modifies H through the effects of TNF-α and perhaps other factors. This model is consistent with the experimental result that the percentage synaptic strength changes induced by Hebbian LTP or LTD protocols were unchanged by modifications of homeostatic plasticity (pre-treatment with TNF-α or knockout of TNF-α receptors, Stellwagen and Malenka 2006).

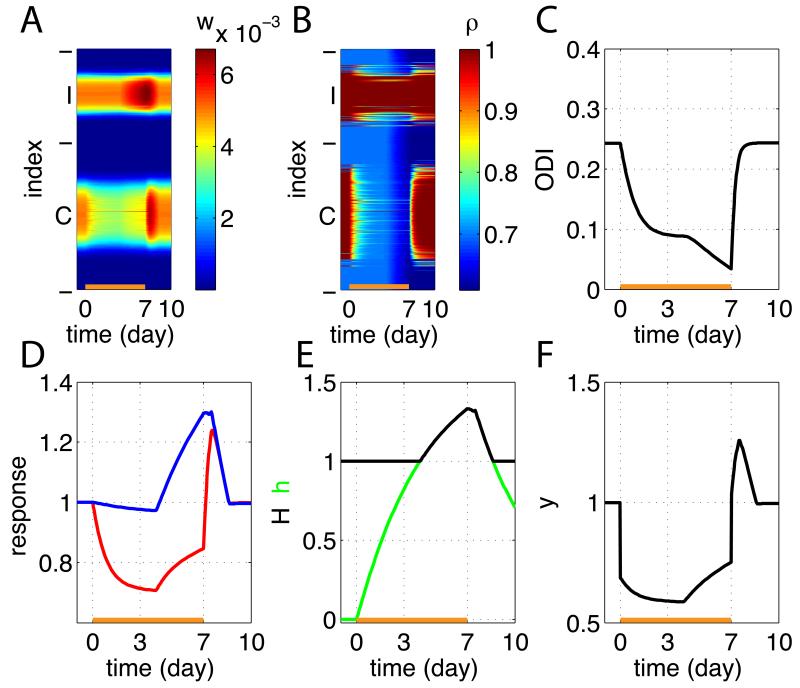
Figure 4.

A schematic description of the two-factor model (A). The ith synaptic strength is described by w_i = Hρ_i, where H is a synapse non-specific homeostatic variable, and ρ_i is a synapse-specific Hebbian variable. Hebbian plasticity rapidly changes ρ_i, while homeostatic plasticity slowly changes H. The slow change in H can build up without being overwritten by the fast Hebbian effect. In models in which Hebbian plasticity and homeostatic plasticity both directly change synaptic strengths, homeostatic plasticity cannot be slow without being overwritten. In the model, both LTP and LTD are mediated by NMDA dependent calcium influx. In addition, BDNF/TrkB signaling is assumed to be required for LTP, and homeostatic plasticity is mediated by TNF-α. (B) A biophysical interpretation of separable factors whose product is the synaptic strength: four overall factors (light blue) and corresponding biophysical elements controlling them (dark blue), including further breakup of some factors into a product of subfactors. Our model could be instantiated if H and ρ each control separate subsets of these factors or subfactors. (C) Simulation results of the two-factor model in the monocular cortex during MD and recovery from MD. Colored regions of plots (days 0-5) represent periods of MD; white region (days 5-12) represents normal vision (x = 1). The plot illustrate the synaptic strength w (red line); and the maximal and minimal possible synaptic strengths, Hρ_min and Hρ_max, which we term the limiting strengths, both represented by dashed lines. Changes in these limiting strengths represent homeostatic plasticity, i.e. changes in the homeostatic factor H. When the weight w reaches a limiting strength, it indicates the Hebbian factor ρ has reached its corresponding limiting value, ρ_max or ρ_min. The synaptic strength was rapidly depressed to the minimum value via the Hebbian component and then this minimum value was slowly potentiated by the homeostatic component. When the eye was reopened (x = 1) after 5 days of MD, the synaptic strength rapidly potentiated to the maximum value by LTP and then this maximum value was slowly depressed by the homeostatic component. x-axis: time in days. Parameters used: θ = 0.6, y₀ = 1, ρ_max = 1, ρ_min = 0.6, T_ρ = 0.2 days and T_H = 8.0 days.

In our proposed model, the dynamics of ρ – the Hebbian dynamics – are stable by themselves, reaching a stable fixed point for a given input statistics. We will assume this stabilization is achieved through saturation of ρ at minimal and maximal allowed values (O’Connor et al. 2005, Petersen et al. 1998), but any stable Hebbian learning rule would suffice. The homeostatic dynamics still involve slow learning, but because of the relationship w = Hρ, such slow dynamics will scale the weights – including the minimal and maximal weights – to bring the overall activity level toward the desired set point without disturbing the intrinsic stability of the Hebbian dynamics. In this model, the synaptic strength does not oscillate because homeostatic plasticity is driven by the instantaneous activity, without the delays of slow time-averaging. In the previous models, the observed slowness of homeostatic plasticity had to arise from slow time-averaging rather than slow learning because slow learning, which means small changes per unit time, would have made the homeostatic term too weak to affect learning. That is, under slow learning, the small changes in w induced by homeostasis in any given time interval would have been easily reversed by the larger changes induced by the faster Hebbian plasticity.

This two-factor model is no doubt still a simplification – an effective model – of the complex dynamics of synaptic learning (e.g., Huganir and Nicoll 2013), and determining the biophysical basis of this model awaits further experimental work. However, we suggest the following overall framework for interpreting the model (Fig. 4B). The postsynaptic density (PSD) is thought to have a certain number of “slots” for alpha-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid receptors (AMPARs). These slots are created by PSD structural proteins (Huganir and Nicoll 2013, Kessels and Malinow 2009), some of which play roles in homeostatic plasticity (Shin et al. 2012, Steinmetz and Turrigiano 2010, Sun and Turrigiano 2011). The synaptic strength, to the extent that it is determined by AMPARs, could be understood as the product of four elements: (1) the area of the PSD (which is increased by Hebbian LTP, which increases spine size: Harvey and Svoboda 2007, Kopec et al. 2007, Matsuzaki et al. 2004, Zhou et al. 2004); (2) the density of AMPARs bound to slots in the PSD; (3) the efficacy of the AMPARs (4) the presynaptic efficacy, which also undergoes activity-dependent modification (Atwood and Karunanithi 2002, Kaneko et al. 2010). If free AMPARs in the membrane and slots bind with first-order kinetics, then the PSD density of bound AMPARs can be further broken down as the product of (2a) membrane AMPAR density, known to be increased by TNF-α (Beattie et al. 2002, Leonoudakis et al. 2008, Stellwagen and Malenka 2006); (2b) PSD slot density; (2c) slot/AMPAR binding affinity. The latter two factors and AMPAR efficacy are likely altered by modulations (e.g., phosphorylation) and/or changes in composition of both AMPARs and PSD structural proteins. The presynaptic efficacy likewise breaks down to a product of subfactors. In sum, if the homeostatic factor H and Hebbian factor ρ each correspond to different subsets of these biophysical factors, then the product ρH would correspond to the synaptic strength.

Such a division of mechanisms fits well with the three working models proposed by Huganir and Nicoll (2013) for how CaMKII activation causes Hebbian LTP. In their “PSD-centric” model, CaMKII alters PSD structural proteins to increase the number of slots at the given synapse (mechanism (2b)). In their “receptor-centric” model, CaMKII phosphorylates AMPAR complexes to increase their binding affinity to the slots (mechanism (2c)). In their “insertion” model, CaMKII drives exocytosis of vesicles containing glutamate receptors, increasing the density of AMPARs in the plasma membrane (mechanism (2a)). Under any of these models, Hebbian plasticity might also control additional mechanisms and homeostasis would control one or more complementary mechanisms.

To study our proposed two-factor model, we continue to consider the framework of Fig. 2A, a single presynaptic input in monocular cortex. The Hebbian factor is modeled as in the previous section, so that LTP and LTD occur for xy > θ and xy < θ, respectively, and both are stabilized by saturation of ρ at maximal or minimal values:

$${\tau }_{\rho }\frac{d\rho }{dt}=({\rho }_{\max }-\rho ){[xy-\theta ]}_{+}-(\rho -{\rho }_{\min }){[\theta -xy]}_{+}$$ (5)

The homeostatic term grows or decays if the activity is respectively below or above the desired set-point level y₀:

$${\tau }_H\frac{dH}{dt}=H\left(1-\frac{y}{y_0}\right)$$ (6)

The proportionality to H on the right side of Eq. 6 is not important in practice, but formally ensures that H remains positive. The speed of Hebbian and homeostatic learning are controlled by the time constants T_ρ and T_H respectively. Note that H depends only on postsynaptic activity y, and not directly on the synaptic weight, so that it provides a set point for y. In a multi-synapse model this will mean that H is a postsynaptic-cell-specific, rather than synapse-specific, factor.

These equations (and also those of a multi-synapse model to be studied below) can be shown to be mathematically equivalent to a model similar to that of Eq. 3, in which Hebbian and homeostatic plasticity both compete to modify a single factor w, but in which homeostatic plasticity also scales the maximal and minimal allowed weights and, while slow, responds to instantaneous rather than time-averaged postsynaptic activity (Supplemental Information, section S5). The former point is critical for homeostatic plasticity to multiplicatively scale synaptic strengths without disturbing intrinsic Hebbian stability and without being overwritten by Hebbian plasticity. The latter point is critical to stability: slow averaging introduces delays which can yield oscillations of synaptic strength.

We will find that this simple model, like the previous model (Fig. 2), still has behavior that varies qualitatively with the strength of MD (the value of x), although in the present case this variation might be physiologically realistic (see Supplemental Information, section S6). The key difference, however, will be that in the present model, the behavior is always stable, approaching a stable fixed point (at which each form of plasticity is separately zero) without oscillations. Further issues with the behavior can be fixed by using a more complex plasticity model, as we will see in the next section, but the stability is intrinsic to the framework of separable factors with a stable Hebbian component (Supplemental Information, section S4). In the previous model, instability was intrinsic to the framework for the reasons outlined above and could not be fixed by a more complex model.

To simulate this model, we assumed that homeostatic learning was quite slow relative to Hebbian learning, to show that no instability results: T_H was 40 times longer than T_ρ (stability for any value of T_H/T_ρ is shown in Supplemental Information, section S4). Before MD, ρ was saturated at its maximal value, ρ = ρ_max.

We simulated MD (x = 0.5) applied for 5 days (colored region), followed by recovery with normal vision (x = 1) for the next 7 days (white region; Fig. 4C). (Behavior of the model for MD with intermediate values of x are examined in Supplemental Information, section S6.) During the 5 days of MD, the synaptic strength was first decreased through Hebbian LTD, reaching about 70% of its initial value, and then was potentiated by homeostatic plasticity, well matching experimental results (Kaneko et al. 2008b). Restoration of normal vision at day 5 led to an overshoot of synaptic strength: a rapid increase through Hebbian LTP, followed by a slower decrease toward baseline through homeostatic plasticity. This overshoot is a robust prediction of our model given slow homeostatic and fast Hebbian plasticity: homeostatic scaling H had increased to compensate for decreased activity and Hebbian synaptic depression during MD; recovery induces a rapid LTP of ρ, yielding an overshoot of w = ρH; H then slowly decreases to return the system to the set-point activity. We present below an experimental test of this prediction of an initial overshoot of synaptic strength following restoration of normal vision.

So far, we have considered the MD result only in the monocular cortex and have also neglected the heterogeneity among synapses, replacing multiple synaptic strengths by a representative value. In the next section, we consider a more realistic network model with multiple presynaptic neurons and consider binocular as well as monocular cortex.

MD effects in multi-synapse plasticity models in the binocular cortex

We now consider multiple presynaptic neurons (N = 500) projecting to a postsynaptic neuron. The i^th input contributes an amount to the postsynaptic firing rate equal to the input’s firing rate x_i times its synaptic weight w_i, and the postsynaptic firing rate is the linear sum of these contributions: $y={\Sigma }_{i=1}^N{w}_i{x}_i$. In the binocular cortex, the postsynaptic neuron receives N_C = 310 synapses from the contralateral eye and N_I = 190 synapses from the ipsilateral eye. This ratio was chosen to reproduce the physiological ocular-dominance index (ODI) under normal rearing (Kaneko et al. 2008b). The i^th synaptic strength is described by w_i = HA_iρ_i, where A_i is the anatomical strength of axonal arborization (Miller et al. 1989) (see Supplemental Information, section S7.2) and is normalized as Σ_i A_i = 1 to keep postsynaptic activity level roughly independent of the choice of N; ρ_i is the synapse-specific Hebbian factor; and H is the synapse-non-specific homeostatic factor characterizing the overall scaling of synaptic strengths onto the given postsynaptic neuron. The arborization function was introduced to reproduce localized receptive fields with continuously decreasing magnitude toward their flanks. The presynaptic firing rates are drawn from a Gaussian distribution with a specific mean and covariance (see Experimental Procedures). Under the normal rearing condition, the mean firing rates ⟨x_i⟩ are identical for all presynaptic neurons (⟨x_i⟩ = 1). The input covariance specifies that two inputs at a given retinotopic separation are more correlated if they are from the same eye than from opposite eyes, while the correlation of two inputs with given ocular identities decreases with their retinotopic separation. MD decreases the input firing rates within the closed eye and the covariance between closed-eye and open-eye inputs by a factor f = 0.5, and decreases the covariance between closed-eye inputs by f². To show the robustness of our learning rule to noise, we added a symmetric Gaussian random matrix (see Experimental Procedures) to the covariance matrix. While this noise heterogeneously perturbs individual synapses, it has only negligible influence on ODP.

We will use a more complex learning rule than used previously to reproduce quantitative aspects that the simpler rule of Eqs. 5-6 could not account for. We emphasize that our point in using this more complex rule is not to argue that it captures the true, complex biological rules (see also discussion of alternatives in Supplemental Information, section S7). Rather, we only wish to demonstrate that (1) the separation of ρ and H variables gives stability despite slow homeostatic plasticity, with each form of plasticity separately zero at the network stable state; and (2) suitable plasticity rules can then replicate the biological behavior without disturbing these features.

The behaviors we wish to capture with the plasticity rules are as follows (further explained in Supplemental Information, section S7): (1) TNF-α-dependent ODP: during days 3-7 of MD, there is continuing ODP toward the open eye in wild-type animals but not in TNF-α knockouts (Kaneko et al. 2008b). Since homeostatic plasticity alone would equally scale both eyes and thus cause no ODP, this suggests that TNF-α-dependent homeostatic plasticity induces further Hebbian plasticity after Hebbian plasticity would otherwise be saturated. (2) Saturation of homeostatic plasticity: under MD in monocular cortex, homeostasis only returns synaptic strength to near its original level, which would not restore original activity levels under continuing MD. (3) Delay in homeostatic onset: no potentiation of open-eye responses is seen in binocular cortex until after day 3 of MD (Kaneko et al. 2008b). Under the simple rule of Eq. 6, homeostatic plasticity, while slow, was active from the initiation of MD, yielding significant homeostatic plasticity by the time of maximal LTD (evident as the rise of ρ_minH by day 2 in Fig. 4C).

To account for TNF-α-dependent ODP, we modified the rule for changes in the Hebbian factor by adding H-dependence to ρ_min

$${\tau }_{\rho }\frac{d{\rho }_i}{dt}=({\rho }_{\max }-{\rho }_i){\left[{\varphi }_i\right]}_{+}-({\rho }_i-{\rho }_{\min }(H\left)\right){\left[{\varphi }_i\right]}_{+}$$ (7)

Here T_ρ = 0.2 day is a characteristic time scale, φ_i is the pre-post covariance minus a threshold, φ_i = Cov[x_i, y] − θ with θ = 0.6, and ρ_max = 1. We set ρ_min(H) = 0.7 for H ≤ 1 and = 0.7H^−1/2 for H > 1, which allows homeostatic plasticity to induce continued LTD and thus continued ODP after LTD has initially saturated. If ρ_min is constant, there would be no ODP once LTD is saturated, while if ρ ~ H⁻¹ there would be no homeostatic strengthening of depressed synapses in monocular cortex (because continued LTD would cancel homeostatic upscaling). Apart from these constraints, the exact functional form of ρ_min(H) does not matter for the results.

To impose saturation of TNF-α-dependent homeostatic plasticity (Beattie et al. 2002), we first note that, without saturation, homeostatic dynamics that reaches the set point y₀ can be written T_HdH/dt = −H + H_target with H_target ≡ Hy₀/⟨y⟩. Here ⟨y⟩ is the instantaneous (i.e., very short time-scale) mean activity (used in place of y simply to average out the Gaussian input noise). To achieve saturation we can modify the dynamics to T_HdH/dt = −H + F(H_target) with some saturating nonlinearity F. To impose a delay in homeostasis, we assume that, after activity decreases (e.g., due to MD), increase of the homeostatic factor H from the baseline level of 1 is delayed until a threshold amount (which we take to be 1) of an underlying factor h has accumulated:

$$H=\mathrm{Max}(h,1)$$ (8)

h is a factor that builds to a saturating value > 1 when activity is below its set-point value. For example, h might be inversely related to the sensing of glutamate concentrations over time by glial cells (Stellwagen and Malenka 2006) and would induce a proportional increase in TNF-α release once it is above a threshold. H would reflect the resulting TNF-α concentration. Note that Eq. 8 incorporates the experimental result that TNF-α is only involved in upscaling strengths in response to too-low activity and not in downscaling strengths in response to too-high activity (Stellwagen and Malenka 2006). To ensure adequate delay in homeostatic onset, h should decay to a baseline level well below 1 when this activity is at or above its set-point value. We take this baseline level to be zero. Note that these assumptions could not solve the problems of oscillations or instability in conventional models (Eqs. 1–4), because those models would not work with delayed homeostatic onset. In those models, the dynamics yield a fixed point that would be unstable under Hebbian plasticity alone. Therefore, for the baseline condition to be stable, they require ongoing fast homeostatic responses to return weights to the fixed point after small weight fluctuations.

Putting these assumptions together, we use the following rule (along with Eq. 8) for changes in the homeostatic factor:

$${\tau }_h\frac{dh}{dt}=-h+F\left(H_{\text{target}}\right)$$ (9)

Here, F(x) is a monotonically increasing function that is 0 for x ≤ 1 (so that h returns to its baseline value of 0 once the homeostatic constraint is achieved), jumps from 0 to 1 when x exceeds 1 and then increases roughly linearly with x until it saturates at around 2 (Eq. S16 and Fig. S5A). We take the time constant of homeostatic plasticity to be T_h = 4 days.

We modeled MD of the contralateral eye initiated at day 0, followed by reopening of that eye at day 7, in binocular cortex. The model reproduced rapid LTD of the closed-eye synapses and slow homeostatic potentiation of the open-eye synapses (Fig. 5). Hebbian LTD reduced closed-eye response by about 30% after 3 days of MD by reduction of the closed-eye’s Hebbian factors ρ (Fig. 5A,B,D). At the same time, the reduction of activity (Fig. 5F) caused h to start increasing from the baseline value of 0. After about 4 days of MD, h reached the threshold value of 1 and homeostatic potentiation via increase of H was initiated (Fig. 5E). The open-eye response accordingly was unchanged for the first 4 days but was potentiated by about 30% after 7 days of MD (Fig. 5A,D). The homeostatic increase of H then started lowering the Hebbian saturation limit ρ_min and decreased the closed-eye Hebbian factor, inducing additional ODP during MD days 3-7 (Fig. 5C). After restoration of normal visual input at day 7, the closed-eye synapses showed rapid LTP (Fig. 5A,B,D) while homeostatic plasticity decreased back to baseline slowly (Fig. 5E), so that synaptic weights overshot their final level and then gradually decreased back to it, as we saw in the previous model of monocular cortex (Fig. 4C). Simulation of MD in the monocular cortex using the present model (Fig. S6) produced a result very similar to the single-synapse model presented in the previous section (Fig. 4C).

Figure 5.

Simulation results in the binocular cortex before, during, and after MD. MD was started at day 0 and the closed eye was reopened at day 7. (A) Synaptic strengths w_i are shown as a function of developmental time. From bottom to top, there are 500 rows, which we label i = 1,…, 500, with the i^th row showing the time course of the strength of weight w_i. Indices i = 1,…, 310 are from the closed eye (contralateral eye, labeled ‘C’) and i = 310,…, 500 are from the open eye (ipsilateral eye, ‘I’). See (D) for time course of the strongest weights. (B) The Hebbian factors ρ_i. (C) the ocular-dominance index (the value 1 means contralaterally dominated and the value −1 means ipsilaterally dominated; see Experimental Procedures). (D) Traces of the sum of weights from the closed eye (red) and the open eye (blue), normalized to have initial value of 1. We refer to this as the “normalized visual response”, because it represents the relative visual response through each eye that would be assayed by an experimenter at any given time. (E) The homeostatic factor H (black) and the underlying glial factor h (green). (F) The average postsynaptic activity ⟨y⟩ during ongoing plasticity.

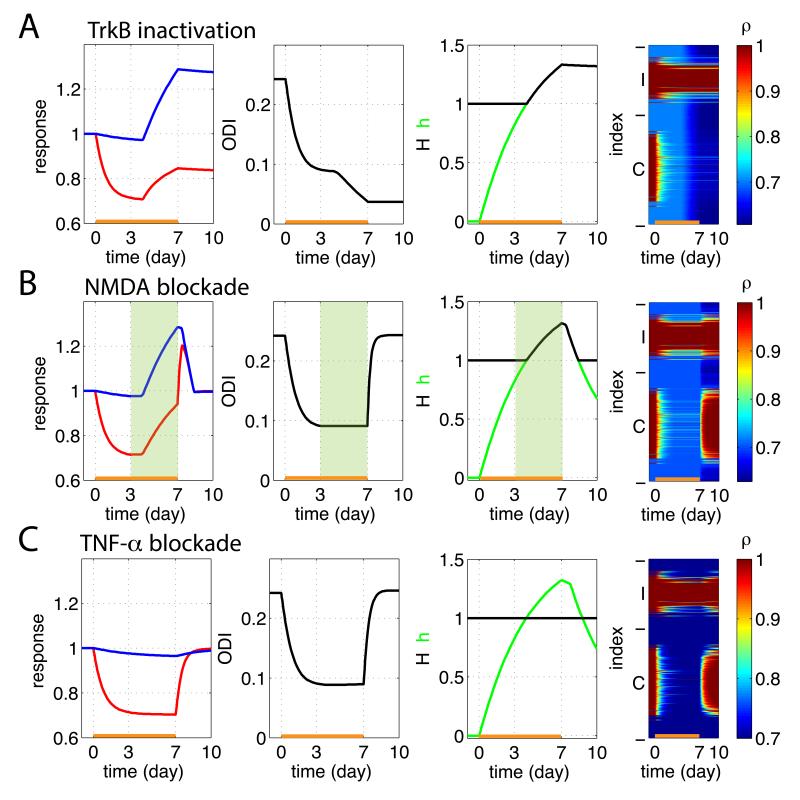
In addition to explaining the MD results in wild-type mice, we also applied the model to ODP under various forms of inactivation (Fig. 6). We modeled blockade of TrkB receptors (Kaneko et al. 2008a) as a lack of Hebbian potentiation (we removed the first, LTP term from the right side of Eq. 7), whether due to a direct block of LTP or to block of anatomical addition of synapses. This is based on the facts that BDNF/TrkB signaling is required for growth of synapses in neuronal cell culture (Meyer-Franke et al. 1998) and for stabilization of LTP in hippocampus (Figurov et al. 1996, Kovalchuk et al. 2002, Lai et al. 2012, Tanaka et al. 2008) and visual cortex (Sermasi et al. 2000). This reproduced the experimental results in TrkB-inactivated mice (Kaneko et al. 2008a): MD e ects (both the initial LTD and the subsequent homeostatic potentiation) were normal, but the recovery from MD after reopening the closed eye was blocked (Fig. 6A).

Figure 6.

Results of MD (days 0-7) and recovery (days 7-10) under various inactivation conditions. Conventions as in Fig. 5. (A) Simulation of TrkB-inactivated mice, modeled as an absence of LTP. MD effects (both LTD and homeostatic plasticity) were normal but synaptic strengths did not recover under binocular vision. (B) Simulation of partial NMDA blockade during MD days 3-7, modeled as no Hebbian plasticity during colored interval. This stopped ODP, increasing closed-eye strengthening (due to block of LTD) and slightly decreasing open-eye strengthening. (C) Simulation of TNF-α inactivation, modeled as H remaining constant at H = 1. No homeostatic potentiation of the open-eye synapses occurred. As a result, overshoot of synaptic strengths did not occur during the recovery period.

To model partial NMDA blockade during MD days 3-7, we assumed no Hebbian plasticity in the corresponding time interval (interval shaded green in Fig. 6B). Purely homeostatic potentiation then equally scaled both eyes without changing ODI. The elimination of closed-eye LTD led to increased closed-eye potentiation, which in turn led to slightly less overall homeostatic upscaling than normal, slightly reducing open-eye potentiation.

To model TNF-α blockade, we assumed that H remained constant at 1, without any homeostatic adjustment. Simulations then showed little or no change in open-eye synapses over 7 days of MD (Fig. 6C), as observed in TNF-α KO mice (Kaneko et al. 2008b). Furthermore, the model predicts that the overshoot of the previously-closed-eye synapses during the recovery phase in wild-type mice (C.f. Fig. 5) should be absent in TNF-α KO mice. Reopening of the previously closed eye causes that eye’s Hebbian factors to be potentiated to the saturating value ρ_max. In the absence of prior homeostatically-induced increase in H, this simply returns those synapses to their original values without any overshoot.

Experimental Tests II: Hebbian depression of closed-eye synapses during 3-7 days of MD and homeostasis-dependent overshoot of closed-eye responses during recovery from MD

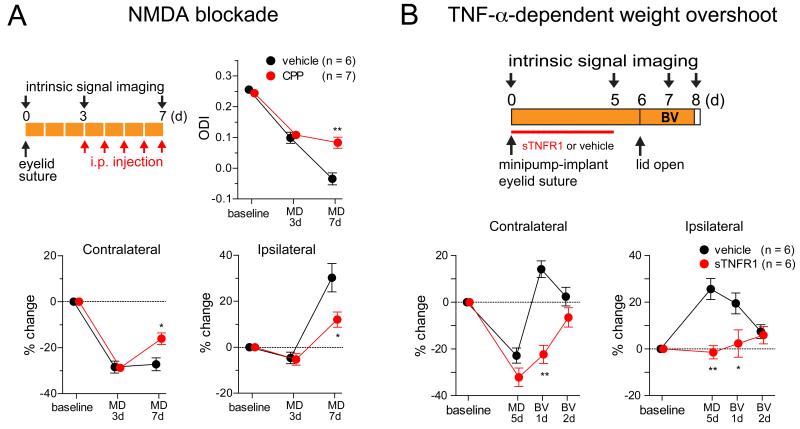
As we have noted, our proposed solution makes several robust, qualitative predictions that are independent of the model complexities that we added to more precisely match details of development. These predictions, which have not previously been tested, are: (1) Blockade of Hebbian plasticity during MD days 3-7 should reveal purely homeostatic plasticity, involving equal percentage increases in each eye’s strengths with no change in ODI (as in Fig. 6B); (2) After MD for 7 days, long enough to yield homeostatic potentiation of synapses, restoration of normal vision should cause a TNF-α-dependent overshoot of closed-eye response above the pre-MD baseline, before it ultimately returns to the baseline (as in Figs. 4C and 5D, compare Fig. 6C).

We tested these predictions using intrinsic-signal imaging from the binocular region of mouse V1 during MD and recovery, with results as predicted by the model (Fig. 7). With intraperitoneal injections of the NMDA blocker CPP during MD days 3-7, equal potentiation of the two eyes occurred without change in ODI and with increased closed-eye potentiation and reduced open-eye potentiation (Fig. 7A). This is consistent with the idea (Fig. 6B) that CPP blocked Hebbian LTD of the closed eye, revealing purely homeostatic plasticity, which is equal in the two eyes, while reducing the overall strength of homeostatic plasticity. Furthermore, normal recovery from MD produced the predicted overshoot of closed-eye responses followed by slow recovery to baseline, whereas if homeostatic plasticity had been blocked during MD by cortical infusion of sTNFR1 (soluble TNF receptor, which scavenges TNF-α), this overshoot did not occur (Fig. 7B). Note that, during normal recovery, both closed- and open-eye synapses showed a similar degree of potentiation from the pre-MD baseline at 24 hours, when the peak of the closed-eye overshoot was measured, and both recovered to near the pre-MD baseline, without further change in ODI (not shown), over the next 24 hours. This is consistent with the idea that, at 24 hours, both eyes have saturated Hebbian LTP and are scaled by the same homeostatic factor, and that over the next day this homeostatic factor subsides to baseline (as in Fig. 5D).

Figure 7.

Experimental verification of model predictions for MD and recovery. (A) Injection of NMDA receptor antagonist CPP during days 3-7 of contralateral-eye MD reveals pure homeostatic plasticity, as judged by equal multiplicative upscaling of both eyes’ responses with no further shift in ODI (upper right panel). Upper left panel indicates the experimental schedule. CPP added closed-eye potentiation and reduced open-eye potentiation (lower panels), as in Fig. 6B (compare with Fig. 5D). Baseline response levels were indistinguishable in CPP and control animals (Fig. S7). (B) Upon recovery from MD, there is a TNF-α-dependent overshoot (blocked by sTNFR1, which scavenges TNF-α) of the closed-eye weight from its pre-MD baseline level, before it returns to baseline. MD: monocular deprivation. BV: binocular vision (to induce recovery of closed-eye responses). Bottom panels: change relative to day 0 baseline. * p< 0.05, ** p < 0.01, between CPP- and vehicle-injected animals in A, between sTNFR1- and vehicle-treated animals in B (two-way ANOVA followed by multiple comparisons with Bonferroni correction). Data are represented as mean ± SEM.

Discussion

Hebbian and homeostatic plasticity work in tandem refining neural circuitry, but their interactions have been unclear. In this paper, we have studied the dynamic interaction of fast NMDA-receptor-dependent Hebbian plasticity and slow TNF-α-mediated homeostatic plasticity, as found in ocular dominance plasticity (ODP) (Kaneko et al. 2008b). While our studies were based on specific, simplified models, they revealed more general principles that we now summarize.

In most existing models, the two forms of plasticity each modify the same factor, the synaptic strength. An equilibrium is reached when the changes induced by the two are equal and opposite, meaning that homeostatic plasticity is stabilizing a set of strengths that would be unstable under Hebbian plasticity alone. We have shown that these models fail to robustly reproduce ODP, because slow homeostatic negative feedback cannot stabilize fast Hebbian plasticity, which is a positive feedback process (Cooper et al. 2004, Zenke et al. 2013).

We show instead that ODP can robustly be captured by a model in which the two forms of plasticity modify separate factors whose product is the synaptic strength. Each form of plasticity then separately reaches its own stable state. This allows homeostatic plasticity to scale synaptic strengths slowly without needing to stabilize Hebbian plasticity. This model is consistent with the apparently multiplicative scaling of weights by homeostatic plasticity (Kaneko et al. 2008b, Stellwagen and Malenka 2006, Turrigiano et al. 1998) and the independence from TNF-levels of the percentage change in weights induced by LTP and LTD (Stellwagen and Malenka 2006), and it has natural biophysical interpretations (Fig. 4). The model can equivalently be regarded as one in which both processes directly modify the synaptic strength, but with two new features: (1) Homeostatic plasticity responds to instantaneous activity, rather than to delayed activity signals (e.g., due to slow temporal averaging), which lead to oscillations and instability. The slowness of homeostatic plasticity then results from slow learning (small weight changes per unit time) and/or delayed onset, neither of which could stabilize fast unstable Hebbian plasticity and thus neither of which could be used in existing models. (2) Homeostatic plasticity also scales the minimal and maximal strengths, allowing multiplicative scaling of all strengths and allowing Hebbian plasticity, which ceases at these limiting strengths, to remain in its own stable state while homeostatic plasticity proceeds. The model can account for ODP in response to MD in both monocular and binocular cortices and under various inactivation conditions.

The model makes several new predictions that we experimentally verified. First, it predicts that both forms of plasticity should be inactive at a steady state of the strengths. We tested this prediction in mouse V1, blocking Hebbian plasticity either during normal rearing or during days 7 to 10 of MD during the critical period for monocular deprivation. In both cases, the blockade did not alter synaptic weights, indicating that both forms of plasticity were inactive under these conditions. Second, as the model predicts, blocking Hebbian plasticity during MD 3-7 days revealed pure homeostatic potentiation of both eyes without any ODP, including closed-eye potentiation and reduced open-eye potentiation (Fig. 7A), as the model predicts (Fig. 6B). Finally, we verified (Fig. 7B) the predictions that, during binocular recovery after 6 days of MD, the previously closed eye’s synaptic strengths will overshoot their pre-MD baseline before returning to baseline (Fig. 5D), and that this overshoot will not occur if TNF-α-mediated homeostasis was blocked during MD (Fig. 6C). In the model, overshoot occurs because eye reopening causes rapid potentiation of the Hebbian factor from its MD-depressed state, while the homeostatic factor only slowly decreases from its MD-elevated state.

A similar two-factor learning rule was previously, independently studied in a model of the development of V1 orientation selectivity and its contrast invariance (Pool and Mato 2010). That paper motivated the rule simply as a means of modeling multiplicative homeostatic scaling, and did not address the dynamical issues we address here.

Additional contributions to cortical plasticity

Many other mechanisms are likely to contribute to cortical plasticity besides the interaction of fast Hebbian and slow homeostatic plasticity studied here. For example, here we did not model plasticity in synapses to or from inhibitory neurons (e.g. Gandhi et al. 2008, Kuhlman et al. 2013, Maffei et al. 2006) or in intrinsic intracortical synapses (e.g. Trachtenberg and Stryker 2001). We have focused on physiological ODP, ignoring mechanisms of anatomical plasticity such as branching and retraction of axons (Antonini and Stryker 1993, Trachtenberg and Stryker 2001). A variety of mechanisms not considered here may contribute to closing the critical period for MD-induced ODP (reviewed in Bavelier et al. 2010, Espinosa and Stryker 2012). Cho et al. (2009) found, in layer 4, that open-eye potentiation after MD is NMDA dependent. Our results partially reconcile this with the result of Kaneko et al. (2008b) that such potentiation depends on TNF-α, showing that partial NMDA blockade reduces open-eye potentiation by eliminating closed-eye LTD and thus reducing homeostatic upscaling. However, Hebbian LTP, laminar differences, or other facts might also play roles (further discussed in Supplemental Information, section S7.1). We have modeled only TNF-α-dependent homeostatic plasticity, which mediates scaling up of strengths in response to reduced activity, while ignoring separate mechanisms that scale synapses down in response to hyperactivity (Stellwagen and Malenka 2006) and other forms of homeostatic plasticity (Turrigiano 2011).

Functional significance

The slow activation of TNF-α may mechanistically result from the diffusive signaling interactions between neurons and glia (Stellwagen and Malenka 2006). Is there a functional reason, a computational benefit, for evolution to select this slow means of maintaining an activity set point? Consider an extreme example: if very fast homeostatic plasticity always set the postsynaptic activity to a constant set-point, this would prevent coding of differing signals with differing firing rates. Similarly, for Hebbian plasticity to learn stimulus statistics that change over minutes, hours, or a day, it may be important that homeostatic plasticity not substantially change activity statistics over these time scales.

Maintaining these two processes through separable factors allows dynamic range for coding to be maintained while allowing Hebbian mechanisms to freely learn synaptic patterns without interference. It allows stable weight patterns to be maintained without constitutively active but cancelling plasticities, which might be metabolically costly. Finally, as we have seen, it allows dynamic range to be maintained slowly, relative to Hebbian learning, without oscillations or instability. Thus, the dynamical interaction we propose here may describe a key biological principle underlying memory and learning in neuronal circuits.

Experimental Procedures

Mathematical model

The single-input models are detailed in Results. For models with N = 500 inputs: we label inputs by i, i = 1, …, 500. The eye that drives a given input is indicated by e_i ∈ {C, I} (C, contralateral eye; I, ipsilateral eye). In simulations of monocular cortex, e_i = C for all i. In simulations of binocular cortex, e_i = C, i = 1: 310; e_i = I, i = 311: 500, which reproduces the experimentally observed ODI of about 0.25 under normal vision (Kaneko et al. 2008b). Inputs are uniformly spaced on a 1D retinotopic axis, with z_i the retinotopic position of the ith input (0 ≤ z_i < 1 ∀i). In monocular cortex, z_i = (i − 1)/500. In binocular cortex, z_i = (i − 1)/310 for i = 1: 310 and z_i = (i − 311)/190 for i = 310: 500.

Input statistics with multiple presynaptic neurons

The input firing rates are assumed to be Gaussian random variables with mean ⟨x_i⟩ and covariance Q̃_ij of the form

$${\tilde{Q}}_{ij}=q_{e_i,e_j}\langle x_i\rangle \langle x_j\rangle \exp \left[-\frac{{(z_i-z_j)}^2}{2{\sigma }_q^2}\right]$$ (10)

The correlation magnitudes are q_C,C = q_I,I = 1, q_C,I = q_I,C = 0.5; σ_q = 0.2. The mean firing rates are ⟨x_i⟩ = 1 for normal rearing and ⟨x_i⟩ = 0.5 for contralateral inputs under MD. To demonstrate the robustness of our plasticity rule to noise and to reproduce some biological heterogeneity, we added noise to the covariance matrix, i.e., Q_ij = Q̃_ij + 2(ξ_i + ξ_j), where {ξ_i} is a set of independent random Gaussian variables with unit variance. Note that, while this noise perturbs individual synapses, it does not effect ODP.

Visual response and ocular dominance index

The visual response C or I of the contralateral or ipsilateral eye, respectively, was defined as the sum of that eye’s synaptic strengths. The ocular dominance index was ODI = (C − I)/(C + I).

Simulation methods

Numerical simulations in Figs. 1-4 (except Fig. 1C) used Mathematica (using NDSolve, which uses the Livermore Solver for Ordinary Differential Equations Adaptive (LSODA) approach). Other simulations used Matlab (a modified Rosenbrock formula of order 2).

In vivo experiments

All procedures were approved by the Institutional Animal Care and Use Committees at University of California San Francisco, in compliance with the NIH guide for the care and use of laboratory animals. C57BL/6 male mice (Charles River Laboratories) were used. Day 0 in all experiments is P25. Eyelid suture, visual stimulation, repeated optical imaging of intrinsic signals and quantification of response amplitude and ocular dominance were performed as described (Kaneko et al. 2008b). For the partial NMDA blockade experiments, intraperitoneal injections of 3-(2-Carboxypiperazin-4-yl)propyl-1-phosphonic acid (CPP, Tocris Bioscience) (15 mg/kg) or the vehicle solution were made every 24 hours for the duration as indicated in Figs. 3 and 7. To inhibit TNF-α signaling, recombinant soluble TNF receptor 1 (R&D Systems, Inc.) at the rate of 8.57 μg/hr or the vehicle solution was continuously infused into the cortex using an osmotic minipump (Alzet model 1002) during MD as indicated in Fig. 7. For details of in vivo procedures, see Supplemental Information, section S9.