Raison d’être of insulin resistance: the adjustable threshold hypothesis

Abstract

The epidemics of obesity and diabetes demand a deeper understanding of insulin resistance, for which the adjustable threshold hypothesis is formed in this paper. To test the hypothesis, mathematical modelling was used to analyse clinical data and to simulate biological processes at both molecular and organismal levels. I found that insulin resistance roots in the thresholds of the cell's bistable response. By assuming heterogeneity of the thresholds, single cells' all-or-none response can collectively produce a graded response at the whole-body level—conforming to existing data. The thresholds have to be adjustable to adapt to extreme conditions. During pregnancy, for example, the thresholds increase consistently to strengthen the mother's insulin resistance to meet the increasing glucose demand of the expanding fetal brain. I also found that hysteresis, a key element of the adjustable threshold hypothesis, can explain reactive hypoglycaemia, which is characteristic of diabetes complications but remains poorly understood. Contrary to the common belief that insulin promotes glucose disposal, the results imply that insulin is the body's ‘ration stamp’ to restricting glucose utilization by peripheral tissues and that insulin resistance is primarily a well-evolved mechanism. The hypothesis provides an intuitive and dynamical description of the previously formless insulin resistance, which may make the detection of pre-diabetes possible and may shed light on the optimal timing of therapeutic intervention. It also provides valuable clues to defining subtypes of type 2 diabetes that might respond differently to specific prevention and intervention strategies.

1. Introduction

The pandemic of type 2 diabetes marks a major healthcare crisis of our time. It was projected that by 2030 some 552 million people, or one adult in 10, would have diabetes [1]. Type 2 diabetes is characterized by insulin resistance, a condition under which certain tissues do not respond adequately to insulin, a peptide hormone secreted by the pancreas to facilitate glucose uptake. Because the pancreas can overproduce insulin for compensation, the insulin-resistant state can remain asymptomatic for many years, until finally the exhausted pancreas can no longer produce the required amount of insulin. The full-fledged diabetes ensues, characterized by abnormal glucose levels (persistent hyperglycaemia, severe hypoglycaemia due to inaccurate treatments, etc.). Type 2 diabetes is closely related to obesity, for which the term ‘twin epidemics' was coined to signify their parallelism [2].

Neel [3] proposed that evolutionary pressure to preserve glucose for use by the brain during starvation leads to a genetic propensity towards insulin resistance in peripheral tissues. Under normal conditions, the neurons depend solely on glucose as their source of energy, and their glucose consumption accounts for some 60% of that of the whole body in the resting state. If the majority of tissues (muscles in particular) were not resistant to insulin, then the brain, which constitutes only about 2.5% of the body weight, would not be able to obtain 60% of glucose. Insulin resistance was even more critical for early hunter–gatherers who had often to deal with prolonged starvation [4,5]. Although illuminative, the evolutionary perspective has not led to any definitive conclusions regarding insulin resistance. Neel's theory has remained speculative since its introduction more than half century ago.

This paper aims to advance our understanding of insulin resistance by using a dynamical perspective. Insulin resistance primarily occurs in muscles, which display interesting dynamical behaviours upon certain types of stimulation. Early in 1871, Henry P. Bowditch observed that muscles respond to electric stimulus in an all-or-none manner: the stimulus either produces the greatest muscle contraction or does not produce any contraction, depending on the intensity of the stimulus [6]. Later, similar dynamics was observed in different processes such as the passage of impulses along nerve trunks (the action potential) and the bursting electrical activity in pancreatic beta cells [7], which led to a series of breakthroughs in these fields. It is thus expected that the dynamical perspective would also provide great insights into insulin resistance and type 2 diabetes.

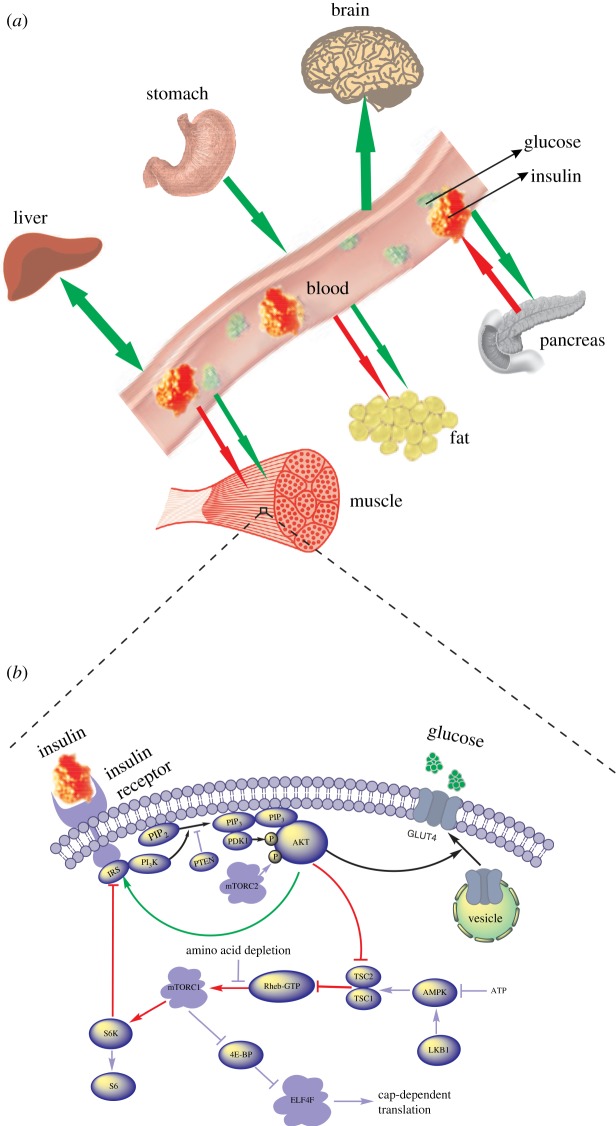
A fundamental question inspired by the dynamical perspective is: ‘how does a typical cell, as the fundamental unit of life, respond to insulin?’ Is the response all-or-none, similar to the response of a muscle fibre to electricity? It was observed that our body responds to insulin in a graded manner [8]. By extrapolation, one would expect that a cell also exhibits a graded response to insulin (the graded response view). To determine the validity of the extrapolation, information spanning multiple levels—from molecules to the organism—is integrated to form a global picture of insulin action. In [9,10], I examined the insulin signalling pathway (figure 1b), a molecular circuit hard-wired into the cell that, when stimulated by insulin, mediates the cell's glucose uptake, among many biological functions. In this paper, I primarily study glucose–insulin homeostasis (figure 1a), which is influenced by both the cells' individual action and the feedback mechanisms at the organismal level. These holistic considerations strongly challenge the graded response view and lead to a unified hypothesis, called the adjustable threshold hypothesis.

Figure 1.

A global picture of glucose–insulin dynamics. (a) Interorgan coordination of glucose and insulin homeostasis. (b) Intracellular insulin signalling pathway.

According to the hypothesis, a typical cell exhibits an all-or-none response to insulin (figure 2b). The switching between all and none occurs at two threshold insulin concentrations I_on and I_off, which render hysteresis: the delayed switch-on to spare glucose for the brain and the delayed switch-off to avoid hyperglycaemia. Insulin resistance, known as a ‘pathologic’ condition underlying type 2 diabetes, is actually a useful mechanism in the first place. Insulin resistance should even be strengthened under harsh metabolic conditions such as pregnancy, during which the expanding fetal brain demands more glucose. This condition demands the adjustability of the thresholds. The adjustable threshold hypothesis provides an intuitive and dynamical description of the previously formless insulin resistance, which may make the detection of pre-diabetes possible.

Figure 2.

The two kinds of response of the insulin signalling pathway. (a) The graded response and (b) the bistable response. (Online version in colour.)

2. Material and methods

Figure 1b illustrates the insulin signalling pathway. Upon binding to its receptor, insulin triggers a chain of molecular interactions inside the cell. The signal propagates through the cytoplasm and eventually renders glucose uptake (the response). Besides the linear cascade from IRS to GLUT4 (highlighted by the black arrows), the pathway also contains a positive feedback (from AKT to IRS directly as highlighted by the green arrow) and a negative feedback (from AKT to IRS indirectly as highlighted by the red arrows). Mathematical modelling of the insulin signalling pathway [9,10] revealed that the pathway can produce two kinds of response curves u(I): the graded response (figure 2a) and the bistable response (figure 2b). Here, I represents the plasma insulin concentration and u represents the response, namely the cell's rate of glucose uptake. The bistable response has two different thresholds I_off and I_on. When the insulin concentration is smaller than I_off, the response is none; when the insulin concentration is greater than I_on, the response is all; when the insulin concentration is between I_off and I_on, the response adheres to its current state, which is either none or all (electronic supplementary material, equation S9). The bistable response is characterized by hysteretic reversal [11]. As the insulin concentration increases from low to high, the response switches from none to all at I_on. As the insulin concentration decreases, the response switches off at I_off—a different route. The difference between the two thresholds, ΔI = I_on − I_off, is used to quantify the degree of hysteresis. Note that hysteresis is even more important to distinguish figure 2b from figure 2a. A graded response, if having a steep slope at some point, can be called approximately all-or-none, but it does not manifest hysteretic reversal. In fact, the graded response is characterized by exact reversal. As the insulin concentration increases, the level of response traces out a curve that is exactly the same as the one traced out by letting the insulin concentration decrease. The modelling work in [9,10] thus narrowed insulin action down to only two basic patterns and justified the fundamentality of the question ‘how does a cell respond to insulin: graded or all-or-none?’

Figure 1a illustrates the coordination of glucose–insulin homeostasis among main organs or tissues in the body, where green (red) arrows indicate flows of glucose (insulin). In the fasting state, plasma glucose is primarily used by the brain, which relies absolutely on glucose as its fuel. The glucose consumption is balanced by hepatic glucose production, which allows the body to maintain a relatively constant glucose concentration. Upon a meal ingestion, the plasma glucose concentration rises dramatically, intensifying its stimulation to the pancreas. Accordingly, the pancreas secretes more insulin and causes a surge of the plasma insulin concentration. The increased insulin concentration drains glucose from the blood into tissue cells (primarily in the muscles, adipose tissues and the liver), which cancels out the initial surge of plasma glucose. The decrease in the glucose concentration is followed by the decrease in the insulin concentration, because the pancreas becomes less stimulated. Finally, both glucose and insulin return to their baseline levels.

To examine glucose–insulin homeostasis, a mathematical model

2.1

2.2

is reported [10,12], where G(t) and I(t) are the glucose and insulin concentrations as functions of time, respectively. See the electronic supplementary material, appendix, for a detailed explanation of the model parameters. The mathematical model can reproduce observed properties of the system, including the maintenance of fasting glucose and insulin concentrations; the rapid restoration of homeostasis upon perturbations such as a meal ingestion, reactive hypoglycaemia, etc. Clinical data related to these properties were used to constrain the parameters of the mathematical model.

In the model, V(I) represents the whole-body's rate of glucose disposal as a function of the plasma insulin concentration. This function is crucial to test the adjustable threshold hypothesis. Because V(I) is the accumulation of every cell's rate of glucose uptake, an agent-based approach is taken to construct such a V(I). A system of N = 10⁵ cells is first created in silico. For a given cell, its I_on value is drawn from a Gaussian probability distribution, which is determined from clinical data (see below); its I_off value is automatically obtained, because a fixed ΔI = I_on−I_off is assumed for all the cells. In this way, the response u(I) of each of the N cells is determined (electronic supplementary material, equation S9), followed by the whole-body's response V(I) (electronic supplementary material, equation S8).

3. Results

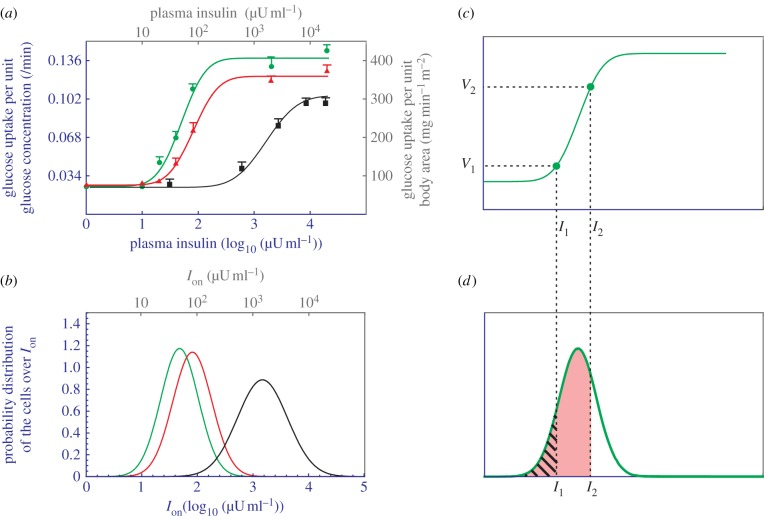
It was taken for granted that a cell exhibits a graded response to insulin (figure 2a), probably because the whole-body's response was found to be graded. Figure 3a presents three sets of dose–response data obtained from euglycaemic insulin clamp studies [8,13]: the green, red and black one is for normal subjects, obese non-diabetes and obese diabetes, respectively. These data all fit well with simple graded curves. By extrapolation, one would expect that a cell also exhibits a graded response to insulin (electronic supplementary material, appendix: the graded response view). Under this view, insulin acts like a fuel for pumping glucose into the cell. When the insulin concentration starts to rise in the blood, the cells start to absorb glucose, and their efforts increase as the insulin concentration increases.

Figure 3.

Analysis of data obtained from insulin clamp experiments. (a) Dose–response relationship between the plasma insulin concentration and the whole-body's rate of glucose uptake in normal (green circles), obese non-diabetes (red triangles) and obese diabetes subjects (black squares). The curves are obtained by using the electronic supplementary material, equation S7, to fit with the data. Two setting of units are used: one from the original data (grey) and the other from the simulation (blue). (b) The Gaussian distribution of cells over their I_on values. The green, red and black colours correspond to normal subjects, obesity non-diabetes and obese diabetes, respectively. (c) A reproduction of the normal subjects' dose–response curve, with only two data points presented. (d) A reproduction of the normal subjects' cell distribution. The hatched area corresponds to V₁ and the pink area corresponds to V₂.

Although intuitively appealing, the graded response view is problematic. If the cell's response curve u(I) is graded, then it must also exhibit exact reversal, as figure 2a clearly indicates. As a consequence, the whole-body's response V(I), as the sum of many u(I), must also exhibit exact reversal (see the proof in electronic supplementary material, appendix). In other words, the graded response view imposes that a single curve, namely the green curve in figure 3a, must account for the body's response to both directions of insulin concentration change. This is still fine—the exact reversal was taken for granted. But a problem emerges when a connection is established between hysteresis and reactive hypoglycaemia.

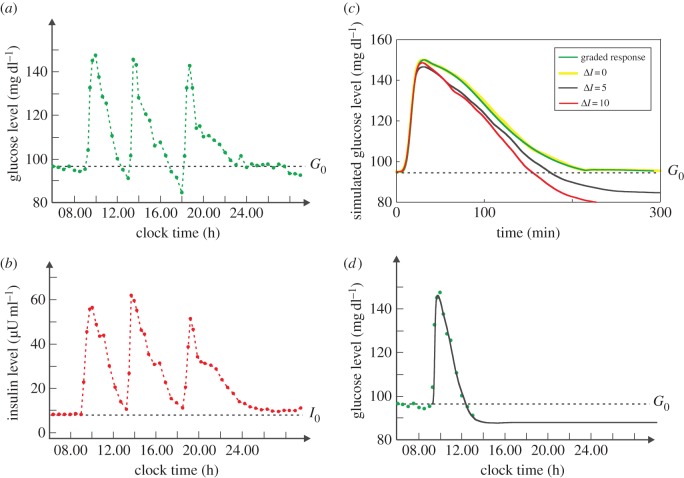
Reactive hypoglycaemia is a recurring phenomenon that remains poorly understood. Figure 4a,b presents 24 h clinical data of plasma glucose concentration G(t) and insulin concentration I(t), respectively, of normal subjects [14]. In the figure, the three spikes were caused by the three meals. One sees that every glucose spike is followed by an undershoot (i.e. the glucose concentration drops below the baseline G₀) that occurs 3–4 h after the meal. If overly large, the undershoot would be perceivable as reactive hypoglycaemia, or postprandial hypoglycaemia [15]. Although often strengthened by complications such as diabetes, moderate reactive hypoglycaemia is normal. Many people often experience mid-afternoon drowsiness [16], an indication of impaired brain function due to post-lunch hypoglycaemia.

Figure 4.

Glucose and insulin homeostasis. (a) Twenty-four hour profile of plasma glucose concentration averaged from 14 normal subjects. The three spikes were caused by the three meals at 09.00, 13.00 and 18.00. The baseline concentration G₀ is indicated by the dashed line. (b) Twenty-four hour profile of plasma insulin concentration. (c) The numerical simulation of plasma glucose homeostasis provoked by a meal beginning at time 0. The green curve is obtained under the graded response view. It is actually a reproduction of the curve in figure 5a. The yellow, black, red curves are obtained under the adjustable threshold hypothesis with ΔI = 0, 5, 10 µU ml⁻¹, respectively. (d) A reproduction of the ΔI = 5 curve with the timescale of (a) and with the assumption that the meal begins at 09.00. The green dots represent the same data as those presented in (a).

It is agreed that reactive hypoglycaemia is caused by the high insulin spike as illustrated in figure 4b. But which part of the spike is the culprit? The peak? Although at the peak concentration insulin is supposed to be most powerful, glucose is also at the peak (cf. figure 4a,b)—no danger of hypoglycaemia at that moment. As the glucose level drops and approaches the baseline G₀ = 95 mg dl⁻¹, the danger of hypoglycaemia increases. But the insulin level also drops and approaches the baseline I₀ = 8 µU ml⁻¹, almost synchronously. According to the green curve in figure 3a, an insulin concentration as low as I₀ elicits almost no glucose disposal (note that the basal rate V₀ is not caused by insulin; see the electronic supplementary material, appendix) and is thus unlikely to cause hypoglycaemia. Instead, G(t) should level off well above the baseline. Finally, even if the glucose level drops slightly below the baseline G₀, the drop should be gentle, which is contradictory to the fact that the undershoot is steep (figure 4a).

This prediction is verified by the mathematical model (equations (2.1) and (2.2)), which contains the whole-body's response V(I). By using the green curve in figure 3a as V(I) and by assuming it reverses exactly, I obtain a simulation run that corresponds to normal glucose and insulin dynamics (figure 5). One sees that the glucose time course G(t) approaches the baseline G₀ but is always above it—no undershoot. Note that the simulation is based on parameter values (electronic supplementary material, table S1) that are biologically plausible. To determine the sensitivity of the result to the parameter values, the simulation is repeated 10⁴ times, each with a new set of parameter values. For every round of simulation, the value of every parameter is drawn randomly from a uniform distribution centring on the standard value (i.e. the value in the electronic supplementary material, table S1) with ±40% variation. That is, every parameter value is generated with equal probability between 1 − 40% and 1 + 40% of its standard value. At the end of the round of simulation, G(T)/G₀ − 1 is calculated to quantify the relative deviation from G₀ of the final glucose level, where T = 1200 min is used. Electronic supplementary material, figure S2A, shows the histogram of the quantity G(T)/G₀ − 1, which is strictly to the right of the longitudinal axis, indicating that the quantity is always positive, i.e. undershoot never occurred. These results imply that the graded response view is problematic. If the graded response view were right, then V(I) would be precisely the green curve in figure 3a and would exhibit exact reversal, and then the glucose dynamics G(t) would never undershoot. This is however contradictory to the fact that even reactive hypoglycaemia (a manifestation of large undershoot) is frequently observed. It should be noted that if the parameters are completely random, then undershoots may occur. But those results are biologically irrelevant, and that is why the constraint of ±40% variation was used.

Figure 5.

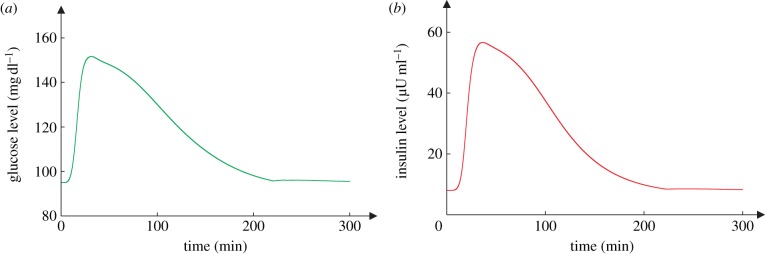
A simulation of normal insulin and glucose homeostasis. (a) The glucose dynamics and (b) the insulin dynamics. (Online version in colour.)

It is counterintuitive that the body's response does not exhibit exact reversal. Nevertheless, there is no evidence of the exact reversal either. Take the green dots in figure 3a as an example of insulin clamp data. Let (I_j, V_j) denote the coordinate of the jth dot. To obtain V_j, one first increases the insulin concentration from the baseline I₀ to the targeted value I_j. The insulin concentration is then ‘clamped’ at I_j, during which period V_j is determined. Therefore, the insulin clamp data only reflect one direction of the dose–response, namely the increase in insulin. The removal of the clamp initiates the reverse process—the insulin concentration decreases to the baseline I₀. But the reverse process involves no measurement, and essentially no data were collected for the reverse process.

The difficulty of the graded response view inspires me to formulate a new hypothesis centring on the thresholds, called the adjustable threshold hypothesis. The hypothesis points out four characteristics of insulin response: all-or-none (the existence of I_on), hysteresis (the existence of I_off < I_on that imparts hysteretic reversal), heterogeneity (the threshold values are different among the cells) and adjustability (the thresholds are subject to regulation in response to certain metabolic changes). To demonstrate the plausibility of adjustable threshold hypothesis, one has to show that individual all-or-none can produce a graded response at the whole-body level. In the following, I shall first give an intuitive explanation, followed by numerical verifications. It turns out that the hypothesis has additional advantages. It can explain the right-shift phenomenon, namely the progressive shift of the whole-body's response to the right, as the health state changes from normal to diabetic (figure 3a). It provides a natural explanation of reactive hypoglycaemia, which is much more difficult to explain using the graded response view.

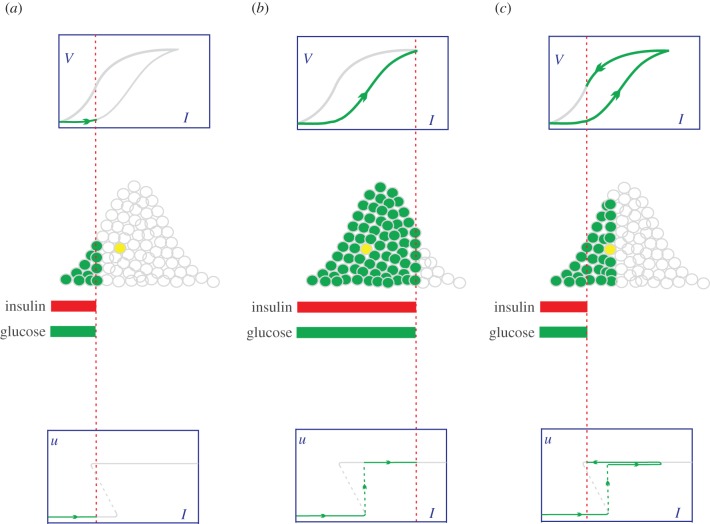
To show that individual all-or-none can produce a graded whole-body response, the cells are distributed over their I_on values to reflect heterogeneity: those with smaller I_on values are placed to the left of those with larger ones (the middle row of figure 6a). The insulin level is indicated by the red dashed line, which divides the activated cells (the green dots with grey periphery) and the inactivated cells (the white dots with grey periphery). As the insulin level increases (figure 6b), the number of activated cells gradually increases, producing a graded dose–response at the whole-body level (the forward branch of V(I)). It appears that insulin acts as a signal to trigger the cells' glucose uptake. The cells are different in their timing of activation. Once activated, they all work with maximal capacity. Therefore, the gradual increase of whole-body glucose utilization is not because every cell works harder as the insulin concentration increases, but because more and more cells become activated. By contrast, the graded response view assumes that insulin is a fuel to power glucose uptake and that a cell's effort is roughly proportional to the insulin level. As the insulin level decreases (figure 6c), the cell deactivates at its I_off. Note that the hysteresis (I_off < I_on) prolongs the cell's activation. To show this, take the yellow-filled cell as an example, and suppose the insulin levels in figure 6a,c are exactly the same. While the cell is inactive in figure 6a (because I < I_on), it is active in figure 6c (because I > I_off). The combined action of all the cells produces the reverse branch of V(I) during the decrease in insulin. The forward and reverse branches together constitute the graded whole-body response that exhibits hysteretic reversal. In the following, V⁺(I) and V⁻(I) are often used to represent the forward and reverse branches of V(I), respectively.

Figure 6.

The adjustable threshold hypothesis. First row: the whole-body dose–response V(I), which exhibits hysteretic reversal. The grey (green) colour indicates unexperienced (experienced) portion of the response curve. Second row: the Gaussian distribution of cells over their I_on values. The cells are represented by white dots (for the inactivated cells) and green dots (for the activated cells). Third row: the bistable response u(I) of the cell represented by the yellow dot. The grey (green) colour indicates unexperienced (experienced) portion of the response curve. (a) The insulin concentration is low and is rising. Only a small fraction of cells are activated. The yellow cell is not activated. (b) The insulin concentration is high and most cells are activated, including the yellow cell. (c) Insulin reduces to a level the same as that in (a). But there are more active cells than those in (a). Notably, the yellow cell is still active.

Threshold heterogeneity is a reasonable assumption and there are at least three sources of heterogeneity. The first is cellular heterogeneity. It is well known that adipocytes are conspicuously different in their sizes, and larger adipocytes are generally less insulin sensitive [17]. It is likely that larger adipocytes have larger I_on values. For myocytes, those having greater intracellular lipid content are generally less insulin sensitive [18]. The second is inhomogeneity of the insulin concentration in the space. Two identical but spatially separated cells switch at different times because their local insulin concentrations are slightly different. Finally, the temporal fluctuation of insulin concentration leads to switching uncertainty, and the uncertainty might be augmented by the energy barrier at the nominal threshold [19,20].

The forward branch of V(I) should fit well with insulin clamp data. Consider normal subjects first, namely the green dots (I_j, V_j) in figure 3a. According to the last paragraph, V_j should be proportional to the number of cells whose I_on values are smaller than I_j. In other words, V_j should be proportional to the area underneath the distribution function and to the left of the I = I_j line. For a clearer presentation, figure 3c shows the putative V⁺(I) of normal subjects, with only two data points (I₁,V₁) and (I₂,V₂) presented; figure 3d illustrates the cells' putative distribution function. One sees that V₁ should be proportional to the hatched area in figure 3d, whereas V₂ should be proportional to the pink area in figure 3d. If the distribution function is taken to be Gaussian with mean μ and s.d. σ, then V⁺(I) is a cumulative Gaussian function represented by the electronic supplementary material, equation S7. By using μ = 1.68, σ = 0.34, V_max = 0.139, V⁺(I) is obtained and is presented as the green curve in figure 3a, which fits well with the green dots. The corresponding Gaussian distribution is illustrated as the green curve in figure 3b. Now consider obese non-diabetes' insulin clamp data, namely the red triangles in figure 3a. By using μ = 1.91, σ = 0.35, V_max = 0.121, V⁺(I) is obtained and is presented as the red curve in figure 3a, which fits well with the red triangles. The corresponding Gaussian distribution is illustrated as the red curve in figure 3b. For obese diabetes' insulin clamp data, namely the black squares in figure 3a, they can be fit by using μ = 3.17, σ = 0.45, V_max = 0.100. The corresponding Gaussian distribution is illustrated as the black curve in figure 3b.

These results not only explain the graded whole-body response, but also explain the right-shift phenomenon [8,13], namely the progressive shift of the whole-body's response to the right, as the health state changes from normal to diabetic (figure 3a). It now appears that the phenomenon was due to the right-shift of the cells' I_on-distribution (figure 3b). What is the molecular basis of the increase of a cell's I_on? It is known that some obesity-related factors (free fatty acids, inflammatory factors such as tumour necrosis factor-α, etc.) can diffuse into a cell and downregulate the interaction between PI3K and the insulin receptor substrate [18,21,22]. The downregulation elevates both I_off and I_on, while keeping ΔI = I_on − I_off roughly fixed [9,10]. Consequently, the cell's response curve shifts to the right (because both thresholds increase) without much distortion (because ΔI is roughly fixed). Take the yellow-filled cell in figure 7 as an example. As the person becomes obese, there is a nearly perfect shift of the cell's bistable response to the right (figure 7c). Because obesity-related factors can diffuse into virtually every cell, the effect is systemic—the majority of cells are evenly affected. Indeed, the red distribution and the green distribution in figure 3b have almost the same shape (σ = 0.34 versus 0.35), indicating that the cells have roughly the same magnitude of I_on-increase. By contrast, the black distribution is more spread (σ = 0.45), indicating that the diabetic state involves more complications.

Figure 7.

A schematic view of four different types of cell and their distribution over I_on. (a) Normality. A pulse of insulin activates only a small portion of the cells. (b) Obesity. The majority of cells have enlarged I_on values. The pancreas has to secrete more insulin to achieve the same level of glucose disposal (i.e. activate the same number of cells). (c) The bistable responses of the yellow cell. The left (right) one is for the normal (obese) person.

The adjustable threshold hypothesis can explain reactive hypoglycaemia through the notion of hysteresis. Although defined at the molecular level, hysteresis is retained in the whole-body's response, as manifested by the two branches of V(I). Because V⁻(I) is above V⁺(I), insulin is more ‘powerful’ during its decrease in concentration, causing hypoglycaemia. I test this idea by using equations (2.1) and (2.2). To take into account the assumption that the cells have heterogeneous I_on values, a system of N = 10⁵ cells is created in silico whose I_on values follow the Gaussian distribution illustrated as the green curve in figure 3b. At a given time t, a cell either absorbs glucose or not, depending on the plasma insulin level I(t), its I_on and I_off values, and of course, the rule of bistability (electronic supplementary material, equation S9). The results demonstrate that hysteresis is essential to cause reactive hypoglycaemia. The yellow, black and red curves in figure 4c correspond to different degrees of hysteresis ΔI = 0, 5 and 10, respectively. By using the same timescale as figure 4a, the black curve (ΔI = 5) is reproduced in figure 4d, which fits well with the clinical data. More importantly, G(t) finally goes below the baseline G₀—an undershoot occurs. To determine the observation's sensitivity to the parameters, the simulation is repeated 10⁴ times. Each simulation is based on a new set of parameter values. Electronic supplementary material, figure S2C, shows the histogram of the quantity G(T)/G₀−1, which is strictly to the left of the longitudinal axis, indicating that the quantity is always negative, i.e. undershoot occurs with a 10⁴/10⁴ = 100% frequency. As hysteresis increases (ΔI = 10), the undershoot occurs earlier and is larger (figure 4c); and it also occurs with a 10⁴/10⁴ = 100% frequency (electronic supplementary material, figure S2D). In the absence of hysteresis (ΔI = 0), undershoot never occurs (electronic supplementary material, figure S2B) and hypoglycaemia is thus impossible. It is clear that hysteresis can explain reactive hypoglycaemia.

With ΔI = 0, all-or-none responses of individual cells collectively produce a whole-body response V(I) almost the same as that produced by cells with graded response, because the forward and reverse branches reduce to the same curve (V⁺ (I) = V⁻(I) = V(I)). As a consequence, G(t) obtained with ΔI = 0 (the yellow curve in figure 4c) should be almost the same with that obtained with the graded response assumption (the green curve in figure 4c), which is indeed the case. Note that the yellow curve is intentionally made thicker to obtain a better contrast with the green curve. As such, the histogram of 10⁴ simulations with ΔI = 0 (electronic supplementary material, figure S2B) is similar to that with the graded response assumption (electronic supplementary material, figure S2A).

Given that hypoglycaemia has no apparent usefulness, what is the purpose of hysteresis? Hysteresis implies I_off < I_on—the delayed termination of glucose uptake. This sustained insulin action is necessary to remove glucose accumulated during the phase of insulin resistance, without which hyperglycaemia would occur. A consequence of hysteresis is some undershoot of the glucose concentration, which may or may not be perceived as reactive hypoglycaemia, depending on the degree of hysteresis.

The undershoot is reminiscent of the after hyperpolarization phase of an action potential in a cell. During this phase, the cell's membrane potential falls below the normal resting potential, owing to the sustained opening of potassium ion channels that permit potassium ions exiting from the cell. This is unusual because the potassium ion channels would close rapidly as the potential falls. As a matter of fact, the falling of membrane potential also triggers an influx of calcium into the cell, which sustains the opening of potassium ion channels. It is the delayed closing of potassium ion channels (hysteresis) that leads to the undershoot of the membrane potential. Likewise, the decrease in insulin concentration would rapidly weaken glucose uptakes, which does not happen because the positive feedback from AKT to IRS sustains the signalling strength (hysteresis) that leads to the undershoot of the glucose level. It now appears that the similarity of response between insulin stimulus and electrical stimulus consists of not only all-or-none but also hysteresis.

4. Discussion

Our body depends upon insulin for glucose disposal. When the body is short of insulin, subcutaneous injection of insulin is needed for glycaemic control. Even when insulin production is normal, tissue cells may respond poorly to the hormone (insulin resistance). The pandemic of diabetes deepens our impression that insulin resistance is a pathologic condition and that insulin is a potent promoter of glucose disposal.

Yet, the adjustable threshold hypothesis emphasizes that insulin is primarily a signal restricting, rather than promoting, glucose uptake. To make sense of the idea, one may draw an analogy with food stamps issued by a government during wartime. From a holder's perspective, the food stamp promotes his/her own food acquisition. In essence, however, the food stamp embodies the government's intention to spare food for the war by restricting the masses' share. By analogue, insulin is essentially ‘glucose stamp’ issued by the body to restrict peripheral glucose utilization so that glucose can be spared for the brain. Just as the amount of food stamp being issued should match the reserve of food, the insulin concentration should reflect well the glucose concentration, which is indeed the case—the glucose dynamics (figure 4a) and the insulin dynamics (figure 4b) are almost synchronized. To realize the restriction, a signalling network downstream of the insulin receptor is used to produce none-then-all: a persistent unresponsiveness switching to a full response at a threshold I_on.

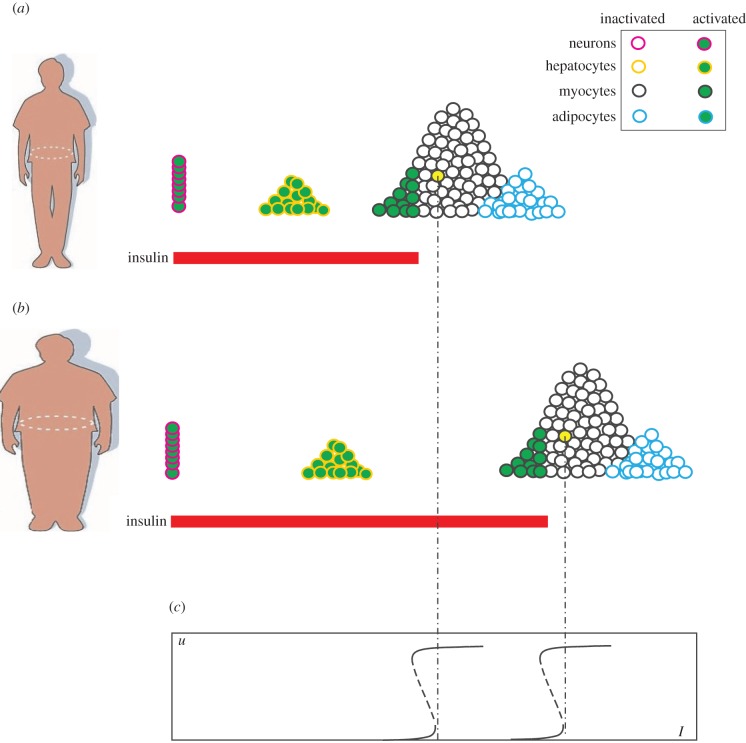
Just as some people can acquire more food because they possess more food stamps, some cells can use more glucose because they have smaller I_on values. In other words, the heterogeneity of I_on has a purpose. It creates an order of glucose uptake, which allows cells more critical to glucose to preempt glucose utilization. Figure 7a illustrates the putative I_on positions of neurons, hepatocytes, myocytes (muscle fibres) and adipocytes (fat cells). Neurons depend absolutely on glucose. Their glucose uptake is unconditional and should not be controlled by insulin (I_on = 0). Because the brain's demands are continuous but our meals are discrete, an organ is needed to store glucose for the later utilization by the brain. That organ is the liver. Therefore, hepatocytes should have small I_on values so that they can easily obtain glucose. Despite these brain-favourable designs, the bulk of muscles still constitute a menace to the brain, owing to their great mass and the fact that they never return glucose to the blood. Therefore, myocytes should have large I_on values. Adipocytes should generally have even larger I_on values. This would allow other tissues to uptake glucose first, followed by adipocytes if the insulin concentration continues to rise (e.g. due to a heavy meal). The primary role of adipocytes is to store surplus glucose and convert it into fat. It is fine if they do not get glucose at all.

The existence of I_on implies that insulin resistance is an inherent property: the cell's response ensues only after the insulin level exceeds I_on. In this event, a global elevation of I_on would strengthen insulin resistance, desired or undesired. Figure 7b illustrates that the majority of tissue cells have their I_on values elevated as the person becomes obese. Because the postprandial glucose resulting from a normal diet can hardly be cleared without the participation of muscles, the plasma insulin concentration (indicated by the red bar) has to elevate to reach the globally elevated muscular I_on. If this condition lasts too long, then the pancreas would reach its maximal capacity and be damaged in the end, leading to the full-blown diabetes. The scenario typically takes place in an obese man, where the ever-increasing adiposity may drive the drift of I_on larger and larger (the right-shift phenomenon). It appears that severe insulin resistance is pathologic, although moderate insulin resistance is necessary.

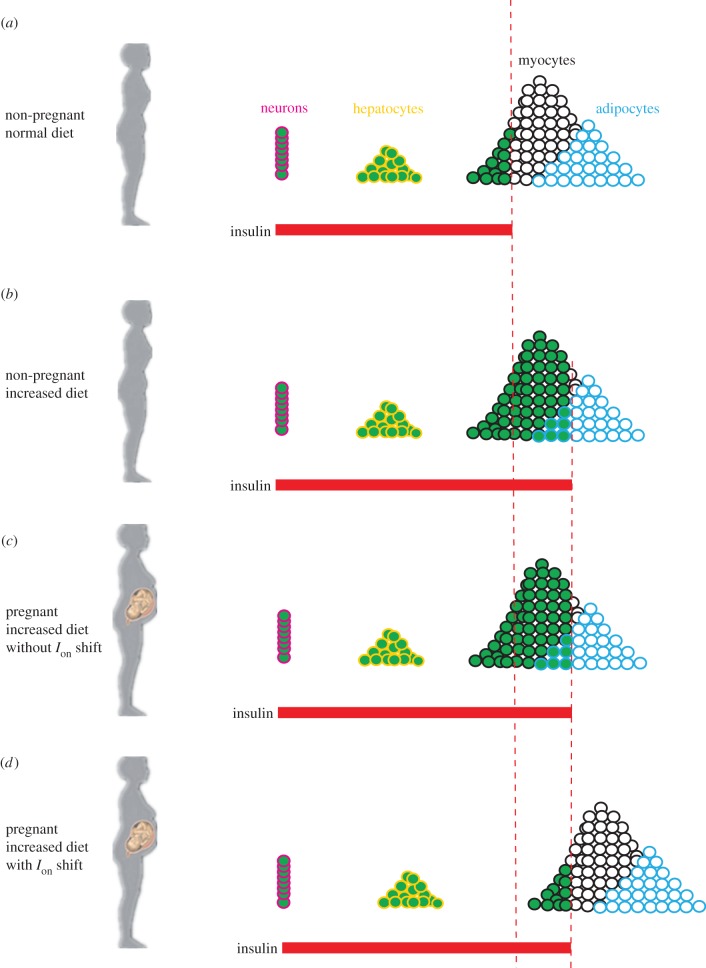
What makes it surprising and interesting is that even severe insulin resistance (even to a degree that diabetes would develop) may become necessary under certain metabolic conditions. During pregnancy, many women exhibit high glucose levels in the blood, although they were not diagnosed diabetes previously. This condition, termed gestational diabetes, is poorly understood [23]. According to the adjustable threshold hypothesis, insulin is developed to spare glucose for the brain. During pregnancy, there are at least two brains: the mother's and the fetus'. For multiple births, there are even more brains. One should not underestimate the fetal brain—it weighs one-fourth to one-third of the adult brain at birth [24]. To protect the expanding brains, the I_on values of the mother's muscles have to be raised accordingly. This can be realized with the help of the placenta, which secretes placental growth factor to downregulate the IRS-PI3K interaction [25], whereby the threshold I_on is raised. Because the brain content increases gradually as pregnancy progresses, the I_on values should drift larger and larger to match the brain growth. This causes a consistent right-shift of the body's insulin response, similar to the right-shift caused by obesity. But unlike the case in obesity, the right-shift usually does not elevate the plasma glucose level, because the extra glucose would be consumed by the expanding fetal brain. However, the possibility exists that the right-shift and the fetal growth are not well matched. If the fetal growth lags behind the right-shift, for example, then gestational diabetes is likely to emerge. Because placental growth factor dissipates as pregnancy completes, gestational diabetes is usually reversible.

One may argue that I_on values need not be raised because the expanding brains' needs can be met by eating more per meal, with the hope that the extra glucose all goes to the fetus. This strategy is unlikely to work for the following three reasons. First, famine is a recurring theme in human history. Even in modern societies that are characterized by food abundance, starvation does occur occasionally. Second, even if food is always abundant and one can always eat more, the majority of the extra glucose would go to the mother; and the fetus is unlikely to benefit from it. This is because the increased meal ingestion increases the peak insulin level, which activates more cells (of the mother) to absorb glucose (figure 8c). Finally, the increased diet may exacerbate reactive hypoglycaemia (the more one eats, the lower the nadir of the plasma glucose level). This exacerbated hypoglycaemic state, although transient, may be deadly to the fetus. With the raised muscular I_on values (figure 8d), the muscles postpone their action, which allows the brains to obtain more glucose. Moreover, the livers can store more glucose. This renders a more sustained hepatic release of glucose during the fasting state. Because the fasting glucose concentration is relatively low, the sustained-release would not provoke the muscles and the released glucose can fully benefit the brains.

Figure 8.

Tissue-specific, insulin-mediated glucose uptake under different conditions. (a) Non-pregnant woman with normal diet. (b) Non-pregnant woman with increased diet. (c) Pregnant woman with increased diet and with unchanged I_on values. (d) Pregnant woman with increased diet and with increased I_on values.

Reactive hypoglycaemia is also dangerous to diabetes patients, especially to those relying on the injection of insulin for glycaemic control. In current clinical practices, the timing and dosage of insulin and/or drug administrations are only empirically determined, because the mechanisms of hypoglycaemia are poorly understood. The notion of hysteresis provides an intriguing clue to its understanding. Further investigations should be performed, on the basis of the notion of hysteresis, to determine the optimal strategies for therapeutic interventions. To this end, hysteresis should be considered together with other dynamical properties such as all-or-none, heterogeneity and adjustability. Therefore, the formation of the adjustable threshold hypothesis is necessary, as well as its further testing.

It is possible that the adjustable threshold hypothesis addresses only one type of insulin resistance, which is a fine mechanism in the first place. There may exist other types of insulin resistance. If bistability vanishes (i.e. the response curve changes from figure 2b into figure 2a) for the majority of cells in the body, then a much higher insulin concentration is needed to render the cell's maximal rate of glucose uptake. Moreover, a high rate of glucose uptake is difficult to maintain, for the rate decreases with the decrease in the insulin concentration (due to the lack of hysteresis). In brief, type 2 diabetes may have different subtypes, which necessitate differential prevention and intervention strategies.

This paper is just a starting point of the adjustable threshold hypothesis. An apparent next step is to test the hypothesis based on single-cell experiments, including the existence of I_on and I_off; the heterogeneity of these thresholds within the same cell type, across different cell types, and even across different species; how these thresholds are regulated in response to fatty acids and certain hormones. On the basis of these single-cell studies, animal experiments can also be done to further test the hypothesis.

Funding statement

This work was partly supported by National Natural Science Foundation of China (no. 61471186) and Shenzhen Municipal Research Funds.