Hybrid Incompatibility Arises in a Sequence-Based Bioenergetic Model of Transcription Factor Binding

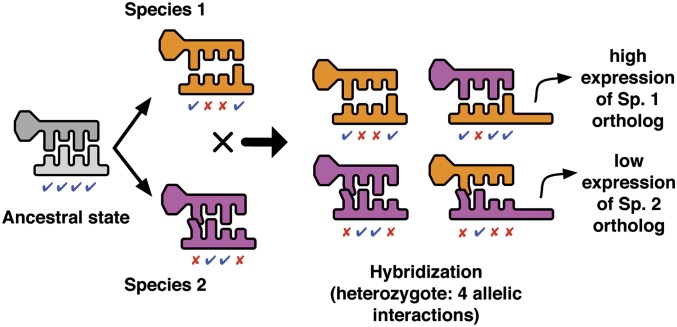
Abstract

Postzygotic isolation between incipient species results from the accumulation of incompatibilities that arise as a consequence of genetic divergence. When phenotypes are determined by regulatory interactions, hybrid incompatibility can evolve even as a consequence of parallel adaptation in parental populations because interacting genes can produce the same phenotype through incompatible allelic combinations. We explore the evolutionary conditions that promote and constrain hybrid incompatibility in regulatory networks using a bioenergetic model (combining thermodynamics and kinetics) of transcriptional regulation, considering the bioenergetic basis of molecular interactions between transcription factors (TFs) and their binding sites. The bioenergetic parameters consider the free energy of formation of the bond between the TF and its binding site and the availability of TFs in the intracellular environment. Together these determine fractional occupancy of the TF on the promoter site, the degree of subsequent gene expression and in diploids, and the degree of dominance among allelic interactions. This results in a sigmoid genotype–phenotype map and fitness landscape, with the details of the shape determining the degree of bioenergetic evolutionary constraint on hybrid incompatibility. Using individual-based simulations, we subjected two allopatric populations to parallel directional or stabilizing selection. Misregulation of hybrid gene expression occurred under either type of selection, although it evolved faster under directional selection. Under directional selection, the extent of hybrid incompatibility increased with the slope of the genotype–phenotype map near the derived parental expression level. Under stabilizing selection, hybrid incompatibility arose from compensatory mutations and was greater when the bioenergetic properties of the interaction caused the space of nearly neutral genotypes around the stable expression level to be wide. F₂’s showed higher hybrid incompatibility than F₁’s to the extent that the bioenergetic properties favored dominant regulatory interactions. The present model is a mechanistically explicit case of the Bateson–Dobzhansky–Muller model, connecting environmental selective pressure to hybrid incompatibility through the molecular mechanism of regulatory divergence. The bioenergetic parameters that determine expression represent measurable properties of transcriptional regulation, providing a predictive framework for empirical studies of how phenotypic evolution results in epistatic incompatibility at the molecular level in hybrids.

POSTZYGOTIC hybrid incompatibility (HI), an important component of reproductive isolation (Coyne and Orr 2004), is usually not due to failure of a single gene, but arises from incompatibilities between interacting genes, as described by the Bateson–Dobzhansky–Muller (BDM) model (Bateson 1909; Dobzhansky 1937; Muller 1942). Recent studies of the genes underlying HI show that this BDM model is well supported and that some form of selection plays a role in the evolution of HI (Johnson 2010; Presgraves 2010; Maheshwari and Barbash 2011). In most cases, however, the molecular basis of HI is unresolved; because incompatibility requires at least two interacting genes under the BDM model, the cause of incompatibility can be understood fully only after all of the interacting partners have been identified.

Gene interactions are of essence in developmental biology. Networks of interacting genes map an organism’s genotype to its phenotype through developmental and physiological processes (Wilkins 2002). Motivated by the pervasive nature of these networks, Johnson and Porter (2000, 2001, 2007) (see also Palmer and Feldman 2009) developed models that connect directional selection on phenotypic traits to the evolution of hybrid incompatibility through the action of gene networks. In these models, BDM incompatibilities can be understood in terms of molecular interactions among the nucleic acid and protein components of these networks. Simplifications in the representation of these interactions in this model yielded several results that limited its generality and its tractability for future empirical work.

Molecular interactions in biological systems are governed by bioenergetic (combining thermodynamics and kinetics, Morowitz 1978) principles inherent to the physics of interacting molecules. In the context of gene regulation (Gerland et al. 2002), these principles require that interactions between transcription factors (TFs) and the promoter sites they associate with be viewed not as binary and static, with prospective TFs always or never bound such that gene expression proceeds at its maximum level or not at all. Rather, bioenergetic principles require that binding be dynamic and expressed in terms of fractional occupancy, the probability that the TF is associated with its binding site at a given moment. The values of bioenergetic parameters themselves depend on the configurations and concentrations of the interacting molecules, which are evolvable in regulatory networks, with the consequence that gene expression evolves on a continuous rather than binary scale (Gerland et al. 2002). Intermediate levels of gene expression are possible and can be favored in environments where the corresponding phenotypes are optimal.

The genotype–phenotype (G–P) map, which describes the relationship between genotypic information and phenotypic expression (Segal et al. 2008), is shaped by the bioenergetic properties of the molecular interactions (Gerland et al. 2002). The fitness landscape, which describes the relationship between fitness and the underlying genetic information and environmental conditions that ultimately determine reproductive success, is mediated through the phenotype. When phenotypes are based upon regulatory interactions, the shape of the fitness landscape is determined by the bioenergetics of the interacting molecules. The fitness landscape is therefore ultimately based upon these bioenergetic properties and subject to bioenergetic constraints (Watt and Dean 2000; Watt et al. 2003, Watt 2013). The evolutionary dynamics of HI depend on the details of its shape.

In this study, we investigate the effects of bioenergetic parameters on evolving genetic regulatory interactions and the evolutionary constraints imposed upon their by-product, BDM incompatibilities. We show the conditions under which BDM incompatibilities are most likely to evolve in the simplest regulatory interaction, the two-locus case. Our results overcome the limitations in the Johnson and Porter (2000, 2001, 2007) models and are well suited to empirical studies of the bioenergetic basis of gene expression (Segal and Widom 2009; Shultzaberger et al. 2012) and bioinformatic data characterizing promoter sequences and TF binding (Segal et al. 2008; Wittkopp and Kalay 2012).

Modeling Approach

To characterize the bioenergetic properties of regulatory molecular interactions, we modify a class of statistical physics models (Von Hippel and Berg 1986; Gerland et al. 2002; Mustonen et al. 2008), originally developed to model the bioenergetics of transcription regulation in terms of the information content of the regulatory site. In these models, the information content represents the fit between the TF’s binding motif and the binding site’s nucleotide sequence, which in turn determines the free energy of formation of bonds between them. In the cell, a TF molecule may interact to varying extents with its target binding site, any spurious binding sites in the remainder of the genome, and other molecules in the intracellular environment. The total free energy of binding to this nonspecific background varies with the motif length and genome size. The binding energy of the TF to the specific site of interest, relative to the collective binding energies to the competing interactors, and in combination with the number of TF molecules available, determines the fractional occupancy—the probability that the TF is associated with its binding site at a given moment. Gene expression occurs while the TF is bound.

We modify this basic statistical physics model by allowing the information content of the TF’s binding motif to vary in the same way as the binding site and represent the information content of both as mutable binary sequences (Figure 1), with fractional occupancies calculated from novel variants of each. The phenotype is proportional to fractional occupancy, and the fitnesses of those phenotypes depend on environmental conditions that may change. Adaptation arises from evolutionary changes in the underlying regulatory interaction responsible for gene expression. Inasmuch as the fitness landscape—the relationship between genotype and fitness—is mediated through the phenotype, the dynamics of adaptation ultimately are subject to the evolutionary constraints imposed by the underlying bioenergetic parameters. As in Johnson and Porter (2000, 2007), we expect hybrid incompatibility, in the form of misregulated gene expression, to arise as a by-product of adaptation if parent populations evolve different and incompatible solutions in response to selection for a given level of expression, but subject to the bioenergetic constraints that act upon adaptation.

Figure 1.

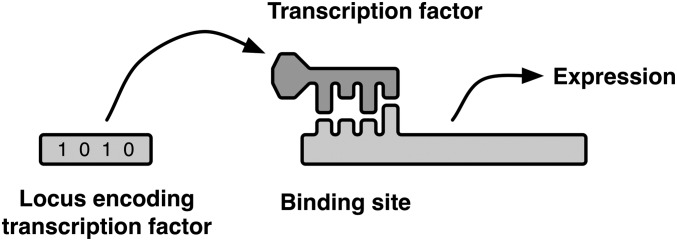
“Lock and key” model of a two-locus regulatory interaction. Expression depends on the fit between the transcription factor, encoded at the first locus, and a binding site in the regulatory region of the second locus. Alleles of the transcription factor and the binding site are represented as binary strings. A perfect match results in the maximum level of expression (but not necessarily the highest fitness).

Model

We model a regulatory interaction between two unlinked diploid loci, where the first locus encodes a mutable TF and the second locus encodes a protein whose expression level determines the organismal phenotype of interest. Expression of the second locus is activated by binding of the TF to a mutable binding site in its regulatory region (Figure 1). Information contained in the alleles of the TF and the binding site is represented using sequences of n = 12 bits, where the constant n is the length of the binding motif. The number of matched bits represents the fit between the binding site’s nucleotide sequence and the TF’s binding motif, which in combination with bioenergetic parameters determines the level of expression and the resulting phenotype.

Fractional occupancy

Expression is calculated from the fractional occupancy of the TF on its target binding site (the proportion of time the TF is bound) following the statistical physics models of Von Hippel and Berg (1986), Gerland et al. (2002), and Mustonen et al. (2008), which model fractional occupancy as a dynamic equilibrium determined by the free energy of binding and the availability of TF molecules in the cell, and take into account the possibility of spurious occupancy of the TF on nontarget sites. Transcription factor molecules may exist freely in solution or in association with the genome, where they may be bound at any position with a sequence-dependent probability. An individual binding site’s sequence distinguishes it from the rest of the genome and determines the relative affinity for that site by a given TF molecule. Following Gerland et al. (2002), we focus on a single functional binding site and treat the rest of the genome as random sequence that may contain whole or partial instances of the binding motif. Attraction to the genomic background and the rest of the intracellular environment is treated as nonspecific binding with no functional consequence except to decrease the fractional occupancy at the focal site.

Equilibrium fractional occupancy, θ, at the focal binding site is determined by how well its sequence matches the TF motif vs. the extent of nonspecific binding. This is expressed in terms of bioenergetic parameters as

$$\theta =\frac{N_{\text{TF}}}{N_{\text{TF}}+e^{\mathrm{\Delta }{G}_{\text{TF}}-\mathrm{\Delta }{G}_{\text{b}}}},$$ (1)

where N_TF is the number of molecules of the transcription factor in the cell, ΔG_TF is the free energy of binding of the TF to the focal site, and ΔG_b is the combined free energy of formation for all binding interactions with the nonspecific background. (ΔG_TF and ΔG_b are in units of k_bT, the Boltzmann constant multiplied by temperature, and by definition take negative values.) To account for the effect of mutation on fractional occupancy, we express the effect of the fit between a TF and its target cis-regulatory site on binding energy as ΔG_TF = (n – m)ΔG₁ = ΔG_match – mΔG₁, where m is the number of mismatched bits between the TF and its target site, ΔG₁ is the contribution of a single bit of information to the free energy of formation, and ΔG_match is the free energy of binding of a perfectly matched TF-focal site pair. Each matched bit increases the negative magnitude of the free energy of formation, increasing the fractional occupancy. Implicit in the ΔG₁ parameter is the simplifying assumption that each position in the TF-binding site interaction has an equal and additive effect on binding energy (Von Hippel and Berg 1986; Gerland et al. 2002; see also Khatri et al. 2009).

Following Gerland et al. (2002), we define a heuristic parameter describing a relationship between two causal free-energy parameters. E_diff = ΔG_b – ΔG_match is the difference in free energies of binding between the nonspecific background and a perfectly matched TF, with its sign chosen such that E_diff < 0 when nonspecific sites are collectively more attractive than the best-matched focal site. (Gerland et al. 2002 show that under plausible regulatory conditions, E_diff ≈ 0 is expected to yield biologically realistic levels of transcriptional control and that empirical estimates are consistent with that or slightly lower.) This allows us to cast fractional occupancy in terms of mismatches, the free-energy contribution of a single match, and the relative attractiveness of the nonspecific background, as

$$\theta =\frac{N_{\text{TF}}}{N_{\text{TF}}+e^{-m\mathrm{\Delta }{G}_1-E_{\text{diff}}}}.$$ (2)

To model the phenotypes of diploid organisms, we need to take into account dominance between allelic forms of the TF. Dominance effects emerge from allelic differences in fractional occupancy and are therefore sensitive to bioenergetic parameters. They play a role in the degree of hybrid incompatibility seen in F₁ vs. F₂ crosses. We model dominance by treating each TF as a competitive inhibitor of the other, reciprocally reducing their fractional occupancies, and scaling $e^{-m\mathrm{\Delta }{G}_1-E_{\text{diff}}}$ accordingly. Following Michaelis and Menten (1913) (Supporting Information, File S1), the fractional occupancy of each allelic form of the TF on its target binding site is reduced from its haploid level to

$${\theta }^{\prime }=\frac{N_{\text{TF}}}{N_{\text{TF}}+\alpha e^{-m\mathrm{\Delta }{G}_1-E_{\text{diff}}}},$$ (3)

where $\alpha =1+N_{\text{TFc}}{e}^{m_{\text{c}}\mathrm{\Delta }{G}_1+E_{\text{diff,c}}}$. N_TF is the number of molecules of the TF allele of interest, N_TFc is the number of molecules of the competing TF allele, m_c is the number of mismatches in the competing TF, and E_diff,c = ΔG_bc – ΔG_match scales the net free energy of formation of nonspecific binding of the competing TF to that of its own perfectly matched, specific binding site. Allelic variation may occur at both TF and binding-site loci, and θ’ is calculated separately for each of the four possible allelic interactions. We used N_TFc = N_TF and E_diff,c = E_diff throughout, tantamount to the assumptions that each TF allele is equally expressed and nonspecific binding is equal among alleles.

Phenotype

We treat the organismal phenotype, P, as equivalent to the level of expression. At each allele of the cis-regulated locus, expression of the trait proceeds if either TF allele is bound; thus, the rate of expression, r, at each equals kΣθ’, the sum of the competition-adjusted fractional occupancies of the TF alleles multiplied by a proportionality constant k. The maximum total fractional occupancy, θ_max, occurs in perfectly matched (m = 0) homozygotes. Expression is assumed to proceed independently from the two binding sites, and keeping all other cellular processes constant, the final level of expression is proportional to the expression rate (Gertz et al. 2009). Thus, we calculate the phenotype P = Σr, the sum of the expression rates of each allele of the cis-regulated locus. To force P to a unary scale, we set k = 1/ 2θ_max such that P = 1 when m = 0 at all four allelic interactions. If the transcription factor were a repressor rather than an activator, P would instead equal (1 – Σr). In the simple two-locus case, this would not change the results except for reversing the effect of expression level, so we do not investigate repressors further here.

The genotype–phenotype map

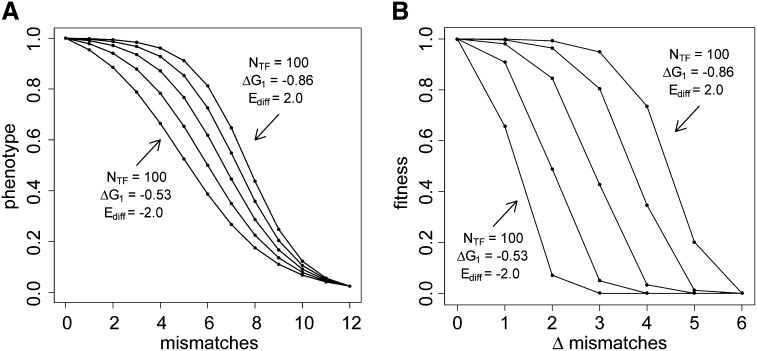
The genotype–phenotype (G–P) map comprises the set of rules governing the translation of genetic information into the realized phenotype (Travisano and Shaw 2012). When those rules follow the bioenergetic principles embodied by Equation 3 the G–P map takes a general sigmoid form (Figure 2), with the details of the shape and position determined by the three bioenergetic parameters, ΔG₁, E_diff, and N_TF. Once a G–P map’s shape is established by assigning values to those parameters, the phenotype it produces depends on the number of mismatches, m, in the binding motif. Figure S1 shows the effects on the phenotype of varying each of these parameters independently. Increasing ΔG₁ (in negative magnitude, because free energies are by definition negative) increases the slope at the inflection point and shifts the overall curve to the left (Figure S1A). Increasing E_diff decreases the attraction of the TF to nonspecific targets and therefore increases its availability at the binding site. This makes the binding interaction more tolerant to mismatches, which shifts the curve to the right without changing the slope at the inflection point (Figure S1B). It follows from Equation 2 that an exponential increase in N_TF has an identical effect as a linear increase in E_diff (Figure S1C); the outcomes are isomorphic. In our analyses, we held N_TF constant and varied E_diff instead. The lateral shifts induced by singly varying the bioenergetic parameters also imply that, for a constant motif length n, the minimum phenotype differs and in some cases considerable gene expression can proceed even when m = n (Figure S1). To explore the effects of variation in the shape of the G–P map while constraining it to its biologically relevant range, such that P ∼0 when m = n, it is necessary to vary ΔG₁ and E_diff concurrently (Figure 2A).

Figure 2.

Effects of the bioenergetic parameters ΔG₁ and E_diff on the genotype–phenotype (G–P) map and the corresponding fitness landscape. ΔG₁ and E_diff are in units of k_bT. (A) Effect on the G–P map. Horizontal axis: the number of mismatched bits between the binding site and the transcription factor’s binding motif. Vertical axis: the phenotype, which in this case is the expression level normalized to a scale of zero to one. ΔG₁ values, in steps of 0.0825 k_bT, were chosen for each E_diff so as to hold constant the expression produced by n = 12 substitutions. (See Figure S1 for the independent effects of these parameters.) (B) The fitness landscapes for the bioenergetic parameter combinations in A, in this case with environmental fitness parameters set to P_opt = 1 and σ_s = 0.05. Horizontal axis: Δ mismatches is the number of mismatches responsible for the difference between an individual’s phenotype P and the optimal phenotype P_opt. The bioenergetic parameters that determine expression level, and therefore the transition from genotype to phenotype, extend further to drive the relationship between genotype and fitness under a given environmental selection regime.

It is useful to adopt a heuristic shorthand to describe qualitative differences between the bioenergetically determined shapes. We use the slope near the top of the G–P map curve, where P = 1, unless otherwise specified. We therefore refer to the “slope” of the G–P map as the difference between phenotypes at m = 0 and m = 1 (Figure 2A), i.e., the phenotypic effect of the first mismatch, such that G–P maps with shallower slopes are broader and flatter at the top. We use the same language to compare fitness landscapes, below.

Fitness and the fitness landscape

Fitness is a function of an organism’s deviation from the optimal expression level, as per Johnson and Porter (2000, 2007),

$$W=\exp \left[\frac{-{\left(P-P_{\text{opt}}\right)}^2}{2{\sigma }_{\text{s}}^2}\right],$$ (4)

where P_opt is the optimal expression level as determined by the environment, and ${\sigma }_{\text{s}}^2$ is the variance of fitness around the optimum, a measure of the degree to which a suboptimal phenotype is tolerated by selection.

The fitness landscape describes the relationship between genotype and fitness across a spectrum of environments (Svensson and Calsbeek 2012). Inasmuch as an organism’s fitness depends on its phenotype, the fitness landscape is mediated through the G–P map and, ultimately, the bioenergetic properties of the molecules that underlie this map (Watt and Dean 2000; Watt et al. 2003, Watt 2013). Figure 2B shows the fitness landscapes corresponding to the G–P maps of Figure 2A when the environmentally determined fitness parameters of Equation 4 are set to P_opt = 1 and σ = 0.05. Changes in the bioenergetic parameters have the same qualitative effects on the slope of the fitness landscape as they have on the G–P map; the fitness landscapes around other values of P_opt share that isomorphism. Fitness landscapes with flatter slopes (such as the top curve in Figure 2B) can result from G–P maps with flatter slopes under a constant value of σ_s or could result from a G–P map with steeper slope and a more permissive environment—a higher value of σ_s. Because of this relationship, we did not study the effect of varying σ_s alone.

Simulations

We used simulations to examine misregulation of the hybrid phenotype in cases where two allopatric populations of diploids were subject to either parallel directional or parallel stabilizing selection for high gene expression. Although divergent selection would also result in HI under our model, we focus on parallel selection to study incompatibility resulting from gene interactions alone, excluding the effect of adaptation to diverging environments. We study selection to intermediate gene expression in File S1.

Each generation consisted of viability selection, using a fitness function with a standard deviation (σ_s) of 0.05, followed by random mating. Population size was kept constant each generation, with no overlap of generations. Mutations occurred in the offspring at a rate of 0.001 per locus, with each mutation changing one bit of information. A high mutation rate was chosen so that populations would be able to respond reliably to selection. Varying the mutation rate should have little effect on hybrid incompatibility under directional selection as long as populations are large enough that sufficient new mutations are available for selection to act upon (Johnson and Porter 2000). Under stabilizing selection, the mutation rate is expected to affect the rate of divergence due to drift, but since this effect is relative to population size and divergence time, we do not test it separately here.

We used n = 12 bits and σ_s = 0.05 throughout the article because these values permit adequate response to selection under the range of bioenergetic parameters and population sizes we studied. The sensitivity of the results to σ_s also depends on the mutation effect size (Johnson and Porter 2000), which, for a specified set of parameter values, is reflected in the number of bits in the binding motif linking the TF to its binding site. Tulchinsky (2013) found that doubling n (and simultaneously halving ΔG₁ to restore the sigmoid shape of the G–P map) had negligible effect on the results in the two-locus interaction, so we do not report those results here.

To assess misregulation of the hybrid phenotype for each replicate, we randomly created 50 F₁ hybrids, and F₂ hybrids from those (without viability selection on the F₁’s), and calculated total hybrid misregulation as the mean absolute deviation from the optimal parental phenotype, P_opt. This total misregulation includes a contribution from residual polymorphism in the parental populations, so we calculated net hybrid misregulation by subtracting the mean parental deviation. Although the evolution of net hybrid misregulation is the central issue in explaining the evolution of BDM incompatibilities, we also report the fitness of hybrids under the assumption that they experience the same viability selection (Equation 4) as do the parental populations. Results are based on 200 replicates of the simulation. To compare stabilizing selection to directional selection, the optimal phenotype of the conserved trait was held constant at a value of P_opt = 1.0 for 40,000 generations and that of the directionally selected trait changed at a rate of ΔP_opt = 1/40,000, from an initial value near zero (corresponding to 12 mismatches) to a final value of 1.0 (corresponding to zero mismatches) over the same time period. (Sensitivity analyses in Tulchinsky 2013 indicate that the choice of ΔP_opt has a small effect unless it is large enough relative to σ_s and the mutation rate that it drives the population toward extinction.) In all cases, the initial genotypes of all individuals were set to identical values such that each phenotype started at the initial optimum.

We tested the effect of the fitness landscape on evolutionary outcomes by varying the bioenergetic parameters that specify the G–P map. For regulatory interactions under directional selection, we performed a series of simulations to test the effect of genetic divergence and the slope of the genotype–phenotype map. (Further tests of the separate effects of ΔG₁ and E_diff can be found in Tulchinsky 2013.) To test the effect of genetic divergence on hybrid incompatibility while holding the G–P map constant, we held N_TF at 100, ΔG₁ at −0.610 k_bT, and E_diff at −1.0 k_bT (corresponding to the second curve from the left in Figure 2A) and varied the starting phenotype so that between one and six substitutions would be required in each parent population to reach the final optimal phenotype after 4000 generations. To test the effect of the slope of the G–P map and fitness landscape while holding genetic divergence constant, we evolved populations toward a phenotype of 1.0, held N_TF at 100, and adjusted ΔG₁ and E_diff to vary the slope at the final optimal phenotype while ensuring that exactly n = 12 substitutions separated the initial and final optima (Figure 2A). The slope of the G–P map at the endpoint phenotype of P_opt = 1.0, represented by the phenotypic difference between zero and one mismatches in Figure 2A, is related to our parameter values as follows: for slope 0.002, ΔG₁ = −0.858 and E_diff = 2.0; for slope 0.004, ΔG₁ = −0.774 and E_diff = 1.0; for slope 0.010, ΔG₁ = −0.692 and E_diff = 0.0; for slope 0.022, ΔG₁ = −0.610 and E_diff = −1.0; for slope 0.046, ΔG₁ = −0.530 and E_diff = −2.0. Under stabilizing selection, the genotypic basis of the regulatory interaction can evolve when one locus compensates in response to a weakly deleterious mutation in the other. We examined the effect on this compensatory evolution of population size crossed with the slope of the G–P map.

Dominance is inherent to bioenergetic models and it allows for the possibility that when parental populations have the same optimal phenotypes, F₁ hybrids may show less net misregulation than F₂’s in proportion to the level of dominance. To examine the effect of allelic dominance, we manipulated competitive binding between alleles by changing the availability of TF’s at their binding sites. We express the degree of dominance as the effect that removing one of the two allele copies of the TF would produce on an individual’s phenotype. We held N_TF at 100 and stepped E_diff from −7.5 k_bT to −1.0 k_bT in increments of 0.5 k_bT. At each value of E_diff, the value of ΔG₁ was chosen such that exactly n = 12 substitutions separated ancestrally from derived phenotypes. These parameter settings vary the degree of dominance in the following way. At E_diff = −7.5 k_bT, the attraction of the TF to the nonspecific background is high, so its availability at the binding site is low and competitive binding between alleles is negligible. A complete loss of binding of one TF allele reduces expression by an average of 49%, so at these parameter values, strongly and weakly binding TF alleles approach codominance. At E_diff = −1.0 k_bT, the attraction of the TF to the nonspecific background is low, an excess is available at the binding site, competitive binding is high, and the stronger-binding TF approaches complete dominance. At these parameter values, a complete loss of binding of one TF allele reduces expression by only 3% (Equation 2). These simulations were run at parental population sizes of 400 for t = 4000 generations, such that ΔP_opt = 1/4000. In File S1, we also study the extent that misregulation apparent in the F₂ generation remains cryptic in F₁ hybrids, obscured by regulatory combinations from parental genotypes.

All simulations were written in C in the XCode environment and run under the Mac OS X operating system, and graphics were produced using the statistical package R.

Results

Under all parameter sets, each parent population tracked the optimal phenotype so that the final deviation from the optimum was <0.05 in at least 99.5% of replicates. HI occurred in the F₁ or F₂ generation under both directional and stabilizing selection, but was more severe and evolved in less time under directional selection. Residual polymorphism remained in the parental populations at the end of each run, but contributed only a very small amount to misregulation in hybrids (File S1). We found that the bioenergetic parameters affected the extent of HI differently depending on the type of selection.

Type of selection

Under parallel directional selection to new optimal phenotypes, how much the hybrid genotype deviated, on average, from the optimal number of TF-to-binding-site matches depended on how far genotypes of the parent populations had diverged from one another, which in turn depended on the number of substitutions separating ancestral from derived phenotypes. The shape of the G–P map determined the phenotypic and fitness effects of too few or too many matches in the hybrid. The effect of changing the slope of the G–P map and fitness landscape can be seen in Figure 3, open bars. In this case, the ancestral and derived phenotypes were kept constant and the G–P map varied as shown in Figure 2A. Median HI increased with increasing slope around the derived phenotype of 1.0. HI occurred primarily in the F₂ generation, because the parameters that determine the shape of the G–P map in our model also determine the dominance of high expression (see dominance results below).

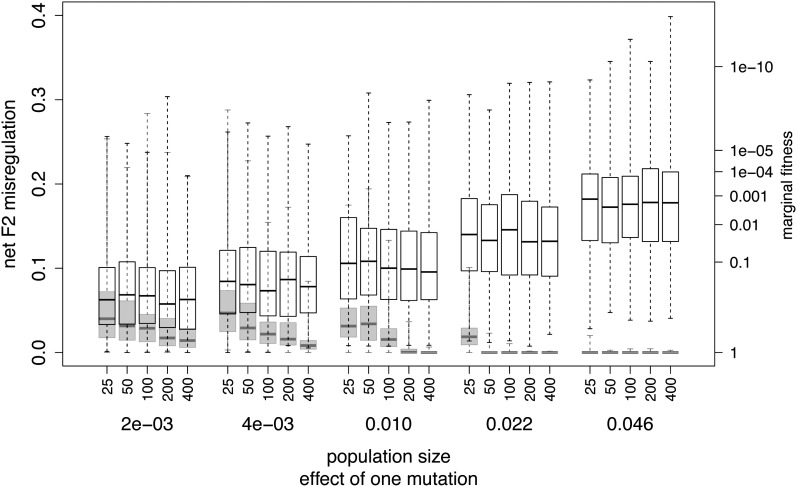
Figure 3.

The effects of the slope the G–P map (phenotypic effect of one mutation) and population size on median F₂ misregulation and corresponding fitness. Open boxes correspond to directional selection from minimal expression (12 mismatches) toward maximal expression (zero mismatches). Shaded boxes correspond to stabilizing selection at maximal expression (zero mismatches). Box plots show median, quartiles, and full ranges. Population size has no effect under directional selection, but smaller populations are more likely to evolve misregulation under stabilizing selection. The slope of the G–P map is represented by the effect of one mutation, which here is the phenotypic difference between a genotype with zero mismatches and a genotype with one mismatch (visible in Figure 2A). Steeper slopes increase hybrid misregulation under directional selection, but decrease misregulation under stabilizing selection. The effect is the same for directional selection toward intermediate expression (not shown). Hybrid fitness follows Equation 4.

Under stabilizing selection, HI can evolve as a consequence of compensatory evolution once a deleterious mutation at either locus becomes common. We found that HI evolved only when the population size was low and the phenotypic effect of a single mutation was small (Figure 3). The latter was possible only when the phenotype was conserved at high or low expression, because the phenotypic and fitness effects of a single mismatch are strongest at intermediate expression (Figure 2). If the effect of a single mutation was too high or the population size was relatively larger, parental genotypes did not diverge enough for HI to evolve (see also Fierst and Hansen 2010), as nearly all mutations were eliminated by selection before a compensatory mutation could arise. Here again, HI occurred primarily in the F₂ generation due to dominance in the F₁.

Direction of selection

In File S1, we report the effects of the direction of selection and evolutionary distance (the number of substitutions needed to reach the final phenotype on a given G–P map) on the evolution of HI. We find that selection from intermediate toward extreme phenotypic expression (from P_opt = 0.5 to P_opt = 1.0) yields much lower values of HI than does selection toward intermediate expression. This effect occurs because the slope of the G–P map at P = 0.5 is steeper, such that each mismatch has a greater effect on the hybrid phenotype and fitness than at P = 1.0. The absolute magnitude of the effect is higher over longer evolutionary distances, but is proportionally stronger over short evolutionary distances.

Allelic dominance

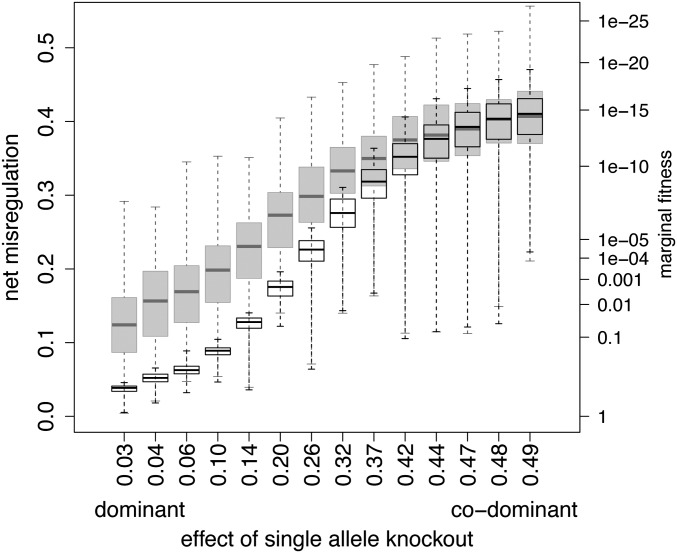
In the above results, bioenergetic parameter settings were such that higher expression was dominant over lower expression (i.e., a single allele of the TF with good fit to the binding site was sufficient to drive expression). As dominance was decreased by altering those parameter values, selection for higher expression shifted median HI in the F₁ upward to match that in the F₂ (Figure 4). Under directional selection for reduced expression, dominance did not change the generation in which HI occurs (data not shown), because our model has no combination of bioenergetic parameter values under which low expression is dominant.

Figure 4.

Effect of allelic dominance on median net phenotypic misregulation in F₁ (open bars) and F₂ (shaded bars) crosses following directional selection from minimal expression (12 mismatches) toward maximal expression (0 mismatches). Dominance is manipulated by changing E_diff and ΔG₁ values and expressed as the average effect on an individual’s phenotype of removing one of its TF allele copies. Dominance is highest on the left. Hybrid fitness follows Equation 4. Box plots show median, quartiles, and full ranges. See Model for details.

Under stabilizing selection for high expression, reducing the degree of dominance reduced HI in both F₁ and F₂ generations because compensatory evolution did not occur when the mutation effect size was too large. For the F₂ generation, this can be seen indirectly in Figure 3 and results are comparable in the F₁ (not shown). A property of the bioenergetic model is that varying the parameters E_diff and ΔG₁ to modify dominance also changes the slopes of the G–P map and fitness landscape (Figure 2). In equivalent biological terms, decreasing the availability of the TF at the binding site decreases dominance and simultaneously increases the effect of a single mismatch on expression; it increases slope of the G–P map. Figure 3 (shaded bars) shows the effect of the slope of the G–P map on HI under stabilizing selection for high expression; HI increases as a consequence of decreasing slope. Dominance, in itself, is likely to enhance this effect, because a mildly deleterious mutation of a given effect size is more likely to reach high frequency if it is recessive.

Cryptic misregulation in F₁ hybrids

Even when the phenotypes of F₁’s tend to resemble their parents’ and HI is low, underlying regulatory divergence can still be indicated if expression levels differ between orthologous combinations of TF/binding-site pairs (Wittkopp et al. 2004; Landry et al. 2005; Graze et al. 2012; Maheshwari and Barbash 2012). We find that the magnitude of these asymmetries depends on whether selection is toward the extreme vs. intermediate phenotype (Figure S3), being strongly constrained when evolving toward P_opt = 1, and it occurs in F₁ hybrids whether or not they exhibit HI. Asymmetry is strongest near P = 0.5 because mismatches there have the greatest effect on expression (Figure 2). These cryptic asymmetries in the F₁ are manifested as HI in the F₂ generation as parental combinations are dissociated. (See Figure S2.)

Discussion

Postzygotic isolation generally results from the accumulation of incompatibilities that arises as a consequence of genetic divergence (Orr 1995; Maheshwari and Barbash 2011; Nosil and Flaxman 2011). Transcription regulation contributes substantially to phenotypic divergence (Wray et al. 2003; Wittkopp and Kalay 2012), and abnormal expression levels observed in hybrids suggest that cis–trans regulatory interactions likely play a role in speciation (Ortíz-Barrientos et al. 2007). In addition to diversification of cis-regulatory regions (Wray 2007), evidence that affects affinity for DNA binding sites is emerging from comparisons within and among TF gene families of sequence evolution (Jovelin 2009; Nakagawa et al. 2013). Because phenotypic divergence often occurs under selection (Schluter 2009; Sobel et al. 2010), it is influenced by the adaptive landscape of the genes involved, including how those genes interact to produce the phenotype (Hansen and Wagner 2001; Gavrilets 2004; Palmer and Feldman 2009). The outcomes of those interactions, at the molecular level, are determined in turn by their local bioenergetic milieu. Thus, to understand at the molecular level how genetic incompatibility evolves between populations, we need a class of models that incorporate the relationship between genotype and phenotype in its bioenergetic context. To this end, we extended the gene-network speciation model of Johnson and Porter (2000, 2007) by incorporating an information-based statistical physics model of transcriptional regulation (Gerland et al. 2002; Mustonen et al. 2008). We show that the evolution of hybrid incompatibility depends on the bioenergetic properties of transcription factors and their binding sites.

The bioenergetic properties of TF–binding site interactions relate genotype to expression (Gertz et al. 2009; Segal and Widom 2009) and therefore affect the potential for adaptation and speciation by shaping the fitness landscape (Gavrilets 2004). Accordingly, we found that the degree to which a regulatory interaction under directional selection produced HI depended primarily on two factors: the number of substitutions separating ancestral and derived populations and the slope of the genotype–phenotype map and corresponding fitness landscape near the derived parental phenotype. HI was stronger when genetic divergence was high and when the G–P map around the derived phenotype was steep. Under stabilizing selection, HI occurred due to compensatory evolution, and its strength depended on the slope of the G–P map and population size. HI in a stabilized phenotype was stronger at low population sizes and, in contrast to the directional-selection case, when the G–P map around the phenotype was shallow. Similar population size effects under stabilizing selection appear in an analytical bioenergetic model (Khatri and Goldstein 2013).

Genetic divergence under selection

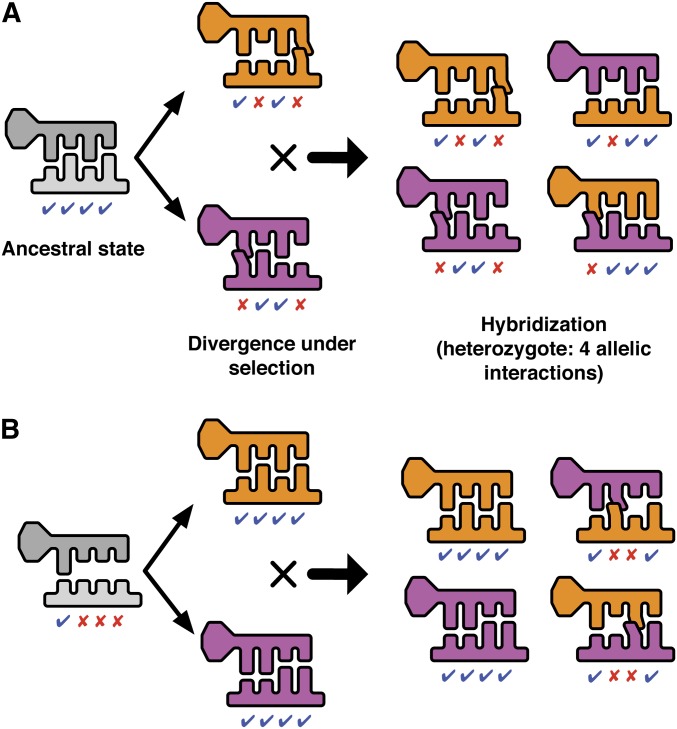
The number of substitutions separating ancestral and derived populations correlated with the genetic divergence between parent populations that evolved in parallel to new optimal phenotypes, and therefore the severity of HI. With selection for increased expression, each newly evolved matching position in the TF–binding site interaction in one population had a 50% chance per bit of information of being mismatched with the corresponding position in the other population. Thus, increasing the accumulated genetic divergence within evolving populations increased the expected number of extraneous mismatches in the cross-species molecular interactions. Similarly, with selection for decreased expression, each favored substitution that produced a beneficial mismatch in a parent had the potential to produce a spurious match in the hybrid, through the recreation of ancestral matches (see Figure 5).

Figure 5.

(A) Evolution toward lower gene expression: each parent population evolves two mismatches between transcription factor and binding site in response to selection for reduced expression. F₁ hybrids may have higher gene expression than either parent population due to reconstructed ancestral matches and accidental matches at derived sites. (B) Evolution toward higher gene expression: each parent evolves new matches between transcription factor and binding site in response to selection for increased expression. Incompatible alleles arise in the F₁ because each parent evolved a different fit between transcription factor and binding site.

Our results differ from those of Johnson and Porter (2000), where HI evolved readily only when reduced phenotypic expression was favored. This is a consequence of how alleles were modeled. In that model, each interacting allele was represented as a vector of one or more real numbers, and binding strength decreased with the Euclidean distance between TF and binding site. Reduced binding could be produced by at least two incompatible evolutionary trajectories; e.g., with one-dimensional alleles, each ortholog could evolve in either of two directions that each increased its distance from its binding partner. However, increased binding could result only from moving the Euclidean distance between alleles toward zero, so little incompatibility could arise between populations. Because alleles are represented in the bioenergetic model in terms of their information content as unique bit sequences (lacking directionality), HI evolved whether selection was for reduced or increased expression. In addition, the directionality of alleles in the Johnson and Porter (2000) model is responsible for their result that HI increased with the number of dimensions used to represent an allele. This outcome did not appear in the results of the bioenergetic model.

Studies of gene expression in hybrids often find asymmetric expression of parental orthologs (Wittkopp et al. 2004; Landry et al. 2005; Graze et al. 2012). This can be indicative of cryptic cis-by-trans regulatory divergence, as was recently revealed by asymmetric expression of the hybrid lethality gene Lhr in Drosophila (Maheshwari and Barbash 2012). Such regulatory divergence may produce asymmetry if, for example, spurious binding occurs between the TF of one species and the regulatory region from the other, but not the reverse. We found this phenomenon (Figure S3) if the relative amount of divergence in cis compared to trans differed between derived parental populations (Figure 6). Asymmetric expression occurred more frequently in our data than symmetric expression (data not shown), because for a given number of mismatches, there are more allelic states that produce asymmetry. Depending on dominance, the overall expression level in F₁ hybrids may be similar to parental expression levels. As in Maheshwari and Barbash (2012), cryptic cis-by-trans divergence may be revealed in the F₁ generation only by asymmetric expression.

Figure 6.

Asymmetric expression of parental orthologs in the F₁ hybrid resulting from cis-by-trans regulatory divergence, when the relative amount of divergence in cis compared to trans differs between species. In the above example, divergence occurred under selection for reduced expression. More spurious matches resulted between the binding site of species 1 and the transcription factor of species 2 (top right interaction in the hybrid) than in the inverse interaction (bottom right). Depending on allelic dominance, the overall expression level in the F₁ generation may be nearly the same in hybrids as in the parent species.

Effect of the fitness landscape

The fitness landscape of evolving populations is determined by the relationship between genotype and phenotype (the G–P map), the relationship between phenotype and fitness (Gavrilets 2004), and thereby, the bioenergetic properties affecting gene expression. Because the phenotype-to-fitness relationship was invariable among our populations at any given time, variation in the fitness landscape in our simulations was determined solely by the G–P map and the underlying bioenergetic parameters that define it. Thus, we can consider the effect of the G–P map on adaptation in evolving populations, as well as on hybrid fitness directly.

The slope of the G–P map and fitness landscape around a given phenotype determines the amount of phenotypic change produced by an additional match (or mismatch) in the TF–binding site interaction. Thus, it determines the robustness of a TF–binding site interaction to mutation, as well as the effect of excess matches or mismatches in hybrids. Under directional selection, a steeper slope near the derived parental phenotype resulted in higher median HI because fewer incompatible positions are needed to produce a given level of misregulation in the hybrid (Figure 3). Likewise, if parent populations evolved toward a highly robust TF–binding site interaction, the result was less HI, because the interaction is also robust to incompatibilities in the hybrid.

The observation that hybrid misregulation occurs in conserved traits (True and Haag 2001) suggests that HI is possible under stabilizing selection (see also Palmer and Feldman 2009; Fierst and Hansen 2010), although it may be less likely (Gavrilets 2004; Schluter 2009). Under stabilizing selection, we found that the amount of HI was determined primarily by the slopes of the G–P map and fitness landscape near the conserved phenotype and by population size (Figure 3). In contrast to directional selection, under stabilizing selection HI was greater when the slope near the parental phenotype was shallow. This is because divergence of parental genotypes under stabilizing selection depends on compensatory evolution, which is less likely to occur when the average fitness effect of a mutation is high; such mutations are eliminated by selection before a compensatory mutation can arise (Haag 2007; Fierst and Hansen 2010). Low population size reduces the efficiency of selection (Wright 1931), increasing the parameter range under which compensatory evolution can occur (Lynch 2007).

Dependence of compensatory evolution on the shape of the fitness landscape is also found in multilocus models where the shape is determined by the strength of epistasis among loci (Palmer and Feldman 2009; Fierst and Hansen 2010). In general, a flatter plateau of near neutrality around a conserved phenotype is expected to increase divergence at the underlying loci (Haag 2007; Palmer and Feldman 2009), which produced HI in our results if the hybrid genotype fell outside of the nearly neutral plateau. This aspect of our model bears similarity to the “holey adaptive landscape” model of Gavrilets (1999, 2004), in which fitness is a step function with a perfectly flat plateau and an infinitely steep threshold. The main difference, in addition to the fact that accounting for bioenergetic parameters results in a sigmoid fitness landscape, is where the holey-landscape model considers the cumulative effect of multiple independent loci, we consider instead the cumulative effect of multiple independent mutations within pairs of epistatically interacting loci.

Under the model of Johnson and Porter (2000), no HI was observed under stabilizing selection. We found this to be a consequence of the way diploid loci were handled to intentionally exclude the effects of dominance. When we permitted dominance in their model, a high amount of HI evolved under stabilizing selection (A. Tulchinsky, N. Johnson, A. Porter, unpublished results). By contrast, the present model resulted in more limited evolution of HI under stabilizing selection (Figure 3). As above, this is a consequence of how alleles are represented in the two models. Compensatory evolution is more likely when alleles are restricted to evolve in a limited number of dimensions; for example, with one-dimensional alleles in the earlier model, half of all possible mutations were at least partially compensatory for a deleterious substitution. In this model, a deleterious mismatch at a given position can be compensated only by a mutation at that same position (or another mismatched position, if any are available). We believe that this reduced probability of compensation is more realistic and consistent with the theoretical difficulties of compensatory evolution (Haag 2007).

Our model includes an assumption (implicit in the ΔG₁ parameter) that each position in the TF–binding site interaction has an equal and additive effect on binding energy (Von Hippel and Berg 1986; Gerland et al. 2002; see also Khatri et al. 2009). Relaxing this assumption may result in increased HI under stabilizing selection, if nonadditivity allows TF–binding site interactions to diverge without any reduction in fitness. Likewise, it may result in decreased HI if TF mutations affect binding to multiple nucleotides, making compensatory evolution more difficult.

Dominance and F₁ vs. F₂ hybrid breakdown

In the absence of any other modifiers of allelic dominance, the same bioenergetic parameters that determine the effect of mismatches on expression (ΔG₁, E_diff, and N_TF) also determine the extent of dominance between TF alleles. Strong binding is dominant over weak binding when N_TF >> $e^{-m\Delta G_1-E_{\text{diff}}}$; in this case a reduction in binding of a single allele of the TF has little effect on expression. In biological terms, the reason is that when E_diff or N_TF are high, an excess of transcription factor is available at the binding site; if one allele of the TF binds poorly, the other allele is sufficient to drive expression. Dominance decreases, asymptotically approaching codominance, as E_diff and N_TF become lower, because fewer TF molecules are available at the binding site and expression is sensitive to further reduction in TF availability. Introducing mismatches into just one allele of the TF is enough to reduce the expression level.

Under the parameter combinations that yielded the above results, F₂ hybrids showed much higher HI than did F₁’s (Figure 4, left). These bioenergetic parameter values promote strong allelic dominance; knocking out one allele copy of a TF has little average effect. Under these conditions, the availability of TF was not limiting and competitive binding among TF alleles for the regulatory sites was strong, so that phenotypic expression in heterozygotes was driven by the allele combination with the tightest binding. F₁ individuals exclusively carry TF and binding-site alleles from both parent populations. Knocking out either TF ortholog eliminates competitive binding so that the hybrid exhibits one parental phenotype or the other, so overall, F₁’s and their two parents had the same phenotypes, and HI was minimal. However, in F₂’s, half of the time, homozygous TF’s of one parental line combine with homozygous binding-site orthologs of the other, so average misexpression in F₂’s was high.

Hybrid incompatibility in the F₁ generation reaches that of the F₂ (Figure 4, right) under bioenergetic parameter values where TF’s become increasingly scarce at the binding sites (E_diff increases or N_TF decreases). This is because competitive binding becomes less important and phenotypic expression in individuals approaches the expression averaged over all TF-to-binding-site pairs. Codominance occurs in parental, F₁, and F₂ individuals, and averaging over individuals, F₁’s and F₂’s are equally misregulated.

This has ramifications when the two-locus regulatory interaction occurs upstream of further regulatory steps (see Ronen et al. 2002). Because dominance is partially dependent on concentration (N_TF), a pathway with more than one step would exhibit evolutionary change in dominance at downstream loci as a consequence of expression changes upstream. This dependence of dominance on the genetic background is consistent with existing theory that indicates that, in general, the contribution of one locus to the phenotype can evolve solely due to changes at other loci (Wagner and Mezey 2000). We did not introduce other determinants of dominance (e.g., dimerization) as additional model parameters, because in our two-locus pathway, the effect of dominance on speciation would be the same regardless of how that dominance was generated. If weak binding were made dominant over strong binding, unfit low-expression hybrids would appear in the F₁ generation but the degree of HI would be unchanged overall.

Parameterization of the model in empirical studies

The parameters of the bioenergetic model represent empirically measurable properties of transcription factors and the genomic background with which they interact (Gerland et al. 2002; Mustonen et al. 2008). Simicevic et al. (2013) document fivefold differences in N_TF among TF loci, roughly corresponding to the range of E_diff values we investigated here. The effect on gene expression of the concentration of TF’s, N_TF, is readily manipulated in the laboratory. The component of E_diff describing the relative competition for the TF from the genomic background is readily estimated by adding increasing concentrations of random genomic DNA to a solution of TF and specific binding-site fragments and measuring the effect on specific binding (Raumann et al. 1995). Binding affinities (corresponding to mΔG₁) of TF and cis-site variants have been indirectly measured in several studies (e.g., Man et al. 2004; Shultzaberger et al. 2012; Samee and Sinha 2013). Empirical measures of these parameters within and between populations showing HI will yield considerable insight into the relationship between the evolution of the misregulation of expression and resulting BDM incompatibilities.

Biological context of the two-locus interaction and HI in F₁’s vs. F₂’s

Because gene networks connect genotype to complex phenotypes via G–P maps, ultimately network-based models are needed for making inferences about the initiation and evolutionary dynamics of speciation (Johnson and Porter 2001; see also Wilkins 2002, 2007). The two-locus regulatory interaction is elemental to all regulatory networks and provides a necessary basis for interpreting the evolution of HI in network settings. In a companion study (A. Tulchinsky, N. Johnson, A. Porter, unpublished results), we examine a bioenergetic model of a simple, three-locus pleiotropic network motif, another ubiquitous element of regulatory networks (Gibson 1996; Wray et al. 2003). Information-based bioenergetic models of other motifs have been studied in the context of the evolution of gene expression per se. These include cases where multiple independent TF’s regulate expression at a single locus (Stewart and Plotkin 2014; Ezer et al. 2014), where single TF’s have multiple binding sites in a single promoter region (He et al. 2012), and where a TF may be inhibited by nucleosomes at the binding site (Raveh-Sadka et al. 2009).

We found that HI evolves more readily in the F₂ than in the F₁ across a broad range of bioenergetic parameter values and that this difference depends on the degree of dominance imposed by those parameters (File S1). Our results apply to cases of parallel selection, where hybrid fitness doesn’t depend on environmental differences between parental populations. To what extent under these conditions, then, do we predict HI in natural systems to be stronger in F₂’s? In this study we held constant the expression level of the upstream TF at N_TF = 100 and instead varied E_diff, the difference in the free energies of binding of the TF to the target site vs. the nonspecific background. The effects on the phenotype of varying E_diff and N_TF are isomorphic, with the effects of varying E_diff on the linear scale equivalent to varying N_TF on the exponential scale (via Equation 4; illustrated in Figure S1). Inasmuch as phenotypic expression evolves in broader network settings, a problem well beyond the scope of this study, we expect the expression level of our upstream TF to respond to phenotypic selection as well. This upstream change in N_TF will alter the baseline bioenergetic properties of the downstream two-locus interaction we model here, affecting its degree of dominance (Figure 6) and the shapes of the G–P map and fitness landscape (Figure S1). We expect this to have downstream effects on the evolutionary dynamics of HI, including the extent that HI can evolve in F₁ relative to F₂ crosses (Figure 4). Nevertheless, this bioenergetic model implies that HI in the F₁ should be equal to or lower than that in the F₂ regardless of the parameter values.

In nature, it is very plausible that the selection imposed by a changing environment will be multifarious, affecting several developmentally independent traits at once (Nosil et al. 2008). Although the bioenergetic bases of these traits are likely to differ and with them, their fitness landscapes, the fitness effects of evolving incompatibilities are likely to be multiplicative in hybrids. The more traits respond to selection, the smaller the incompatibilities need to be in each for significant hybrid incompatibilities to evolve. These multiplicative effects, however, will tend to magnify differences in HI between F₁ and F₂ generations to the extent that dominance effects emerge from the bioenergetic properties that determine expression of those traits. We expect regulatory interactions to exhibit bioenergetic properties favoring allelic dominance in cases where F₁ hybrids resemble their parents more than do F₂’s.