The Influence of Selection for Protein Stability on dN/dS Estimations

Abstract

Understanding the relative contributions of various evolutionary processes—purifying selection, neutral drift, and adaptation—is fundamental to evolutionary biology. A common metric to distinguish these processes is the ratio of nonsynonymous to synonymous substitutions (i.e., dN/dS) interpreted from the neutral theory as a null model. However, from biophysical considerations, mutations have non-negligible effects on the biophysical properties of proteins such as folding stability. In this work, we investigated how stability affects the rate of protein evolution in phylogenetic trees by using simulations that combine explicit protein sequences with associated stability changes. We first simulated myoglobin evolution in phylogenetic trees with a biophysically realistic approach that accounts for 3D structural information and estimates of changes in stability upon mutation. We then compared evolutionary rates inferred directly from simulation to those estimated using maximum-likelihood (ML) methods. We found that the dN/dS estimated by ML methods (ω_ML) is highly predictive of the per gene dN/dS inferred from the simulated phylogenetic trees. This agreement is strong in the regime of high stability where protein evolution is neutral. At low folding stabilities and under mutation-selection balance, we observe deviations from neutrality (per gene dN/dS > 1 and dN/dS < 1). We showed that although per gene dN/dS is robust to these deviations, ML tests for positive selection detect statistically significant per site dN/dS > 1. Altogether, we show how protein biophysics affects the dN/dS estimations and its subsequent interpretation. These results are important for improving the current approaches for detecting positive selection.

Introduction

Zuckerkandl and Pauling (1962) and subsequently Margoliash (1963) observed that the amino acid differences between two orthologous proteins are approximately proportional to the elapsed time since their common ancestor. This apparently steady rate of protein evolution is known as the molecular clock (Zuckerkandl and Pauling 1965). Over the last five decades, the molecular clock has been central to debates in evolutionary biology (i.e., selectionism vs. neutralism), and provided a basis for estimating the divergence time of populations and species, detecting natural selection at genomic scales and understanding the origin of sequence variations (Rannala and Yang 2003; Kumar 2005; Yang and Rannala 2012; Du et al. 2013).

Traditionally, the ratio of the rates of nonsynonymous substitutions and synonymous substitutions (dN/dS) has been used to detect patterns of selection in molecular evolution (Kimura 1977; Yang and Bielawski 2000). A protein is considered under positive selection when the normalized rate of nonsynonymous substitutions (dN) exceeds the rate of synonymous substitutions (dS). Conversely, dN/dS < 1 is usually interpreted as meaning that the protein evolves slowly under negative (purifying) selection (i.e., is more conserved), because most of the nonsynonymous substitutions are detrimental to fitness and consequently have low fixation probabilities. When the normalized dN/dS ∼ 1, the protein is considered to evolve neutrally (Kimura 1977).

Estimating dN/dS in practice requires statistical models of sequence evolution, such as Markov chains (Felsenstein and Churchill 1996; Lio and Goldman 1998; Holder and Lewis 2003). Specifically, maximum-likelihood (ML) and Bayesian methods determine the probabilities of substitutions between orthologous sequences using different nucleotide/amino acid substitution models (Whelan and Goldman 1999; Anisimova et al. 2001; Yang et al. 2005). It is likewise possible to test several biological hypotheses with regards to dN/dS-variation across different sites in a protein and along branches and clades of phylogenetic trees and distinguish between them using the likelihood ratio tests (LRT) (Yang 1998).

Despite the prevalence and utility of these statistical tools, it is still largely unclear when and why rate variations occur, and how they are influenced by real properties of the proteins. From a molecular biophysics perspective, the protein stability (folding free energy, i.e., ΔG) is one of the major determinants of sequence evolution (Dokholyan and Shakhnovich 2001; Taverna and Goldstein 2002a,b; Bloom et al. 2005; Williams et al. 2006; Zeldovich et al. 2007; Goldstein 2008). Regardless of specific function, proteins must be stable enough to preserve their functional native structures, except perhaps the special cases of intrinsically disordered proteins (Dyson and Wright 2005). Furthermore, misfolding is emerging as an important etiological basis of many diseases (Soto 2003; Chiti and Dobson 2006; Serohijos et al. 2008). Selection for protein folding, including selection against detrimental effects of protein aggregation, is an important selection pressure in molecular evolution (Mirny et al. 1998; Li et al. 2000; Drummond et al. 2005; Chen and Dokholyan 2008; Drummond and Wilke 2008; Cherry 2010; Lobkovsky et al. 2010; Serohijos et al. 2012, 2013; Goldstein 2013; Serohijos and Shakhnovich 2014).

To systematically investigate the influence of protein stability on estimating dN/dS in phylogenetic trees, we constructed a population of model organisms whose genomes encode for a single protein Myoglobin (Mb). Similar to prior works (Chen and Shakhnovich 2009; Goldstein 2011; Wylie and Shakhnovich 2011), we assumed that the fitness of the organism is proportional to the total number of folded Mb proteins in the cell and hence a function of the folding stability of Mb (Materials and Methods). The population was subjected to the evolutionary process of mutation, drift, and selection (Materials and Methods). The model explicitly mapped the sequence to folding stability and fitness. This approach enabled us to record complete evolutionary histories and compare dN/dS from simulations (explicit count of mutations that were fixed during simulation) with rates estimated from the trees using standard approaches such as ML.

We used Mb as the model protein because its main functional phenotype (i.e., O₂-binding as measured by the O₂ pressure at half Mb saturation [P₅₀]) is almost constant in mammals (Dasmeh and Kepp 2012), which is also reflected in the conservation of the important functional residues (Suzuki and Imai 1998; Scott et al. 2000). Many of these sites are close to the heme group and are accordingly under strong purifying selection. Thus, Mb provides a good test case for investigating both nearly neutral drift, purifying, and positive selection for folding stability, as was in fact recently found in Mbs of diving mammals (Dasmeh et al. 2013), suggesting that all three types of evolutionary processes can be identified and distinguished in this important protein.

First, we demonstrated that the biophysics-based evolutionary model can recapitulate the pattern of conservation in sequence alignment of real Mbs. We found a strong correlation between ML-estimated per gene dN/dS and the computed dN/dS from simulations when the evolving proteins are very stable. In this regime of high stability, the arising mutations are more neutral, producing the agreement with the ML method. In the regime of less stability, we observed deviation from neutrality and per gene dN/dS < 1 and dN/dS > 1. However, the dN/dS > 1 observations are not statistically significant according to the LRT. Altogether, these observations validate the ML approach for estimating the per gene dN/dS. These statistical approaches are robust to the nonneutral effects of mutations on folding stability at the whole gene level.

Second, we explored per site dN/dS using ML approaches. In the regime where proteins are less stable, stability effects had major influence on the dN/dS estimates, showing that ML methods are highly sensitive to underlying biophysical properties such as stability. Furthermore, the resolution of the phylogenetic tree affected the likelihood of observing positive selection: Specifically, per gene dN/dS > 1 was observed more frequently at higher resolution (i.e., shorter branch lengths). These results are consistent with the molecular clock being constant mainly over longer evolutionary times due to cancellation of low and high rates of evolution and suggest that observations of neutrality may be overestimated due to such averaging effects.

Materials and Methods

Selection for Thermodynamic Stability

To investigate dN/dS of a protein evolving under a selection pressure to maintain folding stability, the fitness F was assumed proportional to the fraction of folded proteins in the cell defined as $F\propto P_{\text{nat}}$ where P_nat is the probability that a sequence is in the native state at equilibrium given the two-state model for protein unfolding (Privalov and Khechinashvili 1974; Shakhnovich and Finkelstein 1989):

$$P_{\text{nat}}=\frac{1}{1+\text{exp}(\text{β}\Delta G)}$$ (1)

Here, ΔG is the free energy of folding and β = 1/RT. The Fermi–Dirac like form of equation 1 suggests that fitness effects of mutations are more dramatic at lower stabilities (Chen and Shakhnovich 2009). The effect of mutations on folding stability is modeled as:

$$\Delta G_{\text{after}}=\Delta G_{\text{before}}+\Delta \Delta G_{\text{mutation}}$$ (2)

An arising mutation would have a selection coefficient s defined as (Goldstein 2011; Wylie and Shakhnovich 2011):

$$s=\frac{F_{\text{after}}-F_{\text{before}}}{F_{\text{before}}}\sim e^{\text{β}\Delta G_{\text{before}}}\left(1-e^{\text{β}\Delta \Delta G_{\text{mutation}}}\right)$$ (3)

which can be positive, negative, or nearly zero corresponding to mutations being beneficial, deleterious, or neutral. In a monoclonal, haploid population, each arising mutation has a probability of fixation described by the Kimura formula (Kimura 1962):

$$P_{\text{fix}}=\frac{1-\text{exp}(-2s)}{1-\text{exp}(-2s\times N_{\text{eff}})}$$ (4)

where N_eff is the effective population size, which is approximately 10⁴−10⁵ for mammals (Lynch and Conery 2003; Mailund et al. 2011).

The effect of all single-point mutations on folding stability was assumed to be additive (Fersht et al. 1992):

$$\Delta G=\Delta G_0+{\displaystyle \sum }_{i=1}^n\Delta \Delta G_i$$ (5)

Here, ΔG₀ is the stability of the protein at time = 0, before simulation, and ΔΔG_i is the change in stability due to single-point mutation i (supplementary table S1, Supplementary Material online). Because of this additivity assumption and the absence of epistatic energetic interactions between residues, any correspondence between calculated stability of proteins using our approach and experimental stability should be taken with caution. Mutation in one site of the protein could affect the propensity of other sites toward mutation and would change the phenotypes of the multisubstituted descendants. Additional terms correcting for such epistasis in the energy function have been suggested by Goldstein et al. (Goldstein 2011; Pollock et al. 2012). However, for computational tractability, we keep our assumption of the additivity of ΔΔG because this still maintains some important features of the biophysics-based evolutionary models (Serohijos et al. 2013) (see the Materials and Methods section for details). We show that despite the simplified assumption, the model recapitulates the pattern of sequence divergence in real Mb sequences and the general results are not influenced by epistasis (see fig. 1C and description below).

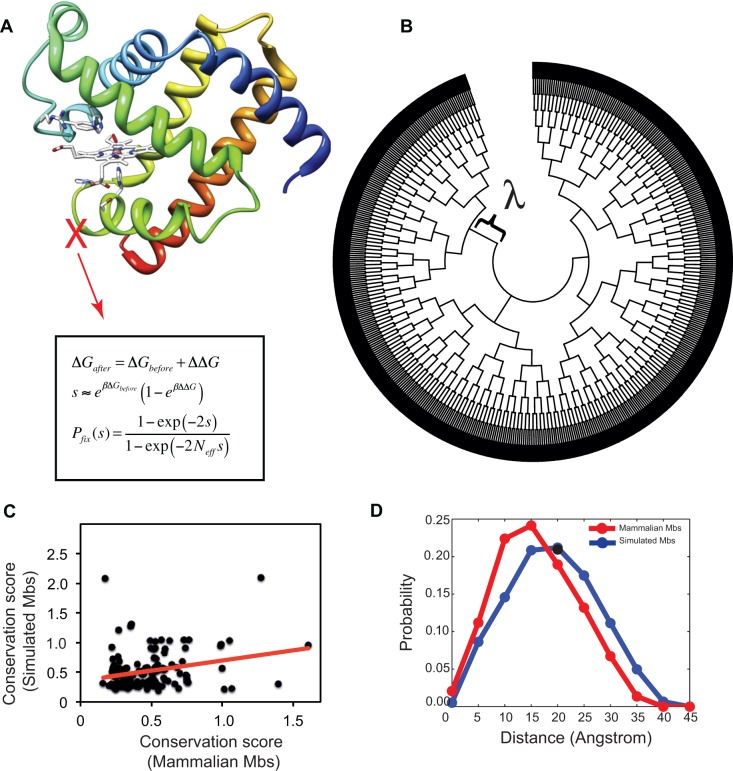
Fig. 1.—

Schematic and performance of structural and evolutionary analyses used in this study. (A) The Mb sequences were evolved in a population of N_eff = 10⁴ cells under monoclonal conditions with selection for folding (eqs. 3 and 4). (B) A bifurcating simulated phylogeny with 1,024 external nodes was constructed from an initial Mb sequence with ΔG = −6.84 kcal/mol. Each bifurcation happens after λ arising mutations in the ancestral sequence. (C) Sequence conservation of simulated Mb sequences calculated with Kullback–Leibler score correlates with mammalian Mbs (see Materials and Methods section and supplementary information, Supplementary Material online). (D) The pairwise distance distribution of subsequent substitutions on branches of simulated (in blue) and real mammalian (in red) phylogenetic trees.

Estimating the Effect of Point Mutations on Protein Folding Stability

We used the structure of sperm whale Mb (PDB code = 1MBO) (Phillips 1980) as our model protein. The assumption of additivity (eq. 5) requires ΔΔG due to single-point mutations. We estimated the folding free energy ΔG_{wild type} using the flexible-back bone method of the ERIS algorithm (Yin et al. 2007a,b). To calculate the ΔG_mutant, we replaced the amino acid in the PDB 1MBO and repacked and optimized the side-chains to within 10Å of the site being mutated. Backbone dihedrals were also allowed to relax to minimize backbone strain. The ΔG was calculated for both wild type and the mutant and ΔΔG reported as ΔG (mutants) − ΔG (wild type). Altogether, we arrived at a 154 × 20 matrix of ΔΔG values where each row corresponded to a specific residue in sperm whale Mb and each column to a possible mutated amino acid (see supplementary table S1, Supplementary Material online).

For mutations in the residues important for O₂ binding (i.e., residues 29, 43, 63, 64, 65, 68, 91, 92, and 93) (Dasmeh and Kepp 2012), we did not calculate the ΔΔG, but a priori assigned P_fix = 0 to mimic full conservation of these sites as seen across mammalia. The obtained distribution of ΔΔG distribution is consistent with experimental ΔΔG values in the ProTherm database (Sarai et al. 2001) and with data from exhaustive computational mutagenesis (Tokuriki et al. 2007).

Protein Evolution Model and the Simulated Phylogenies

We evolved the Mb sequences using a model population of N_eff = 10⁴ individuals, a reasonable effective population size for mammals (Mesnick et al. 1999; Lynch and Conery 2003; Charlesworth 2009). The population is assumed to be monoclonal. Under this assumption, the evolution could require an update upon a mutation (see the Materials and Methods section for details). When a mutation occurs, we randomly picked a site and randomly performed a nucleotide substitution. If the substitution is missense, we estimated the change in protein folding stability ΔΔG using equation 2.

The initial folding stability of the Mb was set to ΔG = −7.5 kcal/mol (experimentally measured by [Scott et al. 2000]). The Mb was evolved under selection for stability (i.e., eqs. 3 and 4) toward the dynamic equilibrium of mutation-selection balance. The last sequence in this equilibration (∼32% identical to the sperm whale Mb (see the supplementary information, Supplementary Material online, for details) became our “ancestor” sequence in simulating the phylogenetic tree, as shown in figure 1B. The ancestor population was bifurcated after λ arising mutations, defined in multiples of population size (e.g., λ = 10N_eff = 10⁵ arising mutations). We refer to λ as resolution parameter throughout the text of this paper. We continued this bifurcation procedure until the simulated phylogenetic tree reached 1,024 external nodes.

Bioinformatics

We used the CODEML program within the PAML suite (Yang 2007) to calculate the ML-based dN/dS (denoted as ω_ML) for the pairwise comparison of Mb sequences obtained from the simulations. We estimated the equilibrium codon frequencies from the products of the average observed nucleotide frequencies in the three-codon positions (F3X4 model). No codon preference was assumed in the model.

To check whether positive selection can be detected in different amino acid sites of Mb sequences, a multiple sequence alignment of 1,024 Mb sequences of external nodes of simulated phylogeny was used along with the tree in Newick format (fig. 1C). The tree branch lengths were first estimated with the M0 model that assumes one ω across all branches. Branches with dN or dS > 1.5 were removed from the total number of branches to avoid problems associated with saturation of synonymous and nonsynonymous sites. We then used the branch lengths estimated by the M0 model in more advanced codon substitution models as described below. Essentially, codon models fit a set of Markov models to the observed data (here: the extant sequences and the phylogenetic tree) and calculate a likelihood function under different assumptions regarding variability of dN/dS across different sites of the protein, branches of the phylogeny, or both (Yang 2006). We investigated five different site-models described as M1, M2, M7, M8, and M8fix. The M1 model assumes two categories of sites undergoing purifying selection (ω < 1) and neutral evolution (ω = 1). In the M2 model, a third set of sites with ω > 1 is added to M1 model. The M7 model partitions all the sites into ten different categories with ω < 1 and fits a beta distribution to ω. M8 adds an 11th category to the M7 model with ω allowed to have values > 1, and finally ω is fixed to 1 for the 11th category of sites in M8fix model. Because these models are inherently nested, different LRT can be designed to investigate different hypotheses on the observed sequences and phylogeny (Nielsen and Yang 1998).

Within a LRT test, twice the log-likelihood difference between two nested models should have a χ² distribution that has a number of degrees of freedom equal to the differences of free parameters in two models. For example, the nested pair of site models M1 and M2, M7, or M8 or more rigorously M8 and M8fix can be used to test whether there are sites evolving under positive selection (i.e., ω > 1) in the protein. It is noteworthy that LRT in these cases only predicts the existence of such sites but not their exact location in the protein. To identify the position of residues with significant dN/dS > 1, an Empirical Bayesian framework is implemented in CODEML that calculates the probability that each site is sampled from a particular site class. We recorded the posterior probabilities of sites putatively under positive selection using the Bayes Empirical Bayes (BEB) method that takes into account uncertainties in the ML estimates of the parameters (Yang et al. 2005).

To compare sequence conservation of simulated Mbs versus real mammalian Mbs, we used the Kullback–Leibler (KL) conservation score (Kullback and Leibler 1951) for each residue:

$$\text{KL}={\displaystyle \sum }_{i=1}^N\text{ln}\left(\frac{P(i)}{Q(i)}\right)$$ (6)

where P(i) is the probability of amino acid i in that specific residue and Q(i) is the background natural frequency of that specific amino acid from the Uniprot database (UniProt Consortium 2008). Eighty-three mammalian Mb sequences were retrieved from the Uniprot database similar to our previous study (Dasmeh et al. 2013), and the KL conservation score was compared with ten independent sets of 1,024 simulated sequences using the MISTIC web server (Simonetti et al. 2013). We excluded the invariable residues in simulations (i.e., residues 29, 43, 63, 64, 65, 68, 91, 92, and 93) from this analysis.

To investigate the importance of epistatic interactions in our model, we calculated the pairwise distance distribution of substitutions on each branch of simulated phylogenetic trees. The distance of beta carbons, C_β, for all residues (except for glycine where we used C_α) was used as the distance measure. For mammalian Mbs, we used the inferred substitutions on each branch of mammalian phylogeny by ancestral sequence reconstruction from the previous study (Dasmeh et al. 2013) and applied the same measure to calculate the distance distribution.

Results

Selection for Folding Stability, Epistasis, and Patterns of Sequence Conservation

From in silico simulations in protein engineering, it is generally known that selection for protein folding stability could reproduce the pattern of sequence conservation in real sequences (Mirny and Shakhnovich 1999; Kuhlman and Baker 2000; Dokholyan and Shakhnovich 2001; Ding and Dokholyan 2006). We first investigated whether our model can recapitulate the pattern of sequence conservation among real Mb sequences. We constructed an alignment of “orthologous” sequences from our evolutionary simulations (i.e., sequences in the external nodes of a simulated phylogenetic tree) and compared the patterns of sequence conservation with real mammalian Mbs using the Kullback–Leibler conservation score (Materials and methods). As shown in figure 1C, sequence conservation of simulated Mb sequences is significantly correlated with real Mb sequences (P value ∼2 × 10⁻⁴ for Spearman rank correlation). We further confirmed this correlation by using ten independent simulated data sets (see supplementary fig. S1, Supplementary Material online).

Epistasis is inherent to the model due to the curvature of fitness landscape. The “Fermi–Dirac” form of equation 1 imposes a noncommutative effect for mutations (Wylie and Shakhnovich 2011). However, the site–site epistasis in the 3D structure is not explicit because of the assumed additivity of ΔΔG. We also investigated to what extent epistatic interactions among residues are recapitulated by the model. Specifically, we asked whether mutations that are fixed in each branch of the simulated phylogenetic tree are correlated in the 3D structure of the Mb. We calculated the pairwise distances of C_β (C_α for glycine) for mutations that were subsequently fixated in the simulations (Materials and Methods). As shown in figure 1D, the average distance between substitutions is approximately 20Å with approximately 5% of mutations having a distance less than 5Å. Therefore, in the simulated trajectories, substitutions are less likely to be affected by a substantial epistasis, although there are cases where such substitution patterns occur. Importantly, these correlations can have both positive and negative effects on total stability and hence, P_fix, which will reduce total epistatic contributions to dN/dS. We also investigated the distance distribution for substitutions occurring in the real evolution of mammalian Mbs. From figure 1D, substitutions in branches of the phylogenetic tree of real Mb occur (on average) in residues closer in the 3D structure compared with simulation. This is expected because real Mbs are under selection for biophysical properties beyond folding stability. Nonetheless, there is still epistasis in real sequences probably due to coevolutionary constraints among the residues (de Juan et al. 2013). Taken together, epistasis has a minor effect in the simulated sequences compared with real Mbs but clearly of relevance in future, more refined approaches, and we conclude that our model is realistic enough for our scope, that is, to capture the effect of selection for protein stability on dN/dS.

Statistical Estimation of dN/dS Is Accurate When Proteins Are Stable

We used the codon models and the ML estimation implemented in CODEML to compute pairwise dN/dS (i.e., ω_ML) for proteins evolving under selection for stability (eqs. 3 and 4) in each branch of simulated phylogenies. Because we know the full history of the simulated population, we can estimate dN/dS (denoted as ω_pop) by counting the number of synonymous and nonsynonymous substitutions normalized by the average number of synonymous and nonsynonymous sites using the sequence information in the simulation trajectories.

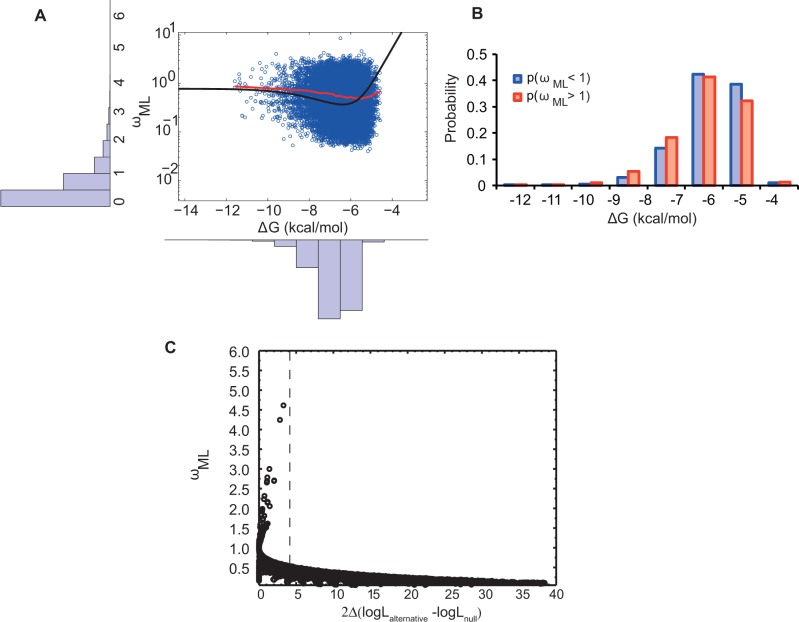
Figure 2A shows the ΔG versus ω_ML for simulated protein sequences. Each point corresponds to ΔG of a protein in internal nodes of the phylogenetic tree with the ω_ML value calculated between the protein sequence itself and its closest extant sequence in the phylogenetic tree. We performed these calculations over 12 simulated phylogenetic trees that originated from the same ancestral Mb sequence. The stability of the ancestral Mb is ΔG = −6.84 kcal/mol. Bifurcations occurred after every λ = 10⁵ mutational attempts (i.e., the resolution parameter) in the Mb sequence, which corresponds to approximately 5 amino acid substitutions. Most branches had ω_ML < 1 with an average of 0.55 and a standard deviation of 0.51 (fig. 2A). These low evolutionary rates imply partial conservation of the initial stability due to selection against destabilizing mutations (eqs. 3 and 4), that is, purifying selection. However, 3,035 out of 20,887 branches displayed an elevated rate of nonsynonymous versus synonymous substitutions. ΔG spanned from approximately −4 kcal/mol to −10 kcal/mol with an average of −6.34 kcal/mol and a standard deviation of 0.83 kcal/mol. The final obtained skewed distribution of ΔG was in good agreement with the empirical distribution of stabilities derived from the Protherm database (see the bottom panel in fig. 2A) (Sarai et al. 2001). This distribution has been articulated in several works (Bloom et al. 2005; Zeldovich et al. 2007; Goldstein 2011; Wylie and Shakhnovich 2011).

Fig. 2.—

dN/dS is more variable for marginally stable proteins. (A) Left insert: distribution of ω inferred by ML estimation for 20,887 branches of 12 independent phylogenetic trees. Bottom insert: Folding stabilities of internal branches of the phylogenies. Main figure: Black line is the molecular clock curve derived from analytical theory (Serohijos et al. 2012) with the scattered ΔG and ω_ML in log-scale from the internal nodes of simulations (in red). The locally weighted scatterplot smoothing line is shown in red. (B) The probability of observing ω_ML > 1 and ω_ML < 1 in proteins at different folding stabilities. (C) dN/dS estimated by ML method, ω_ML, versus twice the difference in log likelihoods of the models when dN/dS is set to 1 versus the case it is left to vary. The value of 2|lnLω = 1–lnLω = 0| > 3.84 (shown as dotted line) corresponds to P < 0.001 for rejecting the null hypothesis of dN/dS = 1.

There is a higher probability of deviation from neutrality (i.e., ω_ML = 1) at lower stabilities (fig. 2B), in agreement with the theoretical prediction (Serohijos et al. 2013). During simulated evolution, Mb spends much of its time under purifying selection (i.e., ω_ML < 1) while traversing to very high and low stabilities as reflected in ω_ML ∼ 1 and ω_ML > 1, respectively. Compared with the regime of stable proteins where evolution is neutral, the probability of observing ω_ML > 1 or ω_ML < 1 increases at intermediate stabilities up to its maximum at ΔG ∼ −6 kcal/mol where ΔG has its most probable value (fig. 2B). Although the molecular clock is expected to tick fastest at the least stable regime (Serohijos et al. 2012), the probability of observing ω_ML > 1 decreases because the probability density (i.e., distribution function of ΔG) approaches 0 at ΔG = 0 kcal/mol (Bloom et al. 2005; Zeldovich et al. 2007; Goldstein 2011; Serohijos et al. 2012, 2013; Serohijos and Shakhnovich 2014) (see supplementary information, Supplementary Material online, for a detailed mathematical analysis). This mechanism shows how the biophysical properties such as folding stability could affect the rate of protein evolution. We note that because the folding stability is a global property of proteins, it has a direct effect on the evolutionary rate even in the absence of selection for particular protein functions.

The recently derived relationship between protein stability and dN/dS (Goldstein 2011; Serohijos et al. 2012, 2013) provides better understanding of these results. For an evolving protein under selection for stability, there are three distinct regimes for dN/dS, and these three regimes are obtained in our simulations as well: First, at high stabilities, most mutations do not have a selective advantage/disadvantage. For a protein with ΔG = −10 kcal/mol, an average mutation with ΔΔG = 1 kcal/mol has a fixation probability of approximately 10⁻⁴, similar to a neutral mutation at moderate population size (i.e., P_fix ≈ 1/N_eff). Thus, within this regime of high stability, most mutations are neutral with dN/dS ∼ 1. However, when proteins are unstable, destabilizing mutations are either purged from the population (i.e., purifying selection and thus dN/dS < 1) or randomly fixated to decrease folding stability. In the latter case, even a slightly beneficial mutations with ΔΔG = −0.5 kcal/mol can be subsequently fixated with probabilities that are approximately 10 times higher than for a neutral mutation with ΔΔG = 0 (see eqs. 3 and 4). As expected, in the regime of very low stability, protein evolution is dominated by substitutions that increase stability (see supplementary fig. S2, Supplementary Material online).

We wanted to investigate whether the current observations of per gene dN/dS > 1 are statistically significant. The ML approach typically assigns significance to the estimated dN/dS by comparison with neutral evolution (e.g., see Nielsen et al. 2005). In figure 2C, we calculated twice the difference of the logarithm of likelihood functions in the null model of ω_ML = 1 and the alternative model of free ω_ML and plotted ω_ML versus this measure. Indeed the observed dN/dS values > 1 are not deemed statistically significant, which shows that ML approaches are robust against false detection of positive selection at the level of the whole gene.

We next compared the estimated dN/dS per gene as explicitly counted in the simulation (Materials and Methods) and the dN/dS estimated using ML. Because the full history of the population is known, one can explicitly count dS, dN, and consequently compute dN/dS (See supplementary table S2, Supplementary Material online, for the statistics of dN and dS themselves). We thus asked whether ML methods could accurately estimate the rates obtained from simulation. Theoretically, in ML estimation of dN/dS, the rate ratio for each site in the protein is treated as a variable in the transition rate matrix of the relevant Markov model. The branch length and transition/transversion ratio are estimated using ML. These estimates are subsequently used in the evaluation of per gene dN/dS as ω_ML (Yang 2006).

Figure 3A shows the distribution of the ratio ω_pop/ω_ML with a peak at ω_pop/ω_ML = 1; specifically, more than 90% of all comparisons show ω_pop/ω_ML ∼ 1 (fig. 3B). However, there are deviants in the ML inference of ω_pop (i.e., ω_ML) that are more frequently observed at lower folding stabilities. The null hypothesis of ω_pop and ω_ML being independent random samples from the same distributions with equal means and equal but unknown variances is strongly rejected when ΔG greater than − 6 kcal/mol (supplementary fig. S3, Supplementary Material online). This indicates a systematic deviation of ω_ML from ω_pop in the regime of modest stability.

Fig. 3.—

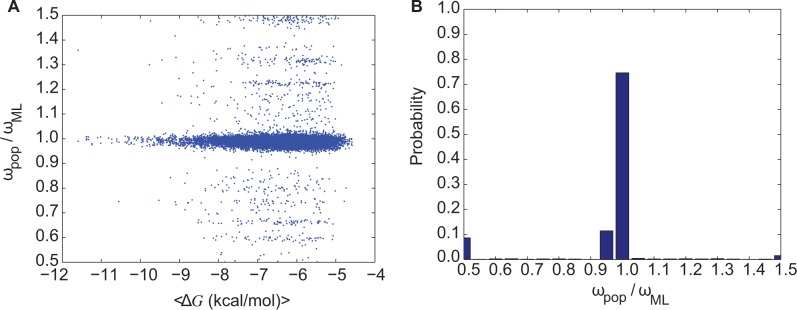
dN/dS values from simulations correlate more strongly with ML-estimated dN/dS when proteins are more stable. (A) The ratio between dN/dS from simulations, ω_pop, and the ML estimation of dN/dS, ω_ML versus ΔG. The Spearman rank correlation between ω_ML and ω_pop shows a correlation coefficient of ρ = 0.96 and the P value of ∼ 0. (B) Frequency distribution of the ratio ω_pop/ω_ML indicating the overall accuracy the Bayesian methods. Deviations between ω_pop and ω_ML are predominantly in the regime when proteins are less stable (panel A). All analyses were performed on branches of 12 simulated bifurcating phylogenetic trees each having 1,024 external nodes.

At higher folding stabilities, most mutations do not have a significant effect on dN/dS. For Mb with ΔG = −9 kcal/mol, dN/dS is only altered by mutations having ΔΔG > 4 kcal/mol which have a probability of occurrence < 0.04 (supplementary fig. S4, Supplementary Material online). For proteins having stabilities close to the average observed stabilities in the simulated phylogenies (i.e., ΔG = −6.34 kcal/mol), dN/dS fluctuates between high and low values due to the more frequent mutations with marginal effects on stability (∼±1 kcal/mol). There is thus a stronger agreement between ML estimation and explicit dN/dS values at higher stabilities where changes in folding stability have neutral effects because of the extra buffer in pre-mutation stability.

To explore the robustness of our method with respect to population sizes, we simulated a phylogenetic tree with 1,024-extant sequences and N_eff = 10⁵. The average and the variance of dN/dS was 0.51 and 0.22, respectively, for larger population size (i.e., N_eff = 10⁵), significantly smaller than 0.55 and 0.26 for N_eff = 10⁴ (two sample t-test at the significance level of 0.05). Furthermore, P(ω_ML > 1) was slightly but significantly higher at the smaller population size with 0.14 and 0.13 for N_eff = 10⁴ and N_eff = 10⁵, respectively. With the larger population size, the average ΔG decreased to approximately −7.66 kcal/mol, consistent with previous studies on the relation between population size and the strength of selection for folding stability (Goldstein 2011; Wylie and Shakhnovich 2011). This effect is mainly due to the fact that in smaller populations, drift is more prevalent and deleterious mutations have a higher chance of fixation. Therefore, on average, proteins are more stable (have a more negative ΔG) at larger population sizes N_eff = 10⁵. Because proteins are more stable in larger populations, we observed a lower probability of ω_ML > 1.

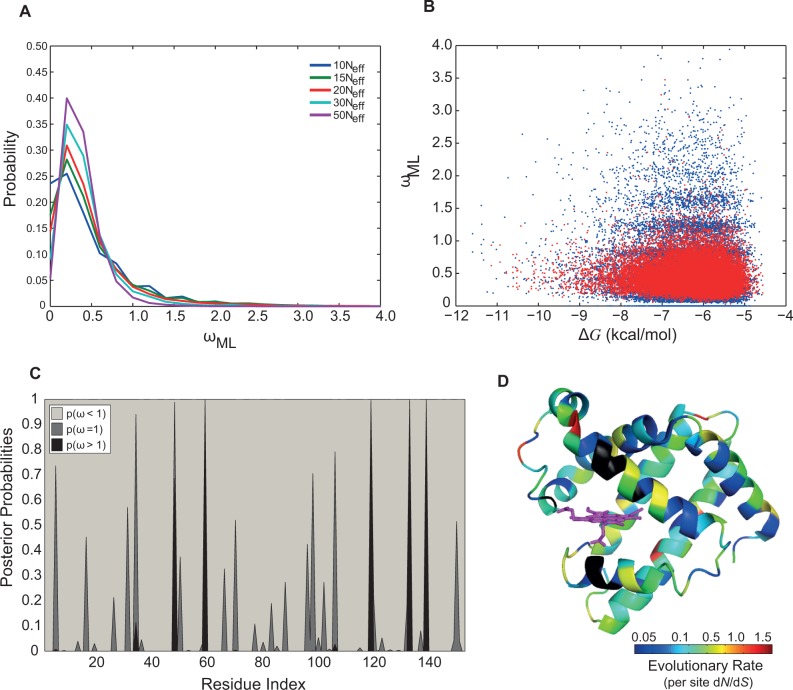
We also checked the sensitivity of our results to the choice of resolution parameter. Figure 4A and table 1 both show that P(ω_ML > 1) increases at higher resolutions (i.e., smaller values for resolution parameter or fewer amino acid substitutions, see supplementary fig. S5, Supplementary Material online). As an example, the distributions of ω_ML for λ = 10⁵ (in blue) and λ = 5 × 10⁵ (in red) shown in figure 4B have averages ± standard deviations of 0.55 ± 0.51 and 0.46 ± 0.24, respectively. The coefficient of variation (the standard deviation divided by the mean) of ω_ML, as a measure of the dispersion of the distribution, is likewise higher at higher resolutions. Because proteins have a longer residence time in intermediate stabilities, lower resolutions (i.e., larger values of resolution parameter), mask infrequent transitions from low to moderate stabilities in simulated phylogenies and hence, we observe ω_ML < 1 more frequently. Furthermore, more finite effects are expected in the calculation of dN/dS at lower resolution (e.g., compare the banding patterns between the blue and the red scatter plots in fig. 4B). For a more systematic comparison of this finite effect artifact see supplementary figure S8, Supplementary Material online.

Fig. 4.—

Observation of branches with dN/dS > 1 depends on the resolution of phylogenetic trees. Histograms of (A) dN/dS inferred from the ML method, ω_ML, and (B) ω_ML versus ΔG for Mb sequences evolved with λ = 10⁵ (in blue) and 5 × 10⁵ (in red) mutations having the coefficient of variation of approximately 0.94 and 0.54, respectively. (C) Posterior probabilities of per site dN/dS from M8 model (Materials and Methods) across the sequence and (D) mapped onto the crystal structure of sperm whale Mb (PDB code = 1MBO) (Phillips 1980). Here, the color spectrum from blue to red is proportional to the value of average per site dN/dS for each sites. Residues in black are the ones excluded in evolutionary simulation due to their importance in O₂-binding and interaction with Heme. Residues 48, 59, 119, 133, and 139 have dN/dS > 1 (shown in red) and are located in C/D loop, E helix, G/H loop and H helix, respectively. For log-scale presentation of ω_ML in panels A and B see supplementary figure S5, Supplementary Material online.

Table 1.

Probability of Observing ω_ML > 1 and Coefficient of Variation of ω_ML at Different Resolutions (i.e., λ-parameter)

	λ = 105	λ = 1.5 × 105	λ = 2 × 105	λ = 3 × 105	λ = 5 × 105
P(ωML > 1)	0.11	0.10	0.08	0.04	0.01
Coefficient of variation of ωML	0.94	0.93	0.89	0.76	0.51

Observation of Residues with Significant per Site dN/dS > 1

We showed in the analysis of ω_ML that the observation of per gene dN/dS > 1 is not statistically significant when compared with neutral evolution. However, it has been shown that proteins with per gene dN/dS values in the range of approximately 0.25 still have signatures of dN/dS > 1 at specific sites (Swanson et al. 2004; Sawyer and Malik 2006). In the same way that rates appear more “neutral” over time, that is, in longer branches, due to cancellation of negative and positive selection processes, they also appear more neutral when averaged over sites in the protein. We then determined if folding stability also affects the estimation of per site dN/dS. To identify residues with dN/dS > 1, we used the codon-based models across different sites (i.e., site models). For an evolving Mb sequence with λ = 10⁵ mutational attempts, three pair-models as M1–M2, M7–M8, and M8fix-M8 were employed to identify sites with dN/dS > 1 as presented in table 2 (Materials and Methods). As shown in table 2, the LRT gave a significant result, with six sites detected to show dN/dS > 1 significantly having high posterior probabilities using the BEB test (Yang et al. 2005). Therefore, substitutions in these residues contribute to dN/dS > 1 and thus to higher ΔΔG when proteins are at low folding stabilities (see fig. 4C and D and supplementary table S3 and fig. S6, Supplementary Material online, for posterior probabilities of per site dN/dS).

Table 2.

Log-Likelihood Values of the Site Models with Detected Sites Having dN/dS > 1

Models (number of parameters)	ln L	2Δl = 2 × (ln L1–ln L2)	P value	Positively Selected Sites (BEB: Pr(ω > 1) > 0.5)a [ωML]
M1a (2)	−65,183.82	—	—	—
M2a (4)	−65,141.86	(M1a vs. M2a) 83.92	<10−16	34 [1.47], 48 [1.49], 59 [1.50], 119 [1.49], 133 [1.50], 139 [1.50]
M7 (2)	−64,591.18	—	—	—
M8 (4)	−64,563.17	(M7 vs. M8) 56.02	6.84 × 10−13	48 [1.32], 59 [1.50], 119 [1.48], 133 [1.50], 139 [1.50]
M8fix (3)	−64,586.49	(M8 vs. M8fix) 46.64	8.53 × 10−12	—

Note.—ln L is the logarithm of likelihood function fitted to the relevant model.

^aPr(ω_ML > 1) > 0.95 is shown in italics.

Finally, we investigated the reproducibility of the results by comparing results obtained from ten different phylogenetic trees with evolving Mb sequences and λ = 10⁵. LRT was significant in all cases, and different sites were detected to be under positive selection (see the supplementary information, Supplementary Material online, for LRT results). As presented in table 2, the maximum ω_ML for the sites under positive selection was 1.5, pointing to a weak yet significantly elevated rate of evolution in these positions (fig. 4C and D). Altogether, this shows that per site dN/dS estimated using ML provides statistically significant dN/dS > 1 values when the entire evolution is under mutation-selection balance. Thus, these results suggest that the observation of per site dN/dS could be due to transient substitutions to maintain the biophysical properties (such as folding stability) under mutation-selection balance, hence, not truly adaptive.

Discussion

Maintenance of folding stability is universal selection pressure acting on all proteins except perhaps intrinsically disordered proteins (Dokholyan and Shakhnovich 2001; Williams et al. 2006; Goldstein 2008; Soskine and Tawfik 2010; Heo et al. 2011; Serohijos et al. 2012, 2013; Serohijos and Shakhnovich 2014). We have shown in this work that such a type of selection pressure can directly influence rates of protein evolution, estimated by dN/dS and distinguish regimes of neutral drift (high stability) from regimes of selection (low stability).

First, at higher folding stabilities, most arising mutations are neutral and do not have tangible effects on fitness (i.e., P_nat): A highly stable protein (e.g., ΔG < −9 kcal/mol) is still “stable enough” after a typical mutation reducing stability by 1 kcal/mol. This stems from the sigmoidal relation between the fraction of folded proteins and folding free energy (eq. 1) (Chen and Shakhnovich 2009). In the process of calculating dN/dS by ML methods, the ratio of the rates of nonsynonymous to synonymous substitutions is assumed to be unchanged for all nonsynonymous substitutions, which is most likely the case at higher folding stabilities. For proteins in this regime, dN/dS inferred from ML methods, ω_ML, correlates more strongly with the dN/dS from simulations calculated by explicitly tracking the number of synonymous and nonsynonymous substitutions and normalizing by the number of synonymous and nonsynonymous sites, ω_POP. Thus, ML estimates of dN/dS using codon models, as widely done in the community, are more reliable in the regime of high folding stability because mutations are neutral and the molecular clock assumption is valid.

Second, in the unstable regime where proteins are prone to unfolding, protein evolution has two forms of selection. One is purifying selection against destabilizing mutations leading to dN/dS < 1, and another is positive selection of stabilizing mutations leading to dN/dS > 1. We showed that per gene ML estimation of dN/dS is robust to such sporadic deviations from neutrality and the proteins as a whole remain in the nearly neutral regime, consistent with the fact that whole-gene estimates are insensitive to local selection patterns and are too coarse-grained to detect selection.

In contrast, per site estimation of dN/dS reveals statistically significant selection signatures in different residues with dN/dS ∼ 1.5. This observation is consistent with the requirement of approximately 1−2 nonsynonymous substitutions to bring the folding stability of Mbs back to its average value, as shown in figure 2A. This contrast between per gene and per site estimation of dN/dS is analogous to the loss of information of the inherent dynamics of the collision of particles when the mean free path is much smaller than the chamber size, and illustrates how gene-averaging destroys selection signatures. We have shown that once these issues are resolved (in the case of protein evolution by looking at per site dN/dS) the fixation dynamics leaves an imprint on genomic sequences via dN/dS ∼ 1.5. Although the observation of dN/dS > 1 is often interpreted as positive selection due to adaptations and niching, our study shows that compensatory substitutions at very low stability regimes can also increase dN/dS significantly. This conclusion is in line with the view that selection of beneficial mutations is necessary in order to compensate for deleterious mutations (Fisher 1999; Sawyer et al. 2007; Mustonen and Lässig 2009).

One limitation of the model is that it does not explicitly account the epistatic interaction among sites in the protein, although the model itself has epistatic interactions because of the curvature of the fitness function (Materials and Methods). Ideally, one should update the folding stability by calculating the ΔΔG of the arising mutation using the physical force field and the crystal structure as input. However, this is computationally prohibitive in evolutionary simulations. Importantly, the major contributions to our observed rate variations come from small groups of compensating substitutions, typically less than a handful. As was shown in this work, the probability that these few sites are close together and thus infer important epistasis to the observed dynamics is small, especially because their effects can be both toward increasing or reducing P_fix. Instead, the global stability compensation drives the rate variations, and these are largely robust to epistasis. Still, epistasis is observed in some instances where substitutions occur in nearby sites. Whether this has any effect on true rate variations, that is, whether these correlations change ΔΔG enough to change the general fixation dynamics, remains to be investigated.

Supplementary Material

Supplementary information, figures S1–S7, tables S1–S3, and trees S1–S10 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).