Inference for Environmental Intervention Studies using Principal Stratification

Abstract

Previous research has found evidence of an association between indoor air pollution and asthma morbidity in children. Environmental intervention studies have been performed to examine the role of household environmental interventions in altering indoor air pollution concentrations and improving health. Previous environmental intervention studies have found only modest effects on health outcomes and it is unclear if the health benefits provided by environmental modification are comparable to those provided by medication. Traditionally, the statistical analysis of environmental intervention studies has involved performing two intention-to-treat analyses that separately estimate the effect of the environmental intervention on health and the effect of the environmental intervention on indoor air pollution concentrations. We propose a principal stratification (PS) approach to examine the extent to which an environmental intervention’s effect on health outcomes coincides with its effect on indoor air pollution. We apply this approach to data from a randomized air cleaner intervention trial conducted in a population of asthmatic children living in Baltimore, Maryland, USA. We find that amongst children for whom the air cleaner reduced indoor particulate matter concentrations, the intervention resulted in a meaningful improvement of asthma symptoms with an effect generally larger than previous studies have shown. A key benefit of using principal stratification in environmental intervention studies is that it allows investigators to estimate causal effects of the intervention for sub-groups defined by changes in the indoor air pollution concentration.

1. Introduction

Previous studies have established an association between outdoor fine particulate matter (PM_2.5) and the risk for mortality and morbidity [1-6]. In particular, research has shown an association between ambient outdoor PM_2.5 and respiratory health [2, 6] and more specifically, found that higher concentrations of particulate matter air pollution (PM_2.5 and PM₁₀) were associated with a greater number of symptom days for asthmatic children [7, 8]. Interventions to lower outdoor PM_2.5 are typically conducted at the national or state level through government regulatory agencies [9]. This process can be time-consuming and may take years to have an effect. Interventions at the individual or community level are more manageable and less expensive to implement. This suggests that environmental interventions to reduce indoor air pollution may be relatively simple and inexpensive ways to improve health. Recent research suggests that environmental interventions reduce indoor air pollution and allergens. It also suggests that they are associated with improved asthma in children [10-14]. However, the health benefits observed in these studies were generally modest and questions remain regarding whether environmental modification provides a significant benefit over standard medication-based treatments. The effectiveness of environmental interventions on health and asthma symptoms continues to be an area of active research [10-15].

The statistical analysis of environmental intervention studies has generally consisted of an intention-to-treat (ITT) analysis for the effect of the intervention on the health outcome and an ITT analysis for the effect of the intervention on the environmental factor(s) of interest [10, 11]. However, this approach does not allow one to simultaneously consider the relationship between the environmental intervention, environmental factor, and asthma morbidity. One can only detect an association between the intervention’s effect on health and the intervention’s effect on environmental factors. Studies performing regression analysis of indoor air pollution and respiratory health, such as in Hunt et al. [16], identify associations between indoor air pollution and respiratory health. Yet, in general, such analyses cannot estimate causal effects and their effect estimates may be biased due to potential confounding.

In many environmental intervention studies, the interventions are implemented to improve health by modifying an environmental factor that has been shown to be associated with health. As discussed in Frangakis and Rubin [17] and Stuart and Jo [18], conditioning on variables that may be affected by treatment assignment can result in biased treatment effect estimates. In Frangakis and Rubin [17], the authors introduced the principal stratification (PS) framework to estimate the effect of treatment when a key post-treatment variable is present. The PS approach estimates causal effects of the treatment by grouping individuals into principal strata based on the potential outcomes of the post-treatment variable. Because we do not observe all the potential outcomes of the post-treatment variable, principal stratum membership is generally not known and must be inferred. Propensity score approaches can be used to estimate principal stratum membership and obtain causal treatment effect estimates [18, 19]. Other studies analyze data with post-treatment variables using a PS framework and Bayesian models [20-23]. A spatial Bayesian PS method to examine the causal effects of outdoor air quality regulations is proposed in Zigler et al. [9].

Another commonly used approach for analysis of data with post-treatment variables, proposed in Baron and Kenny [24], is to test for indirect effects of the post-treatment variable by fitting three regression models and then multiplying the estimates for the effect of the treatment on the post-treatment variable and the effect of the post-treatment variable on the outcome. Other causal analyses use marginal structural models (MSMs) to estimate the direct and indirect causal effects when post-treatment variables are present [25-28]. In Ten Have et al. [29], the authors propose a linear rank preserving model (RPM) approach that avoids making the assumption of sequential ignorability for the relationship between post-treatment variable and outcome as is assumed in MSMs. However, the RPM assumes no interaction between treatment and post-treatment variables.

In this paper, we extend the research examining the effectiveness of environmental interventions on health and asthma symptoms by using PS to analyze data from a randomized trial of air cleaners. The PS framework allows us to estimate the causal effect of an air cleaner on asthma symptoms for sub-populations of interest, such as for individuals for whom the air cleaner would reduce indoor PM_2.5. If the air cleaner improves health by reducing indoor PM_2.5, we would expect the health effect estimate for the sub-population of individuals for whom the air cleaners would meaningfully reduce indoor PM_2.5 to be greater than the health effect estimate found in a traditional ITT. The PS approach allows us to take advantage of the randomized experimental design and avoid bias in the environmental intervention effect estimates that may be introduced by an analysis that simply conditions on the post-treatment variable. Using PS as opposed to testing for mediation as in Baron and Kenny [24] or performing mediation analysis estimating indirect effects as in VanderWeele [26], allows us to examine the relationships between the environmental intervention, indoor PM_2.5, and health while avoiding making assumptions about a priori counterfactuals for interventions on indoor PM_2.5 [26]. Our analysis includes a treatment by post-treatment variable interaction which is assumed not to exist in the RPM proposed in Ten Have et al. [29]. Unlike causal analyses using propensity scores and other causal analysis using PS that assume discrete post-treatment variables, such as in Elliott et al. [21] and Gallop et al. [22], we treat indoor PM_2.5 as a continuous variable. By treating indoor PM_2.5 as continuous as opposed to a discrete outcome, we are able to consider several different cutoffs to define a meaningful reduction in indoor PM_2.5 and obtain causal treatment effect estimates for a multitude of potential PM_2.5 outcome values. Our analysis parallels the work of Zigler et al. [9], Schwartz et al. [20] and Jin and Rubin [23] by considering a PS model with a continuous post-treatment variable and adapts it to the context of environmental intervention studies with a randomized treatment assignment. Section 2 describes the data used in our analysis, Section 3 discusses our PS model and estimation procedure, and Section 4 gives the results obtained from applying the PS analysis to data from a randomized trial in which air cleaners are randomly assigned to inner-city households with asthmatic children and smokers. We end with a discussion and recommendations for using a PS approach in environmental intervention studies in Section 5.

2. PREACH Data

Our analysis uses data collected for the Particulate Reduction Education in City Homes (PREACH) study [11]. Previous studies have suggested that multi-modal intervention programs that combine environmental interventions and asthma education improve the health of asthmatic children [10, 30-32]. The main objective of the PREACH study was to compare the effect of air cleaners, air cleaners and a health coach, and no intervention on measures of second hand smoke exposure and asthma symptoms among children living with a smoker. It was a randomized trial with 3-arms: (1) control group receiving 4 asthma education sessions, (2) air cleaner group receiving 4 asthma education sessions and 2 air cleaners, and (3) air cleaner plus coach group receiving 2 air cleaners and 4 asthma education sessions which also include behavioral interventions with a health coach. Households randomized to the control case received four asthma education sessions during 4 nurse home visits. They served as an attention control group and received the same number of nurse contacts as the treatment arms [11]. For households assigned to the air cleaner groups, an air cleaner was placed in the room in which the child slept for 4 or more nights per week and in the family or living room. In the air cleaner plus coach treatment arm, the health coach worked with the caregiver to reduce the child’s exposure to tobacco smoke and achieve a total home smoking ban.

Children between the ages of 6 and 12 who were physician-diagnosed asthmatics with persistent asthma were enrolled in the study using patient rosters from an urban pediatric emergency department and 2 community practices. The children in the study were limited to children who live with a smoker in the home who smoked at least 5 cigarettes per day and resided in the home at least 4 days a week. There were 126 households enrolled and randomized. Data was collected at baseline and a six month follow-up visit. Data collected at baseline and follow-up includes the number of symptom days for asthmatic child in previous two weeks of visit, the total cotinine concentration in child’s urine in ng/mL, the air nicotine concentration, the concentration of particulate matter air pollution less than 10 micrometers in diameter (PM₁₀), and the concentration of particulate matter air pollution less than 2.5 micrometers in diameter (PM_2.5). PM₁₀ and PM_2.5 were measured using 4-L/min impactors sampling for 7 days within 2 weeks of the clinic visit. The number of symptom days was determined by asking the caregiver how many days in the past two weeks did the child experience ”wheezing, coughing, shortness of breath, or tightness in the chest” and the number of symptom free days (SFDs) was calculated by subtracting the number of symptom days from 14 [11]. More details on the PREACH study can be found in Butz et al. [11]. One outcome of interest in the PREACH study is the change in PM_2.5 concentrations between baseline and follow-up visits. No significant differences in this outcome were detected between the two groups with air cleaners [11]. After combining the two air cleaner groups, a significant decrease in PM_2.5 concentrations between baseline and follow-up for the combined air cleaner group was found with a mean decrease of 18 μg/m³ [11]. The mean change in PM_2.5 for the control group was estimated to be 2.4 μg/m³ and found not to be significantly different than zero. In Butz et al. [11], they also found that the combined air cleaner group had a significant increase in number of SFDs (mean increase of 1.36 SFDs) compared to control group with a mean increase of 0.24 SFDs which was not found to be significantly different than zero. The authors conclude that the significant improvement in health was most likely due to the reduction in indoor PM_2.5 concentrations.

3. Methods

We consider a PS framework and a potential outcomes model [17, 33]. Let A_i be the random variable representing the level of treatment assigned to individual i and Z_i be the s × 1 column vector of observed baseline covariates. In our case, A_i = a_i with a_i ∈ {0, 1} where a_i = 1 indicates that individual i is assigned to the treatment group and receives air cleaners. Let Y_i be the response variable, which in our case is the change in SFD from baseline to follow-up, and let Y_i (a_i) be the potential outcome for the response variable given that individual i is assigned to treatment level a_i. Let X_i be the random variable that is not directly controlled and whose levels depends on treatment assignment. For the PREACH analysis, this is the change in PM_2.5 levels from baseline to follow-up. To simplify the notation throughout the rest of the paper, we will lose the subscript when denoting fine particulate matter and simply refer to PM_2.5 as PM. Let X_i (a_i) be the potential outcome for X_i given individual i is assigned to treatment level a_i.

3.1. Assumptions

We assume the stable unit treatment value assumption (SUTVA) which is a common assumption in causal inference [29, 33]. SUTVA has two parts where the first assumes that there is no interaction between units of the study and thus, the potential outcomes of an individual are not influenced by the treatment assignment of other individuals. The second assumes that there are no other possible treatments or versions of the treatment in the study [33]. We also assume another common but untestable assumption in causal inference, the ignorability of treatment assumption [9, 29, 33]. This assumption implies that conditional on observed covariates, there is no unmeasured confoundedness in the relationship between the treatment and potential health outcomes and there is no unmeasured confoundedness in relationship between the treatment and potential outcomes for the environmental factor. This assumption is often reasonable for data obtained from randomized experiments. Since little is known about the mechanisms that contribute to indoor PM levels, we make a minimal amount of assumptions about indoor PM. We do not assume sequential ignorability since sequential ignorability implies that there does not exist extraneous variables that influence both indoor PM and the health outcome [22, 34]. We also do not assume another common assumption, the exclusion restriction [18, 22, 35]. In this case, the exclusion restriction would imply that there is no treatment effect on individuals whose PM levels are not affected by treatment level assignment. We also avoid making the monotonicity assumption, which would imply that there does not exist individuals for whom indoor PM would increase when assigned to air cleaner and decrease when assigned to the control case [22, 35].

3.2. Model

Note that we do not observe all the potential outcomes for a given individual. Thus, without further assumptions, we will not be able to identify a full joint density with which to draw inference. We, therefore, assume a model for the change in SFDs and the change in PM concentrations. For the model for the change in SFDs, the SFD model, we assume

$$Y_i\left(a_i\right)=Z_i^{\prime }\alpha +{\beta }_1{a}_i+{\beta }_2{X}_i\left(a_i\right)+{\beta }_3{a}_i{X}_i\left(a_i\right)+{\eta }_{a_{i}i}$$ (1)

where η_{ai ,i} is normally distributed with mean 0 and variance ξ , η_{ai ,i} ~ N (0, ξ²). Let X_i = (X_i (0) , X_i (1))′ and Y_i = (Y_i (0) , Y_i (1))′. We assume that Y_i given Z_i and X_i is independent of Y_j given Z_j and X_j for i ≠ j. We further assume that given X_i (0), X_i (1) and Z_i,

$$\left[\begin{array}{c}\hfill Y_i\left(0\right)\hfill \\ \hfill Y_i\left(1\right)\hfill \end{array}\right]~N\left(\left[\begin{array}{c}\hfill {\mathit{Z}}_i^{\prime }\alpha +{\beta }_2{X}_i\left(0\right)\hfill \\ \hfill {\mathit{Z}}_i^{\prime }\alpha +{\beta }_1+({\beta }_2+{\beta }_3)X_i\left(1\right)\hfill \end{array}\right],\left[\begin{array}{cc}\hfill {\xi }^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\xi }^2\hfill \end{array}\right]\right).$$ (2)

For the model for the change in PM, the PM model, we assume

$$\left[\begin{array}{c}\hfill X_i\left(0\right)\hfill \\ \hfill X_i\left(1\right)\hfill \end{array}\right]~N\left(\left[\begin{array}{c}\hfill {\mu }_{0i}\hfill \\ \hfill {\mu }_{1i}\hfill \end{array}\right],\left[\begin{array}{cc}\hfill {\sigma }_0^2\hfill & \hfill \rho {\sigma }_0{\sigma }_1\hfill \\ \hfill \rho {\sigma }_0{\sigma }_1\hfill & \hfill {\sigma }_1^2\hfill \end{array}\right]\right)$$ (3)

where ${\mu }_{0i}={\mathit{W}}_i^{\prime }\gamma ,{\mu }_{1i}={\mathit{W}}_i^{\prime }\gamma +{\delta }_1$ and δ₁ is the effect of the air cleaner on the PM potential outcome. We let W_i be a r × 1 column vector of observed baseline covariate for individual i, which do not necessarily have to be the same as the covariates in Z_i. Note that ρ is the correlation between an individual’s PM potential outcome under treatment and that same individual’s PM potential outcome under control. Larger values of ρ will occur if there are unmeasured factors about an individual or in an individual’s environment that effect PM level concentrations. Since we do not observe an individual under both the treatment and control condition, the data provide no information on ρ. Thus, for our analysis, we will fix the value of ρ and check the sensitivity of our results to different values of ρ. Relaxations of the assumption that ρ is fixed are discussed in Section 5. We assume that X_i given W_i is independent of X_j given W_j for i ≠ j.

3.3. Bayesian Analysis

To estimate the parameters of interest and obtain causal effect estimates, we use a Bayesian approach as in Zigler et al. [9] and Jin and Rubin [23]. Let X be a n × 2 matrix with the ith row equal to the X^I and Y be a n × 2 matrix with the ith row equal to the Y ^I . Note that Y_i (1) and X_i (1) are unknown for the individuals in the control group and that Y_i (0) and X_i (0) are unknown for the individuals in the treatment group. Let Y ^mis be a n × 1 column vector where the ith element, $Y_i^{\mathrm{mis}}$, is the missing SFD potential outcome for individual i and let Y^obs be a n × 1 column vector where the ith element, $Y_i^{\mathrm{obs}}$, is the observed SFD potential outcome for individual i. Likewise, let X^mis be a n × 1 column vector where the ith element, $X_i^{\mathrm{mis}}$, is the missing PM potential outcome for individual i and let X^obs be a n × 1 column vector where the ith element, $Y_i^{\mathrm{obs}}$, is the observed PM potential outcome for X_i for individual i. The unknown potential outcomes, often referred to as counterfactuals, can be thought of as missing data that need to be estimated along with other parameters in the model [26, 33, 36]. Let θ = ⁽γ′, δ₁, σ₀, σ₁, α′, β₁, β₂, β₃, ξ²)′ be a (r + s + 7) × 1 vector of the parameters from the SFD and PM models in (2) and (3), respectively. The posterior distribution for θ is proportional to

$$f\left(\theta \right)\int \int f({\mathit{X}}^{\mathrm{mis}},{\mathit{X}}^{\mathrm{obs}},{\mathit{Y}}^{\mathrm{mis}},{\mathit{Y}}^{\mathrm{obs}}\mid \mathit{Z},\mathit{W},\theta )\partial {\mathit{X}}^{\mathrm{mis}}\partial {\mathit{Y}}^{\mathrm{mis}}$$ (4)

where Z is a n × s matrix with the ith row equal to $Z_i^{\prime }$ and W is a n × r matrix with the ith row equal to $W_i^{\prime }$. Note that this is difficult to integrate since we need to integrate over missing potential outcomes. Thus, similar to the analysis in Zigler et al. [9], we focus on sampling from the joint posterior proportional to

$$f(\theta ,{\mathit{X}}^{\mathrm{mis}},{\mathit{Y}}^{\mathrm{mis}}\mid {\mathit{X}}^{\mathrm{obs}},{\mathit{Y}}^{\mathrm{obs}}\mathit{Z},\mathit{W})\propto f\left(\theta \right)\underset{i=1}{\overset{n}{\Pi }}f({\mathit{X}}^{\mathrm{mis}},{\mathit{X}}^{\mathrm{obs}}{\mathit{Y}}^{\mathrm{mis}},{\mathit{Y}}^{\mathrm{obs}}\mid \theta ,\mathit{Z},\mathit{W}).$$ (5)

Markov Chain Monte Carlo (MCMC) techniques are used to sample from this distribution. We iteratively sample the missing PM potential outcomes followed by the missing SFD potential outcomes. We then update the (r + 1) × 1 column vector θ_X = (γ′, δ₁)^′, followed by the (s + 3) × 1 column vector θ_Y = (α′, β₁, β₂, β₃)^′. Lastly, we update the variance components ξ², σ₀, and σ₁. Details of the sampling algorithm can be found in the Supplemental Material.

3.4. Priors

For the variance parameter in (2), ξ², we select an inverse gamma prior (shape and scale parameters are 0.01 in our analysis). For the standard deviations in the PM model in (3), σ₀ and σ₁, we assume lognormal priors. We let the priors for log (σ₀) and log (σ₁) be normal distributions with mean zero and variance $m_0^2\mathrm{and}{m}_1^2$, respectively ($m_0^2=5\mathrm{and}{m}_1^2=5$ in our analysis). As explained in Section 3.2, ρ is fixed as opposed to a free parameter. By fixing ρ, we are able to check the sensitivity of our causal effects estimates under different values of ρ. As an alternative, one could let ρ be a free parameter, using an inverse-Wishart prior for the covariance matrix in the PM model or by using a Dirichlet process mixture model [20]. If ρ is a free parameter, the causal effect estimate would be found by integrating over ρ as opposed to assuming ρ is equal to a fixed value. This adds a greater computational burden and since no household is observed under both treatment conditions, the data does not provide any additional information on ρ (See Section 5).

For the other parameters, we choose less informative normal priors. We let θ_X be normally distributed with mean equal to the zero vector and a diagonal variance matrix with diagonal elements (${\sigma }_{\gamma 1}^2,\dots ,{\sigma }_{\gamma r}^2,{\sigma }_{\delta }^2$) with σ_γ1 = … = σ_γr = σ_δ = 20 in our analysis. We let θ_Y be normally distributed with mean equal to the zero vector and a diagonal variance matrix with diagonal elements ${\sigma }_{\alpha 1}^2,\dots ,{\sigma }_{\alpha s}^2,{\sigma }_{\beta }^2,{\sigma }_{\beta }^2,{\sigma }_{\beta }^2$ with σ_α1 = … = σ_αs = σ_β = 20 in our analysis. We assume a priori independence among all parameters.

3.5. Causal Effects

We consider the average causal effect of the treatment within principal strata where the principal strata are defined using the PM potential outcomes. The average causal effect can be found for any combination of principal strata [9, 17]. We consider a level ℓ such that if X_i (1) − X_i (0) < l, we conclude that the air cleaner would meaningfully reduce indoor PM. The average causal effect of the air cleaner on SFDs for those individuals for whom there would be a meaningful reduction in indoor PM under treatment is

$${\mathrm{ERE}}_{\ell }=\mathrm{E}[Y_i\left(1\right)-Y_i\left(0\right)\mid X_i\left(1\right)-X_i\left(0\right)<\ell ].$$ (6)

Thus, this is the average causal effect for individuals for whom the treatment would have improved indoor PM levels. We refer to (6) as the expected reduced effect (ERE). If X_i (1) − X_i (0) ≥ ℓ, we conclude that the air cleaner would not meaningfully reduce indoor PM. The average causal effect of the air cleaner on SFDs for those individuals for whom indoor PM would not be meaningful reduced under treatment is

$${\mathrm{ENRE}}_{\ell }=\mathrm{E}[Y_i\left(1\right)-Y_i\left(0\right)\mid X_i\left(1\right)-X_i\left(0\right)\ge \ell ].$$ (7)

Thus, this is the average causal effect for individuals for whom the treatment would not have improved indoor PM levels. We refer to this as a expected not reduced effect (ENRE).

Another principal strata that may be of interest is the principal strata for which there would be no meaningful change in indoor PM under treatment. The average causal effect of the air cleaner on SFDs for those individuals for whom indoor PM would not meaningfully change under treatment is

$${\mathrm{ENCE}}_{\ell }=\mathrm{E}[Y_i\left(1\right)-Y_i\left(0\right)\mid X_i\left(1\right)-X_i\left(0\right)<\mid \ell \mid ].$$ (8)

We refer to this causal effect as the expected no change effect (ENCE). A large ENCE estimate would suggest that the air cleaner is improving health by another mechanism besides reducing indoor air pollution. The regulations for outdoor PM requires that it does not to exceed 35 μg/m³ in a 24 hour time period but indoor PM levels are not regulated in the United States [37, 38]. Thus, there is no clear choice for the value of ℓ so we consider several values for ℓ in our analysis.

4. Results

Our analysis of the PREACH data begins by focusing on the individuals for whom researchers were able to obtain the number of SFDs and PM concentrations for both the baseline and follow-up periods along with certain baseline covariates such as baseline asthma severity. Thus, our analysis focuses on 75 out of 126 trial participants (60%). Like the analysis in Butz et al. [11], we combine the two air cleaner groups in the PREACH study into one group referred to as the air cleaner group giving 46 observations in the treatment group and 29 observations in the control group. Figure 1 summarizes the outcomes of interest by treatment group with the left plot of Figure 1 giving boxplots of the change in SFD from baseline to follow-up (in days) by treatment group. The right plot of Figure 1 gives boxplots of the change in PM concentrations from baseline to follow-up (in μg/m³) by treatment group. Note that the air cleaner group generally has greater increases in SFDs compared with control group and most of the observations for the air cleaner group lie above zero. Also, the air cleaner group appears to have a greater decreases in PM concentrations when compared to control group and most of the observations in the air cleaner group lie below zero.

Figure 1.

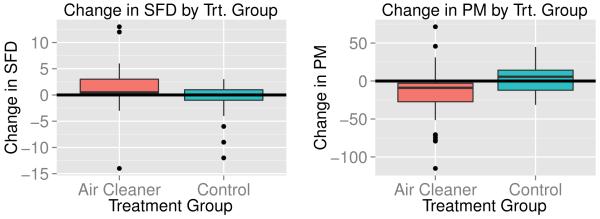
Left plot gives boxplots of the change in symptom free days (SFD) for asthmatic children from baseline to 6 month follow-up by treatment group. Right plot gives boxplots of the change in indoor PM_2.5 concentrations (in μg/m³) from baseline to 6 month follow-up by treatment group.

For our PS analysis, we ran the MCMC algorithm for 200,000 iterations discarding the first 20,000 as burn-in. We let ℓ = −10 in (6), (7) and (8) but look at the sensitivity of the results to the choice of ℓ in Appendix A. We find that our results are generally robust to the choice of ℓ. The baseline covariates used for the PM model in (3) are initial PM_2.5 and initial log₁₀ (cotinine). The baseline covariates used for the SFD model in (1) are initial PM_2.5, initial log₁₀ (cotinine), age, gender, and asthma severity based on national asthma guideline categories: Intermittent Asthma, Mild Persistent Asthma, Moderate Persistent Asthma, and Severe Persistent Asthma [39]. For the PM model, we selected to use only a subset of the covariates used in the SFD model since age, gender and baseline asthma severity are believed to affect the health outcome but are not believed to influence indoor PM levels.

4.1. Principal Stratification Analysis of the PREACH Data

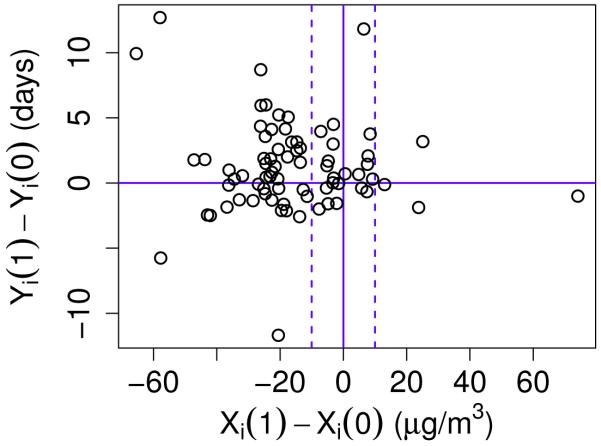
We present the results for our PS analysis assuming ρ = 0.1 in (3), which implies that there is a non-zero correlation between an individual’s PM potential outcome for the treatment group and that same individual’s PM potential outcome for the control group but this correlation is positive and small. We then perform a sensitivity analysis with respect to ρ in Section 4.2. Figure 2 gives the posterior predictive estimates for the difference in the SFD potential outcomes, Y_i (1) − Y_i (0), versus the posterior predictive estimates for the difference in the PM potential outcomes, X_i (1) − X_i (0). For each individual i, the estimate for Y_i (1) − Y_i (0) is found by computing the difference in the potential outcomes for each MCMC iteration and then averaging across the MCMC iterations after discarding burn-in. The same procedure is used to estimate X_i (1) − X_i (0). The dashed vertical lines mark where X_i (1) − X_i (0) = −10 and X_i (1) − X_i (0) = 10.

Figure 2.

Plot of the estimated difference in the SFD potential outcomes between treatment and control case, Y_i (1) − Y_i (0), versus the estimated difference in the PM potential outcomes between treatment and control case, X_i (1) − X_i (0), for each individual i in trial. The solid vertical line denotes where X_i (0) = X_i (1). The left dashed line marks where X_i (1) − X_i (0) = −10 and the right dashed line marks where X_i (1) − X_i (0) = 10. The solid horizontal line marks where Y_i (1) − Y_i(0) = 0.

Using 10 μg/m³ to denote a significant difference in the PM potential outcomes between treatment and control conditions, individuals whose X_i (1) − X_i (0) estimates fall to the left of the dashed lines have PM outcome estimates that would be meaningfully lower when assigned to the air cleaner group. Individuals whose X_i (1) − X_i (0) estimates fall between the dashed lines have PM outcome estimates that would not be meaningfully different when assigned to the air cleaner group compared to control and individuals whose X_i (1) − X_i (0) estimates fall to the right of the dashed lines have PM outcome estimates that would be meaningfully greater when assigned to the air cleaner group compared to control. Note that there are very few individuals for whom we estimate the latter to be the case which is as expected since air cleaners are not likely to increase indoor PM. The estimate for Y_i (1) − Y_i (0) for individuals with X_i (1) − X_i (0) estimates to the left of the dashed lines are of particular interest since we are interested in the health effects for individuals for whom the air cleaner reduces indoor PM. Figure 2 shows that the majority of these individuals also have estimates for Y_i (1) − Y_i (0) > 0 suggesting improvement in the SFD outcome under treatment.

Our causal inference approach also allows us to estimate causal effects as discussed in Section 3.5. Letting ℓ = −10, ERE₋₁₀ is the average effect of the air cleaner on the SFD outcome for all individuals who also would have a meaningful reduction in indoor PM when assigned to the air cleaner. We estimate ERE₋₁₀ to be 1.95 days with a 95% credible interval of (0.14, 3.79) which suggests a rather large increase in SFDs for individuals who are also estimated to have a meaningful reduction in PM when assigned to the air cleaner. We estimate that 59% of the trial participants have a meaningful reduction in PM between treatment and control. This estimate is found by first finding the number of observations for which X_i (1) − X_i (0) < l for each MCMC iteration t, denoted by $n_l^{\left(t\right)}$. We then take the mean of $n_l^{\left(t\right)}∕n$ across all iterations after discarding burn-in where n = 75 is the number of individuals in the trial.

The estimate for the corresponding ENRE when ℓ = −10 is the average causal effect estimate for individuals who would either have no meaningful difference in PM between treatment groups or a meaningful increase in PM under the treatment. We estimate ENRE₋₁₀ to be 0.16 SFDs and the 95% credible interval for ENRE₋₁₀ to be (−2.00, 2.23). This suggests that individuals whose PM would not be meaningfully reduced under treatment do not have a significant improvement in asthma symptoms. Focusing on the subset of individuals who would have no meaningful change in PM between treatment groups, we estimate the ENCE₋₁₀ to be 0.52 SFDs and the 95% credible interval for ENCE₋₁₀ to be (−2.19, 3.19). The relatively large estimate for the ERE compared to the ENRE estimate suggests there is a much greater improvement in asthma symptoms for individuals whose households would have a meaningful reduction in PM compared to those that would not. These results support the hypothesis proposed in Butz et al. [11] that the air cleaner improves asthma symptoms by reducing indoor air pollution.

4.2. Results for different values of ρ

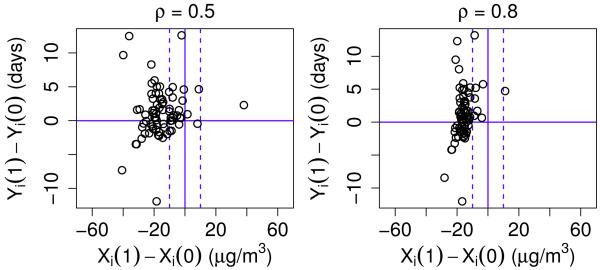
We perform the PS analysis using different values for ρ since, as discussed in Section 3.2, the data does not provide any information on what value of ρ to use in the analysis. We consider four additional values for ρ (−0.1, 0, 0.5, and 0.8). For ρ = 0.5 and 0.8, Figure 3 summarizes the posterior predictive estimates for the difference in the SFD potential outcomes, Y_i (1) − Y_i (0), and the posterior predictive estimates for the difference in the PM potential outcomes, X_i (1) − X_i (0). The plots for ρ = 0 and ρ = −0.1 look similar to Figure 2 and thus are not shown here. Note that the distribution of the estimates for X_i (1) − X_i (0) differs depending on the value of ρ. Compared to Figure 2, the number of individuals whose X_i (1) − X_i (0) estimates are greater than −10 is drastically less when ρ = 0.8 (right plot of Figure 3). Since almost all of the X_i (1) − X_i (0) estimates fall to the left of the dashed lines when ρ = 0.8, it is hard to make comparisons of estimates for Y_i (1) − Y_i (0) between individuals who would have a meaningful reduction in PM and individuals who would not.

Figure 3.

Plots of the estimated difference in the SFD potential outcomes between the treatment and control cases, Y_i (1) − Y_i (0), versus the estimated difference in the PM potential outcomes between the treatment and control cases, X_i (1) − X_i (0), for each individual i in trial when ρ = 0.5 (left plot) and ρ = 0.8 (right plot). In each plot, the solid vertical line denotes where X_i (0) = X_i (1). The left dashed line marks where X_i (1) − X_i (0) = −10 and the right dashed line marks where X_i (1) − X_i (0) = 10. The solid horizontal line marks where Y_i (1) − Y_i (0) = 0.

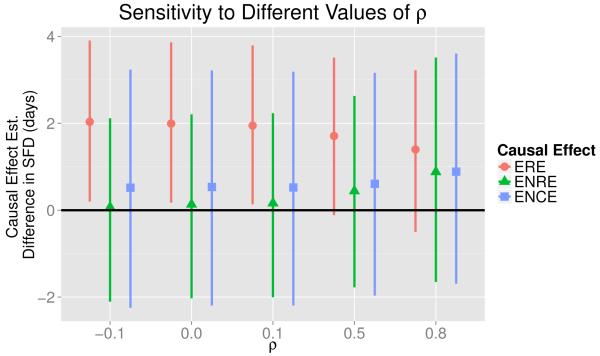
For all values of ρ considered in our analysis, including ρ = 0.1, Figure 4 gives the ERE₋₁₀ estimates (circles) as defined in (6) along with the 95% credible intervals (lines). No matter which value we use for ρ, the estimate for ERE₋₁₀ is relatively large and between 1.4 and 2.0 days. Note that as ρ increases, the ERE₋₁₀ estimate decreases. Figure 4 also summarizes the ENRE₋₁₀ estimates (triangles) for all the values of ρ used in our analysis. For all values of ρ except ρ = 0.8, the ENRE₋₁₀ estimate is much smaller than the corresponding ERE₋₁₀ estimate. Assuming ρ = 0.8 implies that an individual’s PM potential outcome under treatment is extremely correlated with an individual’s PM potential outcome under control. This implies that the air cleaner has little effect on the PM potential outcome levels, which we believe is not a reasonable assumption for the PREACH study. The relatively large ERE estimates and relatively small ENRE estimates suggest that the air cleaner has the strongest effect on health for individuals where it would also meaningfully reduce PM concentrations. The causal effect estimates for individuals whose PM potential outcome would not meaningfully change under treatment (squares) are similar to, but slightly larger than, the ENRE estimates. This suggests that, regardless of the value selected for ρ, the air cleaner would not significantly improve health for individuals whom it also would not meaningfully change the PM potential outcomes.

Figure 4.

Plots of the causal effect estimates for different values of ρ in the PM potential outcomes model in (3). The points give estimates for the expected reduced effect (ERE), the expected not reduced effect (ENRE), and the expected no change effect (ENCE) discussed in Section 3.5. The vertical lines are the corresponding 95% credible intervals.

4.3. Sensitivity Analysis

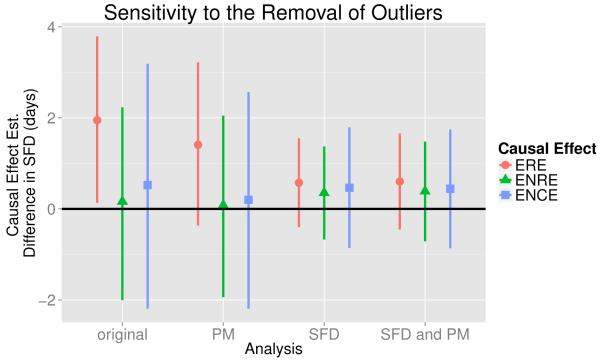
We also perform a sensitivity analysis to see how robust the results are to the removal of outliers. We first perform a PS analysis after removing the observations corresponding to eight individuals whose change in PM appear to be outliers when looking at the boxplot of the distributions of X_i by treatment group given in the right plot of Figure 1 and refer to this as the “remove PM outliers analysis.” Fixing ρ = 0.1, the ERE, ENRE, and ENCE estimates (points) along with their corresponding 95% credible intervals (lines) are given in Figure 5 and denoted by the label ”PM.” The causal effect estimates from the analysis discussed in Section 4.1 are also given in Figure 5 and are denoted by the label ”original.” Note that the ERE estimate for the remove PM outliers analysis is smaller than the corresponding estimate from the original analysis. Though the credible interval does cross zero, the ERE estimate for the remove PM outliers analysis is still relatively large. Figure 5 also shows that the ENRE and ENCE estimates for the remove PM outliers analysis are smaller than their corresponding estimates in the original analysis. However, we still see the pattern of a relatively large ERE estimate and relatively small ENRE and ENCE estimates.

Figure 5.

Plot of the estimated causal effects (points) along with 95% credible intervals (lines) for the sensitivity analysis performed in Section 4.3 with ρ = 0.1 and ℓ = −10. The expected reduced effect (ERE), expected not reduced effect (ENRE), and expected no change effect (ENCE) estimates were calculated from PS analyses performed on data without removing any outliers (original), after removing observations that were outliers in the change in PM distribution (PM), after removing observations that were outliers in the change in SFD distribution (SFD), and after removing observations that were outliers in the change in PM distribution or the change in SFD distribution (SFD and PM).

We also consider two other analyses that remove outliers. For ρ = 0.1, we perform the PS analysis after removing the observations corresponding to the six individuals whose change in SFDs appears to be outliers when looking at the boxplot of the distributions of Y_i by treatment group given in the left plot of Figure 1 and refer to this as the “remove SFD outliers analysis.” The causal effect estimates are summarized in Figure 5 and are denoted by label “SFD.” Likewise, for ρ = 0.1, we perform the PS analysis after removing the observations corresponding to the 13 individuals with values that appear to be outliers when looking at either the change in PM or the change in SFD (only one individual had values which were outliers when looking at both the change in PM and the change in SFD) and refer to this as the “remove SFD and PM outliers analysis.” The causal effect estimates and credible intervals are denoted by label ”SFD and PM” in Figure 5. Note that for both the remove SFD outliers and the remove SFD and PM outliers analysis, the ERE estimates are much smaller than their corresponding values in the original and remove PM outliers analyses but are still positive. Also, for the remove SFD outliers and the remove SFD and PM outliers analyses, the ERE estimates are only slightly larger than their corresponding ENRE and ENCE estimates. Thus, for these two cases, the results no longer strongly support that the air cleaner’s effect on the SFD outcome would be greatest for individuals whom it would also meaningfully reduce PM.

5. Discussion

We used a principal stratification approach to analyze data from a randomized environmental intervention study of children with asthma. We find that amongst children for whom the air cleaner would reduce indoor particulate matter concentrations, the intervention would result in a meaningful improvement of asthma symptoms. We estimate larger health effects for sub-populations of individuals who would have a meaningful decrease in their PM potential outcomes under treatment than for sub-populations that would not which supports the hypothesis that air cleaners improve health by reducing indoor air pollution concentrations. Compared to other environmental intervention study analyses, we estimate a larger effect on SFDs for the air cleaner when we focus on the sub-populations of individuals who would also have a meaningful decrease in indoor PM under treatment. In particular, we estimate the change in SFDs to be 1.95 SFDs more when assigned to the air cleaner compared to control for the sub-population of individuals that would have this meaningful decrease in PM. This estimate is found by defining a meaningful decrease in PM to be a PM potential outcome that would be at least 10 μg/m³ less when assigned to air cleaner compared to control and letting ρ = 0.1.

This estimate is larger than the health effects estimate found by the ITT analysis performed for the same study in Butz et al. [11] that estimates the change in SFD to be 1.12 SFDs more for the combined air cleaner group compared to the control group. This is also larger than the estimated improvement of 0.82 more SFDs per two weeks for asthmatic children in a treatment group receiving an environmental intervention compared to the control group for the study in Morgan et al. [10]. The health effect estimate of a mean difference of 1.95 SFDs between treatment and control over a two week period is similar to the treatment effect estimate found in a study using anti-inflammatory therapies [40]. In this study, they found a mean difference of 2 SFDs per month when comparing a treatment group of asthmatic children receiving an inhaled corticosteroid to a control group given a placebo therapy [40].

Our analysis focuses on a subset of the individuals in the randomized trial that had observations for PM and SFD at both baseline and follow-up and combines two treatment groups from the original study. Thus, there is concern that some covariates may no longer be balanced between the two treatment levels and there is unobserved confounding. There is no evidence to suggest the observations were missing in a systematic way or that combining air cleaner groups will lead to confounding. However, extensions to our analyses are to consider propensity score matching to balance covariates and imputation methods for the missing data.

By fixing ρ in our analysis, we are able to see how the causal effect estimates differ depending on ρ. An alternate approach would be to allow ρ to be a free parameter. However, this makes the relationship between the causal effects and ρ less explicit. Additionally, the fact that for many iterations of the MCMC, we did not estimate any individual to have X_i (1) − X_i (0) < l for ℓ = −25 and −30 when ρ = 0.8 (See Appendix A) illustrates that the values of ℓ for which it is reasonable to estimate ERE_l differs depending on ρ.

As a possible alternative approach, we ran the PS analysis on the PREACH data with ρ a free parameter by assuming an inverse-Wishart prior for the covariance matrix in the PM model in (3). Using the PM model without ρ fixed, we were unable to get the MCMC algorithm to converge. Furthermore, the use of an inverse-Wishart distribution does not allow us to model the correlation and standard deviation components separately. Different results may be obtained if one models the correlation and standard deviation components separately as in Barnard et al. [41]. However, in general, our ability to estimate the correlation and standard deviation components is limited due to the relatively small sample size. As in Schwartz et al. [20], we also ran the PS analysis using a more flexible Dirichlet process mixture (DPM) model for the potential outcomes for indoor PM. For this approach, ρ is a free parameter. The DPM model also relaxes the normality assumption on the PM potential outcomes and provides a more flexible model for the potential outcomes. However, we were similarly unable to get the MCMC algorithm to converge, likely because of the relatively small sample sizes in each of the treatment groups. An extension to our analysis would be to consider non-normal data models for both the SFD and PM potential outcomes. Another extension to our analysis would be to consider two or more environmental factors in the potential outcomes framework. However, we again find the relatively small sample size makes it difficult to fit more complex models and leave these for future analyses.

We found that the ERE, ENRE and ENCE estimates are sensitive to the removal of outliers. They are particularly sensitive to the removal of observations that appear to be outliers when looking at the distribution of the change in SFDs. In the remove SFD outliers analysis, we removed observations from the control group that had relatively large decreases in SFD and removed observations from the treatment group that have relative large increases in SFD giving a smaller mean difference in the SFD outcome for treatment group and the control group (0.85 days) when compared to the original analysis (1.97 days). The mean difference in the SFD outcome when comparing the treatment group to the control group is also smaller for the remove SFD and PM outliers analysis (0.76 days) compared to the original analysis (1.97 days). This may be due to heterogeneity in individuals’ responses to PM reduction. In the remove SFD outliers analysis and the remove SFD and PM outliers analysis, we may be removing individuals that benefit the most from a reduction in PM. It is also important to note that removing outliers reduces the number of observations and increases the uncertainty the parameter estimates. It would be of interest to replicate this analysis for a randomized trial with more observations. In future work, it would also be of interest to perform a simulation study to explore the small sample performance of principal stratification in the context of environmental intervention studies.

Our results are robust to the choice of ℓ used for the cutoff to define a meaningful reduction in PM (Appendix A). Regardless of the value for ℓ, we still have larger ERE estimates than their corresponding ENRE estimates. Our results are also rather robust to the choice of ρ, the correlation between an individual’s PM potential outcomes under treatment and control cases. For all values of ρ, except ρ = 0.8, the PS analysis without removing outliers estimates the ERE to be relatively large (at least 1.5 days) and much larger than the corresponding ENRE estimates (at most 0.79 days). The choice of ρ = 0.8 is rather extreme and suggests a very large correlation between an individual’s PM potential outcomes under both treatment and control conditions. Thus, it implies that there is not a large difference in the potential outcomes for PM between the two treatment levels which is an unreasonable assumption for the PREACH study, since the treatment is believed to affect the PM concentrations.

We elected to use a PS approach to examine the relationship between air cleaners, indoor PM, and asthma symptoms as opposed to using other causal inference tools such as MSM, which would allow for the estimation of indirect effects [25-27]. In particular, a MSM would allow us to estimate the indirect effect of indoor PM on asthma symptoms whereas a PS approach allows us to estimate average causal effects. These average causal effects are not the same as indirect effects unless additional assumptions are made about the relationships between air cleaners, indoor PM, and asthma symptoms [42, 43]. For this reason, there is some concern as to whether a PS analysis is the best approach when your interest is in the effect of the post-treatment variable on the response variable [42, 43]. However, using a causal approach that estimates indirect effects, such as MSMs, requires us to consider indoor PM as a treatment variable itself and assume that there is a process by which we can manipulate the concentrations of indoor PM such that we can achieve a given concentration of indoor PM. Given that the mechanisms that drive indoor PM concentrations are not well understood, we choose not to make this assumption for our analysis and use a PS approach. Furthermore, this assumption may be undesirable in other environmental studies given that the mechanisms that drive many environmental factors are often not well understood. We also note that our PS approach assumes no interaction between baseline PM and treatment. This assumption may be unreasonable for environmental intervention studies with extremely large baseline PM values for some individuals. For these individuals, the reduction in PM caused by the treatment may be negligible compared to the baseline PM resulting in little, if any, improvement in health. Thus, the treatment effect would depend on baseline PM. Also, the correlation between the PM potential outcomes under the control condition and under the treatment condition will be high for individuals with extremely large baseline PM. However, for the levels of baseline PM observed in the PREACH study, we believe the no interaction assumption is reasonable.

In this paper, we demonstrate the effectiveness of using a potential outcomes approach and PS in the analysis environmental intervention studies. However, when applying causal inference techniques to environmental intervention studies, it is important to consider all the assumptions made in the analysis. The PS approach requires an unverifiable ignorability assumption and assumes that, conditional on the covariates in the potential outcomes model, no other covariates confound the treatment and environmental factor relationship or the treatment and health outcome relationship. This assumption may be reasonable for randomized trials, especially for double-blind randomized trials as in Lanphear et al. [13], but becomes more of a concern in observational studies and in randomized trials when there is missing data, different levels of adherence among treatment groups, or poor compliance. To make this assumption more reasonable, it is helpful to have measures of the factors that one believes may confound these relationships in the data and condition on them in the analysis. It is also particularly important to consider whether it is valid to assume that the treatment assignment of one individual, such as receiving an air cleaner or not, will not effect the potential outcomes of other individuals in the study. Environmental interventions at the individual level are not likely to violate this assumption but interventions at the national level, such as setting national air pollution standards, are likely to violate this assumption. We also recommend considering whether it is best to use a discrete variable to model the environmental factor or to use a continuous variable as in Zigler et al. [9] and our analysis. If one assumes a discrete variable for an environmental factor, a simpler model, similar to the model used in Gallop et al. [22], might be appropriate but it does require defining a threshold for the level of the environmental factor that indicates it is meaningfully affected by treatment. If it is unclear what to choose for the threshold, a continuous variable may be preferred. However, regardless of whether the post-treatment environmental factor is treated as discrete or continuous, the causal effect estimates in the PS framework can be used to determine the extent to which the effects of the treatment on the environmental intervention coincides with the effects of the treatment on the environmental factor.

Appendix A

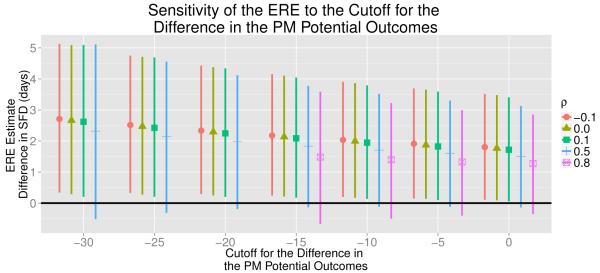
As discussed in Section 3.5, it is not apparent how to specify the value for ℓ when estimating the ERE, ENRE and ENCE. Thus, we find estimates for ERE, ENRE and ENCE specifying several different values for ℓ and 5 different values for ρ. We summarized these estimates for the ERE, ENRE and ENCE in Figures 6, 7 and 8, respectively. For ρ = 0.8, we were unable to estimate ERE for ℓ = −30, −25, and −20 because, for many iterations of the algorithm, no individual was estimated to have X_i (1) − X_i (0) < l. Figure 6 illustrates that as ℓ approaches 0, the ERE estimates decrease. This may be due to the fact that as the cutoff ℓ approaches 0, the individuals included in the principal strata may only have a small differences in their PM potential outcomes between treatment and control conditions. Thus, we may be including individuals for whom there would not be a meaningful reduction in PM under treatment in the principal strata, which may cause us to underestimate the causal effect for sub-population of individuals that would have a meaningful reduction in PM under treatment. Yet, for most of the values for ℓ and ρ, the ERE estimates are relatively large and all the ERE estimates are greater than one. It is important to note that as ℓ changes, the percent of trial participants who are estimated to fall into the sub-population of individuals that would experience a meaningful reduction in PM changes. With fewer trial participants in the principal strata, there is more uncertainty in the ERE estimates, resulting in wider credible intervals. There are far fewer trial participants estimated to be the sub-population of individuals who would experience a meaningful reduction in PM when ℓ = −30 (39% of trial participants) then when ℓ = 0 (71% of trial participants). Thus, one needs to be careful when making inference on the sub-groups in the principal stratification analysis [44]. Additionally, one needs to exercise care when comparing effects estimated in different sub-groups, as these groups may differ from each other on unmeasured covariates.

Figure 6.

Plot of the estimated expected reduced effect (ERE) along with 95% credible intervals for 5 different values of ρ (−0.1, 0, 0.1, 0.5, and 0.8) and 7 different values for the cutoff for the difference in the PM potential outcomes (ℓ). For ρ = 0.8, we were unable to estimate the ERE for ℓ = −30, −25, and −20 because, for many iterations of the algorithm, no individual was estimated to have X_i (1) − X_i (0) < l for these values of ℓ.

Figure 7.

Plot of the estimated expected not reduced effect (ENRE) along with 95% credible intervals for 5 different values of ρ (−0.1, 0, 0.1, 0.5, and 0.8) and 7 different values for the cutoff for the difference in the PM potential outcomes (ℓ). For ρ = 0.8, we were unable to estimate ENRE for ℓ = −5 and 0 because, for many iterations of the algorithm, no individual was estimated to have X_i (1) − X_i (0) ≥ l for these values of ℓ.

Figure 8.

Plot of the estimated expected no change causal effect (ENCE) along with 95% credible intervals for 5 different values of ρ (−0.1, 0, 0.1, 0.5, and 0.8) and 5 different values for the cutoff for the absolute value of the difference in the PM potential outcomes (ℓ).

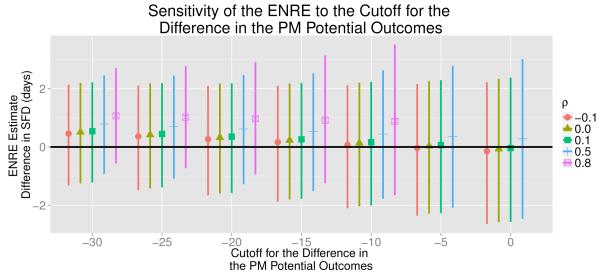
Figure 7 summarizes the ENRE estimates for 7 different values of ℓ and all the values of ρ used in our analysis. For ρ = 0.8, we were unable to estimate the ENRE for ℓ = 0, and −5 because, for many iterations of the algorithm, no individual was estimated to have X_i (1) − X_i (0) ≥ ℓ. Figure 7 shows that as ℓ decreases and moves farther away from 0, the ENRE estimate increases. In this case, as ℓ decreases, we are more likely to include people in the principal strata that actually would have a meaningful reduction in PM. Thus, our estimate for ENRE may be inadvertently inflated. For all values of ρ except ρ = 0.8, the ENRE estimates are relatively small, which suggests that there would be little, if any, improvement in asthma symptoms for individuals who would not experience a meaningful reduction in indoor PM under treatment. For all values of ℓ and ρ except when ρ = 0.8, the ENRE estimates are much smaller than the corresponding ERE estimates. The relatively larger ERE estimates compared to the relatively smaller ENRE estimates suggest the air cleaner would have the strongest effect on health for individuals where it would also meaningfully reduce PM concentrations.

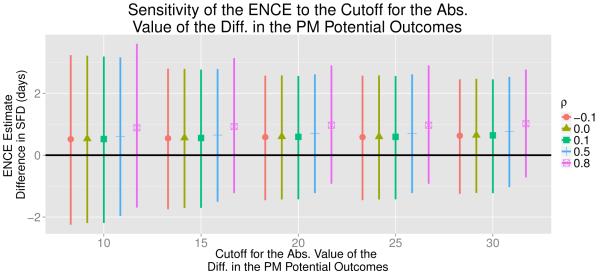
Figure 8 summarizes the ENCE estimates for 5 different values of ℓ (ℓ = 10, 15, 20, 25, and 30) and all the values of ρ used in our analysis. For ℓ = 5, we were unable to estimate the ENCE because, for many iterations of the algorithm, no individual was estimated to have |X_i (1) − X_i (0)| < |ℓ|. Except when ρ = 0.8, these average causal effect estimates of the air cleaner on SFDs for the subpopulation of individuals whose PM would not meaningfully change under treatment are relatively small and similar in magnitude to the ENRE estimates.