Modeling thermophoretic effects in solid-state nanopores

Abstract

Local modulation of temperature has emerged as a new mechanism for regulation of molecular transport through nanopores. Predicting the effect of such modulations on nanopore transport requires simulation protocols capable of reproducing non-uniform temperature gradients observed in experiment. Conventional molecular dynamics (MD) method typically employs a single thermostat for maintaining a uniform distribution of temperature in the entire simulation domain, and, therefore, can not model local temperature variations. In this article, we describe a set of simulation protocols that enable modeling of nanopore systems featuring non-uniform distributions of temperature. First, we describe a method to impose a temperature gradient in all-atom MD simulations based on a boundary-driven non-equilibrium MD protocol. Then, we use this method to study the effect of temperature gradient on the distribution of ions in bulk solution (the thermophoretic effect). We show that DNA nucleotides exhibit differential response to the same temperature gradient. Next, we describe a method to directly compute the effective force of a thermal gradient on a prototypical biomolecule—a fragment of double-stranded DNA. Following that, we demonstrate an all-atom MD protocol for modeling thermophoretic effects in solid-state nanopores. We show that local heating of a nanopore volume can be used to regulate the nanopore ionic current. Finally, we show how continuum calculations can be coupled to a coarse-grained model of DNA to study the effect of local temperature modulation on electrophoretic motion of DNA through plasmonic nanopores. The computational methods described in this article are expected to find applications in rational design of temperature-responsive nanopore systems.

1 Introduction

Nanopores in thin synthetic membranes have emerged as a convenient tool for single molecule characterization experiments [1–3]. Driven by a gradient of the electrostatic potential, charged biomolecules, such as nucleic acids and proteins, can be transported through a nanopore one after another, producing transient reductions of the nanopore ionic current that report on the presence, abundance and, in some cases, the chemical structure of biomolecules. One extreme application of the nanopore method is DNA sequencing [4–6], where the chemical identity of individual DNA nucleotides is determined by the level of the residual ionic current flowing through a nanopore blocked by a DNA strand [7].

The rate of nanopore transport is conditioned by the competition of the electrophoretic force driving a biomolecule through a nanopore and the friction force opposing the electrophoretic motion [8]. Reflecting the charge, size and shape of a biomolecule, the transport rate can vary over several orders of magnitude [9]. The nanopore transport can also be highly selective [10–14]. However, controlling the rate and selectivity of the nanopore transport remains a major challenge. One possibility is to use local temperature gradients that can impart forces on the translocating molecules in a manner that depends on their chemical makeup.

Temperature has already been explored as a mechanism to control molecular transport through nanopores. Lowering the temperature was observed to significantly slow the process of DNA translocation in both biological [15] and solid-state [16] nanopores. Gating of the transport through a biological nanopore α-hemolysin was realized by incorporating temperature-sensitive peptides that opened and closed the nanopore depending on the temperature of the environment [17]. Solid-state nanopores were shown to change their effective dimensions by means of a thermoresponsive coating [18], which enabled regulation of the molecular transport, in particular the ionic current [19–22].

Until recently, the effect of temperature gradients in nanopore transport remained unexplored. Recent advances in nanoscale fabrication have enabled placement of small metallic particles in proximity to nanopores[23,24]. Plasmonic heating [25,26] of such particles was shown to produce steep temperature gradients [27], offering a new means for single molecule manipulation—the nanoscale thermophoresis [28–31].

2 Brief review of thermophoresis

Motion of species in temperature gradients, known as thermophoresis or the Soret effect, is an omnipresent phenomenon that emerges in electrolyte [32–36] and polymer [37,38] solutions, ensembles of micron-size polystyrene particles [39] and nanometer-sized micelles [40]. Since its discovery in 1856 [32], experiments have found that magnitude and direction of motion produced by steady temperature gradients depend sensitively on the physical properties of the solute species and the solvent. Among the many factors that affect thermophoresis are the temperature of the solution [41], the concentration of solutes [42–46], their charge [47], size [48], hydration shell [49], and masses and moments of inertia [50] as well as the interactions between different solutes in the solvent [51]. In recent years, thermodiffusion emerged as a tool for ion separation [41], polymer characterization (thermal field-flow fractionalization) [52], DNA stretching [53] and control of DNA transport [30, 28]. Thermodiffusion is also speculated to play a significant role in prebiological evolution [54,55].

Despite the long history of experimental observations and extensive theoretical efforts, understanding of the microscopic mechanisms of the Soret effect is far from being complete [56,57]. Several models describing thermodiffusion in the same system are still under consideration. In the most general case, the mass flow J of thermally diffusing species can be written as

$$J=-\rho D\nabla c-\rho c(1-c)D_T\nabla T,$$ (1)

where D is the ordinary diffusion coefficient, ρ is the density of the solution, T is the temperature, and D_T and c are the thermal diffusion coefficient and mass fraction of the species, correspondingly. The relation of thermal to normal diffusion coefficients, S_T = D_T/D, is called the Soret coefficient.

To describe the origin of thermal diffusion of dissolved ions, models based on radiation pressure theory [45] and the heat of transport concept [51] were developed. A considerably greater number of models have been proposed to describe thermal diffusion of polymers in aqueous solutions. The list of proposed models includes: a kinetic model based on activation energies for viscous flow and polymer-solvent interactions [38]; a model based on temperature-dependent osmotic-pressure gradients due to nonuniform London-van der Waals interactions [58]; a kinetic model based on activation energies for diffusive flow in the solvent [59]; a model based on activation energies for viscous flow of individual polymer segments [60]; a model based on nonuniform velocity distributions of the solvent surrounding the polymer [39]; a model based on radiation pressure or acoustic sound waves [45]; a model based on temperature dependence of the polymer-solvent interaction parameter [61]; a two-chamber lattice model [62], and a bead-spring model [63]. But of all these models, only that of [38] can predict the negative Soret effect in dilute polystyrene solutions, and even that model fails to correctly describe the magnitude and direction of the effect for many other polymers.

A number of models have been developed to describe thermodiffusion of particles in liquids, e.g. models based on: an interfacial-tension driven mechanism (Marangoni-type) [64]; the concept of asymmetrical electric potential near charged particles [47]; the formalism of hydrodynamic fluctuations theory [65]; radiation pressure concepts [45]; the formalism of local pressure gradients produced by nonuniform London-van der Waals interactions [66]; the concept of minimization of the free energy of the double-layer [67,68], and still other ideas [69,70]. Most of these models, however, predict different thermodiffusive behavior for the same systems.

Computer simulations present a reliable way to verify, test and even stimulate the development of new theoretical approaches. Various MD simulation methods have already been tested: non-equilibrium MD simulations (NEMD) [71,72], reverse NEMD [73], and equilibrium MD [74,75]. The essence of non-equilibrium MD is the presence of an external bias that drives the system away from its thermodynamic equilibrium. In case of thermodiffusion, such a bias could be a non-uniform distribution of temperature. However, introducing such a non-uniformity is not a straightforward task. In the reverse NEMD algorithm, the real-life cause-and-effect picture is swapped. For the study of thermal diffusion, the heat flux is imposed on the system whereas the temperature gradient is obtained from the simulation. Both NEMD and reverse NEMD methods typically yield results consistent with each other. Equilibrium MD simulations allow computation of the Soret effect using the Green-Kubo formalism [74].

The bulk of computational methods previously employed to study thermophoresis lacked explicit description of the solvent molecules. Instead, a solution was described as a continuous medium in which an imposed temperature gradient produced thermal forces that acted on the solute particles or molecules. On the one hand, such an approach offered flexibility in choosing a functional form to describe the thermal force. On the other hand, not only does such an approach becomes invalid when the size of the solute approaches the size of the solvent molecules, but the method offers only a test of the ad hoc assumptions about the functional form of the thermal force, making its evaluation impossible a priori.

All-atom molecular dynamics simulations explicitly account for the solvent molecules surrounding the solute species, allowing the thermophoresis process to be fully described at the microscopic level. Such a detailed description requires significant computational power, which became available only recently. The explicit description of solvent molecules allows one to compute practically any quantity that has been experimentally measured or theoretically considered. The same all-atom simulation simultaneously tests a number of theoretical models. Furthermore, physical properties of the solvent or the solute can be easily adjusted in the MD method, which allows one to determine how such changes affect the response of the system to thermal gradients.

3 Modeling methods

In this article, we describe several protocols for modeling thermophoretic effects using MD simulations. By explicitly considering every atom of the solvent and solute molecules, all-atom molecular dynamics simulations allow to observe directional motion of molecules in a temperature gradient. With the advent of high-performance computer codes [76] and massively parallel supercomputer systems, thermophoresis can be finally simulated at the ultimate, atomic resolution.

Our description of modeling thermophoretic effects is organized as follows:

Bulk solutions

In this section we introduce multiple temperature baths approach to model thermophoretic effects using all-atom MD. We demonstrate the applications of the method to the study of electrolyte solutions, mixture of DNA nucleotides and direct measurement of the effective thermophoretic force on double-stranded DNA.

Solid-state nanopore systems

In this section we show that a similar modeling approach can be applied to solid-state nanopore systems. We compute temperature and concentration profiles of solute species to verify the presence of temperature gradients and demonstrate the effect of temperature gradients on ionic current.

Device-level simulations

Finally, we use the results of direct thermophoretic force measurements and continuum modeling performed in COMSOL to run μs-long coarse-grained (CG) simulations of double-stranded DNA permeation through plasmonic nanopores [23].

3.1 Thermophoretic effects in bulk solutions

The study of thermophoretic effect begins with describing the behavior of single particles or molecular species under a constant temperature gradient. In this section we describe the methods of producing constant temperature gradients in all-atom MD, determining the Soret coefficients of ions and DNA nucleotides and measuring the effective thermophoretic force on double-stranded DNA (dsDNA).

3.1.1 Temperature gradients in all-atom MD

In a thermally conducting media, temperature gradients are established between boundaries held at different temperature. Bulk solutions, however, lack any internal boundaries by definition. Furthermore, periodic boundary conditions, which are typically employed in all-atom MD, imply absence of external boundaries as well. Therefore, some mathematical abstractions have to be employed when modeling such systems using an all-atom level. In a boundary-driven non-equilibrium molecular dynamics (BD-NEMD) [77], boundaries are modeled as regions where local mechanisms control temperature, chemical potential, concentration, or any other experimentally measurable quantity. BD-NEMD has been successfully applied to model heat conduction [78–80] in fluids and study polarization of fluids induced by thermal gradients [81,82].

Realizing temperature gradient in all-atom MD simulations requires a mechanism for maintaining spatially separated regions of the system at different temperatures. One such approach is to apply individual thermostats to fixed sets of atoms (fixed thermostats). The atoms can be additionally restrained to remain within the same temperature-controlled volumes of the system (for example, a solid-state membrane) or to form compact objects that can move about the system (for example, freely diffusing particles subject to radiative heating). Alternatively, one can employ thermostats that act on every particle in predefined volumes (local thermostats). In such a case, atoms can enter and leave the temperature controlled regions and can be subject to the thermostats only within those regions. Modeling the thermophoretic effect in all-atom MD simulations can employ either or both of the above approaches, depending on the nature of the system or process considered.

All simulations reported in this article were performed using the molecular dynamics program NAMD2 [76]. Unless stated otherwise, the simulations employed periodic boundary conditions, CHARMM27 [83] parameter set for water, ions and nucleic acids, and CHARMM-compatible parameters for silicon nitride [11]; ion-pair specific corrections to the Lennard-Jones parameter σ [84], a 2–2–6-fs multiple timestepping, SETTLE algorithm to keep water molecules rigid [85], RATTLE algorithm to keep rigid all other covalent bonds involving hydrogen atoms [86], a 7–8 Å cutoff for van der Waals and short-range electrostatic forces. In the simulations of bulk solutions we instructed NAMD2 to remove net momentum before every full electrostatics calculation with the zeroMomentum [87] feature. Long-range electrostatic interactions were computed using the particle mesh Ewald (PME) method [88] over a 1.0 Å resolution grid.

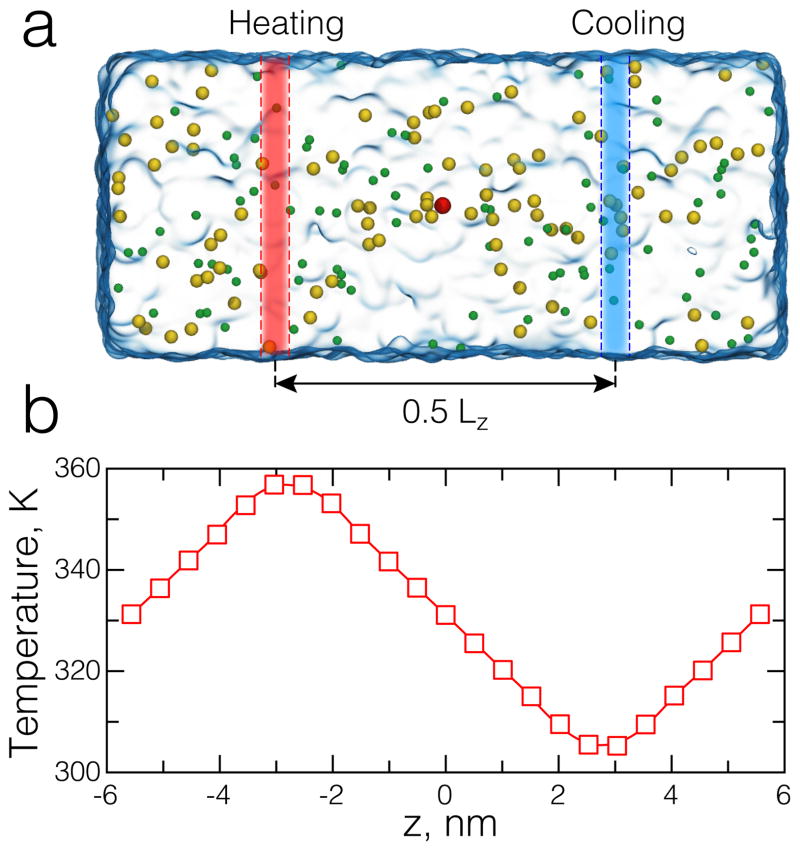
To compute temperature distributions, we recorded the velocities of all atoms along with their coordinates. Then, the system was split into bins and instantaneous local temperature was computed as: T = 2 K/(N_DOF k _B), where K and N_DOF are the total kinetic energy and the number of degrees of freedom, respectively, for all atoms in a particular bin and k_B is the Boltzmann constant. In bulk solutions (Figure 1b), the temperature was averaged over 5 Å-wide slabs arranged perpendicular to the z-axis; in solid-state nanopore systems (Figure 5a,b), we used cubic bins with a side of ~ 5 Å, which allowed us to differentiate between temperature profiles through the membrane and the nanopore. Although stable temperature gradients established in our systems within ~ 1 ns from the beginning of the simulation, we typically performed averaging over 10 ns intervals.

Fig. 1.

Dual temperature bath all-atom MD simulation. (a) All-atom system containing 1 M aqueous solution of potassium chloride. The system is a hexagon prism. Semi-transparent red and blue stripes illustrate two thermostat regions maintained at different temperature (T_H = 365 K and T_C = 295 K). Water is shown as a semitransparent molecular surface. Potassium and chloride ions are shown as green and yellow spheres, respectively. (b) Steady-state distribution of temperature in the system shown in panel a. The temperature is averaged over slabs of equal thickness (5 Å).

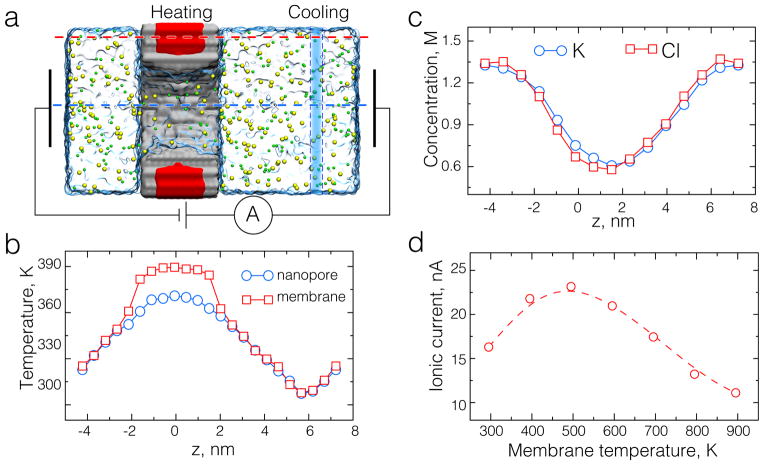
Fig. 5.

All-atom MD simulations of locally heated solid-state nanopores. (a) Cut-away view of an all-atom model of a solid-state nanopore. A Si₃N₄ membrane is shown as a gray molecular surface. Atoms of the Si₃N₄ membrane located 5 Å away from the membrane surface (shown with red) are thermostatted at 395 K. Potassium and chloride ions are shown as green and yellow spheres, respectively. Water is shown as a semitransparent molecular surface. The blue rectangle illustrates a thermostat region where temperature is set to 295 K. (b) The profile of local temperature along the axis of the nanopore (blue) and through the solid-state membrane (red). The profiles were computed using cubic bins ~ 5 Å on side; centers of the bins lie along the dashed red and blue lines shown in panel (a). (c) The concentration of ions along the nanopore axis in a locally heated solid-state nanopore system; the temperature profile is shown in panel b. (d) Ionic current through a locally heated Si₃N₄ nanopore system as a function of the Si₃N₄ temperature at a transmembrane bias of 1.0 V.

To define regions where local thermostats couple to the bulk system, we used the Grid Forces feature [89] of NAMD2. This feature was originally designed to apply forces to specific sets of atoms based on grid-based potentials. We modified the code of the Grid Forces feature and instructed NAMD2 to couple atoms inside the volumes defined by the grid-based potentials to local thermostats. The protocol allows us to use any local temperature control mechanisms, couple them to arbitrary sets of atoms, and provides multiple ways to define target temperatures. As particles in our bulk systems were expected to enter and leave the volumes of predefined temperature we chose to use Lowe-Andersen [90] dynamics for local temperature controls. No special regulation of energy injection and withdrawal has been made in the thermostatted regions. However, once established, the temperature distributions did not change in the course of the simulations indicating that energy injection in one region compensated energy withdrawal from the other. As a results, the temperatures established in the thermostatted regions did not reach their target values. Typically, the “heated” region was cooler and the “cooled” region was hotter than initially planned. The difference between the target and established temperatures were approximately equal in magnitude and did not exceed several percents of the target temperature values.

In the simulations of bulk solutions, the thermostats were coupled to water molecules only. In practice, the target temperature was specified using a temperature factors column of Protein Data Bank file, which was prepared for each thermostat individually. In every such file, temperature factors of all water molecules were set to identical values—target temperature of the thermostat however, only those molecules that located within the thermostat volume defined by the grid potentials were subject to the thermostat.

3.1.2 The effect of temperature gradient on ionic solutions

Using the MD protocols described above, we simulated the thermophoretic effect in 1 M solutions of KCl, NaCl, and LiCl. In these simulations we employed Joung and Cheatham [91] parameter set for ion interactions and custom NBFIX corrections [84]. The setup of the simulations is illustrated in Figure 1a: a box (hexagonal prism) of water with dissolved ions is subject to dual temperature control. Using the Grid Forces feature, we defined two 5 Å-wide temperature-controlled slabs. The slabs, effectively infinite in xy-plane and perpendicular to the z axis, were positioned so that the distance between their centers is half the system size along the z axis (0.5 L_z ), see Figure 1a. The temperatures of the hot and cold regions were set to 365 and 295 K, respectively. Under periodic boundary conditions, such a placement of local thermostats results in formation of two equal-magnitude opposite-direction temperature gradients between the regions, Figure 1b.

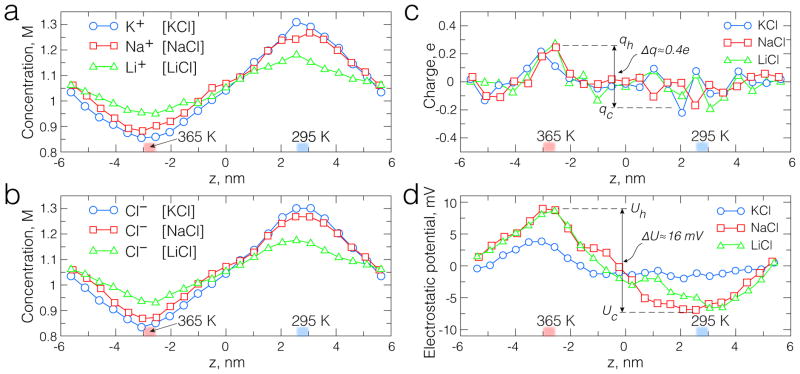
The results of our dual temperature control simulations are shown in Figure 2. For all ionic solutions, we observed positive thermodiffusion, i.e. ions moved away from the slab with higher temperature, increasing the concentration in the cooled volume, Figure 2a. The simulations have shown a clear difference in the thermophoretic effect experiences by different ions: potassium ions were most responsive to the temperature gradient, followed by sodium and then lithium ions. The thermophoretic response of anions was strongly correlated with that of cations: the distributions of chloride ions in our simulations followed the distributions of cations and was different for all three ionic solutions, Figure 2b. Local electric neutrality was at the origin of such coupling. Figure 2c shows the distribution of the electric charge in the simulations of bulk solutions. The solutions appear to be electroneutral at the scale of 5 Å, although some minor separation of the electrical charge is apparent, as evident from the plot of the average electrostatic potential, Figure 2d. The maximum difference in the electrostatic potential of the two temperature controlled regions was observed in the simulations of 1 M NaCl and LiCl solutions and corresponded to an effective electric bias of ~ 16 mV. The response of KCl solution was significantly less pronounced, indicating the importance of ion-specific interactions.

Fig. 2.

The effect of temperature gradient on ion distribution. (a–b) The local concentration of potassium, sodium and lithium ions (a) and chloride ions (b) in the dual-temperature simulations of 1 M KCl, NaCl and LiCl. Each system was simulated for at least 40 ns. The ion concentration was averaged over 5 Å slabs arranged perpendicular to the z-axis. The number of ions within each bin was averaged over the corresponding MD trajectory and divided by the bin volume. (c) The local electric charge of ions in the dual-temperature simulations of 1 M KCl, NaCl and LiCl. (d) The profile of the electrostatic potential along the temperature gradient. The maximum/minimum values are marked with q_h/q_c in panel c and U_h/U_c in panel d for the charge and potential distributions, correspondingly.

3.1.3 The effect of temperature gradient on the distribution of DNA nucleotides

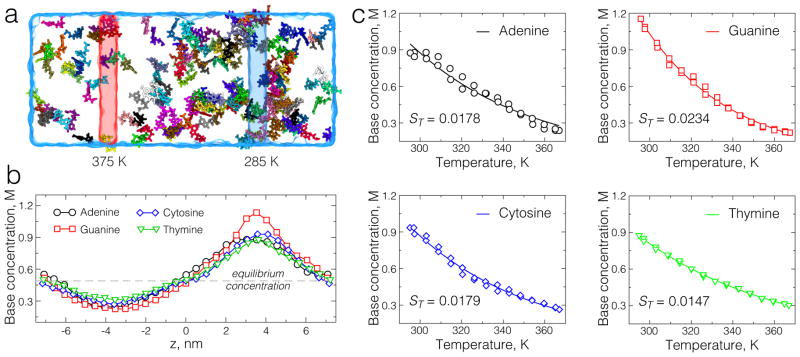
Separation of DNA nucleotides according to their chemical makeup has been the key problem in the field of DNA sequencing. We have applied our dual bath temperature protocol to determine if DNA nucleotides of different types respond differently to the same temperature gradient. Figure 3a shows a snapshot from an all-atom MD simulation of a concentrated (0.5 M) solution of adenine nucleotides and potassium counterions. As in the case of ionic solutions, we found DNA nucleotides to diffuse away form the region of higher temperature, thus exhibiting positive thermodiffusion. The concentration profiles extracted from the simulations of A, C, G and T DNA nucleotides are shown in Figure 3b. Despite having the same starting concentration, the resulting concentration profiles appear to be different, indicating that response of DNA nucleotides to the same temperature gradient depends on the nucleotide type. The Soret coefficients for individual nucleotide species can be extracted from the dependence of the nucleotide concentration on the local temperature [56], see Figure 3c.

Fig. 3.

Dual temperature control simulation of DNA nucleotide solutions. (a) All-atom system containing 0.5 M solution of adenine nucleotides and potassium counterions. Water is shown as a semitransparent molecular surface. Temperature controlled regions are highlighted as semitransparend red and blue rectangles. Individual bases are shown in different colors. (b) The concentration profiles of A, C, G, and T nucleotides along the temperate gradient. The profiles were computed using 5-Å slabs normal to the direction of the temperature gradient (the z axis). Each profile was determined from a separate ~ 70 ns-long simulation. (c) The Soret coefficients extracted from the fit of the dependence of nucleotide concentration on local temperature value c = c₀e^−S_TT.

So far, we have applied our dual temperature bath simulation protocol to the study of the thermophoretic effect in solutions where more than one molecular specie was present (for example, cations and anions in the case of bulk electrolytes). These simulations, however, measured the thermophoretic response of the mixture, which still needs to be connected to the thermophoretic response of individual molecular species. It can be desired to measure the thermophoretic effect for individual species or particles. The most straightforward setup for doing that is to place a single solute particle (ion, monomer, etc.) between the temperature controlled regions and observe its stochastic motion. The motion of an unrestrained particle will be highly diffusive and, as a consequence, the particle will move in and out of the thermostatted regions, experiencing a changing temperature gradient. To draw statistically significant conclusions about the magnitude of the thermophoretic effect, a large number of independent simulations will be required. While straightforward for modeling the thermophoretic effect of uncharged particles, simulations of a single charged particle should be done with care to account for the long-range electrostatic interactions of the particle with its periodic images.

3.1.4 Direct measurements of the thermophoretic force

The dual temperature bath protocol permits direct measurement of the effective thermophoretic force. To perform such measurements, one needs to restrain a single particle to a reference point via harmonic potential. The average displacement of the particle from its equilibrium position would then indicate the effective force experienced by the particle due to the thermal gradient. Due to the small values of the forces (typically ~ pN), such an approach requires a large number of simulations to obtain a statistically significant value of the force. Since many identical systems can be simulated in parallel, these calculations are well within the reach of modern computer systems.

The typical distribution of temperature in a dual temperature bath simulations, Figure 1b, has two regions of equal-magnitude, opposite direction constant temperature gradients. By placing a molecule in one of these regions and harmonically restraining it to its initial position, Figure 4a, one can estimate the effective force it experiences as F_th = −F_sp = kΔz, where F_th and F_sp are the thermophoretic and harmonic spring forces, respectively, k is the spring constant of the harmonic potential and Δz is the displacement of the molecule from its initial (Δz = 0) position along the direction of the temperature gradient (z axis). Such simulations would provide a direct measurement of the force experienced by the molecule due to the temperature gradient. Since the extent of the regions having a constant temperature gradient depends only on the dimensions of the system and the parameters of the local thermostats, such a protocol can be applied to a molecule of an arbitrary size.

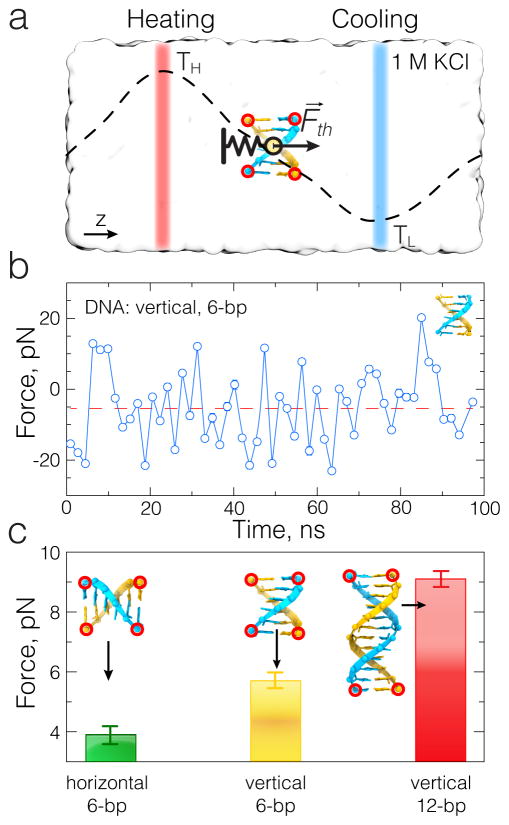
Fig. 4.

Direct measurement of the thermophoretic force using the dual temperature bath setup. (a) Schematic illustration of the direct measurement approach. A model molecule (6 base-pairs fragment of dsDNA) is placed in electrolyte solution shown as a semi-transparent molecular surface. The molecule is harmonically restrained to have its z coordinate equidistant from the two thermally-regulated subvolumes of the system (highlighted as semi-transparent red and blue slabs). The mean displacement of the molecule along the direction of the temperature gradient $\overline{\mathrm{\Delta }\mathrm{z}}$ reports the direction and magnitude of the effective thermophoretic force: $\overline{F_{\mathrm{th}}}=k\overline{\mathrm{\Delta }\mathrm{z}}$, where k is the spring constant of the harmonic restrain. (b) A typical time dependence of the effective force experienced by the model molecule (6-bp dsDNA) in a dual bath thermostat simulation. Each data point in the trace corresponds to the average of 400 instantaneous force measurements recorded during a 2 ns interval. (c) The average force experienced by three fragments of dsDNA in a temperature gradient of 0.42 K/Å( T = 25 K over 6 nm distance). The linear increase of the effective force with the number of basepairs is consistent with the expectations. The dependence of the effective force on the orientation of DNA signifies the asymmetric structure of dsDNA.

Figure 4 illustrates direct measurement of the thermophoretic force on fragments of dsDNA 6 and 12 base pairs long in two orientations relative to the direction of the temperature gradient. In each simulation, the DNA fragments were submerged in 1 M KCl solution. Four carbon atoms (one in each of the DNA’s 5′ and 3′ ends) were restrained in xy plane to preserve DNA orientation during the simulations. The center of mass of the entire DNA molecule was harmonically restrained (k ≈ 10 pN/Å) to its equilibrium position with steered molecular dynamics (SMD) feature of NAMD2. In these simulations, we employed CHARMM36 [92] parameters set to describe interactions between water, ions and nucleic acids, and corresponding ion-pair specific corrections to the Lennard-Jones parameter σ [84]. The fragments were prepared using the 3D-DART program [93]. The sequence of one of the 6 base-pair strands was chosen as 5′–AGGACT–3′; the sequence was duplicated for the 12 base-pair DNA fragment, 5′–AGGACTAGGACT–3′. To prevent dsDNA molecules from melting, hydrogen bonds within the basepairs were reinforced using the Extrabonds feature of NAMD. The system size (~60×60×120 ų) was large enough for every DNA fragment to fit into the the region of a constant temperature gradient. Although it was possible to place a second DNA fragment in the region of the opposite temperature gradient (see Figure 4a), one would have to consider possible interactions between the DNA fragments and therefore we refrained from doing that.

A typical trace of the effective force (along z axis) on a 6-bp DNA fragment oriented perpendicular to the direction of the temperature gradient is shown in Figure 4b. The force fluctuates considerably, requiring averaging times of 100 ns or longer to obtain statistically significant values of the mean force. The results of these simulations suggest that the thermophoretic force not only linearly depends on the length of the DNA fragment but also on its orientation. The above estimates of the thermophoretic force will be used in our CG description of dsDNA transport through locally heated solid-state nanopores.

3.2 All-atom studies of thermophoresis in nanopore systems

Multiple thermostats can be combined to study the effect of temperature on the electrophoretic transport through solid-state nanopores. One such simulations is illustrated in Figure 5, where the membrane surrounding the nanopore is considered to be a heat source. The point source nature of heating justifies the use of linear gradient approximation [28], although the multi-thermostat method is not limited to realizing linear temperature gradients.

The setup of our dual bath temperature control is shown in Figure 5a. A 3.5 nm-thick Si₃N₄ membrane was built according to procedures described elsewhere [11]. A double-cone pore of a 3.5 nm-diameter in its center and 4.3 nm-diameter openings at both sides was cut by removing atoms from the membrane. The system was then solvated using the Solvate plugin of VMD [94]. Following that, the system was neutralized by adding K⁺ and Cl⁻ ions in the amounts necessary to produce a 1 M solution. The final system was a 117 Å-long hexagonal prism with a side of 79 Å; hexagonal periodic boundary conditions were applied in the xy-plane. In all simulations of the Si₃N₄ systems, atoms of the membrane were harmonically restrained to their initial coordinates. The spring constant of the harmonic constraints that were applied to the surface or bulk atoms of the membrane was 10 and 1 kcal/(mol·Å ²), respectively.

To generate temperature gradients in the system, a set of Si₃N₄ membrane atoms was coupled to a Langevin thermostat. The second, local Lowe-Andersen, thermostat controlled the temperature of water molecules in a 5-Å-wide slab away from the membrane. The slab was arranged parallel to the membrane and positioned such that under the periodic boundary conditions two equal-magnitude opposite-direction temperature gradients were formed on both sides of the membrane, see Figure 5b. Water and ions could freely enter and exit the volume subject to the Lowe-Andersen thermostat, whereas the Langevin thermostat was applied to a fixed set of membrane atoms independent of their position.

One-dimensional profiles of temperature averaged over bins, the centers of which pass through the nanopore and membrane, are shown in Figure 5b. The difference in the profiles can be attributed to the difference in vibrational properties of membrane and solution (thermal boundary resistance). As in simulations of bulk ionic solutions, we observe positive thermodiffusion: both ionic species moved away from the higher temperature region, producing a clear well and a peak in the concentration profiles, see Figure 5c.

The dual bath method is well suited for a study of the thermophoretic effect on electrophoretic transport in solid-state nanopore systems. In such systems, the motion of ions through the nanopore is driven by a transmembrane gradient of the electric potential. Local heating and the associated thermophoretic forces can be used to modulate the electrophoretic transport. We performed all-atom MD simulations of Si₃N₄ nanopore system subject to the dual temperature bath control under an external electric bias of 1 V, see Figure 5a. The transmembrane bias generates the ionic current, which we find to depend on the distribution of temperature, Figure 5d. Interestingly, the ionic current exhibits a nonlinear dependence on the membrane temperature. Certainly, the heating conditions used in these exploratory simulations are beyond the experimental ones.

The temperature gradients in nanopore systems determine the conformation and electrophoretic mobility of molecules passing through the nanopores. In our studies of a 54-nucleotide single-stranded DNA molecule in locally heated nanopore systems [28] we observed rapid (~20 ns) and significant stretching (unwinding) of the molecule. Upon switching off the heat source, DNA relaxed to a compact structure over a much longer period (~200 ns). Local heating was also observed to increase the speed of DNA transport while unraveling the DNA molecule, suggesting that slow single-file translation of ssDNA can be achieved by combining local heating with ultra-low (10 mV or less) transmembrane biases.

3.3 Device-level simulations of the thermophoretic effect

To study the effect of thermophoresis on nanopore transport at the device scale, i.e. 100 nm and up, the all atom MD approach is prohibitory expensive. In our previous study, we have shown that the temperature distributions derived from continuum and all-atom models are in good agreement with one another [28]. Thus, instead of simulating the heat transport using an all-atom model, it is computationally more efficient to determine the distribution of temperature from a continuum model and apply it in a CG simulation of nanopore transport [28]. In the case of a CG model (which typically lacks explicit solvent molecules), the coupling between the temperature gradient and the effective thermophoretic force can be derived from all-atom simulations, Section 3.1.4.

Figure 6 illustrates our multi-scale simulation of a nanopore transport. A continuum model of a heated solid-state nanopore system was built using the COMSOL software package (COMSOL Multiphysics 4.3). A cylindrical pore of 4 nm radius was made in a 20 nm-thick membrane (Figure 6a). The membrane material was set to silicon nitride with the following parameters: specific heat capacity ${\mathrm{c}}_p^m=710\mathrm{J}{(\text{kg}·\mathrm{K})}^{-1}$, density ρ^m = 3310 kg·m⁻³, and thermal conductivity k^m= 2 W·(m·K)⁻¹. The membrane was surrounded by 1 M KCl solution. The entire simulation volume was a cubic box 2 μm on each side, which was large enough to minimize boundary effects. The heating element was modeled as a gold bow tie sitting at the nanopore entry on the membrane [23], with ${\mathrm{c}}_p^m=129\mathrm{J}{(\text{kg}·\mathrm{K})}^{-1}$, ρ^m = 19300 kg·m⁻³, and k^m= 317 W·(m·K)⁻¹. Each of the two parts of the bow tie had the shape of a triangular prisms with rounded corners. The triangles were separated from the center of the nanopore by 4 nm, which was the nanopore radius. Both prisms were 86.6 nm on each side and 30 nm in height.

Fig. 6.

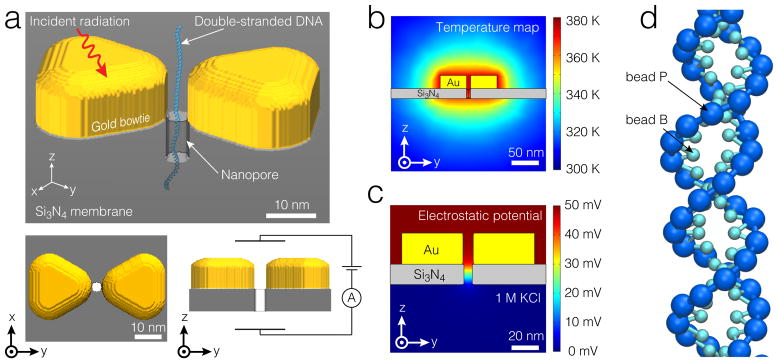
Device-scale simulation of DNA translocation through locally heated solid-state nanopores. (a) An image illustrating a dsDNA molecule passing through a nanopre in a Si₃N₄membrane surrounded by a gold bow tie. Plasmonic heating of the bow tie serves as a heat source [23]. (b,c) The z-y cross section of the temperature (b) and electric potential (c) maps obtained from continuum description. The temperature of the gold bow tie was set to 373.15 K. The voltage bias was 50 mV. (d) A two beads per nucleotide CG model of dsDNA [95].

After building a standard mesh, a steady-state solution to the system of coupled heat transfer, electrostatics, and ion diffusion equations was found using the COMSOL 4.3 software package [96]. Specifically, the temperature distribution was derived from the heat transfer equations for fluid and solid (the Heat Transfer in Fluids interface). The temperature of the entire gold bow tie was fixed at 373.15 K, while the initial temperature of the solution was set to 295.65 K and the temperature of the box boundaries were set to the same (constant) value. The electrostatic potential was determined by solving the Poisson’s equation (the Electrostatic interface), using the temperature input from the Heat Transfer in Fluids interface. A transmembrane bias of 50 mV was applied across the entire simulation domain. The Nernst-Planck equation was used to describe ion diffusion and ion migration (the Transport of Diluted Species interface), which had temperature and electrostatic potential coupled from the prior two interfaces. The solution was obtained using the PARDISO direct solver and damped Newton’s method. The hydrodynamic effects were ignored in these proof-of-principle calculations.

Figure 6b,c shows the distributions of temperature and electric potential resulting from the continuum model calculations. The temperature drops nonlinearly from the heat source (the bow tie prisms) towards the boundary of the simulation domain. The gradient of the electric potential is localized to the vicinity of the nanopore, as expected. In order to apply the derived thermal/electrical gradient in our MD simulations, the numerical solutions obtained with COMSOL were converted into grid-based potentials with the grid spacing of 2 nm. To increase the computational efficiency of the subsequent MD runs, only the central part (352 nm on each side) of the COMSOL simulation domain was represented by the grid-based potentials.

A CG representation of a 250 base pair fragment of dsDNA was constructed using our model featuring two interaction sites per nucleotide [95], Figure 6d. The thermal and electrical gradients derived from the continuum simulations were taken into account in our CG MD simulation using the standard Grid Forces feature [89] of NAMD. An additional grid-based potential was introduced to represent the steric effect of the solid state membrane and the gold bow tie. In the simulation, the thermophoretic force on each bead was calculated by multiplying the local temperature gradient with a force-per-gradient factor derived from atomistic simulations (Section 3.1.4). In this approximation, the thermophoretic force scales linearly with the temperature gradient and does not depend on the absolute value of the temperature. The electrophoretic driving force was calculated based on the local gradient of the electrostatic potential assuming each backbone bead carries a nominal charge of a DNA nucleotide.

At the beginning of the simulation, a double-stranded DNA was partially-threaded into the nanopore (Figure 7a). To elucidate the effect of thermophoresis on DNA translocation velocity, an ensemble of 19 independent simulations was performed with and without the heat source. With the temperature gradient applied, the average translocation time, defined as the time required for the entire DNA strand to exit the nanopore, was 1.02 μs, while in the system without heating the translocation time was 1.08 μs, with a standard error of 0.02 μs for both systems. In other words, heating was observe to speed up the DNA translocation, which could be attributed to the repression of lateral fluctuation by the thermophoretic effect. A detailed description of the physical mechanisms will be the subject of a future study.

Fig. 7.

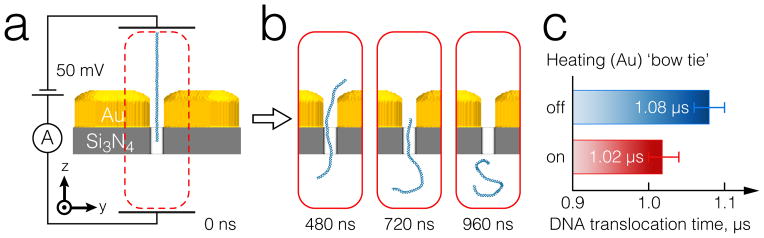
The effect of thermophoresis on DNA transport through a plasmonic nanopore. (a) Setup of a CG MD simulation. Each simulation started with dsDNA partially threaded into the nanopore. (b) A series of snapshots illustrating a single DNA translocation event. (c) Average time to complete translocation with and without heating of the bow tie. The translocation velocity was increased by heating the gold bow tie to 78 K higher than the surrounding solution. The data was obtained by averaging over 19 independent runs for each simulation condition.

4 Concluding remarks

We have shown a hierarchy of computational methods to study the thermophoretic effect at three different levels: thermophoresis of individual particles or their mixture, thermophoretic effect in solid-state nanopores and device-scale simulations of the thermophoretic effect. In addition to measuring the direct effect of the thermal gradient on the behavior of a particle, all-atom MD trajectories can also reveal the microscopic origin of the observed phenomena. An analysis of this kind is of ultimate interest to the field of thermal diffusion; such a level of detail is still unachievable in experiments and has not been possible with prior computational methods. Among the many effects that can be examined are the role of configurational entropy, the presence of acoustic waves or the change in the solute’s electrical double layer in response to a thermal gradient. The all-atom studies of nanopore thermophoresis have already revealed a possible application of the locally heated nanopores for DNA sequencing [28]. Combined with a device-scale description, atomistic and CG simulations can accelerate the deployment of thermophoretic effects in biosensing.