Two-Stage Adaptive Cutoff (TACO) Design for Building and Validating a Prognostic Biomarker Signature

Abstract

Cancer biomarkers are frequently evaluated using archived specimens collected from previously conducted therapeutic trials. Routine collection and banking of high quality specimens is an expensive and time-consuming process. Therefore, care should be taken to preserve these precious resources. Here we propose a novel two-stage adaptive cutoff (TACO) design that affords the possibility to stop the biomarker study early if an evaluation of the model performance is unsatisfactory at an early stage, thereby allowing one to preserve the remaining specimens for future research. In addition, our design integrates important elements necessary to meet statistical rigor and practical demands for developing and validating a prognostic biomarker signature, including maintaining strict separation between the datasets used to build and evaluate the model and producing a locked-down signature to facilitate future validation. We conduct simulation studies to evaluate the operating characteristics of the proposed design. We show that under the null hypothesis when the model performance is deemed undesirable, the proposed design maintains type I error at the nominal level, has high probabilities of terminating the study early, and results in substantial savings in specimens. Under the alternative hypothesis, power is generally high when the total sample size and the targeted degree of improvement in prediction accuracy are reasonably large. We illustrate the use of the procedure with a dataset in patients with diffuse large-B-cell lymphoma. The practical aspects of the proposed designs are discussed.

1. Introduction

Increased understanding of cancer biology and advances in biotechnology have revolutionized the landscape of oncology drug development and brought us closer to the realization of “precision medicine”. A major thrust to this new paradigm involves development of biomarkers that will improve our ability to identify patients who are at an elevated risk of developing cancer (screening biomarkers), have a poor prognosis (prognostic biomarkers), or who are more likely to benefit from specific therapies (predictive biomarkers). The oncology community has committed expansive resources to biomarker studies during the last decade. Ideally the development of a biomarker would be synchronized with the development of cancer therapy, but in reality biomarker development often lags behind therapeutic development. The reasons for this asynchrony may include an incomplete understanding of the mechanism of action of a drug, the uncertainty about what form of a marker is most relevant, and technical difficulties with marker assay development. As such, it is common for cancer biomarkers to be identified using archived specimens collected from previously conducted therapeutic trials. While routine collection and banking of high quality specimens from clinical trials provides a rich resource for conducting biomarker research, the development of the specimen banking system involves an expensive and time-consuming process. Therefore, care should be taken to preserve these valuable and scarce specimens. Motivated by the use of early looks in treatment clinical trials, here we propose a two-stage adaptive cutoff (TACO) design that affords the possibility to stop the biomarker study early if an evaluation of the model performance is unsatisfactory at an early stage, thereby allowing one to preserve the remaining specimens for future research.

A prognostic signature is a collection of biomarkers that are combined through some mathematical model to provide either a continuous score or a categorical classifier. Prognostic signatures can be used to identify patients receiving standard treatment (or no treatment if that is the standard of care) into subgroups with distinct clinical outcomes. In spite of the considerable increase in the number of cancer biomarker studies in recent years, the pace of adoption of new biomarkers into clinical practice has been slow. This phenomenon can, in part, be attributable to the lack of rigorous statistical design and analysis in many biomarker studies. In a comprehensive review of published studies reporting gene expression-based prognostic signatures for non-small cell lung cancer, Subramanian and Simon [1] identified common methodological deficiencies which included the failure to maintain a strict separation between the data used for model development from the data for model evaluation and the lack of a completely specified prognostic model to allow an independent validation on a separate dataset. The performance measurement of a prognostic model computed based on the same data used to develop it is known to be severely biased in an optimistic direction (the resulting estimates of the performance measure are referred to as the “resubstitution statistics”). This is especially problematic when the number of variables is much larger than the number of samples due to the risk of overfitting the data [2]. Re-sampling methods (e.g. split sample, K-fold cross-validation, leave-one-out cross-validation (LOOCV), Monte Carlo cross-validation and bootstrapping), when used properly, provide an almost unbiased estimate of the generalization error of the full sample classifier built using the entire dataset [3]. There is often a desire, however, to evaluate this “final” locked-down signature on an independent dataset where the effects of other sources of variability can be appreciated. The full model specification should include a list of variables in the model (including any interaction or non-linear terms), their weights in the multivariable model (e.g. regression coefficients) and any cutoff used to define risk groups. Clinical decision-making regarding treatment options often relies on the application of a cutoff (to some continuous score) to classify patients into “high” or “low” risk groups. In practice, however, the determination of cutoffs often suffer the lack of statistical rigor. A common pitfall is to search all possible cutoffs within the entire spectrum of the continuous predicted outcome and select one that maximizes the model performance in the same dataset. This practice is well-known to give inflated measure of the model performance and should be avoided [4].

The two-stage design we propose here represents a framework that integrates all the aforementioned elements necessary to meet the practical demands and statistical rigor for a prognostic biomarker signature. Specifically, in Stage 1, a statistically valid procedure based on the unbiased 10-fold cross-validated error is employed to evaluate the model performance. If the initial model performance based on Stage 1 data proves to be unsatisfactory, the study is terminated early. Otherwise, the study proceeds to Stage 2. In Stage 2, a final prognostic signature is built based on the entire Stage 1 data including the identification of a cutoff for classifying patients into distinct risk groups. This locked-down prognostic signature (including the cutoff) is then independently validated with Stage 2 data. The technical aspects of the design focus mainly on development of prognostic signatures in the context of a binary outcome, although with suitable adjustment similar approaches may be contemplated for other types of biomarker signatures or clinical outcomes (e.g. time-to-event). To date, we are aware of only one paper in the literature that incorporates the idea of early stopping into the development of biomarker signatures [5]. However, their work does not build in a formal statistical test for model performance in an early stage and hence the decision as to whether the model holds sufficient promise to be further validated in the second stage is somewhat arbitrary.

Conservation of biospecimens is a relatively less pertinent issue in exploratory or hypothesis-generating studies involving high-dimensional data (e.g. gene-expression profiling studies) since such studies are typically based on smaller datasets readily accessible by the investigators. For this reason, the technical development of our design focuses mainly on settings in which the number of specimens is much larger than the number of biomarker variables (i.e. “large n, small p”) such that an early stopping will result in a sizable saving of specimens. In particular, we assume that biomarker discoveries have been carried out previously with smaller datasets and a small panel of biomarkers (e.g. 5 to 20) has been identified to be of prognostic value. The primary interest is to combine these promising biomarkers into a prognostic signature and to evaluate the ability of the signature to accurately predict patient outcomes. These candidate markers may be selected based on biological insight, data-driven approaches, or the combination of both.

This paper is organized as follows: In Section 2, we describe the two-stage adaptive cutoff design. In Section 3, we present a simulation study to evaluate the operating characteristics of the design. In Section 4, we illustrate the use of the proposed design with a real dataset. We conclude with a discussion on practical aspects of the proposed design in Section 5.

2. Methods

2.1. Theoretical Framework

We start with notational set-up and a brief overview of the theoretical framework underlying the class prediction problem in which the goal is to predict some clinical outcome of a patient (or associated specimen) from a set of covariates. Suppose one observes n independent and identically distributed random variables O = (O₁, …, O_n) with unknown distribution 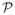. Each observation in O consists of a dichotomized outcome Y ∈ {0, 1} and a p-dimensional vector (p ≪ n) of measured covariates X ∈ 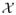, such that O_i = (X_i, Y_i) for i = 1, …, n. In a biomarker study, the outcome Y may indicate some disease status (e.g. disease relapse by 5 years) and the covariates X may include standard clinico-pathological variables, molecular variables such as genetic variations, or imaging variables. The observations o = (o₁, …, o_n) are realizations of underlying random variables O = (O₁, …, O_n).

Define a classifier f(X) = I[m(X|β) > C] as a rule that maps the covariate space 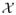onto the class space {0, 1}, where m(X|β) denotes a parametric statistical model that can be built, for example, via regression techniques (linear or non-linear) and C is the cutoff. Given the observations (o₁, …, o_n), the classifier f̂(x) = I(m(x|β̂) > Ĉ) is obtained by substituting the parameters (β, C) with their estimates (β̂, Ĉ) from the data. We are interested in the performance of the given classifier f̂(x) in terms of its prediction accuracy in the population. Let L(Y, f̂(X)) denote the loss function for measuring errors between Y and f̂(X). For a given loss function L, define the conditional risk for a given f̂ as

$$\theta =E[L(Y,\widehat{f}(X))]=\int L(y,\widehat{f}(x))dP(x,y).$$ (1)

Note that here the conditional risk refers to the expected error for a fixed classifier f̂ constructed based on observed data o = (o₁, …, o_n). In the technical development that follows, we focus on the indicator loss function L(Y, f̂(X)) = I[Y ≠ f̂(X)]. The indicator loss function is a common choice of a loss function with a binary outcome Y although other choices are possible (e.g. the squared error loss (Y – f̂(X))²) [6].

A naive estimator of the conditional risk θ for the classifier f̂(x) is the resubstitution error which averages the loss over the observed data (o₁, …, o_n) used to build the classifier

$${\widehat{\theta }}_{RE}=\frac{1}{n}\sum _{i=1}^{n}L(y_i,\widehat{f}(x_i)).$$ (2)

It has been shown that the resubstitution error can severely underestimate the expected error in finite sample situations [2].

One of the most widely used methods for estimating the conditional risk θ is cross-validation. Cross-validation involves using part of the available data to build a classifier and a different part of the data to evaluate its performance. For example, in a K-fold cross-validation, one splits the data into K roughly equal-sized and mutually exclusive subsets each with size (s₁, …, s_K), respectively, such that ${\sum }_{k=1}^K{s}_k=n$. For the kth subset, we develop a classifier with combined data from the remaining K–1 subsets, and calculate the misclassification error of the classifier when predicting the kth part of the data. This process is repeated for k = 1, 2, …, K and the K estimates of the misclassification error are then combined to get the K-fold cross-validated error. In the case of a binary outcome and indicator loss, for example, the K-fold cross-validated error can be written as

$${\widehat{\theta }}_{\mathit{KCV}}=\frac{1}{K}\sum _{k=1}^K\left[\frac{1}{s_k}\sum _{i=1}^{s_k}I\left(y_i\ne {\widehat{f}}^{(k)}(x_i)\right)\right]$$ (3)

where f̂^(k)(x) denotes the classifier developed with kth part of the data removed. Note that the case K = n is known as the leave-one-out cross-validated error.

The performance of the classifier f̂(x) is evaluated in the following statistical hypothesis testing framework:

$$H_0:\theta \ge {\theta }_0\text{vs}.H_1:\theta <{\theta }_0,$$ (4)

where θ₀ is a pre-specified threshold below which the performance of a classifier would be deemed acceptable. In the context of a biomarker study, the alternative hypothesis would correspond to the scenario in which the probability that the classifier f̂(x) built on the observed data (o₁, …, o_n) misclassifies a future specimen is less than θ₀ (see Discussion for the choice of θ₀).

Dudoit and van der Laan proposed asymptotic confidence intervals for the conditional risk θ using a class of resampling methods including cross-validation [7]. They showed that these methods have good asymptotic properties when using common loss functions to assess the performance of the classifier f̂. The asymptotic results were derived under the assumption that the size of the test set in the resampling methods converges to infinity which should apply well to the “large n, small p” setting. Based on their results, an asymptotic 100(1– α)% confidence interval for the conditional risk θ can be written as s

$${\widehat{\theta }}_{\mathit{KCV}}\pm z_{1-\alpha /2}\sqrt{\frac{\widehat{{\sigma }^2}}{n}}$$ (5)

where θ̂_KCV is the K-fold cross-validated error defined in (18), Φ(z_1−α/2) = 1–α/2 for the standard normal cumulative distribution function Φ(.) and the estimated variance term is

$${\widehat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n{\left[I\left(y_i\ne \widehat{f}(x_i)\right)-{\widehat{\theta }}_{RE}\right]}^2,$$ (6)

where ${\widehat{\theta }}_{RE}=\frac{1}{n}{\sum }_{i=1}^{n}I[y_i\ne \widehat{f}(x_i)]$ is the resubstitution error.

2.2. The TACO Design

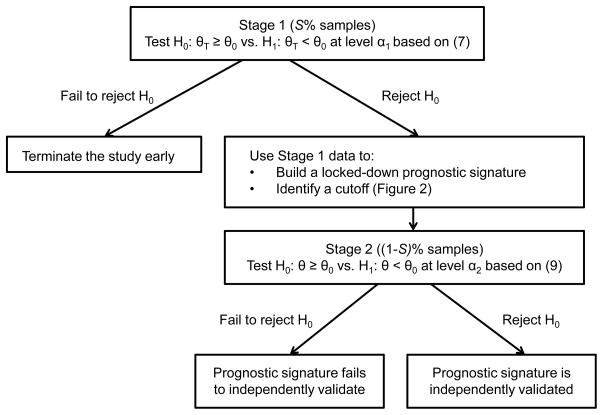
Assume a total of N specimens are available for the study. In Stage 1, S% of the total N samples (n₁ samples) are used to obtain an unbiased estimate of the conditional risk based on 10-fold cross-validation. A test for (4) is performed using a statistical procedure. If H₀ is not rejected (indicating an unacceptable performance of the classifier), the study is terminated early. Otherwise, the study continues to Stage 2. In Stage 2, all data in Stage 1 are combined to develop a prognostic classifier (or signature) including the identification of a cutoff. This locked-down signature is then validated using the remaining independent (1–S)% samples in Stage 2 (n₂ = N–n₁ samples). The significance levels for Stage 1 (α₁) and Stage 2 (α₂) are chosen so that (α₁ × α₂) does not exceed some pre-specified type I error α (e.g. 0.05). A flow chart of the design is given in Figure 1. Below we describe the technical steps of the procedure in detail.

Figure 1.

Flow chart of the two-stage adaptive cutoff (TACO) procedure. θ₀ denote a pre-specified error rate below which a model would be deemed acceptable. The significance levels α₂ and α₂ are chosen so that (α₁ × α₂) does not exceed some pre-specified type I error α (e.g. 0.05).

Stage 1

1-1. First layer (10-fold cross-validation)

The samples are divided randomly into 10 groups with roughly equal size. Nine of the groups (i.e. 90% of the samples) serves as the “training set” while the remaining group (i.e. 10% of the samples) constitutes the “test set”. For each training set, develop a prognostic signature based on p biomarkers using standard statistical techniques suitable for a binary outcome (e.g. logistic regression). The performance of the signature as measured by misclassification error is computed on the test set in each iteration.

1-2. Second layer (cutoff identification)

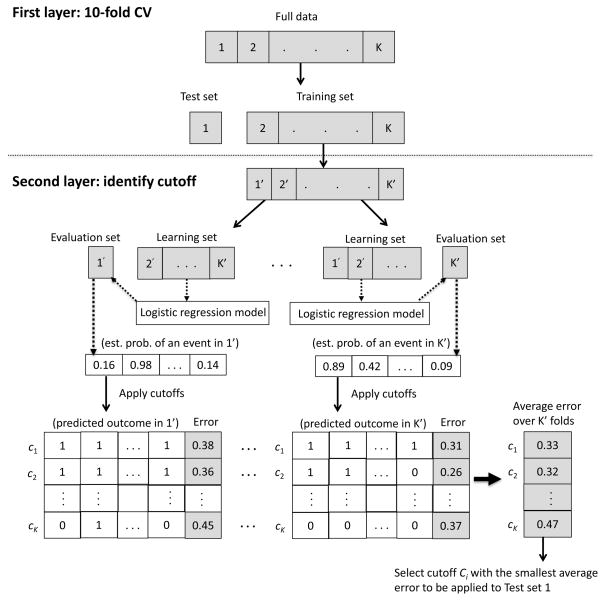
To identify a cutoff to dichotomize the estimated probability for each specimen in the test set, each training set is further subdivided into a “learning set” (90% of the training set) and an “evaluation set” (10% of the training set) [8]. For each learning set, a prognostic signature is developed. The estimated probability of an event for each specimen in the evaluation set is then predicted based on the signature. A fine grid of cutoffs in the range [0, 1] are applied to the predicted probability for each specimen in the evaluation set and the misclassification error with each cutoff is recorded. This process is repeated for each split of data within the training set. For each fixed cutoff, the average misclassification error across the 10 learning-evaluation splits is computed. The cutoff that yields the minimum average misclassification error is the chosen cutoff to be applied to the test set. A diagram of the two-layer procedure in Stage 1 of the TACO design is given in Figure 2.

Figure 2.

A diagram of the two-layer procedure in Stage 1 of the TACO design.

1-3. Early test of model performance

Repeat steps 1-1 and 1-2 until all 10 training-test splits are exhausted. The average misclassification error across the ten test sets constitutes the unbiased 10-fold cross-validated error. Perform a statistical test at significance level α₁ based on the Dudoit and van der Laan procedure [7]. Specifically, we will reject the null hypothesis H₀ in (4) and proceed to Stage 2 if

$$Z_1=\frac{{\widehat{\theta }}_1-{\theta }_0}{{\widehat{\sigma }}_1/\sqrt{n_1}}<z_{{\alpha }_1},$$ (7)

where θ̂₁ is the 10-fold cross-validated error defined in (18) (with K = 10) and σ̂₁ is the estimated standard error term defined in (6) using Stage 1 data. Otherwise, if H₀ is not rejected (the initial signature performance is unsatisfactory), terminate the study early.

Stage 2

2-1. Locked-down signature

Build a prognostic signature using all Stage 1 data, including the selection of a cutoff based on the second-layer procedure described in step 1-2.

2-2. Independent validation

Apply the locked-down prognostic signature in step 2-1 to Stage 2 data, {( $x_i^{\prime },y_i^{\prime }$), i = 1, …, n₂}. Since Stage 2 data are completely independent from Stage 1 data and are not used for signature building, the estimated misclassification error ${\widehat{\theta }}_2=\frac{1}{n_2}{\sum }_{i=1}^{n_2}I(y_i^{\prime }\ne \widehat{f}(x_i^{\prime }))$ follows a binomial distribution, where f̂ denotes the signature built based on Stage 1 data. Based on normal approximation, we have

$${\widehat{\theta }}_2~N\left({\theta }_0,\frac{{\widehat{\theta }}_2(1-{\widehat{\theta }}_2)}{n_2}\right)$$ (8)

We will reject H₀ at significance level α₂ and conclude that the prognostic value of the signature is validated if

$$Z_2=\frac{{\widehat{\theta }}_2-{\theta }_0}{\sqrt{\frac{{\widehat{\theta }}_2(1-{\widehat{\theta }}_2)}{n_2}}}<z_{{\alpha }_2}.$$ (9)

Otherwise, if H₀ is not rejected, we will conclude that the prognostic signature fails to validate.

3. Simulation Studies

We conducted a simulation study to evaluate the operating characteristics of the proposed design under a variety of settings. We assumed that X is a 10-dimensional vector of biomarkers. We simulated the biomarkers from independently and identically distributed standard normal distributions. Assume that the collective ability of the 10-dimensional biomarkers to accurately classify patients into good (Y = 0) versus poor (Y = 1) prognosis subgroups is determined by the following logistic regression model

$$log\left(\frac{p(y_i=1\mid x_{i1},\dots ,x_{i10})}{1-p(y_i=1\mid x_{i1},\dots ,x_{i10})}\right)={\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{10}{x}_{i10}$$ (10)

The binary outcome for the ith patient, y_i, is thus drawn from a Bernoulli distribution with the probability of being in a poor prognosis subgroup:

$$p_i=p(y_i=1\mid x_{i1},\dots ,x_{i10})=\frac{e^{{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{10}{x}_{i10}}}{1+e^{{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{10}{x}_{i10}}}$$ (11)

We evaluate the operating characteristics of the design under the following four scenarios:

• Null Hypothesis (NH): θ = 0.35

• Alternative Hypothesis 1 (AH1): θ = 0.20

• Alternative Hypothesis 2 (AH2): θ = 0.25

• Alternative Hypothesis 3 (AH3): θ = 0.30

Here we include three alternative scenarios representing varying magnitudes of improvement in order to evaluate the impact of the effect size on the operating characteristics of the design. In each scenario, we also vary the total sample size (n = 200, 300, 400) and the proportion of samples used in Stage 1 (S% = 25%, 50%, 75%).

The ability of the prognostic signature to discriminate patient status is influenced by the β’s coefficients in the logistic regression model (10). However, there are infinitely many combinations of β’s values that would give rise to a specified true conditional risk θ. To simplify, we fixed the values of nine β’s coefficients in (10) and performed a fine grid search of the remaining β coefficient (with an increment 0.02) such that the true conditional risk is equal to the desired value. This is possible by recognizing that the true conditional risk θ decreases with increasing values of the remaining β. Details on the determination of the set of (β₁, β₂, …, β₁₀) values that correspond to the true conditional risk in each of the above scenario are given in the Appendix (see Appendix 1).

For each hypothesis scenario and (N, S%) configuration, we simulated 1,000 independent realizations of {(x_i1, …, x_i10, y_i), i = 1, …, N}. With each simulated dataset, we applied the proposed procedure using significance levels α₁ = 0.25 and α₂ = 0.2 for Stage 1 and Stage 2, respectively. A fine grid with 0.01 increment was used in the search of the cutoff value. In each setting, we recorded the empirical probability of stopping the study early, the probability of declaring that the prognostic signature is independently validated (this would represent the type I error under the null hypothesis and power under the alternative hypothesis), and the expected sample size E(SS). A reasonable design should terminate the study early with a high probability under the null hypothesis and hence minimizes the expected sample size but provides sufficient statistical power to detect a meaningful improvement in the prediction error of the classifier under the alternative hypothesis.

Table 1 and Table 2 present the results of the simulation studies. Under the null hypothesis, we note that the type I error is maintained under the overall level of 0.05 in all settings. Further, the probability of terminating the study early ranges from 77% to 84%. The percentage of saving in sample size (computed as the percent reduction in sample size compared with the total sample size) ranges from 19% to 62%, with an average of about 39%. Under AH1 (an improvement of 15% in prediction error), the power exceeds 92% in all settings. Under AH2 (an 10% improvement), the power is generally acceptable (exceeds 81% in most cases) except when the sample size in either stage is only 50 (power is 67% and 68%). Power is generally low when the targeted degree of improvement is as low as 5% (AH3). In AH1 and AH2, we note that for a fixed sample size N, the power tends to be maximized when sample size is equally split between the two stages. Intuitively this is because the power of the procedure depends on allocating adequate sample sizes to reject the null hypothesis in both stages. Overall, our simulation results demonstrate that desirable operating characteristics of the proposed design can be achieved when the total sample size is reasonably large (i.e. N > 200) with an equal split of sample size between the two stages. The power of the procedure in most cases is reasonable when the targeted degree of improvement in prediction error is at least 10%.

Table 1.

Operating characteristics of the TACO design under various hypotheses

N	S(%)	n1	n2	Null Hypothesis: θ = 0.35				Alternative Hypothesis 1: θ = 0.20
				β3	% Early Stop	Type I error	E(SS)	β3	% Early Stop	Power	E(SS)
200	25%	50	150	1.26	0.77	0.02	97	3.38	0.06	0.93	191
	50%	100	100	0.90	0.80	0.03	120	2.26	0.01	0.98	199
	75%	150	50	0.76	0.84	0.02	158	1.82	0.001	0.92	200
300	25%	75	225	1.02	0.83	0.02	114	2.54	0.02	0.97	295
	50%	150	150	0.76	0.81	0.03	179	1.82	0.002	0.99	300
	75%	225	75	0.66	0.77	0.04	242	1.78	0.001	0.98	300
400	25%	100	300	0.90	0.80	0.02	159	2.26	0.004	0.99	399
	50%	200	200	0.70	0.79	0.03	243	1.82	0	1	400
	75%	300	100	0.62	0.81	0.04	319	1.70	0	1	400

Table 2.

Operating characteristics of the TACO design under various hypotheses

N	S(%)	n1	n2	Alternative Hypothesis 2: θ = 0.25				Alternative Hypothesis 3: θ = 0.30
				β3	% Early Stop	Power	E(SS)	β3	% Early Stop	Power	E(SS)
200	25%	50	150	1.84	0.24	0.68	164	1.78	0.45	0.40	133
	50%	100	100	0.94	0.08	0.85	192	1.38	0.34	0.43	166
	75%	150	50	0.40	0.06	0.67	197	1.18	0.37	0.25	182
300	25%	75	225	1.20	0.16	0.81	265	1.52	0.42	0.45	205
	50%	150	150	0.40	0.05	0.90	293	1.18	0.40	0.39	241
	75%	225	75	0.24	0.02	0.81	299	1.14	0.23	0.41	283
400	25%	100	300	0.94	0.10	0.89	371	1.38	0.37	0.52	289
	50%	200	200	0.40	0.02	0.96	397	1.18	0.22	0.59	357
	75%	300	100	1.24*	0.01	0.92	399	1.10	0.16	0.51	384

Note: The unusual β₃ value (*) may be due to the relatively small number of simulation runs (1,000 simulations).

4. Example: An Application to a Dataset

We illustrate the proposed design with a real dataset in patients with diffuse large-B-cell lymphoma (DLBCL). DLBCL is a curable disease for many patients using anthracycline-based chemotherapy regimens such as a combination of cyclophosphamide, doxorubicin, vincristine and prednisone (CHOP) [9]. Recently, the addition of rituximab immunotherapy (R-CHOP) has also been shown to substantially prolong patient survival [10]. DLBCL is a biologically diverse disease and much research has been devoted to identify molecularly distinct subtypes. Rosenwald et al. described a study in which gene-expression profiling was performed in pre-treatment tumor-biopsy specimens of 181 newly-diagnosed DLBCL patients who received CHOP or similar treatment regimens [11]. In that study, two biologically and clinically distinct molecular subtypes of DLBCL were identified, namely the germinal-center B-cell-like (GCB) subtype and the activated B-cell-like (ABC) subtype. Patients with the GCB disease tend to have better long-term prognosis than those with the ABC disease (5-year overall survival were 60% and 30%, respectively). We refer to this signature as the “subtype” signature henceforth. Using the same training dataset but different analytical approaches, the same investigators discovered a number of other gene expression-based signatures: the “germinal-center B-cell” signature, the “proliferation” signature, the “major histocompatibility complex class II” (MHC) signature, the “stromal-1” signature and “stromal-2” signature. For a detailed description of the biological basis of these signatures, see Lenz et al. [12]. In addition to molecular signatures, many clinical variables such as patient age, ECOG status and Ann Arbor Stage have also been shown to have prognostic value for this disease population [13].

We obtained access from the investigators to an independent dataset of 175 newly diagnosed DLBCL patients. No aspect of identification of the gene-expression signatures or development of the survival model was performed with this dataset. These patients constituted an R-CHOP cohort that received similar chemotherapy plus rituximab. We illustrate the use of the proposed TACO design in this dataset with the goal to combine putative clinical prognostic variables with discoveries from the previous training dataset into one signature. The clinical outcome of interest is death at 18 months (a time point by which 25% of the patients have deceased). ECOG status and Ann Arbor stage were analyzed as binary variables (≤ 1 or > 1). The subtype signature was binary in nature (GCB vs. ABC). Age and all other gene-expression signatures were analyzed as continuous variables. We test the null hypothesis that the conditional risk of the prognostic signature is greater than or equal to 35% (H₀: θ ≥ 0.35) against the alternative hypothesis that the conditional risk is smaller than 35% (H₁: θ < 0.35).

We split the dataset roughly equally between the two stages. Significance levels 0.25 and 0.2 were used to test the performance of the prognostic signature in Stage 1 and Stage 2, respectively. Stepwise logistic regression, implemented with the step function in the R software [14], was used to build all prognostic models. In Stage 1, the resubstitution prediction error was 0.25 which represented an optimistically downwards estimate of the true conditional error. The 10-fold cross-validated error was 0.29. The test statistic in Stage 1 based on (7) was Z₁ =−1.14 (p-value = 0.13) leading to the rejection of H₀ and continuation to Stage 2. A final prognostic signature was built based on all Stage 1 data. Table 3 gives the final locked-down multivariable logistic regression model. Stage 1 data were also used to identify the cutoff based on the procedure described in step 1-2 of Section 2.2. A fine grid with an 0.01 increment was applied and the resulting cutoff was 0.79.

Table 3.

The final locked-down prognostic signature based on Stage 1 data of the DLBCL dataset

Coefficients	Estimate	Standard Error	p-value
Intercept	−8.48	2.97	0.004
ECOG (> 1 vs. ≤1)	1.61	0.58	0.005
Subtype (GCB vs. ABC)	−1.74	0.61	0.004
Stromal-2 (continuous)	0.96	0.37	0.009

In Stage 2, the probability of death by 18 months for each specimen was estimated using the logistic regression model developed in Stage 1, i.e.

$$\widehat{p}(y_i=1)={\text{logit}}^{-1}(-8.48+1.61\times I[\text{ECOG}>1]-1.74\times I[\text{Subtype}=\text{GCB}]+0.96\times \text{Stromal}-2).$$ (12)

The cutoff 0.79 was applied to the estimated probabilities to classify each specimen in Stage 2 into either a “short survivor” (y_i = 1) or a “long survivor” (y_i = 0). The estimated prediction error using Stage 2 data was 0.26. The test statistic in Stage 2 based on (9) was Z₂ =−1.81 (p-value = 0.04) leading to the rejection of H₀. Thus, the prognostic signature in (12) (including the cutoff 0.79) was independently validated.

5. Discussion

In practice, the suitable choice of the conditional risk θ₀ depends on the particular clinical scenario and the targeted degree of improvement in signature performance. For example, suppose that the goal of the study is to develop a prognostic signature to predict 10-year disease recurrence. Assume that 35% of the patients are expected to experience disease recurrence within 10 years. The investigators consider a positive predictive value (PPV) (i.e. the probability that a patient truly experiences an event given that the signature predicts an event) and a negative predictive value (NPV) (i.e. the probability that a patient does not experience an event given that the signature predicts the patient to be event-free) of 70% to be unsatisfactory. Suppose an improvement in PPV by 10% and in NPV by 20% (i.e. PPV of 80% and NPV of 90%, respectively) would be deemed clinically meaningful to warrant further assay development. In this case, the conditional risk under the null and the alternative hypothesis would be 30% and 14%, respectively (see Appendix 2).

Various components of the proposed design may be altered although further simulation studies are needed to evaluate the impact such changes have on the overall properties of the design. For example, the 10-fold cross-validation in Stage 1 may be substituted with other resampling methods such as bootstrap. In a more confirmatory setting where a reasonably large number of specimens is available, the difference in signature performance among different resampling methods may not be profound [3]. The use of stepwise logistic regression as a model building technique may also be replaced by other methods suitable for binary outcomes. For example, when a large number of input variables is present in the dataset, penalized regression methods such as LASSO or the Elastic Net are useful to help avoid overfitting [15, 16]. A vast literature on statistical model building exists [6]. While it is beyond the scope of this work to compare among different model building approaches, we stipulate that simplicity or complexity of the model should not dictate choice of a particular approach; rather, the overall performance of the model should serve as the primary consideration. We have chosen an indicator loss function for its practical appeal and ease of interpretation, but other loss functions are possible. For example, the mean squared error can be used to measure the difference between the true binary outcomes and the predicted probabilities. In this case, a cutoff to dichotomize the predicted probability of an event into a binary outcome is not needed, hence obviating the need for the cutoff search in step 1-2. The choice of the signature performance metric may be context dependent. In this work, we focus on the conditional risk mainly because of its mathematical simplicity. For a binary classifier, other choices of performance metrics may include NPV, PPV and Area Under the ROC Curve (AUC). Minimizing the conditional risk θ may not be relevant to some clinical questions. In those settings, other performance metrics may be considered. Our general TACO framework may be tailored to test other performance metrics as long as a loss function can be properly defined. It should be noted, however, that the theoretical development of the TACO procedure is greatly simplified due to the choices of the loss function and performance metric necessary to construct the statistical testing procedure in Stage 1 and Stage 2. Any adaptations may not be mathematically trivial and will require further methodological development. Finally, the overall framework of the proposed design may be applied to “large p, small n” settings, although again the operating characteristics of the design will require further investigation.

Note that when α₁ → 1 and α₂ → α, the TACO design reduces to a simple split-sample approach in which Stage 1 data are used to build a prognostic signature without the possibility for early stopping and Stage 2 data are used to evaluate the signature performance. We evaluated the operating characteristics of the contrasting one-stage design (α₁ = 1, α₂ = 0.05) for each scenario in Table 1 and Table 2. In general, we found that the one-stage competing designs control the type I error at the nominal 0.05 level in all scenarios. Under all of the alternative hypotheses considered, the one-stage designs have slightly higher statistical power compared with their TACO counterparts when a larger percentage of specimens are allocated to Stage 2 (S = 25%). However, this power gain is accompanied by an increase in the sample size, which is equal to the total planned sample size since the one-stage design does not allow the possibility of stopping the study early. The TACO designs have higher statistical power than their competing one-stage designs in all other scenarios when the sample split is equal between the two stages (S = 50%) or when a larger percentage of specimens is allocated to Stage 1 (S = 75%).

In the data example and simulation studies, we chose the significance levels α₁ and α₂ such that the multiplication of the two is equal to some desired overall type I error (e.g. α = 0.05) (as a consequence of the independence between the datasets in two stages). In practice, the choice of α₁ may be guided by the scarcity and the difficulty involved in obtaining the specimens. For example, for certain specimens that are extremely rare, one may choose a more stringent α₁ (e.g. 0.25) to ensure that a reasonably promising prognostic value of the signature needs to be established at the early stage before attempting the rest of the specimens. The choice of α₁ should be made in conjunction with α₂ to ensure that sufficient rigor can be achieved in the validation of the signature at the second stage. Under the guiding principle that a more stringent statistical criterion should be reserved for the final validation of the signature, we recommend using the general rule: α₁ ≤ 0.50 and α₂ ≤ 0.20. A few examples that may be useful in practice are: (α₁, α₂) = (0.25, 0.2), (0.30, 0.17), (0.35, 0.14). Further, when sample size permits, (α₁, α₂) may be chosen so that the product of the two values may be smaller than the conventional 0.05 level.

A larger sample size in Stage 1 will on average result in a locked-down signature with higher classification accuracy in independent data. However, the trade-off is an inevitably smaller sample size for validating the signature performance in Stage 2. While the impact this trade-off has on the statistical power of the overall procedure may be context-dependent, in the limited number of scenarios we considered in our simulation studies, an equal split of sample size between the two stages appeared to yield optimal power. This finding is consistent with Dobbin and Simon who suggested that “the optimal proportion of cases for the training set tended to be in the range of 40% to 80% for the wide range of conditions studied”, although their investigation was focused on high dimensional data problems and did not consider a formal statistical test for the training data [17]. Furthermore, the marginal gain in classification accuracy as a result of a larger Stage 1 sample size may be less profound when the true conditional risk is closer to the zero boundary (or equivalently, when the true classification accuracy is closer to 100 %). This implies that the effect a larger Stage 1 sample size has on the observed effect size (and consequently the Stage 2 test statistic) may depend on the value of the true conditional risk. In general, for fixed α₁ and α₂, the operating characteristics of TACO are jointly influenced by the true conditional risk, the Stage 1 sample size, and the Stage 2 sample size. Therefore, while the classification accuracy of the locked-down signature may be improved by maximizing the sample size in Stage 1, it is important to note that this strategy does not always lead to an optimal design. In practice, we encourage the investigators to conduct simulation studies based on the particular clinical setting of interest to calibrate the design parameters (e.g. total sample size, sample split between the two stages) so as to optimize the operating characteristics of the design (i.e. power, type I error and expected sample size). The R functions for implementing our procedure and programs for simulating the operating characteristics of the design are available upon request from the authors.

In this article, we have studied the properties of the proposed design in settings where a relatively large sample size is available (N > 200). In reality it may be practically infeasible to set up large prospective studies with building a prognostic signature as the primary objective since the collection of clinical outcomes is a costly, resource-intensive and time-consuming process. As such, we envision that the most suitable setting for the TACO design would be retrospective studies of biomarker signature development using archived specimens and clinical data previously collected in large single-arm therapeutic trials where patients are uniformly treated with some treatment regimen (or a sub-study on one treatment arm of a large randomized trial). Alternatively, our design can also be built into a prospective therapeutic clinical trial as a secondary objective with the goal to develop a prognostic biomarker signature using data collected during the trial. While the general framework of the two-stage design may be extended to include more than one treatment arms, the development of such predictive signatures requires more thought and is beyond the scope of this work.

A salient feature of our design is that it produces a single locked-down signature at the end of Stage 1 to facilitate future independent validations. In practice, the two-stage nature of the design can also help facilitate the implementation of an “honest broker” system in which the signature builder(s) in Stage 1 remains strictly blinded to the clinical outcomes in the confirmatory dataset in Stage 2 until after individual predictions have been made for each specimen. Finally, some caution is required when interpreting the results of the study. While the term “validation” is widely used in practice, it may mean different things in different contexts or to different investigators. Within the context of our design, a “validated” signature by TACO would mean that it is highly probable that the signature in hand achieves certain accuracy (i.e. true positive + true negative), as defined by the hypothesis testing set-up. In some situations, minimizing the misclassification error rate may not be most relevant to the underlying clinical question of interest. For example, in some disease settings, PPV and NPV may be more relevant metrics that investigators will rely on to judge if a signature is satisfactory. The meaning of PPV and NPV may also be different to the investigators depending on the specific signature. For some signatures or tests, a higher PPV may be desirable while a slightly lower NPV may be tolerated. For other signatures, NPV may be deemed more important on the contrary. In real life applications, it is likely that a more comprehensive assessment of various aspects (e.g. PPV, NPV, accuracy, etc.) is necessary depending on the specific disease setting and the intended clinical use of the signature. Even if the clinical validity is established by demonstrating that the signature has a suitable strong association with a clinical outcome of interest, it does not imply that the signature is ready to direct patient care [18]. Establishing the clinical utility of a signature will require evidence that the use of the signature to direct patient care will result in favorable balance between benefits and harm, thereby leading to meaningful improvement in health outcomes such as quality of life, prolonged survival or reduced cost.

In summary, we propose a two-stage design useful for developing and validating a prognostic biomarker signature which includes an early stopping in the event of a poor signature performance. Novel statistical designs like this are needed to allow rigorous evaluation of prognostic biomarker signatures while ensuring efficient use of specimens.

6. Appendix 1: Determination of β’s coefficients that give rise to a true conditional risk θ

Assume there are ten biomarkers of interest and these markers are independently and identically distributed as a standard normal distribution. Assume further that the collective ability of the 10-dimensional biomarkers to accurately classify a patient into a good (Y = 0) or a poor (Y = 1) prognosis subgroup is determined by the following logistic regression model

$$\mathit{log}\left(\frac{p(y_i=1\mid x_{i1},\dots ,x_{i10})}{1-p(y_i=1\mid x_{i1},\dots ,x_{i10})}\right)={\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{10}{x}_{i10}$$ (13)

The binary outcome for the ith patient, y_i, is thus drawn from a Bernoulli distribution with the probability of being in a poor prognosis subgroup:

$$p_i=p(y_i=1\mid x_{i1},\dots ,x_{10i})=\frac{e^{{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{10}{x}_{i10}}}{1+e^{{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_{10}{x}_{i10}}}$$ (14)

Note that the ability of the prognostic signature to discriminate patient outcomes is influenced by the β’s coefficients in the logistic regression model. We wish to devise a data generating mechanism that gives rise to the true conditional risk θ in each of the following four scenarios:

• Null Hypothesis (NH): θ = 0.35

• Alternative Hypothesis 1 (AH1): θ = 0.20

• Alternative Hypothesis 2 (AH2): θ = 0.25

• Alternative Hypothesis 3 (AH3): θ = 0.30

There are infinitely many combinations of β’s values that would correspond to a specified θ. To simplify, we fix the values of nine β’s coefficients and perform a fine grid search of the remaining β coefficient (with an increment 0.02) such that the true conditional risk is equal to the desired value. This is possible by recognizing that θ decreases with increasing values of the remaining β. Specifically, in all scenarios we fix β₄ = β₅ = ··· = β₁₀ = 0. Further, we fix β₁ = β₂ = 0.5 for NH and AH3 and β₁ = β₂ = 1.3 for AH1 and AH2 such that the only β coefficient free to vary is β₃. The following steps are then followed to search for the solution of β₃ in each scenario:

1. For each fixed value of β₃, simulate a very large dataset D₁ = {(x_i1, …, x_i10, y_i), i = 1, …, M} (e.g. M = 10, 000) which represents the “universe” in which the conditional risk of a signature will be evaluated.

2. For the same fixed β₃, simulate 1,000 datasets D₂ = {(x_i1, …, x_i10, y_i), i = 1, …, n₁} where n₁ represents the sample size in Stage 1 of the TACO procedure.

3. For each simulated dataset D₂, build a prognostic signature, identify the cutoff based on the procedure described in step 1-2 of Section 2.2, and estimate the conditional risk of the signature (including the cutoff) in the “universe” D₁.

4. Average the estimated conditional risks across 1,000 simulated D₂ datasets.

5. If the average conditional risk in step 4 exceeds the targeted θ, increment β₃ by a small amount (e.g. we used 0.02 in our simulation studies) and repeat above steps 1-4. The search stops when the smallest β₃ value that yields an average conditional risk smaller than θ is found.

7. Appendix 2: Translating PPV and NPV into conditional risk θ

In calculating the value of θ under H₀ and H_A, we first set up a 2 × 2 table as follows in which the rows represent the true disease status (Y = 0 if event-free, Y = 1 if event) and the columns represent the predicted disease status based on the signature (X = 0 if predicted to be event-free, X = 1 if predicted to be an event).

		Predicted Status
		X = 0	X = 1
True Status	Y = 0	a	b	(a + b)
	Y = 1	c	d	(c + d)
		(a + c)	(b + d)	(a + b + c + d)

Let π₁, π₂ and w denote, respectively, the PPV, NPV, and the prevalence of disease, then

$$\{\begin{array}{c}{\pi }_1=d/(b+d)\\ {\pi }_2=a/(a+c)\\ w=(c+d)/(a+b+c+d)\end{array}$$ (15)

With some algebraic manipulations, we have

$$\{\begin{array}{c}b=\left(\frac{1-{\pi }_1}{{\pi }_1}\right)d\\ c=\left(\frac{1-{\pi }_2}{{\pi }_2}\right)a\\ a=\left(\frac{{\pi }_2}{1-{\pi }_2-\omega }\right)\left(\frac{w-{\pi }_1}{1-{\pi }_1}\right)b\end{array}$$ (16)

Re-expressing a, b and c in terms of d in (16) gives

$$\{\begin{array}{c}a=\left[\frac{{\pi }_2(w-{\pi }_1)}{{\pi }_1(1-{\pi }_2-w)}\right]d\\ b=\left(\frac{1-{\pi }_1}{{\pi }_1}\right)d\\ c=\left[\frac{(1-{\pi }_2)(w-{\pi }_1)}{{\pi }_1(1-{\pi }_2-w)}\right]d\end{array}$$ (17)

Note that since a, b, c, d > 0, the system of equations in (17) requires that either Condition (i): 1–π₂ < w < π₁, or Condition (ii): π₁ < w < 1–π₂ to be satisfied.

Theoretical bounds for w depend on the disposition of π₁ and π₂. Specifically, consider the following scenarios:

S1π1, π2 ≥ 0.5 S2πi < 0.5 < πj(i ≠ = j) and π1 + π2 > 1 S3π1, π2 ≤ 0.5 S4πi < 0.5 < πj(i = ≠ j) and π1 + π2 < 1

It can be shown that w is bounded by Condition (i): 1–π₂ < w < π₁ for S1 or S2, and w is bounded by Condition (ii): π₁ < w < 1–π₂ for S3 or S4.

Finally, using expressions in (17), the conditional risk θ can be expressed as a function of π₁, π₂ and w as follows:

$$\theta =\frac{b+c}{a+b+c+d}=\frac{(1-{\pi }_1)(1-{\pi }_2-w)+(1-{\pi }_2)(w-{\pi }_1)}{(1-{\pi }_1-{\pi }_2)},$$ (18)

where 1–π₂ < w < π₁ if S1 or S2, and π₁ < w < 1–π₂ if S3 or S4. Note a special case when π₁ = π₂(≠ 0.50), it can be easily shown that θ in (18) reduces to (1–π₁).