On identification of natural direct effects when a confounder of the mediator is directly affected by exposure

Abstract

Natural direct and indirect effects formalize traditional notions of mediation analysis into a rigorous causal framework and have recently received considerable attention in epidemiology and in the social sciences. Sufficient conditions for identification of natural direct effects were formulated by Judea Pearl under a nonparametric structural equations model, which assumes certain independencies between potential outcomes. A common situation in epidemiology is that a confounder of the mediator-outcome relationship is itself affected by the exposure, in which case natural direct effects fail to be nonparametrically identified without additional assumptions, even under Pearl's nonparametric structural equations model. In this paper, we show that when a single binary confounder of the mediator is affected by the exposure, the natural direct effect is nonparametrically identified under the model, assuming monotonicity about the effect of the exposure on the confounder. A similar result is shown to hold for a vector of binary confounders of the mediator under a certain independence assumption about the confounders. Finally, we show that natural direct effects are more generally identified if there is no additive mean interaction between the mediator and confounders of the mediator affected by exposure. When correct, this latter assumption is particularly appealing because it does not require monotonicity of effects of the exposure. Additionally, it places no restriction on the nature of the confounders of the mediator which can be continuous or polytomous.

There is a fast growing literature in causal inference concerned with the definition, identification and estimation of direct and indirect effects in fully non-parametric models^1,15 based primarily on ideas developed by Robins and Greenland¹ and Pearl.² The recent literature uses the language of potential outcomes to give a non-parametric definition of effects involved in mediation analysis known as controlled direct effects, natural direct and indirect effects, and path-specific effects. Sometimes, these effects, despite being defined in a fully non-parametric way, can nevertheless be sometimes identified and estimated from observational data.²

The current paper concerns natural direct effects, also known as pure direct effects, that capture the effects of an exposure when one intervenes to set a mediator to the (random) level it would have been in the absence of exposure.^1,2 Such effects generally differ from controlled direct effects, which refer to exposure effects that arise upon intervening to set the mediator to a fixed level that may differ from its observed value.^1,2,4 Natural direct and indirect effects combine to produce an exposure total effect. As Pearl has previously noted, total effects may be more useful than controlled direct effects for understanding the underlying mechanism by which the exposure operates.²

Sufficient conditions for nonparametric identification of natural direct and indirect effects were given by Pearl,² under a nonparametric structural equations model that assumes certain independencies between potential outcomes. A common situation in epidemiology is that a confounder of the mediator is affected by the exposure. In such cases, Avin et al⁴ have established that natural direct effects fail to be nonparametrically identified without additional assumptions, even under Pearl's nonparametric structural equations model. In this paper, we show that when a single binary confounder of the mediator is affected by the exposure, natural direct effects are nonparametrically identified under a monotonicity assumption about the effect of the exposure on the confounder. In the Appendix, a similar result is shown to hold for a vector of binary confounders of the mediator under a certain independence assumption of the confounders, and the result is also shown to like-wise extend to an additive hazards model for survival data. Finally, we show that natural direct effects are more generally identified if there is no additive interaction between the mediator and the confounders of the mediator affected by the exposure in the outcome regression. When correct, this latter assumption is appealing because it does not require monotonicity of effects of exposure; additionally, it places no restriction on the nature of the confounders, which can be continuous or polytomous.

Notation and definitions

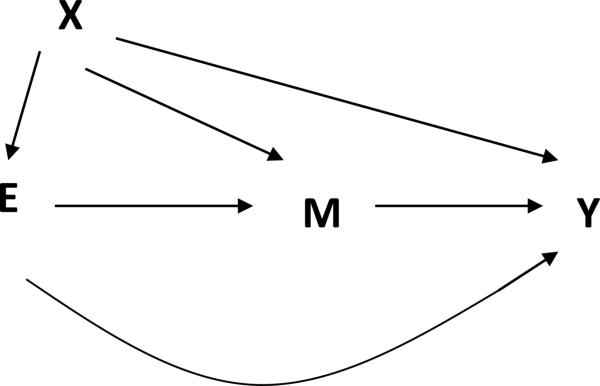
We introduce notation and definitions we will use throughout. Let E denote the exposure or treatment received by a person, let Y denote a post-treatment outcome, and let M denote the value of a post-treatment intermediate variable that may serve as a mediator for the treatment-outcome relationship. Let C denote the value of a set of pre-exposure confounding variables of the effects of E and M. Throughout, we will assume independent and identically distributed sampling of C, E, M and Y . If there is no confounder of the mediator effect on the outcome that is itself affected by the exposure, then the relationships between these variables may be depicted in the causal diagram in Figure 1.

Figure 1.

No confounder of M-Y relation is affected by E.

We now consider counterfactuals or potential outcomes, under possible interventions on the variables.^16,17 Let Y (e) denote a subject's outcome if treatment E were set, possibly contrary to fact, to e. In the context of mediation there will also be potential outcomes for the intermediate variable. Let M(e) denote a subject's counterfactual value of the intermediate M if treatment E were set to the value e. Finally, let Y (e, m) denote a subject's counterfactual value for Y if E were set to e and M were set to m. Similar definitions hold for Y (e, m, c) and M(e, c).

Identification under a nonparametric structural equations model with no exposure-dependent confounding

The exposition is framed around a nonparametric structural equation theory of causal inference, described by Judea Pearl.¹⁸ Structural equations provide a nonparametric algebraic interpretation of the diagram of Figure 1 corresponding to four functions, one for each variable on the causal graph:

$$C=g_C\left({\epsilon }_C\right)$$ (1)

$$E=g_E(C,{\epsilon }_E)$$ (2)

$$M=g_M(C,E,{\epsilon }_M)$$ (3)

$$Y=g_Y(C,E,M,{\epsilon }_Y)$$ (4)

Each of the nonparametric functions {g_C, g_E, g_M, g_Y} represents a causal mechanism that determines the value of the left-hand-side variable (known as the output) from variables on the right (known as the inputs). The errors (ε_C, ε_E, ε_M, ε_Y ) stand for all factors not included on the graph that could possibly affect their corresponding outputs when all other inputs are held constant. To be consistent with the causal graph presented in Figure 1, we require that these errors be mutually independent, but we allow their distribution to remain arbitrary. If they were not independent, we would include an additional unmeasured variable U on the diagram with arrows into the relevant variables to induce dependence. Lack of a causal effect of a given variable on an output is encoded by an absence of the variable from the right-hand side. For example, consider a modification of Figure 1 obtained by deleting the arrow E → Y, thus indicating the absence of a direct effect of E on Y. This no-direct-effect is encoded by replacing equation (4) with Y = g_Y (C, M, ε_Y ) in the nonparametric structural equation model. The absence of E from the arguments of g_Y encodes the assumption that variations in E will leave Y unchanged, as long as variables C, M and ε_Y remain constant, which is also consistent with the assumption that there are no unmeasured common causes of Y and E.

As stated by Pearl,¹⁸ the invariance of structural equations permits their use as a basis for modeling causal effects and potential outcomes. In fact, to emulate the intervention in which setting {E = e} for all persons simply amounts to replacing the equation for E with E = e, producing the following set of modified equations:

$$C=g_C\left({\epsilon }_C\right)$$

$E=e$

$$M\left(e\right)=g_M(C,e,{\epsilon }_M)$$

$$Y\left(e\right)=g_Y(C,e,M\left(e\right),{\epsilon }_Y)$$

with {M (e) , Y (e) = Y (e, M (e))} denoting the potential outcomes had the exposure been set to e.

Under the above nonparametric structural equations model, the independence of errors ε_M ⊥ ε_Y implies independence of so-called “cross-world” potential outcomes, which are potential outcomes for various exposure values:

$$Y(e,m,c)⫫M(e^{\ast },c)$$ (5)

where M (e* , c) = g_M(c, e* , ε_M) and Y (e, m, c) = g_Y (c, e, m, ε_Y ) are obtained upon intervening on (E, C) and (E, M, C), respectively, and e, e* take values in f0, 1g. The assumption encoded in equation (5) is a strong assumption, because it is not empirically verifiable. Unlike the assumption of no unobserved confounding routinely made in causal inference¹⁹, the assumption encoded in equation (5) cannot be enforced by experimental design, such as by randomization. For this reason, Robins and Richardson²⁰ have warned against identification results that rely on cross-world independences encoded in an nonparametric structural equations model, since no experimental scientific study can ever be conducted to validate the findings. Nonetheless, this type of assumption is required to make empirical statements about natural direct and indirect effects without adding other assumptions.

Robins and Greenland¹ and Pearl² considered the following decomposition of individual total effect of exposure:

$$\begin{array}{cc}\hfill Ye)-Y\left(e^{\ast }\right)=& Y(e,M\left(e\right))-Y(e^{\ast },M\left(e^{\ast }\right))\hfill \\ \hfill =& \underset{\text{Natural direct effect}}{\underbrace{Y(e,M\left(e^{\ast }\right))-Y(e^{\ast },M\left(e^{\ast }\right))}}+\underset{\text{Natural indirect effect}}{\underbrace{Y(e,M\left(e\right))-Y(e,M\left(e^{\ast }\right))}}\hfill \end{array}$$

where e* indicates a reference or baseline value of E. For instance, it is common to choose e* = 0 for binary E, where e represents an active value of treatment. The first contrast on the right-hand side of the second line displayed above defines the natural direct effect of treatment E on outcome Y in a given person. The potential outcome Y (e* , M (e*)) captures the behavior of Y under the baseline treatment value, while Y (e, M (e*)) describes the behavior of Y under the active treatment value, in a hypothetical situation where the mediator behaves as if treatment were set to baseline. Conceptually, for e = 1 and e* = 0, the potential outcome Y (e, M (e* )) could be obtained if it were possible in an intervention to deactivate the component of the exposure that affects solely the mediator, so that the mediator would take the value M (e* ), while at the same time leaving active the component of the exposure, which affects only the outcome, so that we would observe Y (1, M (0)). The second contrast on the right-hand side of the expression in the display above corresponds to the natural indirect effect of treatment E on outcome Y . The potential outcome Y (e, M (e)) describes the behavior of Y under the active treatment value, while the second “subtracts off” the behavior of Y under the active treatment value, in a hypothetical situation where the mediator behaves as if treatment were set to its baseline value. In graphical terms, the individual natural indirect effect quantifies for the person, the effect of E on Y along the indirect causal pathway E → M → Y , but not along the direct arrow from E to Y . Because potential outcomes under confficting exposure status are never jointly observed, individual causal effects are generally not identified. However, one can hope that, under certain assumptions, population average causal effects would become identified. It is well known that the average total effect of E on Y is identified given data on (C, E, Y ) in the causal diagram of Figure 1, and is given by the g-formula of Robins¹⁹ :

$$TE(e,e^{\ast })\equiv \mathbb{E}\{Y\left(e\right)-Y\left(e^{\ast }\right)\}=\sum _c[\mathbb{E}\{Y\mid e,c\}-\mathbb{E}\{Y\mid e^{\ast },c\}]\mathrm{Pr}(C=c)$$ (6)

where E stands for expectation. Pearl² proved that under the nonparametric structural equations model for the causal graph of Figure 1, the average natural direct effect is identified by

$$\begin{array}{cc}\hfill NDE(e,e^{\ast })\equiv & \mathbb{E}\{Y(e,M\left(e^{\ast }\right))-Y(e^{\ast },M\left(e^{\ast }\right))\}\hfill \\ \hfill =& \sum _c[\mathbb{E}\{Y\mid e,m,c\}-\mathbb{E}\{Y\mid e^{\ast },m,c\}]\mathrm{Pr}(M=m\mid E=e^{\ast },C=c)\mathrm{Pr}(C=c)\hfill \end{array}$$

Therefore the average natural indirect effect is obtained under the nonparametric structural equations model by NIE (e, e* ) = T E (e, e* ) NDE (e, e* ) . Numerous statistical methods for estimating NDE (e, e* ) and NIE (e, e* ) have been proposed in recent literature.^6,9,15 Tchetgen Tchetgen and Shpitser¹⁴ compare several of these methods and develop a semiparametric approach with attractive robustness and efficiency properties.

Non-identifiability under a nonparametric structural equations model with exposure-dependent confounding

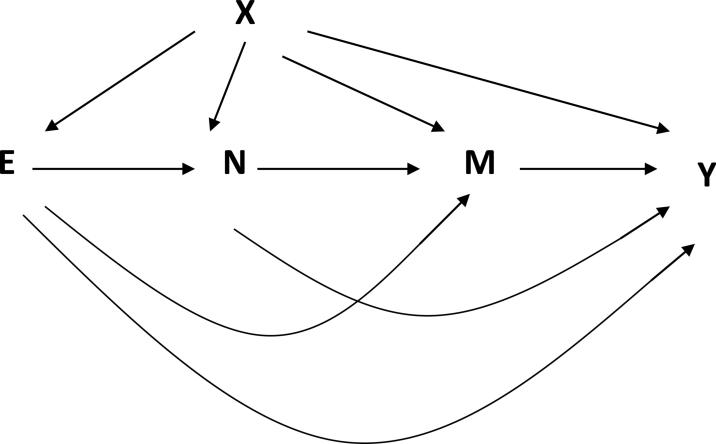
Next, we consider a common setting in epidemiology as displayed in Figure 2. In this causal diagram, a common cause N of the mediator and outcome is directly affected by exposure. In other words, N is simultaneously a confounder of the effects of the mediator M on Y, and on the causal pathway from exposure to outcome.

Figure 2.

A setting where N is a confounder of M-Y relation that is affected by E.

Similar to Figure 1, we suppose the nonparametric structural equations model for this causal diagram is given by:

$$C=g_C\left({\epsilon }_C\right)$$ (7)

$$E=g_E(C,{\epsilon }_E)$$ (8)

$$N=g_N(C,E,{\epsilon }_N)$$ (9)

$$M=g_M(C,E,N,{\epsilon }_M)$$ (10)

$$Y=g_Y(C,E,M,N,{\epsilon }_Y)$$ (11)

where, as before, {g_C, g_E, g_N, g_M, g_Y} are nonparametric functions, and the errors (ε_C, ε_E, ε_N, ε_M, ε_Y ) are mutually independent. The total effect of E on Y remains identified by equation (6) using data (C, E, Y ) only, so that the presence of N brings no new difficulty. The situation is quite different if identification of natural direct effect $NDE(e,e^{\ast })=\mathbb{E}\{Y(e,M\left(e^{\ast }\right))-Y(e^{\ast },M\left(e^{\ast }\right))\}$ is in view. In particular, according to a result by Avin et al,⁴ a causal effect along a specific path is not identifiable in a fully observable nonparametric structural equations model if and only if there is no so-called firecanting witness,flnamely a random variable that mediates the causal pathway of interest from E to Y , while at the same time mediating another causal pathway from E to Y that is not of interest.⁴ Note that the direct effects of E on outcome Y with respect to the mediator of interest M, in Figure 2, consists of the two pathways E → Y and E → N → Y. But the variable N also mediates the indirect effect E → N → M → Y, which is not of interest when direct effects are in view, and therefore the exposure-dependent confounder N is a recanting witness for the direct-effect path E → N → Y . This in turn implies that NDE (e, e* ) is not nonparametrically identified without an additional assumption under nonparametric structural equations model defined by the equations (7)-(11) for the causal diagram in Figure 2. As shown, the recanting witness is an exposure-dependent confounder of the mediator-outcome relation. Thus, we can conclude that if there is such a variable present in a given application, the NDE (e, e* ) is not identifiable even under a nonparametric structural equations model without an additional assumption.

To understand why identification fails, it is useful to consider the following expression for the average of the potential outcome $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$, under the nonparametric structural equations model given by Robins and Richardson²⁰:

$$\sum _{m,n,n^{\prime },c}\mathbb{E}(Y\mid e,m,n,c)\mathrm{Pr}(M=m\mid e^{\ast },n^{\prime },c)\mathrm{Pr}(N\left(e\right)=n,N\left(e^{\ast }\right)=n^{\prime }\mid c)\mathrm{Pr}(C=c)$$ (12)

Therefore, although $\mathbb{E}(Y\mid e,m,n,c)$, Pr(M = m| e* , n′, c) and Pr(C = c) are identified from data (Y, E, M, N, C), identification of NDE (e, e* ) fails because it requires the conditional joint density Pr(N (e) = n, N(e* ) = n′|c) that involves the potential outcomes of the recanting witness N for confficting exposure values, and therefore is not identified even under the nonparametric structural equations model. The rest of this paper will consider various assumptions that make the unidentified term in this equation identified.

Robins and Richardson²⁰ show that equation (12) becomes identified under either of the fol lowing two assumptions:

1. if N(e) ⫫ N(e* ), then $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$ is identified by the following formula

   $$\sum _{m,n,n^{\prime },c}\mathbb{E}(Y\mid e,m,n,c)\mathrm{Pr}(M=m\mid e^{\ast },n^{\prime },c)\mathrm{Pr}(N=n\mid e,c)\mathrm{Pr}(N=n^{\prime }\mid e^{\ast },c)\mathrm{Pr}(C=c)$$
2. or if N(e) is a deterministic function of N(e* ), say N(e) = h(N(e* )), in which case, $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$ is given by

   $$\sum _{m,n,n^{\prime },c}\mathbb{E}(Y\mid e,m,n,c)\mathrm{Pr}(M=m\mid e^{\ast },n^{\prime },c)\mathrm{Pr}(N=n^{\prime }\mid e^{\ast },c)I(n=h\left(n^{\ast }\right))\mathrm{Pr}(C=c)$$

For scalar N taking values in a continuous state space, Robins and Richardson²⁰ showed that, under a condition of rank preservation, there will always exist a function h such that (ii) holds. However, rank preservation is often not biologically plausible, and even if the assumption holds, it is not clear whether h can be determined empirically. Likewise, assumption (i) seems unrealistic for applications in the health sciences. In such applications, it is usual that potential outcomes under various exposure values are correlated because of unknown behavioral or environmental risk factors, or unknown genetic risk factors for the outcome. In the following sections, we will explore somewhat less stringent assumptions for identification of NDE (e, e* ) under an nonparametric structural equations model.

Identification under monotonicity of the effect of E on N

Suppose that N is binary. Then consider the following monotonicity assumption.

$$E-NMonotonicityAssumption:If{e}^{\ast }<ethenN\left(e^{\ast }\right)\le N\left(e\right)forallpersons.$$

This type of monotonicity assumption is often used in recent epidemiologic literature, particularly in the context of causal inference.^{21 – 24} The monotonicity assumption is particularly easy to interpret for binary exposure and counfounder E and N. Then it simply states that there is no one in the population with counterfactual response type N(0) = 1 but N(1) = 0. That is, if a person experienced the confounder when unexposed, i.e. N(0) = 1, then he or she must also experience the confounder when exposed, that is N(1) = 1. However, for a person without the confounder when unexposed, that is N(0) = 0, the potential outcome N(1) can either be 0 or 1. In the eAppendix, we use this assumption to show the following result.

Result 1: Assuming the nonparametric structural equations model (7) – (11), suppose that N is binary, and E N Monotonicity Assumption holds, then $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$ is nonparametrically identified by the following formula

$$\sum _{m,n,n^{\prime },c}\mathbb{E}(Y\mid e,m,n,c)\mathrm{Pr}(M=m\mid e^{\ast },n^{\prime },c)f(n,n^{\prime },e,e^{\ast },c)\mathrm{Pr}(C=c)$$ (13)

where

$$f(n,n^{\prime },e,e^{\ast },c)=[\begin{array}{c}\hfill \mathrm{Pr}\{N=1\mid e^{\ast },c\}if{n}^{\prime }=n=1\hfill \\ \hfill \mathrm{Pr}\{N=1\mid e,c\}-\mathrm{Pr}\zeta \{N-1\mid e^{\ast },c\}if{n}^{\prime }=0andn=1\hfill \\ \hfill 0if{n}^{\prime }=1andn=0\hfill \\ \hfill \mathrm{Pr}\{N=0\mid e,c\}if{n}^{\prime }=n=0\hfill \end{array}\phantom{]}$$

The theorem states that under the nonparametric structural equations model (7) – (11) for which E – N monotonicity holds, the joint conditional density Pr(N(e) = n, N(e*) = n′|c) of potential outcomes for conflicting values E = e, e* is identified by f (n, n′, e, e*, c), and therefore, by equation (12), $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$ is nonparametrically identified by equation (13). Note that because of monotonicity Pr{N = 1|e, c} ≥ Pr{N = 1|e* , c} and therefore Pr(N (e) = 1, N(e* ) = 0|c) = f (1, 0, e, e* , c) = Pr{N = 1|e, c} – Pr{N = 1|e* , c} ≥ 0. In addition, since E {Y (e* , M (e* ))} is nonparametrically identified by the g-formula given in equation (6), we conclude that NDE (e, e* ) is nonparametrically identified. Likewise, it follows that NIE (e, e* ) is also nonparametrically identified by T E (e, e* ) – NDE (e, e* ).

As we show in the Appendix, Result 1 generalizes somewhat beyond the simple case of a single binary recanting witness. Specifically, we show with Result 2 that a similar result continues to hold if N consists of multiple independent binary variables. However, we recognize that the assumption of independent confounders is quite stringent, as it requires that the baseline covariates C also include all common causes of each pair of variables in N, as illustrated in Figure 3 of the Appendix. Crucially, we note that the above Result 1 and its multivariate extension, Result 2, place no restriction on the functional form of the regression function $\mathbb{E}(Y\mid e,m,n,c)$, and therefore interactions are easy to accommodate as well as nonlinearities in the effect of covariates, but also in terms of the link function defining the regression. In the Appendix, the results obtained above are further extended to the survival context under an additive hazards model. The mononiticity assumption again suffices for identification of direct and indirect effects (Result 3).

Recall that NDE(e, e* ) captures the aggregate effect along the following two pathways, E → Y and E → N → Y. In the Appendix, we further establish that under monotonicity, one can identify the respective contribution of each path-specific effect to NDE(e, e* ). There we derive formulae for the portion of the direct effect not mediated by N, i.e. E → Y , and the portion of the direct effect mediated by N, i.e. E → N → Y. These path-specific effects may be of independent scientific interest, as they further clarify the extent to which the exposure directly affects the outcome without involving any other pathway on the graph.

Next, we brieffy describe analogous expressions for conditional natural direct effects NDE(e, e* , c) = E {Y (e, M (e* )) – Y (e* , M (e* )) jc} . Similar to marginal effects, the challenge in identification of such effects lies in the need to identify E fY (e, M (e* )) jcg , which can be shown under the non-parametric structural equations model to be equal to:

$$\sum _{m,n,n^{\prime }}\mathbb{E}(Y\mid e,m,n,c)\mathrm{Pr}(M=m\mid e^{\ast },n^{\prime },c)\mathrm{Pr}(N\left(e\right)=n,N\left(e^{\ast }\right)=n^{\prime }\mid c)$$

Under monotonicity, it essentially follows from the proof of Result 1 for binary N that the above formula is identified by

$$\sum _{m,n,n^{\prime }}\mathbb{E}(Y\mid e,m,n,c)\mathrm{Pr}(M=m\mid e^{\ast },n^{\prime },c)f(n,n^{\prime },e,e^{\ast },c)$$

In epidemiologic applications, confounders (including the mediator-outcome confounders included in Figure 2) are routinely measured as polytomous factors, or as continuous factors, in which case Results 1 and 2 may not be particularly useful. In the following section, we give an alternative assumption that identifies NDE (e, e* ) even if the exposure dependent confounder N, i.e. the recanting witness, is polytomous or continuous.

Identification assuming no mediator-recanting-witness interaction

To state the identification result, we require additional notation. Let (c* , m* , n* ) denote a reference value of (c, m, n) and define

$$\begin{array}{cc}\hfill {\beta }_m(e,m,c)=& \mathbb{E}(Y\mid e,m,n^{\ast },c)-\mathbb{E}(Y\mid e,m^{\ast },n^{\ast },c)\hfill \\ \hfill {\beta }_m(e,n,c)=& \mathbb{E}(Y\mid e,m^{\ast },n,c)-\mathbb{E}(Y\mid e,m^{\ast },n^{\ast },c)\hfill \\ \hfill {\beta }_{m,n}(e,m,n,c)=& \mathbb{E}(Y\mid e,m,n,c)-\mathbb{E}(Y\mid e,m^{\ast },n,c)-\mathbb{E}(Y\mid e,m,n^{\ast },c)+\mathbb{E}(Y\mid e,m^{\ast },n^{\ast },c)\hfill \\ \hfill {\overline{\beta }}_{e,c}(e,c)=& \mathbb{E}(Y\mid e,m^{\ast },n^{\ast },c)\hfill \end{array}$$

β_m (e, m, c) and β_n (e, n, c) encode, on the additive scale, the average main effects of M and N on Y within levels of E and C, when n = n* and m = m* , respectively. β_m,n (e, m, n, c) encodes the interaction between m and n on the additive scale, within levels of E and C, and ${\overline{\beta }}_{e,c}(e,c)$ is the average outcome within levels of E and C. The average outcome can be decomposed on the additive scale in terms of β_m, β_n, β_m,n, ${\overline{\beta }}_{e,c}$:

$$\mathbb{E}(Y\mid e,m,n,c)={\beta }_m(e,m,c)+{\beta }_n(e,n,c)+{\beta }_{m,n}(e,m,n,c)+{\overline{\beta }}_{e,c}(e,c)$$ (14)

Crucially, note that this decomposition is fully nonparametric. Consider the following “no-M -N average interaction assumption” on the additive scale.

No M-N average interaction: The average additive interaction between M and N is zero, that is

$${\beta }_{m,n}(e,m,n,c)=0$$

Result 4: Assuming the nonparametric structural equations model (7)-(11), if “no M -N average interaction” assumption also holds, then $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$ is identified by the following formula

$$\sum _{m,c}{\beta }_m(e,m,c)\mathrm{Pr}(M=m\mid e^{\ast },c)\mathrm{Pr}(C=c)+\sum _{n,c}{\beta }_n(e,n,c)\mathrm{Pr}(N=n\mid e,c)\mathrm{Pr}(c=c)+\sum _c{\overline{\beta }}_{e,c}(e,c)\mathrm{Pr}(C=c)$$

The “no- M-N average interaction” assumption is testable, since the assumption places a restriction on the observed data distribution. In principle, a nonparametric test of interaction could be performed to assess this restriction as long as the observed data are not too highly dimensional. In practice, a simple parametric test of interaction could be used, or, alternatively, a semiparametric multiply robust test of additive interaction could be used to accommodate high-dimensional data, which also utilizes simple parametric models while minimizing the risk for bias due to modeling error.²⁵ The above result, which we prove in the eAppendix, states that when the assumption of no interaction holds, $\mathbb{E}\left\{Y(e,M\left(e^{\ast }\right))\right\}$ is identified under the nonparametric structural equations model and therefore NDE (e, e* ) is identified by the following simple expression

$$\begin{array}{cc}\hfill & NDE(e,e^{\ast })=\sum _{m,c}\{{\beta }_m(e,m,c)-{\beta }_m(e^{\ast },m,c)\}\mathrm{Pr}(M=m\mid e^{\ast },c)\mathrm{Pr}(C=c)\hfill \\ \hfill & +\sum _{n,c}\{{\beta }_n(e,n,c)\mathrm{Pr}(N=n\mid e,c)-{\beta }_n(e^{\ast },n,c)\mathrm{Pr}(N=n\mid e^{\ast },c)\}\mathrm{Pr}(C=c)\hfill \\ \hfill & +\sum _c\{{\overline{\beta }}_{e,c}(e,c)-{\overline{\beta }}_{e,c}(e^{\ast },c)\}\mathrm{Pr}(C=c)\hfill \end{array}$$

Comparison with the approach of Imai and Yamamoto

Imai and Yamamoto²⁶ have recently considered the issue of identification of NDE(e, e* ) in the context of exposure-dependent confounding of the mediator, and have proposed an alternative approach for inference. Brieffy, Imai and Yamamoto²⁶ relax the independence assumptions encoded in the nonparametric structural equations model defined by equations (7)-(11) corresponding to the causal diagram in Figure 2.

Specifically, using potential outcomes to encode their identifying assumptions, those authors assume that,

$$E⫫\{Y(e,m),M\left(e\right)\}\mid C=c,$$ (15)

$$Y(e,m)⫫M\mid C=c,E=e,N=n,$$ (16

$$N⫫\{Y(e,m),M\left(e\right)\}\mid C=c,E=e$$ (17)

These assumptions would be satisfied, for instance in a sequential randomized trial, in which E is randomized conditional on C, subsequently N is randomized conditional on (C, E), and finally M is randomized conditional on (C, E, N). Note that these assumptions are satisfied under the non-parametric structural equations model (7)-(11), however, as mentioned before, the nonparametric structural equations model encodes additional independence assumptions such as (5), which are not implied by assumptions (15)-(17).

In their paper, Imai and Yamamoto²⁶ adopt a linear-model specification with random effects for the outcome and the mediator, and establish that NDE(e, e* ) becomes identified under as sumptions (15) – (17), and an additional assumption that a nonidentified sensitivity parameter is known. They then obtain a sensitivity analysis by varying the sensitivity parameter and propose to report inferences about NDE(e, e* ) over a range of values of the nonidentified parameter. In the Appendix, we show that in the simple case of a binary mediator, which renders the linear-model specification of Imai and Yamamoto²⁶ unnecessary, NDE(e, e* ) is identified up to the unknown parameter:

$$\chi \left(e\right)=\mathbb{E}\left(\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\}M\left(e\right)\right)$$ (18)

The above parameter is not identified because it is a sum of the expectation of terms that involve counterfactuals under confficting exposure values, which are of general form $\mathbb{E}\left\{\left(Y(e^{\ast },m)M\left(e\right)\right)\right\}$, and are not identified under assumptions (15) – (17). In the Appendix, we show that the above sensitivity parameter is closely related to the sensitivity parameter of Imai and Yamamoto,²⁶ which can be written

$$\vartheta \left(e\right)=\mathbb{E}\left(\{Y(1,1)-Y(0,1)-Y(1,0)+Y(0,0)\}\left(e\right)\right)$$

for e = 0, 1, in fact, we also have that χ (1) = ν (1). We establish that using χ (e) as a sensitivity parameter is a more parsimonous approach, since only assumptions (15) and (16) are needed, and since χ (0) = 0, only χ (1) would need to be varied. Imai and Yamamoto require not only a linear-model specification and assumptions (15) – (17), but also that one vary both ν (0) and ν (1) .²⁶

As previously established by Robins and Greenland,¹ NDE(e, e* ) is identified under assumptions (15) and (16) and the additional assumption

$$\{Y,(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\}=0$$

of no individual causal additive interaction between E and M. The result holds because this latter assumption clearly implies that χ (e) is then known to be identically zero. In contrast, the approach of Imai and Yamamoto²⁶ allows for inferences about direct and indirect effects, without necessarily making the no-interaction assumption of Robins and Greenland¹, however as mentioned above, it requires that χ (e) takes on a known, albeit non-null value, which is subsequently varied to produce a sensitivity analysis.

In this paper we have also shown that NDE(e, e* ) is identified under the nonparametric structural equations model (7)-(11), assuming either monotonicity about the effects at the individual level of E on N, or no average interaction between N and M within levels of E and C. Thus, one should expect that either of our identifying assumptions also identifies χ (e) . We show in the Appendix that this is in fact the case. We emphasize that our result holds without the linearity assumption made by Imai and Yamamoto,²⁶ and without the untestable no-interaction assumption of Robins and Greenland,¹ and therefore our identifying assumptions are in fact distinct from these other conditions. Note, however, that our result relies on the nonparametric structural equations model independencies, which are themselves not experimentally enforceable nor verifiable. An instructive interpretation of the no-interaction assumption, is presented in the Appendix. The as sumption in essence states that, while the average causal main effect of the mediator may depend on N, the average exposure-mediator causal interaction does not, i.e.

$$\begin{array}{cc}\hfill & \mathbb{E}(\{Y(e,m)-Y(0,m)-Y(e,0)+Y(0,m)\}\mid M=m.C=c,E=e,N=n)\hfill \\ \hfill & =\mathbb{E}(\{Y(e,m)-Y(0,m)-Y(e,0)+Y(0,m)\}\mid M=m,C=c,E=e).\hfill \end{array}$$

Estimation of NDE (e, e*)

For estimation under the monotonicity assumption, first suppose that the vector of covariates C is of sufficiently low dimension to allow nonparametric inference. Focusing on the expression for $\mathbb{E}\left\{Y(1,M\left(0\right))\right\}$, needed to estimate NDE(e, e* ), with e = 1 and e* = 0, the following estimator is obtained using Result 1 according to the plug-in principle of maximum likelihood theory,

$$\begin{array}{cc}\hfill & n^{-1}\sum _i\sum _m[\widehat{\mathbb{E}}(Y\mid E=1,m,N=1,C_i)\widehat{\mathrm{Pr}}(M=m\mid E=0,N=1,C_i)\widehat{\mathrm{Pr}}(N=1\mid E=0,C_i)\phantom{]}\hfill \\ \hfill & +\widehat{\mathbb{E}}(Y\mid E=1,m,N=1,C_i)\widehat{\mathrm{Pr}}(M=m\mid E=0,N=0,C_i)\left\{\widehat{\mathrm{Pr}}(N=1\mid E=1,C_i)-\widehat{\mathrm{Pr}}(N=1\mid E=0,C_i)\right\}\hfill \\ \hfill & +\widehat{\mathbb{E}}(Y\mid E=1,m,N=0,C_i)\widehat{\mathrm{Pr}}(M=m\mid E=0,N=0,C_i)\widehat{\mathrm{Pr}}(N=0\mid E=1,C_i)\hfill \end{array}$$

where $\widehat{\mathbb{E}}(Y\mid e,m,n,c)$, $\widehat{\mathrm{Pr}}(M=m\mid e,n,c)$, $\widehat{\mathrm{Pr}}(N=1\mid e,c)$ are empirical versions of $\mathbb{E}(Y\mid e,m,n,c)$, Pr (M = m| e, n, c) , Pr (N = 1|e, c) , obtained, say, using saturated models.

In applications, C will often have too many levels for nonparametric inference to be practical, in which case a straightforward parametric approach is described below. To ground the discussion, consider a setting with continuous Y and M, and binary E, N. Suppose one posits the following regression models:

$$\mathbb{E}(Y\mid e,m,n,c)={\alpha }_0+{\alpha }_c^{\prime }c+{\alpha }_{e}e+{\alpha }_{m}m+{\alpha }_{n}n+{\alpha }_{mn}mn$$ (19)

$$\mathbb{E}(M\mid e,n,c)={\theta }_0+{\theta }_c^{\prime }c+{\theta }_{e}e+{\theta }_{n}n$$ (20)

$$\mathrm{logit}\mathrm{Pr}\{N=1\mid e,c\}={\eta }_0+{\eta }_{e}e+{\eta }_{c}c$$ (21)

where for simplicity we allow for a potential interaction between M and N in the model for Y, and all covariates are otherwise assumed to enter the models linearly. These assumptions could of course be relaxed to accommodate additional interactions and possible nonlinearities. Closed-form expressions for NDE(e, e* ) and NDE(e, e* , c), upon taking e = 1 and e* = 0 for models (19)-(21) are:

$$\begin{array}{cc}\hfill NDE(1,0)=& {\alpha }_e+\mathbb{E}\left\{({\alpha }_{mn}{\theta }_0+{\alpha }_{mn}{\theta }_c^{\prime }C+{\alpha }_n)\omega \left(C\right)\right\}\hfill \\ \hfill NDE(1,0,c)=& {\alpha }_e+({\alpha }_{mn}{\theta }_0+{\alpha }_{mn}\theta {\sigma }_c^{\prime }c+{\alpha }_n)\omega \left(c\right)\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \omega \left(c\right)=& \mathrm{Pr}\{N=1\mid e=1,c\}-\mathrm{Pr}\{N=1\mid e=0,c\}\hfill \\ \hfill =& [{\{1+\exp (-{\eta }_0-{\eta }_e-{\eta }_{c}C)\}}^{-1}-{\{1+\exp (-{\eta }_0-{\eta }_{c}C)\}}^{-1}]\hfill \end{array}$$

Above, α_e captures the effect of E along the direct path E → Y in Figure 2, whereas

$$({\alpha }_{mn}{\theta }_0+{\alpha }_{mn}{\theta }_c^{\prime }c+{\alpha }_n)\omega \left(c\right)$$

captures the effect of E along the path E → N → Y accounting for interaction between M and N. Regression parameters in (19) and (20) can be estimated via ordinary least squares using standard statistical software, and the parameters in (21) can similarly be obtained via maximum likelihood estimation of logistic regression. The estimator of NDE(1, 0) is then obtained upon replacing unknown parameters by their estimates. A standard application of the delta method can be used to compute standard errors, or, alternatively, one could apply the nonparametric bootstrap. In the Appendix, we provide SAS code (SAS, Cary, NC) and a simple data illustration of the methods described in this section using Proc NLMIXED in SAS, which also delivers valid standard error estimates and 95% confidence intervals.

Inference about NDE(1, 0) and NDE(1, 0, c) can likewise be obtained even when the monotonicity assumption does not apply, provided that the no-interaction assumption of Result 4 holds. Specifically, if N is now continuous, assume:

$$\mathbb{E}(Y\mid e,m,n,c)={\alpha }_0+{\alpha }_c^{\prime }c+{\alpha }_{e}e+{\alpha }_{m}m+{\alpha }_{n}n+{\alpha }_{em}em+{\alpha }_{en}en$$ (22)

$$\mathbb{E}(N\mid e,c)={\eta }_0+{\eta }_{e}e+{\eta }_{c}c$$ (23)

The regression model for Y in the above display differs from the previous model in that it now includes possible interactions between E and M, and between E and N, but no interaction between M and N. Additionally, suppose that M is modeled as in Equation (20), which implies that

$$\mathbb{E}(M\mid e,c)={\theta }_0^{†}+{\theta }_c^{†\prime }c+{\theta }_e^{†}e$$

where

$$\begin{array}{cc}\hfill {\theta }_0^{†}=& {\theta }_0+{\theta }_n{\eta }_0\hfill \\ \hfill {\theta }_0^{†}=& {\theta }_c+{\theta }_n{\eta }_c\hfill \\ \hfill {\theta }_e^{†}=& {\theta }_e+{\theta }_n{\eta }_e\hfill \end{array}$$

Applying Result 4, we obtain the following simple expressions:

$$\begin{array}{cc}\hfill NDE(1,0)=& {\alpha }_e+{\alpha }_{em}\left({\theta }_0^{†}+{\theta }_c^{†\prime }\mathbb{E}\left(C\right)\right)+{\alpha }_n{\eta }_e+{\alpha }_{en}({\eta }_0+{\eta }_e+{\eta }_c\mathbb{E}\left(C\right))\hfill \\ \hfill NDE(1,0,c)=& {\alpha }_e+{\alpha }_{em}\left({\theta }_0^{†}+{\theta }_c^{†\prime }c\right)+{\alpha }_n{\eta }_e+{\alpha }_{en}({\eta }_0+{\eta }_e+{\eta }_{c}c)\hfill \end{array}$$

As was the case under monotonicity, the coefficients in the above regression models for Y , M and N can be obtained using ordinary least squares estimation. NDE(1, 0) and NDE(1, 0, c) are estimated using the expression in the above display, evaluated at the estimated parameter values. In principle, the delta method could be used to derive analytical estimates of standard errors. Alternatively, the nonparametric bootstrap could be used and may be more convenient in practice. In the Appendix, we provide SAS code illustrating how these estimators and their standard errors can be obtained using Proc NLMIXED in SAS.

Final Remarks

Natural direct effects have previously been shown not to be nonparametrically identified under a nonparametric structural equations model when a variable affected by exposure confounds the mediator effects on the outcome. The primary contribution of this paper has been to show that natural direct effects are nonparametrically identified in the simple case of a binary recanting witness, but also in the case where the recanting witness is a vector of binary variables that satisfy a certain independence condition, provided that the exposure is known to have a monotonic effect on the recanting witness. For more general settings outside of these special cases, the situation of no additive interaction between exposures, mediator and recanting witness assumptions is required for identification. For instance, we have established that if the average interaction between the exposure and the mediator is independent of the recanting witness, natural direct effects are identified under a nonparametric structural equations model. Sample SAS code is provided to facilitate the use of proposed methods, together with the analysis of a simulated data set that confirms good finite-sample performance of the proposed methods.

These results are relevant to questions of mediation in observational epidemiology in the context of an exposure-induced mediator-outcome confounder. In addition, the results are of relevance to a broad class of intervention trials. Particularly within the context of experiments in psychology and the behavioral sciences, an intervention (e.g. cognitive behavioral therapy) is randomized to evaluate whether it improves some outcome (e.g. depressive symptoms). Often the theory behind the intervention is motivated by a belief that the intervention will principally operate through some intermediate process (e.g. attitudes toward negative life experience), and the intervention is often designed so as to target this intermediate. In the context of such trials, it is then of interest to assess mediation. Typically these trials involve some degree of non-compliance. Compliance to treatment is itself, of course, affected by the treatment, but compliance will likely affect both the intermediate and the outcome. Compliance in these trials serves as a mediator-outcome confounder affected by treatment. Our results are relevant to assessing mediation in such trials whenever compliance is all-or-none (i.e. a binary mediator-outcome confounder), or when compliance status and the mediator do not interact in their effects on the outcome (though the treatment and the mediator or the treatment and compliance status, would still be allowed to interact). The methods developed here provide useful tools for mediation analysis in such settings.

Finally, we should note that the methods described herein assume that the exposure-dependent confounder is observed. If this is not the case, one can still report a sensitivity analysis for unob served exposure-dependent confounding of the mediator-outcome relation using the semiparametric sensitivity analysis technique of Tchetgen Tchetgen and Shpitser.¹⁴

APPENDIX

Technical details of comparison to the approach of Imai and Yamamoto²⁶

Focusing on binary exposure and mediator variables, we begin by stating a key counterfactual representation of the natural indirect effect similar to that given in VanderWeele and Tchetgen Tchetgen²⁷:

$$\begin{array}{cc}\hfill & Y(e^{\ast },M\left(e\right))-Y(e^{\ast },M\left(e^{\ast }\right))\hfill \\ \hfill & =\{Y\left(e\right)-Y\left(e^{\ast }\right)\}+Y(e^{\ast },M\left(e\right))-Y(e,M\left(e\right))\hfill \\ \hfill & =\{Y\left(e\right)-Y\left(e^{\ast }\right)\}+\{Y(e^{\ast },1)-Y(e,1)-Y(e^{\ast },.0)+Y(e,0)\}M\left(e\right)\hfill \\ \hfill & +Y(e^{\ast },0)-Y(e,0)\hfill \end{array}$$

Thus, we have that

$$\begin{array}{cc}\hfill & \mathbb{E}[Y(e^{\ast },M\left(e\right))-Y(e^{\ast },M\left(e^{\ast }\right))]\hfill \\ \hfill & =\mathbb{E}\{Y\left(e\right)-Y\left(e^{\ast }\right)\}-\mathbb{E}\{Y(e,0)-Y(e^{\ast },0)\}\hfill \\ \hfill & -\mathbb{E}\left[\{Y(e,1)-Y(e^{\ast },1)-Y(e,0)+Y(e^{\ast },0)\}M\left(e\right)\right]\hfill \end{array}$$

It is well known that assumptions (15) and (16) are sufficient to identify $\mathbb{E}\{Y\left(e\right)-Y\left(e^{\ast }\right)\}$ and $\mathbb{E}\{Y(e,0)-Y(e^{\ast },0)\}$,¹⁹ and therefore assumptions (15)-(17) clearly suffice to identify these two terms.

The term $\chi \left(e\right)=\mathbb{E}\left[\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\}M\left(e\right)\right]$ is, however, not identified under assumptions (15) (17). This parameter is closely related to the sensitivity parameter of Imai and Yamamoto,²⁶ who, under a linear model specification, recover identification of the direct and indirect effects, upon fixing the sensitivity parameter:

$$\begin{array}{cc}\hfill & \mathrm{Cov}[\{Y(1,1)-Y(0,1)-Y(1,0)+Y(0,0)\},M\left(e\right)]∕\sqrt{\mathrm{Var}\left(M\left(e\right)\right)}\hfill \\ \hfill & =\mathbb{E}\left[\{Y(1,1)-Y(0,1)-Y(1,0)+Y(0.0)\}[M\left(e\right)-\mathbb{E}\left\{M\left(e\right)\right\}]\right]∕\sqrt{\mathrm{Var}\left(M\left(e\right)\right)}\hfill \\ \hfill & =\mathbb{E}\left[\{Y(1,1)-Y(0,1)-Y(1,0)+Y(0.0)\}[M\left(e\right)-\mathbb{E}\left\{M\left(e\right)\right\}]\right]∕\sqrt{\mathrm{Var}\left(M\left(e\right)\right)}\hfill \\ \hfill & =\vartheta \left(e\right)∕\sqrt{\mathrm{Var}\left(M\left(e\right)\right)}-\mathbb{E}\left\{M\left(e\right)\right\}∕\sqrt{\mathrm{Var}\left(M\left(e\right)\right)}.\hfill \end{array}$$

where

$$\vartheta \left(e\right)=\mathbb{E}\left[\{Y(1,1)-Y(0,1)-Y(1,0)+Y(0,0)\}M\left(e\right)\right]$$

is not identified under assumptions (15) – (17), while $\mathbb{E}\left\{M\left(e\right)\right\}$ and Var (M (e)) are identified.

Then, we note that Imai and Yamamoto²⁶ essentially vary the nonidentified parameters ν (e), e = 0, 1, in a sensitivity analysis. In contrast, we have shown that (for binary M) it actually suffices to fix χ (1) = ν (1) in order to recover identification of natural direct and indirect effects, since χ (0) = 0, resulting in a more parsimonous sensitivity analysis than that suggested by Imai and Yamamoto.²⁶

Furthermore, next we show that χ (1) is identified under the nonparametric structural equations model defined by equations (7) – (11) and the no-average N M interaction assumption, which allows for an alternative proof of the identification result in Result 4, which is more clearly related to Imai and Yamamoto.²⁶

Consider the nonparametric structural equations model defined by equations (7)-(11), then one can verify that

$$\begin{array}{cc}\hfill & \mathbb{E}\{Y,(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,e,n,c\}\hfill \\ \hfill & =\mathbb{E}\{Y(e,1,n,c)-Y(0,1,n,c)-Y(e,0,n,c)+Y(0,0,n,c)\}\hfill \\ \hfill & ={\beta }_m(1,m,c)+{\beta }_{m,n}(e,m,n,c)\hfill \end{array}$$

Therefore, the no-average N –M interaction β_m,n (e, m, n, c) = 0, is equivalent to

$$\begin{array}{cc}\hfill & \mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,e,n,c\}\hfill \\ \hfill & =\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,e,c\}\hfill \end{array}$$

Furthermore,

$$\begin{array}{cc}\hfill \chi \left(e\right)=& \mathbb{E}\left[\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\}M\left(e\right)\right]\hfill \\ \hfill =& \chi \left(e\right)=\mathbb{E}\left[\mathbb{E}\{Y(e,1)-Y(e,0)+Y(0,0)\mid M\left(e\right),C\}M\left(e\right)\right]\hfill \\ \hfill =& \sum _c\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,c\}\mathrm{Pr}(M(e,c)=1\mid c)\mathrm{Pr}(C=c)\hfill \\ \hfill =& \sum _c\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,e,c\}\mathrm{Pr}(M(e,c)=1\mid e,c)\mathrm{Pr}(C=c)\hfill \end{array}$$

(by nonparametric structural equations model independence)

$$\begin{array}{cc}\hfill =& \sum _c\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M=1,e,c\}\mathrm{Pr}(M(e,c)=1\mid c,e)\mathrm{Pr}(C=c)\hfill \\ \hfill =& \sum _c\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M=1,e,c,n\}\mathrm{Pr}(M=1\mid c,e)\mathrm{Pr}(C=c)\hfill \end{array}$$

(by interaction independence)

Next, we have

$$\mathbb{E}\{Y(e,1)\mid M=1,e,c,n\}=\mathbb{E}\{Y\mid M=1,e,c,n\};$$

$$\begin{array}{cc}\hfill \mathbb{E}\{Y(0,1)\mid M=1,e,c,n\}& =\mathbb{E}\{Y(0,1,c,n)\mid M(e,c,n)=1,E\left(c\right)=e,c,N(e,c)=n\}\hfill \\ \hfill & =\mathbb{E}\{Y(0,1,c,n)\mid M(0,c,n)=1,E\left(c\right)=0,c,N(0,c)=n\}\hfill \\ \hfill & \left(\text{by nonparametric structural equations model independence}\right)\hfill \\ \hfill & =\mathbb{E}\{Y\mid M=1,E=0,c,n\};\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathbb{E}\{Y(e,0)\mid M=1,e,c,n\}& =\mathbb{E}\{Y(e,0,c,n)\mid M(e,c,n)=1,E\left(c\right)=e,c,N(e,c)=n\}\hfill \\ \hfill & =\mathbb{E}\{Y(e,0,c,n)\mid M(e,c,n)=0,E\left(c\right)=e,c,N(e,c)=n\}\hfill \\ \hfill & \left(\text{by nonparametric structural equations model independence}\right)\hfill \\ \hfill & =\mathbb{E}\{Y\mid M=0,e,c,n\};\hfill \end{array}$$

and likewise

$$\begin{array}{cc}\hfill \mathbb{E}\{Y(0,0)\mid M=1,e,c,n\}& =\mathbb{E}\{Y(0,0,c,n)\mid M(e,c,n)=1,E\left(c\right)=e,c,N(e,c)=n\}\hfill \\ \hfill & =\mathbb{E}\{Y(e,0,c,n)\mid M(0,c,n)=0,E\left(c\right)=0,c,N(0,c)=n\}\hfill \\ \hfill & \left(\text{by nonparametric structural equations model independence}\right)\hfill \\ \hfill & =\mathbb{E}\{Y\mid M=0,E=0,c,n\};\hfill \end{array}$$

proving the identification result.

Under the nonparametric structural equations model defined by equations (7) – (11) and the monotonicity assumption, we have that

$$\begin{array}{cc}\hfill \chi \left(e\right)=& \mathbb{E}\left[\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\}M\left(e\right)\right]\hfill \\ \hfill =& \chi \left(e\right)=\mathbb{E}\left[\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M\left(e\right),C\}M\left(e\right)\right]\hfill \\ \hfill =& \sum _c\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,c\}\mathrm{Pr}(M(e,c)=1\mid c)\mathrm{Pr}(C=c)\hfill \\ \hfill =& \sum _c\mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,N(e,c)=n,N(e^{\ast },c)=n^{\prime },c\}\hfill \\ \hfill & \times \mathrm{Pr}(N(e,c)=n,N(e^{\ast },c)=n^{\prime }\mid c,M(e,c)=1)\mathrm{Pr}(M(e,c)=1\mid c)\mathrm{Pr}(C=c)\hfill \end{array}$$

Note that

$$\mathrm{Pr}(N(e,c)=n,N(e^{\prime },c)=n^{\prime }\mid c,M(e,c)=1)=\frac{\mathrm{Pr}(M(e,c)=1\mid N(e,c)=n,N(e^{\ast },c)=n^{\prime },c)\mathrm{Pr}(N(e,c)=n,N(e^{\ast },c)=n^{\prime }\mid c)}{{\sum }_m\mathrm{Pr}(M(e,c)=m\mid N(e,c)=n,N(e^{\ast },c)=n^{\prime },c)\mathrm{Pr}(N(e,c)=n,N(e^{\ast },c)=n^{\prime }\mid c)}$$

which is identified by monotonicity (see the proof of Result 1) and the nonparametric structural equations model assumptions. Likewise,

$$\begin{array}{cc}\hfill & \mathbb{E}\{Y(e,1)-Y(0,1)-Y(e,0)+Y(0,0)\mid M(e,c)=1,N(e,c)=n,N(e^{\ast },c)=n^{\prime },c\}\hfill \\ \hfill & =\mathbb{E}\{Y(e,1)\mid M(e,c)=1,e,N(e,c)=n,c\}\hfill \\ \hfill & -\mathbb{E}\{Y(0,1)\mid M(e,c)=1,E=0,N(0,c)=n^{\prime },c\}\hfill \\ \hfill & -\mathbb{E}\{Y(e,0)\mid M(e,c)=0,e,N(e,c)=n,c\}\hfill \\ \hfill & +\mathbb{E}\{Y(0,0)\mid M(0.c)=1,e=0,N(0,c)=n^{\prime },c\}\hfill \end{array}$$

is identified by the nonparametric structural equations model assumptions.