Dynamic Treatment Regimes

Abstract

A dynamic treatment regime consists of a sequence of decision rules, one per stage of intervention, that dictate how to individualize treatments to patients based on evolving treatment and covariate history. These regimes are particularly useful for managing chronic disorders, and fit well into the larger paradigm of personalized medicine. They provide one way to operationalize a clinical decision support system. Statistics plays a key role in the construction of evidence-based dynamic treatment regimes – informing best study design as well as efficient estimation and valid inference. Due to the many novel methodological challenges it offers, this area has been growing in popularity among statisticians in recent years. In this article, we review the key developments in this exciting field of research. In particular, we discuss the sequential multiple assignment randomized trial designs, estimation techniques like Q-learning and marginal structural models, and several inference techniques designed to address the associated non-standard asymptotics. We reference software, whenever available. We also outline some important future directions.

1 Introduction

Personalized medicine is an increasingly popular theme in today’s health care. Operationally, personalized treatments are decision rules that dictate what treatment to provide given a patient state (consisting of demographics, results of diagnostic tests, genetic information, etc.). Dynamic treatment regimes (DTRs) [1, 2, 3, 4, 5, 6] generalize personalized medicine to time-varying treatment settings in which treatment is repeatedly tailored to a patient’s time-varying – or dynamic – state. DTRs are alternatively known as adaptive treatment strategies [7, 8, 9, 10, 11] or treatment policies [12, 13, 14]. These decision rules offer an effective vehicle for personalized management of chronic conditions, e.g. alcohol and drug abuse, cancer, diabetes, HIV infection, and mental illnesses, where a patient typically has to be treated at multiple stages, adapting the treatment (type, dosage, timing) at each stage to the evolving treatment and covariate history. DTRs underpin clinical decision support systems – described as a key element of the chronic care model [15].

A simple example of a DTR arising in the treatment of alcohol dependence is: After the patient completes an intensive outpatient program, provide the medication naltrexone along with face-to-face medical management. If within the following two months the patients experiences 2 or more heavy drinking days, then immediately augment the naltrexone with a cognitive behavioral therapy. Otherwise at the end of the two months, provide telephone disease management in addition to the naltrexone. A second example given in Rosthøj et al. [16] is a DTR for use in guiding warfarin dosing to control the risk of both clotting and excessive bleeding. Here the decision rules input summaries of the trajectory of International Normalized Ratio (a measure of clotting tendency of blood) over the recent past and output recommendations concerning how much to change the dose of warfarin (if any). The third example, provided by Robins et al. [17] concerns a DTR with decision rules that input summaries of the trajectories of plasma HIV RNA and CD4 counts over the recent past and output when to start an asymptomatic HIV-infected subject on highly active antiretroviral therapy. In Section 3 different statistical methods for constructing the decision rules in a DTR are reviewed.

1.1 Decision Problems

Traditionally personalized medicine concerns single stage decision making. In a single-stage (non-dynamic) decision problem one observes a random vector, the first observation, O₁, then one selects an action (here a treatment action), a₁, from a set ${\mathcal{A}}_1$ of actions and then depending on which action was selected, observes a second observation, O₂(a₁). To avoid technical details and for simplicity, here and below, we assume sufficient regularity for all statements. A decision rule, say d₁, is a mapping from the range of O₁ into ${\mathcal{A}}_1$. The quality of a treatment for a particular value of O₁ is evaluated in terms of its utility, say r(O₁, a₁, O₂(a₁)), for r a known function. The utility may be a summary of one outcome, such as percent days abstinent in an alcohol dependence study or a composite outcome; for example, in Wang et al. [18] the utility is a compound score numerically combining information on treatment efficacy, toxicity, and the risk of disease progression. The optimal decision rule outputs the treatment (action) that maximizes the expected utility, $\mathcal{U}(o_1;a_1)=E\left[r\right(O_1,a_1,O_2\left(a_1\right))\mid O_1=o_1]$; this is personalized decision making since the choice of optimal treatment depends on o₁. Equivalently the optimal decision rule is given by arg max_d1 $E\left[\mathcal{U}\right(O_1;d_1\left(O_1\right)\left)\right]$, where the maximum is taken over all functions on the range of O₁. $E\left[\mathcal{U}\right(O_1;d_1\left(O_1\right)\left)\right]$ is called the Value of the decision rule d₁.

Constructing DTRs involves solving, or estimating quantities relevant in, a multi-stage decision problem. In multi-stage decision problems, observations are interweaved with action selection; denote such a sequence by $O_1,a_1,O_2\left(a_1\right),a_2,O_3\left({\stackrel{‒}{a}}_2\right),\dots ,O_k\left({\stackrel{‒}{a}}_{K-1}\right),a_K,O_{K+1}\left({\stackrel{‒}{a}}_K\right)$ where ${\stackrel{‒}{a}}_j=\{a_1,\dots ,a_j\}$ and $O_{j+1}\left({\stackrel{‒}{a}}_j\right)$ denotes the observation made at stage j + 1 subsequent to the selection of the action sequence ${\stackrel{‒}{a}}_j$. A DTR is a sequence of decision rules, ${\stackrel{‒}{d}}_K=(d_1,\dots ,d_K)$; the decision rule d_j is a mapping from the range of $(O_1,a_1,\dots ,O_j({\stackrel{‒}{a}}_{j-1}\left)\right)$ into the jth action space, ${\mathcal{A}}_j$. When K = 2 and the treatment actions are discrete, the Value of the DTR (d₁, d₂) can be written on one line as

$$E\left[\sum _{a_1\in {\mathcal{A}}_1}{1}_{a_1=d_1\left(O_1\right)}\sum _{a_2\in {\mathcal{A}}_2}{1}_{a_2=d_2{(O_1,a_1,O_2(a_1\left)\right)}^r}(O_1,a_1,O_2(a_1),a_2,O_3(a_1,a_2\left)\right)\right]$$ (1)

(the generalization to more than two stages is straightforward). Using this formula we might compare two or more DTRs in terms of their Value or equivalently their expected utility. The optimal DTR is the set of decision rules, ${\stackrel{‒}{d}}_K$, that maximize the Value.

Constructing the optimal decision rules in multi-stage decision problems is challenging due to the time-varying or dynamic nature of this problem. Historically, an early method for solving (e.g. construct the optimal decision rules) multi-stage decision problems is dynamic programming (DP), which dates at least back to Bellman [19]. The primary reason why classical DP algorithms have seen little use in DTR research is due to the fact that these algorithms require complete knowledge of, or a full model for, the multivariate distribution of the data for any set of actions; this is impractical in many application areas (curse of modeling) [20]. Secondly, DP methods are computationally very expensive, and they become hard to manage in moderately high-dimensional problems; in other words, they suffer from the curse of dimensionality [21]. But DP provides an important theoretical and conceptual foundation for research in multi-stage decision problems; in fact, as will be seen, many present day estimation methods build on classical DP algorithms, while relaxing its stringent requirements.

2 Data Sources for Constructing DTRs

Most statistical research in the arena of DTRs concerns: (a) the comparison of two or more preconceived DTRs in terms of their Value; and (b) the estimation of the optimal DTR, i.e. to estimate the sequence of decision rules, one per stage, that result in the highest Value, within a class of DTRs. In each case the data used in comparing or constructing DTRs are usually from: (i) sequentially randomized studies, or (ii) longitudinal observational studies, or (iii) dynamical system models. Research based on the first source of data, that from sequentially randomized studies, is experiencing a period of rapid growth, due to the increasing number of clinical trials in which many of the patients are randomized multiple times, in a sequential manner. However, by far, the majority of statistical research, led by Robins’ pioneering work [1, 2, 3, 4] concerns the use of data from longitudinal, observational studies. The third data source, based on simulating from or otherwise using existing dynamical system models has seen much less use in DTR development. In this section we briefly review the first two types of data sources, their advantages and drawbacks, and the assumptions required to perform valid analyses in each, along with some examples. Dynamical system models will be discussed in Section 3.

2.1 Sequentially Randomized Trials (SMART)

Initially, beginning with Robins’ work [1, 2, 3, 4], sequentially randomized trials were used as a conceptual tool to precisely state the inferential goals in DTR research. More recently trial designs, known as Sequential Multiple Assignment Randomized Trial (SMART) designs [7, 22, 11], have been implemented in practice. SMART designs involve an initial randomization of patients to available treatment actions, followed by re-randomizations at each subsequent stage of some or all of the patients to treatment actions available at that stage. The re-randomizations and set of treatment actions at each subsequent stage may depend on information collected in prior stages such as how well the patient responded to the previous treatment.

Recent SMARTs include: a smoking cessation study [23]; a study involving treatment of autism among children [24, 25]; a study involving interventions for children with attention deficit hyperactivity disorder [26, 27]; a study involving treatment for pregnant drug abusers [28, 25]; and a study involving alcohol-dependent individuals [25]. For a list of some further SMARTs see the website http://methodology.psu.edu/ra/adap-treat-strat/projects.

To make the discussion more concrete, see Figure 1 for a hypothetical SMART design based on the addiction management example introduced earlier. In this trial, each participant is randomly assigned to one of two possible initial treatments: cognitive behavioral therapy (CBT) or naltrexone (NTX). A participant is classified as a non-responder or responder to the initial treatment according to whether s/he does or does not experience more than two heavy drinking days during the next two months. A non-responder to NTX is re-randomized to one of the two subsequent treatment options: either a switch to CBT, or an augmentation of NTX with CBT (CBT+NTX). Similarly, a non-responder to CBT is re-randomized to either a switch to NTX, or an augmentation (CBT+NTX). Responders to the initial treatment receive telephone monitoring (TM) for an additional period of six months. One goal of the study might be to construct a DTR leading to a maximal mean number of non-heavy drinking days over 12 months.

Figure 1.

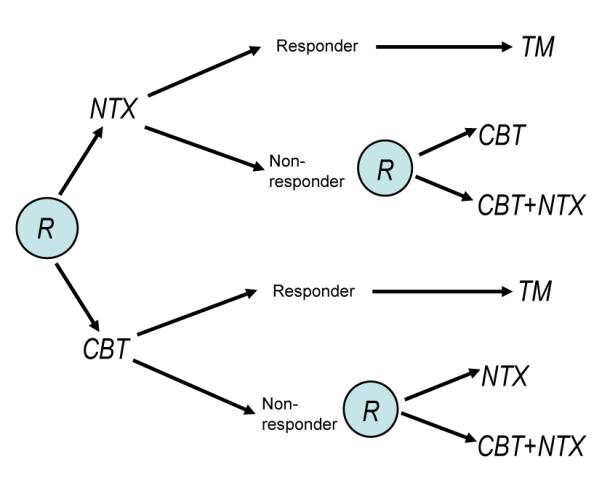
Hypothetical SMART design schematic for the addiction management example (an “R” within a circle denotes randomization at a critical decision point).

Denote the observable data trajectory for a participant in a two-stage SMART by (O₁, A₁, O₂, A₂, O₃), where O₁, O₂ and O₃ are the pretreatment information, intermediate outcomes and final outcomes, respectively. The randomized treatment actions are A₁ and A₂ and the primary outcome is Y = r(O₁, A₁, O₂, A₂, O₃) for r a known function. For example, in the addiction management study above, O₁ may include addiction severity and co-morbid conditions, O₂ may include the participant’s binary response status, side effects and adherence to the initial treatment, and Y may be the number of non-heavy drinking days over the 12-month study period.

To connect the distribution of the data collected in the above SMART to the distributions considered in the multistage decision problem in Section (1.1), we make a short digression into the field of causal inference. Recall that in the case of two stages, in Section (1.1), we denoted the sequence of random observations by (O₁, a₁, O₂(a₁), a₂, O₃(a₁, a₂)) for the selected actions (a₁, a₂). These observations are potential outcomes [29, 1]. Potential outcomes or counterfactual outcomes are defined as a person’s outcome had s/he followed a particular treatment (sequence), possibly different from the treatment (sequence) s/he was actually observed to follow. Consider, for example, a single-stage randomized trial in which participants can receive either a or a’. Accordingly, any participant in this study is conceptualized to have two potential second observations, O₂(a) and O₂(a’). However, only one of these – the one corresponding to the treatment a participant is randomized to – will be observed. Clearly, it is not possible to observe the O₂ under both treatments a and a’ without further data and assumptions (e.g. in a crossover trial with no carryover effect). Now suppose that participants are treated over two stages, and can receive at each stage either a or $a^{\prime }({\mathcal{A}}_1={\mathcal{A}}_2=\{a,a^{\prime }\left\}\right)$. In this case there are four sequences of potential observations, (O₂(a), O₃(a, a)), (O₂(a), O₃(a, a’)), (O₂(a’), O₃(a’, a)), (O₂(a’), O₃(a’, a’)); only one of these sequences will be observed on any given participant.

To connect the potential observations to the observations made during the conduct of a SMART, we make two assumptions [4]:

1. Consistency: The potential outcome under the observed treatment and the observed outcome agree.

2. No unmeasured confounders: For any treatment sequence ${\stackrel{‒}{a}}_K$, treatment A_j is independent of future (potential) outcomes, $O_{j+1}\left({\stackrel{‒}{a}}_j\right),\dots ,O_K\left({\stackrel{‒}{a}}_{K-1}\right),O_{K+1}\left({\stackrel{‒}{a}}_K\right)$, conditional on the history $H_j=({\stackrel{‒}{O}}_j,{\stackrel{‒}{A}}_{j-1})$. That is, for any possible treatment sequence ${\stackrel{‒}{a}}_K$,

$$A_j\perp \phantom{\mid }\left(O_{j+1}\right({\stackrel{‒}{a}}_j),\dots ,O_K({\stackrel{‒}{a}}_{K-1}),O_{K+1}({\stackrel{‒}{a}}_K\left)\right)\mid H_j{\forall }_j=1,\dots ,K.$$

The consistency assumption subsumes Rubin’s [30] more explanatory Stable Unit Treatment Value Assumption (SUTVA), which is: each participant’s potential outcome is not influenced by the treatment applied to other participants. In clinical trials SUTVA is most often violated when the treatment is not well defined. For example the treatment as defined may not specify that some aspects of the treatment are provided in a group setting containing multiple participants from the trial. In this case the response of one participant to treatment may influence the response of another participant if they are in the same group.

Under the consistency assumption, the potential outcomes in a two stage SMART are connected to the observable data by O₂ = O₂(A₁) and O₃ = O₃(A₁, A₂). The “no unmeasured confounders” assumption holds in a SMART design if the randomization probabilities depend at most on the past observations; more precisely, the randomization probabilities for A₁ and A₂ may depend on O₁ and (O₁, A₁, O₂), respectively. Under this assumption, P(O₂(a₁) ≤ o₂∣O₁ = o₁) = P(O₂ ≤ o₂∣O₁ = o₁, A₁ = a₁), and P(O₃(a₁, a₂) ≤ y∣O₁ = o₁, O₂(a₁) = o₂) = P (O₃ ≤ y∣O₁ = o₁, A₁ = a₁, O₂ = o₂, A₂ = a₂). This implies that the Value for a DTR can be written as a function of the multivariate distribution of the observable data obtained from a SMART; in the case of two stages (1) can be written as

$$E\left[E\left[\sum _{a_1\in {\mathcal{A}}_1}{1}_{a_1=d_1\left(H_1\right)}E\left[\sum _{a_2\in {\mathcal{A}}_2}{1}_{a_2=d_2\left(H_2\right)}E\left[r\right(H_2,A_2,O_3)\mid H_2,A_2=a_2]\mid \right]\mid H_1,A_1=a_1\phantom{\mid }\right]\right]$$

(recall H₁ = O₁ and H₂ = (O₁, A₁, O₂)). A similar result holds for settings with more than two stages. Thus the validity of the two assumptions ensures that data from SMARTs can be effectively used to evaluate pre-specified DTRs or to estimate the optimal DTR within a certain class.

2.1.1 Some Practical Considerations in Designing a SMART

A variety of authors recommend that the design of a SMART be no more complicated than necessary. Indeed the class of treatment options at each stage should not be unnecessarily restricted [22, 11]. For example it is better to use a low dimensional summary criterion (e.g. responder/non-responder status, as used in the example addiction management SMART) instead of all intermediate outcomes (e.g. improvement of symptom severity, side-effects, adherence etc.) to restrict the class of possible treatments. Furthermore a SMART is best viewed as one trial among a series of randomized trials intended to develop and/or refine a DTR. It should eventually be followed by a confirmatory randomized trial that compares the developed regime and an appropriate control [11]. That is, the construction of DTRs is a developmental endeavor as opposed to confirmatory. In this sense a scientist employing a SMART design has a similar goal to Box’s [31] goal of developing multicomponent treatments. Indeed the SMART can be viewed as an extension of the factorial design to the setting in which time and sequencing of treatments play a crucial role [32]. As a result often the primary hypothesis, that is, the hypothesis used to determine the sample size for the trial, concerns a main effect. However due to the multiple randomizations, a variety of interesting secondary research questions can be addressed with randomized data. Note that the SMART may or may not be powered to address these secondary hypothesis questions.

Most often the primary hypothesis concerns the main effect of the first stage treatment. For example, in the addiction management study an interesting primary research question would be: “marginalizing over secondary treatments, what is the best initial treatment on average?”. In other words, here the researcher wants to compare the mean primary outcome of the group of patients receiving NTX as the initial treatment with the mean primary outcome of those receiving CBT. Another interesting primary question could concern the main effect of a second stage treatment: “on average what is the best secondary treatment, a ‘switch’ or an ‘augmentation’, for non-responders to initial treatment?”. Here the researcher might compare the mean primary outcome of non-responders assigned to switch with the mean primary outcome of non-responders assigned to augmentation. In all of these cases sample size formulae are standard or easily derived.

Alternatively the primary research question may concern the comparison of two of the embedded DTRs. In the example addiction management SMART there are 4 embedded DTRs, corresponding to 2 options for the first stage treatment and 2 options for the second stage treatment for nonresponders (note that there is only one option for the responders). For example, one embedded regime in this SMART is: ‘treat the patient with NTX at stage 1; give TM at stage 2 if the patient is a responder, and give CBT at stage 2 if the patient is a non-responder’; other embedded regimes can be described similarly. Determining appropriate sample sizes to compare two embedded DTRs in terms of a continuous outcome was considered by Murphy [11], Oetting et al. [33], and Dawson and Lavori [34, 35]. A web application that calculates the required sample size for a SMART design for a continuous endpoint can be found at http://methodologymedia.psu.edu/smart/samplesize. Much work has concerned survival endpoints [12, 13, 14, 36]. Relevant sample size formulae can be found in Feng and Wahed [37] and Li and Murphy [38]. A web application for sample size calculation in this case can be found at http://methodologymedia.psu.edu/logranktest/samplesize.

2.1.2 SMART versus Other Designs

The SMART design discussed above involves stages of treatment and/or experimentation. In this regard, it bears superficial similarity with adaptive designs [39]. The term, “adaptive design” is an umbrella term used to denote a variety of trial designs that allow certain trial features to change based on accumulating data while maintaining statistical, scientific, and ethical integrity of the trial [39]. In a SMART design, each participant moves through multiple stages of treatment, while in adaptive designs each stage involves different participants. The goal of a SMART is to develop a good DTR that could benefit future patients. Many adaptive designs try to provide the most efficacious treatment to each patient in the trial based on the current knowledge available at the time that a participant is randomized. In a SMART, unlike in an adaptive design, the design elements such as the final sample size, randomization probabilities and treatment options are pre-specified. SMART designs involve within-participant adaptation of treatment, while adaptive designs involve between-participant adaptation. While in some settings it is possible to incorporate some adaptive elements into a SMART design [10, 40], how to optimally do this is an open question that warrants further research.

SMART designs have some operational similarity with classical crossover trial designs; however they differ greatly in the scientific goal. In particular a crossover design is typically used to contrast the effects of stand-alone treatments whereas the SMART is used to develop a DTR, that is, a sequence of treatments. Note that treatment allocation at any stage after the initial stage of a SMART typically depends on a participant’s intermediate outcome (response/non-response). However, in a crossover trial, participants receive all the candidate treatments irrespective of their intermediate outcomes. And most importantly, it is crucial in a crossover trial to attempt to wash out the carryover effects, whereas the process of constructing a DTR involves harnessing carryover effects so as to lead to improved outcomes. That is, carryover effects such as synergistic interactions between treatments at different stages may lead to a better DTR as compared to a DTR in which there are no carryover effects.

2.2 Observational Studies

In observational studies the treatments are not randomized; in particular, the reasons why different individuals receive differing treatments or the reasons why one individual receives different treatments at different times are not known with certainty. Certainly data in which the treatments are (sequentially) randomized, when available, is preferable for making inferences concerning DTRs. However observational studies are the most common source of data for constructing DTRs and indeed most research in statistics has concentrated on how best to use observational data.

In observational data associations observed in the data (e.g., between treatment and outcome) may be partially due to the unobserved or unknown reasons why individuals receive differing treatments as opposed to the effects of the treatments. Thus to conduct inference, assumptions are required. Assumptions such as the consistency assumption and the no unmeasured confounders assumption discussed earlier can be used to justify estimation and inference based on observational data; the plausibility of these assumptions is generally best justified by scientific, expert knowledge. A variety of studies aimed at constructing DTRs from observational data have been undertaken. Data sources include hospital databases [16, 17, 41, 42], randomized encouragement trials [43], and cohort studies [44].

The assumption of no unmeasured confounders must be given careful consideration and thought in the observational data setting. Recall the no unmeasured confounders is the assumption that conditional on the past history, treatment received at stage j is independent of future potential observations and outcome: $P(A_j=a\mid H_j,O_{j+1}({\stackrel{‒}{a}}_j),\dots ,O_K({\stackrel{‒}{a}}_{K-1}),O_{K+1}({\stackrel{‒}{a}}_K\left)\right)=P(A_j=a\mid H_j)$. This assumption allows us to effectively view the observational data as coming from a sequentially randomized trial, albeit with unknown as opposed to known randomization probabilities at stage j. The assumption may be (approximately) true in observational settings where all relevant common causes of outcomes and treatment have been observed.

In addition to careful consideration of causal inference issues, using observational data to construct DTRs requires careful thought concerning how the data may restrict the set of DTRs that can be assessed absent further assumptions. This set is called the feasible [45] or viable [18] DTRs. Feasibility of a DTR ${\stackrel{‒}{d}}_K$ requires a positive probability that some participants in the study will have followed ${\stackrel{‒}{d}}_K$.

3 Data Analysis

As mentioned in Section 2, two common goals are: (a) the estimation/comparison of a small number of DTRs in terms of their Value; and (b) to estimate the optimal DTR within a certain class. In the following, we review the analysis strategies for both. Throughout we assume that both the no-unmeasured confounding and consistency assumptions hold and that all DTRs considered are feasible.

Weighting is often used to address both (a) and (b). Weights or inverse probability of treatment weights (IPTW) were originally developed to estimate the Value of non-dynamic regimes [46, 47], but later adapted to the problem of estimating the Value of DTRs. IPTWs were used to estimate the Values of a small number of DTRs in Murphy et al. [48] and Wang et al. [18]. To see why weights might be used, consider a SMART as in Figure 1, with only one option for responding participants (e.g. telephone monitoring). Suppose that the treatment assignment probabilities at stage 1 and also for the non-responders are uniform (randomization probability is 0.5). Suppose further that we want to estimate the Value of the embedded DTR, “treat the patient with NTX at stage 1; give TM at stage 2 if the patient is a responder, and give CBT at stage 2 if the patient is a non-responder.” To estimate the Value we utilize the outcome of all participants with treatment patterns consistent with this DTR. However within this group of participants there is an over-representation of responders compared to non-responders because the non-responders were subdivided in the trial but the responders were not. The IPTWs are used to adjust for over-representation of participants across the treatment patterns consistent with a given DTR. In this example, data from responders would have a weight of $\frac{1}{0.5}$ as responders have been randomized only in stage 1 (with a probability of 0.5) whereas data from non-responders would have a weight of $\frac{1}{\left(0.5\right)\left(0.5\right)}$ as they have been randomized twice (each with a probability of 0.5). See Wang et al. [18] and Nahum-Shani et al. [26] for detailed explanations of how IPTWs can be used to account for this over/under representation in SMARTs. Lunceford et al. [12], Wahed and Tsiatis [13, 14], and Miyahara and Wahed [49] use ITPW weights in estimating the Value of DTRs in the survival analysis setting. Improved versions of IPTW estimator are available in papers by Robins and colleagues [48, 17, 41, 50] and Zhang et al. [51].

3.1 Direct Methods for Estimating an Optimal DTR

For notational simplicity, let d denote the DTR, ${\stackrel{‒}{d}}_K$, in the following. Recall from Section 1 that the Value of a DTR is the mean of the utility, marginalized over all observations that might be impacted by the treatment. In direct methods one specifies a class of DTRs $\mathcal{D}$ (see below for an example), estimates the Value for each candidate DTR $d\in \mathcal{D}$, say ${\widehat{V}}^d$ and then selects the DTR in $\mathcal{D}$ with maximal estimated Value.

The use of IPTWs for estimating an optimal DTR was pioneered by Robins and colleagues [17, 41]. For a simple example consider DTRs that use a risk score to indicate when to initiate treatment. At the clinic visit at which the risk score is greater than or equal to x, treatment is initiated. The Value varies by DTR, that is, by x. In Robins et al. [17] the Value is parameterized as a polynomial function in x and pretreatment variables; for example, V(x; β) = β₀ + β₁x + β₂x². The optimal DTR is to initiate treatment when the risk score is greater than or equal to x₀ where x₀ = arg max_x V(x, β). To estimate the optimal DTR, we need estimators of the β’s. In the simplest setting the β’s are estimated by solving an IPTW weighted estimating equation. To improve efficiency in the estimation of the β’s, Robins et al. [17] take advantage of the fact that some individuals’ treatment sequence will be consistent with more than one DTR. For example if the individual initiates treatment with a risk score of 12 and at the prior office visits the individual’s risk score was always lower than 10, then this individual has a treatment sequence consistent with x = 10, 11 and 12. To improve efficiency this individual’s data is used to estimate the Value V (x; β) for x = 10, 11, 12. Operationally, the estimating equation uses three replicates of this individual’s data. In the above example the individual is replicated twice to produce three replicates and the replicated outcome Y is relabeled as Y₁₀, Y₁₁, Y₁₂ (Y₁₀ = Y₁₁ = Y₁₂). In general the number of replicates of an individual’s data is equal to the number of DTRs with which their observed treatment is consistent.

The β’s can be estimated by solving the weighted estimating equation

$$0={\mathbb{P}}_n\left[\sum _x{w}_{d^x,\pi }\cdot \frac{\partial }{\partial \beta }V(x;\beta )\left(Y_x-V(x;\beta )\right)\right]$$

where the ${\mathbb{P}}_n$ is an average over the augmented data set (containing the replicates). Nahum-Shani et al. [26], in the context of SMART, provides an intuitive discussion of why replication of participants can be used to account for the fact that a participant’s observed treatment is consistent with more than one DTR. The observational data setting can be more complicated; see Robins et al. [17] and Shortreed and Moodie [52] for detailed expositions. Related work that compares a range of candidate DTRs by incorporating a treatment-tailoring threshold can be found in Hernán et al. [53], Petersen et al. [54], van der Laan and Petersen [55], and Cotton and Heagerty [42].

Direct methods for a one-stage decision making setting (e.g. K = 1) has seen a great deal of research; here the single decision rule is often called an individualized decision rule. As highlighted by Qian and Murphy [56], the one stage decision making problem has a close connection with classification. Subsequently, methods based on classification [57, 58] have been proposed for estimating the decision rule. Other work in the one-stage decision setting include Cai et al. [59] and Imai and Ratkovicz [60].

3.2 Indirect Methods for Estimating an Optimal DTR

Indirect approaches to estimating the optimal DTR are commonly employed when scientists wish to consider decision rules that may depend on multiple covariates or depend on covariates in a complex manner. In the indirect approach the stage-specific conditional mean outcomes (called Q-functions) or contrasts thereof are modeled first, and then the optimal decision rules are found via maximization of these estimated conditional means or contrasts. These methods were originally developed in the reinforcement learning literature within computer science, but later adapted to statistics. One such procedure that has become particularly popular in the DTR literature is Q-learning [21]. Q-learning is an approximate dynamic programming method – approximate because the Q-functions are approximated by the use of data and models. In its simplest incarnation, Q-learning uses linear models for the Q-functions, and can be viewed as an extension of least squares regression to multi-stage decision problems [61]. However, one can use more flexible models for the Q-functions, e.g. regression trees [62] or kernels [63]. The version of Q-learning considered in the DTR literature is most similar to the fitted Q-iteration algorithm [62] in the reinforcement learning literature.

3.2.1 Q-learning with Linear Models

For clarity, here we will define Q-functions and describe Q-learning for studies with two stages only; generalization to K (≥ 2) stages is straightforward [61]. For simplicity, assume that the data come from a SMART with two possible treatments at each stage, A_j ∈ {−1, 1) and that the treatment is randomized with known randomization probabilities. The data from a SMART involving n subjects will consist of n data trajectories of the form (O₁, A₁, O₂, A₂, O₃); as before the histories are defined as H₁ = O₁ and H₂ = (O₁, A₁, O₂). The study can have either a single terminal utility (primary outcome) Y observed at the end of stage 2, or two stage-specific utilities Y₁ and Y₂ adding up to the primary outcome Y = Y₁ + Y₂ (in general Y can be any known function of the data). The interest lies in estimating a two-stage DTR (d₁, d₂), with d_j(H_j) ∈ {−1, 1}.

The optimal Q-functions for the two stages are defined as: Q₂(H₂, A₂) = E[Y₂∣H₂, A₂], and Q₁(H₁, A₁) = E[Y₁ + max_a2 Q₂(H₂, a₂)∣H₁, A₁]. A backwards induction argument [21] can be used to prove that the optimal treatment at a particular stage is given by the value of the action that maximizes the associated Q-function. In particular, if these two Q-functions were known, the optimal DTR (d₁, d₂) would be d_j(h_j) = arg max_aj Q_j(h_j, a_j), j = 1, 2. In practice, the true Q-functions are not known and hence must be estimated. Since Q-functions are conditional expectations, a natural approach to model them is via regression models. A dynamic programming (moving backwards through the stages) approach is used to estimate the parameters. Consider linear regression models for the Q-functions. Let the stage j (j = 1, 2) Q-function be modeled as $Q_j(H_j,A_j;{\beta }_j,{\psi }_j)={\beta }_j^T{H}_{j0}+\left({\psi }_j^T{H}_{j1}\right)A_j$, where H_j0 and H_j1 are two (possibly different) features of the history H_j.

There are many versions of the Q-learning algorithm depending on whether there are parameters that are common across the stages and depending on the form of the dependent variable used in the stage 1 regression. One form for the Q-learning algorithm consists of the following steps:

1. Stage 2 regression: $({\widehat{\beta }}_2,{\widehat{\psi }}_2)=\arg {\min }_{{\beta }_2,{\psi }_2}\frac{1}{n}{\sum }_{i=1}^n{\left(Y_{2i}-Q_2(H_{2i},A_{2i},;{\beta }_2,{\psi }_2)\right)}^2$.

2. Stage 1 dependent variable: ${\widehat{Y}}_{1i}=Y_{1i}+{\max }_{a_2}{Q}_2(H_{2i},a_2;{\widehat{\beta }}_2,{\widehat{\psi }}_2),i=1,\dots ,n$.

3. Stage 1 regression: $({\widehat{\beta }}_1,{\widehat{\psi }}_1)=\arg {\min }_{{\beta }_1,{\psi }_1}\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{Y}}_{1i}-Q_1(H_{1i},A_{1i};{\beta }_1,{\psi }_1)\right)}^2$.

Note that in step 2. above, the quantity ${\widehat{Y}}_{1i}$ is a predictor of the unobserved random variable Y_1i + max_a2 Q₂(H_2i, a₂), i = 1, … , n. The estimated optimal DTR using Q-learning is given by $({\widehat{d}}_1,{\widehat{d}}_2)$, where the stage j optimal rule is specified as ${\widehat{d}}_j\left(h_j\right)=\arg {\max }_{a_j}{Q}_j(h_j,a_1;{\widehat{\beta }}_j,{\widehat{\psi }}_j),j=1,2$.

Q-learning (with K = 2) has been implemented in the R package qLearn, freely available from: http://cran.r-project.org/web/packages/qLearn/index.html, and in the SAS procedure QLEARN: http://methodology.psu.edu/downloads/procqlearn. Q-learning can be extended for application to observational data by incorporating appropriate adjustments to account for confounding; more precisely, this can be done either by including all the measured confounders – or simply the propensity score as a proxy for all measured confounders – in the models for Q-functions, or instead weighting the stage-specific regressions by the inverse of the propensity scores [64]. Q-learning is a version of Robins’ optimal structural nested mean model [6] developed in the causal inference literature; see Chakraborty et al. [23] for a detailed discussion and derivation.

Q-learning has been generalized in a variety of ways. Lizotte et al. [65, 66] generalize Q-learning for use when different patients may make different tradeoffs between multiple outcomes and thus a data analysis of one composite outcome is insufficient. Q-learning has also been generalized to settings in which Y is a, possibly censored, survival time [67, 68]; both these papers provide a Q-learning method with the aim of maximizing a truncated survival time.

3.2.2 Approaches based on Dynamical Systems Models

An alternate indirect approach to estimating an optimal DTR is to use dynamical systems models. By dynamical systems models we mean a time-ordered sequence of nested conditional models (each model conditions on past data) for the multivariate distribution of the data. In this approach one first develops a dynamical systems model; this model may be constructed using expert opinion or may be estimated using observational or sequentially randomized data sets. Indeed these types of models are quite attractive when there are strong biological, behavioral or social theories that can be employed to guide the formation of the nested conditional models. Once the dynamical systems model is in hand, algorithms from control theory, such as dynamic programming or constrained optimization algorithms are used to estimate the optimal DTR [69]. This is a common approach in applications in engineering, economics and business. In the clinical field there has been much less development. Bayesian methods have been employed in simple, low dimensional problems; one example is Thall et al. [70].

Rosenberg et al. [71], and Banks et al. [72] discussed how a variety of data sources with models based on ordinary differential equations can be used to build a dynamical systems model for use in estimating an optimal DTR in AIDS treatment. In this setting the treatment is a continuous dose of antiviral therapy, and the optimal DTR is chosen to bring the dynamical system to its “steady state”. Rivera and colleagues, in a series of presentations available at http://csel.asu.edu/node/13 and papers [69, 73], discussed how common dynamical systems models might be used to describe behaviorial dynamics and thus form the basis for DTRs involving behavioral treatments in obesity and addiction treatment. Gaweda et al. [74, 75] discussed the use of control theoretic approaches to anemia management in patients with end-stage renal disease. Bennett and Hauser [76] discussed a framework for simulating clinical decision making from electronic medical records data. In summary, while the dynamical systems approaches to develop DTRs are emerging, from a statistical perspective they still lag behind the other approaches presented earlier; hence this area is ripe for further development.

4 Confidence Sets

High quality measures of confidence are needed in the development of DTRs both for (i) the parameters indexing the optimal DTR; and (ii) the Value of a DTR – either a pre-specified DTR, or an estimated DTR. Inference for the Values of pre-specified regimes has been addressed by numerous authors [12, 13, 14, 9, 10]; however there is little work on inference for the Value of an estimated regime. We return to this problem after discussing the construction of confidence intervals (CIs) for the parameters indexing the optimal regime. Measures of confidence for these parameters are important for the following reasons. First, if the CIs for some of these parameters contain zero, then the corresponding patient variables need not be collected in future, thus lowering the data collection burden. Second, CIs for the coefficient of the treatment variable can be used to indicate if there is insufficient support in the data to recommend one uniquely best treatment over another, thereby suggesting considerations other than the treatment effect be used to decide on treatment, e.g. cost, patient/clinician familiarity, preference etc.

Orellana et al. [41] discussed construction of confidence sets for parameters indexing the optimal DTR when direct methods of estimation using IPTW are employed. These confidence sets are based on standard Taylor series arguments, and are asymptotically valid under a set of smoothness assumptions. Robins [6] pointed out that non-regularity arises in the indirect estimation of DTRs. By non-regularity, we mean that the asymptotic distribution of the estimator of the treatment effect parameter does not converge uniformly over the parameter space; see below for further details. Indeed the treatment effect parameters at any stage prior to the last can be non-regular. This phenomenon has practical consequences, including bias in estimation and poor frequentist properties of Wald-type or other standard CIs in small samples. Any inference technique that aims to provide good frequentist properties such as nominal Type I error and/or nominal coverage of CIs in small samples has to address this problem of non-regularity. The problem can be better understood with a simple but instructive example discussed by Robins [6]; here we present a slightly modified version as presented by Chakraborty et al. [23]. Consider the problem of estimating ∣μ∣ based on n i.i.d. observations X₁, … , X_n from $\mathcal{N}(\mu ,1)$. Note that $\mid {\stackrel{‒}{X}}_n\mid$ is the maximum likelihood estimator of ∣μ∣, where ${\stackrel{‒}{X}}_n$ is the sample average. The asymptotic distribution of $\sqrt{n}(\mid {\stackrel{‒}{X}}_n\mid -\mid \mu \mid )$ for any μ ≠ 0 is a standard normal, whereas for μ = 0 it is nonnormal; that is, the change in the distribution as a function of μ is abrupt. Thus $\mid {\stackrel{‒}{X}}_n\mid$ is a non-regular estimator of ∣μ∣; an exact proof of non-regularity of this estimator uses local alternatives as in Leeb and Pötscher [77]. Also, for $\mu =0,{\lim }_{n\to \infty }E\left[\sqrt{n}\right(\mid {\stackrel{‒}{X}}_n\mid -\mid \mu \mid \left)\right]=\sqrt{\frac{2}{\pi }}$. This asymptotic bias [6] is one symptom of the underlying non-regularity.

Next we review the problem of non-regularity in the context of Q-learning. Suppose we want to construct CIs for the parameters ψ_j’s appearing in the model for Q-functions. In a two-stage set-up, the inference for the stage 2 parameters ψ₂ is straightforward since this falls in the standard linear regression framework. In contrast, inference for ψ₁ is complicated. Note that the stage 1 dependent variable in Q-learning for the i-th participant is ${\widehat{Y}}_{1i}=Y_{1i}+{\max }_{a_2}{Q}_2(H_{2i},a_2;{\widehat{\beta }}_2,{\widehat{\psi }}_2)=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ,i=1,\dots ,n$, which is a non-differentiable function of ${\widehat{\psi }}_2$ (due to the presence of the absolute value function). Since ${\widehat{\psi }}_1$ is a function of ${\widehat{Y}}_{1i},i=1,\dots ,n$, it is in turn a non-smooth function of ${\widehat{\psi }}_2$. As a consequence, the distribution of $\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ does not converge uniformly over the parameter space [6]. More specifically, the asymptotic distribution of $\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ is normal if φ₂ is such that $p\triangleq P[H_2:{\psi }_2^T{H}_{21}=0]=0$, but is non-normal if p > 0, and this change in the distribution happens abruptly. Below we present several different approaches to address the problem.

4.1 Adjusted Projection Confidence Intervals

As discussed in Robins [6], a joint CI for all of the parameters (in our two stage example both the first and second stage regression coefficients) can be formed by inverting hypothesis tests. That is, if the parameters are φ = (φ₁, φ₂) and a hypothesis test of φ = φ⁰ for each value of φ⁰ is well behaved, then a joint (1 − α)% CI, $\mathcal{C}$ for φ can be constructed. This is the case in Q-learning since it is easy to construct a well-behaved hypothesis test statistic when all of the regression coefficients are set to fixed values (the test statistic is based on a quadratic form involving the estimating functions evaluated at the fixed values). Next a projected CI for φ₁ is given by ${\bigcup }_{{\psi }_2}\{{\psi }_1:({\psi }_1,{\psi }_2)\in \mathcal{C}\}$. Unfortunately this interval is very conservative. As a result, Robins [6] using ideas as advanced by Berger and Boos [78] adjusts the usual projection CI. We discuss this idea in the context of the two stage Q-learning method presented above.

Recall that we are interested in a CI for φ₁. In this context, φ₂ is a nuisance parameter. If the true value of φ₂ were known, then the asymptotic distribution of $\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ would be regular (in fact, normal), and standard procedures could be used to construct an asymptotically valid CI. Let $\mathcal{C}\left({\psi }_2\right)$ denote a (1 − α)% asymptotic CI for φ₁ if φ₂ were known. Let $\mathcal{S}$ be a (1 − ∊)% asymptotic CI for φ₂. Then, it follows that ${\bigcup }_{{\psi }_2\in \mathcal{S}}\{{\psi }_1:{\psi }_1\in \mathcal{C}({\psi }_2\left)\right\}$ is a (1 − α − ∊)% CI for φ₁. To see this, note that $P\left({\psi }_1\in {\bigcup }_{{\psi }_2\in \mathcal{S}}\mathcal{C}\left({\psi }_2\right)\right)\ge 1-\alpha +o_P\left(1\right)+P({\psi }_2\notin \mathcal{S})=1-\alpha -∊+o_P\left(1\right)$. Thus, this CI is the union of the CIs $\mathcal{C}\left({\psi }_2\right)$ over all values ${\psi }_2\in \mathcal{S}$, and is an asymptotically valid (1 − α − ∊)% CI for φ₁. The main downside of this approach is that it appears to be computationally di cult to implement; to our knowledge this CI has not yet been implemented.

4.2 Adaptive Confidence Intervals

Laber et al. [79] developed an adaptive bootstrap procedure to construct CIs for linear combinations $c^T{\psi }_1$, where c is a known vector. In this procedure, they decomposed the asymptotic expansion of $c^T\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ as ${\mathbb{W}}_n+{\mathbb{U}}_n$, where the first term ${\mathbb{W}}_n$ is smooth and asymptotically normally distributed, while the distribution of the second term ${\mathbb{U}}_n$ depends on the underlying data-generating process “non-smoothly”. The adaptive confidence intervals (ACIs) are formed by first constructing smooth data-dependent upper and lower bounds on ${\mathbb{U}}_n$, and thereby on $c^T\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$. The data-dependent upper/lower bounds use a pretest [80] that partitions the data into two sets: (i) patients for which there appears to be a treatment effect, and (ii) patients where it appears there is no treatment effect. The pretests are performed using a critical value λ_n, which is a tuning parameter of the procedure and can be varied; Laber et al. [79] used λ_n = log log n in their analysis.

Let the upper and lower bounds on $c^T\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ be given by $\mathcal{U}\left(c\right)$ and $\mathcal{L}\left(c\right)$ respectively; both these quantities are functions of λ_n. Laber et al. [79] showed that the asymptotic distributions of $c^T\sqrt{n}({\widehat{\psi }}_1-{\psi }_1),\mathcal{U}\left(c\right)$ and $\mathcal{L}\left(c\right)$ are all equal in the regular case when p = 0. That is, when there is a large treatment effect for almost all patients then the bounds are asymptotically tight. However, when there is a non-null subset of patients with no treatment effect, then the asymptotic distribution of $\mathcal{U}\left(c\right)$ is stochastically larger than the asymptotic distribution of $c^T\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$, and likewise the asymptotic distribution of $\mathcal{L}\left(c\right)$ is stochastically smaller. This adaptivity between non-regular and regular settings is a key feature of this procedure. The distributions of $\mathcal{U}\left(c\right)$ and $\mathcal{L}\left(c\right)$ are approximated using the bootstrap. Let $\widehat{u}$ be the 1 − α/2 quantile of the bootstrap distribution of $\mathcal{U}\left(c\right)$, and let $\widehat{l}$ be the α/2 quantile of the bootstrap distribution of $\mathcal{L}\left(c\right)$. Then $(c^T{\widehat{\psi }}_1-\widehat{u}∕\sqrt{n},c^T{\widehat{\psi }}_1-\widehat{l}∕\sqrt{n})$ is the ACI for $c^T{\psi }_1$ Laber et al. [79] proved the consistency of the bootstrap in this context, and in particular that $P\left(c^T{\widehat{\psi }}_1-\widehat{u}∕\sqrt{n}\le c^T{\psi }_1\le c^T{\widehat{\psi }}_1-\widehat{l}∕\sqrt{n}\right)\ge 1-\alpha +o_P\left(1\right)$, where the probability statement is with respect to the bootstrap distribution. Furthermore, if p = 0, then the above inequality can be strengthened to equality. This result shows that the adaptive bootstrap method can be used to construct valid – though potentially conservative – CIs regardless of the underlying parameters of the generative model. This method is implemented in the SAS procedure QLEARN: http://methodology.psu.edu/downloads/procqlearn.

4.3 m-out-of-n Bootstrap Confidence Intervals

The m-out-of-n bootstrap is a tool for producing valid CIs for non-smooth functionals [81]. This method is the same as the ordinary bootstrap except that the resample size (m) satisfies: m → ∞ as n → ∞, but m = o(n). Chakraborty et al. [82] proposed a data-driven method for choosing m in the context of Q-learning that is directly connected to an estimated degree of non-regularity. This method is adaptive in that it leads to the usual n-out-of-n bootstrap in regular settings (p = 0) and the m-out-of-n bootstrap otherwise.

In this approach, Chakraborty et al. [82] considered a class of resample sizes of the form $m=n^{\frac{1+\eta (1-p)}{1+\eta }}$, where η > 0 is a tuning parameter. For implementation, one first needs to estimate p using a plug-in estimator, $\widehat{p}={\mathbb{P}}_n\mathbb{I}[n{\left(H_{21}^T{\widehat{\psi }}_2\right)}^2\le (H_{21}^T{\widehat{\Sigma }}_{{\widehat{\psi }}_2}{H}_{21})\cdot {\chi }_{1,1-\nu }^2]$, where $n^{-1}{\widehat{\Sigma }}_{{\widehat{\psi }}_2}$ is the plug-in estimator of the asymptotic covriance matrix of ${\widehat{\psi }}_2$ and ${\chi }_{1,1-\nu }^2$ is the (1 − ν) × 100 percentile of a χ² distribution with 1 degree of freedom. Then the data-driven choice of the resample size is given by $\widehat{m}=n^{\frac{1+\eta (1-\widehat{p})}{1+\eta }}$. Note that for fixed $\widehat{m}$ is a monotone decreasing function of $\widehat{p}$, taking values in the interval $[n^{\frac{1}{1+\eta }},n]$. Thus, η governs the smallest acceptable resample size. The procedure has been shown to be robust to the choice of ν. Once $\widehat{m}$ is computed, a (1 − α) × 100% m-out-of-n bootstrap CI for $c^T{\psi }_1$ is given by $(c^T{\widehat{\psi }}_1-\widehat{u}∕\sqrt{\widehat{m}},c^T{\widehat{\psi }}_1-\widehat{l}∕\sqrt{\widehat{m}})$ where $\widehat{l}$ and $\widehat{u}$ are the (α/2) × 100 and (1 − α/2) × 100 percentiles of $c^T\sqrt{m}({\widehat{\psi }}_1^{\left(b\right)}-{\widehat{\psi }}_1)$ respectively $({\widehat{\psi }}_1^{\left(b\right)}$ is the m-out-of-n bootstrap analog of ${\widehat{\psi }}_1)$. This bootstrap procedure is consistent, and $P\left(c^T{\widehat{\psi }}_1-\widehat{u}∕\sqrt{\widehat{m}}\le c^T{\psi }_1\le c^T{\widehat{\psi }}_1-\widehat{l}∕\sqrt{\widehat{m}}\right)\ge 1-\alpha +o_P\left(1\right)$, where the probability statement is with respect to the bootstrap distribution. Furthermore, if p = 0, then the procedure possesses the adaptive property in that the above inequality is an equality. The method has been implemented in the R package qLearn on http://cran.r-project.org/web/packages/qLearn/index.html.

See the online Supplemental Materials for a simulation study that illustrates the performance of the above approaches to forming a CI.

4.4 Confidence Intervals for the Value of an Estimated DTR

The topic of constructing CIs for the Value of an estimated DTR has not been adequately addressed in the literature yet, but some insight can be gained by exploiting its connection with classification. As highlighted by Qian and Murphy [56] and Zhao et al. [58], the Value of a DTR can be expressed in a similar form as the misclassification error rate in a weighted classification problem. Thus constructing a CI for the Value of an estimated DTR is equivalent to constructing a CI for the test error of an estimated weighted classifier. Unfortunately even in an unweighted classification problem, constructing a CI for the test error is di cult due to the inherent non-smoothness; standard methods like normal approximation or usual bootstrap fail. Laber and Murphy [83] developed a method for constructing such CIs using smooth data-dependent upper and lower bounds on the test error; this method is similar to the ACI method described in Section 4.2. While intuitively one can expect that this method could be successfully adapted for the Value of an estimated DTR, more targeted research is needed to extend and fine-tune the procedure to the current setting.

5 Discussion and The Future

Dynamic treatment regimes comprise an increasingly active area of current statistical research with much interest from the clinical science community. SMART studies are increasing in number indicating that for some time the design of, and data analysis for, these trials will provide a steady source of new statistical problems. For example, many interventions are administered in group settings; in case of DTRs this requires the design and analysis of cluster-randomized SMARTs. At the design level, cluster randomization would imply increased sample size requirements due to intra-class correlation. At the analysis level, it would open up questions as to how best to incorporate random effects models or generalized estimating equations into the existing framework of estimation, how the intra-class correlation would impact the non-regularity in inference, and so on. Furthermore the development of statistical methods that can be used in the analysis of longitudinal observational data sets will likely continue to be necessary in this area. In either case methods for variable selection and model checking in the context of constructing data-driven DTRs, both of which pose slightly different issues than similar topics in the prediction literature are under-developed, and warrant further research.

Inference in the domain of DTRs is a particularly challenging problem due to non-regularity of the estimators under certain underlying longitudinal data distributions. This challenge occurs both when the targets of inference are the parameters indexing the optimal DTR and when the target is the Value of an estimated DTR. Optimality principles and statistical methods aiming to achieve optimal CIs in these non-regular problems is an open area of research. There is growing interest in confidence intervals for other parameters. One example is data-dependent parameters such as the first stage regression coefficients that would result in a future study in which the estimated second stage decision rule is used to assign treatment. Confidence intervals for this type of parameter is as yet undeveloped.

In today’s health care, there is an increasing use of sophisticated mobile devices (e.g. smart phones, actigraph units containing accelerometers, etc.) to remotely monitor patients’ chronic conditions and to intervene, when needed. This is an instance in which methods from online reinforcement learning in the infinite horizon setting may be useful. Development of sound estimation and inference techniques for such a setting is an important future research direction.

The field of DTRs is in its infancy and is quickly evolving. These methods and trial designs hold much promise for informing sequential decision making in health care. To achieve this promise many of the problems discussed above require further efforts on the part of the statistical community. In addition, dissemination of the newly developed methods into the medical domains and collaboration with clinical scientists will be crucial.