Abstract
High intensity focused ultrasound (HIFU) operated in thermal mode has been reported to reduce interstitial fluid pressure and improve the penetration of large macromolecules and nanoparticles in tumor and normal tissue. Little is understood about how the interstitial fluid pressure and velocity as well as the interstitial macromolecule transport are affected by HIFU exposure. A mathematical model is presented here which sheds light on the initial biophysical changes brought about HIFU. Our continuum model treats tissue as an effective poro-elastic material that reacts to elevated temperatures with a rapid drop in interstitial elastic modulus. Using parameters from the literature, the model is extrapolated to derive information on the effect in tumors, and to predict its impact on the convective and diffusive transport of macromolecular drugs. The model is first solved using an analytical approximation with step-wise changes at each boundary, and then solved numerically starting from a Gaussian beam approximation of the ultrasound treatment. Our results indicate that HIFU causes rapid drop in interstitial fluid pressure that may be exploited to facilitate convection of macromolecules from vasculature to the exposed region. However, following a short recovery period in which the interstitial fluid pressure is normalized, transport returns to normal and the advantages disappear over time. The results indicate that this effect is strongest for the delivery of large molecules and nanoparticles that are in the circulation at the time of treatment. The model may be easily applied to more complex situations involving effects on vascular permeability and diffusion.
Keywords: focused ultrasound, hyperthermia, drug delivery, tissue transport
1. Introduction
The ability of HIFU to concentrate the acoustic energy on a focal spot, measuring a few millimeters in diameter, deep inside a number of soft tissues in a minimally invasive way has been investigated for several decades largely for application to tumor thermal ablation (Ter Haar 2007). An emerging application of HIFU currently under investigation is targeted drug delivery. Efficient delivery of therapeutic agents into target cells or tissues still remains a big challenge in medicine. HIFU has been reported to increase the uptake of therapeutic agents in a number of tumor models in vivo (Dittmar el al 2005, Frenkel el al 2006, Khaibullina et al 2008, Lai et al 2010, Nelson et al 2002, Wang et al 2012). A promising technology is the combined use of HIFU and magnetic resonance (MR) imaging and thermometry, since MR imaging can provide high-resolution images for HIFU treatment planning and post-treatment evaluation and MR thermometry provides a way to estimate the acoustic energy deposited at the focal volume. HIFU guided by MR imaging has been shown to be effective in assessing the increased delivery of temperature sensitive liposomes (Grüll and Langereis 2012, Ranjan et al 2012) and the antitumor drug doxorubicin (Chen et al 2012) to tumor models in vivo.
The mechanisms responsible for this observed increased uptake of therapeutic agents are still a matter of investigation and debate in the literature. In general, ultrasound bio-effects are thought to arise from contributions of thermal and mechanical origin with longer pulses that generate higher thermal losses and shorter pulses that minimize such losses (O’Brien 2007, Ter Haar 2004). In the literature, traditional hyperthermia has long been studied for drug and nanoparticle delivery (Kong et al 2001, Chang et al 2005, Song et al 2005, Li et al 2013). In these studies, improved vascular permeability is generally considered as the major effect. While the treatments discussed here are not traditional hyperthermia, they are hypothermic in the sense that they involve elevated temperatures and thermal doses. However, generally the heat duration is much shorter (1–2 minutes rather than 30–60 minutes) and the temperatures higher than traditional hyperthermia, and because of this the thermal profile is much more localized.
The present work does not address the general mechanisms responsible for the reported increased uptake but it focuses on some aspects that may contribute to it.
Rapid edema formation (fluid accumulation in the interstitium) as a result of HIFU thermal ablation has also been reported in a number of studies in muscle and brain (Chen et al 1999, McDannold et al 2001, Vykhodtseva et al 2000, O’Neill et al 2009, O’Neill et al 2013). It is interesting to consider the processes that might be responsible for such a rapid reaction to thermal and mechanical stresses, and possibly take advantage of them to improve delivery of therapeutic agents. A drop in the IFP with no visible edema formation as a consequence of HIFU exposure under mild hyperthermia conditions with associated increase in nanoparticle delivery in a mouse tumor model has been recently reported (Watson et al 2012).
In order to gain some insight into these effects we present here a general mathematical model. The model is based on the linear biphasic model developed by Netti el al. (1995, 1997) to describe fluid transport in solid tumors when the tumor is treated as a poroelastic solid. The Netti model is an extension to time dependent situations of the mathematical model developed by Baxter and Jain (1989). These models have been adapted for analysis of hyperthermia treatments and drug delivery, sometimes with extensions for discrete rather than distributed vasculature (El-Kareh and Secomb 2004, Gasselhuber et al 2012), and other times including drug released from low temperature sensitive liposomes (Gasselhuber et al 2012a). In our study, we adapt this model to understand the initial rapid edema formation observed in the HIFU experiments referenced above. We will investigate mathematically these phenomena to see if they could be responsible for enhancing localized drug delivery. A major difference with general hyperthermia and other drug delivery models is that we must somehow take into account the limited spatial and temporal duration of our treatment if we are to have any hope of replicating the experimental conditions. This was not the case in previous models.
Our model consists of (i) a macroscopic fluid transport model able to predict the IFP and the interstitial fluid velocity (IFV) in tissue and (ii) a macroscopic solute transport model that describes the tissue concentration profiles of macromolecules with no extravascular binding. A focused ultrasound heating model was combined with experimental data to predict the change in tissue elastic properties. This same approach was extended a simplified case of a homogeneous, alymphatic tumor.
2. Materials and Methods
2.1. Governing Equations
It is assumed that the tissue is composed by two phases: a fluid phase, and a solid phase that is porous-permeable, isotropic and linearly elastic. Blood and lymphatic capillaries are not explicitly taken into account but are represented as a continuous, spatially distributed fluid source/sink throughout the tissue. The tissue as a whole is compressible only through exudation of fluid.
The physiological parameters that control the fluid transport are the hydraulic permeability of the vascular wall (Lp), the hydraulic conductivity of the interstitium (K), and the aggregate modulus of the interstitium: H = 2μ+λ where μ and λ are the Lamé constants of the solid matrix. We provide here the basic equations of the model. Additional details about the model and its computer implementation can be found in the Supplementary Information.
2.1.1. Macroscopic Fluid Transport
The transient evolution of inhomogeneous tissue deformation is modeled by a diffusion-type equation with a chemical reaction given by
| (1) |
where the dilatation is defined by with Vt and the volumes of the deformed and undeformed tissue element respectively. With interstitial fluid pressure defined as Pi = He (see Supplementary Information), and assuming constant conductivity, we can rewrite (1) as:
| (1a) |
The right-hand side of (1) or (1a), accounting for the trans-capillary fluid exchange, is the source/sink term of the Baxter and Jain model (1989) given by
| (2) |
where φv and φL represent the transcapillary flow (Starling equation) and the lymphatic drainage, respectively; Lp and LpL are the average hydraulic conductivity coefficients of the capillary and the lymphatic walls; S/V and SL/V are the vascular and lymphatic surface densities in the tissue (vessel surface area S per unit of tissue volume (V)); Pe (mmHg) is the effective vascular pressure Pe = PV − σ(πV − πi) where the difference between the average vascular pressure PV and the average IFP, Pi, is countered by the effective oncotic pressure (σ(πV − πi)). The parameters σ, πV and πi are, respectively, the average osmotic reflection coefficient of plasma proteins, the colloid osmotic pressure of plasma, and the colloid osmotic pressure of interstitial fluid and PL is the average lymphatic pressure.
The left-hand side of (1) describes the transient evolution of the tissue dilatation (deformation) due to fluid percolation through the tissue. A redistribution of the dilatation of tissue occurs via two mechanisms: a pseudo-diffusion process through the solid matrix with a pseudo-diffusion coefficient given by KH and a pseudo-fluid-generation process given by the term on the right hand side of (1).
Netti and collaborators solved (1) for two particular cases, both involving the source term Ω, an abrupt change of the macrovascular pressure from an initial value Pv0 to a final value Pvf and also an abrupt cessation of the trans-vascular fluid exchange. In our study, we focused instead on the effects resulting from changes occurring in the interstitial matrix. Owing to ultrasound exposure, we have assumed that the tissue in the focal region experiences a sudden change in the interstitium aggregate modulus H from a value H0 to a final value Hf. Eq. (1a) is then solved numerically for both normal and tumor tissue using a finite element technique.
The calculation of Pi from (1a) allows us to determine the tissue dilatation from e = Pi/H, the displacement u from e = ∇ · u, and the convective IFV, v, from the generalized form of Darcy’s law:
| (3) |
2.1.2. Macroscopic Solute Transport
The transport of macromolecules (solute) in the interstitium is modeled using the macroscopic convective-diffusion equation proposed by Baxter and Jain (1989)
| (4) |
where Ci is the interstitial solute concentration (in g/ml) and v is fluid velocity as determined by the fluid transport model. Similar to the fluid transport model, the discrete vessel source term is replaced by a distributed solute (macromolecular) source term ϕS. The remaining variables in (4) are: the solute diffusion coefficient, D, the retardation factor (ratio of solute velocity to the fluid velocity), rF, and an extravascular binding (reaction) term, ϕR (in g/ml s). In the pore model for transcapillary exchange (see for example, Taylor and Granger (1984), for a review), the solute source term ϕS can be written in terms of diffusion and convection sources as
| (5) |
where ξ is the vascular (diffusive) permeability coefficient, Cp is the plasma solute concentration and σ, σL are the reflection coefficients for the solute across the capillary and lymphatic membranes. The last term is most often excluded from the literature, but we include it here to make the obvious comparison to (2). It is useful to rewrite (5) explicitly in terms of the fluid flow, Ω:
| (6) |
from which it is immediately clear that the convective components are negligible in tumor but not in normal tissue. Under steady state in both tissues types, Ω = 0, however, only in normal tissues is there some inflow, and the third term ensures that this leads to a convective build-up of solute in the tissue. Note that we are neglecting the reaction term ϕR, which describes permanent binding of drug rather than transient build-up due to finite tissue filtration and permeability. For the steady state, an effective diffusion is most often used, and the lymphatic filtration term is mostly ignored in the literature. In terms of the excess drug concentration, Cex = Ci − CiC, defined as the difference in uptake between ultrasound treated and control or steady state tissue, (4) becomes (see Supplemental):
| (7) |
where is an effective “reflection” coefficient that determines the fraction of plasma solute that is transported into the interstitium along with the fluid and Ω is given by the right hand side of either (1) or (1a).
2.2. Analytical Approximation
We can rewrite the inhomogeneous pressure PDE conveniently as:
| (8) |
with and , so that Ω = −α (Pi − PSS). Clearly, the steady state solution is just Pi = PSS. With limited data, little is precisely known about the change in H through space and time. However, based on changes in T2-weighted and contrast enhanced MR images, we can make the following general statements: that a change occurs that allows for an influx in fluid (edema) to occur at the treatment site, that this process is quite rapid (<2 minutes), and that there is a quite sharp boundary demarcating the treated spot on T2-weighted images. We have also observed that contrast injected shortly following treatment does not build up preferentially in the treated region. Our hypothesis is that these observations may be explained by a change in phase in the treated tissue that results in a rapid reduction in the tissue modulus, H. Without knowing the details, we can also approach this problem analytically using distinct domains in space and time. Writing:
| (9) |
where h() is step function that goes from 0 to 1 as the argument crosses 0 from negative to positive, ΔH = Hf − H0, and t0, ri are the coordinates of the interface in time and space. The derivative of such a step is here written as δ(), and is Dirac delta function, the integral of which is the unit step. The advantage of this formalism is that it keeps track of the step while being agnostic as to its precise nature. One can at any time replace it with an appropriate sigmoidal function to find a specific solution. In general, the steps in the various dimensions are not numerically identical, however, for convenience we use the same notation for all step functions used here. The main point is that far from the boundaries, in both space and time, H is a constant, either H0 or Hf = H0 + ΔH. The choice of sigmoidal step function, and its derivatives, determines only how things match across boundaries.
Extending this formalism to the tumor case is trivial. There, we have two different steady state pressures. The pressure inside the tumor is derived by removing the lymphatic terms (setting SL = 0) and the vascular osmotic pressure (setting Pe = Pv). From this, it is trivial to show that, inside the tumor, PSS = Pv, and Ω = 0, that is the convective flow of fluid is zero. Similar to the approach above, the steady state pressure at the tumor boundary may be approximated as some step function. Netti’s solution amounts to solving (1) for a particular choice of step function between the tumor and normal tissue pressures. For an ultrasound treatment spot completely inside the tumor and far from the tumor boundary, we just solve (8) replacing PSS with Pv.
2.3. Computer Model Implementation
2.3.1. Experimental estimate of the function H
Although the general behavior of tissue following ultrasound thermal treatment may be generally predicted from a step function given in (9), a result relevant to a particular situation requires that we specify H(r, t) more precisely and solve (1) or (1a) numerically. In our case, heat was gradually building up over a period of 60–120 s, a situation that requires a numerical approach. We implemented this approach in Comsol Multiphysics 3.5a by employing four different modules in cylindrical symmetry with , z = r cos ϕ, with ϕ the polar angle, simulating, in turn, the heating of the tissue that causes protein denaturation, the change in IFP, the resulting tissue displacement/IFV, and, finally, the movement of solute (drug) due to diffusion and convection. The solution was found using a segregated solver with manual specification of steps, that is, by ignoring the possible effects of tissue and fluid movement on the heat distribution, etc. All of this hinges on some estimation of the change in tissue bulk modulus due to the heating. While there is no way to estimate H(r, t) or Pi(r, t) directly in living tissue, it is possible to estimate relative changes e(r, t) from MR imaging, with some limits in temporal and spatial resolution. Since, in the model, the solid and fluid phases are considered intrinsically incompressible, tissue deformation can occur only with an increase of fluid content in the affected tissue, i.e. the amount of edema can be associated with the dilation e. The relative increase in fluid content in tissue immediately after HIFU exposure can be roughly estimated from T2 weighted (or better, proton density) MR images. Here, we have considered a particular set of data which shows the increment of fluid content in the focal plane at 2.5 minutes after a pulsed HIFU treatment of rabbit thigh. More details about this experiment can be found in O’Neill et al (2013). The focal spot considered in our analysis was obtained with an HIFU exposure lasted about 60 s and resulting in a temperature increase (hottest pixel) of about 15 °C as measured by MRI thermometry. From this, and other similar observations, edema already appears in the T2 images taken 2.5 minutes post treatment and remains relatively static for several hours (see Supplemental Information). The change in H can therefore be estimated by matching the results of the simulation to this data. We also know, from the physics of protein denaturation, that this process should be thermal dose dependent. In a previous paper looking at over 200 such sonications, we estimated the critical thermal dose at 159 cumulative equivalent minutes at 43 °C. We were also able to show that for our particular treatment (single focal spot from a 1 MHz beam treated over 60–120 s), the same transition will occur with temperatures peaking at 49 °C or greater. Although a phase change based on thermal dose is more accurate and universal, for our simulation we chose to work with temperature since it is easier to implement in Comsol Multiphysics. Without further guidance from experiment, we set:
| (10) |
with , where erf () is the error function, that is, the integral of a normal Gaussian, with σ as the parameter controlling the width of the transition. The parameters ΔH and σ were chosen to reasonably fit the experimental data (see Supplemental Information), beginning with σ = 2°C and ΔH = 0.5 H0. Tmx(t) is the maximum temperature reached from start of insonation to time t –and ensures the effect is irreversible. This was implemented in Comsol by running separate solutions during heating and cooling, using the final temperature map from the heating phase as Tmx for the cooling phase.
2.3.2. Acoustic model and heating
In order to make use of (10) we must have as input T(r, t). This may, in principle, be obtained directly from MRI thermometry data of the treatments, however, for simulation purposes in Comsol Multiphysics, it is easier to model the temperature rise due to a theoretical acoustic beam than work with noisy data. This may be done using the bioheat equation, that is, we can solve (see O’Neill et al 2012, Wissler 1998):
| (11) |
with boundaries in the +R direction fixed at 37 °C, in the ±z direction set to 21 °C, and an insulation condition at the R=0 axis. For simplicity, we modeled the ultrasound as a Gaussian beam (Wu and Du 1990, O’Neill et al 2012) in cylindrical coordinates, that is:
| (12) |
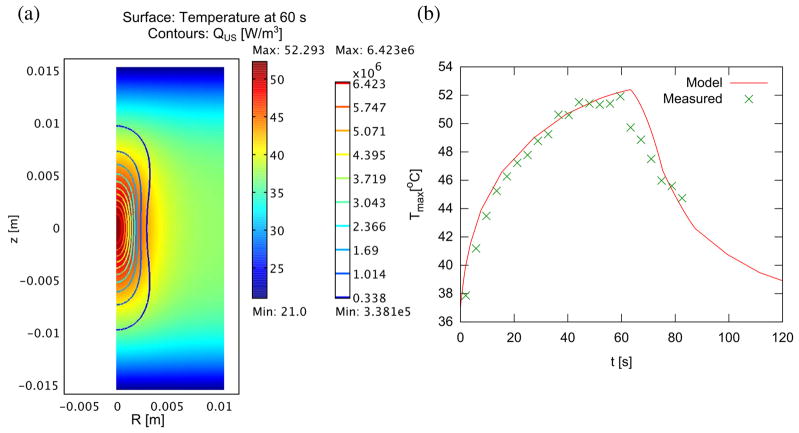
This expression places the focus at (0,0), with focal width approximately σR and length σz, and acoustic absorption αz. The constants used in the simulation come from literature and earlier studies that fit our experimental thermometry data to a similar expression (see O’Neill et al 2012). The total acoustic power, Ptap, was set so that the peak temperature reached 52 °C at the end of 60 s of sonication, matching several of our experimental data sets. The parameters used may be found in table 1.
Table 1.
Simulation parameters. Literature sources are noted.
| Variable [Unit] | Description | Normal Value | Tumor Value | |
|---|---|---|---|---|
|
Bioheat Equation,
Eq. (11), (12)
| ||||
| ρ [kg/m3] | Tissue densitya | 1050 | 1050 | |
| C[J kg−1K−1] | Tissue heat capacitya | 3600 | 3600 | |
| k[W m−1K−1] | Thermal conductivitya | 1.0 (0.7) | 1.0 | |
| ωb[s−1] | Perfusion ratea | 0.006(0.007) | 0.006 | |
| Tb[°C] | Blood temperature | 37 | 37 | |
|
| ||||
| Ultrasound Treatment Parameters Eq. (12) | ||||
|
| ||||
| Ptap[W] | Acoustic powera | 12 | 12 | |
| αz[m−1] | Ultrasound absorptiona | 2.6 | 2.6 | |
| σR[mm] | Beam waist half-widtha |
|
1.13 | |
| σz[mm] | Focal spot half-lengtha |
|
5.27 | |
|
| ||||
| Fluid Transfer Equation, Eqs. (1) – (3), (6) | ||||
|
| ||||
| Tc[°C] | Transition temperatureb | 49 | 49 | |
| λ,μ [mmHg] | Lamé coefficientsc | 684, 15.2 | 684, 15.2 | |
| H0[mmHg] | Aggregate modulus | 714 (= λ + 2μ) | 714 | |
| f = −ΔH/H0 | Fractional change in H | 0.53 | 0.53 | |
|
|
Fluid conductivityd | 2.5× 10−7 | 2.5× 10−7 | |
|
|
Filtration coefficientd | 3.6 × 10−8 | 1.86 × 10−6 | |
| S/V[cm−1] | Vascular surface densityd | 100 [50–250] | 100 [50–250] | |
|
|
Effective filtrationd | 3.6 × 10−6 | 1.86 × 10−4 | |
| σ | Osmotic reflection (BSA)d | 0.91 | 8.7× 10−5 | |
| πv, πi [mmHg] | Osmotic pressuresd | 20, 10 | 19.8, 17.3 | |
| PSS[mmHg] | Steady state IFP | 1.0 | 10 | |
| ϕ0 | Volume fraction of fluide | 0.13–0.3 | 0.35–0.55 | |
|
| ||||
| Solute Transport Equation, Eqs. (4), (5), (9) | ||||
|
| ||||
| D [cm2/s] | Solute diffusivityf | 4.8 × 10−10 | 1.3 × 10−8 | |
| rF | Convection efficiency | 1.0 | 1.0 | |
| ζeff [cm/s] | Effective permeabilityf | 7.3 × 10−8 | 5.73 × 10−7 | |
| Σ | Effective solute reflection | 0.9 | 0.0001 | |
| τp[hr] | Solute plasma half-lifef | 72 | 72 | |
Data taken from O’Neill et al (2012)
Data taken from O’Neill et al (2013)
Data taken from Netti et al (1997)
Data taken from Jain et al (2007)
Data taken Jain (1987)
Data taken from Baxter and Jain RK (1989)
2.3.3. IFP and fluid transfer
From (10), we find: , where . These expressions were substituted, with , in (6) to give the following PDE that, given T(r, t) from (ii) may be solved numerically to find IFP:
| (13) |
where h and δ are defined above. The initial and boundary conditions here are that Pi = PSS, except at R=0, where we used a “no flux” boundary condition. The parameters used here and below are given in table 1.
Having solved for Pi(r, t) in (13), it is possible to obtain the strain, tissue displacement and IVF. The tissue displacement u can be determined by solving ∇ · u = e(r, t) with ∇ × u = 0. This set of equations can be solved in Comsol Multiphysics by expressing Δu = u − u0 as a gradient of a potential, Δ u = ∇ φ, and solving the Poisson equation, ∇ · ∇φ = e(r, t), at each time t, with initial and boundary conditions that Δ u = 0 everywhere. Substituting the result (with ) and the gradient of Pi in (3), we can obtain the IVF: . In general the tissue volume fraction, ϕ, is not constant, but depends on dilatation. An estimate of this change is given in Netti al al (1997) as , with ϕ0 the steady-state value and . This may be alternatively expressed in terms of IFP as .
2.3.4. Drug Delivery
Having the flow of fluid from the vasculature, Ω = − α(Pi − PSS), and from neighboring tissue, , from the solution to Eq. (13), it is possible to determine the changing concentrations of a drug or solute provided one knows the parameters for (5), the initial conditions, and the plasma concentration Cp(t). Since we are only interested in the increase in drug accumulation, we instead solve (7), in which case, the initial and boundary conditions are Cex= 0, except at R=0 where we instead set the flux to zero. Anticipating that, for useful therapeutics, the decay of the plasma concentration will take much longer than any accumulation process, we here set Cp uniformly with a 72 h half-life starting from a concentration of 1 at t0. The effective reflection coefficient, Σ, is taken to be 0.9 for normal tissue and 0.0001 for tumor based on the measured reflection coefficients for bovine serum albumin in these tissues (see table 1), while the coefficients for diffusion from the vasculature and through the tissue are taken from values estimated for IgG. Estimates are also made for small molecule drugs with diffusion and permeability increased 100-fold compared to IgG, and nanoparticles with diffusion and permeability decreased 100 fold.
Total drug accumulation may be found by adding the excess accumulation calculated here to the steady state accumulation found by solving (4) with Pi = PSS and spatial gradients set to 0.
2.3.5. Parameter Values for Model
The parameters used in the simulations are given in table 1. Acoustic and thermal parameters are taken from previous studies, see O’Neill et al (2012). Most of the values for the tissue flow parameters have been taken from Jain et al (2007) since these are, to the best of our knowledge, the most updated estimated or measured values. The remaining values have been taken from Baxter and Jain (1989), Jain (1987) and Netti al al (1997). A discussion and justification for these values can be found in the cited references. Dreher et al (2006) was used to extrapolate the range of permeability and diffusion coefficients from IgG to small molecules and nanoparticles. In Dreher et al (2006), ξeff ranges from 154 × 10−7cm/s for a 3.3 kDa (hydrodynamic radius ~1.8 nm) dextran to 1.7 × 10−7cm/s for a 2 MDa (24 nm) dextran, compared to the value used here of 5.73 × 10−7cm/s for 150 kDa IgG. Based on extrapolating permeability and diffusion as 1/volume, we estimate that our range of values should correspond to particles between about 1.7 kDa (2 nm radius) and 17 MDa (50 nm) in size. The corresponding range in diffusion coefficient yields results reasonably similar to Figure 6 in the Dreher paper (2006). Because they have been evaluated experimentally, each of these parameters refers to macroscopic values. These are only representative values and one should expect a wide variability among different tissues and tumors with significant variations even at the local level. The same simulations are valid for tumor tissue using the tumor appropriate parameters, provided the ultrasound treatment is considered to be “far away” from the tumor boundary.
3. Results
3.1 Analytical results
Using the step approximation (9) in (8) gives:
| (14) |
Outside the treatment zone given by t > t0 and r < ri, Pi(r, t) = PSS = H0e0. Inside the treatment zone:
| (15) |
with matching (initial) condition at t0 (see Supplemental Information)
| (16) |
That is, e = Pi/H is continuous across t0, while the pressure “instantaneously” changes due to the change in elastic modulus. This is due to the finite flow which limits the response of e. Note that for pressure to fall, Hf < H0.
Far from the boundary, or for small conductivity K, we can take K∇2Pi = 0. In that case, for example, near the center of the treatment, , with the initial condition given in (16). The solution in spatial domains far from ri is therefore:
| (19) |
Most generally, the dynamics near the boundary require a numerical solution, however, it is possible to approximate what is happening there as well. It makes sense that an expression for Pi across the boundary will look also like a step across the boundary and therefore (see Supplemental Information):
| (20) |
with formal solution to (15) in space and time:
| (21) |
In the limits r ≪ ri and r ≫ ri, this reverts to (19). Around r = ri, this represents a softening of the boundary due interstitial fluid transfer with the pressure gradient, since δ′(r − ri) is greater than zero inside the boundary and less than zero outside the boundary. If Kδ′> α, on the other hand, the major contribution to the fluid build-up is flow from the tissue outside the treatment zone rather than the vasculature. The enhanced IFP is clearly transient, returning to Pi = PSS at long times, with the scenario above indicating the optimal level of fluid exchange. During the transient phase, when IFP is low, excess fluid enters the tissue from the vasculature, given by Ω, and from neighboring tissue near the boundary, given by − K∇2Pi. The excess from these two sources is the cause of the swelling and edema, (see (1)). The total amount of excess fluid can then be found by integrating over time, that is, the excess fluid is just the change in e. Since the dilatation inside the treatment zone ultimately goes to e = PSS/Hf, the net volume fraction of excess fluid is just , with . This is just enough fluid to rebalance the pressure. Based on our experimental results, the excess fluid is typically 70– 100% of the baseline (see Supplemental Information). From the data set selected, and Hf = 0.5H0. Using this with the parameters in table 1 implies the time-scale of this process, given by 1/(Hfα), is 778 s or ~13 minutes for normal tissue with α = 3.6 × 10−6 mmHg−1s−1, but just 15 s in tumors with α = 1.86 × 10−4mmHg−1s−1. This time only gets shorter near the treatment boundary. Once the pressure has stabilized back to steady state, transport in the region returns to normal and any compound administered after this point will not show any excess build-up in the treated region. Clearly there exists a very narrow window in which to take advantage of this phenomenon.
Using the solution above, far from the treatment boundary, the expression for excess compound delivered from the vasculature over time, assuming Cp, the concentration of compound in the blood at the time of treatment, is constant (see Supplemental Information):
| (24) |
with . Unfortunately, these parameters are not all available in the literature (and depend in general on the solute being transported), however, it is clear that for normal tissue, Σ ≈ 1, whereas for tumors, Σ ≈ 0. This expression makes it obvious that under the best circumstances, that is, without any damping of the diffusion (setting ), there will be a net excess of compound in the treated region that is proportional to the expansion of the tissue following the treatment. In general it is clear, however, that the reduction in diffusion (due to loss of concentration gradient) will eventually remove any advantage of this effect over time. Using the parameters from table 1, we have, for IgG in normal tissue, and for tumors, , implying time constants of 38 and 4.8 hours, respectively, over which the improved uptake effect return to normal.
3.2 Simulation Results
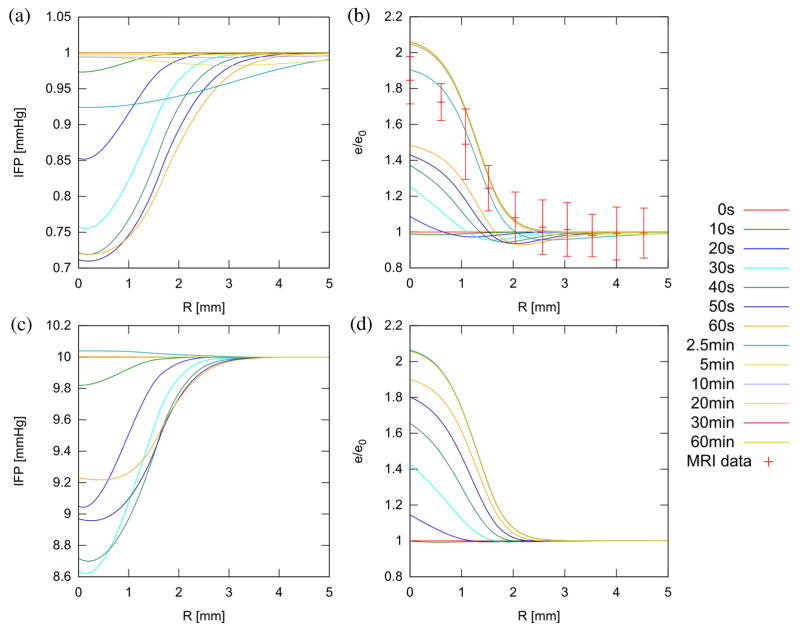
The tissue temperature found by solving the bioheat equation with a Gaussian acoustic beam is shown in figure 1(a) for normal and tumor tissue at 60 s, along with the peak temperature over time in figure 1(b). To match the experimental data of e(r = 0, t = 2.5 min) ≈ 1.9 e0, it was necessary to set f = 0.53 (Hf = 0.47H0) and σ = 2.0. –Using the result from the thermal simulation, the IFP, as expected, initially falls upon heating, then rises over time. Figure 2 shows the IFP and dilatation at treatment end (60 s). Figure 3 shows the time evolution of IFP and dilatation in the radial cross section up to 1 hour. Compared to the ideal case of instantaneous denaturation discussed in the analytical approximation, the IFP does not drop quite as far (0.72 PSS vs. 0.47 PSS) and, due to the prolonged nature of the heat treatment, the IFP in the center of the treatment zone is recovering while the edge is still falling. Eventually, IFP returns to normal and dilatation eventually goes to , as predicted analytically.
Figure 1.
Temperature distribution in model tissue with cylindrical symmetry (complete domain shown) after 60s sonication (a). Interfaces at z = ±1.5 cm are assumed in contact with room temperature bath, while interfaces at R = 0, 1.5 cm are connected to other tissue, with axial symmetry at R = 0. The ultrasound beam is directed along the R = 0 axis, and is focused at z = 0, with a focal spot size of radius 1.5 mm and length 7 mm. (b) Peak temperature over time during heating and cooling, compared to actual temperature measured during sonication with MR thermometry. Denaturation is assumed to occur between 48 and 50 °C.
Figure 2.
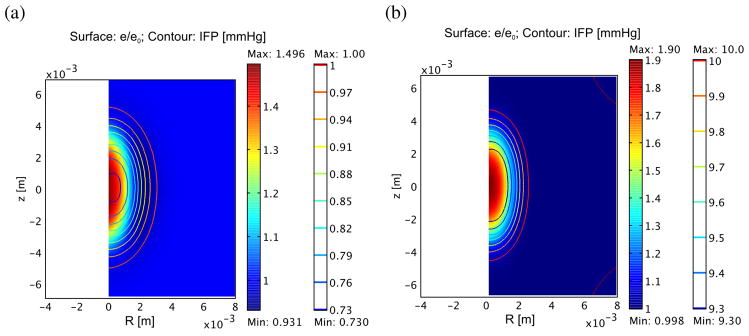
Relative dilatation (surface plot) and interstitial pressure (contours) for normal (a) and tumor (b) following 60 s treatment as described in figure 1. For simplicity, steady state IFP is assumed to be 1 mmHg for normal tissue and 10 mmHg for tumor.
Figure 3.
Radial IFP (a, c) and relative dilatation (b, d) at various times during and after treatment in normal (a, b) and tumor tissue (c, d). Experimental data showing normalized (to background) T2-weighted signal in the proximity of a treated spot at 2.5 min is included in (b) for comparison (see Supplemental Information). Recovery of IFP is much more rapid in tumors (~ 2.5 min rather than 10 min) due to greater influx of fluid from the vasculature.
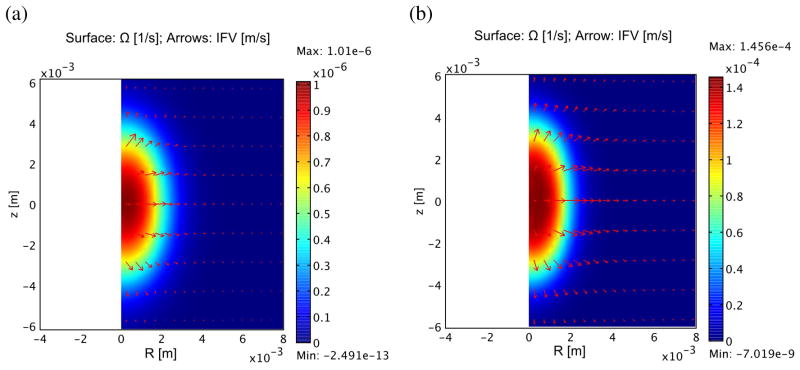
Figure 4 compares the components of flow arising from the vasculature and neighboring tissue at 60 s. Vascular fluid flow clearly dominates, particularly in the case of the tumors where the permeability is much greater. The net motion of IFV is surprisingly positive, as indicated by the arrows in the figure. The reason for this is that the IFV comes from two components, one is the expansion of the tissue ( ), which is clearly outward as the treated spot swells, the other is the movement of the fluid through the tissue (−K∇P), which is directed into the treatment spot. The first of these is slightly larger in normal tissue (7.2e-9 m/s vs. −5.45e-9 m/s in the radial direction), resulting in a net loss of fluid in the treated spot due to interstitial convection. This tendency may reverse later as the tissue expansion stops.
Figure 4.
Influx of fluid into treated zone from vasculature (surface) and convection from surrounding tissue (arrows) in normal muscle (a) and tumor tissue (b). The largest arrow in the normal tissue represents a flow of 2.5 × 10−9m/s, while in the tumor it is 6.0 × 10−8m/s. Note that in spite of the inward fluid flow relative to the tissue (−K∇Pi · r < 0), the net IFV still outward because the tissue itself is expanding at a greater rate ( ). Fluid influx from the vasculature is the major component of this process and is significantly more rapid in the tumor due to high vascular permeability.
The build-up of excess IgG-like compound due to the treatment at 60 s is shown in figure 5 and, in figure 6, at 60 minutes. In tumors, build-up due to vascular convection is much larger than in normal muscle, both in absolute terms (9.786 × 10−3 Cp vs. 4.062 × 10−6 Cp) and relative to steady-state, untreated tissue build-up (275% vs. 1%) (compare figure 5(a) vs. 5(b)). The build-up lasts a significant time, long after the pressure and dilatation have apparently stabilized. Eventually, however, the greater influx due to convection results in a loss of diffusion gradient that gradually wipes out any advantage over several hours. This is beginning to happen in both normal and tumor tissue by 1 hour (figure 6). Also observed is a significant increase in concentration in the tissue peripheral to the treated spot, presumably due to diffusion. The tissue build-up in excess of diffusion vs. radial distance is illustrated at different times for normal and tumor tissue in figure 7(a) and (b). It is generally much lower in the less permeable normal tissue compared to the tumor tissue, however, the advantage in tumor tissue is already reversing by 5 min compared to 60 min in normal tissue. The higher permeability and diffusion in tumor leads to rapid tumor uptake of these particles even without treatment, therefore the advantage of treatment is more transient. Figure 8 illustrates the different behavior of small molecules and nanoparticles in treated tumor tissue. Because small molecules diffuse easily even without treatment, the relative advantage is quickly lost, returning to near zero in under 20 minutes. On the other hand, for large nanoparticles, which have both low permeability and low diffusion, the advantage lasts much longer since, first, without treatment, very little actually gets into the tissue, and second, whatever gets in via convection cannot easily diffuse away.
Figure 5.
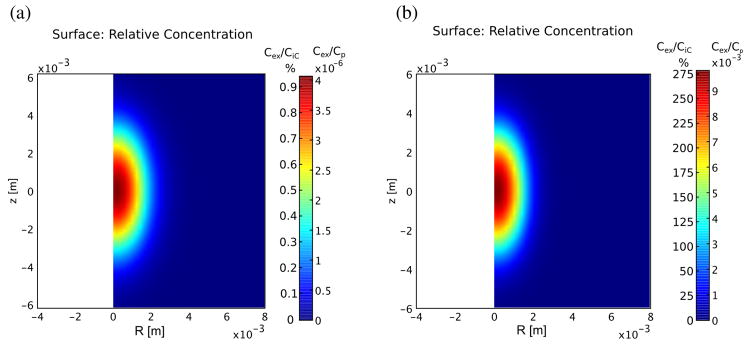
Excess concentration of IgG in at the end of treatment for normal (A) and tumor (B) tissue assuming the plasma concentration is 1 mol/m3. Influx into the tumor is three orders of magnitude greater due to the much greater permeability of the vascular source. The concentration due to steady state diffusion at 60 s is 4.45 × 10−4Cp for normal muscle and 3.5 × 10−3Cp for tumor tissue, so the peak values in (a) and (b) above represent almost 1% and over 275% of the background concentrations.
Figure 6.
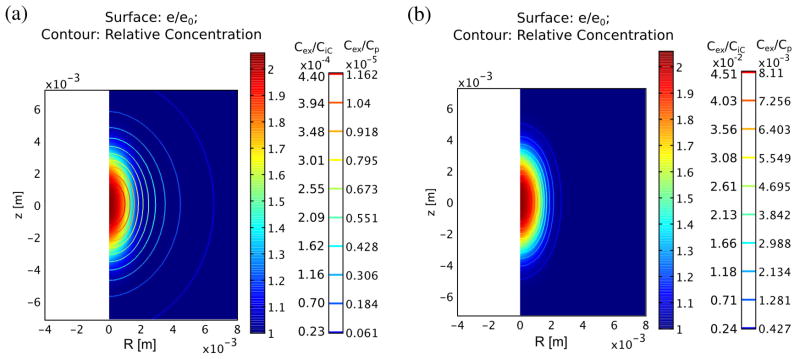
Distribution of excess concentration after 1 hour in normal (a) and tumor tissue (b). Contours indicate excess concentration while relative dilatation is shown as the surface color at the same time point. These numbers represent maximum increases of almost 0.05% and 4.5% over the background values of 0.0264 Cp and 0.18 Cp, respectively, in normal and tumor tissues.
Figure 7.
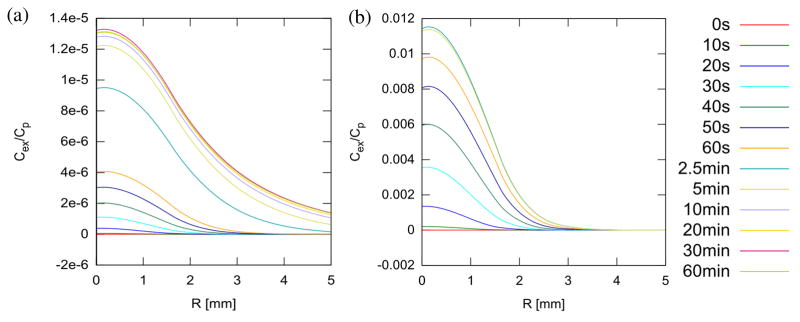
Excess concentration in the focal plane at various times during and after treatment in normal (a) and tumor tissue (b). Note that concentration peaks around 30 min in normal tissue and 2.5 min in tumor tissue, after which the advantage relative to untreated tissue starts to decay.
Figure 8.
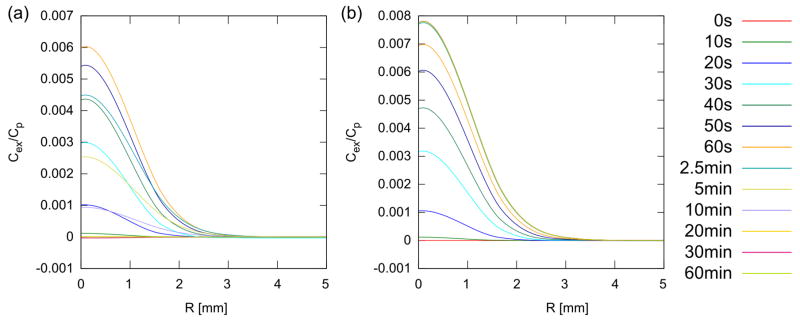
Excess concentration in the focal plane of tumor at various times during and after treatment for model small molecules (a, assuming D and ζeff are increased by factors of 100 compared to IgG) and nanoparticles (b, assuming D and ζeff are decreased by factors of 100). Note that the concentration advantage peaks around 60 seconds for small molecule then rapidly drops back to zero by 20 minutes, whereas for the nanoparticles, the advantage peaks at 2.5 min and remains there. Because small molecules will diffuse into the tissue quite rapidly even in the absence of any treatment, the delivery advantage for them is overall limited. Macromolecules and nanoparticles, however, having limited diffusion, do not penetrate into the tissue, and therefore any delivery advantage is sustained.
4. Discussion
4.1. Ultrasound Mechanism of Action in Lowering the IFP
The results of our simulations show that in the regions of tissue where the IFP becomes negative, the convective flow favors drug accumulation. In order to understand how ultrasound might induce a sudden lowering of the IFP, it is useful to keep in mind the mechanisms that regulate the IFP and the interstitial fluid volume and to relate them to the physical chemistry of ultrasound interaction with tissue.
The interstitium is a connective tissue which is primarily composed of two phases: the interstitial fluid (IF), consisting of interstitial water and its solutes, and the extracellular matrix (ECM). The ECM is primarily composed by a hydrated gel of negatively charged macromolecules, the glycosaminoglycan chains (GAGs) (long polymer of amino sugars), in a framework of fibrous proteins and connective tissue cells (Aukland and Reed 1993). Collagen is the most abundant fibrous protein of the interstitium and forms a network of collagen fibers. The characteristic cell type of the interstitial connective tissue is the fibroblast, but mast cells and cells of the immune system are also present in varying numbers.
Studies have shown that the fibroblasts have an important function for IFP control and tissue homeostasis (Wiig et al 2003). Fibroblasts exert a tension on collagen fibers via the β1-integrins (Reed et al 1992) and the intracellular actomyosin contractility (Berg et al 2001). This tension in the fibrils opposes the inherent tendency of interstitium to attract water and swell. The gel swelling pressure is caused by the osmotic activity of the GAGs, which is due mainly to Na+ ions attracted by their fixed negative charges (the Gibbs-Donnan effect).
During the rapid development of edema in thermally injured tissue and in the initial swelling of acute inflammation, several studies have shown that the relative IFP sharply decreases to negative values before the IFP rises again as the fluid accumulates (Wiig et al 2003, Lund et al 1988). In thermal injury, this could be attributed at least in part to the thermal denaturation of collagen to gelatin, i.e. conversion of fibrillar collagen from water insoluble to random coil denaturated collagen and water soluble α-chains and degradation products (Lund et al 1989). Since collagen denaturation does not play a role in acute inflammation, other mechanisms should also be involved. It has been suggested that the initial fall in the IFP may be caused by the release of bonds between the fibroblast α2β1-integrin and the collagen fibrils. This eliminates the gel-compressing action of the fibroblasts and allows a fuller expression of the glycosaminoglycan swelling pressure. This hypothesis has been confirmed by several in vivo and in vitro experiments (for a review, see, for example, Wiig et al 2003).
Several studies (Bamber 2004, Carstensen et al 1953, Goss et al 1980, Pauly and Schwan 1971, Sarvazyan and Hill 2004) have shown that ultrasound absorption by the protein content of tissue is significant. Therefore, it may be expected that ultrasound action can easily damage even temporarily the structure of the proteins involved in keeping the swelling pressure of the GAGs under control, resulting in a drop of the IFP until repair mechanisms can re-establish pre-existing conditions.
4.2. Comparison to Experimental Observations
The hypothesis that ultrasound can affect the IFP and the IFV is a novel concept that needs to be further investigated and confirmed experimentally. The mathematical model presented in this paper can predict the IFP and the IFV once the dilatation is known through measurement of edema. Consequently, it can provide guidance for future experiments that test this hypothesis. It can also explain some experimental facts reported in the literature.
For example, McDannold et al (2001) have shown that pulsed HIFU sonications in rabbit thigh muscle produce a rapid tissue swelling. For sonication times longer than 60 s, the swelling was significant. For a 60 s sonication time, out of the 33 lesions, only 13 had no evident swelling. However, the swelling was small in the rest of the lesions and was observed between 30–63 s after the start of the sonication with an average time from the starting of the swelling of 45 s. Other studies referenced in the Introduction also report such rapid swelling without providing an explanation. The investigation presented in our paper suggests that this initial rapid swelling may be attributed to the initial fall of the IFP resulting from the damage of some key connective proteins during HIFU exposure.
In a previous work (O’Neill et al 2013), it was concluded that the largest increase in local uptake of MR contrast was correlated with the effects described in this paper, but not directly caused by them. This conclusion was arrived at by two observa. First, the edema itself occurred on the timescales in this paper, that is, within a few minutes. However, contrast injected at this time did not show significant accumulation. This effect is explained here by the rapid recovery of IFP that normalizes the flow over a relatively short time. Contrast injected at 24 hours, however, did show significant accumulation. The second observation has been the spatial correlation of the improved uptake with inflammatory pathology (O’Neill et al 2013). Inflammation is known to alter vascular permeability. In this model, inflammation suggests a change in Lp, and a resulting alteration of the α parameter and PSS that should set in on a timescale of 6–24 hours. Unlike the transient effect of altering H, a change in PSS results in a permanent alteration of fluid transport, in other words, an artificial “enhanced permeability and retention” (EPR) effect. In tumors, however, there is no or at best limited room for improvement, since, as shown in (8), the changes in α and PSS work against each other and cancel out for a system already without lymphatics. Alternative explanations need to be considered for enhanced accumulation in tumors. One likely possibility that is particularly relevant for nanoparticles is that they can be actively carried to the site of inflammation by macrophages.
Recently, Watson et al (2012) reported a 1.5-fold increase in accumulation of liposomes in epithelial and epithelial–mesenchymal (EMT) tumors in mice when the tumors where exposed to HIFU under mild-hyperthermia conditions, typically 5–18 minutes at 42 °C. The authors of this study concluded that although more studies are required, this reduction is likely due to the effect of insonation and hyperthermia on the extracellular matrix. Interestingly, the intratumoral water content did not appear to change as a result of ultrasound exposure in their study of a tumor mouse model. This is in contrast with the experiments in thermally injured tissue and in tissue undergoing HIFU thermal ablation, where fast developing of edema was observed. Assuming that the effects discussed here, that is edema and inflammation, are truly not present, the only remaining parameter that may be impacted is the fluid conductivity, K. It is clear that a change in e should result in a concomitant change in K due to the increase in fluid volume fraction and tissue porosity. This effect was ignored in our analysis above, but could be important in some instances. It is difficult to conceive of a change in K that might occur without a significant change in e, but it is not impossible. Given this possibility, the resulting change in flow according to (8) would then be limited to regions with a significant gradient in Pi, such as at tumor boundaries or heterogeneities. It is also possible that the diffusion or reflection coefficients for the macromolecular transport might be altered by some as yet unknown mechanism, such as active biological transport.
The study of hyperthermia related improved transport of nanoparticles and drugs has a long history, going back at least to Kong et al 2001. The general result of such studies has been to pinpoint changes in vascular permeability as the major effect (Kong et al 2001, Chang et al 2005, Song et al 2005, Li et al 2013, Gasselhuber et al 2012). We discount this possibility as an explanation for our effect because of our observed lack of contrast uptake immediately following treatment. Any changes in vascular permeability would result in increased flow through the affected region, and consequently greater uptake in contrast compared to normal tissue. Our proposed change, on the other hand, produces a convective inflow due to decreased IFP that returns to normal within minutes, thus having little or no impact on transport of drug or contrast agent injected after the treatment. While our previous work (O’Neill et al 2013) clearly relates the increased edema to hyperthermic conditions rather than mechanical effects, the short duration, high temperature, small volume treatments produced by HIFU are quite different from traditional hyperthermia. Our observed effects may be unique to this type of treatment. Alternatively, because of the duration of traditional hyperthermia, it may be that these effects are being masked, and mistakenly attributed to vascular changes.
4.1. Model Limitations
Our model is based on the linear biphasic model implemented by Netti et al. (1995, 1997). As described in more details in the Supplementary Information, the Netti model can be derived from the conservation of continuum mechanics assuming the Lame’s parameters μ and λ of the solid matrix to be constant in space. In our model, in order to reproduce the MRI data, we assumed H = λ + 2μ to be a function of space and time. This amounts to neglecting, in the basic equations of continuum mechanics, certain terms related to shear that might arise due to the differential variation of the Lamé parameters in time and space (see Supplemental Material).
An important limitation in our study lies in the source of our experimental data. Parameters for the function H were estimated by comparing the model-derived relative dilatation to the relative signal intensity in a T2-weighted image of the focal plane of a treatment spot. This approach is based on the assumption that the signal intensity is linearly related to fluid content, an assumption that is not entirely accurate. The use of a proton density scan would be an obvious improvement. The thermal model is also based on focal plane MR thermometry, with all out of plane data inferred from the geometry of the acoustic focal spot. Including other planes in the both the thermometry and the imaging of the edema would result in greater confidence in the thermal model and the derived function H, but would not substantially change the conclusions of this paper.
From the mathematical modeling side, more sophisticated tissue models could be developed. Triphasic models that also include the presence of mobile ions in the interstitium and can therefore simulate the electrokinetic phenomena that give rise to the swelling pressure have been developed (Mow et al 2002, Lai et al 1991, Sun et al 1999) and might also be useful in our case. In a tri-phasic model, an additional term is introduced into the effective tissue stress tensor to represent the ion induced swelling pressure. Therefore, besides the Lamé constants (μ, λ) of the solid matrix, the IFP and IFV would also depend on the ion concentration in the interstitium.
Additionally, the present tumor tissue model has all the limitations of the Baxter and Jain model and Netti’s model, including simplified geometry and the assumption of homogeneity. In reality, a tumor is highly heterogeneous, and there can be avascular and necrotic regions. A tumor can also have variability in growth rate, vascular permeability, and interstitial components. These can lead to variable transport properties throughout the tumor as well as a heterogeneous fluid source, thus affecting the shape of interstitial fluid pressure and velocity profiles. Although many groups are approaching this problem with models of discrete vasculature, it could also be approached macroscopically with spatially varying parameters in the present model. Imaging, such as with MRI, may provide much of the information needed to realize a more realistic heterogeneous model of tumors.
Solute distributions were obtained under the assumption of a uniformly perfused region. If the tumor were heterogeneously perfused, there would be little IgG delivered to poorly perfused regions; also, little IgG will be delivered to these regions by interstitial diffusion from well-perfused regions, since a long time is required for this diffusion. Furthermore, binding which slows down the interstitial transport, has been taken into account only approximately through the parameter rF.
4.4. Implications for Drug Delivery
It is well known that IFP is elevated in tumors (Boucher et al 1990) and this phenomenon may influence the efficient delivery of therapeutic agents in tumors (Jain et al 2007). If one assumes that the delivery of anti-tumor agents is dependent at least in part on the pressure gradient for filtration into a tumor, one way to enhance tumor uptake is to reduce the IFP. Our simulations indicate that a lowering of the IFP induces fluid convection from the vasculature and facilitates penetration of macromolecules. The effect is strongest and lasts longest for macromolecules and nanoparticles and is relatively transient for small molecule drugs because they already diffuse quite easily. However, this beneficial outcome disappears once the IFP rises again, thus only molecules or particles already in the bloodstream at the time of treatment will benefit. If these results are confirmed experimentally, then ultrasound exposure conditions need to be investigated to slow down the rising of the IFP and identify the precise timing when the lowering of the IFP occurs. Further benefits for drug delivery (or detriments, depending on the application) may be obtained from the biological reaction to treatment, for example inflammation. These were discussed in an earlier paper (O’Neill et al, 2013), but are not analyzed here. The model could be extended to include biological effects once the link between the heat applied and subsequent biological changes in tissue transport is better established.
5. Conclusions
Despite its limitations, the mathematical model presented in this study provides a coherent picture describing improved fluid convection and macromolecule distribution inside a tumor during the initial lowering of the IFP resulting from ultrasound exposure that well explains experimental observations. It can therefore represent a preliminary mathematical framework upon which more complex mathematical models may be built and, more importantly, it can offer valuable guidance for experiments aimed at developing strategies that employ HIFU (or any other means able to lower IFP) for improving drug delivery to solid tumors.
Supplementary Material
Acknowledgments
This work was partially funded by the National Institutes of Health (NIH) through a National Institute of Biomedical Imaging and Bioengineering grant R01-EB009009. The authors gratefully acknowledge the support of Dr. King Li.
Contributor Information
E Sassaroli, Email: elisabettasassaroli@gmail.com.
B E O’Neill, Email: beoneill@houstonmethodist.org.
References
- Aukland K, Reed RK. Interstitial-lymphatic mechanisms in the control of extracellular fluid volume. Physiol Rev. 1993;73:1–78. doi: 10.1152/physrev.1993.73.1.1. [DOI] [PubMed] [Google Scholar]
- Bamber JC. Attenuation and Absorption. In: Bamber JC, ter Haar GR, editors. Physical Principles of Medical Ultrasonics. 2. John Wiley & Sons; 2004. pp. 93–166. [Google Scholar]
- Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvasc Res. 1989;37:77–104. doi: 10.1016/0026-2862(89)90074-5. [DOI] [PubMed] [Google Scholar]
- Berg A, Rubin K, Reed RK. Cytochalasin D induces edema formation and lowering of interstitial fluid pressure in rat dermis. Am J Physiol Heart Circ Physiol. 2001;281:H7–13. doi: 10.1152/ajpheart.2001.281.1.H7. [DOI] [PubMed] [Google Scholar]
- Boucher Y, Baxter LT, Jain RK. Interstitial pressure gradients in tissue-isolated and subcutaneous tumors: implications for therapy. Cancer Res. 1990;50:4478–84. [PubMed] [Google Scholar]
- Carstensen EL, Li K, Schwan HP. Determination of the Acoustic Properties of Blood and Its Components. J Acoust Soc Am. 1953;25:286–9. [Google Scholar]
- Chang E, Chalikonda S, Friedl J, Xu H, Phan GQ, Marincola FM, Alexander HR, Bartlett DL. Targeting vaccinia to solid tumors with local hyperthermia. Hum Gene Ther. 2005;16:435–44. doi: 10.1089/hum.2005.16.435. [DOI] [PubMed] [Google Scholar]
- Chen L, Bouley D, Yuh E, D’Arceuil H, Butts K. Study of focused ultrasound tissue damage using MRI and histology. J Magn Reson Imaging. 1999;10:146–53. doi: 10.1002/(sici)1522-2586(199908)10:2<146::aid-jmri6>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- Chen X, Cvetkovic D, Ma CM, Chen L. Quantitative study of focused ultrasound enhanced doxorubicin delivery to prostate tumor in vivo with MRI guidance. Med Phys. 2012;39:2780–6. doi: 10.1118/1.4705346. [DOI] [PubMed] [Google Scholar]
- Dittmar KM, Xie J, Hunter F, Trimble C, Bur M, Frenkel V, Li KC. Pulsed high-intensity focused ultrasound enhances systemic administration of naked DNA in squamous cell carcinoma model: Initial experience. Radiology. 2005;235:541–6. doi: 10.1148/radiol.2352040254. [DOI] [PubMed] [Google Scholar]
- Dreher MR, Liu W, Michelich CR, Dewhirst MW, Yuan F, Chilkoti A. Tumor vascular permeability, accumulation, and penetration of macromolecular drug carriers. J Natl Cancer Inst. 2006;98:335–44. doi: 10.1093/jnci/djj070. [DOI] [PubMed] [Google Scholar]
- El-Kareh AW, Secomb TW. A theoretical model for intraperitoneal delivery of cisplatin and the effect of hyperthermia on drug penetration distance. Neoplasia. 2004;6:117–27. doi: 10.1593/neo.03205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frenkel V, Etherington A, Greene M, Quijano J, Xie J, Hunter F, Dromi S, Li KC. Delivery of liposomal doxorubicin (Doxil) in a breast cancer tumor model: Investigation of potential enhancement by pulsed-high intensity focused ultrasound exposure. Academic Radiol. 2006;13:469–79. doi: 10.1016/j.acra.2005.08.024. [DOI] [PubMed] [Google Scholar]
- Gasselhuber A, Dreher MR, Rattay F, Wood BJ, Haemmerich D. Comparison of conventional chemotherapy, stealth liposomes and temperature-sensitive liposomes in a mathematical model. PLoS One. 2012;7:e47453. doi: 10.1371/journal.pone.0047453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasselhuber A, Dreher MR, Partanen A, Yarmolenko PS, Woods D, Wood BJ, Haemmerich D. Targeted drug delivery by high intensity focused ultrasound mediated hyperthermia combined with temperature-sensitive liposomes: computational modelling and preliminary in vivovalidation. Int J Hyperthermia. 2012;28:337–48. doi: 10.3109/02656736.2012.677930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goss SA, Frizzell LA, Dunn F. Dependence of the ultrasonic properties of biological tissue on constituent proteins. J Acoust Soc Am. 1980;67:1041–4. [Google Scholar]
- Grüll H, Langereis S. Hyperthermia-triggered drug delivery from temperature-sensitive liposomes using MRI-guided high intensity focused ultrasound. J Control Release. 2012;161:317–27. doi: 10.1016/j.jconrel.2012.04.041. [DOI] [PubMed] [Google Scholar]
- Jain RK, Tong RT, Munn LL. Effect of Vascular Normalization by Antiangiogenic Therapy on Interstitial Hypertension, Peritumor Edema, and Lymphatic Metastasis: Insights from a Mathematical. Model Cancer Res. 2007;67:2729–35. doi: 10.1158/0008-5472.CAN-06-4102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain RK. Transport of molecules in the tumor interstitium: a Review. Cancer Res. 1987;47:3039–51. [PubMed] [Google Scholar]
- Khaibullina K, Jang BS, Sun H, Le N, Yu S, Frenkel V, Carrasquillo JA, Pastan I, Li KC, Paik CH. Pulsed high intensity focused ultrasound enhances uptake of radiolabeled monoclonal antibody to human epidermoid tumor in nude mice. J Nucl Med. 2008;49:295–302. doi: 10.2967/jnumed.107.046888. [DOI] [PubMed] [Google Scholar]
- Kong G, Braun RD, Dewhirst MW. Characterization of the Effect of Hyperthermia on Nanoparticle Extravasation from Tumor Vasculature. Cancer Res. 2001;61:3027–32. [PubMed] [Google Scholar]
- Lai CY, Kruse DE, Caskey CF, Stephens DN, Sutcliffe PL, Ferrara KW. Noninvasive thermometry assisted by a dual-function ultrasound transducer for mild hyperthermia. IEEE Trans Ultrason Ferroelectr Freq Control. 2010;57:2671–84. doi: 10.1109/TUFFC.2010.1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113:245–58. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- Li L, ten Hagen TLM, Bolkestein M, Gasselhuber A, Yatvin J, van Rhoon GC, Eggermont AMM, Haemmerich D, Koning GA. Improved intratumoral nanoparticle extravasation and penetration by mild hyperthermia. J Control Release. 2013;167:130–7. doi: 10.1016/j.jconrel.2013.01.026. [DOI] [PubMed] [Google Scholar]
- Lund T, Wiig H, Reed RK. Acute postburn edema: role of strongly negative interstitial fluid pressure. Am J Physiol. 1988;255:H1069–74. doi: 10.1152/ajpheart.1988.255.5.H1069. [DOI] [PubMed] [Google Scholar]
- Lund T, Onarheim H, Wiig H, Reed RK. Mechanisms behind increased dermal imbibition pressure in acute burn edema. Am J Physiol. 1989;256(4 Part 2):H940–8. doi: 10.1152/ajpheart.1989.256.4.H940. [DOI] [PubMed] [Google Scholar]
- McDannold NJ, Hynynen K, Jolesz FA. MRI Monitoring of the Thermal Ablation of Tissue: Effects of Long Exposure Times. J Magn Reson Imaging. 2001;13:421–7. doi: 10.1002/jmri.1061. [DOI] [PubMed] [Google Scholar]
- Mow VC, Guo XE. Mechano-electrochemical properties of articular cartilage: Their Inhomogeneities and Anisotropies. Annu Rev Biomed Eng. 2002;4:175–209. doi: 10.1146/annurev.bioeng.4.110701.120309. [DOI] [PubMed] [Google Scholar]
- Nelson JL, Roeder BL, Carmen JC, Roloff F, Pitt WG. Ultrasonically activated chemotherapeutic drug delivery in a rat model. Cancer Res. 2002;62:7280–3. [PubMed] [Google Scholar]
- Netti PA, Baxter LT, Boucher Y, Skalak R, Jain RK. Time-dependent behavior of interstitial fluid pressure in solid tumors: implications for drug delivery. Cancer Res. 1995;55:5451–8. [PubMed] [Google Scholar]
- Netti PA, Baxter LT, Boucher Y, Skalak R, Jain RK. Macro- and microscopic fluid transport in living tissues: application to solid tumors AIChE. J Bioeng Food Nat Prod. 1997;43:818–34. [Google Scholar]
- O’Brien WD., Jr Ultrasound–biophysics mechanisms. Prog Biophys Mol Biol. 2007;93:212–55. doi: 10.1016/j.pbiomolbio.2006.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Neill BE, Karmonik C, Sassaroli E, Li KCP. Translational studies of pulsed HIFU enhanced tissue permeability: mechanisms in mouse and rabbit models. Proceedings of the IEEE International Ultrasonics Symposium (IUS ’09); 2009. pp. 1795–8. [Google Scholar]
- O’Neill BE, Karmonik C, Sassaroli E, Li KC. Estimation of thermal dose from MR thermometry during application of nonablative pulsed high intensity focused ultrasound. J Magn Reson Imaging. 2012;35:1169–78. doi: 10.1002/jmri.23526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Neill BE, Vo H, Shao H, Karmonik C, Zhou X, Li KC. MRI-based prediction of pulsed high-intensity focused ultrasound effect on tissue transport in rabbit muscle. J Magn Reson Imaging. 2013;38:1094–102. doi: 10.1002/jmri.24087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pauly H, Schwan HP. Mechanism of Absorption of Ultrasound in Liver Tissue. J Acoust Soc Am. 1971;50:692–9. doi: 10.1121/1.1912685. [DOI] [PubMed] [Google Scholar]
- Ranjan A, Jacobs GC, Woods DL, Negussie AH, Partanen A, Yarmolenko PS, Gacchina CE, Sharma KV, Frenkel V, Wood BJ, Dreher MR. Image-guided drug delivery with magnetic resonance guided high intensity focused ultrasound and temperature sensitive liposomes in a rabbit Vx2 tumor model. J Control Release. 2012;158:487–94. doi: 10.1016/j.jconrel.2011.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed RK, Rubin K, Wiig H, Rodt SA. Blockade of beta 1-integrins in skin causes edema through lowering of interstitial fluid pressure. Circ Res. 1992;71:978–83. doi: 10.1161/01.res.71.4.978. [DOI] [PubMed] [Google Scholar]
- Sarvazyan AP, Hill CR. In: Physical Chemistry of the Ultrasound-Tissue Interaction Physical Principles of Medical Ultrasonics. 2. Bamber JC, ter Haar GR, editors. John Wiley & Sons; 2004. pp. 223–35. [Google Scholar]
- Song CW, Park HJ, Lee CK, Griffin R. Implications of increased tumor blood flow and oxygenation caused by mild temperature hyperthermia in tumor treatment. Int J Hyperthermia. 2005;21:761–7. doi: 10.1080/02656730500204487. [DOI] [PubMed] [Google Scholar]
- Sun DN, Gu WY, Guo XE, Lai WM, Mow VC. A mixed finite element formulation of triphasic mechano-electrochemical theory for charged, hydrated biological soft tissues. Int J Num Methods Eng. 1999;45:1375–402. [Google Scholar]
- Taylor A, Granger D. Exchange of macromolecules across the microcirculation. In: Renkin EM, Michel CC, editors. Handbook of Physiology The Cardiovascular System Volume IV: Microcirculation, Part 1. American Physiological Society; 1984. pp. 467–520. [Google Scholar]
- Ter Haar GR. In: Therapeutic and Surgical Applications Physical Principles of Medical Ultrasonics. 2. Bamber JC, ter Haar GR, editors. John Wiley & Sons; 2004. pp. 407–56. [Google Scholar]
- Ter Haar GR. Therapeutic applications of ultrasound. Prog Biophys Mol Biol. 2007;93:111–29. doi: 10.1016/j.pbiomolbio.2006.07.005. [DOI] [PubMed] [Google Scholar]
- Vykhodtseva N, Sorrentino V, Jolesz FA, Bronson RT, Hynynen K. MRI detection of the thermal effects of focused ultrasound on the brain Ultrasound. Med Biol. 2000;26:871–80. doi: 10.1016/s0301-5629(00)00216-7. [DOI] [PubMed] [Google Scholar]
- Wang S, Shin IS, Hancock H, Jang BS, Kim HS, Lee SM, Zderic V, Frenkel V, Pastan I, Paik CH, Dreher MR. Pulsed high intensity focused ultrasound increases penetration and therapeutic efficacy of monoclonal antibodies in murine xenograft tumors. J Control Release. 2012;162:218–24. doi: 10.1016/j.jconrel.2012.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson KD, Lai CY, Qin S, Kruse DE, Lin YC, Seo JW, Cardiff RD, Mahakian LM, Beegle J, Ingham ES, Curry FR, Reed RK, Ferrara KW. Ultrasound increases nanoparticle delivery by reducing intratumoral pressure and increasing transport in epithelial and epithelial-mesenchymal transition tumors. Cancer Res. 2012;72:1485–93. doi: 10.1158/0008-5472.CAN-11-3232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiig H, Rubin K, Reed RK. New and active role of the interstitium in control of interstitial fluid pressure: potential therapeutic consequences. Acta Anaesthesiol Scand. 2003;47:111–21. doi: 10.1034/j.1399-6576.2003.00050.x. [DOI] [PubMed] [Google Scholar]
- Wissler EH. Pennes’ 1948 paper revisited. J Appl Physiol. 1998;85:35–41. doi: 10.1152/jappl.1998.85.1.35. [DOI] [PubMed] [Google Scholar]
- Wu J, Du G. Temperature elevation generated by a focused gaussian beam of ultrasound Ultrasound. Med Biol. 1990;16:489–98. doi: 10.1016/0301-5629(90)90171-8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.