Design and control of compliant tensegrity robots through simulation and hardware validation

Abstract

To better understand the role of tensegrity structures in biological systems and their application to robotics, the Dynamic Tensegrity Robotics Lab at NASA Ames Research Center, Moffett Field, CA, USA, has developed and validated two software environments for the analysis, simulation and design of tensegrity robots. These tools, along with new control methodologies and the modular hardware components developed to validate them, are presented as a system for the design of actuated tensegrity structures. As evidenced from their appearance in many biological systems, tensegrity (‘tensile–integrity’) structures have unique physical properties that make them ideal for interaction with uncertain environments. Yet, these characteristics make design and control of bioinspired tensegrity robots extremely challenging. This work presents the progress our tools have made in tackling the design and control challenges of spherical tensegrity structures. We focus on this shape since it lends itself to rolling locomotion. The results of our analyses include multiple novel control approaches for mobility and terrain interaction of spherical tensegrity structures that have been tested in simulation. A hardware prototype of a spherical six-bar tensegrity, the Reservoir Compliant Tensegrity Robot, is used to empirically validate the accuracy of simulation.

1. Introduction

Prior work has investigated the unique structural properties of tensegrity systems, their role in biology and control strategies for different tensegrity morphologies. One of the centres for this research is NASA Ames Research Center, Moffett Field, CA, USA, where there is interest in these systems for planetary exploration missions.

1.1. Tensegrity structures

Tensegrity structures are composed of compression elements encompassed within a network of tensional elements; consequently, each element experiences either pure compression or pure tension. This allows individual elements to be extremely lightweight, as designs do not need to resist bending or shear forces. Active motion in tensegrity structures can be performed with minimal energy expenditure as actuators work linearly along load paths in tension elements, avoiding torques caused by long lever arms of traditional robotic designs.

A unique property of tensegrity structures is how they internally distribute forces. As there are no lever arms, forces do not magnify around joints or other common points of failure. Rather, externally applied forces distribute through the structure via multiple load paths, creating system-level mechanical robustness and tolerance to forces applied from any direction or failure of individual actuation elements [1]. Thus, tensegrity structures are ideally suited for operation in dynamic environments where contact forces cannot always be predicted.

1.2. Tensegrity and biology

Tensegrity structures are being discovered in many aspects of biological systems, which motivate this work's bioinspired modelling and control approaches. The tensegrity concept appears at various scales, from the cytoskeleton of individual cells (figure 1) [2–4] to mammalian physiology [5]. Emerging biomechanical theories are shifting focus from bone-centric models to fascia-centric models. Fascia is the connective tissue in our bodies (including muscles, ligaments, tendons, etc.) that forms a continuous web of tension, even surrounding and supporting bones, which, unlike traditional mechanical systems, have no rigid connections between them [6]. This new view is challenging the ‘common-sense’ view of skeletal structures as the primary load-bearing elements of human and mammalian bodies (figure 2). In the emerging ‘bio-tensegrity’ model, bones are still under compression, but they are not passing compressive loads to each other; rather, it is the continuous tension networks of fascia that are the primary load-bearers [5,6].

Figure 1.

Computer simulations of a nucleated tensegrity cell model exhibits mechanical coupling between the cell, the cytoskeleton and the nucleus. (Adapted from [2], with permission from Macmillan Publishers Ltd.) (Online version in colour.)

Figure 2.

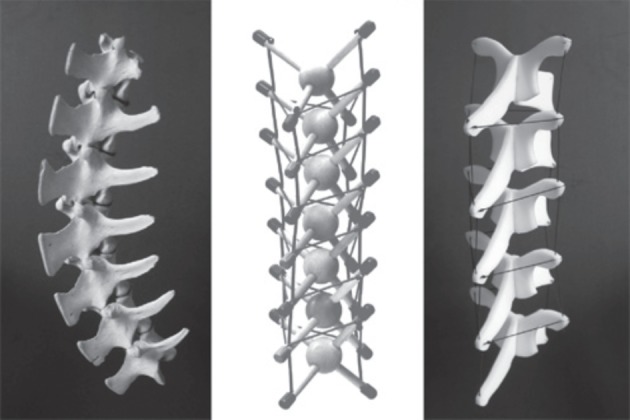
Tensegrity models of the spine show how vertebrae float without touching. (Image courtesy of Tom Flemons. © copyright 2006 [7].)

1.3. Tensegrity robotics for space exploration

NASA is supporting research into tensegrity robotics to create planetary rovers with many of the same qualities that benefit biological systems. The high strength-to-weight ratio of tensegrity structures is attractive due to the impact of mass on mission launch costs. Likewise, large tensegrity structures are deployable from compact configurations, enabling them to fit into space-constrained spacecraft. While these qualities have inspired studies of deployable antennae and other large space structures [8], the unique force distribution of tensegrity robots has only recently been investigated for planetary exploration [9]. Initial work in the NASA Innovative Advanced Concepts project [10] shows that controllable compliance and force distribution properties allow for reliable and robust environmental interactions during landing and planetary surface exploration.

A key goal of this NASA work is to develop a tensegrity probe with an actively controlled tensile network, enabling compact stowage for launch followed by deployment for landing. Compliant tensegrity probes can safely absorb significant impact forces, enabling high-speed entry, descent and landing scenarios where the probe acts like an airbag [9]. However, unlike an airbag that must be discarded after a single use, the tensegrity also provides rolling mobility (figure 3). This enables compact and lightweight planetary exploration missions with the capabilities of traditional wheeled rovers, but with a mass and cost similar to a stationary probe. Dual use of structure allows a tensegrity mission to have a high mass fraction between science payload and overall weight (as measured at atmospheric entry). This reduces mission cost and enables new forms of surface exploration using the tensegrity's natural tolerance to impacts [9].

Figure 3.

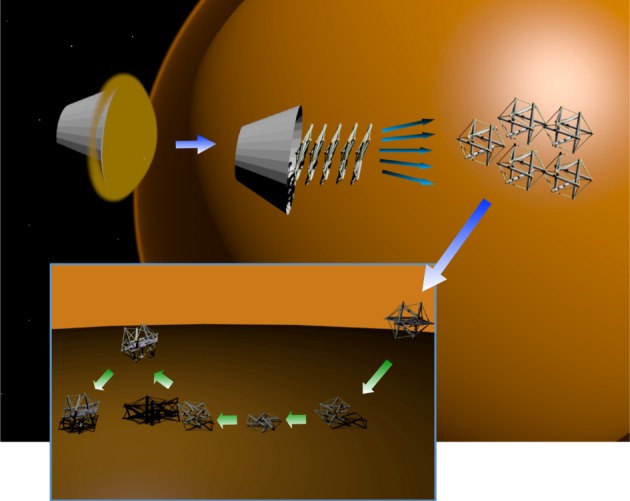
Mission scenario—a tightly packed set of tensegrities expands, spreads out, falls to the surface of the Moon and then safely bounces on impact. The same tensegrity structure cushioning landing is then used for exploration.

1.4. Tensegrity control

Tensegrity structures are a fairly modern concept, having been initially explored in the 1960s by Buckminster Fuller [11] and the artist Kenneth Snelson [12]. Initial tensegrity research was mostly concerned with form-finding techniques [13] and the design and analysis of static structures [14,15]. Research into control of tensegrity structures began in the mid-1990s, with initial efforts at formalizing the dynamics of tensegrity structures only recently emerging [15]. The very properties that make tensegrities ideal for physical interaction with the environment (compliance, multi-path load distribution, nonlinear dynamics, etc.) also present significant challenges to traditional control approaches. A recent review shows that there are still problems actively controlling tensegrities [16]. Work has continued in the analytical understanding of the equations of motion and dynamics of tensegrity structures [17]. However, environmental interactions cause additional modelling difficulties, typically limiting the effectiveness of such approaches. Consequently, successful demonstrations of tensegrity mobility have primarily used non-analytical methods [1,18–20]. Our approach to these problems is therefore to develop control algorithms based on central pattern generators (CPGs), distributed learning and genetic algorithms instead of more traditional control approaches.

1.4.1. Central pattern generators

CPGs are neural circuits found in both vertebrate and invertebrate animals that produce rhythmic patterns of neural activity without receiving rhythmic inputs. CPGs have been studied from a biological perspective and have been used extensively in robotics [21]. The term central indicates that rhythms of the CPG are not driven by sensory input, but are self-generated. CPGs are the fundamental building blocks for locomotor neural circuits in many animals and are also key to other fundamental rhythmic activities such as chewing, breathing and digesting. Recent research shows a close relationship between CPGs and motion primitives in the spine that enable both rhythmic and discrete motions [22]. Alongside their biological inspiration for use in robotic motion, CPGs present several interesting and useful properties including distributed control, robustness to perturbations, inherent tolerance to redundancies, fast control loops and the ability to modulate locomotion by simple control signals.

CPGs are therefore well suited for controlling tensegrities [23] and other biomimetic structures [24]. Additionally, there is intuition for pairing tensegrity robots with CPG networks: the dynamics of physical forces propagating through a tensegrity structure are similar to the dynamics of control patterns propagating through CPG networks.

1.4.2. Evolutionary algorithms

Instead of defining a control policy directly, evolutionary algorithms can be used to learn a control policy. This is accomplished through an iterative cycle, where in simulation a control policy is run and evaluated, and this evaluation is fed back into the genetic algorithm so that it can improve the control policy. Evolutionary algorithms have the following advantages:

• (1) Complex, nonlinear control policies can be learned.

• (2) Underlying dynamics need not be known.

• (3) Control policies can be learned or parameters of existing control policies can be optimized.

• (4) Distributed learning can be used to scale to larger tensegrities and to accelerate learning.

Moreover, coevolutionary algorithms provide distributed learning for multi-agent problems [25]. Each component can individually learn a control policy that decides how to actuate its individual end cap in such a way that global performance is maximized [26]. Challenges controlling tensegrity robots using traditional approaches have led some researchers to consider biologically inspired evolutionary or coevolutionary algorithms [1,27–29].

1.5. Outline

This paper is organized as follows: §2 introduces our simulators and hardware platform; §3 presents our simulator validation results; §4 describes our various control strategies; and §5 discusses our future work and our results and control strategies in context of other work. And last, §6 presents our conclusion.

2. Systems and models

We introduce three systems to evaluate the design and control of tensegrity structures. The first two are simulation environments, while the third is an untethered, lightweight robot prototype.

2.1. Spring–cable assemblies

All tensile members of the structures we study in this work are compliant and we refer to them as spring–cable assemblies. Although various implementations are possible, all spring–cable assemblies in this work can be modelled as a zero rest-length passive spring in series with a non-elastic cable. The tension on spring–cable assembly i is given by

2.1

where k_i is the spring stiffness, 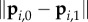is the Euclidean distance between the attachments of the spring–cable assembly and ℓ_i is the cable length. Actuated members have a controllable rest length ℓ_i.

2.2. Euler–Lagrange simulator

We extended the Euler–Lagrange formulation described in Skelton's reference work on tensegrity systems by adding support for ground contacts and gravity [15]. In Skelton's work, the tensegrity structure struts are modelled as cylinders with infinitesimal radius. Strut-to-strut contacts are not modelled, which is an acceptable approximation for NASA-scale missions.

We found that this environment provides particularly accurate results for two types of experiments: tests of structural forces and tests of effective structural stiffness. This simulator is used for payload acceleration prediction during impacts from drop tests, as well as stiffness analyses and form-finding. However, its simple underlying model makes it unsuited for the study of complex environmental interactions.

2.3. NASA Tensegrity Robotics Toolkit

Our main simulation environment, the NASA Tensegrity Robotics Toolkit (NTRT), is built on the discrete time Bullet Physics engine (a game physics simulator) [30].

As game physics requires real-time simulation, Bullet is designed to handle collisions without excessive processing power. However, the Bullet physics library does not currently provide models of ropes, cables or springs with realistic material properties and stress analysis. Instead of using these default soft body models, we built an additional library to simulate spring–cable assemblies as two-point tensional elements that apply directional forces to rigid bodies.

This approach gives the ability to calculate the amount of stretch and tension for each simulated cable, as well as the force exerted to the bodies, using more mathematically rigorous models. A current limitation of this method is that the cables do not exist in the simulation world as physical bodies. Thus, their collisions and interaction with rigid bodies are not simulated. For locomotion tasks and terrain types we have explored so far, this is not a problem, but will be addressed in the future to simulate more extreme terrain interactions.

2.4. Prototype

In addition to these two software environments, a physical prototype of the six-bar tensegrity was constructed. Reservoir Compliant Tensegrity Robot (ReCTeR) is a highly compliant, lightweight (1.1 kg), underactuated tensegrity icosahedron robot, as shown in figure 4. The robot's 24 outer tensile elements are passive spring–cable assemblies with low-stiffness springs (28.4 N m⁻¹) under moderate pretension (≈10 N). Six actuated spring–cable assemblies run through the robot connecting active and passive end caps (also see §2.5). Their rest length is adjusted by a rotational DC motor (4.5 W, 4.4 : 1 gear ratio) that spins a snag-resistant bobbin (5.5 mm diameter). The other end of the cable attaches to a stiffer spring (81 N m⁻¹) affixed to a passive end cap. We use low-stiffness springs to allow active folding (figure 4) without plastic deformation of the 24 passive tensile members or excessive motor power requirements.

Figure 4.

ReCTeR: an untethered, highly compliant, spherical tensegrity robot. Top left: deployed robot. (Credit: NASA Ames/Eric James.) Centre right: active folding. Bottom: ReCTeR rolling from right to left.

The six active spring–cables run through the robot and connect non-parallel struts in an advantageous way. Stiffness analysis revealed that this pattern allows for large shape deformations with low motor power requirements. As a consequence of low spring stiffnesses, the lowest natural frequencies of oscillatory modes for the structure are of the order of a few hertz.

Sensing and feedback control are achieved by 24 tension sensors using strain gauges, six ground reaction-force sensors and three six-DOF inertial measurement units distributed evenly among the actuated end caps. To allow dynamic motion and rolling, each self-contained strut holds a hardware module with battery power and wireless communication. The battery is mounted at the centre of the strut to minimize the moment of inertia around its longitudinal axis. This makes ReCTeR fully untethered.

2.5. Robot models

Our control methods are implemented on platforms with varying configurations. Figure 5 shows the three tensegrity icosahedra analysed in this paper.

Figure 5.

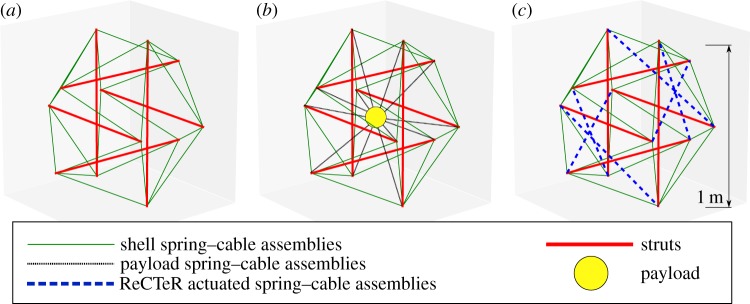
The various tensegrity configurations used in this paper. (a) Tensegrity icosahedron with only outer-shell members. (b) Tensegrity icosahedron with a payload by inner elements. (c) ReCTeR configuration with passive outer-shell and actuated spring–cable assemblies. (Online version in colour.)

We put a particular emphasis on spherical icosahedron tensegrities. This symmetric configuration provides a large interior volume with a moderate number of members and can be folded easily. It lends itself naturally to rolling locomotion because of its triangular faces. Additionally, tensile-member failure will result in reduced locomotion capabilities instead of full failure, due to its redundant number of tensile members [31].

The basic tensegrity icosahedron is shown in figure 5a. This structure has 24 spring–cable assemblies and six rigid rods. The spring–cable assemblies are also referred to as outer-shell elements.

A tensegrity icosahedron with a payload is displayed in figure 5b. This structure has an additional 12 spring–cable assemblies to suspend the payload in the centre of the robot. We also refer to these as inner members.

Figure 5c displays the model ReCTeR's configuration with actual dimensions. ReCTeR has the basic tensegrity icosahedron configuration with six extra actuated spring–cable assemblies.

3. Validation of simulations

3.1. Experimental set-up

To track the full state of the robot, an active marker motion capture set-up was used. Passive struts were fitted with two markers, and active struts received three markers.

3.2. Kinematics

The forward kinematics of the Euler–Lagrange and NTRT simulators were compared against motion capture data from ReCTeR.

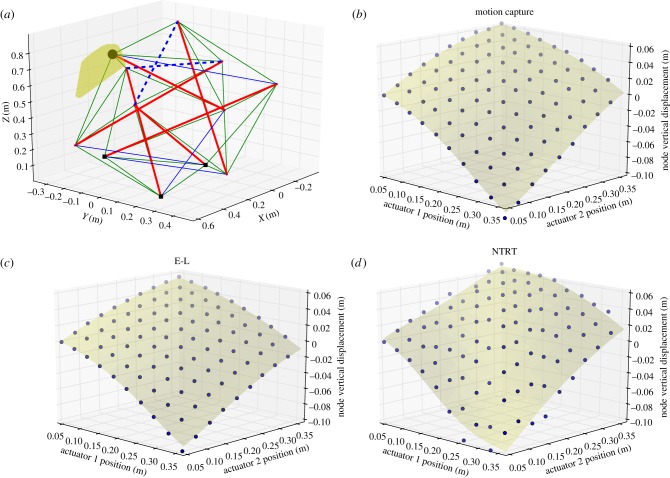
The six-strut ReCTeR robot was placed on one of its triangular faces and two top spring–cable assemblies were actuated, as shown in figure 6. We tracked vertical displacement of an end cap not directly actuated by one of these two members. The incident strut was suspended in air by a total of 10 springs.

Figure 6.

(a–d) Kinematic comparison of Euler–Lagrange (E-L) and NTRT simulators and ReCTeR motion capture data. (a) shows the experimental set-up. The rest length of two actuated spring–cable assemblies (dashed lines) is modified. The full range of tracked end-cap motion during the experiment is shown in transparent yellow (convex hull). The end caps indicated by small squares are on the ground. (b–d) show vertical displacement of the end cap indicated by the large black dot in (a) as a function of the lengths of the two actuated cables. The end cap where we trace the displacement is not directly actuated and is floating. The nodal displacement as a function of the actuator position is nonlinear, even for modest displacements. Note that the left-most point (0.05, 0.05, 0) is the reference point; displacements are relative to this initial state. (Online version in colour.)

Lengths of the two actuated spring assemblies were varied from the point of no tension in the given configuration (slack) to 0.32 m beyond this length. Each range was sampled at 10 equally spaced lengths, resulting in 100 measurement positions. Ranges were manually tuned to maximally deform the robot without causing it to roll. This experiment was repeated three times with no meaningful difference in observed displacements.

The average observed difference between motion capture data and the Euler–Lagrange simulator was 6.5 mm. For NTRT, we obtained an average error of 15 mm (0.5% and 1.3% of ReCTeR's diameter).

3.3. Dynamics

Next, we compared the dynamics of the NTRT simulator with the ReCTeR hardware. This experiment was designed for two purposes: first, to verify that the simulator can replicate ground interactions; and second, that it can simulate conversion of potential energy into kinematic energy when a spring is released. The experimental set-up is shown in figure 7. The robot initially has a non-minimal ground contact (four end caps on the ground instead of just three), and three actuated springs are tensioned. Next, one of the tensioned, actuated springs is loosened by its actuator, causing the robot to roll over.

Figure 7.

Comparing the dynamics of the robot and NTRT. The tensioned spring–cable assembly indicated by the dashed line is released (0.32–0.535 m at 0.6 m s⁻¹), causing the robot to topple. Two other actuated members are also tensioned, while the other three actuated springs are at their initial lengths, resulting in two slack springs. We observed a time-averaged error of the end caps' vertical positions of less than 5% of ReCTeR's diameter for all end caps. (Online version in colour.)

As the experiment also depends on ReCTeR's initial state, the observed initial state from the motion capture data was copied to the NTRT simulator. The ReCTeR model in the NTRT simulator was then released from this initial configuration, allowing it to reach the simulated, predicted equilibrium. Recorded motor positions from the physical test were then applied into the simulator, causing a similar roll-over motion.

4. Locomotion control

Once it had been determined that the NTRT simulator modelled these robotic dynamics reasonably well, locomotion experiments were performed with tensegrity robots in both simulation and hardware. The algorithms described in §4.1 apply to various configurations, but are presented here in simulation for the first configuration, as shown in figure 5 with 1.5 m rods, weighing 15 kg. The controls in §4.2 were applied to simulations of the second configuration. Section 4.3 presents hardware results on ReCTeR and a comparison of those results with previously simulated implementations. Appendix A provides a summary of the control methods in this work and an overview of related work.

4.1. Coevolutionary control

The first control method from our group is based on coevolutionary algorithms [25]. We demonstrated successful rolling locomotion of a tensegrity icosahedron with this technique in the NTRT [29]. In this scheme, each spring–cable assembly is active and has a controller that evolves independently from the other controllers (i.e. in independent pools), but cooperation is used to optimize behaviour of the entire robot. The objective function for this maximization was set to be ReCTeR's distance travelled during a fixed amount of time. The simplest implementation of this technique is an optimization of open-loop control signals that are only a function of time; sinusoidal functions performed well.

After this method was explored, the effects of different complexities and frequencies of these open-loop signals were analysed. More precisely, we optimized stepwise functions with varying numbers of via points. This enables the study of computational load and scaling properties needed to estimate power consumption of various controllers, as well as to investigate the effects of actuator failure. Figure 8 shows the learning curve of this process. In this case, optimized rest-length signals had four via points. An analysis of practical aspects of these results (power consumption, actuator failure, etc.) is underway.

Figure 8.

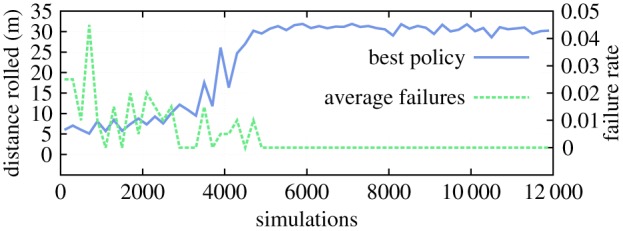
Distance covered by the robot in 60 s with distributed learning of open-loop controllers based on coevolutionary algorithms. Each of the 24 outer-shell spring–cable assembly controllers has a different evolution pool, but their combined behaviour is optimized. (Online version in colour.)

While these open-loop controllers demonstrated basic rolling behaviour, they commonly failed in the presence of external forces or unexpected terrain conditions. To solve this problem, we developed a simple rolling algorithm that uses ground-contact sensors located on the simulated end caps. Preliminary results have shown steerable rolling on various terrains.

This brief analysis of coevolutionary learning for icosahedral tensegrity locomotion demonstrates that learning-based controls can provide robust rolling locomotion without analytical knowledge of the robot's dynamics.

4.2. Bioinspired control

In contrast to the direct learning technique presented above, our second set of approaches is more designer-involved and specific to this structure. State feedback was used to increase rolling performance of the tensegrity robot with payload simulated with the NTRT (figure 5).

The idea behind these control laws is to create torque by moving the robot's centre of mass with respect to the ground-contact surface to cause the robot to roll, as illustrated in figure 9. This motion is achieved with a two-layer control architecture: the robot's heading and speed are controlled by displacement of the central payload using the inner spring–cable assemblies, and motion is simplified by actuating the outer shell.

Figure 9.

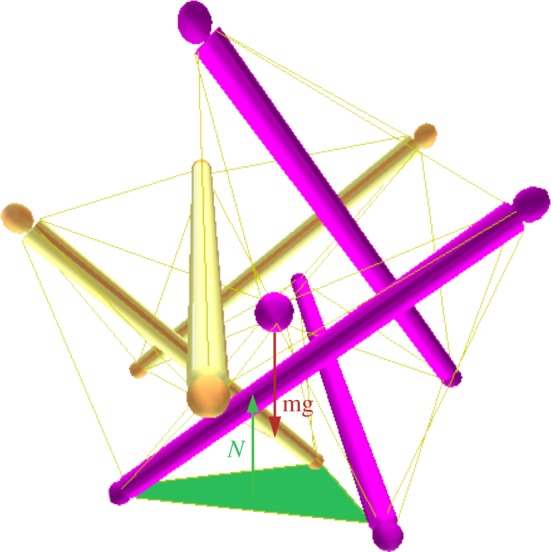
Regular icosahedron tensegrity shape with central payload (figure 5b). The highlighted contact surface with the ground creates a reaction force N (upwards arrow) that, at rest, balances the weight of the structure, represented on the figure by the downwards arrow mg. Torque is created on the whole structure when displacement of the centre of mass from its rest position occurs. (Online version in colour.)

Three control approaches test inner spring–cable assemblies: reactive controls, inverse kinematics (IK)-based controls and CPG-based controls. Outer spring–cable assemblies are controlled with hand-tuning. Actuation of the outer shell reduces ground contacts, not directly influencing heading or speed. This affects motion in several ways. First, it allows for creation of greater torques with the same payload displacement. Second, it smoothens rolling behaviour of the structure by preventing discontinuities due to excessive ground contact.

For each control approach, inputs were taken as functions of the robotic state. The height of each strut was computed using simulated omnidirectional distance sensors located at the end of each rod. The height assigned to each spring–cable assembly was computed as the average of the two endpoints' height. We understand that omnidirectional distance sensors can be difficult to realize in hardware; it is not practical to rely on the full state of the robot as input. However, multiple solutions to this problem exist. An interesting approach is to embed ground reaction-force sensors in a protective soft cap on each rod end. A second possibility, motivated by the separation principle of control theory [32], is to estimate system states from other sources, such as accelerometer and gyroscope measurements. This second approach could be augmented with the knowledge that this icosahedron robot often rolls over an edge of a face triangle [20]. Finally, one could use a CPG to emulate rhythmic activation of sensors, similar to the approach in §4.2.2.

The control for the outer-shell cables was designed to tighten the bottom part of the structure when rolling, changing the lever arms of the gravitational force from the robot's centre of mass, requiring less force to induce a roll. Typically in the presence of a slope, reduction of ground-contact surface is sufficient to cause a roll down the slope. In order to take this into account, we added a measure of speed, which is computed as the dot product between the centre-of-mass position and the robot's overall heading direction vector. With this method, speed is a scalar number and its sign depends on the robot's heading (positive in the desired direction and negative otherwise). Speed can then be used as feedback to influence the spring actuator command. Rest lengths of the shell spring–cable assemblies are computed using the following actuation rule:

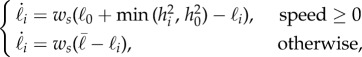4.1

where h_i is the height of spring–cable assembly i as measured from the distance sensors; ℓ_i is its current rest length; ℓ₀, h₀ and 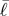are constant parameters; and 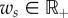accounts for the time scale where length corrections occur. ℓ₀ and h₀ represent the offset-rest length of the spring and the maximum height measurement. The parameter 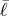represents the default rest lengths of the springs that, if given as a command to all motors, puts the tensegrity in a stable position on the ground. Input and output parameters of this control law are updated continuously through feedback control. Impedance control, which was adapted to tensegrities previously [24,33], is used to modify spring–cable rest lengths.

4.2.1. Reactive controls

The first technique for actuation of inner payload spring–cable assemblies was the use of reactive controllers. We note that the only controllable parameter is cable length. The variables ℓ_i here are the rest length of the inner springs. Global heading direction in a chosen inertial reference frame is defined by the unit vector v and the orientation of each spring in this same reference frame, represented by the vector v_i. For each inner spring–cable assembly, we use the dot product 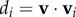as feedback to control the position of the payload as follows:

4.2

4.3

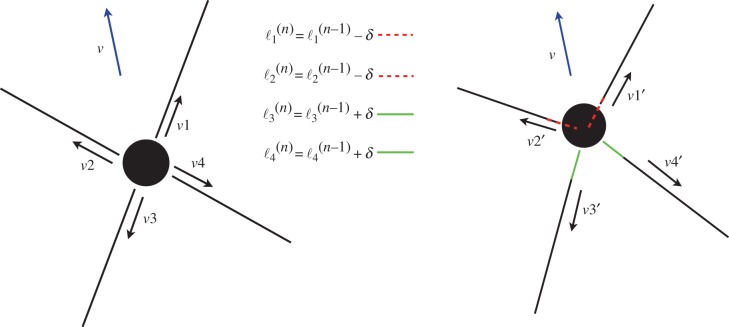
where the weight w_r determines reactivity of the system and γ < 0 is a fixed parameter. Thus, without any external perturbation, the system has a stable equilibrium position at 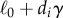. Rest length of the spring–cable assemblies where the orientation aligns with the global heading is reduced. Vice versa, springs pointing in the opposite direction are elongated. The global result is displacement of the payload in the direction of the heading vector, as shown in figure 10. Note that the heading direction v can be chosen arbitrarily and adjusted dynamically. This method resulted in stable and smooth rolling gaits, allowing a roll of up to 1 m s⁻¹ (≈1 body-length per second) over flat terrain. The robot could also handle slopes up to 8°, bumpy terrain, obstacles and collisions.

Figure 10.

Computation of new rest lengths according to the spring–cable assemblies’ individual orientations v_i (time t^(n–1)). Length modification is indicated by coloured lines, dashed red if reduced and light green if elongated. The resulting effect is displacement of the central payload in the desired direction v (time 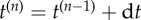). (Online version in colour.)

The main disadvantage of the reactive method is the type and amount of sensor feedback required to implement this approach in hardware. This issue is addressed by the control methods presented next, which are based on the same physical principle but require less feedback information.

4.2.2. Central pattern generator controls

CPGs have been successfully used in past tensegrity systems [23]. Such controls are a feasible alternative to reactive controllers that enable generation of regular motion patterns. For this control, full-state information is used to generate smooth motion under reactive controls. Then, resulting periodic commands were stored as a stable limit cycle of a CPG. Once this process completes, the tensegrity can be driven by CPG output with much less feedback. We used an adaptive frequency Hopf oscillator [34] during the learning phase where the tensegrity was reactively control-driven. The underlying dynamical system reads

4.4

4.5

4.6

where u, g and ω are state variables of the dynamical system, γ is a time constant, μ is the target frequency and ω is the target pulsation of the signal. Note the element and time indices are dropped to simplify notation: u designates u_i(t), with i the index of the spring–cable assembly. The output u can synchronize to any periodic input signal b(t) and replaces the feedback signal from the previous section,

4.7

Once the signal is learned, time dependency of the pulsation is removed, i.e. ω is held constant and a term accounting for ground-contact coupling is added to the dynamical system

4.8

4.9

4.10

where h(t) denotes the height signal fed back by the omnidirectional ranging sensors and 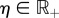is a coefficient. This method has the advantage of requiring minimal feedback and, thus, minimal computations. However, it is important to note that the dynamical system runs on a much larger time scale than perturbations disturbing the system. A tensegrity driven only by a CPG would then, in the best case, only have a stable rolling gait on a flat, obstacle-free terrain. Consequently, it is necessary to include a second control method that works on this smaller time scale and gives an appropriate response to external perturbations.

4.2.3. Hybrid central pattern generator: inverse kinematics controls

The final control method we tested is a hybrid technique with inverse kinematics. First, the position of the central payload 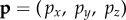is defined as a function of the inner cable lengths 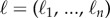. We can write this as a small displacement δp of the payload

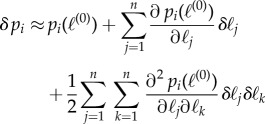4.11

or

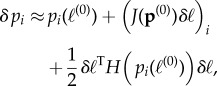4.12

for 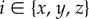and where 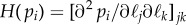is the Hessian matrix associated with p_i and .

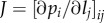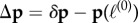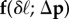Considering equation (4.12), we additionally define and as

4.13

Computation of the spring–cable rest-length changes δℓ for a desired payload displacement Δp corresponds to finding the δℓ that cause f = 0. As this last equation is over-determined, nonlinear and might not possess a real solution, we employed a quasi-Newtonian iterative method to approximate the solution. Starting from a candidate solution, e.g. 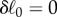, the next iteration is computed as

4.14

until convergence. J⁻¹ here denotes the Moore–Penrose pseudo-inverse of the Jacobian defined by

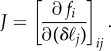4.15

Note that this matrix is not the same as the one in the Taylor expansion of p(ℓ).

The outputs of the IK algorithm 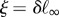(where ∞ indicates convergence) represent length corrections that have to be made to reposition the payload at the desired location. The outputs ξ can be used together with the adaptive frequency oscillator as presented in §4.2.2. This approach is inspired by two previous works by Ajallooeian et al. [35] and Gay et al. [36]. We update ξ if and only if the payload position lies on the opposite side of the robot's centre of mass, and we continuously adjust ξ with time according to the following evolution rule:

4.16

with 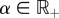. In this way, corrections are made only if the tensegrity can potentially roll in an undesired direction. Note also that, in order to use this method, both the position of the payload and the centre of mass are required inputs. Combining a corrective term with the output of the oscillator, the resulting dynamical system reads

4.17

and

4.18

If the value of ξ(t) is constant over time, the dynamical system converges asymptotically to u(t) = ξ [36]. While the pure CPG implementation does not allow any steering control, this implementation enables guidance on a desired trajectory on flat terrain (figure 11).

Figure 11.

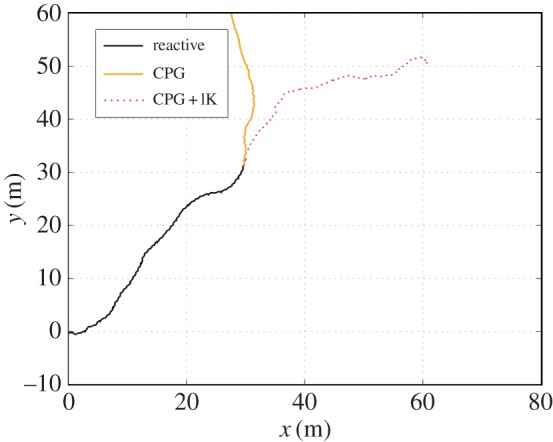
Trajectory of the tensegrity (top view). The dark curve represents the trajectory while the robot is driven by the reactive control algorithm and the CPG is in the learning mode (50 s). Motion is regular and the heading is maintained throughout the entire period. Light solid (yellow) and dashed (red) trajectories represent the path travelled once the CPG controller takes over (40 s). When the CPG is coupled to the height signal and receives inputs from the second-order inverse kinematics algorithm (dashed red curve), the resulting trajectory is a long and relatively straight line extending well the reactive control. (Online version in colour.)

Table 1 provides a summary of results obtained with different control strategies over regular, flat terrain.

Table 1.

Bioinspired control strategies summary.

	reactive	CPG	hybrid
average speed (m s−1)	1.00	0.50	0.38
complex terrain	yes	no	no

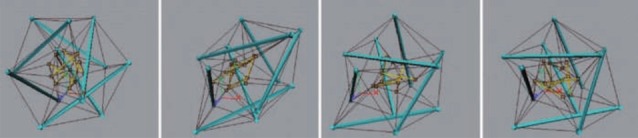
Note that results do not take the trajectory of the path into account and, consequently, even if the distance travelled using the CPG controller without any trajectory control is larger than with hybrid control, the ‘quality’ of the path is worse (e.g. figure 11). Interestingly, we observe that the stable gait pattern obtained in simulation is a sequence of contacts defined as energetically optimal by Koizumi et al. [20] for a tensegrity icosahedron. With the current implementation, only the reactive controller manages to induce rolling efficiently over complex terrain and obstacles. To the best of our knowledge, this last result is the only implementation of a tensegrity robot controller demonstrating such capabilities. Figure 12 presents such results from within the NTRT simulator.

Figure 12.

Examples of successful locomotion over complex terrains, such as slopes, bumps and obstacles. (Online version in colour.)

Experimentation demonstrated that the hybrid controller's performance is highly sensitive to some parameters appearing in the CPG equations, such as the ones presented in equations (4.17) and (4.18). As a result, future work will incorporate other methods to optimize feedback data and compute corrections to more accurately navigate complex environments. A good example of such an improvement can be found in Gay et al. [37], where sensory information is preprocessed by a neural network and trained using particle-swarm optimization methods before being fed back to the CPG. In the same idea, reservoir computing (RC) can also be a suitable tool for feedback computation, as detailed in the following section.

4.3. Learning a Matsuoka oscillator with physical reservoir computing

This section presents the final control results of this work: an implementation of the physical RC (PRC) principle on the ReCTeR hardware prototype. These results validate use of the NTRT in an untethered, underactuated feedback control of tensegrity icosahedra with string force sensors [38, §5.1.1]. Here, closed-loop feedback control is used when motor signals are generated by a Matsuoka oscillator. This demonstrates a successful adaptation of our simulation results to a physical platform (ReCTeR), with similar learning times and robustness.

A static linear feedback controller is designed, which robustly generates a set of desired oscillatory motor signals after a short learning phase. For this experiment, the target spring–cable rest lengths (ℓ_i) are generated using a random Matsuoka oscillator [39] (see [38, §3.1], for oscillator parameters and motivation). These signals represent desired actuator signals. We manually scaled target signals so that the resulting behaviour corresponds to a motion pattern with large shape deformations while keeping the physical structure from moving too fast (as this impeded motion tracking). The resulting gait was a slow crawling motion that allowed motion-capture tracking of the full experiment.

The algorithm proceeds by first applying target rest lengths to actuators in an open-loop set-up, inducing the robot to start moving. Next, online learning is applied to approximate desired signals based on sensor readings. These approximations are the feedback signals. The ratio of open-loop to feedback signals is gradually decreased until signals are generated by the feedback loop alone. At this point, the robot will robustly maintain oscillatory patterns. The precise equations and parameters used in the experiment are provided in [38] and the electronic supplementary material.

In our prior simulation work, we used the term PRC to describe how nonlinear computations, which are inherently performed by a physical system, can be easily exploited to simplify control of tensegrities [38]. PRC extends the RC concept that, at its origin, is a simple technique to train recurrent neural networks [40,41]. The common idea is that a system with complex dynamics is perturbed externally, but is otherwise left untouched. Instead, a simple readout mechanism is trained to perform the desired computational task. A number of related demonstrations have recently appeared in the soft robotics fields, e.g. RC applied to a soft, simulated octopus arm [42,43].

Controller feedback signals are obtained from ReCTeR's 24 force transducers. As these sensors are mounted perpendicularly to the robot's struts, output values depend on the angle of attack and tension of the attached spring–cable assembly. Thus, the sensors provide a readout of the robot's state, similar to state observations in RC. The robot's behaviour was evaluated using the motion-capture set-up described in §3.1.

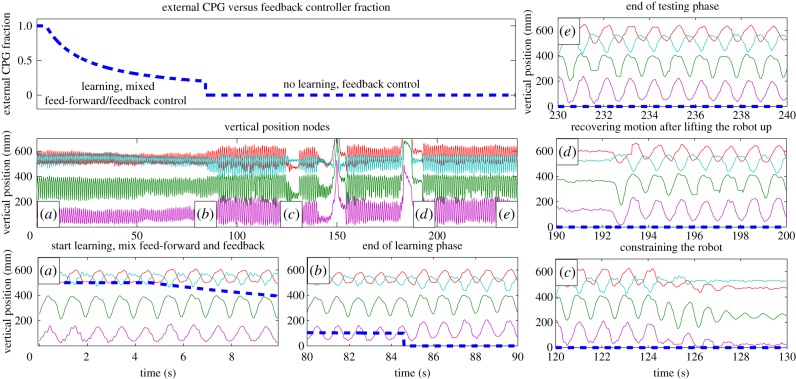
Figure 13 shows the result of an experiment where we first outsourced motor-signal generation to the feedback loop by online learning of the feedback weights. After training, we disturbed the system (lifting and constraining the robot). In this case, the robot stops moving and switches back to its original oscillatory mode when released, demonstrating robustness of the learned feedback controller, corresponding to our simulation results.

Figure 13.

Fast online learning of a static feedback controller for a Matsuoka oscillator on ReCTeR based on uncalibrated strain-gauge sensors. The top left plot shows the fraction of feed-forward versus feedback control. During learning, both feedback and feed-forward controllers (training signals) are active. The influence of the open-loop feed-forward controller decreases, and when its fraction is below 0.2, learning stops and only the trained feedback controller is active. The left plot on the second row shows vertical coordinates (in millimetres) of the four end caps with the largest vertical displacements as a function of time. The five surrounding plots are details of this plot, showing different training and testing phases. (a) Fully open-loop control. (b) Switch from partially open-loop and feedback control to full feedback control, learning stops. (c) We perturb the robot by pushing it down, preventing all movements. (d) The feedback controller recovers after the robot was lifted from the ground. (e) Behaviour of the robot after 250 s (170 s closed loop).

This experiment is a first demonstration of a simple, robust feedback control strategy implemented in both hardware and simulation for this class of untethered tensegrity robots. Additionally, this result shows the usefulness of tension sensors for tensegrity control. These PRC experiments are part of a continuous effort to develop low-level controllers for compliant robots that maximally exploit the robots' proper dynamics and that allow mitigation of stringent sensor requirements. We discussed many variations and extensions on the hardware experiment presented here in our prior simulation work [38].

5. Future work

Current prototype hardware allows for multiple verification levels of NTRT simulations. However, a more capable robot design is required to implement fully dynamic controls from the CPG systems and related work. ReCTeR has a maximum tension–force limit in its cables, as well as with the number of cables actuated. We are currently working on a redesigned six-strut robot with twice the number of actuators, with torque and velocity capabilities an order of magnitude higher than ReCTeR [44]. This robot will be able to implement the more advanced control schemes described in this paper. Design of this new robot will also target payload protection, a crucial feature for space exploration.

On the control side, one of our future goals is further integration of CPG and RC approaches, to maximally exploit the advantages of both.

6. Conclusion

Tensegrity is a curious design concept, spanning art, science and biology. This work presented the tensegrity workflow developed at the NASA Ames Research Center. Our simulator set-ups were described and demonstrated, and a new, highly compliant, untethered tensegrity robot—ReCTeR—was used to validate simulator set-ups in both dynamic and kinematic situations. Next, various control strategies were presented, based on evolutionary algorithms and CPGs, and a feedback controller was implemented on the hardware platform to demonstrate sensor capabilities. The biologically inspired control approaches we are exploring appear naturally suited for biologically inspired tensegrity structures, due to their matching nonlinear and oscillatory qualities.

An important aspect of this work is the creation of an Open Source simulation environment (the NTRT) for tensegrity-based mobility and manipulation controls research that has now been validated against hardware. This simulation environment enables us to develop an understanding of the structure and qualities of successful control approaches. Using evolutionary exploration of parameters for different structural and biologically inspired control approaches, this system can be used to develop performance-driven hardware requirements, such as the forces experienced in the rods, speed and torque requirements for actuators, elasticity constants for springs and sensor requirements and placements. Developing the right toolset and design workflow enables progress beyond tensegrity robots that merely move, and into a realm where tensegrity systems purposefully interact with the environment and execute tasks.

Appendix A. Tensegrity control methods overview

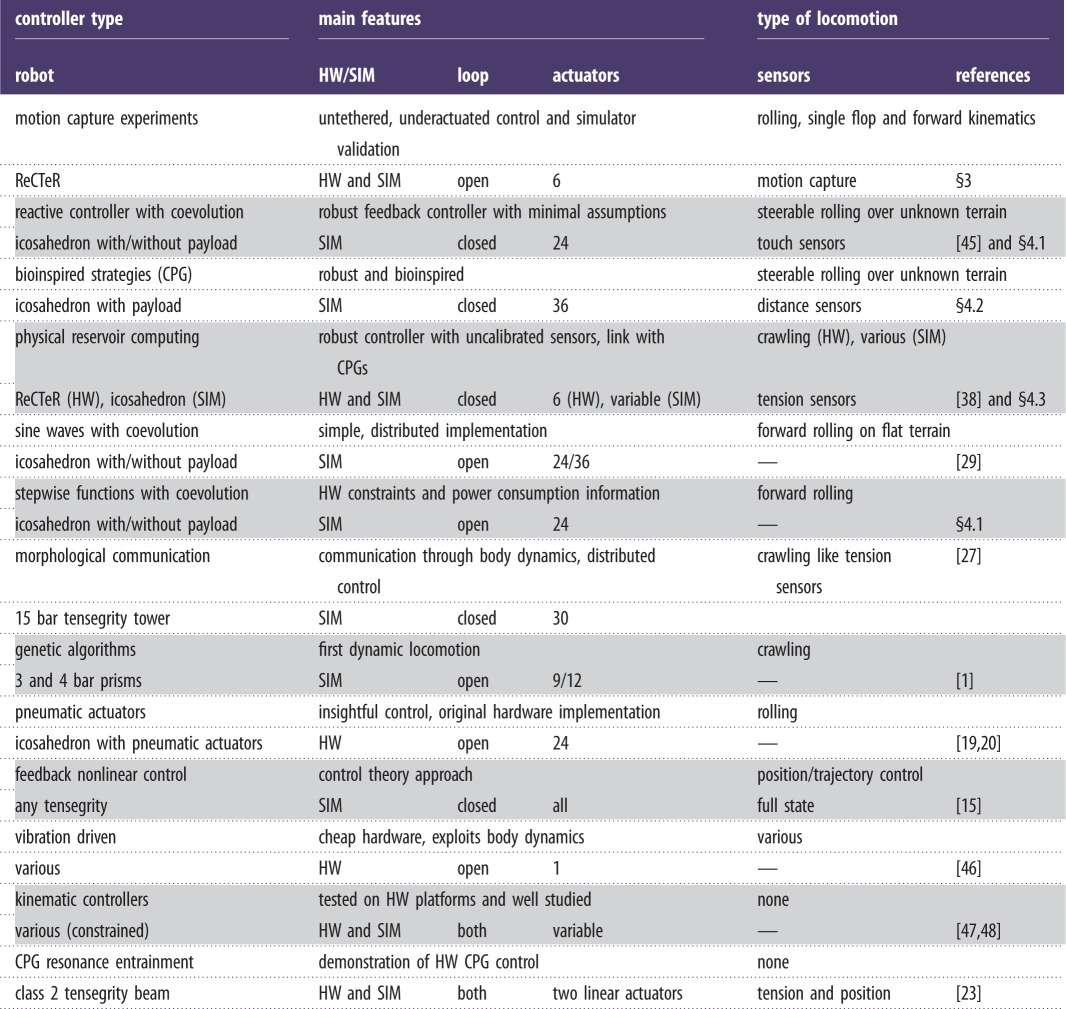
Table 2 provides an overview of various control methods for tensegrity structures. We list their main features and the type of locomotion.

Table 2.

Overview of various types of controllers for tensegrity robots and our experiments.

Data accessibility

Our simulators and the ReCTeR robot hardware designs are Open Source and can be obtained from our website: http://ti.arc.nasa.gov/tech/asr/intelligent-robotics/tensegrity/.

Funding statement

This research was supported by the European Commission's FP7 programme under grant agreement no. 248311—AMARSi and the NASA Innovative Advanced Concepts program. K.C. was supported by a PhD fellowship of the Research Foundation—Flanders (FWO). Support also came from NSF Graduate Research Fellowship no. DGE1106400, and from NASA Prime Contract no. NAS2–03144 awarded to the University of California, Santa Cruz, University Affiliated Research Center.