Timing and heterogeneity of mutations associated with drug resistance in metastatic cancers

Significance

Metastatic dissemination to surgically inaccessible sites is the major cause of death in cancer patients. Targeted therapies, often initially effective against metastatic disease, invariably fail due to resistance. We use mathematical modeling to study heterogeneity of resistance to treatment and describe for the first time, to our knowledge, the entire ensemble of resistant subclones present in metastatic lesions. We show that radiographically detectable metastatic lesions harbor multiple resistant subclones of comparable size and compare our predictions to clinical data on resistance-associated mutations in colorectal cancer patients. Our model provides important information for the development of second-line treatments that aim to inhibit known resistance mutations.

Abstract

Targeted therapies provide an exciting new approach to combat human cancer. The immediate effect is a dramatic reduction in disease burden, but in most cases, the tumor returns as a consequence of resistance. Various mechanisms for the evolution of resistance have been implicated, including mutation of target genes and activation of other drivers. There is increasing evidence that the reason for failure of many targeted treatments is a small preexisting subpopulation of resistant cells; however, little is known about the genetic composition of this resistant subpopulation. Using the novel approach of ordering the resistant subclones according to their time of appearance, here we describe the full spectrum of resistance mutations present in a metastatic lesion. We calculate the expected and median number of cells in each resistant subclone. Surprisingly, the ratio of the medians of successive resistant clones is independent of any parameter in our model; for example, the median of the second clone divided by the median of the first is $\sqrt{2}-1$. We find that most radiographically detectable lesions harbor at least 10 resistant subclones. Our predictions are in agreement with clinical data on the relative sizes of resistant subclones obtained from liquid biopsies of colorectal cancer patients treated with epidermal growth factor receptor (EGFR) blockade. Our theory quantifies the genetic heterogeneity of resistance that exists before treatment and provides information to design treatment strategies that aim to control resistance.

Acquired resistance to treatment is a major impediment to successful eradication of cancer. Patients presenting with early-stage cancers can often be cured surgically, but patients with metastatic disease must be treated with systemic therapies (1). Traditional treatments such as chemotherapy and radiation that exploit the enhanced sensitivity of cancer cells to DNA damage have serious side effects and, although curative in some cases, often fail due to intrinsic or resistance acquired during treatment. Targeted therapies, a new class of drugs, inhibit specific molecules implicated in tumor development and are typically less harmful to normal cells compared with chemotherapy and radiation (2–5). In the case of many targeted treatments, patients initially have a dramatic response (6, 7), only to be followed by a regrowth of most of their lesions several months later (8–10). Acquired resistance is often a consequence of genetic alterations (usually point mutations) in the drug target itself or in other genes (10–14).

Recently, mathematical modeling and clinical data were used to show that acquired resistance to an epidermal growth factor receptor (EGFR) inhibitor panitumumab in metastatic colorectal cancer patients is a fait accompli, because typical detectable metastatic lesions are expected to contain hundreds of cells resistant to the drug before the start of treatment (10). These cells would then expand during treatment, repopulate the tumor, and cause treatment failure. Similar conclusions should hold for targeted treatments of other solid cancers (15). Successful treatment requires drugs that are effective against the preexisting resistant subpopulation and must take into account the (possible) heterogeneity of resistance mutations present in the patient’s lesions. In this article we use mathematical modeling to investigate the heterogeneity of drug-resistant mutations in patients with metastatic cancers.

First mathematical investigations of the evolution of resistance to cancer therapy were concerned with calculating the probability that cells resistant to chemotherapy are present in a tumor of a certain size (16). Later studies expanded these results to include the effects of a fitness advantage or disadvantage provided by resistance mutations (17, 18), multiple mutations needed to achieve resistance to several drugs (15, 19–21), and density limitations caused by geometric constraints (22). These studies used generalizations of the famous Luria–Delbrück model for accumulation of resistant cells in exponentially growing bacterial populations (23). Probability distribution for the number of resistant cells in a population of a certain size in the fully stochastic formulation of the Luria–Delbrück model was recently calculated in the large population size limit (24, 25). The focus of above studies was describing the total number of all resistant cells, rather than the composition of the resistant population (26).

Results

We model the growth of a metastatic lesion as a branching process (27) that starts from a single cell (the founder cell of the metastasis) that is sensitive to treatment. Sensitive cells divide with rate b and die with rate d. The net growth rate of sensitive cells is $r=b-d$. During division, one of the daughter cells receives a resistance mutation with probability u. Resistant mutations can be neutral in the absence of treatment, which means they have the same birth and death rates as sensitive cells, and we initially focus on this case. We also expand our theory to the more general case where resistant cells are nonneutral, which means they have birth and death rates $b_R$ and $d_R$, respectively. If $c=\left(b_R-d_R\right)/\left(b-d\right)>1$, then resistance mutations are advantageous before treatment; if $c<1$, they are deleterious.

A resistant cell may appear in the population and be lost due to stochastic drift or it can establish a resistant subclone. We number the resistant subclones that survive stochastic drift by the order of appearance (Fig. 1A). A reasonable assumption for the number of point mutations that can provide resistance to a targeted drug is on the order of 100 (10, 28). Thus, the different resistant subclones will typically contain different resistance mutations, especially if we only focus on the largest ones.

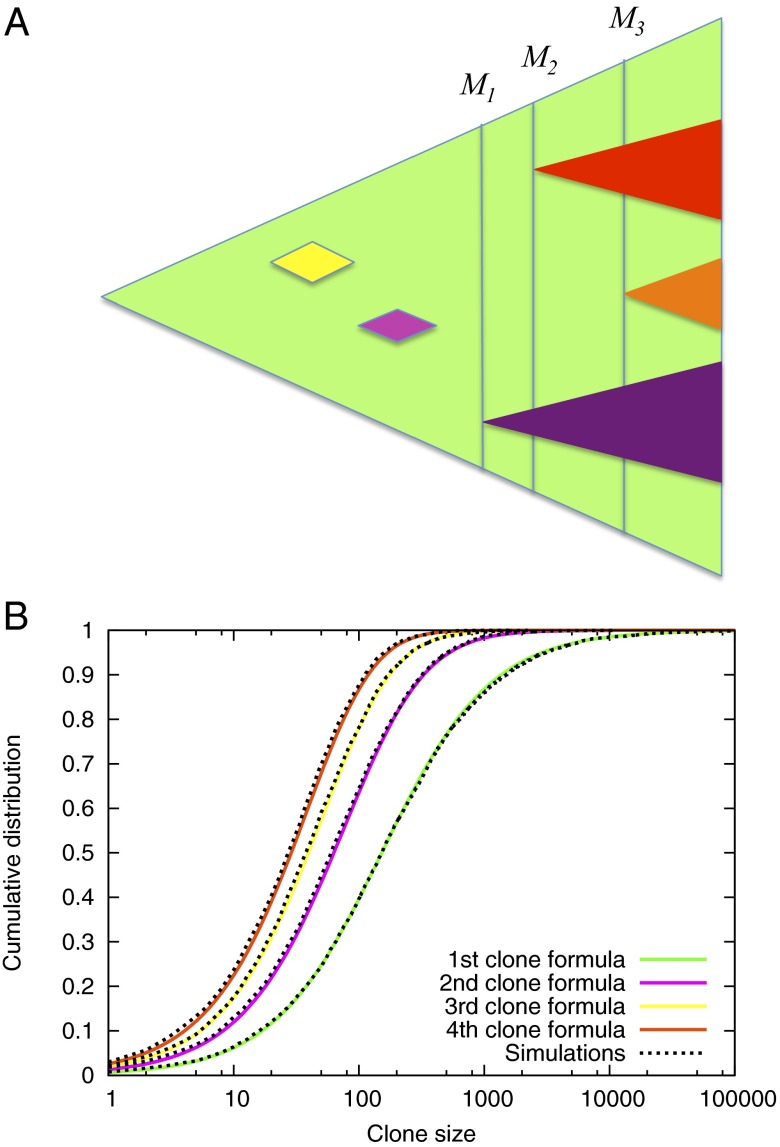
Fig. 1.

Evolution of resistance in a metastatic lesion. (A) As the lesion (green) grows from one cell to detectable size, new resistant subclones appear. Some of them are lost to stochastic drift (yellow and pink), while others survive (purple, red and orange triangle). Instead of looking at the time of appearance of new clones, our approach takes into account the total size of the lesion when the resistance mutation first occurred. (B) Agreement between computer simulations and formula (1) for the cumulative distribution function for the number of cells in the first four resistant clones. The first subclone contains 10 or fewer cells with probability 0.06, between 10 and 100 cells with probability 0.34, between 100 and 1000 cells with probability 0.47 and more than 1000 cells with probability 0.13. The second subclone contains more than 100 cells with probability 0.36. Parameters $b=0.25$, $d=0.181$, $M={10}^9$, $u=42\cdot {10}^{-9}$.

We calculate the number and sizes of resistant subclones in a metastatic lesion containing M cells. Typical radiographically detectable lesions are $\sim 1$ cm in diameter and contain $\sim {10}^9$ cells. The mutation rate, u, leading to resistance is the product of the point mutation rate μ, which is on the order of $\sim {10}^{-9}$ per base pair per cell division, and the number of point mutations that can confer resistance, which is $\sim 100$. In our analysis we will assume a large M and small u limit and mostly focus on the case when $Mu\gg 1$.

Tumor sizes at which successful resistant mutants are produced can be viewed as a Poisson process on $\left[0,M\right]$ with rate u (SI Text) (10, 17). The number of successful mutant lineages is thus Poisson distributed with mean $\lambda =Mu$. If $M_k$ is the number of cancer cells in the lesion when the kth mutant appeared, which survived stochastic drift (Fig. 1A), then $M_{k+1}-M_k$ is exponentially distributed with mean $1/u$. Therefore, we expect that the kth clone appeared when the total population size was $M_k\sim k/u$ and that roughly the size of the first clone is k times the size of the kth clone. The probability that exactly k clones are present in the population of size M is ${\lambda }^k{e}^{-\lambda }/k!$.

Counting new successful resistant clones in the order of appearance, we calculate the probability distribution for the number of cells in the kth resistant clone. In particular, if $k\ll Mu$, the cumulative distribution function for the number of resistant cells in the kth clone simplifies to

$$F_k\left(y\right)\approx 1-{\left(\frac{Mu}{Mu+y-dy/b}\right)}^k.$$ [1]

The excellent agreement between Formula 1 and exact computer simulations of the stochastic process is shown in Fig. 1B.

The mean number of cells in the kth resistant clone is $\text{E}\left(Y_1\right)\approx \left[bMu/r\right]\left[\log \left(r/bu\right)-1\right]$ and $\mathrm{E}\left(Y_k\right)\approx bMu/\left[r\left(k-1\right)\right]$ for $k\ge 2$. The median for the number of cells in the kth subclone is given by

$$\mathrm{Med}\left(Y_k\right)\approx \frac{bMu}{r}\left(2^{1/k}-1\right).$$ [2]

Interestingly, the ratio of the means of the two subclones k and j is $\left(j-1\right)/\left(k-1\right)$ for $k,j>1$. The ratio of their medians is

$$\frac{\mathrm{Med}\left(Y_k\right)}{\mathrm{Med}\left(Y_j\right)}=\frac{2^{1/k}-1}{2^{1/j}-1}.$$ [3]

These ratios are independent of any parameters of the process. In particular, the ratio of the medians of the first and second clone is $\sqrt{2}-1$, which implies that they have comparable size (same order of magnitude).

Liquid biopsy data were used to obtain estimates for the birth and death rates of cells in metastatic lesions and the number of point mutations providing resistance to the EGFR inhibitor panitumumab in colorectal cancer (10). The resulting parameter values ($b=0.25\hspace{0.5em}\text{and}\hspace{0.5em}d=0.181$ per day, point mutation rate $\mu ={10}^{-9}$ per base pair per replication, and 42 point mutations conferring resistance) can be used to calculate the mean and median sizes of the resistant subclones in a metastatic lesion containing $M={10}^9$ cells. The mean numbers of cells in the first, second, and third appearing resistant clone are $\text{E}\left(Y_1\right)\approx 2237$, $\text{E}\left(Y_2\right)\approx 152$, and $\text{E}\left(Y_3\right)\approx 76$, respectively. However, the mean for $Y_1$, the size of the first resistant clone, is heavily influenced by the realizations of the stochastic process in which the first resistance mutation appeared early and is not a good summary of the probability distribution for $Y_1$. Namely, the realizations in which the number of cells in the first clone is greater than the mean (2,237) account for less than $7\text{\%}$ of all cases. The median number of cells in the first resistant clone [$\text{Med}\left(Y_1\right)$] for the above parameters is 152, whereas the medians for $Y_2$ and $Y_3$ are 63 and 40, respectively.

In SI Text, we calculate the probability distribution for the ratio of resistant clone sizes $Y_1/Y_k$ and show that it is also independent of the parameters of the process. Even though the first appearing clone is expected to be the largest, followed by the second clone and so on, we show that this ordering is often violated. In $31\text{\%}$ of lesions, the first successful subclone is smaller than the second one; on the other hand, in $24\text{\%}$ of lesions the first subclone is at least 10 times larger than the second one.

Fig. 2 shows different realizations of the stochastic process of evolution of resistance in metastatic lesions containing ${10}^8$ and ${10}^9$ cancer cells. The same parameters were used to generate all lesions. The size of each subclone is shown (in number of cells), and the subclones are ordered by their time of appearance. In lesion L1, the first three subclones are the largest, and each have around 100 cells. Lesion L5 contains only two subclones, whereas L6 contains seven subclones, but none has more than 10 cells. In each lesion of total size ${10}^9$ cells, there are more than 10 resistant subclones. In L7, the two largest subclones contain 1,500 and 460 cells. In L8, there are five subclones of about 100 cells.

Fig. 2.

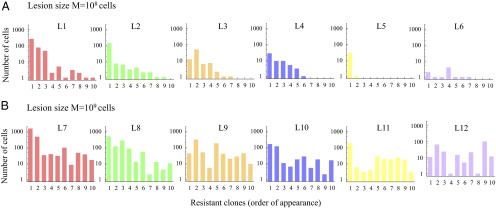
Resistant subclones in metastatic lesions. Different realizations of the same stochastic process are shown in each panel. (A) Six lesions of size ${10}^8$ and (B) six lesions of size ${10}^9$ cells. The first ten resistant clones are shown, which survived until time of detection. They are ordered according to their time of appearance. Parameter values for all simulations: $b=0.25$, $d=0.181$, $u=42\cdot {10}^{-9}$.

In Table 1, we show clinical data for the number of circulating tumor DNA (ctDNA) fragments harboring mutations in five genes associated with resistance to anti-EGFR treatment in 18 colorectal cancer patients who developed more than one mutation in those genes (29). These mutations were not detectable in patients’ serum before therapy, but became detectable during the course of anti-EGFR treatment. The number of ctDNA fragments correlates with the number of tumor cells harboring that mutation: it was previously estimated (using the tumor burdens and pretreatment ctDNA levels measured in patients who had KRAS mutations in their tumors before therapy) that one mutant DNA fragment per milliliter of serum corresponds to 44 million mutant cells in the patient’s tumor (10). Thus, the ratios of the resistant clone sizes can be obtained from the ratios of the numbers of ctDNA fragments harboring resistance-associated mutations. These data provide a unique opportunity to test our theory and compare the relative sizes of resistant clones inferred from the data with those predicted using our model. Assuming that resistance-associated mutations with higher ctDNA counts appeared before those with lower ctDNA counts, we find excellent agreement between the data and our model predictions. For example, the median ratio of the sizes of the first two resistant clones inferred from clinical data (29) is 2.21, whereas our model predicts 2.51. The median ratio of the sizes of the first and third clones from clinical data are 4.3, and our model predicts 4.12 (Table 1). This comparison is parameter free, as we showed that the ratio of resistant clone sizes is independent of parameters.

Table 1.

Comparison of predicted ratios of resistant clone sizes and ratios obtained from clinical data

Patient	$Y_1$*	$Y_2$	$Y_3$	$Y_4$	$Y_1/Y_2$	$Y_1/Y_3$	$Y_1/Y_4$
1	168	90			1.87
2	129	120			1.08
3	82	80	30		1.03	2.73
4	948	120	104	100	7.9	9.12	9.48
5	28	15			1.87
6	114	40			2.85
7	6,760	4,940	4,100	3,900	1.37	1.65	1.73
8	220	30			7.33
9	848	374	135	133	2.27	6.28	6.38
10	61	25			2.44
11	244	83	57		2.94	4.28
12	429	400	100		1.07	4.29
13	394	13	4		30.31	98.5
14	308	265	208	139	1.16	1.48	2.22
15	130	13			10
16	28	13			2.15
17	131	45	12	11	2.91	10.92	11.91
18	250	173	58	31	1.45	4.31	8.06
Median from patients					2.21	4.3	7.22
Predicted median					2.51	4.12	5.74
Predicted median (order by size)					2.05	3.63	5.25

^*Number of circulating tumor DNA (ctDNA) fragments per milliliter ($Y_1$ to $Y_4$) harboring different mutations associated with resistance to anti-EGFR agents in colorectal cancer patients treated with EGFR blockade (29). Ratio of resistant clone sizes is given by the ratio of the ctDNA counts for any two resistance-associated mutations. We assumed that mutations with higher ctDNA counts in the patient data appeared before mutations with smaller ctDNA counts. We also report predicted median ratios obtained from computer simulations when clones are ordered by size (parameters: $b=0.25$, $d=0.181$, $M={10}^9$, $u=42\times {10}^{-9}$).

Our mathematical results describe the relative sizes of resistant clones ordered by age, whereas the experimental data in Table 1 are ordered by size, which serves as a proxy for age, because exact clonal age is unknown. We quantify the extent to which this difference in clonal ordering by size vs. age influences our statistics using exact computer simulations (Table 1). In the relevant parameter regime of large lesion size, M, and small mutation rate, u, with $Mu\gg 1$, the results are largely independent of parameters (median ratios of clone sizes vary by $<10\text{\%}$ for different parameter combinations). We show simulation results for median ratios of clone sizes when clones are ordered by size for typical parameter values (10). As we see in Table 1, the ordering of experimental data by size does not significantly change the results of our analysis.

We can generalize our approach to the case when resistance mutations are not neutral, but provide a fitness effect already before treatment (formulas shown in SI Text). In Table 2, we compare the predicted medians for the first five resistant clones in a metastatic lesion containing $M={10}^9$ cells when resistance is deleterious, neutral, or advantageous. We see from Table 2 that even if resistant cells are only $10\text{\%}$ as fit as sensitive cells, they will still be present in typical lesions. The average number of resistant cells produced until the lesion reaches size M is $Mu/s$. Here $s=1-d/b$ is the survival probability of sensitive cells, which is the probability that the lineage of a single sensitive cell will not die out. For typical parameter values (i.e., those used in Table 2), the number of resistant cells produced by sensitive cells in a single lesion is $\sim 150$. Resistant cells that are $10\text{\%}$ as fit as sensitive cells have a survival probability of $\sim 4\text{\%}$; so on average, six of them will form surviving clones. The effect that mutations can cause treatment failure, although they have high fitness cost is a consequence of the high number of resistant mutants produced by billion(s) of sensitive cells in a lesion and the specific properties of the branching process, namely the independence of lineages.

Table 2.

Sizes of resistant clones when resistance is deleterious, neutral, or advantageous

$c=\left(b_R-d_R\right)/\left(b-d\right)$	First clone*	Second clone	Third clone	Fourth clone	Fifth clone
0.01	0	0	0	0	0
0.1	10	6	4	2	1
0.5	27	17	13	11	10
0.7	50	26	19	15	13
0.9	103	46	30	23	18
0.95	125	54	35	26	20
1	152	63	40	29	23
1.05	186	74	45	33	25
1.1	229	87	52	37	28

^*Median number of cells in the first five successful resistant clones in a metastatic lesion with $M={10}^9$ cells when resistant cells are less fit than sensitive cells ($c<1$), neutral ($c=1$), and more fit than sensitive cells ($c>1$). We fix the birth and death rate of sensitive cells, $b=0.25$ and $d=0.181$, and the death rate of resistant cells $d_R=d$. We vary the relative fitness of resistant cells, c, and let the birth rate of resistant cells be $b_R=d_R+c\left(b-d\right)$. Mutation rate $u=42\times {10}^{-9}$. For $c=0.1$ we report simulation results, and for $c>0.1$, we use Eq. S13; see SI Text for details.

Discussion

In this paper we describe the heterogeneity of mutations providing resistance to cancer therapy that can be found in any one metastatic lesion. Our results can be generalized to take into account all of the patient’s lesions, assuming that they evolve according to the same branching process and that the number of lesions is much smaller than $1/u$. In that case, the probability distribution for the size of the kth appearing resistant clone in the patient’s cancer is given by Formula 1 if we let M be the number of cancer cells in all of the patient’s lesions. All our results generalize similarly.

Although the mean and median clone sizes in our model depend on the parameters of the process, their ratios are generally parameter free. The universality of the clone ratio statistics follows from the fact that the skeleton of our branching process, which includes only cells with infinite line of descent, can be approximated by a Yule (pure birth) process (30). It has been shown that in the limit of large lesion size M and small mutation rate u, the statistics of the relevant clones in a branching process with death remain approximately Yule (31). Similarly, it can be shown that in the Yule process, in the above limits, the mean size of the kth largest clone is $\sim Mu/\left(k-1\right)$, and the ratio of the mean sizes of the kth and jth largest clones is $\sim \left(j-1\right)/\left(k-1\right)$ (31, 32). This formula is exactly the result we obtain for the ratio of mean clone sizes even though we order clones by age.

A few recent investigations studied the dynamics of single clones resistant to therapy (28, 33). In one of the studies (33), the authors used a generalization of the Luria–Delbrück model in which sensitive cells grow deterministically and calculated the number of individual resistant clones and the probability distribution for the number of cells in a single resistant clone after time t. In another study (28), mathematical modeling along with in vitro growth rates of cells harboring 12 point mutations providing resistance to BCR-ABL (fusion of breakpoint cluster region gene and Abelson murine leukemia viral oncogene homolog 1) inhibitor imatinib were used to calculate the number of resistant clones and the expected number of resistant cells with a particular resistance mutation at the time of diagnosis of chronic myeloid leukemia. The authors found that at most one resistant clone is expected to be present, as the total number of CML stem cells at diagnosis is estimated to be approximately $M\sim \mathrm{100,000}$ cells and is much smaller than the billions of cells typically present in a single detectable lesion of a solid tumor. In this paper, we use a different mathematical technique and the novel approach of ordering the resistant clones according to their time of appearance, which allows us for the first time, to our knowledge, to describe the full spectrum of resistance mutations present in a lesion.

Our study is challenging the conventional view of the evolution of resistance in cancer. For every therapy that is opposed by multiple potential resistance mutations, which is the case for every targeted drug developed thus far, we can expect multiple resistant clones of comparable size in every lesion. Our theory provides a precise quantification of the relative sizes of those resistant subclones. The heterogeneity of resistance mutations is further amplified when taking into account multiple metastatic lesions in a patient. This information is pertinent to the development of second line treatments that aim to inhibit known resistance mutations.

Materials and Methods

Model.

We model the growth and evolution of a metastatic lesion as a continuous time multitype branching process (34). The growth of a lesion is initiated by a single cell sensitive to the drug. Sensitive cells produce a resistant cell at each division with probability u and each resistant cell produced by sensitive cells starts a new resistant type.

Analysis.

In our analysis, we use the approximation that resistant cells produced by sensitive cells appear as a Poisson process on the number of sensitive cells (17). For more details and derivations of our results, please see SI Text.

Simulations.

We perform Monte Carlo simulations of the multitype branching process using the Gillespie algorithm (35). Between 5,000 and 10,000 surviving runs are used for each parameter combination.