Functional Mixed Effects Models for Candidate Genetic Mapping in Imaging Genetic Studies

Abstract

The aim of this paper is to develop a functional mixed effects modeling (FMEM) framework for the joint analysis of high-dimensional imaging data in a large number of locations (called voxels) of a three-dimensional volume with a set of genetic markers and clinical covariates. Our FMEM is extremely useful for effciently carrying out the candidate gene approaches in imaging genetic studies. FMEM consists of two novel components including a mixed effects model for modeling nonlinear genetic effects on imaging phenotypes by introducing the genetic random effects at each voxel and a jumping surface model for modeling the variance components of the genetic random effects and fixed effects as piecewise smooth functions of the voxels. Moreover, FMEM naturally accommodates the correlation structure of genetic markers at each voxel, while the jumping surface model explicitly incorporates the intrinsically spatial smoothness of the imaging data. We propose a novel two-stage adaptive smoothing procedure to spatially estimate the piecewise smooth functions, particularly the irregular functional genetic variance components, while preserving their edges among different piecewise-smooth regions. We develop weighted likelihood ratio tests and derive their exact approximations to test the effect of the genetic markers across voxels. Simulation studies show that FMEM significantly outperforms voxel-wise approaches in terms of higher sensitivity and specificity to identify regions of interest for carrying out candidate genetic mapping in imaging genetic studies. Finally, FMEM is used to identify brain regions affected by three candidate genes including CR1, CD2AP, and PICALM, thereby hoping to shed light on the pathological interactions between these candidate genes and brain structure and function.

1 Introduction

Common mental and neurological disorders, such as autism and schizophrenia, are highly heritable and strongly associated with brain structure and function, but it has been diffcult to unravel the genetic factors of these complex illnesses in that many genetic factors may contribute to the susceptibility of the disease while the contribution of each factor is small. Since imaging data provide the most effective measures of brain function and structure, such data may serve as an important intermediate phenotype that ultimately can lead to discoveries of genes for these complex disorders. Imaging genetic studies, which collect both imaging and genetic data, have recently attracted extensive research interest for dissecting the genetic basis of neurological disorders [Gilmore and et al, 2010, Loth et al., 2011, Savitz and Drevets, 2009]. The common and important themes of both the imaging and genetic data include ultra-high dimensionality and complex correlation structures determined by the physical location. However, most of the existing methods for genetic association studies focus on low dimensional phenotypes (e.g. case-control status) and thus cannot account for high-dimensional imaging phenotypes, while accounting for spatial smoothness of the imaging measurements. On the other hand, most existing association methods in the neuroimaging literature do not study the joint effects of multiple genetic markers, while accommodating their correlations due to linkage disequilibrium (LD).

There are two main genetic association approaches including i) the candidate gene approaches and ii) the genome-wide association studies (GWAS) for correlating imaging phenotype with genotype at one or more polymorphic markers in order to uncover genetic predispositions to disease [Zhu and Zhao, 2007, Amos et al., 2011]. Both approaches enjoy a combination of advantages and disadvantages. Candidate genes are commonly selected for study based on either a priori knowledge of their biological functional impact on the phenotype or disease in question or previous GWAS studies, such as the NHGRI GWAS catalog [Hindor et al., 2009]. The candidate gene approach tends to have rather high statistical power, but is incapable of discovering new genes or gene combinations. A standard statistical method for the candidate approach in imaging genetics is the voxel-wise analysis (VWA) framework. The voxel-wise analysis consists of Gaussian smoothing the imaging data and subsequently fitting a statistical model at each voxel. However, the voxel-wise analysis is generally not optimal in power and the use of Gaussian smoothing may introduce a substantial bias in the statistical results [Jones et al., 2005, T. Ball et al., 2012, Li et al., 2011, 2013].

Most imaging genetic studies have used the candidate gene approach, although more recently, more studies are beginning to scan the entire genome for common genetic variation [Thompson et al., 2013, Zhang et al., 2014]. A standard statistical method for GWAS in imaging genetics is the massive univariate linear modelling (MULM) framework [Hibar and et al, 2011, Shen et al., 2010]. This approach repeatedly fits a linear regression model for each pair of imaging voxels and genetic markers. MULM entails a large number of comparisons, and thus MULM can only detect extremely significant imaging-marker pairs. Moreover, MULM ignores both the spatial information of the imaging data and the correlation among genetic markers. See more detailed discussions in [Vounou et al., 2010, Ge et al., 2012, Thompson et al., 2013]. Recently, in Ge et al. [2012], a cluster-wide, marker set association framework was proposed by integrating cluster size inferences based on random field theory in order to utilize the spatial smoothness of the imaging data [Worsley et al., 2004] and a marker set analysis based on least-squares kernel machines in order to assess the joint association of potentially correlated and interacting loci [Liu et al., 2007].

The aim of this paper is to develop a functional mixed effects modeling (FMEM) framework for the joint analysis of high-dimensional imaging data with a set of genetic markers and clinical covariates. Our FMEM is extremely useful for effciently carrying out the candidate gene approaches in imaging genetic studies. FMEM consists of two novel components including a mixed effects model and a jumping surface model. Specifically, at each voxel, we use the mixed effects model with genetic random effects to assess the nonlinear association of potentially correlated and interacting loci with imaging phenotypes and the variance component (VC) of genetic random effects to detect the nonlinear effects of a marker set on imaging measures across voxels [Liu et al., 2007, Tzeng and Zhang, 2007, Wang and Chen, 2012]. To account for the spatial smoothness of the imaging data, we use the jumping surface model to explicitly model both the genetic variance component and fixed effects as piecewisel smooth functions of the voxels with unknown edges and possible jumps. We develop a novel two-stage adaptive smoothing procedure to spatially estimate the genetic variance component function, while preserving its edges among different piecewise-smooth regions. We also develop weighted likelihood ratio tests and derive their exact approximations to test the effect of the genetic markers across the brain. Our numerical examples show that FMEM significantly outperforms voxel-wide approaches in terms of detection of meaningful effect regions.

The rest of the paper is organized as follows. In Section 2, we describe the proposed FMEM and its adaptive estimation procedure. Then, we develop our hypothesis testing procedure to assess the genetic effects as well as the effect of clinical variables on the imaging phenotypes. In Section 3, we evaluate the finite-sample performance of FMEM by using simulation studies and analyzing a real data set from the Alzheimer’s Disease Neuroimage Initiative (ADNI). A few concluding remarks are given in the Discussion section.

2 Methods

2.1 Functional Mixed Effects Model

Suppose that we observe imaging measures, clinical variables, and genetic markers from n unrelated subjects. Let $\mathcal{V}$ be the whole brain and v be a voxel in $\mathcal{V}$. For each individual i (i = 1, …, n), an N_V × 1 vector of imaging measures is observed and denoted by $Y_i=\left\{y_i\right(v):v\in \mathcal{V}\}$. For notational simplicity, we only consider univariate imaging measures and thus, N_V equals the number of voxels in $\mathcal{V}$. Moreover, a K × 1 vector of clinical covariates x_i = (x_i1, …x_iK)^T and a G × 1 vector g_i = (g_i1, …g_ig)^T for genetic markers are also collected for each individual. For instance, imaging measures can be brain structural and functional data at each location [Friston, 2009, Ashburner and Friston, 2000], and genetic markers can be various polymorphism types, such as single nucleotide polymorphisms (SNPs), block substitutions, and copy number variants [Liu et al., 2007, Tzeng and Zhang, 2007, Wang and Chen, 2012]. The objective of this paper is to develop FMEM to quantify genetic contributions to high-dimensional imaging measures.

Our FMEM framework consists of two novel components including a mixed effects model (MEM) at each voxel and a jumping surface model (JSM) for varying coefficient functions across the brain. First, at each voxel v in $\mathcal{V}$, a mixed effects model is introduced as

$$y_i\left(v\right)={\mathbf{x}}_i^T\beta \left(v\right)+{\mathbf{z}}_i^T\gamma \left(v\right)+e_i\left(v\right),$$ (1)

where β(v) = (β₁(v), …, β_K(v))^T is a K × 1 vector, $\gamma \left(v\right)~N(0,{\sigma }_{\gamma }^2(v\left){\mathit{I}}_L\right)$, $e_i\left(v\right)~N(0,{\sigma }_e^2(v\left)\right)$, and $\left\{e_i\right(v):v\in \mathcal{V}\}$ are independent across subjects i and independent of γ(v) for all $v\in \mathcal{V}$, in which I_L is an identity matrix. Let Z = (z₁, …,z_n) be an L × n matrix and Y(v) = (y₁(v), …, y_n(v))^T be an n × 1 vector. Thus, under model (1), we have

$$\mathrm{Var}\left(\mathbf{Y}\right(v\left)\right)={\Sigma }_Y\left(v\right)={\sigma }_{\gamma }^2\left(v\right){\mathbf{Z}}^T\mathbf{Z}+{\sigma }_e^2\left(v\right){\mathbf{I}}_n.$$

Model (1) can be regarded as an alternative representation of the variance component models used in the literature [Liu et al., 2007, Tzeng and Zhang, 2007, Kang et al., 2010, Wang and Chen, 2012]. For instance, when Z^TZ equals a kernel matrix K = (K(g_i, g_i′)), model (1) reduces to the linear mixed model considered in [Liu et al., 2007, Ge et al., 2012], where K(·,·) is a kernel function, such as the polynomial kernel, identity-by-state (IBS) kernel, or the Gaussian kernel. For instance, the IBS kernel is used in [Ge et al., 2012].

Model (1) has a strong connection with a nonparametric fixed effects model given by

$$y_i\left(v\right)={\mathbf{x}}_i^T\beta \left(v\right)+h(g_i;v)+e_i\left(v\right)\text{for}i=1,\cdots ,n,$$ (2)

where h(·; v) is an unknown centered function corresponding to the genetic effects at voxel v. To estimate the unknown functions h(·; v) in model (2), a common approach is to express them as linear combinations of some pre-specified basis functions (e.g., splines or kernels), that is $h({\mathbf{g}}_i;v)={\mathbf{z}}_i^T\gamma \left(v\right)$, where γ(v) = (γ₁(v), …, γ_L(v))^T is an L × 1 vector for genetic random effects and z_i is a pre-specified L × 1 vector of functions of g_i. The variation of h(g_i; v) is then controlled by the variation of their basis coefficients in γ(v). Moreover, a penalty function (e.g., L₂ or L₁) coupled with a tuning parameter is usually introduced to impose certain constraints on γ(v) and such penalty function can be regarded as a prior distribution of random effects. Thus, this connection provides a simple way to connect the nonparametric fixed effects model (2) with model (1) [Liu et al., 2007, Tzeng and Zhang, 2007, Kang et al., 2010, Wang and Chen, 2012]. We focus on model (1) from now on.

We also assume spatial correlation as follows. For v and v′ in $\mathcal{V}$, we assume

$$\mathrm{Cov}\left(\gamma \right(v),\gamma (v^{\prime }\left)\right)={\sigma }_{\gamma }\left(v\right){\sigma }_{\gamma }\left(v^{\prime }\right)1(v=v^{\prime }){\mathit{I}}_L\text{and}\mathrm{Cov}\left(e_i\right(v),e_i(v^{\prime }\left)\right)={\sigma }_e\left(v\right){\sigma }_e\left(v^{\prime }\right){\rho }_e(v,v^{\prime }),$$

where 1(·) is an indicator function and ρ_e(v, v′) characterizes the spatial correlation between the measurement errors. Therefore, the covariance structure of y_i(v) is given by

$${\Sigma }_{y,i}(v,v^{\prime })=\mathrm{Cov}\left(y_i\right(v),y_i(v^{\prime }\left)\right)={\sigma }_{\gamma }\left(v\right){\sigma }_{\gamma }\left(v^{\prime }\right)1(v=v^{\prime }){\mathbf{z}}_i^T{\mathbf{z}}_i+{\sigma }_e\left(v\right){\sigma }_e\left(v^{\prime }\right){\rho }_e(v,v^{\prime }).$$ (3)

Following Zhu et al. [2014], we propose a JSM for the genetic varying coefficient function ${\sigma }_{\gamma }^2(\cdot )=\left\{{\sigma }_{\gamma }^2\right(v):v\in \mathcal{V}\}$ and the fixed effect varying coeffcient functions ${\beta }_j(\cdot )=\left\{{\beta }_j\right(v):v\in \mathcal{V}\}$ for j = 1, …, K. For notational simplicity, we only introduce JSM for ${\sigma }_{\gamma }^2(\cdot )$ as follows:

• (i) (Disjoint Partition) There is a finite and disjoint partition $\{{\mathcal{V}}_l:l=1,\cdots ,L_{\gamma }\}$ of V such that $\mathcal{V}={\cup }_{l=1}^{L_{\gamma }}{\mathcal{V}}_l$.

• (ii) (Piecewise Smoothness) ${\sigma }_{\gamma }^2\left(v\right)$ is smooth within each ${\mathcal{V}}_l$ for l = 1, …, L_γ, but ${\sigma }_{\gamma }^2\left(v\right)$ is discontinuous on ${\cup }_{l=1}^{L_{\gamma }}\partial {\mathcal{V}}_l$, where $\partial {\mathcal{V}}_l$ is the boundary of ${\mathcal{V}}_l$ and the jumping surface of ${\sigma }_{\gamma }^2\left(v\right)$.

A similar JSM can be defined for each β_j(·) for j = 1, …, K.

We use JSM to explicitly delineate the fact that imaging data $\left\{y_i\right(v):v\in \mathcal{V}\}$ can be regarded as a noisy version of a piecewise-smooth function of $v\in \mathcal{V}$ with the possible existence of jumps or edges. In many neuroimaging datasets, those jumps or edges often reflect the functional and/or structural changes, such as white matter (WM) and grey matter (GM), across the brain. Therefore, the varying coefficient functions in model (1) may inherit the piecewise-smooth features from the imaging data. Furthermore, it is more reasonable to assume that different varying coefficient functions have different jumps or edges, since they may play different roles in characterizing the piecewise-smooth pattern of the imaging data.

Our FMEM consisting of model (1) and JSM can be regarded as a novel extension of the existing FMEMs and varying coefficient models in the literature [Zhu et al., 2011, Yuan et al., 2014, Morris and Carroll, 2006, Guo, 2002, Greven et al., 2010, Zhu et al., 2014, 2012], even though all of them are developed to model functional responses (of time or voxel) measured either cross-sectionally or longitudinally. However, at each voxel, the jumping surface model is introduced to spatially characterize the piecewise smoothness of the imaging data. In contrast, most existing FMEMs and varying coefficient models reduce to a parametric model at each voxel, while most FMEMs do not explicitly model the piecewise smoothness of the imaging data. Moreover, the primary interest of our FMEM is to estimate the genetic varying coefficient function ${\sigma }_{\gamma }^2(\cdot )$, whereas that of other FMEMs and varying coefficient models is to estimate the fixed effects varying coefficient functions β_j(·). Estimating the function ${\sigma }_{\gamma }^2(\cdot )$ is computationally and theoretically much harder than estimating the varying coefficient functions, since ${\sigma }_{\gamma }^2(\cdot )$ satisfies a nonnegative constraint.

2.2 Two-stage Estimation Procedure

We propose a two-stage estimation procedure to estimate all varying coefficient functions and test their effects on imaging phenotypes. The key ideas of each stage are given as follows:

• Stage I. Estimate ${\sigma }_e^2(\cdot )$, develop an adaptive smoothing method to estimate ${\sigma }_{\gamma }^2(\cdot )$, and test the null hypothesis ${\sigma }_{\gamma }^2\left(v\right)=0$ across all voxels.

• Stage II. Develop an adaptive smoothing method to spatially and adaptively estimate $\beta (\cdot )=\left\{\beta \right(v):v\in \mathcal{V}\}$ and then test associated hypotheses.

Moreover, after calculating ${\widehat{\sigma }}_e^2(\cdot )$, ${\widehat{\sigma }}_{\gamma }^2(\cdot )$ and $\widehat{\beta }(\cdot )$, we can estimate $\widehat{\gamma }\left(v\right)=\mathbf{Z}{\widehat{\Sigma }}_Y{\left(v\right)}^{-1}\left\{\mathbf{Y}\right(v)-{\mathbf{X}}^T\widehat{\beta }(v\left)\right\}$, where ${\widehat{\Sigma }}_Y\left(v\right)={\widehat{\sigma }}_{\gamma }^2\left(v\right){\mathbf{Z}}^T\mathbf{Z}+{\widehat{\sigma }}_e^2\left(v\right){\mathbf{I}}_n$ and X = (x₁, …,x_n) is a p × n matrix. To approximate ρ_e(v, v′), we calculate the empirical correlation between $\left\{{\widehat{e}}_i\right(v):i=,\cdots ,n\}$ and $\left\{{\widehat{e}}_i\right(v^{\prime }):i=,\cdots ,n\}$ where ${\widehat{e}}_i\left(v\right)=y_i\left(v\right)-{\mathbf{x}}_i^T\widehat{\beta }\left(v\right)+{\mathbf{z}}_i^T\widehat{\gamma }\left(v\right)$. Since γ(v) and ρ_e(v, v′) are nuisance parameters, we do not focus on them throughout. Since our primary interest lies in the genetic effect, we focus on Stage I and only briefly discuss Stage II for the sake of space.

The key novelty of our estimation procedure is the adaptive smoothing method in Stage I for smoothing ${\sigma }_{\gamma }^2(\cdot )$. Since the true variance components σ_γ(v) can be zero in some regions of interest and their estimates are always non-negative, directly applying standard smoothing methods, such as splines or kernel smoothing, to these nonnegative variance component estimates can introduce substantial bias in the estimation of functional genetic variance components. Thus, most existing smoothing methods cannot be successfully used in such smoothing problems [Zhu et al., 2011, Yuan et al., 2014, Morris and Carroll, 2006, Guo, 2002, Greven et al., 2010, Zhu et al., 2014, 2012, Polzehl and Spokoiny, 2000, Polzehl et al., 2010, Yue et al., 2010].

2.2.1 Stage I

The first stage consists of three major steps as follows:

• Step I.1. Calculate the restricted maximum likelihood (REML) estimator of $\eta \left(v\right)=\left({\sigma }_{\gamma }^2\right(v),{\sigma }_e^2(v\left)\right)$ across all voxels $v\in \mathcal{V}$.

• Step I.2. Spatially and adaptively re-estimate $\left\{{\sigma }_{\gamma }^2\right(v):v\in V\}$ by incorporating information from neighboring voxels.

• Step I.3. Construct weighted likelihood ratio statistics and derive their approximate distributions to test the null hypothesis of $H_0\left(v\right):{\sigma }_{\gamma }^2\left(v\right)=0$ across all voxels.

In Step I.1, we calculate the REML estimator of η(v) across voxels. There exists an (n – p) × n matrix K_x such that K_xX^T = 0 and rank(K_x) = n – p. A mixed effects model for Y* (v) = K_xY(v) is given by

$${\mathbf{Y}}^{\ast }\left(v\right)=K_x{\mathbf{Z}}^T\gamma \left(v\right)+K_{x}E\left(v\right),$$ (4)

where E(v) = (e₁(v), …, e_n (v))^T. Based on the distributional assumptions in (1), we have Y* (v) ~ N(0, Σ_Y* (v)), where ${\Sigma }_{Y^{\ast }}\left(v\right)={\sigma }_{\gamma }^2\left(v\right)K_x{\mathbf{Z}}^T\mathbf{Z}{K}_x^T+{\sigma }_e^2\left(v\right)K_x{K}_x^T$. Thus, at each voxel v, the REML estimate of η(v), denoted by $\widehat{\eta }\left(v\right)={\left({\widehat{\sigma }}_{\gamma }^2\right(v),{\widehat{\sigma }}_e^2(v\left)\right)}^T$, is to maximize the REML function given by

$${\ell }_{REML}\left({\mathbf{Y}}^{\ast }\right(v)\mid \mathbf{Z},\eta (v\left)\right)=-0.5\log \mid {\Sigma }_{Y^{\ast }}\left(v\right)\mid -0.5{\mathbf{Y}}^{\ast }{\left(v\right)}^T{\Sigma }_{Y^{\ast }}{\left(v\right)}^{-1}{\mathbf{Y}}^{\ast }\left(v\right).$$ (5)

Since our primary interest lies on ${\sigma }_{\gamma }^2\left(v\right)$, we fix ${\sigma }_e^2\left(v\right)$ as ${\widehat{\sigma }}_e^2\left(v\right)$ from here on.

In Step I.2, we construct a weighted REML function to estimate ${\sigma }_{\gamma }^2\left(v\right)$ by incorporating the spatial information in a neighborhood B(v, h) for each voxel v with a specific radius h as follows:

$$L_{REML}\left({\sigma }_{\gamma }^2\right(v)\mid {\mathbf{Y}}^{\ast },B(v,h\left)\right)=\sum _{v^{\prime }\in B(v,h)}{\omega }_{\gamma }(v,v^{\prime };h){\ell }_{REML}\left({\mathbf{Y}}^{\ast }\right(v^{\prime })\mid \mathbf{Z},{\sigma }_{\gamma }^2(v),{\widehat{\sigma }}_e^2(v^{\prime }\left)\right),$$ (6)

where ω_γ (v, v′; h) is a weight function of voxels v, v′, and the radius h. We maximize $L_{REML}\left({\sigma }_{\gamma }^2\right(v)\mid {\mathbf{Y}}^{\ast },B(v,h\left)\right)$ in order to calculate the weighted REML estimator of ${\sigma }_{\gamma }^2\left(v\right)$, denoted by ${\widehat{\sigma }}_{\gamma }^2(v,h)$. The weight function ω_γ (v, v′; h) measures the data similarity between the two voxels v and v′ such that Σ_{v′∈B(v,h)}ω_γ(v,v′; h) = 1 and ω_γ (v, v′; h) ≥ 0. A large value of ω_γ (v, v′; h) means that the information contained in the voxels v and v′ is very similar, whereas ω_γ (v, v′; h) ≈ 0 indicates that the data in voxel v′ do not have too much information for σ_v (v). The adaptive weight ω_γ (v, v^′; h) plays a critical role in preventing over-smoothing estimation of ${\sigma }_{\gamma }^2\left(v\right)$ and preserving the edges of significant regions of $\left\{{\sigma }_{\gamma }^2\right(v):v\in \mathcal{V}\}$.

In Step I.3, to assess the genetic effects on imaging phenotypes across all voxels, we formulate it as testing the following null and alternative hypotheses:

$$H_{0,\gamma }\left(v\right):{\sigma }_{\gamma }^2\left(v\right)=0v.s.H_{1,\gamma }\left(v\right):{\sigma }_{\gamma }^2\left(v\right)>0.$$ (7)

We test (7) by using the weighted REML ratio statistic defined by

$${\mathrm{RLRT}}_{{\sigma }_{\gamma }^2}\left(v\right)=2\left\{L_{REML}\right({\widehat{\sigma }}_{\gamma }^2\left(v\right)\mid {\mathit{Y}}^{\ast },B(v,h))-L_{REML}(0\mid {\mathit{Y}}^{\ast },B(v,h)\left)\right\}.$$ (8)

Since all the subjects share the same random effect γ(v), the standard asymptotic results in Stram and Lee [1994] are invalid and can perform very poorly even for the unweighted REML ratio statistics for testing random effects in model (1). However, we provide an exact null distribution of ${\mathrm{RLRT}}_{{\sigma }_{\gamma }^2}\left(v\right)$ below.

2.2.2 Step I.2 Adaptive Estimation of ${\sigma }_{\gamma }^2\left(v\right)$

Following the adaptive estimation (AET) procedure proposed in [Li et al., 2011], we adaptively determine $\left\{{\omega }_{\gamma }\right(v,v^{\prime };h):v,v^{\prime }\in \mathcal{V}\}$ and then calculate ${\widehat{\sigma }}_{\gamma }(v;h)$ as h increases from h₀ = 0 to a predetermined value h_S = r₀. The key novelty of AET is to build a sequence of $L_{REML}\left({\sigma }_{\gamma }^2\right(v)\mid {\mathbf{Y}}^{\ast },B(v,h\left)\right)$ for h₀ = 0 < h₁ < … < h_S = r₀ at each voxel $v\in \mathcal{V}$ and then sequentially determine ω_γ (v, v′; h_s) for all v′ ∈ B(v, h_s) based on $\left\{{\widehat{\sigma }}_{\gamma }^2\right(v^{\prime },h_{s-1}):v^{\prime }\in B(v,h_s\left)\right\}$ for all $v\in \mathcal{V}$ and s = 1, …, S. However, one cannot apply many existing smoothing methods, such as local kernel or the propagation-seperation method [Zhu et al., 2014, Polzehl and Spokoiny, 2000, Polzehl et al., 2010, Fan and Gijbels, 1996], to directly smooth $\left\{{\widehat{\sigma }}_{\gamma }^2\right(v):v\in \mathcal{V}\}$ in the non-activation region ${\mathcal{V}}_{NA}=\{v:{\sigma }_{\gamma }(v)=0,v\in \mathcal{V}\}$. Specifically, since ${\widehat{\sigma }}_{\gamma }^2\left(v\right)$ is always non-negative even in the voxels of ${\mathcal{V}}_{NA}$, directly calculating the weighted means of ${\widehat{\sigma }}_{\gamma }^2\left(v\right)$ does not lead to the bias reduction in ${\mathcal{V}}_{NA}$. A path diagram of AET is given as follows:

$$\begin{array}{ccccc}\hfill h_0=0\hfill & \hfill <\hfill & \hfill h_1\hfill & \hfill <\cdots <\hfill & \hfill h_S=r_0\hfill \\ \hfill B(v,h_0)=\left\{v\right\}\hfill & \hfill \subset \hfill & \hfill B(v,h_1)\hfill & \hfill \subset \cdots \subset \hfill & \hfill B(v,h_S)\hfill \\ \hfill \Downarrow \hfill & \hfill \hfill & \hfill \Downarrow \hfill & \hfill \nearrow \cdots \nearrow \hfill & \hfill \Downarrow \hfill \\ \hfill \left\{{\widehat{\sigma }}_{\gamma }^2\right(v):v\in \mathcal{V}\}\hfill & \hfill \Rightarrow \hfill & \hfill {\omega }_{\gamma }(v,v^{\prime };h_1)\hfill & \hfill \cdots \hfill & \hfill {\omega }_{\gamma }(v,v^{\prime };h_S=r_0)\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \Downarrow \hfill & \hfill \nearrow \cdots \nearrow \hfill & \hfill \Downarrow \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \left\{{\widehat{\sigma }}_{\gamma }^2\right(v;h_1):v\in \mathcal{V}\}\hfill & \hfill \cdots \hfill & \hfill \left\{{\widehat{\sigma }}_{\gamma }^2\right(v;h_S):v\in \mathcal{V}\}.\hfill \end{array}$$

The three key steps of AET, including weight adaptation, estimation, and termination checking, are presented as follows.

• In the weight adaption step (i), we select a series $\{h_s=c_h^s:s=1,\cdots ,S\}$ of radii with c_h ∈ (1, 2), say c_h = 1.125. We use a relatively small c_h in order to increase estimation robustness and prevent oversmoothing. We then set s = 1 and h₁ = c_h. The adaptive weights in (6) are given by

  $${\omega }_{\gamma }(v,v^{\prime };h_s)=K_{loc}({\mid \mid v-v^{\prime }\mid \mid }_2∕h_s)K_{st}\left(D_{\gamma }\right(v,v^{\prime };h_{s-1})∕C_n),$$ (9)

  where K_loc(u) = (1 – u)₊ and K_st(u) = min(1, 2(1 – u²))₊, and ∥·∥₂ denotes the Euclidean norm of a vector (or a matrix). Moreover, D_γ (v, v^′; h_s−1) is set as ${\left\{{\widehat{\sigma }}_{\gamma }^2\right(v;h_{s-1})-{\widehat{\sigma }}_{\gamma }^2(v^{\prime };h_{s-1}\left)\right\}}^2∕\mathrm{var}\left[\widehat{{\sigma }_{\gamma }^2}\right(v\left)\right]$ so that the difference between consecutive ${\widehat{\sigma }}_{\gamma }^2(v;h_{s-1})s$ is within the precision of $\sqrt{\mathrm{var}\left[\widehat{{\sigma }_{\gamma }^2}\right(v\left)\right]}$, where $\mathrm{var}\left[\widehat{{\sigma }_{\gamma }^2}\right(v\left)\right]$ is estimated by using the inverse of the Fisher information matrix of $\left({\sigma }_{\gamma }^2\right(v),{\sigma }_e^2(v\left)\right)$ from the likelihood function (5) with h = h₀. We choose C = n^1/3 χ²(1)^0.5 for D_γ (v, v′; h_s−1) defined in (9), where χ²(1)^0.5 is the 0.5-percentile of the χ²(1) distribution. These quantities are fixed for subsequent updates of h_s.

The rationale for choosing different tuning parameters given above is given as follows. The weight K_st(D_γ (v, v′; h_s−1)/C_n) downweights the role of a voxel v′ ∈ B(v, h_s) in the REML functions if D_γ (v, v′; h_s−1) is large. The weight K_loc(∥v – v′∥₂/h_s) gives less weight to the voxel v′ ∈ B(v, h_s), whose location is far from the voxel v. The scale C_n is used to penalize the similarity between any two voxels v and v′ in a similar manner to bandwidth, and an appropriate choice of C_n is crucial for the behavior of the adaptive smoothing method in Stage I. As discussed in Zhu et al. [2014] and Li et al. [2011], C_n should satisfy C_n/n = o(1) and $C_n^{-1}\log \left(N_V\right)=o\left(1\right)$.

• In the estimation step (ii), for each $v\in \mathcal{V}$ and for the radius h_s given ω_γ (v, v′; h_s), we calculate ${\widehat{\sigma }}_{\gamma }(v;h_s)$ by maximizing $L_{REML}\left({\sigma }_{\gamma }^2\right(v)\mid {\mathbf{Y}}^{\ast },B(v,h\left)\right)$ defined in equation (6).

• In the termination checking step (iii), after the S₀–th iteration, we calculate a stopping criterion based on a distance between ${\widehat{\sigma }}_{\gamma }^2(v;h_{S_0})$ and ${\widehat{\sigma }}_{\gamma }^2(v;h_s)$ given by

  $$D\left({\widehat{\sigma }}_{\gamma }^2\right(v;h_{S_0}),{\widehat{\sigma }}_{\gamma }^2(v;h_s\left)\right)={\left\{{\widehat{\sigma }}_{\gamma }^2\right(v;h_{S_0})-{\widehat{\sigma }}_{\gamma }^2(v;h_s\left)\right\}}^{2}var{\left[\widehat{{\sigma }_{\gamma }^2}\right(v\left)\right]}^{-1}$$ (10)

  for s > S₀. Then, we compare $D\left({\widehat{\sigma }}_{\gamma }^2\right(v;h_{S_0}),{\widehat{\sigma }}_{\gamma }^2(v;h_s\left)\right)$ with a benchmark, denoted by $\tilde{C}\left(s\right)$, for s > S₀. If $D\left({\widehat{\sigma }}_{\gamma }^2\right(v;h_{S_0}),{\widehat{\sigma }}_{\gamma }^2(v;h_s\left)\right)>\tilde{C}\left(s\right)$, then we set ${\widehat{\sigma }}_{\gamma }^2\left(v\right)={\widehat{\sigma }}_{\gamma }^2(v,h_{s-1})$ and the estimation for this voxel v is terminated. If s = S and $D\left({\widehat{\sigma }}_{\gamma }^2\right(v;h_{S_0}),{\widehat{\sigma }}_{\gamma }^2(v;h_s\left)\right)\le \tilde{C}\left(s\right)$, ${\widehat{\sigma }}_{\gamma }^2\left(v\right)$ is set as ${\widehat{\sigma }}_{\gamma }^2(v,h_S)$ and the estimation process terminates. The algorithm stops when the estimation is finished for all v in V. If s ≤ S₀ or $D\left({\widehat{\sigma }}_{\gamma }^2\right(v;h_{S_0}),{\widehat{\sigma }}_{\gamma }^2(v;h_s\left)\right)\le \tilde{C}\left(s\right)$ for s < S₀ S – 1, then we go back to the weight adaptation step (i) with an increased radius $h=h_{s+1}=c_h^{s+1}$. Throughout the paper, we set S₀ = 2, $\tilde{C}\left(s\right)={\chi }^2{\left(p\right)}^{0.7∕(s-1)}$, and S = 10. Note that $\tilde{C}\left(s\right)$ is a decreasing function in s which makes the stopping criteria more and more stringent when the radius increases in order to prevent over-smoothing.

2.2.3 Step I.3: Testing $H_{0,\gamma }\left(v\right):{\sigma }_{\gamma }^2\left(v\right)=0$

We perform hypothesis testing in (7) by using the testing statistics ${\mathrm{RLRT}}_{{\sigma }_{\gamma }^2}\left(v\right)$ and their corresponding p-values. Let $\Omega =K_x{Z}^{T}Z{K}_x^T=U{D}_0{U}^T$ be the spectral decomposition of such that D₀ = diag(d₁, …, d_n-p) is the diagonal matrix of eigenvalues d_k and U is an (n – p) × (n – p) orthonormal matrix. Without loss of generality, we choose K_x such that $K_x{K}_x^T={\mathbf{I}}_{n-p}$. We obtain the following theorem, whose proof is included in the supplementary document.

Theorem 1. Under model (1), RLRT_n(v) can be written as

$$RLR{T}_n\left(v\right)=\underset{\lambda \left(v\right)\ge 0}{\sup }\left\{\sum _{v^{\prime }\in B(v,h)}\omega \right(v,v^{\prime };h\left)D\right(v^{\prime };\lambda \left(v\right)∕{\sigma }_e^2\left(v^{\prime }\right)\left)\right\},$$ (11)

where $\lambda \left(v\right)={\sigma }_{\gamma }^2\left(v\right)$ and D(v′; t) is given by

$${\sigma }_e^{-2}\left(v^{\prime }\right){\mathbf{Y}}^{\ast T}\left(v^{\prime }\right)Udiag\left(\frac{t{d}_1}{1+t{d}_1},\cdots ,\frac{t{d}_{n-p}}{1+t{d}_{n-p}}\right)U^T{\mathbf{Y}}^{\ast }\left(v^{\prime }\right)-\sum _{l=1}^{n-p}\log (1+t{d}_l).$$ (12)

Moreover, under the null hypothesis H_0,γ, (v), we have

$$D(v^{\prime };t)\stackrel{\mathcal{D}}{=}\sum _{l=1}^{n-p}\frac{{\delta }_l^2\left(v^{\prime }\right)t{d}_l}{1+t{d}_l}-\sum _{l=1}^{n-p}\log (1+t{d}_l),$$ (13)

where $\stackrel{\mathcal{D}}{=}$ means equality in distribution and the δ_l(v)’s are i.i.d N(0, 1) random variables.

Although Theorem 1 provides an effcient way of approximating the null distribution of RLRT_n(v), a complex issue arises from the complex spatial correlations among the ${\delta }_l^2\left(v^{\prime }\right)$ across voxels v′ ∈ B(v, h). One approach for dealing with such an issue is to estimate the spatial correlation for any pair of voxels, which can be computationally intensive. To avoid calculating spatial correlations, we develop a wild bootstrap method to effciently simulate the null finite sample distribution of RLRT_n(v). The detailed steps of this bootstrap method are presented in the supplementary document. After the p-values for all voxels $v\in \mathcal{V}$ are computed, either a false discovery rate (FDR) method or random field theory (RFT) is applied to correct for multiple comparisons [Ge et al., 2012].

2.3 Stage II

The second stage is to estimate β(v) and carry out statistical inference on β(v). At each voxel v, we consider model (1) given by

$$\mathbf{Y}\left(v\right)=\mathbf{X}\beta \left(v\right)+{\mathbf{Z}}^T\gamma \left(v\right)+E\left(v\right).$$ (14)

After calculating $\left\{{\widehat{\sigma }}_{\gamma }\right(v;h_S),{\widehat{\sigma }}_e(v\left)\right):v\in \mathcal{V}\}$, we can calculate ${\widehat{\Sigma }}_Y\left(v\right)={\widehat{\sigma }}_{\gamma }^2(v;h_S){\mathbf{Z}}^T\mathbf{Z}+{\widehat{\sigma }}_e^2\left(v\right){\mathbf{I}}_n$. Since all components of β(v) and Σ_Y (v) are statistically orthogonal to each other, we fix Σ_Y (v) at ${\widehat{\Sigma }}_Y\left(v\right)$ from here on. Since the true β(v) is not on the boundary of parameter space, different adaptive smoothing methods can be used here [Zhu et al., 2014, Polzehl and Spokoiny, 2000, Polzehl et al., 2010]. For simplicity, we put the detailed steps of Stage II in the supplementary document.

3 Results

3.1 Simulation Studies

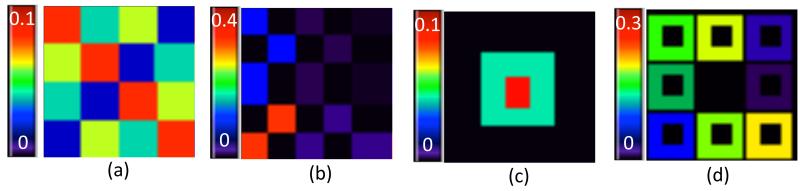
We simulated data at all N_V = 5, 808 voxels on a 44×44×3 phantom image. Each z-slice contains the same effect regions. At each voxel, we simulated the univariate imaging measures according to model (1) with β(v) = (β₀(v), β₁(v), β₂(v), β₃(v))^T and x_i = (1, x_i1, x_i2, x_i3)^T. Moreover, the covariates x_i1, x_i2, and x_i3 were generated from a Gaussian distribution with mean 40 and standard deviation 10, a Bernoulli distribution with success probability 0.5, and a Bernoulli distribution with success probability 0.3, respectively. These three covariates were designed to mimic the common clinical variables: age, gender, and disease status. For a slice of the phantom image, the effect areas for β₀(v) were divided into 16 regions with 4 different values ranging from 0.02 to 0.08, increasing by 0.02 (Figure 1(a)); for β₁(v), the effect regions were divided into 25 regions ranging from 10^−2.5 to 10^−12.5, decreasing by a rate of 10^−2.5 (Figure 1(b)); for β₂(v), the whole space was separated into 3 regions with values 0, 0.05, and 0.1 (Figure 1(c)); the effect area of β₃(v) was divided into 9 regions with values ranging from 0 to 0.1, increasing by differences of 0.025 (Figure 1(d)).

Fig. 1.

Simulation setting: (a) True image of β₀; (b) true image of β₁, in which the colors represent the values of β₁(v) × 10⁴; (c) true image of β₂; and (d) true image of β₃.

The genetic information was simulated according to the SNP data obtained from the public accessible data of the Alzheimer’s Disease Neuroimage Initiative (ADNI). It is an ongoing longitudinal study with the primary purpose of exploring the genetic and neuroimaing information associated with late-onset Alzheimer’s disease (LOAD). The study recruited elderly subjects older than 65 years of age consisting about 400 subjects with mild cognitive impairment (MCI), about 200 subjects with Alzheimer’s disease (AD), and around 200 healthy controls. Each subject was followed for at least 3 years. During the study period, the subjects were assessed with magnetic resonance imaging (MRI) measures and psychiatric evaluation to determine the diagnosis status at each time point. Genetic information was also collected from each subject at baseline and is genotyped by the Illumina 610 Quad array with more than 620,000 single nucleotide polymorphisms (SNPs). More information on ADNI is provided in the real data analysis of Section 3.2. We simulated the genetic information based on the two following scenarios:

• Scenario I. To preserve the linkage disequilibrium among SNPs, we utilize all of the SNPs on chromosome 1 from 197 Caucasian controls to generate the genetic effects. After eliminating the SNPs with minor allele frequency (MAF) less than 5%, there were 31554 out of 45627 SNPs left. Then, we randomly chose 20 SNPs and 100 subjects among the 197 healthy controls as the simulated genetic data z_i in (1). In this case, n = 100. If any of these 20 SNPs have MAF less than 5%, then the genetic data was resampled until all of the 20 SNPs have MAF ≥ 5%.

• Scenario II. To evaluate the performance of FMEM in the case of high LD, we selected the SNPs from the same gene in the second scenario. Searching the SNPs on the gene PICALM, which has been found to be relevant for Alzheimer’s disease in many studies [Harold et al., 2009] using the gene list “glist-hg18” provided by PLINK, there were 23 SNPs on PICALM with MAF larger than 5%. After eliminating the missing values, there are 176 healthy controls with complete genotype data at these 23 SNPs. We randomly selected 7 SNPs from 75 healthy controls to be z_i in (1). Although there is strong LD among these 7 SNPs, no SNP has perfect correlation (1 or −1) with any other SNPs in these 75 subjects. In this case, n = 75.

In both scenarios, the SNP effects were assumed to be additive. The γ(v)’s were generated from a multivariate normal distribution with mean zero and covariance matrix ${\sigma }_{\gamma }^2\left(v\right){\mathit{I}}_L$. Different ${\sigma }_{\gamma }^2\left(v\right)$ values, which represent di erent signal-to-noise ratios, were chosen to examine the finite sample performance of our method at different signal-to-noise ratios and also to test whether FMEM can perform well for different shapes. See Figure 3 (b) and Figure 3 (e) for Scenarios I and II. Moreover, we overlay some of the effect areas of β₃(v) and ${\sigma }_{\gamma }^2\left(v\right)$ in order to account for the fact that the brain phenotype is an intermediate expression of disease progression. The $\left\{{\sigma }_{\gamma }^2\right(v):v\in \mathcal{V}\}$ of the effect regions in Scenario I ranged from 0.005 to 0.025, increasing by 0.0025, whereas the $\left\{{\sigma }_{\gamma }^2\right(v):v\in \mathcal{V}\}$ of effect regions in Scenario II ranged from 0.005 to 0.045, increasing by 0.005. The random error e_i(v) was independently distributed as a univariate normal distribution with mean 0 and standard deviation 3 for all voxels. We set the number of bootstrap samples M and the number of repetitions to be 200.

Fig. 3.

Simulation results for testing the genetic effects: Scenario I: the rejection rate image at a selected slice by using (a) voxel-wise approach and (b) FMEM; Scenario II: the rejection rate image by using (c) voxel-wise approach and (d) FMEM.

Tables 1 and 2 summarize the estimation results of ${\sigma }_{\gamma }^2\left(v\right)$ obtained from FMEM and the voxel-wise method for both scenarios. The tables include the average absolute value of the bias, the root mean square error (RMS), standard deviation (SD), and the ratio of RMS to SD. RMS is based on the empirical mean and the SD is based on the theoretical mean. As shown in both tables, FMEM produces smaller estimation bias, RMS, and SD compared with the voxel-wise method, which indicates that FMEM yields much more accurate estimation.

Table 1.

Simulation results: the estimation results of ${\sigma }_{\gamma }^2\left(v\right)$ in Scenario I using FMEM and the voxel-wise method in terms of average absolute value of bias (BIAS), root mean square error (RMS), standard deviation (SD), and the ratio between RMS and SD (RE).

	FMEM				Voxel-wise
${\sigma }_{\gamma }^2\left(v\right)$	|BIAS|	RMS	SD	RE	|BIAS|	RMS	SD	RE
0	0.001	0.002	0.002	1	0.007	0.005	0.005	1
0.005	2.36e-06	0.003	0.003	1	0.005	0.005	0.005	1
0.0075	0.0005	0.003	0.003	1	0.005	0.006	0.006	1
0.01	0.001	0.004	0.004	1	0.006	0.008	0.008	1
0.0125	0.001	0.004	0.004	1	0.006	0.008	0.008	1
0.015	0.002	0.005	0.005	1	0.008	0.010	0.010	1
0.0175	0.003	0.005	0.005	1	0.008	0.010	0.010	1
0.020	0.002	0.006	0.006	1	0.010	0.012	0.012	1
0.0225	0.003	0.006	0.006	1	0.010	0.013	0.013	1
0.025	0.004	0.006	0.006	1	0.010	0.014	0.014	1

Table 2.

Simulation results: the estimation results of ${\sigma }_{\gamma }^2\left(v\right)$ in Scenario II by using FMEM and the voxel-wise method in terms of average absolute value of bias (BIAS), root mean square error (RMS), standard deviation (SD), and the ratio between RMS and SD (RE).

	FMEM				Voxel-wise
${\sigma }_{\gamma }^2\left(v\right)$	|BIAS|	RMS	SD	RE	|BIAS|	RMS	SD	RE
0	0.002	0.003	0.003	1	0.003	0.008	0.008	1
0.005	0.0001	0.004	0.004	1	0.007	0.126	0.126	1
0.010	0.001	0.006	0.006	1	0.011	0.016	0.016	1
0.015	0.002	0.008	0.008	1	0.014	0.020	0.02	1
0.020	0.002	0.010	0.010	1	0.024	0.017	0.017	1
0.025	0.003	0.020	0.020	1	0.020	0.029	0.029	1
0.030	0.005	0.013	0.013	1	0.023	0.032	0.032	1
0.035	0.004	0.014	0.014	1	0.026	0.035	0.035	1
0.040	0.015	0.006	0.006	1	0.028	0.040	0.040	1
0.045	0.007	0.016	0.016	1	0.031	0.040	0.040	1

We tested the hypotheses H₀ : ${\sigma }_{\gamma }^2\left(v\right)=0$ and H₁ : ${\sigma }_{\gamma }^2\left(v\right)\ne 0$ for all voxels in V based on FMEM and its corresponding voxel-wise method, and the score test based on the IBS kernel used in Ge et al. [2012]. Moreover, we evaluated their finite-sample performance in cluster-based thresholding [Silver et al., 2011]. Specifically, we first thresholded the p-values for all voxels in V by using an initial p-value of 0.01 as suggested by Silver et al. [2011] in order to identify clusters of contiguous supra-threshold voxels. Then, the thresholded clusters were matched with the 9 true effect areas in Figure 3 (b) or (e). If a specific thresholded cluster overlaps with at least one voxel in any of the 9 true effect regions, we call such cluster as a “true positive”. In contrast, if a specific thresholded cluster does not overlap with any voxels of the 9 effect regions, we call a cluster a “false positive”. We summarized the hypothesis testing results by the average dice overlap ratio (DOR), the average number of false positive clusters, and the average size in the number of voxels of false positive clusters. DOR is the ratio between the number of true positive clusters over the true number of effect areas, which is 9 in this simulation setting. Thus, the higher DOR means the higher the probability of detecting the true effect regions.

As shown in Tables 3 and 4, if we set the cluster size threshold as one voxel, FMEM has smaller DOR and a smaller number of false positive clusters compared with the voxel-wise method. When the cluster size threshold increases to 10 voxels, FMEM has a similar DOR value as that of the no threshold case, whereas the DOR of the voxel-wise approach reduces by about 20%. The score test based on the IBS kernel has little power to detect the nine effect regions with subtle effects. It may be caused by both the relatively low sensitivity of the score test itself and the misspecified IBS kernel.

Table 3.

Simulation results: comparisons of FMEM, voxel-wise method, and the score test based on the IBS kernel (Score) for Scenario I: the dice overlap ratio (DOR), average number of false positive clusters, and average size of false positive clusters with different cluster size thresholds.

		FMEM		Voxel-wise		Score
Threshold		Mean	SD	Mean	SD	Mean	SD
		Scenario I
	DOR	0.94	0.05	0.99	0.02	0	0
Voxel Size = 1	False Positive Cluster Number	1.88	6.12	21.30	12.29	0	0
	False Positive Cluster Size	1.03	0.04	1.06	0.06	NA	NA
	DOR	0.91	0.04	0.83	0.10	0	0
Voxel Size = 10	False Positive Cluster Number	0	0	0	0	0	0
	False Positive Cluster Size	NA	NA	NA	NA	NA	NA

Table 4.

Simulation results: comparisons of FMEM, voxel-wise method, and the score test based on the IBS kernel (Score) for Scenario II: the dice overlap ratio (DOR), average number of false positive clusters, and average size of false positive clusters for Scenario II with different cluster size thresholds.

		FMEM		Voxel-wise		Score
Threshold		Mean	SD	Mean	SD	Mean	SD
		Scenario II
	DOR	0.86	0.06	0.996	0.02	0.49	0.21
Voxel Size = 1	False Positive Cluster Number	1.35	4.85	15.45	12.92	0	0
	False Positive Cluster Size	1.07	0.08	1.05	0.07	NA	NA
	DOR	0.85	0.07	0.78	0.11	0.01	0.03
Voxel Size = 10	False Positive Cluster Number	0	0	0	0	0	0
	False Positive Cluster Size	NA	NA	NA	NA	NA	NA

Table 5 summarizes the number of significant voxels identified by the three methods in each effect region of Scenarios I and II. In Table 5, FMEM identifies less voxels in the non-effect regions, while detecting more voxels in the effect regions in both scenarios. For FMEM, its computational time is around 30 minutes for the first scenario and 20 minutes for the second one. Table 5 also confirms that the score test based on the IBS kernel has little statistical power in detecting the nine effect regions. Therefore, FMEM significantly outperforms the voxel-wise method and the score test based on the IBS kernel [Ge et al., 2012] in terms of detecting the true effect regions and controlling the false positive error rate.

Table 5.

ADNI data analysis: global power calculation for number of significant voxels detected by voxel-wise approach and FMEM in both scenarios.

Number of Voxels	4749	207	135	111	147	75	48	144	111	81
Scenario I
${\sigma }_{\gamma }^2\left(v\right)$	0	0.005	0.0075	0.010	0.0125	0.015	0.0175	0.020	0.0225	0.025
Score	0	0	0	0	0	0	0	0	0	0
Voxel-wise	123.91	36.3	38.25	43.08	72.245	42.98	31.535	104.32	86.1	65.97
FMEM	68.43	50.52	77.32	83.09	133.7	69.51	45.57	142.26	110.07	80.54
Scenario II
${\sigma }_{\gamma }^2\left(v\right)$	0	0.005	0.010	0.015	0.020	0.025	0.030	0.035	0.040	0.045
Score	0.165	0.905	2.475	5.11	11.065	7.91	6.715	24.135	21.655	17.81
Voxel-wise	110.93	27.08	33.105	40.05	65.92	39.06	27.51	90.69	73.42	56.59
FMEM	76.57	8.11	46.05	71.82	124.42	66.15	43.182	139.51	108.35	79.49

3.2 ADNI Data Analysis

The ADNI study began in 2004 and has three phases thus far, including ADNI-1, ADNI GO, and ADNI-2. The overall objective of the ADNI study is to determine the relationships among the clinical, cognitive, imaging, genetic and biochemical biomarker characteristics of the entire spectrum of AD as the pathology evolves from normal aging through early mild cognitive impairment, to mild cognitive impairment, to late mild cognitive impairment, to dementia or AD. The Principal Investigator of this initiative is Dr. Michael W. Weiner, MD, VA Medical Center and University of California San Francisco. For up-to-date information, see www.adni-info.org for details.

The aim of this ADNI data analysis is to use FMEM to identify brain regions affected by candidate genes, thereby hoping to shed light on the pathological interactions between these candidate genes and brain structure and function. The data we employed to evaluate the performance of FMEM was from ADNI-1. About 800 subjects with age older than 65 were recruited and followed at least 3 years. The 800 subjects included 200 healthy controls, 400 subjects with different levels of mild cognitive impairment (MCI), and 200 subjects with Alzheimer’s disease (AD). Besides the SNPs and the T1 weighted MRI imaging measurements, the subjects were assessed with demographic information and psychiatric examination scores to determine the diagnosis status at each scheduled visit.

The raw magnetic resonance image (MRI) data was collected from a variety of 1.5 Tesla MRI scanners with protocols individualized for each scanner, including standard T1-weighted images obtained using volumetric 3-dimensional sagittal MPRAGE or equivalent protocols with varying resolutions. The typical protocol included: repetition time (TR) = 2400 ms, inversion time (TI) = 1000 ms, flip angle = 80, field of view (FOV) = 24 cm, with a 256 × 256 × 170 acquisition matrix in the x-,y-, and z-dimensions yielding a voxel size of 1.25 × 1.26 × 1.2 mm³.

The T1-weighted MRI images were preprocessed by standard image processing steps including AC (anterior commissure) and -PC (posterior commissure) correction, bias field correction, skull-stripping, intensity inhomogeneity correction, cerebellum removal, segmentation, and nonlinear registration [Wang et al., 2011]. After segmentation, the brain was segmented into four different tissues: grey matter (GM), white matter (WM), ventricle (VN), and cerebrospinal fluid (CSF). We quantified the local volumetric group differences by generating RAVENS maps [Davatzikos et al., 2001] for the whole brain and each of the segmented tissue type (GM, WM, VN, and CSF) respectively, using the deformation field which we obtained during registration. RAVENS methodology is based on a volume-preserving spatial transformation, since this process changes an individual[prime]s brain morphology to conform it to the morphology of the Jacob template.

We are interested in detecting meaningful brain regions of interest that are associated with several candidate genes. We included only the subjects whose diagnostic status was healthy control or Alzheimer’s disease at baseline and had no status change during ADNI1. After screening, the total number of subjects we included was 372 (195 Healthy Controls (HCs) and 177 ADs). The clinical covariates of interest included gender, baseline age, square of baseline age, handedness, education, baseline intracranial volume, and the risk of Apolipoprotein E (ApoE). Specifically, handedness was treated as a binary variable, the education information was the self-reported years of education by the subjects, and the risk of APOE is assumed to be additive. Specifically, the risk of APOE for a subject was 3 if he/she carries ε4 at both alleles; it was 2 if he/she carries ε3 and ε4 in two alleles, the risk would be considered 0 if the two APOE alleles were the combination of ε2 and ε3, and other combinations of APOE alleles are assumed to have risk 1.

Many genes have been reported to be causal in the progression of Alzheimer’s disease. We selected three candidate causal genes including CR1 on chromosome 1, CD2AP on chromosome 6, and PICALM on chromosome 11 due to their strong association with the progression of Alzheimer’s disease [Harold et al., 2009, Naj et al., 2011, Lambert et al., 2009]. Specifically, PICALM encodes the protein phosphatidylinositol-binding clathrin assembly and is highly correlated with the emergence of late-on-set AD, which is possibly due to the perturbation at synapse triggering its function change [Harold et al., 2009]. The gene CD2AP encodes the CD2-asscociated protein and involves in the process of cell membrane, including endocytosis, that plays critical roles in neurodegeneration and Aβ clearance from the brain [Naj et al., 2011]. The gene CR1 encodes the complement component (3b/4b) receptor 1 and the pathways involving CR1 are involved in the AD process, specifically in clearance of Aβ peptides, which is the primary composition of amyloid plaques [Lambert et al., 2009].

We first matched the SNPs in ADNI with the gene list “glist-hg18” provided by PLINK [Purcell and et al, 2007] and were able to locate 16, 15, and 23 SNPs on the selected CR1, CD2AP, and PICALM genes, respectively. All these SNPs pass the quality control procedure with MAF > 5% and the Hardy Weinberg Equilibrium (HWE) test p-value> 0.01. The MAFs of the SNPs of the selected genes vary from 0.1 to 0.5. After deleting missing values, there are 335, 299 and 328 subjects corresponding to the CR1, CD2AP, and PICALM genes, respectively. The MAFs of all selected SNPs and demographic information are included in the supplementary document.

For each selected gene, we fitted FMEM (1) with z coded as the number of minor alleles in order to detect its associated brain regions of interest (ROIs). For comparisons, we fitted the same model by using the classical voxel-wise method and Ge’s method to the same data sets. To formally detect significant ROIs, by following Ge et al. [2012], we used a cluster-form of threshold of 0.1% with a minimum voxel clustering value of 50 voxels. The names of the brain regions were included in Tables 6-8 of the supplementary document. FMEM is able to to detect 45, 45, and 27 significant clusters for CR1, CD2AP, and PICALM, respectively, whereas the standard voxel-wise method can only identify 6, 14, and 2 significant clusters, and none from Ge’s method for CR1, CD2AP, and PICALM, respectively. We also fitted FMEM on the same data but only with the HC and AD samples only to investigate white noise signal. For HC samples only, FMEM detected 15, 8 and 31 significant clusters for CR1, CD2AP and PICALM, respectively. For AD samples only, FMEM detected 9, 8 and 41 significant clusters for CR1, CD2AP and PICALM, respectively. Although there are some discrepancies between the results based on the HC and AD samples only and those based on the combined sample, the results are highly similar to each other. The results obtained from the combined sample are generally more significant due to a larger sample size.

Finally, we overlapped these significant clusters with the 96 predefined ROIs in the Jacob template and were able to detect several predefined ROIs for CR1, CD2AP, and PICALM. For CD2AP, based on the combined sample, FMEM identified relatively large clusters with more than 150 voxels of right superior temporal gyrus, left and right inferior temporal gryus, left and right precentral gyrus, left and right middle frontal gyrus, right postcentral gyrus, right fusiform, left angular, left inferior frontal gyrus, left inferior occipital gyrus, left and right postcentral gyrus, left and right superior frontal gyrus, left anterior cingulate and paracingulate gyri, left median cingulate and paracingulate gyri, right calcarine fissure and surrounding cortex, right cuneus, right superior occipital gyrus, right middle occipital gyrus, right caudate, and right middle temporal gyrus.

For CR1, based on the combined sample, FMEM identified relatively large clusters with more than 150 voxels of right superior temporal gyrus, left and right putamen, left inferior temporal gyrus, left angular, left inferior occipital gyrus, right postcentral gyrus, right superior frontal gyrus, left anterior cingulate and paracingulate gyri, left median cingulate and paracingulate gyri, left cuneus, left middle occipital gyrus, and right caudate.

For PICALM, based on the combined sample, FMEM identified relatively large clusters with more than 150 voxels of right inferior frontal gyrus- triangular and orbital parts, right insula, right fusiform, right superior temporal gyrus, right temporal pole, right middle temporal gyrus, right inferior temporal gyrus, right precentral gyrus, right supramarginal gyrus, right middel occipital gyrus, right angular, right middle frontal gyrus, and right middle frontal gyrus.

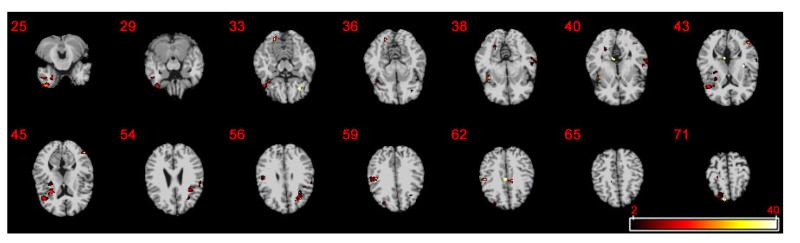
As shown in the supplementary document, we were able to detect several major ROIs, such as superior temporal gyrus, inferior temporal gyrus, middle frontal gyrus, angular, anterior cingulate and paracingulate gyri, hippocampus, putamen, and fusiform. Our finding of these ROIs are highly similar to previous reports on brain morphology in Alzheimer’s disease in the AD literature [Ohnishi et al., 2001, Convit et al., 2000, Jones et al., 2006, Fennema-Notestine et al., 2009]. The superior temporal gyrus is an essential structure involved in auditory processing, in social cognition processes, as well as in the function of language. The inferior temporal gyrus is one of the higher levels of the ventral stream of visual processing. The middle frontal gyrus plays a role in sustaining attention and working memory. The angular gyrus is involved in a number of processes related to language, number processing and spatial cognition, memory retrieval, attention, and theory of mind. The anterior cingulate and paracingulate gyri in rational cognitive functions, such as reward anticipation, decision-making, empathy, impulse control, and emotion. The hippocampus is known to be associated with memory and cognition. The fusiform is associated with color recognition, word and body recognition and the putamen is associated with motor skills. Figure 4 shows the −log₁₀(p) map of selected slices with significant clusters for testing the genetic effects of CD2AP on RAVEN images identified by FMEM.

Fig. 4.

ADNI data analysis: the −log₁₀(p) maps for testing the genetic effect of CD2AP on RAVEN images by using FMEM from 14 selected slices.

4 Discussion

We have developed FMEM to carry out an association analysis between neuroimaging phenotypes and a group of genetic markers, while adjusting for the clinical variables of interest. We have proposed a multiscale adaptive procedure with three features: spatial, hierarchical, and adaptive. Our simulation results have shown substantial gains in parameter estimation precision and statistical power in detecting the true effect of ROIs compared to the voxel-wise method. More research is needed for optimizing the choice of the tuning parameters in FMEM. We will borrow some key ideas of FMEM to develop a fast procedure to carry out GWAS for imaging genetic studies. We will also develop fast FMEM for the joint analysis of neuroimaging and genetic data with rare or common variants [Fan et al., 2013, 2012].

Fig. 2.

Simulation results for estimation accuracy: Scenario I: (a) estimated ${\sigma }_{\gamma }^2\left(v\right)$ by using voxel-wise approach; (b) true ${\sigma }_{\gamma }^2\left(v\right)$ image; and (c) estimated ${\sigma }_{\gamma }^2\left(v\right)$ by using FMEM. Scenario II: (d) estimated ${\sigma }_{\gamma }^2\left(v\right)$ by using voxel-wise approach; (e) true ${\sigma }_{\gamma }^2\left(v\right)$ image; (f) estimated ${\sigma }_{\gamma }^2\left(v\right)$ by using FMEM.