Skip to main content
PMC home page
PLOS ONE logoLink to PLOS ONE
. 2014 Nov 19;9(11):e113400. doi: 10.1371/journal.pone.0113400

Processing Deficits of Motion of Contrast-Modulated Gratings in Anisometropic Amblyopia

Yong Tang 1,2,#, Caiyuan Liu 2,#, Zhongjian Liu 2, Xiaopeng Hu 3, Yong-Qiang Yu 3,*, Yifeng Zhou 1,2,4
Editor: Benjamin Thompson5
PMCID: PMC4237427  PMID: 25409477

Abstract

Several studies have indicated substantial processing deficits for static second-order stimuli in amblyopia. However, less is known about the perception of second-order moving gratings. To investigate this issue, we measured the contrast sensitivity for second-order (contrast-modulated) moving gratings in seven anisometropic amblyopes and ten normal controls. The measurements were performed with non-equated carriers and a series of equated carriers. For comparison, the sensitivity for first-order motion and static second-order stimuli was also measured. Most of the amblyopic eyes (AEs) showed reduced sensitivity for second-order moving gratings relative to their non-amblyopic eyes (NAEs) and the dominant eyes (CEs) of normal control subjects, even when the detectability of the noise carriers was carefully controlled, suggesting substantial processing deficits of motion of contrast-modulated gratings in anisometropic amblyopia. In contrast, the non-amblyopic eyes of the anisometropic amblyopes were relatively spared. As a group, NAEs showed statistically comparable performance to CEs. We also found that contrast sensitivity for static second-order stimuli was strongly impaired in AEs and part of the NAEs of anisometropic amblyopes, consistent with previous studies. In addition, some amblyopes showed impaired performance in perception of static second-order stimuli but not in that of second-order moving gratings. These results may suggest a dissociation between the processing of static and moving second-order gratings in anisometropic amblyopia.

Introduction

Amblyopia is a developmental visual disorder, which may be a consequence of sensory impediment to visual development, such as strabismus (ocular misalignment) or anisometropia (unequal refractive error), occurring early in life [1]. It is often characterized by reduced spatial vision [2]–[5], which cannot be significantly improved by refractive correction, and is believed to be a cortical disorder [6]–[8].

It has been indicated that alterations in response properties of neurons in V1, including reduced spatial resolution [9] and contrast sensitivity [10], [11], as well as a loss of proportion of cells driven by amblyopic eyes [12], [13] underlie the visual deficits in patients with amblyopia. In addition to this, many studies on human amblyopia [14]–[20] and animals with experimental amblyopia [13], [21], [22] have suggested that functions of extra-striate cortex may also be affected by amblyopia. Now, the cortical loci for processing deficits in amblyopia remain an open question.

Investigations of the perception of first- and second-order stimuli in amblyopia may be helpful to the understanding of the cortical deficits in amblyopia. First-order stimuli are defined by modulation of luminance, while second-order stimuli are defined by changes in image features, such as contrast or texture [23]. It is generally recognized that the first-order processing mechanism involves linear neurons in area V1 that detect spatial luminance variations across their receptive fields, while the processing of second-order stimuli involves three successive stages: a first-stage linear filter which is identical to first-order processing and can be conducted in area V1, a pointwise nonlinearity such as rectification, and a second-stage linear filter which has been associated with computations at extra-striate cortex [24], [25].

A large amount of studies [2], [3], [5], [26]–[28] have indicated a significant first-order loss in amblyopia, consistent with the physiological evidence described above that functions of striate cortex are affected by amblyopia. Similarly, some studies [29]–[34] have indicated substantial deficits in perception of second-order stimuli in amblyopia. By measuring the detection threshold of 5 amblyopes, Wong and his colleagues found that four amblyopic eyes and two non-amblyopic eyes showed second-order loss relative to the control eyes [29]. Additionally, they found that the second-order loss was greater than the first-order loss at the carrier spatial frequency, i.e. first-order input to second-order processing systems. Similar results were also obtained by Mansouri and his colleagues in a coarse second-order orientation (vertical vs. horizontal) discrimination task [30]. In two other studies [31], [32], Simmers and her colleagues found substantial deficits in processing of global second-order motion in amblyopes by using a specific method, which could exclude the influence of the deficits in spatial contrast sensitivity, i.e. first-order processing deficits, on motion perception. These findings were further supported by Aaen-Stockdale and his colleagues, who found significant processing deficits of translational, radial and rotational motion in amblyopia with the use of second-order random dots [33]. Simmers and her colleagues also measured the contrast sensitivity for first-order and second-order motion over a five-octave range of spatial and temporal frequencies in three patients with strabismus amblyopia [34]. They found that compared to normal controls, amblyopes were not only impaired in the processing of first-order motion, but overall they exhibited both higher thresholds and a much narrower window of visibility to second-order motion. These findings improved our understanding of the visual problems in amblyopes, and suggested that there are substantial second-order processing deficits, part, if not most, of which may originate from extra-striate cortex, in amblyopia.

Most of the studies described above have focused on the perception of static second-order stimuli [29], [30] and the global processing for second-order stimuli [30]–[33]. In contrast, less is known about the perception of second-order moving gratings in amblyopia. We therefore evaluated this issue using a motion direction discrimination task in the present study. Contrast sensitivity for second-order moving gratings was measured and compared between the AEs and NAEs of amblyopic subjects and CEs of normal control subjects. To exclude the possible influence of low-level processing deficits, i.e. first-order deficits, on the perception of second-order motion, both non-equated carriers (with a full contrast of 1.0) and a series of equated carriers were used. The setting of the equated carriers was similar to that by Wong and his colleagues [29]. And for comparison, the sensitivity for first-order motion and static second-order stimuli were also measured.

Methods

Subjects

Seven anisometropic amblyopes and ten normal controls with appropriate optical correction participated in this experiment. The visual characteristics of all amblyopes were given in Table 1. The average age of the amblyopes was 23.7±0.3 years, and that of the normal controls was 24.6±2.1 years. All observers were naïve to the purpose of experiment.

Table 1. Visual Characteristics of Amblyopic subjects.

Subject Sex Age Type Optical Correction Visual acuity (MAR)
S1 M 23 A AE +2.00DS/+3.00DC×42 2.0
NAE −0.50DS×165 1.0
S2 M 25 A AE +6.00/+0.75×42 2.5
NAE −0.75/−0.50×161 0.8
S3 M 23 A AE +2.00DS/+2.50DC×95 4.0
NAE −3.75DS/−0.75DC×10 1.0
S4 F 24 A AE +2.50DS/1.50DC×85 2.5
NAE plano 0.8
S5 M 24 A AE +1.00DS/+1.50DC×95 2.0
NAE Plano 1.0
S6 F 23 A AE +4.00DS 6.7
NAE Plano 1.0
S7 M 24 A AE +4.00DS/+1.00DC×85 8.3
NAE Plano 1.0
Open in a new tab

F, female; M, male; A, anisometropic amblyopia; AE, amblyopic eyes; NAE, non-amblyopic eyes; MAR, minimum angles of resolution.

Ethics statement

This research has been approved by the ethics committee of the University of Science and Technology of China (We cannot provide the permit number because our institution regulations do not require such numbers), and was performed in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki. The written informed consent was obtained from all participants before participation.

Apparatus

All stimuli were generated in real time using programs in Matlab 6.5 with Psychtoolbox (version 2.50) extensions [35], [36]. The computer was a P4 PC, with an ATI 7500 video card and a 17-inch Sony G220 monitor. A special circuit was used to combine two 8-bit output channels of the video card to produce 14 bits of gray levels [37]. Luminance calibration was performed by using a psychophysical procedure in combination with a photometer (UDT 161) [37], [38]. The mean background luminance was set to 50 cd/m2. When measuring the spatial contrast sensitivity function, the screen resolution was 1600×1200 pixels with a frame rate of 75 Hz, and the eye-screen distance was 228 cm. When measuring the contrast sensitivity for first- and second-order motion, the screen resolution was 640×480 pixels with a frame rate of 160 Hz, and the viewing distance was 114 cm. A chin rest was used to fix head position. All viewing was monocular in a dimly lit room.

Stimuli

The stimuli used for spatial contrast sensitivity measurements were sine-wave gratings with different spatial frequencies, which were 0.5, 1, 2, 4, 8, 16 and 24 c/d for amblyopic eyes, and were 0.5, 1, 2, 4, 8, 16, 24 and 32 c/d for non-amblyopic eyes. These stimuli subtended 3.8°×3.8°, and were presented at the center of the screen.

The noise carrier (Figure 1a) was a 1-bit, spatially 2-d, static noise pattern generated by assigning individual (single) screen pixels (0.025 degree of visual angle) to be either ‘white’ or ‘black’ with equal probability to ensure that there was no spatial variation in luminance within individual noise elements. A new stochastic noise sample was used for each trial. Note that the use of this noise size would not significantly introduce luminance artifacts [39], [40].

Figure 1. Illustration of stimuli used in this experiment.

Figure 1

Open in a new tab

(a) noise carrier, (b) first-order stimulus, (c) second-order stimulus. All stimuli are presented at screen center, subtended 2.51°×2.51°.

The first-order motion stimulus (Figure 1b) was a noise carrier whose luminance was modulated by a sinusoidal grating, while the second-order motion stimulus (Figure 1c) was a noise carrier whose contrast was modulated by a sinusoidal grating. The luminance profile at point (x, y) of the first- (Equation 1) and second-order (Equation 2) stimuli are defined as:

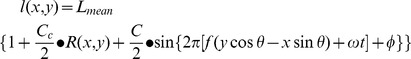graphic file with name pone.0113400.e001.jpg (1)
graphic file with name pone.0113400.e002.jpg (2)

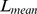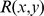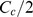where Inline graphic is the background luminance of the display; Inline graphic is the carrier; Inline graphic is the contrast of the carrier (The Michelson contrast is Inline graphic for first-order motion); 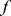Inline graphic is the spatial frequency of the envelope grating (here set to 1 cycle/degree); Inline graphic represents the orientation of the envelope grating (here set to 90°); 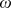Inline graphic is the temporal frequency of the envelope grating (1.0, 2.0, 4.0, 8.0, 16.0, and 30.0 Hz for first-order stimuli; 1.0, 2.0, 4.0, 8.0, and 16.0 Hz for second-order stimuli; 0 Hz for static stimuli); 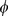Inline graphic is the (random) initial spatial phase; and Inline graphic is the contrast of the envelope, i.e. first-order or second-order modulation depth. These stimuli subtended 2.51°×2.51°, and were presented at the center of the screen. The edges of the square window in which these stimuli were displayed were abrupt.

Experimental design and procedure

With a stimulus detection task, the spatial contrast sensitivity function was first measured in amblyopic eyes (AE) and non-amblyopic eyes (NAE) of amblyopic subjects and dominant eyes (CE) of normal control subjects (The results of spatial contrast sensitivity function were not shown here because they were very similar to those described in previous studies [28], [41]). A carrier detection task was then used to measure the contrast threshold for the noise carriers. Subsequently, a static stimuli orientation discrimination task and a motion direction discrimination task were applied. The order of two discrimination tasks was counter-balanced between subjects. For each eye, the discrimination threshold was first measured with non-equated carriers, i.e. the noise carrier contrast 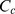Inline graphic was set to 1.0. Following this, it was measured with a number of carrier contrast levels in order to equate carrier visibility, i.e. with equated carriers. Levels were specified in carrier contrast threshold units (CCTU), which were multiples of carrier contrast threshold measured in the carrier detection task.

A two-alternative-forced-choice design was used in this experiment. In the noise carrier detection task, subjects were asked to detect the presence of the stimulus, which was presented in one of two successive presentation intervals each lasting 250 ms and separated by a 500 ms inter-stimulus interval (ISI). In the stimulus discrimination task, subjects were required to indicate the orientation of the static second-order stimulus, horizontal or vertical, and the direction of first-order or second-order motion, leftwards or rightwards. The duration of all stimuli was 250 ms with 25 ms linear ramps in the beginning and the end.

Contrast thresholds were measured using a two-down one-up staircase procedure [42], which decreased the signal contrast by 10% (ct+1 = 0.90ct) following every two consecutive correct responses and increased the signal contrast by 10% (ct+1 = 1.10ct) after every incorrect answer, converging on 70.7% correct. The starting contrast of the staircase was determined by a prior study. Each staircase ran through 100 trials, usually generating about 20 reversals. When measuring the spatial contrast sensitivity and the contrast thresholds for first- and second-order motion, trials for the staircases associated with each spatial or temporal frequency condition were intermixed randomly. Contrast sensitivity (reciprocal of contrast threshold) was used for data analysis.

All trials were initiated by the subjects. In each trial, the stimulus was preceded by a short beep. Then the subject indicated her/his decision with a keyboard button press. No feedback was provided. Before the measure, each subject received a short practice session.

Statistical analysis

Between-subject ANOVA and t-test were used to compare data in the amblyopic eyes of the amblyopic subjects and the dominant eyes of the control subjects. The same statistical tests were also used to compare data in the non-amblyopic eyes of the amblyopic subjects and the dominant eyes of the control subjects. Within-subject ANOVA and t-test were used to compare data in the amblyopic and the non-amblyopic eyes of the amblyopic subjects. All data were expressed as Mean±SEM.

Results

First-order motion

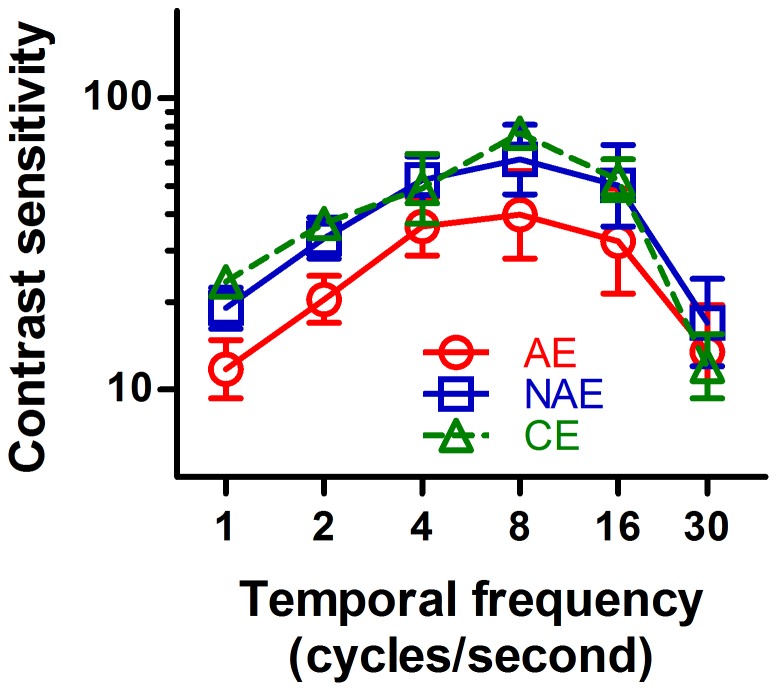
The average contrast sensitivity for first-order motion is plotted as a function of the temporal frequency for AEs, NAEs and CEs in Figure 2. As shown in the figure, all curves exhibit inverted U-shaped patterns, and the peaks of all curves occur around 8 Hz.

Figure 2. Average contrast sensitivity for the identification of the direction of first-order motion for amblyopic eyes (AE, Circles), non-amblyopic eyes (NAE, Squares), and control eyes (CE, Triangles).

Figure 2

Open in a new tab

Error bars represent one standard error of the mean.

In this condition, although the sensitivity function of the AEs is slightly lower than those of NAEs and CEs, the differences were not statistically significant (AE vs. NAE, within-subject ANOVA, F 1,6 = 2.948, p = 0.137; AE vs. CE, between-subject ANOVA, F 1,15 = 2.600, p = 0.128). And there were no significant differences in the sensitivity functions between the NAEs and the CEs (between-subject ANOVA, F 1,15 = 0.015, p = 0.904). In all cases, the two-way interactions were not statistically significant (all p's>0.05). These results indicated that the contrast sensitivity for sine-wave moving gratings, i.e. first-order motion, at the spatial frequency of 1 c/d was relatively normal in these amblyopic subjects.

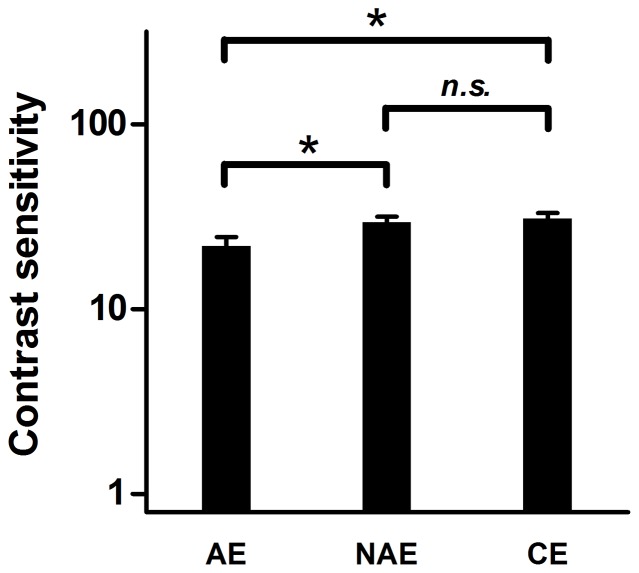
Sensitivity for the carriers

To evaluate the first-order processing deficits in the perception of second-order motion in anisometropic amblyopia, the detection threshold for the noise carriers was measured, with the results shown in Figure 3. For the noise carrier, the average contrast sensitivity was 22.77±2.77, 30.10±1.90 and 31.56±2.09 for AEs, FEs, and CEs, respectively. There was no significant difference between the sensitivity of the NAEs and CEs (between-subject t-test, t 15 = 0.492, p = 0.630), whereas the sensitivity of the AEs were significantly lower than those of the NAEs (within-subject t-test, t 6 = 4.220, p = 0.006) and those of the CEs (between-subject t-test, t 15 = 2.585, p = 0.021). These results indicated substantial deficits in perception of the noise carriers in AEs but not in NAEs, consistent with the previous result [30].

Figure 3. Averaged contrast sensitivity for carriers in amblyopic eyes, non-amblyopic eyes and control eyes.

Figure 3

Open in a new tab

AE, amblyopic eyes; NAE, non-amblyopic eyes; CE, control eyes. *, statistically significant (p<0.05); n.s., non-significant (p>0.05). Error bars represent one standard error of the mean.

Second-order motion

Data for second-order motion with non-equated and a series of equated carriers are shown in Figure 4. For comparison, the sensitivity for static second-order stimuli was also shown. From this figure, it is clear that all eyes exhibited a better performance at a higher CCTU, both for second-order motion and for static second-order stimuli. Note that there are different numbers of participants in each condition tested, which can be clearly seen in Table 2 and Figure 5.

Figure 4. Average contrast sensitivity for second-order motion and static second-order stimuli for amblyopic eyes (AE, Circles), non-amblyopic eyes (NAE, Squares), and control eyes (CE, Triangles).

Figure 4

Open in a new tab

Error bars represent one standard error of the mean.

Table 2. Comparisons of contrast sensitivity for static second-order gratings.

df t p
AE vs. CE* non-equated 15 6.986 <0.001
CCTU20 12 4.840 <0.001
CCTU15 15 4.674 <0.001
CCTU10 14 3.128 0.007
CCTU5 13 3.674 0.003
AE vs. NAE# non-equated 6 6.556 0.001
CCTU20 3 0.531 0.012
CCTU15 6 7.027 <0.001
CCTU10 5 4.011 0.010
CCTU5 4 3.577 0.023
Open in a new tab

AE, amblyopic eyes; NAE, non-amblyopic eyes; CE, dominant eyes of control subjects.

*, between-subject t-test;

#

, within-subject t-test.

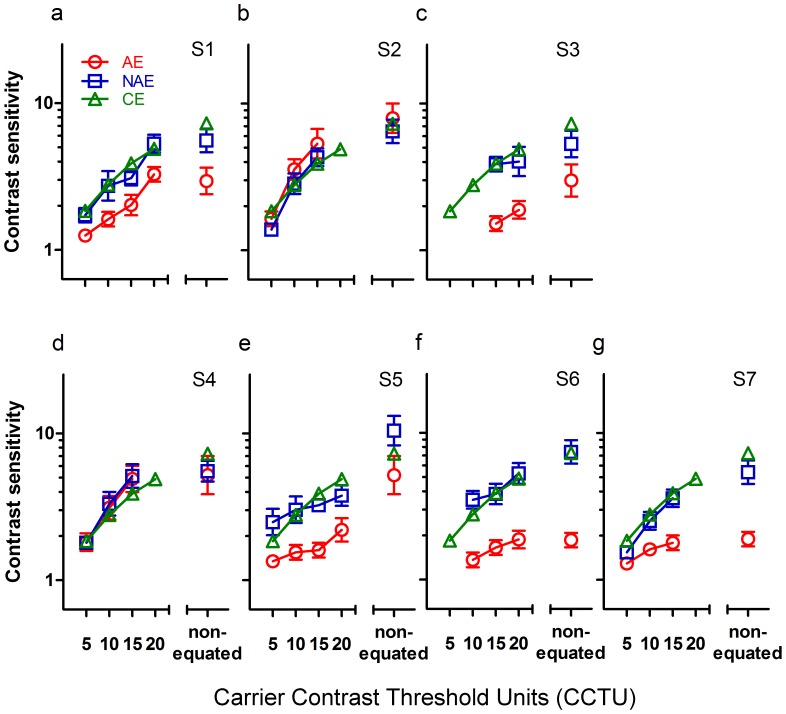
Figure 5. Contrast sensitivity for second-order motion at all carrier contrast levels for each amblyopic subject.

Figure 5

Open in a new tab

The data points for control eyes (CE, Triangles) were averaged across subjects and temporal frequencies. While the data points for amblyopic eyes (AE, Circles) and non-amblyopic eyes (NAE, Squares) were only averaged across temporal frequencies. Note that for some subjects (S3 and S6) the sensitivity for second-order motion could not be measured at some low carrier contrast levels because of the floor effect. And for some other subjects (S2, S4 and S7) the data could not be measured at the highest carrier contrast levels because in this condition the expected contrast of the noise carriers is larger than 1. Error bars represent one standard error of the mean.

As expected, the AEs showed significantly reduced sensitivity to static second-order stimuli relative to the CEs and NAEs at all carrier contrast levels, and there were no significant differences in sensitivity between the NAEs and CEs (Table 2). These findings suggest substantial processing deficits in static second-order stimuli, consistent with the previous studies [29], [30].

Similar to those for first-order motion, all curves for second-order motion show inverted U-shaped patterns, and most of them peak at around 8 Hz. In all carrier contrast levels, sensitivity for second-order motion seems to be comparable between the NAEs and CEs (between-subject ANOVA, non-equated, F 1,15 = 1.200, p = 0.291; CCTU20, F 1,12 = 0.354, p = 0.563; CCTU15, F 1,15 = 0.038, p = 0.847; CCTU10, F 1,14 = 0.549, p = 0.471; CCTU5, F 1,13 = 0.176, p = 0.682). In contrast, AEs showed significantly reduced performance relative to CEs (between-subject ANOVA, non-equated, F 1,15 = 19.9820, p<0.001; CCTU20, F 1,12 = 33.199, p<0.001; CCTU15, F 1,15 = 7.762, p = 0.014; CCTU10, F 1,14 = 5.084, p = 0.041) except for the lowest carrier contrast levels (CCTU5, F 1,13 = 4.263, p = 0.059). Similarly, significant differences were also found between the AEs and the NAEs at high carrier contrast levels (within-subject ANOVA, non-equated, F 1,6 = 14.882, p = 0.008; CCTU20, F 1,3 = 31.067, p = 0.011; CCTU15, F 1,6 = 9.152, p = 0.023) but not at low levels (CCTU10, F 1,5 = 5.520, p = 0.066; CCTU5, F 1,4 = 1.877, p = 0.243).

It seems that the performance gap between high and low carrier contrast levels described above was mainly caused by the performance variance between these amblyopic subjects, which can be clearly seen in Figure 5. In this figure, the data points for control eyes were averaged across 10 subjects and 5 temporal frequencies. While the data points for amblyopic eyes (AE, Circles) and non-amblyopic eyes (NAE, Squares) were only averaged across temporal frequencies. For most of the amblyopic subjects (S1, S3, S5, S6 and S7), NAEs and CEs showed much better performance than AEs in all conditions (in all cases, p<0.05). Whereas for S2 and S4, AEs had similar sensitivity to NAEs (within-subject ANOVA, S2, F 1,4 = 3.037, p = 0.156; S4, F 1,4 = 0.493, p = 0.521), and even to the CEs (between-subject ANOVA,S2, F 1,53 = 0.953, p = 0.333; S4, F 1,53 = 0.001, p = 0.990). In addition, because of the floor effect, the sensitivity for second-order motion could not be measured at low carrier contrast levels, such as CCTU5 and CCTU10, for amblyopic subjects (S3 and S6) with worse performance. As a result, the group-averaged performance included less data from these subjects at low carrier contrast levels, and therefore biased to “normal performance” in these conditions.

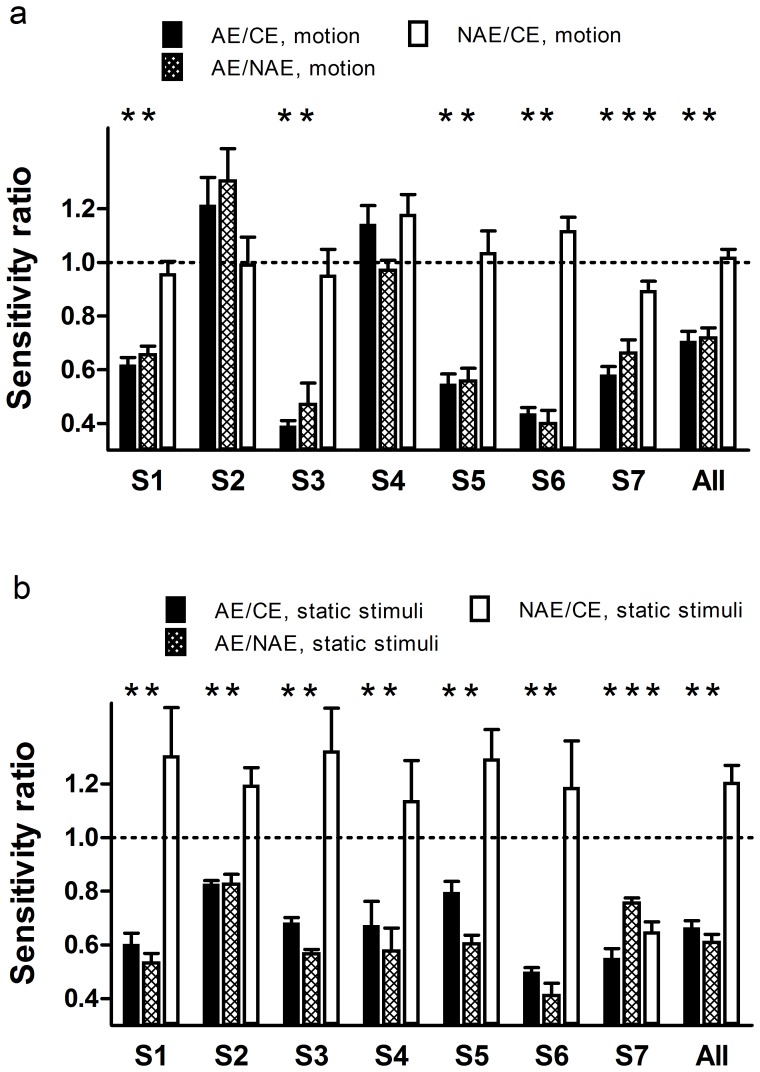
Contrast sensitivity ratios

To get a more clear sense of the deficits in perception of second-order motion in anisometropic amblyopia, the sensitivity ratios between the AEs, NAEs and CEs were calculated for each amblyopic subject (Figure 6a). The ratios were averaged across 4 carrier contrast levels (CCTU5, CCTU10, CCTU15 and CCTU20) and 5 temporal frequencies. Note that data from measures with non-equated carriers were not included. From Figure 6a, it is clear that most of the AE/CE and AE/NAE ratios (5/7, except S2 and S4) were significantly (all p's<0.05) lower than 1, and that most of the NAE/CE ratios (6/7, except S7) were statistically (all p's>0.1) comparable to 1. As a group, the AE/CE and AE/NAE ratios were 0.71±0.03 and 0.72±0.03, respectively, significantly different from 1 (two-tailed one-sample t-test, AE/CE ratios, t 109 = −8.561, p<0.001; AE/NAE ratios, t 109 = −8.077, p<0.001), and the NAE/CE ratio was 1.02±0.03, statistically comparable to 1 (two-tailed one-sample t-test, t 109 = 0.828, p = 0.409). These results suggest that the processing of second-order motion is substantially impaired in AEs of anisometropic amblyopes. In contrast, most of the NAEs are relatively spared.

Figure 6. Averaged sensitivity ratios between the amblyopic eyes (AE), non-amblyopic eyes (NAE), and control eyes (CE) for second-order motion (a) and static second-order stimuli (b).

Figure 6

Open in a new tab

Dash line, the value (1) used in t-test. *, statistically different from 1 (p<0.05) and a mean value lower than 1.

For comparison, the sensitivity ratios between the AEs, NAEs and CEs were also calculated for static second-order stimuli, which were shown in Figure 6b. The AE/CE and AE/NAE ratios varied between subjects, from 0.41 (S6, AE/NAE) to 0.83 (S2, AE/CE and AE/NAE), and were all lower than 1 in statistics (two-tailed one-sample t-test, all p's<0.05). As to NAE/CE ratios, most were slightly larger than 1, and only those of S7 were not (S7, 0.61, 0.62 and 0.72 at CCTU15, CCTU10 and CCTU5, respectively; two-tailed one-sample t-test, t 2 = −10.000, p = 0.01). All these findings suggest that the perception of static second-order stimuli was strongly impaired in AEs and part of the NAEs of anisometropic amblyopes, consistent with the previous study [29].

It should be noted that, in Figure 6, the AEs of S2 and S4 had “normal” sensitivity for second-order motion (S2, AE/CE ratios = 1.21±0.10, AE/NAE ratios = 1.30±0.12; S4, AE/CE ratios = 1.14±0.07, AE/NAE ratios = 1.18±0.07). In contrast, this is not the case for static second-order stimuli. In most cases, their ratios were significantly lower than 1 (S2, AE/CE ratios = 0.83±0.01, two-tailed one-sample t-test, t 2 = −15.248, p = 0.004; AE/NAE: 0.83±0.03, two-tailed one-sample t-test, t 2 = −5.076, p = 0.037; S4, AE/CE: 0.58±0.08, two-tailed one-sample t-test, t 3 = −5.136, p = 0.036; AE/NAE: 0.67±0.09, two-tailed one-sample t-test, t 2 = −3.696, p = 0.066), indicating that the processing of static second-order stimuli was substantially impaired in their AEs. These results might suggest a dissociation between the processing of static second-order stimuli and second-order motion in anisometropic amblyopia.

Discussion

In the present study, we found poor contrast sensitivity for second-order moving gratings in amblyopic eyes of anisometropic amblyopes, even after eliminating the influence of low-level processing deficits. In contrast, the non-amblyopic eyes were relatively spared. We also found that contrast sensitivity for static second-order stimuli was strongly impaired in AEs and part of the NAEs of anisometropic amblyopes, consistent with previous studies. Moreover, some amblyopes showed impaired performance in perception of static second-order stimuli but not in that of second-order moving gratings. All these results suggest that the core mechanisms for second-order processing are strongly affected by amblyopia.

Sensitivity for first- and second-order motion

A number of previous studies have measured the contrast sensitivity for first- and/or second-order motion in normal adults [34], [43]–[46] and amblyopes [34], [46]. The sensitivity functions shown in the present study were similar to those found previously, except for two minor points.

First, the contrast sensitivity for first-order motion in this study was a little lower than that in previous studies. With monocular viewing and a slightly larger stimulus size (3.1 degrees), our previous study [46] has shown that, for normal controls, the peak value of the sensitivity function for moving gratings at 1 c/d is larger than 100. However, the first-order stimulus was only a sine-wave grating in that study, whereas the stimulus was composed of a sine-wave grating and a random noise carrier in the present study. We emphasize that an added noise carrier could greatly reduce the contrast sensitivity for first-order stimuli, no matter static or moving [45]. Additionally, the stimulus duration was 250 ms in the present study, which is much smaller than those (>600 ms) used in some other previous studies [34], [43], [44]. On this basis, it is not surprising that the contrast sensitivity for first-order motion in the present study seems to be a little lower than previously found.

Second, the peak of the sensitivity function for second-order motion occurs at 8 Hz in some conditions of the present study, which was a little higher than previously found in normal adults [34], [43], [44]. This difference may be associated with the refresh rate of the monitor used in the experiment. It was 160 Hz in the present study, much higher than previously used (75 Hz). A high refresh rate may provide more precise information about the motion at high temporal frequencies, such as 8 Hz, which may therefore improve the sensitivity at high temporal frequencies and change the peak location. This peak difference may also be associated with the contrast of the noise carriers. In previous studies [34], [43], [44], the carrier contrasts were 0.15–0.30. While in the present study, a much wider range was employed, from about 0.15 (CCTU5) to 1 (non-equated). Note that in conditions with high carrier contrasts (non-equated carriers, CCTU15 and part of CCTU20) in the present study, the peak occurs at around 8 Hz, whereas in conditions with low contrasts (CCTU10 and CCTU5), the peak moved to lower temporal frequencies, which were similar to previously results. This idea was also supported by one previous study [47] which used a carrier contrast of 1 and found similar sensitivity in normal adults for contrast-modulated motion at 3.75 Hz and 7.5 Hz.

Second-order processing deficits in amblyopia

As described in the Introduction, the previous studies [29], [30], [34] have investigated the processing of second-order gratings with various tasks and several types of amblyopia. Wong and his colleagues employed a static stimulus detection task and patients with both anisometropic and strabismic amblyopia. Mansouri and his colleagues used a coarse orientation discrimination task (vertical vs. horizontal) to investigate the perception of static second-order stimuli in both anisometropic and strabismic amblyopia. In Simmers and her colleagues' study, a motion direction discrimination task with four different varieties of second-order motion (modulations of either the contrast, flicker, size or orientation of visual noise) were used, but only patients with strabismic amblyopia participated in their study. In the present study, we used a coarse contrast-defined motion direction discrimination task (leftwards vs. rightwards), and only patients with anisometropic amblyopia were employed. Despite these different types of tasks and amblyopia, all these studies found poor perception of second-order gratings in amblyopic eyes, no matter static or moving, suggesting substantial deficits in the early processing of second-order stimuli.

Perception of second-order translational motion has been studied by Simmers and her colleagues [31], [32]. Again, significantly reduced performance has been found in amblyopic eyes. Some of these deficits (‘motion deficits’ as referred to in their studies) have also been indicated to be independent of low-level visibility loss, which seems to be consistent with our findings. However, it should be noted that there are some differences between their findings and ours. With the same method, Simmers and her colleagues also found similar processing deficits for first-order global motion [32], and for both first-order and second-order global orientation integration [31] in amblyopia, indicating that these deficits are not constrained to second-order motion and may be associated with the global processing. In line with this idea, it was found that amblyopic eyes exhibited normal performance levels in similar tasks when the requirements on global processing were decreased [17], [48]. Therefore, it is reasonable to speculate that the processing deficits revealed by Simmers and her colleagues occur at a later processing stage of second-order information, and are different from those for second-order moving gratings, which has been suggested by the present study.

Aaen-Stockdale and his colleagues have evaluated the perception of second-order radial and rotational motion, which are often referred to as optic flow, in amblyopia [33]. Similar to the findings by Simmers and her colleagues described above, they found substantial processing deficits, which were independent of the amblyopic contrast sensitivity deficits, underlying the perception of radial and rotational motion. They further indicated that the deficits in second-order optic flow processing were equivalent to those for first-order stimuli, and were comparable in both eyes, which is clearly different from the deficit pattern found in the present study. Additionally, they found that radial motion deficits were significantly correlated with translational motion deficits, which may suggest that the impairment at the level of global translational motion processing may underlie the radial motion deficits. On this basis, it is clear that the findings of Aaen-Stockdale and his colleagues may suggest a high-level binocular locus underlying the processing deficits of second-order optic flow in amblyopia, which is different from those suggested in the present study.

Despite some differences, a number of previous studies have indicated some deficits of non-amblyopic eyes in the perception of static/moving second-order stimuli. With a detection task, Wong and his colleagues found 2 out of 5 non-amblyopic eyes showed second-order loss relative to the control eyes [29]. Mansouri and his colleagues found that, as a group, eight amblyopes showed reduced contrast sensitivity relative to normal controls in a second-order orientation discrimination task [30]. As for second-order motion, the fellow eye of one amblyopic subject participated in Simmers and her colleagues' study showed poorer performance averaged across four types of second-order stimuli than normal controls [34]. Similar to all these findings, we also find impaired contrast sensitivity of one non-amblyopic eye (S7) for second-order moving gratings and of three eyes (S2, S4 and S7) for static second-order stimuli in the present study. This result adds to the literature that the perception of second-order gratings could be affected by amblyopia for both the amblyopic and the non-amblyopic eyes, supporting the hypothesis proposed by Wong and his colleagues that a binocular mechanism may be involved in the early processing deficits of second-order stimuli in amblyopia.

Static and moving second-order stimuli

To date, few studies have focused on the processing difference between static and moving second-order stimuli, although the sensitivity difference between second-order form perception and motion perception has been clearly indicated [39], [49]. The proposed systems for the processing of static second-order stimuli [50], [51] share formal properties with the systems for second-order motion processing [23], [52], [53], at least in the initial three processing stages, i.e. filter-rectify-filter. On this basis, the perception of static and moving second-order gratings may have the same characteristics in amblyopic eyes. However, we found that in the present study some amblyopes (S2 and S4) showed impaired contrast sensitivity for static but not for moving second-order gratings, inconsistent with the idea described above. Interestingly, Ellemberg and his colleagues have also found that subjects who experienced early visual deprivation exhibited impaired performance in second-order motion tasks, but not in static tasks [54]. These findings may suggest a dissociation between the processing of static and moving second-order gratings in amblyopia.

Studies on development and aging have also indicated some differences in processing between static and moving second-order gratings. Bertone and his colleagues found a faster developmental rate for perception of moving than of static second-order gratings in school-aged children [55]. Tang and Zhou have also indicated that during adulthood, contrast sensitivity for moving second-order gratings degrades with a much faster rate than for static gratings, although they may have the similar onset age of degradation [45]. These findings support the hypothesis that there may be different neural basis underlying the perception of static and moving second-order stimuli.

Allard and Faubert have shown that there may be two fundamentally different mechanisms underlying the processing of second-order motion: one low-pass and distinct from the mechanisms processing first-order motion and the other common to the mechanisms for first-order motion processing [56]. The former works at all temporal frequencies, whereas the latter only at high frequencies. This might be a possible explanation of the differences in the perception of static (i.e. a temporal frequency of 0) and moving (including many temporal frequencies, from low to high, as in the present study) second-order stimuli described above. Consistent with this idea, it has been indicated that, during adulthood, the sensitivity decline rates were more similar between first-order and second-order moving gratings than between static and moving second-order gratings [45]. This idea has also been supported, indirectly, by studies on perceptual learning in normal adults, which have shown that the effect of training can be transferred, at least partially, from second-order to first-order motion [57]–[59], but not from static second-order to first-order letters [60]. And studies of adaptation, which have shown that cross-over (i.e. from second-order to first-order) adaptation effects occurs, at least partially, for motion [61] but not for static patterns [62], also lend some support to this idea.

Visual processing in extra-striate cortex in amblyopia

Many studies [23], [50], [63], [64] have suggested that first- and second-order information are separately encoded, in parallel, in the mammalian visual system, and that more processing stages, such as rectification and a second filter, are required for the latter. These additional stages are critical for second-order processing, and are believed to be conducted mainly in extra-striate cortex. This idea is supported by a number of animal electrophysiological studies which have found neurons selective for second-order properties in extra-striate cortex, such as V2 [25], [65], [66] and MT [67], but little in striate cortex [68]. In the present study by eliminating possible influence of low-level processing deficits, we still found poor perception of second-order moving gratings in anisometropic amblyopia, suggesting that the core mechanisms for second-order processing, which may mainly originate from extra-striate cortex, are strongly affected by amblyopia. In other words, our findings support the idea that the processing deficit is not constrained in V1, but also involves large regions of the extra-striate cortex in amblyopia, which has been suggested by a large amount of evidence from animal [13], [21], [22], fMRI [16], [19], [69]–[71] and human psychophysical studies [14], [15], [17], [18], [20], [31]–[33], [72]–[76].

The extra-striate cortex are also involved in the plaid perception. Although some studies [77], [78] have suggested that a number of neurons in primate V1, whose receptive fields are short and wide, could directly encode the plaid stimuli, it has been widely accepted that the plaid patterns are mainly encoded at extra-striate cortex, where a combination of motions of component gratings is implemented [50], [79], [80]. Recently, some studies have reported relatively normal plaid perception in amblyopia. Thompson and his colleagues investigated the plaid coherent perception in 15 patients with strabismic or strabismic-anisometropic amblyopia [81]. Based on the results of three experiments, they found nearly comparable performance between amblyopic, fellow and normal control eyes, and therefore concluded that the neural mechanisms underlying plaid perception are only subtly abnormal in amblyopia. With a motion direction discrimination task, we also found [46] that the loss of contrast sensitivity for moving plaids was statistically equivalent to that for moving component gratings in amblyopic eyes, suggesting the integration of motion information conveyed by component gratings of moving plaids, which is processed at extra-striate cortex, may be intact in amblyopia. All these findings seem to be against the idea described above. However, by using fMRI, another study by Thompson and his colleagues [82] suggested that compared to the normal visual system, the amblyopic visual system may recruit some extra visual areas, such as V3, to support the plaid perception. On this basis, the findings of relatively normal plaid perception in amblyopia do not conflict with the idea that there are substantial processing deficits in extra-striate cortex in amblyopia. Furthermore, it suggests that the visual processing in extra-striate cortex in amblyopia may be more complex than we expected.

Implications on the treatment of amblyopia

It has been proposed that perceptual learning is a potential therapy for amblyopia. Various visual functions, such as vernier acuity [83], [84], position discrimination in noise [85]–[87], spatial contrast sensitivity [88], [89], visual acuity [88], [90], [91], the perception of first-order motion [92], and binocular vision [93], [94] can be improved through perceptual learning. As for second-order perception, Chung and her colleagues have indicated that it can benefit from training with static letters, both luminance-defined and contrast-defined [95], [96], suggesting substantial plasticity in the visual pathway for processing second-order spatial information. On this basis, it is reasonable to speculate that the poor contrast sensitivity for second-order motion in amblyopia may also be improved with similar training, but with the use of moving stimuli, rather than static ones.

Conclusion

In this study, we found poor contrast sensitivity for second-order moving gratings in anisometropic amblyopia, which could not be attributed to the impaired first-order input. These results suggest substantial processing deficits for second-order moving gratings, part, if not most, of which might originate from extra-striate cortex. We also found that some amblyopes showed impaired performance in perception of static second-order stimuli but not in that of second-order moving gratings, which may suggest a dissociation between the processing of static second-order stimuli and second-order motion in anisometropic amblyopia.

Acknowledgments

The authors would like to thank Dr. Tzvetomir Tzvetanov for his critical comments and valuable suggestions in preparation of this manuscript.

Data Availability

The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper.

Funding Statement

This work was supported by National Natural Science Foundation of China grants (NSFC 31300913) to YT and (NSFC 81261120562) to YZ. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  • 1. Wu C, Hunter DG (2006) Amblyopia: diagnostic and therapeutic options. Am J Ophthalmol 141: 175–184. [DOI] [PubMed] [Google Scholar]
  • 2. Hess RF, Howell ER (1977) The threshold contrast sensitivity function in strabismic amblyopia: evidence for a two type classification. Vision Res 17: 1049–1055. [DOI] [PubMed] [Google Scholar]
  • 3.Ciuffreda KJ, Levi DM, Selenow A (1991) Amblyopia: Basic and clinical aspects. Boston: Butterworth-Heinemann. [Google Scholar]
  • 4. Campos E (1995) Amblyopia. Surv Ophthalmol 40: 23–39. [DOI] [PubMed] [Google Scholar]
  • 5. McKee SP, Levi DM, Movshon JA (2003) The pattern of visual deficits in amblyopia. J Vis 3: 380–405. [DOI] [PubMed] [Google Scholar]
  • 6. Daw NW (1998) Critical periods and amblyopia. Arch Ophthalmol 116: 502–505. [DOI] [PubMed] [Google Scholar]
  • 7. Kiorpes L (2006) Visual processing in amblyopia: animal studies. Strabismus 14: 3–10. [DOI] [PubMed] [Google Scholar]
  • 8. Kiorpes L, McKee SP (1999) Neural mechanisms underlying amblyopia. Curr Opin Neurobiol 9: 480–486. [DOI] [PubMed] [Google Scholar]
  • 9. Crewther DP, Crewther SG (1990) Neural site of strabismic amblyopia in cats: spatial frequency deficit in primary cortical neurons. Exp Brain Res 79: 615–622. [DOI] [PubMed] [Google Scholar]
  • 10. Movshon JA, Eggers HM, Gizzi MS, Hendrickson AE, Kiorpes L, et al. (1987) Effects of early unilateral blur on the macaque's visual system. III. Physiological observations. J Neurosci 7: 1340–1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11. Chino YM, Shansky MS, Jankowski WL, Banser FA (1983) Effects of rearing kittens with convergent strabismus on development of receptive-field properties in striate cortex neurons. J Neurophysiol 50: 265–286. [DOI] [PubMed] [Google Scholar]
  • 12. Eggers HM, Blakemore C (1978) Physiological basis of anisometropic amblyopia. Science 201: 264–267. [DOI] [PubMed] [Google Scholar]
  • 13. Kiorpes L, Kiper DC, O'Keefe LP, Cavanaugh JR, Movshon JA (1998) Neuronal correlates of amblyopia in the visual cortex of macaque monkeys with experimental strabismus and anisometropia. J Neurosci 18: 6411–6424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. Mussap AJ, Levi DM (2000) Amblyopic deficits in detecting a dotted line in noise. Vision Res 40: 3297–3307. [DOI] [PubMed] [Google Scholar]
  • 15. Sharma V, Levi DM, Klein SA (2000) Undercounting features and missing features: evidence for a high-level deficit in strabismic amblyopia. Nat Neurosci 3: 496–501. [DOI] [PubMed] [Google Scholar]
  • 16. Barnes GR, Hess RF, Dumoulin SO, Achtman RL, Pike GB (2001) The cortical deficit in humans with strabismic amblyopia. J Physiol 533: 281–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17. Mansouri B, Hess RF (2006) The global processing deficit in amblyopia involves noise segregation. Vision Res 46: 4104–4117. [DOI] [PubMed] [Google Scholar]
  • 18. Simmers AJ, Ledgeway T, Mansouri B, Hutchinson CV, Hess RF (2006) The extent of the dorsal extra-striate deficit in amblyopia. Vision Res 46: 2571–2580. [DOI] [PubMed] [Google Scholar]
  • 19. Li X, Dumoulin SO, Mansouri B, Hess RF (2007) Cortical deficits in human amblyopia: their regional distribution and their relationship to the contrast detection deficit. Invest Ophthalmol Vis Sci 48: 1575–1591. [DOI] [PubMed] [Google Scholar]
  • 20. Aaen-Stockdale C, Hess RF (2008) The amblyopic deficit for global motion is spatial scale invariant. Vision Res 48: 1965–1971. [DOI] [PubMed] [Google Scholar]
  • 21. Schroder JH, Fries P, Roelfsema PR, Singer W, Engel AK (2002) Ocular dominance in extrastriate cortex of strabismic amblyopic cats. Vision Res 42: 29–39. [DOI] [PubMed] [Google Scholar]
  • 22. Kozma P, Kiorpes L (2003) Contour integration in amblyopic monkeys. Vis Neurosci 20: 577–588. [DOI] [PubMed] [Google Scholar]
  • 23. Lu ZL, Sperling G (2001) Three-systems theory of human visual motion perception: review and update. J Opt Soc Am A Opt Image Sci Vis 18: 2331–2370. [DOI] [PubMed] [Google Scholar]
  • 24. Lin LM, Wilson HR (1996) Fourier and non-Fourier pattern discrimination compared. Vision Res 36: 1907–1918. [DOI] [PubMed] [Google Scholar]
  • 25.Li G, Wang Z, Yao Z, Yuan N, Talebi V, et al.. (2011) Form-cue invariant second-order contrast envelope responses in macaque V2. in Neuroscience meeting 2011. Washington, D.C.: Society for Neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26. Howell ER, Mitchell DE, Keith CG (1983) Contrast thresholds for sine gratings of children with amblyopia. Invest Ophthalmol Vis Sci 24: 782–787. [PubMed] [Google Scholar]
  • 27. Xu P, Lu ZL, Qiu Z, Zhou Y (2006) Identify mechanisms of amblyopia in Gabor orientation identification with external noise. Vision Res 46: 3748–3760. [DOI] [PubMed] [Google Scholar]
  • 28. Qiu Z, Xu P, Zhou Y, Lu ZL (2007) Spatial vision deficit underlies poor sine-wave motion direction discrimination in anisometropic amblyopia. J Vis 7: 1–16, 7, 1-16. [DOI] [PubMed] [Google Scholar]
  • 29. Wong EH, Levi DM, McGraw PV (2001) Is second-order spatial loss in amblyopia explained by the loss of first-order spatial input? Vision Res 41: 2951–2960. [DOI] [PubMed] [Google Scholar]
  • 30. Mansouri B, Allen HA, Hess RF (2005) Detection, discrimination and integration of second-order orientation information in strabismic and anisometropic amblyopia. Vision Res 45: 2449–2460. [DOI] [PubMed] [Google Scholar]
  • 31. Simmers AJ, Ledgeway T, Hess RF (2005) The influences of visibility and anomalous integration processes on the perception of global spatial form versus motion in human amblyopia. Vision Res 45: 449–460. [DOI] [PubMed] [Google Scholar]
  • 32. Simmers AJ, Ledgeway T, Hess RF, McGraw PV (2003) Deficits to global motion processing in human amblyopia. Vision Res 43: 729–738. [DOI] [PubMed] [Google Scholar]
  • 33. Aaen-Stockdale C, Ledgeway T, Hess RF (2007) Second-order optic flow deficits in amblyopia. Invest Ophthalmol Vis Sci 48: 5532–5538. [DOI] [PubMed] [Google Scholar]
  • 34. Simmers AJ, Ledgeway T, Hutchinson CV, Knox PJ (2011) Visual deficits in amblyopia constrain normal models of second-order motion processing. Vision Res 51: 2008–2020. [DOI] [PubMed] [Google Scholar]
  • 35. Brainard DH (1997) The Psychophysics Toolbox. Spat Vis 10: 433–436. [PubMed] [Google Scholar]
  • 36. Pelli DG (1997) The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis 10: 437–442. [PubMed] [Google Scholar]
  • 37. Li X, Lu ZL, Xu P, Jin J, Zhou Y (2003) Generating high gray-level resolution monochrome displays with conventional computer graphics cards and color monitors. J Neurosci Methods 130: 9–18. [DOI] [PubMed] [Google Scholar]
  • 38. Colombo E, Derrington A (2001) Visual calibration of CRT monitors. Displays 22: 87–95. [Google Scholar]
  • 39. Smith AT, Ledgeway T (1997) Separate detection of moving luminance and contrast modulations: fact or artifact? Vision Res 37: 45–62. [DOI] [PubMed] [Google Scholar]
  • 40. Nishida S, Ledgeway T, Edwards M (1997) Dual multiple-scale processing for motion in the human visual system. Vision Res 37: 2685–2698. [DOI] [PubMed] [Google Scholar]
  • 41. Volkers AC, Hagemans KH, van der Wildt GJ, Schmitz PI (1987) Spatial contrast sensitivity and the diagnosis of amblyopia. Br J Ophthalmol 71: 58–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42. Levitt H (1971) Transformed up-down methods in psychoacoustics. J Acoust Soc Am 49:Suppl 2: 467+. [PubMed] [Google Scholar]
  • 43. Hutchinson CV, Ledgeway T (2006) Sensitivity to spatial and temporal modulations of first-order and second-order motion. Vision Res 46: 324–335. [DOI] [PubMed] [Google Scholar]
  • 44. Schofield AJ, Ledgeway T, Hutchinson CV (2007) Asymmetric transfer of the dynamic motion aftereffect between first- and second-order cues and among different second-order cues. J Vis 7: 1. [DOI] [PubMed] [Google Scholar]
  • 45. Tang Y, Zhou Y (2009) Age-related decline of contrast sensitivity for second-order stimuli: Earlier onset, but slower progression, than for first-order stimuli. J Vis 9: 11–15, 18, 11-15. [DOI] [PubMed] [Google Scholar]
  • 46. Tang Y, Chen L, Liu Z, Liu C, Zhou Y (2012) Low-level processing deficits underlying poor contrast sensitivity for moving plaids in anisometropic amblyopia. Vis Neurosci 29: 315–323. [DOI] [PubMed] [Google Scholar]
  • 47. Lu ZL, Sperling G (1995) The functional architecture of human visual motion perception. Vision Res 35: 2697–2722. [DOI] [PubMed] [Google Scholar]
  • 48. Hess RF, Mansouri B, Dakin SC, Allen HA (2006) Integration of local motion is normal in amblyopia. J Opt Soc Am A Opt Image Sci Vis 23: 986–992. [DOI] [PubMed] [Google Scholar]
  • 49. Ledgeway T, Hutchinson CV (2005) The influence of spatial and temporal noise on the detection of first-order and second-order orientation and motion direction. Vision Res 45: 2081–2094. [DOI] [PubMed] [Google Scholar]
  • 50. Wilson HR, Ferrera VP, Yo C (1992) A psychophysically motivated model for two-dimensional motion perception. Vis Neurosci 9: 79–97. [DOI] [PubMed] [Google Scholar]
  • 51. Sutter A, Graham N (1995) Investigating simple and complex mechanisms in texture segregation using the speed-accuracy tradeoff method. Vision Res 35: 2825–2843. [DOI] [PubMed] [Google Scholar]
  • 52. Chubb C, Sperling G (1989) Two motion perception mechanisms revealed through distance-driven reversal of apparent motion. Proc Natl Acad Sci U S A 86: 2985–2989. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53. Solomon JA, Sperling G (1995) 1st- and 2nd-order motion and texture resolution in central and peripheral vision. Vision Res 35: 59–64. [DOI] [PubMed] [Google Scholar]
  • 54. Ellemberg D, Lewis TL, Defina N, Maurer D, Brent HP, et al. (2005) Greater losses in sensitivity to second-order local motion than to first-order local motion after early visual deprivation in humans. Vision Res 45: 2877–2884. [DOI] [PubMed] [Google Scholar]
  • 55. Bertone A, Hanck J, Cornish KM, Faubert J (2008) Development of static and dynamic perception for luminance-defined and texture-defined information. Neuroreport 19: 225–228. [DOI] [PubMed] [Google Scholar]
  • 56. Allard R, Faubert J (2008) First- and second-order motion mechanisms are distinct at low but common at high temporal frequencies. J Vis 8: 11–17, 12, 11-17. [DOI] [PubMed] [Google Scholar]
  • 57. Zanker JM (1999) Perceptual learning in primary and secondary motion vision. Vision Res 39: 1293–1304. [DOI] [PubMed] [Google Scholar]
  • 58. Chen R, Qiu Z, Zhang Y, Zhou Y (2009) Perceptual Learning and Transfer Study of First- and Second-order Motion Direction Discrimination. Progress in Biochemistry and Biophysics 36: 1442–1450. [Google Scholar]
  • 59. Petrov AA, Hayes TR (2010) Asymmetric transfer of perceptual learning of luminance- and contrast-modulated motion. J Vis 10: 11. [DOI] [PubMed] [Google Scholar]
  • 60. Dosher BA, Lu ZL (2006) Level and mechanisms of perceptual learning: learning first-order luminance and second-order texture objects. Vision Res 46: 1996–2007. [DOI] [PubMed] [Google Scholar]
  • 61. Ledgeway T, Smith AT (1997) Changes in perceived speed following adaptation to first-order and second-order motion. Vision Res 37: 215–224. [DOI] [PubMed] [Google Scholar]
  • 62. Larsson J, Landy MS, Heeger DJ (2006) Orientation-selective adaptation to first- and second-order patterns in human visual cortex. J Neurophysiol 95: 862–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 63. Baker CL Jr, Mareschal I (2001) Processing of second-order stimuli in the visual cortex. Prog Brain Res 134: 171–191. [DOI] [PubMed] [Google Scholar]
  • 64.Landy MS, Graham N (2004) Visual perception of texture, in The visual Neuroscience, Chalupa LM and Werner JS, Editors. Cambridge, MA: MIT press. p. 1106–1118. [Google Scholar]
  • 65. Zhou YX, Baker CL Jr (1993) A processing stream in mammalian visual cortex neurons for non-Fourier responses. Science 261: 98–101. [DOI] [PubMed] [Google Scholar]
  • 66. Mareschal I, Baker CL Jr (1998) A cortical locus for the processing of contrast-defined contours. Nat Neurosci 1: 150–154. [DOI] [PubMed] [Google Scholar]
  • 67. O'Keefe LP, Movshon JA (1998) Processing of first- and second-order motion signals by neurons in area MT of the macaque monkey. Vis Neurosci 15: 305–317. [DOI] [PubMed] [Google Scholar]
  • 68. Zhou YX, Baker CL Jr (1994) Envelope-responsive neurons in areas 17 and 18 of cat. J Neurophysiol 72: 2134–2150. [DOI] [PubMed] [Google Scholar]
  • 69. Hess RF, Li X, Lu G, Thompson B, Hansen BC (2010) The contrast dependence of the cortical fMRI deficit in amblyopia; a selective loss at higher contrasts. Hum Brain Mapp 31: 1233–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 70. Ho CS, Giaschi DE (2009) Low- and high-level motion perception deficits in anisometropic and strabismic amblyopia: evidence from fMRI. Vision Res 49: 2891–2901. [DOI] [PubMed] [Google Scholar]
  • 71. Bonhomme GR, Liu GT, Miki A, Francis E, Dobre MC, et al. (2006) Decreased cortical activation in response to a motion stimulus in anisometropic amblyopic eyes using functional magnetic resonance imaging. J Aapos 10: 540–546. [DOI] [PubMed] [Google Scholar]
  • 72. Popple AV, Levi DM (2000) Amblyopes see true alignment where normal observers see illusory tilt. Proc Natl Acad Sci U S A 97: 11667–11672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 73. Hess RF, Demanins R, Bex PJ (1997) A reduced motion aftereffect in strabismic amblyopia. Vision Res 37: 1303–1311. [DOI] [PubMed] [Google Scholar]
  • 74. Hess RF, Demanins R (1998) Contour integration in anisometropic amblyopia. Vision Res 38: 889–894. [DOI] [PubMed] [Google Scholar]
  • 75. Constantinescu T, Schmidt L, Watson R, Hess RF (2005) A residual deficit for global motion processing after acuity recovery in deprivation amblyopia. Invest Ophthalmol Vis Sci 46: 3008–3012. [DOI] [PubMed] [Google Scholar]
  • 76. Ellemberg D, Lewis TL, Maurer D, Brar S, Brent HP (2002) Better perception of global motion after monocular than after binocular deprivation. Vision Res 42: 169–179. [DOI] [PubMed] [Google Scholar]
  • 77. Tinsley CJ, Webb BS, Barraclough NE, Vincent CJ, Parker A, et al. (2003) The nature of V1 neural responses to 2D moving patterns depends on receptive-field structure in the marmoset monkey. J Neurophysiol 90: 930–937. [DOI] [PubMed] [Google Scholar]
  • 78. Pack CC, Livingstone MS, Duffy KR, Born RT (2003) End-stopping and the aperture problem: two-dimensional motion signals in macaque V1. Neuron 39: 671–680. [DOI] [PubMed] [Google Scholar]
  • 79.Movshon JA, Adelson EH, Gizzi MS, Newsome WT (1985) The analysis of moving patterns, in Pattern recognition mechanisms, In Chagass C, Gattass R, and Grossberg S, Editors. Vatican Press: Rome. [Google Scholar]
  • 80. Adelson EH, Movshon JA (1982) Phenomenal coherence of moving visual patterns. Nature 300: 523–525. [DOI] [PubMed] [Google Scholar]
  • 81. Thompson B, Aaen-Stockdale CR, Mansouri B, Hess RF (2008) Plaid perception is only subtly impaired in strabismic amblyopia. Vision Res 48: 1307–1314. [DOI] [PubMed] [Google Scholar]
  • 82. Thompson B, Villeneuve MY, Casanova C, Hess RF (2012) Abnormal cortical processing of pattern motion in amblyopia: Evidence from fMRI. Neuroimage 60: 1307–1315. [DOI] [PubMed] [Google Scholar]
  • 83. Levi DM, Polat U (1996) Neural plasticity in adults with amblyopia. Proc Natl Acad Sci U S A 93: 6830–6834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 84. Levi DM, Polat U, Hu YS (1997) Improvement in Vernier acuity in adults with amblyopia. Practice makes better. Invest Ophthalmol Vis Sci 38: 1493–1510. [PubMed] [Google Scholar]
  • 85. Li RW, Levi DM (2004) Characterizing the mechanisms of improvement for position discrimination in adult amblyopia. J Vis 4: 476–487. [DOI] [PubMed] [Google Scholar]
  • 86. Li RW, Young KG, Hoenig P, Levi DM (2005) Perceptual learning improves visual performance in juvenile amblyopia. Invest Ophthalmol Vis Sci 46: 3161–3168. [DOI] [PubMed] [Google Scholar]
  • 87. Li RW, Klein SA, Levi DM (2008) Prolonged perceptual learning of positional acuity in adult amblyopia: perceptual template retuning dynamics. J Neurosci 28: 14223–14229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 88. Zhou Y, Huang C, Xu P, Tao L, Qiu Z, et al. (2006) Perceptual learning improves contrast sensitivity and visual acuity in adults with anisometropic amblyopia. Vision Res 46: 739–750. [DOI] [PubMed] [Google Scholar]
  • 89. Huang CB, Zhou Y, Lu ZL (2008) Broad bandwidth of perceptual learning in the visual system of adults with anisometropic amblyopia. Proc Natl Acad Sci U S A 105: 4068–4073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 90. Polat U, Ma-Naim T, Belkin M, Sagi D (2004) Improving vision in adult amblyopia by perceptual learning. Proc Natl Acad Sci U S A 101: 6692–6697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 91. Polat U, Ma-Naim T, Spierer A (2009) Treatment of children with amblyopia by perceptual learning. Vision Res 49: 2599–2603. [DOI] [PubMed] [Google Scholar]
  • 92. Hou F, Huang CB, Tao L, Feng L, Zhou Y, et al. (2011) Training in contrast detection improves motion perception of sinewave gratings in amblyopia. Invest Ophthalmol Vis Sci 52: 6501–6510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 93. Hess RF, Mansouri B, Thompson B (2010) A new binocular approach to the treatment of amblyopia in adults well beyond the critical period of visual development. Restor Neurol Neurosci 28: 793–802. [DOI] [PubMed] [Google Scholar]
  • 94. Knox PJ, Simmers AJ, Gray LS, Cleary M (2012) An exploratory study: prolonged periods of binocular stimulation can provide an effective treatment for childhood amblyopia. Invest Ophthalmol Vis Sci 53: 817–824. [DOI] [PubMed] [Google Scholar]
  • 95. Chung ST, Li RW, Levi DM (2006) Identification of contrast-defined letters benefits from perceptual learning in adults with amblyopia. Vision Res 46: 3853–3861. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 96. Chung ST, Li RW, Levi DM (2008) Learning to identify near-threshold luminance-defined and contrast-defined letters in observers with amblyopia. Vision Res 48: 2739–2750. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper.

Articles from PLoS ONE are provided here courtesy of PLOS

RESOURCES